사다리꼴 주름판의 최적형상 및 엄밀진동에 관한 연구
© The Korean Society for Noise and Vibration Engineering
Abstract
In this study, the refined rigidities, optimal shapes, and free vibration of trapezoidal corrugated plates were analyzed. The rigidities of trapezoidal corrugated plates by material mechanical analysis have large errors as compared with practical behavior. Thus, the refined rigidities of the plates are proposed by calculating two-variable functions by surface fitting for the correction of errors. These rigidities were applied in analyzing the optimal shapes and free vibration of the plates. In addition, a Visual Basic program was developed for the vibration analysis.
Keywords:
Corrugated Plate, Orthotropy, Surface Fitting, Correction of Error, Refined Rigidity, Optimal Shape, Natural Frequency키워드:
주름판, 직교이방성, 곡면피팅, 오차보정, 엄밀강성, 최적형상, 고유진동수1. 서 론
주름판(corrugated plate)은 평판을 파형(wave form)으로 주름잡아 강성(rigidity)을 크게 증대시킨 판구조물로 많은 산업분야에서 널리 사용되고 있다.
주름판은 평판이 등방성(isotropy)인 반면에 주름방향의 직각방향 강성이 증대된 것으로 기하학적 특성상 직교이방성(orthotropy) 구조물로서 분류된다. 이와 같은 직교이방성판으로서의 주름판에 대한 강성 및 진동 데이터는 재료역학적 해석으로 어느 정도의 정확치로 도출되는 데는 한계가 있으며 그 기하학적 형상에 따라 큰 오차가 뒤따른다.
이러한 주름판의 파형 종류는 정현파(sine wave), 사다리꼴파(trapezoid wave), 방형파(square wave), 삼각파(triangle wave), 톱니파(sawtooth wave) 등이 있다.
그동안 발표된 연구논문들을 살펴보면, 주름판의 진동해석은 직교이방성판으로서 강성해석이 선행되어야 하는데, Seydel은(1) 파형 주름판에 대하여 압축실험으로 강성을 규명하고자 하였고, Fung은(2) 파형 주름판을 평판에 부착시킨 패널에 대하여 기하학적 해석방법을 제시하였다. Kinloch는(3) 사다리꼴 주름판과 평판이 조립된 패널에 대하여 강성해석을 하고자 하였으며, Perel은(4) 사다리꼴 주름판에 대하여 비교적 단순하게 기하학적으로 강성을 구하고자 하였다.
주름판 등 직교이방성판에 대한 진동을 해석한 논문의 경우는 Hoppmann 등이(5) 보강판에 대하여 실험으로 강성을 결정하고 단순지지 경계조건에 대해 진동해석을 하였고, Hearmon 등은(6~8) 직교이방성판에 대하여 강성을 임의로 가정하고 특정 경계조건에 대해 고유진동수를 해석하였다. 또한, Chen 등은(9) 사다리꼴 주름판과 평판이 조립된 완전 자유의 경계조건을 갖는 패널(panel)에 대하여 유한요소 해석 및 진동실험을 하였다.
그 외에도 주름판에 대하여 등가의 개념을 적용시켜 근사적으로 정적 및 동적 해석한 논문(10~12), 주름요소 판 하나의 길이가 두께에 비하여 상당히 긴 장방형 절판(folded plate)의 진동해석 논문(13~15) 등을 살펴볼 수 있다.
그동안, 이 저자 등은(16,17) 연결 판을 보강재로, 연결 볼트를 집중질량으로 취급하여 주름판에 대한 진동해석을 하였고, 적층복합 주름판을 균일한 두께를 지닌 직교이방성판의 균질화 모델로 취급하여 강성을 해석을 하는 등, 주름판의 강성 및 진동 해석과 관련한 연구를 지속적으로 진행하고 있다.
그러나 주름판의 강성은 이전의 논문(18)에서도 언급하였듯이 기하학적 특성과 기본가정 그리고 등가의 개념만을 고려하여 재료역학적으로 해석함으로써 제시되는 것은 엄밀성(exactitude) 차원에서 큰 오차를 유발하는 문제를 지닐 수 있고, 근사적 해석 또는 실험적 방법에 의하여 제시되는 것은 특정 경계조건, 모델에 대해서만 도출 가능한 적용 한계성(application limit)을 가질 수 있다.
따라서 이 연구에서는 사다리꼴 주름판에 대한 재료역학적 해석결과에서 유발되는 오차를 보정하기 위하여 곡면피팅(surface fitting)에 의한 2변수 오차보정(correction of error)식을 산출함으로써 엄밀강성(refined rigidity)을 제시함과 아울러 주름판의 최적형상(optimal shape)을 결정한다. 또한, 이러한 엄밀강성을 적용하여 Ritz법에 의한 주름판의 진동해석 및 비주얼베이직(visual basic) 프로그램을 완성하고, 이 결과는 유한요소 해석 코드인 ANSYS의 결과와 비교함으로써 그 타당성을 검증한다.
2. 주름판의 강성 및 진동
2.1 주름판의 강성
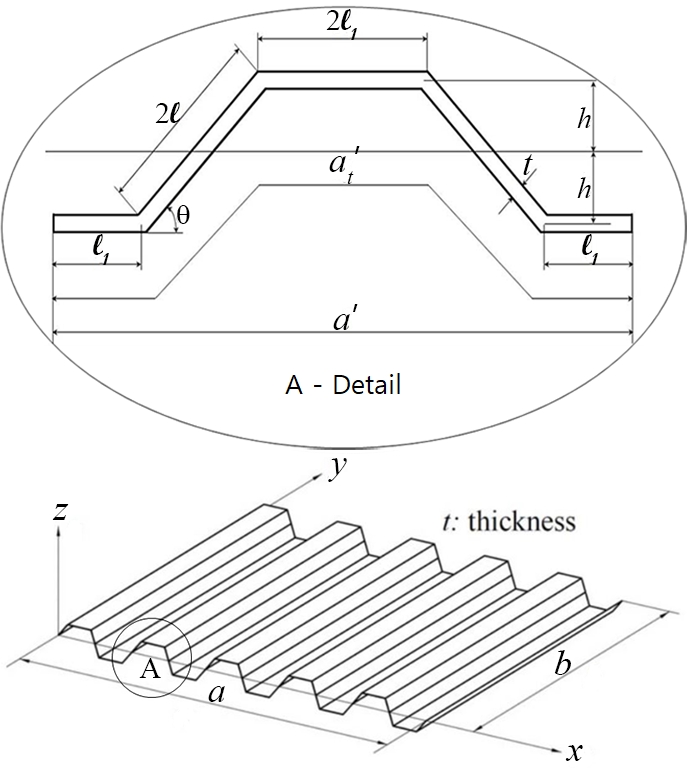
이 연구에서의 사다리꼴 주름판 해석모델은 다음 Fig. 1과 같으며 여기서, a는 주름판의 주름진 x방향 길이, b는 주름판의 y방향 길이다. 또한, 주름판 하나의 주름요소에서 주름각은 θ, 판의 두께는 t, 수평 및 경사 길이 비는 mc(= l1/l), 주름높이는 h이며, a′는 주름요소의 길이, at′는 주름요소의 전체 길이다.
이 연구에서의 해석모델인 사다리꼴 주름판의 재료역학적 해석에 의한 강성은 다음과 같다(18).
주름판의 x축에 대하여 순수 굽힘모멘트가 작용하는 경우, 주름판의 x면에 대한 굽힘강성(flexural rigidity) Dx는 다음 식 (1)과 같다.
| (1) |
여기서, E는 탄성계수, v는 푸아송비이다.
주름판 하나의 주름요소에 대한 y면의 단위길이 당 면적관성모멘트는, 수평면의 경우 평행축 정리를, 경사면의 경우는 경사축에 대한 면적관성모멘트를 각각 중립축에 대하여 적용하면, 주름판의 y면에 대한 굽힘강성 Dy는 다음 식으로 표현할 수 있다.
| (2) |
주름판의 x면에 대한 비틀림모멘트는 경사길이의 비틀림각을 x축에 등가하고 수평길이의 비틀림각과 합하여 유도될 수 있고, 따라서 다음과 같은 x면의 비틀림강성(torsional rigidity) Dxy를 구할 수 있다.
| (3) |
y면에 대한 비틀림모멘트는 경사면의 경우 중립축에 등가의 개념을 적용하고 수평면의 경우와 합하여 구함으로써, Dyx는 다음과 같이 결정된다.
| (4) |
2.2 엄밀강성을 위한 오차보정식
주름판의 최대변형에너지(Vmax)와 최대운동에너지(Tmax)는 다음과 같이 나타낼 수 있다.
| (5) |
| (6) |
여기서, D1 = vyDx + vxDy이고, ρ는 밀도, ω는 각진동수(angular frequency)이다. 그리고 Betti의 상반작용의 정리(Betti’s reciprocal theorem)에 의하여 vyDx = vxDy로 나타낼 수 있다. 여기서의 푸아송비 vx, vy는 재료성질이 아닌 구조 시스템의 기하학적 환경에 따라 좌우되는 탄성상수로서, 각각 주름판의 직교이방성에 따른 x 및 y 방향의 푸아송비이다.
주름판의 처짐함수 W(x, y)는 다음과 같이 가정할 수 있다.
| (7) |
여기서, Amn은 상수이고, Xm(x)과 Yn(y)는 각각 x 및 y 방향의 직교성(orthogonality)과 경계조건을 만족시키는 보함수(beam function)이다.
따라서 보함수의 직교성을 고려하고 식 (7)을 식 (5)와 식 (6)에 대입하여 Rayleigh법을 이용하면, 다음 식 (8)과 같이 나타낼 수 있다.
| (8) |
여기서, , 이고
| (9) |
| (10) |
또한, (a/b)는 주름판의 형상비(aspect ratio)이고, km, kn은 각각 x, y방향의 경계조건에 따른 보함수의 파수(wave numbers), fmn은 주름판의 고유진동수(natural frequencies)이다.
앞서 언급한 바와 같이 기하학적 특성과 기본가정 그리고 등가의 개념만을 고려한 주름판의 재료역학적 강성은 실제거동과 큰 오차를 나타낼 수 있고, 유한요소 해석에 의한 방법으로도 강성을 직접 해석할 수 없다.
따라서 이 연구에서는 임의로 선정한 경계조건, 즉 x방향 고정-자유, y방향 고정-자유의 경계조건에 대하여 주름각 θ와 수평 및 경사 길이 비 mc (=l1/l)에 따른 4차까지의 고유진동수 fmn을 유한요소 해석으로 구한 후, 이에 대응하는 Xm(x)와 Yn(y)에 대한 미적분을 행하고 식 (8)에 적용, 4차 연립방정식을 통해 α, β, δ, γ를 구함으로써 강성을 도출한다. 그리고 이러한 강성을 앞서의 재료역학적 강성과 비교함으로써 오차보정식을 산출하고, 다음과 같은 주름판의 엄밀강성 식 (11)을 제시한다.
| (11) |
여기서, Cx (θ, mc), Cy (θ, mc), Cxy (θ, mc)는 곡면피팅에 의한 2변수 오차보정식으로서 θ와 mc를 2차식으로 나타내면, 다음 식 (12)와 같다.
| (12) |
여기서, (p00, p10, p01, p20, p11, p02)는 다음과 같다.
- Cx의 경우 (1.001, -0.149, 0.042, -0.311, 0.299, -0.058)
- Cy의 경우 (1.001, -0.346, 0.035, -0.133, 0.176, -0.037)
- Cxy의 경우 (1.054, -0.608, 0.246, 0.481, -0.017, -0.067)
2.3 주름판의 진동해석
이 연구에서는 Ritz법에 의한 주름판의 진동해석을 함에 있어, 처짐함수를 다음과 같이 가정한다.
| (13) |
다음의 최소에너지원리(minimum total energy principle)를 도입한다.
| (14) |
따라서 식 (13)을 식 (5)와 식 (6)에 대입하고 식 (14)에 적용하면 다음과 같은 고유치문제가 된다.
| (15) |
여기서, λ2 = ρtω2a4/D
δmn = 1 (m = k와 n = l), δmn = 0 (m ≠ k와 n ≠ l)
- 1) m = k와 n = l인 경우
| (16) |
- 2) m ≠ k와 n ≠ l인 경우
| (17) |
여기서, 식 (10)과 함께
| (18) |
또한, αr, βr, δr, γr는 (Dx)r, (Dy)r, (D1)r, 2(Dxy)r를 각각 D로 나눈 무차원 엄밀강성이다.
3. 결과 및 고찰
3.1 사다리꼴 주름판의 최적형상
앞서 언급한 바와 같이 주름판은 평판을 주름잡아줌으로써 y면의 강성을 크게 증대시킨 것으로, 재료역학적 해석에 의한 강성은 실제 거동과는 큰 차이를 나타낸다. 따라서 이 연구에서는 오차보정식을 통한 엄밀강성식을 제시하였다. Table 1은 a/b = 1, a = 1000 mm, t = 2 mm이고, 주름수 nc = 10개, 재료물성치 ρ = 7850 kg/m3, E = 200 000 MPa인 경우의 y면에 대한 재료역학적 무차원 강성 β과 무차원 엄밀강성 βr을 mc = 1인 경우의 주름각 θ에 따라 비교하여 나타낸 것으로 그 차이가 매우 큼을 알 수 있다.
또한, 이러한 주름판의 강성은 동일중량 하에서 그 형상에 따라 큰 차이를 나타낼 수 있다.
Tables 2 ~ 3은 주름판의 동일중량 상태에서의 θ와 mc에 따른 무차원 엄밀강성 βr을 나타낸 것이다. 산형 주름판 즉, mc = 0인 경우의 θ = 30°와 동일중량인 사다리꼴 주름판의 강성은 θ = 34°, mc = 0.2761에서, 각각 θ = 40°인 경우는 θ = 45°, mc = 0.2519에서, θ = 45°인 경우는 θ = 50°, mc = 0.2196에서, θ = 60°인 경우는 θ = 66°, mc = 0.1865에서 최대치임을 알 수 있다.
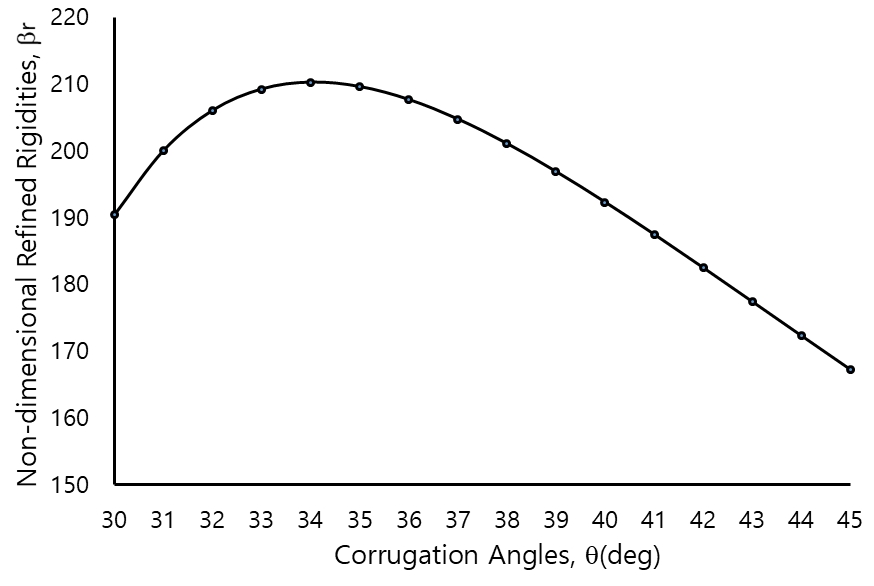
Fig. 2는 Table 2에서의 θ = 30°, mc = 0와 동일중량인 사다리꼴 주름판의 엄밀강성을 주름각 θ에 따라 그래프로 나타낸 것이다.
3.2 사다리꼴 주름판의 엄밀진동
재료역학적 해석에 의한 강성 Dy는 실제거동보다도 상당히 큰 값을 나타냄으로써 진동해석에 있어서도 그 오차는 매우 크게 발생한다.
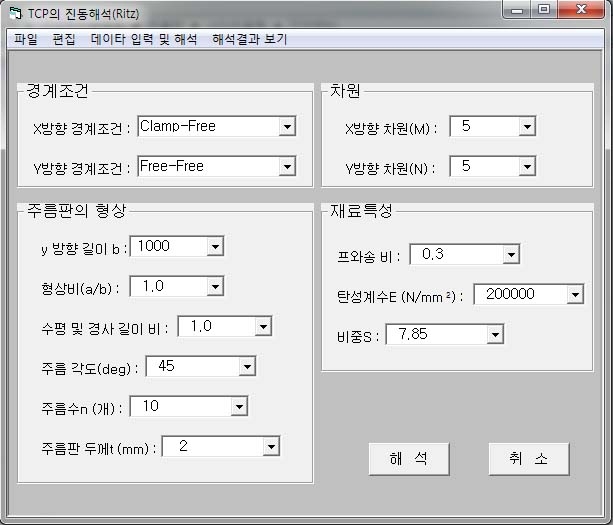
따라서 이 연구에서는 (Dx)r, (Dy)r, (D1)r, 2(Dxy)r 등의 엄밀강성을 사다리꼴 주름판의 진동해석에 적용하여 비주얼베이직 프로그래밍을 하였다. Fig. 3은 완성된 진동해석 프로그램의 입력창을 나타낸 것이다.
Table 4는 a/b = 1, a = 1000 mm, t = 2 mm이고, 주름수 nc = 10개, 재료물성치 ρ = 7850 kg/m3, E = 200 000 MPa,v = 0.3인 사다리꼴 주름판에 대하여, θ = 45°, mc = 1이고 F-F&C-F의 경계조건에 대한 이 연구에서의 해석결과와 유한요소 해석결과로서 5차까지의 고유진동수를 비교하여 나타낸 것인데, 그 오차는 2 %대 이내로 매우 잘 일치하고 있음을 알 수 있다. 여기서, F-F&C-F (x방향 경계조건 & y방향 경계조건)는 자유(free), 고정(clamp)의 경계조건을 이니셜로 표시한 것으로서, 각각 x = 0와 a에서 F와 F, y = 0와 b에서 C와 F의 경계조건을 나타낸다.
Table 5는 주름판에서 가능한 36개 경계조건 중 임의의 3가지 경계조건에 대하여 주름각 θ가 각각 30°, 40°, 50°, 60°인 경우의 mc가 0.5, 1, 2일 때의 기본진동수(fundamental frequency)를 유한요소 해석결과와 비교하여 나타낸 것이다. 그 결과는 마찬가지로 상당히 잘 일치하고 있음을 알 수 있고, 그 밖의 경계조건 및 임의의 형상에 대해서도 이 연구에서의 결과와 유한요소 해석의 결과는 매우 잘 일치함을 알 수 있었다. 여기서, S는 단순지지(simply support) 경계조건을 나타내는 이니셜이다.
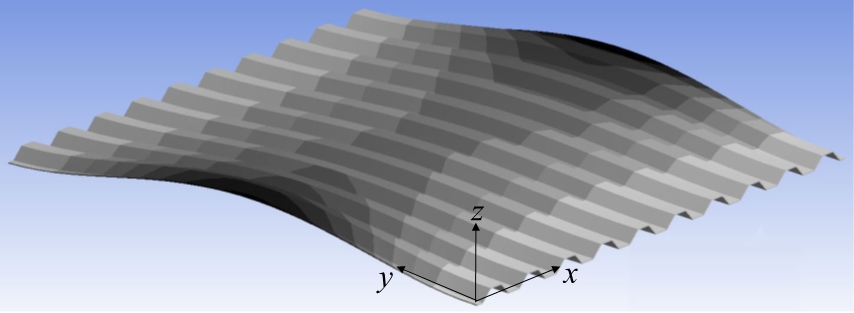
Fig. 4는 경계조건이 F-F&C-C인 사다리꼴 주름판의 유한요소 해석에 의한 1차 진동 모드(mode)를 나타낸 것이다.
4. 결 론
이 연구에서는 사다리꼴 주름판에 대한 엄밀강성과 최적형상을 결정하고 진동해석을 하였다. 그 결과, 다음과 같은 결론을 얻었다.
- (1) 곡면피팅에 의한 2변수 오차보정식을 산출함으로써 사다리꼴 주름판의 엄밀강성을 제시하였다.
- (2) 산형 주름판 즉, mc = 0인 경우의 θ = 30°와 동일중량인 사다리꼴 주름판의 강성은 θ = 34°, mc = 0.2761, θ = 40°인 경우는 θ = 45°, mc = 0.2519, θ = 45°인 경우는 θ = 50°, mc = 0.2196, θ = 60°인 경우는 θ = 66°, mc = 0.1865가 최적형상이다.
- (3) 비주얼베이직에 의한 엄밀강성 및 진동해석 프로그램을 완성함으로써 임의의 경계조건 및 형상을 갖는 사다리꼴 주름판의 실용적이고 효율적인 설계데이터 추출이 가능하다.
References
- Seydel, E. B., (1931), Schubknickversuche mit Wellblechtafeln (Tangential Stress Experiments on Corrugated Steel Panels), Jahrbuch, d. Deutsch. Versuchsanstallt für Luftfahrt, E. V. München und Berlin p233-235.
- Fung, Y. C., (1962), On Corrugation-Stiffened Panels, Calif. Inst. Tech. GA..
- Kinloch, H., (1967), An Experimental and Theoretical Investigation of Orthotropic Plate Structure, Proceedings of Thin Walled Structure Symposium at Swansea, p213-299.
- Perel, D., (1976), The General Instability of Infinitely Long Trapezoidally Corrugated Plates Under Shear, Ph. D. Degree Thesis, Syracuse University, New York, USA.
- Hoppmann, W. H., Huffington, N. J., and Magness, L. S., (1956), A Study of Orthogonally Stiffened Plates, J. Appl. Mech., 78, p343-350.
- Hearman, R. S. F., (1959), The Frequency of Flexural Vibration of Rectangular Orthotropic Plates with Clamped or Supported Edges, J. Appl. Mech., 26, p537-540.
-
Vijayakumar, K., (1974), Natural Frequency of Rectangular Orthotropic Plates with a Parallel Edges Simply Supported, J. Sound Vib., 35(3), p379-394.
[https://doi.org/10.1016/0022-460X(74)90067-4]

-
Dickinson, S. M., (1978), The Buckling and Frequency of Flexural Vibration of Rectangular Isotropic and Orthotropic Plates Using Rayleigh’s Method, J. Sound Vib., 61(1), p1-8.
[https://doi.org/10.1016/0022-460X(78)90036-6]

- Chen, F. H. K., and Carne, T. G., (1979), Vibration Analysis of Corrugation-stiffened Panels, SAE Trans., 87(2), p1705-1717.
-
Briassoulis, D., (1986), Equivalent Orthotropic Properties of Corrugated Sheets, Computers & Structures, 23(2), p129-138.
[https://doi.org/10.1016/0045-7949(86)90207-5]

-
Peng, L. X., Liew, K. M., and Kitipornchai, S., (2007), Analysis of Stiffened Corrugated Plates Based on the FSDT via the Mesh-free Method, Int. J. of Mechanical Sciences, 49, p364-378.
[https://doi.org/10.1016/j.ijmecsci.2006.08.018]

-
Liew, K. M., Peng, L. X., and Kitipornchai, S., (2009), Vibration Analysis of Corrugated Reissner–Mindlin Plates Using a Mesh-free Galerkin Method, Int. J. of Mechanical Sciences, 51, p642-652.
[https://doi.org/10.1016/j.ijmecsci.2009.06.005]

-
Samanta, A., and Mukhopadhyay, M., (1999), Finite Element Static and Dynamic Analyses of Folded Plates, Engineering Structures, 21, p277-287.
[https://doi.org/10.1016/S0141-0296(97)90172-3]

-
Haldar, S., and Sheikh, A. H., (2011), Bending Analysis of Composite Folded Plates by Finite Element Method, Finite Elements in Analysis and Design, 47(4), p477-485.
[https://doi.org/10.1016/j.finel.2010.12.006]

-
Lee, S. Y., Wooh, S. C., and Yhim, S. S., (2004), Dynamic Behavior of Folded Composite Plates Analyzed by the Third Order Plate Theory, Int. J. of Solids and Structures, 41(7), p1879-1892.
[https://doi.org/10.1016/j.ijsolstr.2003.11.026]

-
Jung, K., and Kim, Y.-W., (2014), Vibration Analysis of Trapezoidal Corrugated Plates with Stiffeners and Lumped Masses, Transactions of the Korean Society for Noise and Vibration Engineering, 24(5), p414-420.
[https://doi.org/10.5050/KSNVE.2014.24.5.414]

-
Park, K.-J., Jung, K., and Kim, Y.-W., (2016), Evaluation of Homogenized Effective Properties for Corrugated Composite Panels, Composite Structures, 140, p644-654.
[https://doi.org/10.1016/j.compstruct.2016.01.002]

-
Kim, Y.-W., and Jung, K., (2016), Analysis on Exact Rigidity and Free Vibration of Trapezoidal Corrugated Plates, Transactions of the Korean Society for Noise and Vibration Engineering, 26(7), p787-794.
[https://doi.org/10.5050/KSNVE.2016.26.7.787]


Young-Wann Kim received his Ph.D. degree from Chungnam National University in 1997. He is a professor of Department of Mechanical Design Engineering, Chonnam National University. His research interest includes the structural dynamics & vibration, FSI problems.

Kang Jung received his Ph.D. degree from Hongik University in 1990. He is a professor of Department of Mechanical Design Engineering, Chonnam National University. His research interest includes the structural vibration, fracture behavior.