Vibration Analysis for an Ultrasonic Transducer Coupled with Interior and Exterior Piezoelectric Discs
© The Korean Society for Noise and Vibration Engineering
Abstract
This research deals with an ultrasonic transducer coupled with piezoelectric discs of two types, solid and hollow. The interior solid disc is an exciter and the exterior hollow disc is an ultrasound sensor. The characteristics of the radial and axial vibrations in the axisymmetric motions were investigated theoretically, and verified experimentally. The piezoelectric governing equations were derived theoretically by virtue of mechanical displacements and electric potential, and their solutions produced characteristic equations yielding natural frequencies. The theoretical analysis was enhanced by three-dimensional mode shapes obtained using finite element analysis. The experimental results verified the theoretical analysis. Another experiment showed that the transducer excites ultrasound at the interior disc, and senses it at the exterior disc. The study showed that an ultrasonic transducer coupled with piezoelectric solid and hollow discs could be designed by determining a suitable diameter for each disc.
초록
이 논문은 압전 원판과 환판이 결합된 초음파 트랜스듀서를 다룬다. 내부 원판은 초음파 가진기이고 외부 환판은 감지기이다. 축대칭 운동에서 반경방향과 축방향 진동 특성을 이론적으로 파악하고 실험으로 검증하였다. 이론적으로, 역학적 변위 및 전기적 포텐셜로써 압전 지배방정식을 유도하고 특성방정식을 구하여 고유진동수를 산출하였다. 유한요소해석으로 3차원 모드 형상을 구하여 이론적 해석을 보강하였다. 이론적 결과를 실험 결과와 비교하여 이론적 해석을 검증하였다. 부가적인 실험으로, 트랜스듀서가 내부 원판에서 초음파를 방출하고 외부 환판에서 감지하는 것을 확인하였다. 압전 원판과 환판이 결합된 트랜스듀서가 적절한 지름 치수로 설계될 수 있게 되었다.
Keywords:
Vibration, Ultrasound, Piezoelectricity, Transducer, Disc, Resonance키워드:
진동, 초음파, 압전, 트랜스듀서, 원판, 공진1. Introduction
Piezoelectric discs are used in many ultrasonic sensors(1). In many cases of distance measurement, such as liquid-level measurement(2) and vehicle obstacle detection(3,4), a piezoelectric transducer simultaneously plays the role of an ultrasound transmitter and receiver. Some transducers consist of a single piezoelectric disc that alternately generates and receives ultrasound(2,3). They have to use special signal forms to prevent overlapping transmission and reception signals. Others consist of a couple piezoelectric discs located nearby each other, where one generates and another receives ultrasound(4). They have slightly different transmitter and receiver center locations. This work aims to design a disc-shape transducer consisting of separate transmitter and receiver which have same operating frequency and same center location.
Kim et al.(5) studied the radial-mode in-plane vibration characteristics of piezoelectric disc transducers. They reported theoretical and experimental results for the natural frequencies and mode shapes. Piao et al.(6) presented the radial vibration characteristics for ring-shaped piezoelectric transducers. Li et al.(7) considered concentric electrode patterns on ring-shaped piezoelectric transducers and reported vibration characteristics obtained using finite element analysis. These literatures considered either a disc or a ring made of piezoelectric material. Theoretical approaches concerning piezoelectric disc vibration characteristics appear in much of the literatures. Meitzler et al.(8) explained the coupling factor of radial modes in piezoelectric discs. Kunkel et al.(9) showed the dependence of the vibrational mode on the disk diameter-to-thickness ratio calculated by the finite element method. Lee et al.(10) reported vibration characteristics depending on the thickness-graded material properties. Ho(11) presented a generalized form of Hamilton’s principle for a coupled electromechanical system. He compared theoretically and experimentally obtained impedance curves. Lin and Ma(12) compared experimental results obtained using several techniques with numerical ones. They displayed mode shapes qualitatively to show vibration distribution. Piezoelectric rings, which mean hollow-disks, were also considered theoretically in much of literature(7,13,14). The previous works(5~13) considered only a single disc or ring.
Based on the analysis for a single piezoelectric disc, Piao and Kim studied the vibration characteristics of a piezoelectric disc covered with an elastic disc(15) and a stack transducer made of two piezoelectric discs and coupled axially(16). Guo et al.(17) used finite element and modal analysis to predict the piezoelectric disc vibration characteristics. In that study they identified five types of modes, including radial mode, according to the mode shape characteristics. Heyliger and Ramirez(18) introduced a numerical model to compute natural frequencies of free vibration of laminated circular piezoelectric discs. They combined one dimensional finite elements in the thickness direction for approximation and analytic functions in the plane. Wang et al.(19) investigated resonance frequencies of piezoelectric hollow-disc stack. Laoratanakul and Uchino(20) fabricated the laminated piezoelectric devices and designed a high power transformer. These stacked transducers includes the piezoelectric discs or plates with the same sizes in thickness and planar dimensions.
The transducer suggested in this paper is composed of radially coupled interior and exterior piezoelectricdiscs. The interior disc is solid and transmits ultrasound. The exterior disc is hollow and receives the returning ultrasound. The hollow disc is also called ring shaped. This research investigates the vibration characteristics of the transducer theoretically, numerically and experimentally.
2. Theoretical Analysis
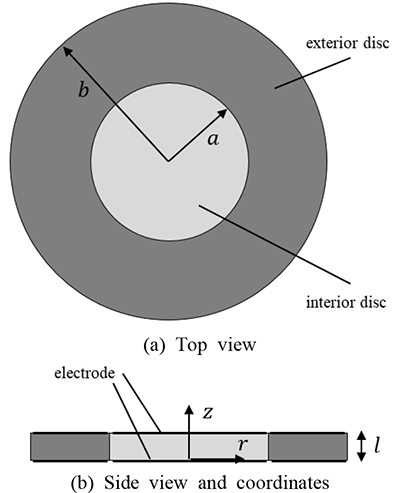
As schematically shown in Fig. 1, an ultrasonic transducer consists of piezoelectric interior and exterior discs; a and b are the inner and outer radii, and l is the thickness. The adhesive thickness between the discs is about 10 μm, and it is negligible compared to the PZT disc diameter, which is larger than 15 mm. The transducer is coated with electrodes uniformly on each surface at z = 0 and l. The piezoelectric differential equations are derived in terms of radial and axial displacements of motion and electric potential. The equations satisfying boundary conditions are solved to obtain characteristic equations. Radial modes of in-plane vibration are considered in the analysis, and the result predicts vibration characteristics depending on the geometric parameters.
The constitutive equations for piezoelectric discs are summarized in the Appendix. The equation of motion is derived from force equilibrium in the radial direction as follows(21):
| (1) |
where ρ is the mass density. Eqs. (A8a) and (A8b) are inserted in Eq. (1) and yield the following governing equation for the interior disc (i = 1) and exterior disc(i = 2):
| (2) |
where , which is the speed of wave propagating in the radial direction.
The radial displacement at the center is zero and circumferential outer face is free of traction. Boundary conditions are therefore
| (3a) |
| (3b) |
At the interface of the two discs, the radial displacement and normal stress are continuous; therefore,
| (3c,d) |
When the electrodes are derived by the voltage of a harmonic function of time with frequency ω, the displacement u and electric potential ϕ are also regarded as harmonic functions with the same frequency. It was reported that the radial displacement does not depend on the axial coordinate z in a piezoelectric transducer excited by a uniform electric field in the thickness direction(5,6). Therefore, via separation of variables u(r,t) and σr(r,t) can be expressed as follows:
| (4a) |
| (4b) |
The electric field is regarded to vary linearly in the thickness direction, and it is expressed as
| (5) |
Eq. (4a) is inserted in Eq. (2) and yields the following Bessel equation:
| (6) |
where ki(= ω/Ci) is the wavenumber. This equation describes the radial mode of the transducer related to the radial boundary conditions. Eqs. (3a) ~ (3d) reduce to
| (7a) |
| (7b,c) |
| (7d) |
For the interior disc, the solution of Eq. (6) with the boundary condition (7a) has the following form of radial motion(5):
| (8) |
where J1is the Bessel function of the first kind of order 1. For the exterior disc, the solution of Eq. (6) has the following form of radial motion(6):
| (9) |
Inserting Eqs. (8) and (9) into Eqs. (7b), (7c), (7d) yields the following equations:
| (10a) |
| (10b) |
| (10c) |
where
| (11a) |
| (11b) |
The condition for Eqs. (10a), (10b), (10c) to have nontrivial solutions yields the following characteristic equation:
| (12a) |
where
| (12b) |
and
| (12c) |
where radius ratio q = b/a and property ratio s =k2/k1.
The expressions of A2and B2in terms of A1are inserted into Eq. (9), and then
| (13a) |
or
| (13b) |
The natural frequencies of the radial mode can be calculated from Eq. (12). Frequency f is related with wavenumber ki and wave speed Ci as follows:
| (14) |
3. Numerical Calculations
The theoretical analysis described in Section 2 is the basis for numerically calculating the vibration characteristics of the transducer in this section. The theoretical results are enhanced by a finite element analysis as a complementary work.
3.1 Theoretical Calculations
The diameter and thickness of the transducer specimens composed of the piezoelectric discs are listed in Table 1. The outer diameter is 10 times larger than the thickness. Three specimens are shown in Fig. 2. The interior disc material is PZT-4. This material is a hard piezoelectric ceramic usually used in ultrasonic actuators. The exterior disc material is PZT-5A. This material is a soft piezoelectric ceramic usually used in ultrasonic sensors. Their properties are well known and listed in Table 2.The material properties in Table 2 were converted for insertion into the equations, and the resulting properties(22) are in Table 3.
The unknown variable k1a in the characteristic equation (12) can be determined using a numerical tool. We used Mathematica(23) in this work. The calculated results are displayed in Table 4.
3.2 Finite-element Analysis
The theoretical analysis explained in Section 2 has the advantage that the expressions can be conveniently used to calculate the natural frequencies and mode shapes. However, the analysis has the disadvantage that the real physical phenomenon was simplified by some assumption. Therefore, the theoretical analysis was complemented using a finite element analysis. Then the analysis results were compared with the experimental ones.
We used a commercial software ANSYS to calculate natural frequencies and mode shapes. Modal analysis and harmonic analysis were carried out with suitable boundary conditions. Mechanically, all outer boundaries are traction free. Electrically, a uniform electric field is formed in the thickness direction by the electrodes on the top and bottom surfaces of the transducer. The analysis model of specimen A is shown in Fig. 3 for example. It consists of 10 668 nodes and 9504 SOLID185 elements.
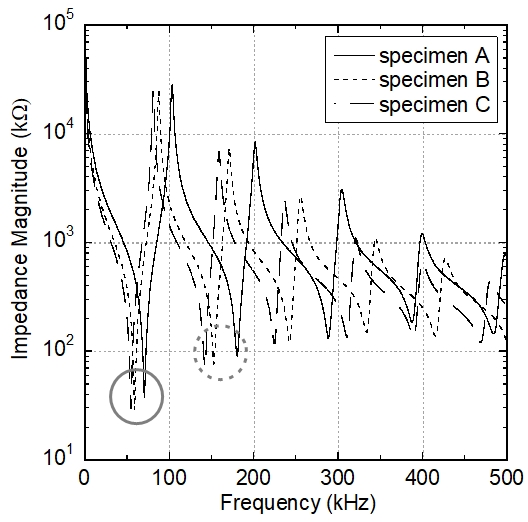
The results of the harmonic analysis are displayed in Fig. 4 in the form of impedance curves for three specimen models. The curves of impedance magnitude indicate the resonances of the transducers at the minimum points.
4. Experiments
This section experimentally determines the ultrasonic transducer vibration characteristics using two methods. The specimens used in the experiments were listed in Table 1 and shown in Fig. 2.
4.1 Impedance Analysis
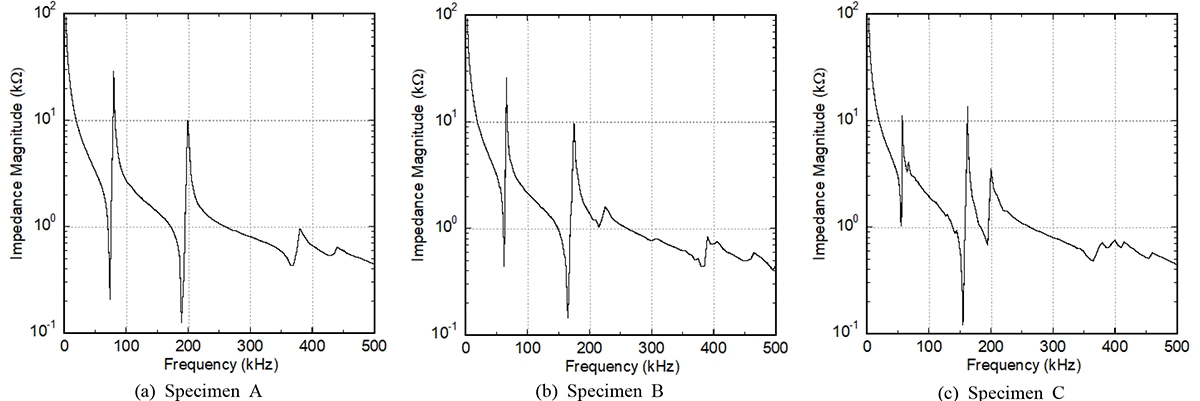
We used an impedance analyzer (Agilent Technology 4192A) to measure natural frequencies. Measurements were carried out with three pieces of three kind specimens. The experimentally obtained impedance curves using one piece of three specimens are displayed in Fig. 5. The minimum points of the impedance magnitude curves indicate the resonances.
4.2 Laser In-plane Interferometry
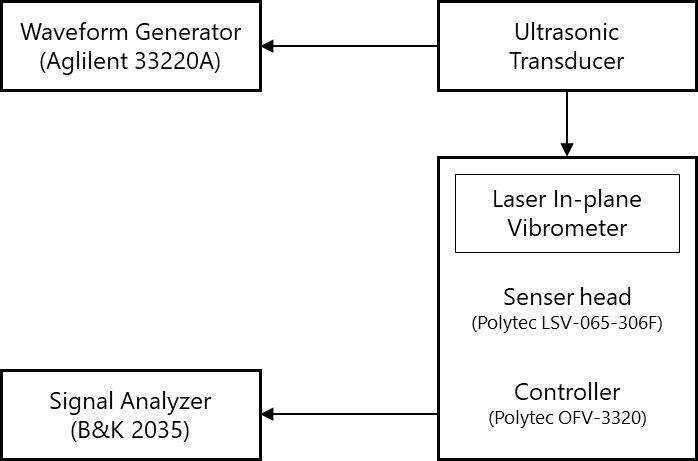
The shape of the first radial mode was measured by laser interferometry. We used a laser in-plane vibrometer, which consists of Polytec LSV-065-306F optical sensor head and Polytec OFV-3320 controller. As described in Ref. [5], the apparatus measured the velocity of the moving plane normal to the central line of laser beams. The experimental equipment was connected as shown in Fig. 6.
A waveform generator (Agilent 33220A) generated electric signals with variable frequencies and a constant voltage onto a transducer. The controller output was monitored on B&K 2035 signal analyzer. The measured amplitude was proportional to the vibration velocity, and it was converted to the vibration displacement. The measurement was performed along a radial line from the center to the outside at every 1 mm. The vibration amplitude was measured and normalized to the maximum amplitude.
4.3 Transmission and Reception of Ultrasound
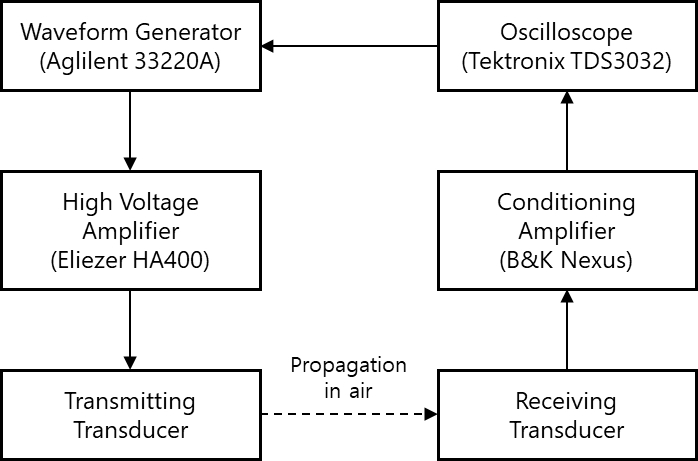
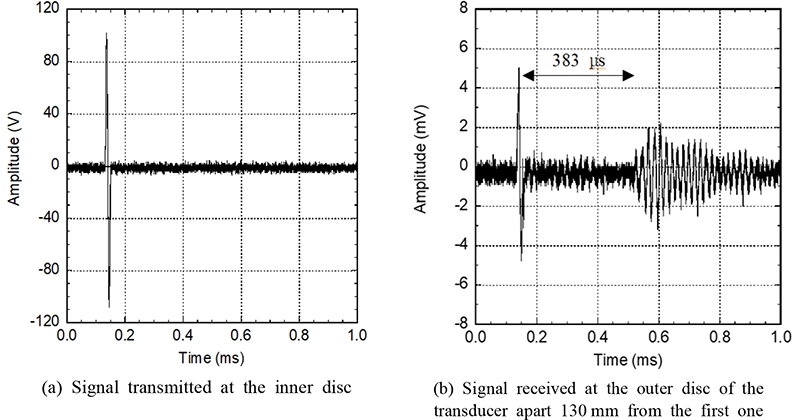
Other experiment was performed to demonstrate the separate transmission and reception of ultrasound in a transducer. The experimental equipment was composed of the devices as shown in Fig. 7. The transducer specimen chosen for the experiment is type C in Table 1. The interior solid disc of the transducer is a transmitter, and it is excited by the high frequency signal generated and amplified by a waveform generator and high voltage amplified, respectively. The signal is one-period harmonic wave of 55 kHz, which corresponds to the fundamental frequency of the transducer. Fig. 8(a) shows the signal exciting the interior solid disc of the transducer.
Second transducer of same type was located at a specific distance from the first transducer. The exterior hollow disc detects the ultrasound and converts it to the electric signal. Fig. 8(b) shows an example of the received signal monitored at the oscilloscope. The time 383 μs corresponds to the flight time of the wave to 130 mm at the speed 340 m/s with the error less than 1 %.
5. Results
Natural frequencies calculated from Eq. (14) are listed in Tables 5, 6 and 7 for various values of the radius ratio q. They are compared with the finite element analysis and experimental results in the tables and discussed in Section 6. Mode shapes are calculated from Eqs. (8) and (13), and the results are displayed in Figs. 9(a) and 10(a).
Comparison of radial mode natural frequencies obtained by theoretical calculation, finite element analysis, and measurement for specimen A(q = 2.0)

Comparison of radial mode natural frequencies obtained by theoretical calculation, finite element analysis, and measurement for specimen B(q = 2.4)

Comparison of radial mode natural frequencies obtained by theoretical calculation, finite element analysis, and measurement for specimen C(q = 2.5)
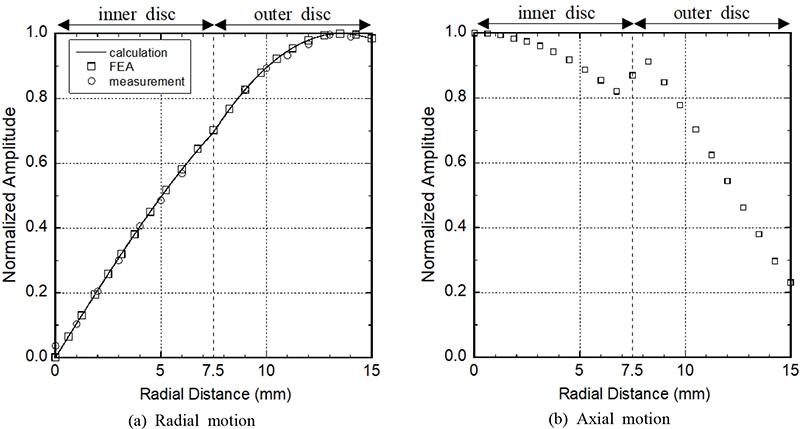
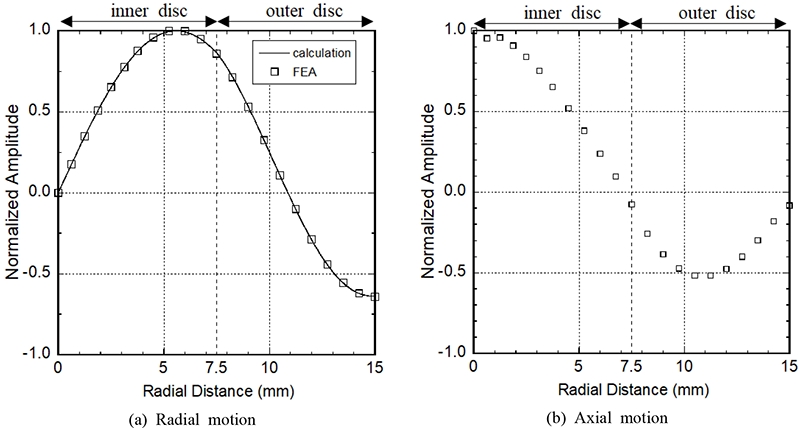
The first mode shape is compared with the finite element analysis and experimental results in Fig. 9(a) and discussed in Section 6.
Figs. 9 and 10 display the mode shapes of the radial and axial vibrations in the radial first and second modes. The axial vibration in the interior disc would be used to radiate ultrasound into the air. The axial vibration in the exterior disc would be used to detect ultrasound from the air.
6. Discussions
The natural frequencies and mode shapes obtained theoretically in Section 3 and experimentally in Sections 4 are compared with each other in this section.
The natural frequencies of the in-plane radial modes obtained by calculations, finite element analysis, and measurements are listed in Tables 5, 6 and 7 for three specimens. The theoretical and experimental results agree well within a 3.2 % discrepancy of each other. The natural frequencies listed in Tables 5, 6 and 7 are displayed in Fig. 11. It is clearly shown that the natural frequencies are smaller when the outer radius of the piezoelectric disc is larger. This trend is same as that observed for a single piezoelectric disc(5).
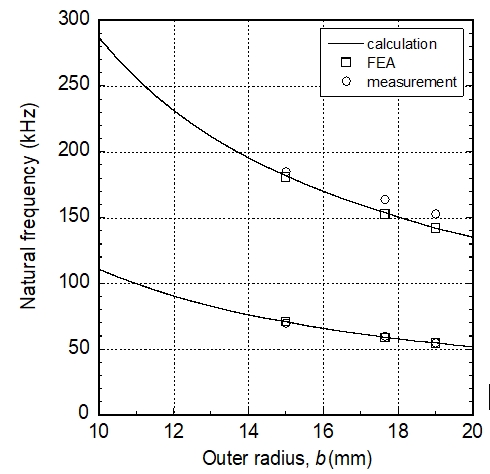
Comparison of natural frequencies obtained by calculations, finite element analysis, and measurements for the radial first and second modes of three specimens
The radial in-plane motion of the first radial mode obtained using the laser vibrometer was compared with the calculated results in Fig. 9(a). It is observed that the results agree well within 1.0 % with each other. In addition, the displacement distribution was not monotonic from the center to the outer surface. The location of the maximum amplitude is 0.7 % away from the perimeter, as observed in a single disc(5).
If the material of the exterior disc is same as that of the interior disc, the characteristics of the transducer are the same as those of a single piezoelectric disc. This statement was confirmed by repeating the calculations and measurements of natural frequencies with the specimens of interior and exterior discs made of PZT-4 only. The results, listed in Tables 8, 9 and 10, were compared with the natural frequencies of a single piezoelectric disc having the same radius as the outer radius of the exterior hollow disc.

Comparison of radial mode natural frequencies obtained by theoretical calculation, finite element analysis, and measurement for specimen A made of PZT-4

Comparison of radial mode natural frequencies obtained by theoretical calculation, finite element analysis, and measurement for specimen B made of PZT-4
7. Conclusions
This research presented the vibration characteristics of an ultrasonic transducer composed of interior and exterior piezoelectric discs. In-plane radial vibration characteristics were investigated theoretically and experimentally, and natural frequencies and mode shapes were compared.
In the theoretical analysis, the equations of piezoelectric motions were derived by using radial displacements and electric potential. With boundary conditions the equations were solved and produced characteristic equations providing the natural frequencies and mode shapes. In the experiments, the natural frequencies were measured at an impedance analyzer and the first radial in-plane mode were measured using a laser in-plane vibrometer. The theoretical and experimental results agreed with each other within 1.0 %. Experiments also confirmed that the transducer transmits ultrasound at the interior disc and receives it at the exterior disc.
Similarly as observed in a single piezoelectric disc, the radial vibration distribution of the first mode was not monotonic from the center to the outer surface, and the maximum amplitude appears 0.2 % away from the outer surface. We found that the characteristics of the transducer is similar to those of a single piezoelectric disc.
The frequencies of the radial modes were shown as a function of outer radius of the disc. It is concluded that the vibration in the interior solid disc would radiate ultrasound into air and that in the exterior hollow disc would detect ultrasound from air.
Nomenclature
| C : | Speed of wave propagation |
| J, K : | Bessel functions of the first kind |
| V0 : | Applied voltage |
| a, b : | Inner and outer radii of the discs |
| cE : | Elastic stiffness |
| e : | Piezoelectric stress constant |
| f : | Natural frequency |
| k : | Wave number |
| l : | Thickness of the transducer |
| u : | Radial displacement |
| ϕ : | Electric potential |
| ρ : | Mass density |
| σ : | Normal stress |
| ω : | Angular velocity |
References
-
Busch-Vishniac, I. J., (1999), Electromechanical Sensors and Actuators, Springer, New York, p140-154.
[https://doi.org/10.1007/978-1-4612-1434-2]

- Lynnworth, L. C., (1989), Ultrasonic Measurements for Process Control, Academic Press, Boston, p487-507.
-
Alonso, L., Milantes, V., Torre-Ferrero, C., Godoy, J., Oria, J. P., and Pedro, T., (2011), Ultrasonic Sensors in Urban Traffic Driving-aid Systems, Sensors, 11(1), p661-673.
[https://doi.org/10.3390/s110100661]

- Shrivastava, A. K., Verma, A., and Singh, S. P., (2010), Distance Measurement of an Object or Obstacle by Ultrasound Sensors Using P89C51RD2, International Journal of Computer Theory and Engineering, 2(1), p64-68.
-
Kim, D. J., Oh, S. H., and Kim, J. O., (2015), Measurements of Radial In-plane Vibration Characteristics of Piezoelectric Disc Transducers, Transactions of the Korean Soc. for Noise and Vibration Engineering, 25(1), p13-23.
[https://doi.org/10.5050/ksnve.2015.25.1.013]

-
Piao, C., and Kim, J. O., (2014), In-plane Vibration Characteristics of Piezoelectric Ring Transducers, Transactions of the Korean Soc. for Noise and Vibration Engineering, 24(10), p780-787.
[https://doi.org/10.5050/ksnve.2014.24.10.780]

- Li, H. H., Hu, J. H., and Chan, H. L. W., (2004), Finite Element Analysis on Piezoelectric Ring Transformer, IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 51(4), p1247-1254.
- Meitzler, A. H., O’Bryan, H. M. Jr., and Tiersten, H. F., (1973), Definition and Measurement of Radial Mode Coupling Factors in Piezoelectric Ceramic Materials with Large Variations in Poisson’s Ratio, IEEE Transactions on Sonics and Ultrasonics SU-20, 12(1), p233-239.
-
Kunkel, H. A., Locke, S., and Pikeroen, B., (1990), Finite-element Analysis of Vibrational Modes in Piezoelectric Ceramic Disks, IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 37(4), p316-328.
[https://doi.org/10.1109/58.56492]

-
Lee, P. C. Y., Yu, J.-D., Li, X., and Shih, W.-H., (1999), Piezoelectric Ceramic Disks with Thickness-graded Material Properties, IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 46(1), p205-215.
[https://doi.org/10.1109/58.741534]

- Ho, S.-T., (2007), Modeling of a Disk-type Piezoelectric Transformer, IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 54(10), p2110-2119.
- Lin, Y.-C., and Ma, C.-C., (2004), Experimental Measurement and Numerical Analysis on Resonant Characteristics of Piezoelectric Disks with Partial Electrode Designs, IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 51(8), p937-947.
-
Iula, A., Lamberti, N., and Pappalardo, M., (1996), A Model for the Theoretical Characterization of Thin Piezoceramic Rings, IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 43(3), p370-375.
[https://doi.org/10.1109/58.489393]

- Ho, S.-T., (2007), Modeling and Analysis on Ring- type Piezoelectric Transformers, IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 54(11), p2376-2384.
-
Piao, C., and Kim, J. O., (2016), Vibration Characteristics of a Piezoelectric Disk Laminated with an Elastic Disk, Journal of Mechanical Science and Technology, 30(12), p5351-5362.
[https://doi.org/10.1007/s12206-016-1102-9]

-
Piao, C., and Kim, J. O., (2017), Vibration Characteristics of an Ultrasonic Transducer of Two Piezoelectric Discs, Ultrasonics, 74, p72-80.
[https://doi.org/10.1016/j.ultras.2016.09.021]

-
Guo, N., Cawley, P., and Hitchings, D., (1992), The Finite Element Analysis of the Vibration Characteristics of Piezoelectric Discs, Journal of Sound and Vibration, 159(1), p115-138.
[https://doi.org/10.1016/0022-460x(92)90454-6]

-
Heyliger, P. R., and Ramirez, G., (2000), Free Vibration of Laminated Circular Piezoelectric Plates and Discs, Journal of Sound and Vibration, 229(4), p935-956.
[https://doi.org/10.1006/jsvi.1999.2520]

- Wang, L. K., Wang, G., and Dong, T. X., (2011), Analyses for Radial Vibration of Piezoceramic Disc Stack, Ferroelectrics, 413(1), p443-451.
-
Laoratanakul, P., and Uchino, K., (2004), Designing a Radial Mode Laminated Piezoelectric Transformer for High Power Application, IEEE International Ultrasonics, Ferroelectrics, and Frequency Control Joint 50th Anniversary Conference, p229-232.
[https://doi.org/10.1109/isaf.2004.1418378]

-
Achenbach, J. D., (1975), Wave Propagation in Elastic Solids, North Holland, Amsterdam, p73-75.
[https://doi.org/10.1016/0003-682x(75)90007-9]

-
Hussein, M., and Heyliger, P. R., (1996), Discrete Layer Analysis of Axisymmetric Vibrations of Laminated Piezoelectric Cylinders, Journal of Sound and Vibration, 192(5), p995-1013.
[https://doi.org/10.1006/jsvi.1996.0230]

- Wolfram, S., (1999), The Mathematica Book, 4th ed., Wolfram Media Inc., Champaign, p100-107.
Appendix
Appendix
A.1 Piezoelectric Constitutive Equations
Piezoelectric relations were well formulated from the general electromechanical relation(1). The piezoelectric constitutive equations are expressed as follows:
| (A1) |
| (A2) |
where T, S, D, and E are the matrix forms of stresses, strains, electric displacements, and electric fields, respectively. In addition, e is the matrix form of piezoelectric stress constants, cE is the coefficient matrix of stiffness with a constant electric field, and εS is the matrix of permittivity with constant strain.
Vibrations with axisymmetry can be formulated with cylindrical coordinates r, θz, and time t in terms of radial displacement u(r, z, t) and axial displacement w(r, z, t). Normal strains εr, εθ, εz and shear strains γθz, γzr, γrθ are related as follows:
| (A3a,b,c) |
| (A4a,b,c) |
Electric field Ez is related with electric potential ϕ(z, t) in the piezoelectric transducer as follows:
| (A5) |
Eqs. (A3) ~ (A5) are inserted in Eqs. (A1) and (A2) and they yield normal stresses σr, σθ, σz, and electric displacement Dz as follows(8):
| (A6a) |
| (A6b) |
| (A6c) |
| (A6d) |
| (A6e) |
A.2 Constitutive Equations under Plane Stress Condition
When the thickness of a disc is much larger than its diameter, i.e. the diameter-to-thickness ratio is bigger than 10, the disc is assumed to satisfy plane stress conditions in the thickness direction, and thus, σz = 0. Eq. (A6c) is rewritten to present the normal strain εS as(8):
| (A7) |
Eq. (A7) is inserted in Eqs. (A6a), (A6b) and (A6e) and they are rewritten as follows:
| (A8a) |
| (A8b) |
| (A8c) |
In Eq. (A8) superscript p is used to define the constants as follows:
| (A9a) |
| (A9b) |
| (A9c) |
| (A9d) |

Chunguang Piao received the M.S. and Ph.D. degrees in mechanical engineering from Soongsil University in 2013 and 2017, respectively. During his stay at Soongsil as a graduate student, he worked on ultrasonic wave propagation and vibration characteristics of piezoelectric transducers. He is now working as a post-doctoral researcher at Seoul National University,

Jin Oh Kim received the B.S. and M.S. degrees in mechanical engineering from Seoul National University in 1981 and 1983, respectively, and the Ph.D. degree from University of Pennsylvania in 1989. For ten years he has got research experiences at Korea Research Institute of Standards and Science, Northwestern University, and Samsung Advanced Institute of Technology. Since 1997, he has been working at Soongsil University, where he is currently a Professor of mechanical engineering. His research interests are in the areas of ultrasonic sensors and actuators using mechanical vibrations and waves.