항공기용 MR 댐퍼의 스카이-그라운드 훅 제어기 설계
© The Korean Society for Noise and Vibration Engineering
Abstract
In this paper, a semi-active magnetorheological (MR) damper is proposed that can be applied to main landing gear suspension system of the aircraft. For the modeling of MR damper, a damping force in the annular orifice and an air force in the damper strut are derived. A MR damper with two magnetic cores is designed to control the damping force with sufficient dynamic range. After modeling the damper, its structural design with the annular type bypass for fast tension speed is determined considering the characteristics of the landing situation of the aircraft. In addition, through the magnetic field analysis of two magnetic cores, controllable yield force of MR fluid is proposed, designed by the magnetic intensity considering the input current. Next, superior performance of the semi-active damper is demonstrated by calculating the aircraft landing efficiency of passive and semi-active dampers by the damper excitation and aircraft drop simulations. To maximize the landing efficiency of drop simulation, the sky-ground control logic is established. The sky hook and ground hook coefficients can be adjusted by tuning the sky-ground hook weighting factor. After calculating the sky-ground hook force with the best-tuned sky hook and ground hook coefficients, the damping force of the MR damper is controlled by the calculated input current. Consequently, the optimized efficiency plot was obtained in comparison with controlled and passive dampers.
Keywords:
MR Damper, Aircraft Landing Gear, Sky Hook, Ground Hook, Sky-ground Hook, Magneto-rheological Fluid키워드:
MR 댐퍼, 항공기 랜딩 기어, 스카이 훅, 그라운드 훅, 스카이-그라운드 훅, 자기유변유체1. 서 론
현재 항공기 착륙장치로 가장 많이 사용되고 있는 공기-유압식 완충장치(oleo-strut)는 수동형 댐퍼가 적용된다. 그러나 완충장치의 성능이 설계단계에서 결정되어 설계 조건 외의 착륙조건에서는 착륙 안정성 저하가 발생한다는 단점을 갖는다(1). 이러한 단점을 극복하기 위해 1970년대 미항공우주국(National Aeronautics and Space Administration, NASA)에서 능동형 착륙장치에 대한 연구가 진행되었으나, 과중량, 구조의 복잡성, 및 안정성 문제 등으로 인하여 상용화되지 못하였다(2).
1970년대 처음 소개된 반 능동형 댐퍼는 구조적으로 단순하며 댐핑력이 가변 가능한 댐퍼로서, 수동형 댐퍼와 능동형 댐퍼의 장점을 가지고 있다(3). 반-능동형 댐퍼에는 자기유변유체(magneto-rheological damper, MR 유체)를 사용한 자기유변댐퍼(magneto-rheological, MR 댐퍼)가 주를 이루고 있으며, 최근 MR 유체를 활용한 항공기용 MR 댐퍼의 연구가 활발히 진행되고 있다(4~6).
MR 유체란 실리콘 베이스의 오일과 스틸 계열의 입자의 혼합물로서 자기장에 반응하는 스마트 유체이다. MR 유체는 자기장이 인가되지 않은 경우 뉴턴 유체(Newtonian fluid)의 거동을 하지만, 자기장이 인가될 경우 MR 유체 내 스틸 입자가 체인을 형성하여 유체의 유동에 저항하는 항복 응력을 갖는 빙햄 유체의 특성을 갖는다(7).
MR 댐퍼는 반-능동형 댐퍼의 일종으로서, 자기장을 인가할 경우 체인을 형성하는 MR 유체의 특성을 응용하여 댐핑력을 가변할 수 있는 댐퍼를 의미한다. 2002년 차량용 댐퍼로 최초 상용화되어 현재 수많은 차종에 적용되어 가변 댐퍼로의 우수성이 입증되었다(8,9).
스카이-그라운드 훅 제어란 착륙 시의 항공기 무게를 충분히 지지해주어 탑승감을 향상시켜주는 스카이 훅 제어와 지면 접지력을 향상시키는 그라운드 훅 제어를 융합한 하이브리드 제어기 일종이다(10). 항공기의 착륙 특성을 고려하여 스카이-그라운드 훅 제어기를 설계하였다.
이 논문에서는 MR 유체가 적용된 항공기용 MR 댐퍼를 수학적으로 모델링한 후, 스카이 훅 제어기, 그라운드 훅 제어기, 스카이-그라운드 훅 제어기를 제안된 MR 댐퍼에 각각 적용하여 제어성능을 비교, 스카이-그라운드 훅 제어기의 우수성을 입증하였다.
2. 항공기용 MR 댐퍼 모델링
항공기용 MR 댐퍼의 설계에 앞서, 댐퍼 설계 기준을 항공기 착륙 시 항공기 착륙 안정성을 개선하기 위하여 착륙 효율(landing efficiency)로 정의하였다. 착륙 효율이란 인가된 최대 에너지와 흡수한 에너지의 비를 의미하며, 식 (1)과 같이 나타낼 수 있다.
| (1) |
Fs는 완충기력(strut force)을 의미하며, Fs,max는 최대 완충기력, s는 스트로크(stroke), smax는 최대 스트로크를 의미한다. 식 (1)에서 볼 수 있듯이, 착륙 효율을 증가시키기 위해서는 최대 완충기력과 최대 스트로크를 줄이는 것이 중요하다.
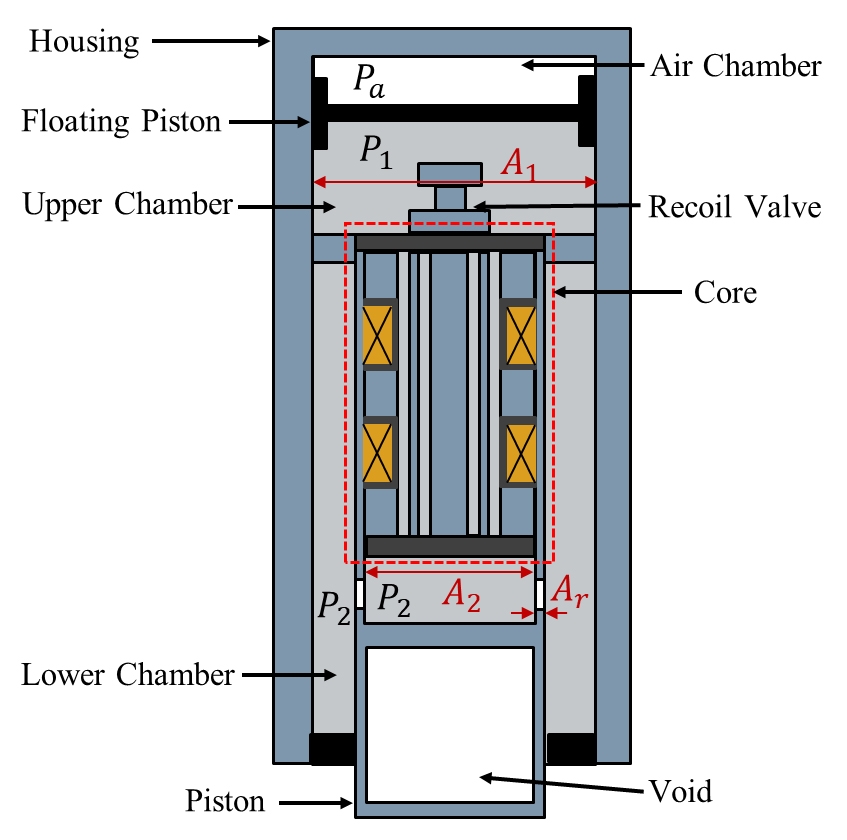
Fig. 1은 이 연구에서 제안하는 항공기용 MR 댐퍼의 개념도를 보여준다. 제시된 MR 댐퍼는 MR 유체를 포함하는 하우징(housing) 부와 피스톤 부로 이루어져 있으며, 피스톤에 의해 공간이 분리되어 상부 챔버(upper chamber)와 하부 챔버(lower chamber)로 나뉘어져 있다. 또한 상부 챔버는 플로팅 피스톤(floating piston)으로 분리되어 압축성 유체를 충진할 수 있는 에어 챔버(air chamber)가 존재한다. 댐퍼 피스톤은 코어(core)부로 통칭할 수 있는 공간과 리코일 밸브(recoil valve)로 구성되어 있다. 코어부 내부에는 MR 유체가 흐를 수 있는 오리피스 홀(orifice hole)과 바이패스 홀(bypass hole)이 환형(annular type)으로 존재하며, 전류 인가 시 자기장(magnetic field)을 형성할 수 있는 두 개의 자기코일(magnetic coil)이 존재한다.
MR 댐퍼 내에 작용하는 힘은 가스압축에 의해 발생하는 공압력(pneumatic force, Fa)과 압력강하로 발생하여 MR 유체의 흐름상태를 결정하는 점성력(viscous force, Fvis), 항복력(yield force, Fy), 오일 씰 및 플로팅 피스톤 등의 마찰에 의해 발생하는 마찰력(friction force, Ff)으로 이루어진다. 여기서 마찰력은 다른 힘 성분에 비해 그 크기가 미소하므로, 마찰에 대한 영향은 무시하도록 한다.
2.1 MR 댐퍼 완충기력(strut force)
피스톤 스트로크에 의해 댐퍼는 인장 또는 압축되게 되고 하우징 내 부피가 변화하게 된다. 하우징 내 부피변화에 대한 부피를 보상을 위해 에어챔버 내 압축성 유체인 가스가 압축되게 되는데, 이를 이용하여 스프링을 대체할 수 있다. 폴리트로픽 법칙에 근거하여 공압을 식 (2)와 같이 유도할 수 있다.
| (2) |
Pa는 에어 챔버에서의 압력이며, Va는 상부 챔버의 체적, Pa0와 Va0는 각각 에어 챔버의 초기 압력과 상부 챔버의 초기 체적을 의미한다. A1과 A2, Ar은 각각 상부 챔버 단면적과 피스톤 내부 단면적, 피스톤 벽면 단면적을 의미한다. n은 폴리트로픽 지수(polytropic index)로, n은 에어 챔버를 단열로 가정하여 1.3을 적용하였다.
오리피스 홀(orifice hole)에서의 압력강하는 근사적으로 MR 유체의 흐름에 의해 발생하는 점성압력강하(viscous pressure drop)와 흐름에 저항하는 항복압력강하(yield pressure drop)의 중첩으로 표현될 수 있다.
| (3) |
| (4) |
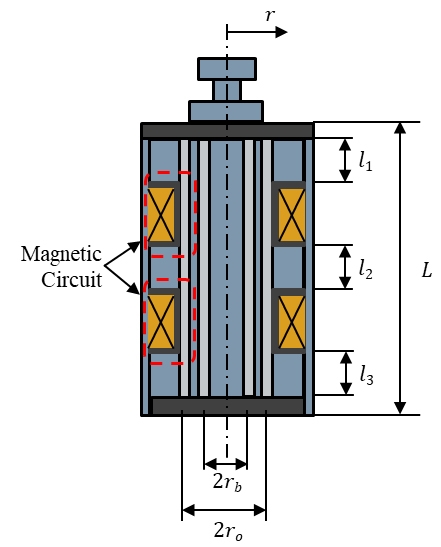
Fig. 2는 코어부의 개략도를 보여준다. ro는 오리피스 반지름, to는 오리피스 두께, L은 오리피스 및 바이패스 홀 길이, lt는 전체유효자극길이(total effective pole length)를 나타낸다. lt는 유효자극길이(l1, l2, l3)의 합으로 구할 수 있다. P1 및 P2는 상부 및 하부 챔버의 압력, μ는 점성계수(viscosity), τy는 자기장에 의한 항복전단응력(yield shear stress), Q는 피스톤 스트로크에 의한 MR 유체의 유량, c는 MR 유체의 흐름속도의 함수를 의미한다. Q와 c는 다음과 같이 나타낼 수 있다.
| (5) |
| (6) |
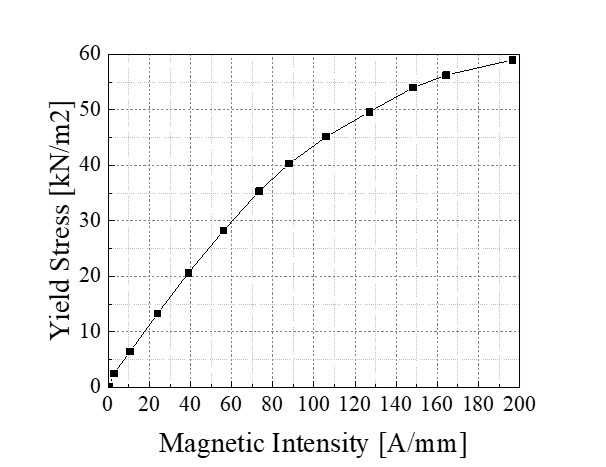
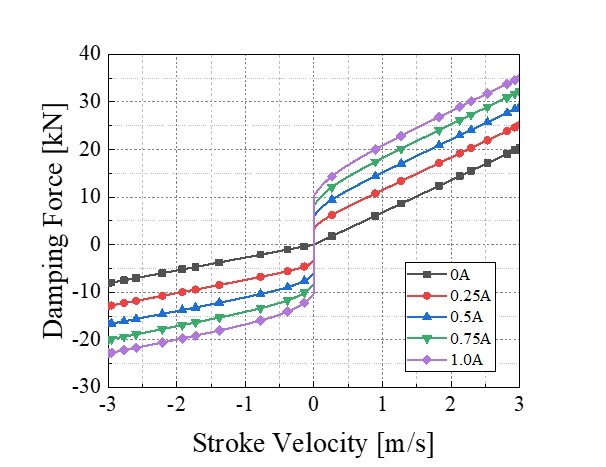
MR 유체는 항공기 착륙조건에 부합하기 위해 점도가 높고 인가전류 대비 높은 항복력을 갖는 LORD사의 MRF-140CG를 적용하였다. MRF-140CG의 점성계수는 0.28 pa·s이다. 항복응력은 MR 유체에 걸리는 자기장 세기에 관련된 함수로서, Fig. 3과 같은 특성곡선을 가진다. 최소자승법(least square method)을 통해 항복응력-자기장 세기 곡선을 다음과 같은 식으로 도출하였다.
| (7) |
H는 자기장 세기(magnetic intensity)를 의미한다.
또한 기존 랜딩기어 완충장치에서 주로 적용되는 리코일 밸브(recoil valve)를 적용하였다. 리코일 밸브는 스트로크 속도에 따른 댐핑력의 비대칭성을 구현하는 장치이다. 항공기 댐퍼는 압축될 시 항공기의 무게를 받쳐줘야 하므로 높은 댐핑력을 요구하여, 댐퍼가 인장될 시 타이어가 안정성 측면에서 항상 노면에 접지되어 있는 상태를 유지해야 하므로 낮은 댐핑력으로 빠른 스트로크 속도를 요구한다. 댐퍼 인장 시 점성압력강하는 리코일 밸브가 열려 바이패스 홀을 통해 흐르는 MR 유체를 고려하여 다음과 같이 정리할 수 있다.
| (8) |
rb는 바이패스 반지름, tb는 바이패스 두께를 나타낸다. 바이패스 홀의 두께는 댐퍼 인장 시 점성력을 압축 시의 점성력의 40 %만 작용하도록 설정하였다.
완충기력을 피스톤에 작용하는 힘 성분을 통해 다음과 같이 유도할 수 있다.
| (9) |
힘 PaA1과 힘 P1A1는 준평형(semi-equilibrium) 상태에 있으며, 압력강하는 식 (3)과 같으므로 완충기력을 다음과 같이 정리할 수 있다.
| (10) |
따라서 최종 정리된 완충기력 및 공압력, 점성력, 항복력은 다음과 같다.
| (11) |
| (12) |
| (13) |
| (14) |
2.2 코어 자기장 해석 및 댐퍼 특성 분석
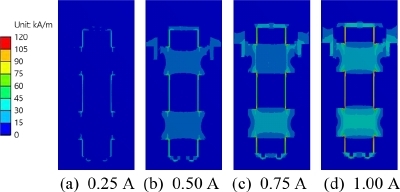
이 논문에서 제안한 항공기용 MR 댐퍼는 착륙 시 충분한 항복력을 가질 수 있도록 두 개의 자기코일을 갖도록 설계하였으며, 각각의 자기코일은 700번의 권선으로 이루어진 솔레노이드 코일을 갖는다. 솔레노이드 코일은 AWG(American wire gauge) 규격의 AWG27(0.35ø) 구리선이 사용되었으며, FEM 기법을 이용하여(Ansys) 자기장 해석이 진행되었다. Fig. 4와 Table 1은 자기장 해석 결과를 보여준다.
자기장 해석 결과를 이용하여 제안된 MR 댐퍼의 특성 시뮬레이션이 수행하였다. 미국연방항공국 소형 항공기 인증 절차(FAR23)의 착륙 기준인 최대 착륙속도 3 m/s를 만족하는 시뮬레이션을 진행하였다. Fig. 5는 시뮬레이션 결과를 보여준다. 댐핑력-가진속도 그래프에서 확인할 수 있듯, 항공기 안정성을 증대시키기 위한 가진속도 비대칭성이 적용되었으며, 전류에 따른 MR 댐퍼의 항복력 제어 범위(dynamic range)가 14.4 kN으로 항공기 특성에 맞게 넓은 제어범위를 보장하는 것을 확인할 수 있다.
3. 제어기 설계 및 착륙 시뮬레이션
3.1 항공기 착륙장치 2-자유도 모델링
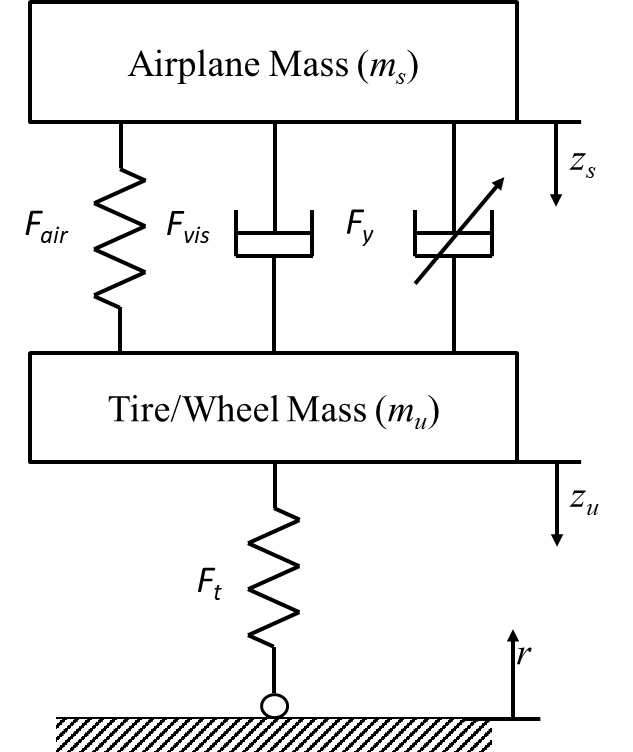
MR 댐퍼의 항공기 착륙 시뮬레이션을 위해 항공기 착륙장치 모델링이 수행되었다. Fig. 6은 이 연구에서 사용한 1/2 항공기 모델을 보여주며, 그에 따른 운동 방정식은 다음과 같이 나타낼 수 있다.
| (15) |
zs는 항공기 질량의 변위, zu는 타이어 질량의 변위, g는 중력가속도, Ft는 노면에서 전달되는 타이어 스프링력을 의미한다. 항공기 질량(airplane mass, ms)를 680 kg으로 결정하였으며, 휠을 포함한 타이어 질량(tire mass, mu)을 18 kg으로 산정하였다.
3.2 스카이-그라운드 훅 제어기 설계
스카이 훅 제어는 Karnopp에 의해 제안되었으며, 현재 수 많은 자동차 진동제어 및 항공기 착륙 제어에 사용되고 있다(11). 이 제어기법은 스프링 상 질량(sprung mass)을 가상의 댐퍼와 연결하여 차량의 감쇠를 담당하는 것으로, 차량의 탑승감을 향상시키나 타이어의 접지력을 떨어뜨려 조향성 및 안정성을 저하시킨다. 스카이 훅 댐핑력의 제어로직은 다음과 같은 논리곱으로 나타낼 수 있다.
| (16) |
Fsky는 스카이 훅 제어에 대한 댐핑력(damping force of sky hook control)을, Csky는 스카이 훅 제어의 게인(gain of sky hook control)을 의미한다. 식 (16)에 의하면, 스카이 훅 제어에 대한 댐핑력은 항공기 및 댐퍼의 운동속도에 따라 항공기 기체의 운동에 저항하는 점성력에 의해 결정되며, 스카이 훅 게인에 따라 그 크기가 결정된다.
그라운드 훅 제어는 Valášek에 의해 제안되었으며, 스프링 하 질량(unsprung mass)을 가상의 댐퍼와 연결하여 타이어의 댐핑력을 제어하는 제어기법이다(12). 이 제어기법은 타이어의 접지력을 향상시켜 타이어의 자운스-리바운드를 줄이고 조향성을 향상시키나 심각한 탑승감 저하 효과를 유발한다. 그라운드 훅 댐핑력의 로직은 다음과 같다.
| (17) |
여기서 Fgrd는 그라운드 훅 제어에 대한 댐핑력(damping force of ground hook control)을, Cgrd는 그라운드 훅 제어의 게인(gain of ground hook control)을 의미한다. 식 (17)에 의하면, 그라운드 훅 제어에 대한 댐핑력은 타이어 및 댐퍼의 운동속도에 따라 타이어의 운동에 저항하는 점성력에 의해 결정되며, 그라운드 훅 게인에 따라 그 크기가 결정된다.
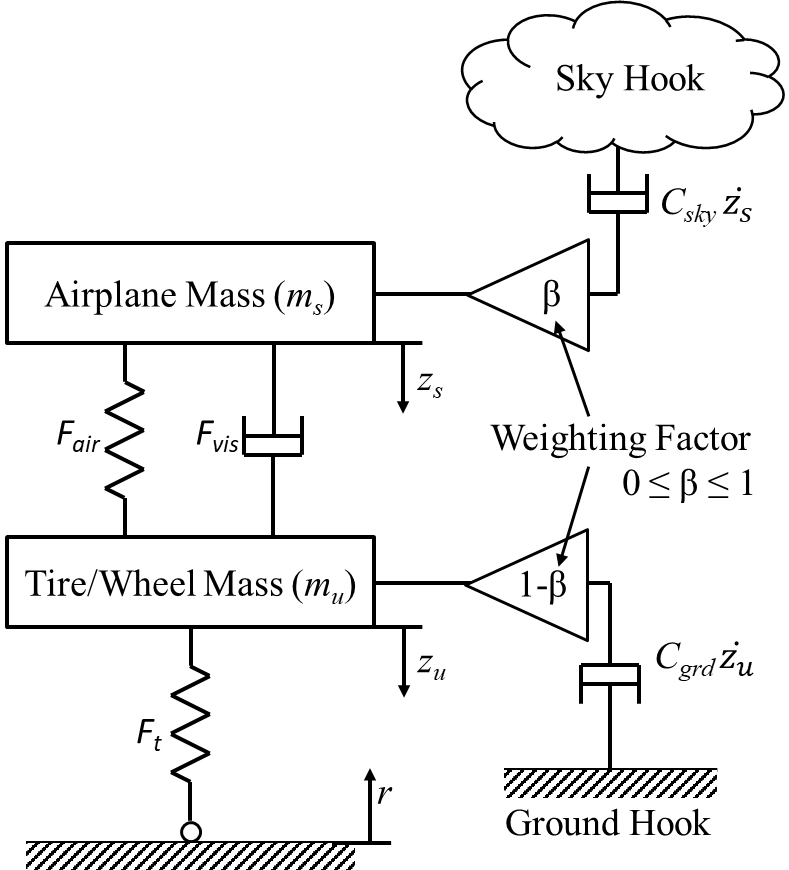
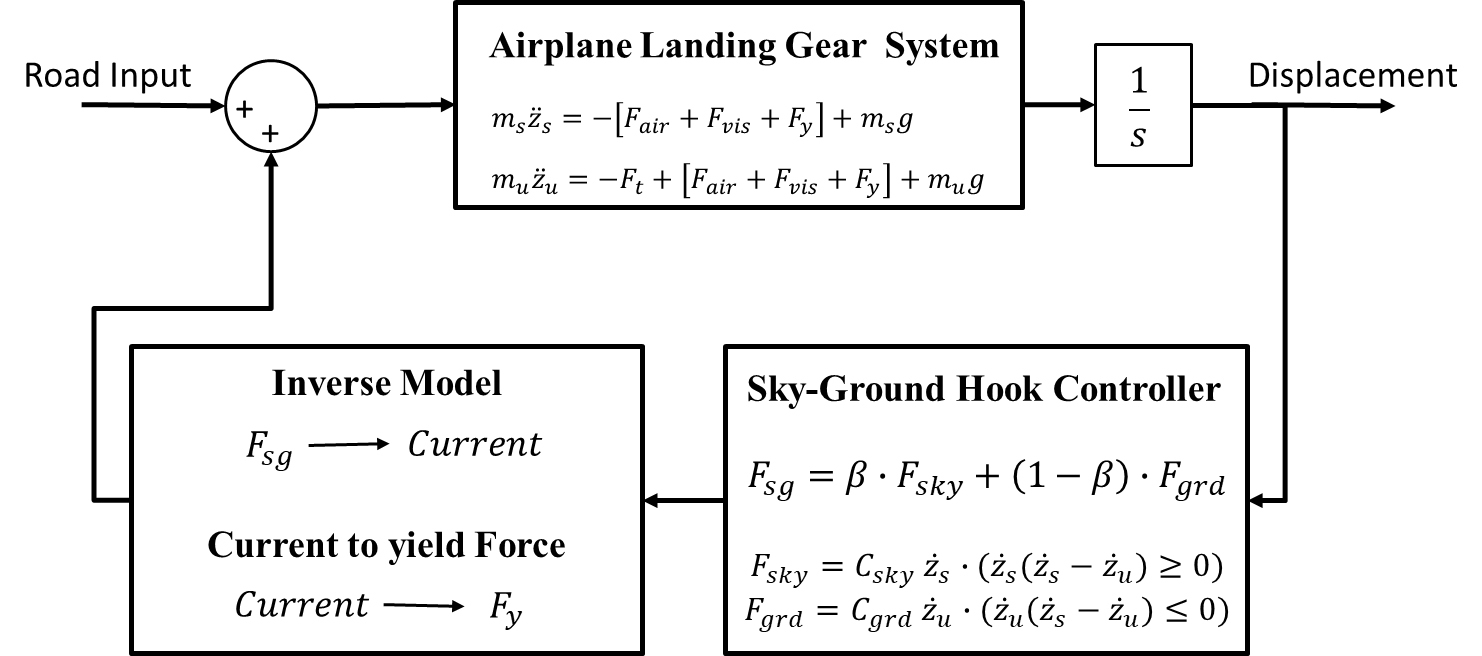
이 연구에서는 항공기의 착륙 효율 및 안전성 증가를 위하여 스카이-그라운드 훅 제어(sky-ground hook control) 기법이 적용되었다. 스카이-그라운드 훅 제어기는 스카이 훅 제어기와 그라운드 훅 제어기의 가중치 제어를 통하여 스카이 훅 제어와 그라운드 훅 제어의 장점을 이용할 수 있는 하이브리드 제어기의 일종이다. 이 연구에서는 항공기 착륙 시 항공기 기체에 가해지는 힘을 최소화하고 타이어의 접지력을 향상시키기 위해 스카이-그라운드 훅 제어기를 적용하였다. Fig. 7은 스카이-그라운드 훅 제어의 개념도를 보여주며, 스카이-그라운드 훅의 댐핑력은 다음과 같이 나타낼 수 있다.
| (18) |
Fsg는 스카이-그라운드 훅 댐핑력(damping force of sky-ground hook), β는 스카이-그라운드 훅 가중치(weighting factor of sky-ground hook)을 의미한다. 식 (18)에 따르면, 스카이-그라운드 훅 댐핑력은 가중치가 1일 경우 스카이 훅 댐핑력이 되며, 가중치가 0일 경우 그라운드 훅 댐핑력이 됨을 확인할 수 있다. 따라서 가중치를 0에서 1의 범위 내에서 적절히 조정하여 댐핑력의 경향성을 제어하여 최적의 감쇠 효과를 얻을 수 있다. Fig. 8과 같이 스카이-그라운드 훅 제어 및 역 모델링된 모델에 전체 상태 되먹임(full state feedback) 제어 로직으로 스카이-그라운드 훅 댐핑력이 실시간으로 계산되며, MR 댐퍼의 항복력으로 변환된다.
3.3 착륙 시뮬레이션
착륙 시뮬레이션은 FAR23 착륙조건을 충족하기 위하여 3 m/s 착륙상황에 대한 드랍 시험조건을 준수하였다. 제어로직은 제어를 하지 않은 수동형 댐퍼의 경우와, 스카이 훅 제어, 그라운드 훅 제어, 스카이-그라운드 훅 제어가 적용된 반-능동형 댐퍼 순서로 적용하였다.
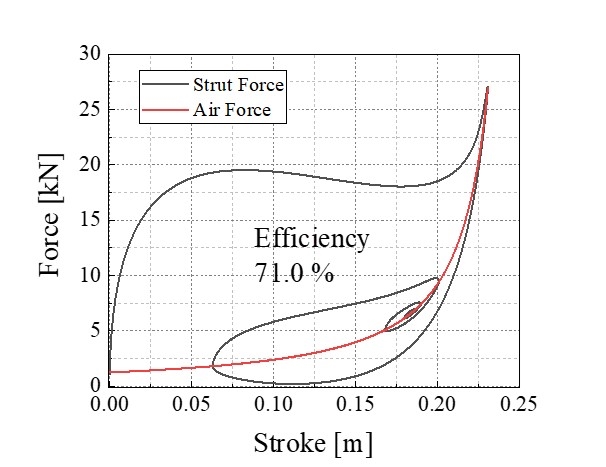
Fig. 9는 제어를 하지 않은 경우의 시뮬레이션 결과를 보여준다. 항공기 특성상, 제어하지 않았을 때에도 항공기를 항상 지지하여 착륙에 대한 안정성을 확보할 수 있어야 하므로 완충기력이 항상 양수의 값을 갖도록 설계됨을 확인할 수 있다. 결과에서 확인할 수 있듯이, 0.23 m의 스트로크와 27 kN의 완충기력이 발생함을 확인할 수 있었다. 그에 따른 착륙 효율은 71.0 %의 착륙 효율을 갖는 것을 확인하였다.
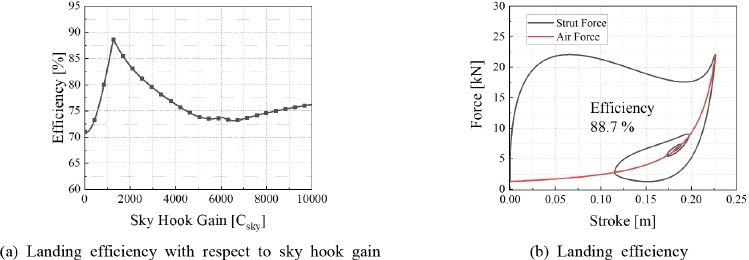
Fig. 10은 스카이 훅 제어의 시뮬레이션 결과를 보여준다. Fig. 10(a)는 스카이 훅 게인에 따른 효율을 계산한 결과를 보여준다. Csky가 1260일 때 최대 88.7 %의 효율을 얻을 수 있는 것을 확인할 수 있었다. 최대 효율을 갖는 게인을 이용하여 착륙 시뮬레이션을 수행하였다. Fig. 10(b)는 Csky가 1260일 때의 착륙 시뮬레이션 결과를 보여준다. 결과에서 알 수 있듯이 0.225 m의 스트로크와 22 kN의 완충기력이 발생함을 확인하였다. 스카이 훅 제어에 대한 항복력이 발생하는 구간에서 댐퍼의 최대 댐핑력이 증가하여 최대 공압력과 동일 선상에 있어 효율이 증가하는 것을 확인할 수 있다.
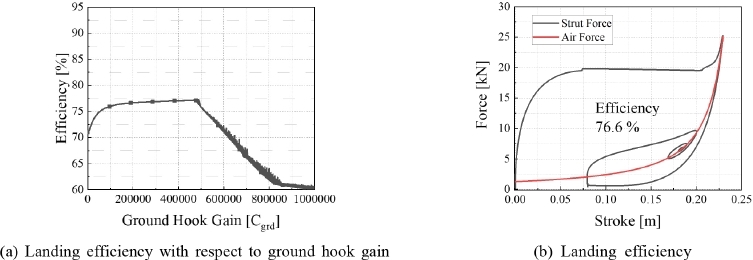
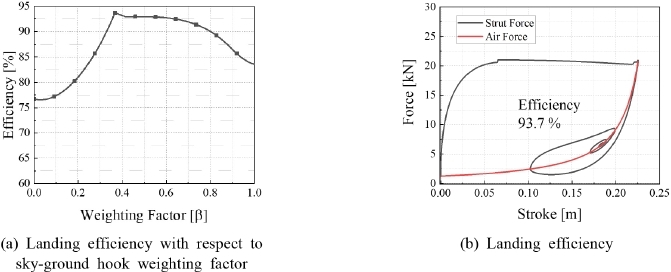
Fig. 11은 그라운드 훅 제어의 시뮬레이션 결과를 보여준다. Fig. 11(a)는 그라운드 훅 게인에 따른 효율을 보여준다. 결과와 같이 Cgrd가 200 000일 때 최대 76.6 %의 효율을 얻을 수 있는 것을 확인하였으며, Fig. 11(b)와 같이 착륙 시뮬레이션을 수행하였다. 0.23 m의 스트로크와 그에 따른 최대 약 25 kN의 완충기력이 발생한 것을 확인할 수 있다. 댐퍼의 점성력이 작아지고 공압력이 증가하는 구간에서 그라운드 훅에 대한 항복력이 발생하여 효율곡선이 평평해져 효율이 증가하는 것을 확인할 수 있다. Fig. 12는 스카이-그라운드 훅 제어의 시뮬레이션 결과를 보여준다. Csky를 2000으로, Cgrd를 200 000으로 설정하고 가중치에 대한 시뮬레이션을 Fig. 12(a)와 같이 수행하였다. 시뮬레이션 결과에서 볼 수 있듯이, β가 0.369일 때 최대 93.7 %의 효율을 얻을 수 있는 것을 확인하였다. Fig. 12(b)와 같이 가중치를 0.369로 설정하여 시뮬레이션을 진행한 결과 0.225의 스트로크와 21 kN의 완충기력이 발생하는 것을 확인하였다. 스카이 훅 제어의 항복력과 그라운드 훅 제어의 항복력에 의한 효과로 효율성능이 증가함을 확인할 수 있다.
4. 결 론
이 논문에서는 항공기용 MR 댐퍼와 2자유도 항공기 착륙장치를 수학적으로 모델링하였으며, FAR23 규준 착륙조건을 충족하기 위하여 3 m/s 착륙상황에 대한 착륙효율을 분석하였다. 또한 스카이-그라운드 훅 제어기의 최적 게인 및 가중치를 확보하고, 스카이-그라운드 훅 제어의 우수성을 입증하였다. 착륙 시뮬레이션을 통해 분석한 결과, 제어를 하지 않은 경우 착륙효율은 71.0 %로 나타났으며, 스카이 훅 제어를 적용한 경우 88.7 %의 착륙효율을 갖는 것을 확인하였다. 또한 그라운드 훅 제어를 적용한 경우 착륙효율은 76.6 %로 나타났으며, 스카이-그라운드 훅 제어를 적용한 경우 93.7 %의 착륙효율을 갖는 것을 확인하였다. 결과적으로 스카이 훅 제어의 최대 댐핑력이 증가하는 효과와 그라운드 훅 제어의 효율곡선이 평평해지는 효과에 의해 스카이-그라운드 훅 제어에서 높은 착륙효율을 얻을 수 있었다. 추후 다양한 착륙 속도 및 노면 상황 등 다양한 착륙상황에 대한 최적 게인을 확보하여 스카이-그라운드 훅 제어기에 대한 적응형 제어기를 구축하고, 항공기 전 기체(full model)에 대한 다양한 착륙 상황에서의 착륙 및 택싱(taxiing) 시뮬레이션을 진행할 계획이다.
Acknowledgments
A part of this paper was presented at the KSNVE 2018 Annual Autumn Conference.
이 논문은 산업통상자원부의 항공우주 부품기술 개발사업 지원을 받아 수행된 연구이며, 이에 감사드립니다.
References
- Young, D. W., (1986), Aircraft Landing Gears - The Past, Present and Future, Proceedings of the Institution of Mechanical Engineers, Part D: Transport Engineering, 200(2), p75-92.
- McGehee, J. R., and Carden, H. D., (1976), A Mathematical Model of an Active Control Landing Gear for Load Control During Impact and Roll-out, NASA Technical Note, NASA TN D-8080.
- Yi, K., (1993), Semi-active Suspension System, Daehan Gigye Haghoeji, 33(10), p902-911.
-
Kim, B. K., Han, C., and Choi, S. B., (2018), Design and Analysis of MR Damper for Airplane Landing Gear, Transactions of the Korean Society for Noise and Vibration Engineering, 28(1), p102-109.
[https://doi.org/10.5050/ksnve.2018.28.1.102]

-
Mikułowski, G., and Jankowski, Ł., (2009), Adaptive Landing Gear: Optimum Control Strategy and Potential for Improvement, Shock and Vibration, 16(2), p175-194.
[https://doi.org/10.1155/2009/732803]

-
Han, C., Kim, B. K., and Choi, S. B., (2018), Design of a New Magnetorheological Damper Based on Passive Oleo-pneumatic Landing Gear, Journal of Aircraft, 55(6), p2510-2520.
[https://doi.org/10.2514/1.c034996]

- Choi, S. B., and Han, Y. M., (2012), Magnetorheological Fluid Technology: Applications in Vehicle Systems, Boca Raton, FL, CRC Press.
-
Choi, S. B., Lee, S. K., and Park, Y. P., (2001), A Hysteresis Model for the Field-dependent Damping Force of a Magnetorheological Damper, Journal of Sound Vibration, 245(2), p375-383.
[https://doi.org/10.1006/jsvi.2000.3539]

-
Han, C., Shin, D. K., Shin, C. S., and Choi, S. B., (2017), Robust Vibration Control of Vehicle Seat Suspension System Using MR Damper, Transactions of the Korean Society for Noise and Vibration Engineering, 27(3), p286-296.
[https://doi.org/10.5050/ksnve.2017.27.3.286]

- Choi, S. B., Park, K. W., and Suh, M. S., (2002), Fuzzy Sky-ground Hook Control of a Tracked Vehicle Featuring Semi-active Electrorheological Suspension Units, Journal of Dynamic Systems, Measurement, and Control, 124(1), p150-157.
-
Karnopp, D., Crosby, M. J., and Harwood, R. A., (1974), Vibration Control Using Semi-active Force Generators, Journal of Engineering for Industry, 96(2), p619-626.
[https://doi.org/10.1115/1.3438373]

-
Valášek, M., Novak, M., Šika, Z., and Vaculin, O., (1997), Extended Ground-hook – New Concept of Semi-active Control of Truck’s Suspension, Vehicle System Dynamics, 27(5-6), p289-303.
[https://doi.org/10.1080/00423119708969333]


Seung-Bok Choi received the B.S. degree in Mechanical Engineering from Inha University in 1979, MS degree and Ph.D. degrees from Michigan State University in 1986 and 1990, respectively. He is currently Dean of the Graduate School and fellow professor in Inha University. He is a fellow of NAEK (National Academy Engineering of Korea), KAST (The Korean Academy of Science and Technology). His research interests are robust controller design and control of various systems using smart actuators.