연속사용 금지범위 통과 시 추진축계의 과도 비틀림 진동 해석
© The Korean Society for Noise and Vibration Engineering
Abstract
To analyze the transient torsional vibration of the propulsion shafting system in the barred speed range (BSR), a method to analyze the non-periodic load condition in the time domain instead of the existing frequency domain analysis is applied. In this paper, the average excitation torque of the engine during acceleration is estimated by the proportional integral controller, whose gains are adjusted by the result of ship acceleration test. The fluctuating excitation torque is calculated using the torque harmonics provided by the engine manufacturer. The test results of the torsional vibration in the BSR are compared with the simulation results performed using varying system damping and bollard resistance.
Keywords:
Barred Speed Range, Transient Torsional Vibration키워드:
연속사용 금지범위, 과도 비틀림 진동1. 서 론
최근 환경 규제로 인해 초장행정 적용, 저속 운전, 엔진 정격조정이 적용된 신형 엔진이 개발되면서 연속사용 금지범위 통과 시 증속이 지연되는 현상이 관찰되었다. 조선업계의 입장에서 이 구간에 증속 지연 현상이 발생하면 추진축계의 피로 수명에 대한 추가적인 검증이 필요하게 되므로, 이를 설계 단계에서 판단할 필요가 있다. 과도 비틀림 진동에 대한 연구는 1960년대 동기 모터의 시동 중 발생하는 펄스토크 현상에 대한 연구로부터 시작되었으며(1), 최근 이돈출 등은 저속 2행정 디젤엔진의 과도 비틀림 진동에 대한 이론적인 해석을 수행하여 이를 정상상태 해석 결과와 최대 응답 토크의 크기를 비교한 바 있다(2). 또한 이돈출 등은 계측된 연속사용 금지범위 통과 시간과 비틀림 응력을 이용하여 축계의 피로수명을 평가한바 있다(3). 하지만 아직까지 연속사용 금지범위에서의 증속 상황을 시뮬레이션하는 연구는 진행된 바 없다. 따라서 이 논문에서는 MAN(Man Energy Solution)사의 G-type 엔진이 적용된 선박의 연속사용 금지범위 통과 시 증속 조건에서 과도 비틀림 진동 해석을 수행하고, 그 결과를 실제 선박의 시운전 시에 계측한 결과와 비교하여 설계 단계에서 선박의 연속사용 금지범위 통과 시간을 예측하는 시뮬레이터를 개발하였다.
또한 계산된 연속사용 금지범위의 통과 시간을 이용하여 증속 시 추진축계에 부과되는 비틀림 응력을 계산하였는데, 이는 향후 선급 규정에 의거한 축계의 피로수명 평가에 사용될 수 있다.
2. 추진축계 과도 비틀림 진동 해석
2.1 계측 데이터 정규화
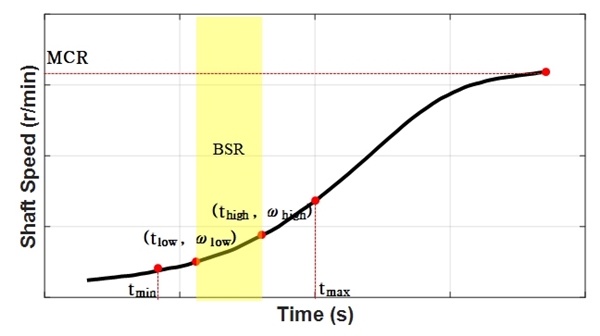
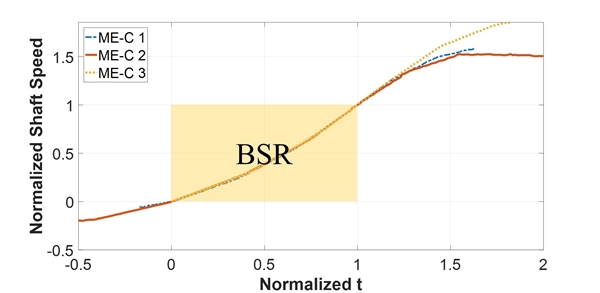
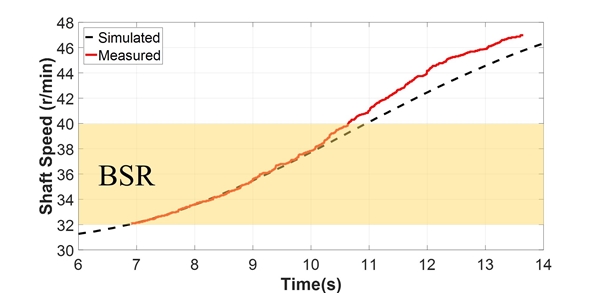
이 연구에서는 MAN 사의 G-type 엔진이 탑재된 선박에 대하여 해석을 수행하였다. 해석에 앞서 동종 엔진이 적용된 선박의 실제 계측 데이터를 정규화하여 연속사용 금지범위 통과 시 이들이 동일한 패턴으로 증속하는지 살펴볼 필요가 있다. 따라서 실제 계측 데이터를 정규화하여 그 패턴을 살펴보았다. Fig. 1은 선박이 정지속도부터 연속사용 금지범위를 통과하여 최대정격속도(maximum continuous rating, MCR)까지 도달하는 과정을 보여주고 있다. 정규화에 사용된 수식은 식 (1)과 식 (2)와 같다. 정규화한 계측 데이터를 Fig. 2에 나타내었고, 그림을 살펴보면 연속사용 금지범위인 [0 ~ 1] 구간에서 선박 세 척의 증속 패턴이 유사함을 확인할 수 있다. 따라서 이 연구에서는 증속 패턴의 유사함이 검증된 선박 세 척의 선박 중 한 척을 선택하여 해석 코드를 작성하고, 이를 나머지 두 척의 선박에 적용하여 정확도를 검증하였다.
| (1) |
| (2) |
여기서,
- tmeasure, ωmeasure = 실제 계측한 시간 및 축 각속도 데이터
2.2 비틀림 진동 해석 모델
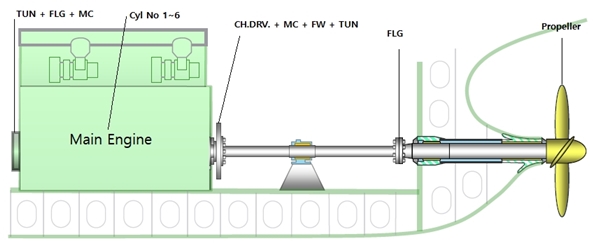
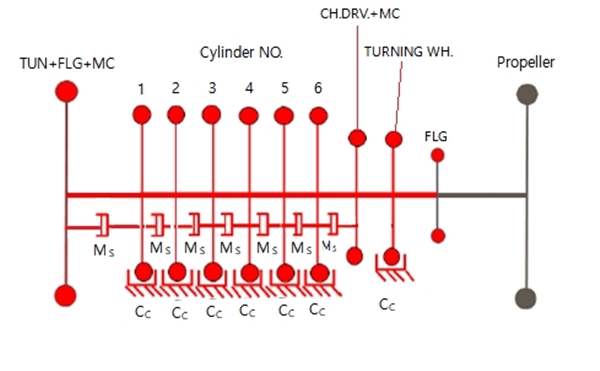
Fig. 3에 해석 대상 선박의 추진축계 개략도를 나타내었다. 좌측부터 주 기관(main engine)과 중간축, 프로펠러축, 그리고 프로펠러가 부착되어 있으며 그 외 터닝 휠, 플렌지 등이 부착되어 있다. 일반적으로 축계의 비틀림 진동을 해석할 때에는 유한요소 해석법과 집중질량 해석법 등을 사용하나, 선박의 추진축계에서 발생하는 비틀림 진동은 30 Hz미만의 저주파 영역이므로 집중질량 해석법을 통해서도 충분히 실제 상황을 시뮬레이션할 수 있다. 따라서 이 논문에서는 해석 대상 선박의 추진축계를 동역학적으로 등가인 집중질량으로 치환하여 해석 모델을 구성하였다. 이에 대한 상세 제원은 주 기관과 프로펠러에 대해 구분하여 각각 Table 1과 Table 2에 주어졌으며, 집중질량 모델은 Fig. 4에 나타내었다. 이에 대한 운동 방정식은 식 (3)과 같이 표현되며, 연속사용 금지범위 통과 시와 같은 비주기적인 하중을 받을 때에 대한 해석을 위해 상태 공간식으로 변환하여 시간 영역에서 해석을 수행하였다.
| (3) |
여기서,
- J = 관성 모멘트 행렬
- Ct = 비틀림 감쇠 행렬
- Kt = 비틀림 강성 행렬
- θ = 각 변위 벡터
- T = 기진력 벡터
식 (3)에 관성 행렬의 역행렬을 곱해주면 식 (4)와 같이 나타난다.
| (4) |
여기서,
- B = 기진력의 작용위치를 나타내는 벡터
- u = 기진력의 크기를 나타내는 벡터
각 변위 벡터의 1차 미분과 2차 미분을 상태 변수 X로 나타내면 식 (5)와 같다.
| (5) |
식 (4)를 상태변수 X로 표현하면 식 (6)과 같으며, 최종적으로 식 (7)의 상태-공간식으로 나타낼 수 있다.
| (6) |
| (7) |
여기서,
또한, 계가 임의의 순간(t초)부터 미소시간(Δt)이 지난 후의 상태를 나타내기 위하여 Taylor 급수 전개를 하면 식 (8)과 같이 단순하게 표현이 가능하다.
| (8) |
식 (7)을 식 (8)에 대입하면 식 (9)와 같은 이산 상태-공간식 (discrete state-space equation)을 유도할 수 있고, 계의 시간 응답을 구할 수 있다.
| (9) |
여기서, DA = 1 + A • dt, DB = B* • dt
2.3 프로펠러 감쇠
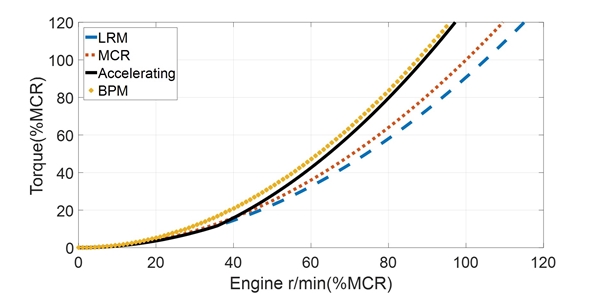
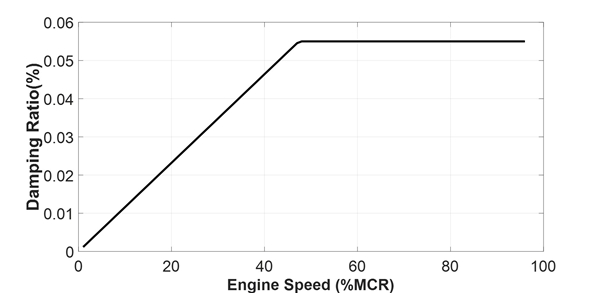
감쇠의 경우, 추진축계에 작용하는 기타 감쇠에 비해 프로펠러 감쇠가 상대적으로 매우 크기 때문에 이 논문에서는 질점에 직접 작용하는 마찰감쇠와 질점 사이에 작용하는 히스테리시스 감쇠를 무시하고 프로펠러 감쇠만을 적용하여 해석을 수행하였다. 평균 성분인 축 회전속도 계산 시 프로펠러 토크는 DNVGL 선급에서 제시한대로 Fig. 5의 검은색 실선과 같이 3 % ~ 5 %의 LRM(light running margin)과 15 % ~ 20 %의 BPM(bollard pull margin) 사이에서 정의하였으며(4), 변동 성분인 비틀림 변동 응력 계산시에 감쇠계수와 감쇠비는 Fig. 6과 같이 MAN사에서 권장한 방법대로 MCR의 50 % 미만에서는 감쇠비가 0 %부터 5.5 %까지 선형 증가하고 그 이후부터는 감쇠비가 5.5 %로 고정되는 방법을 적용하였다(5).
2.4 엔진 평균 기진력
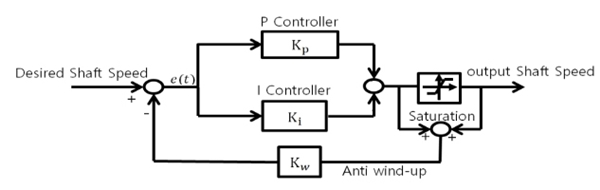
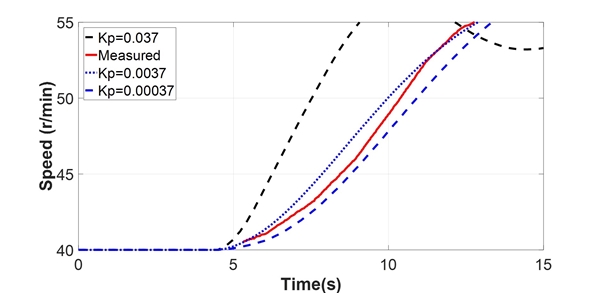
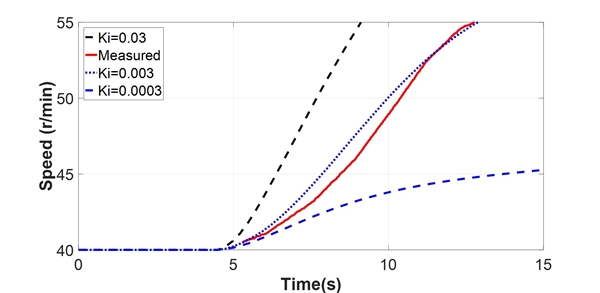
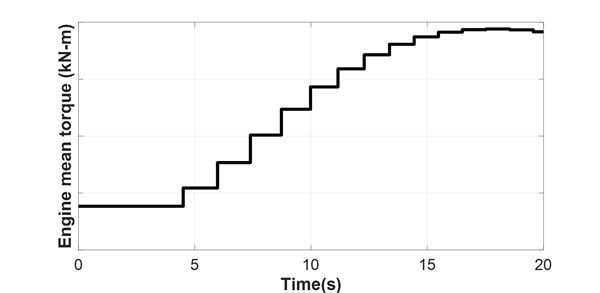
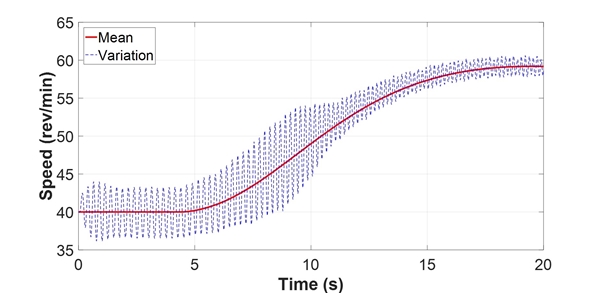
이 논문에서 해석 대상 선박은 전자제어 엔진인 G-type ME-C 엔진을 적용한 선박이다. 일반적으로 선박 엔진의 경우 항해 중 수시로 변화하는 외부 환경 요인에 대해 엔진의 기진력을 제어한다. 따라서 이 논문에서는 선박의 연속사용 금지범위 통과 시 엔진의 기진력을 추정하기 위하여 PI(proportional integral)제어기를 설계하여 해석을 수행하였다. 이 때 Fig. 4와 같이 다자유도계의 추진축계에서 엔진 기진력을 추정하기에는 가관측성(observability) 측면에서 비효율적이므로, 추진축계를 1자유도계의 단일 질량계로 치환하여 해석을 수행하였다. 해당하는 단일질량 모델은 Fig. 7에 나타나 있으며, 엔진 평균 기진력의 패턴은 엔진 제작사에서 제시한 문헌과 같이 계단 모양으로 적용하였다(6). 또한, 제어기 내에서 적분(I) 제어기의 포화를 방지하기 위하여 anti-windup을 추가하였으며, 이에 대한 블록 다이어그램을 Fig. 8에 나타내었다. 게인 변수 2개(P, I)에 대하여 1/1000단위로 전수 조사(exhaustive search)를 통하여 계측치와 유사한 결과가 나오는 값을 취하였다. 비례제어 게인은 0.0037, 적분제어 게인으로는 0.0030을 취하였다. 게인 변수에 대한 변화 양상을 Fig. 8과 Fig. 9에 나타내었다. 최적의 게인 변수를 적용하였을 때의 결과와 이 때의 엔진 기진력 평균값을 각각 Fig. 11과 Fig. 12에 나타내었다.
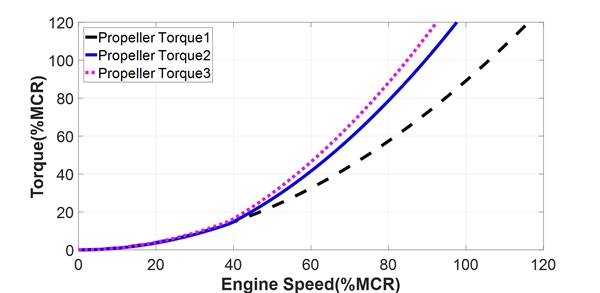
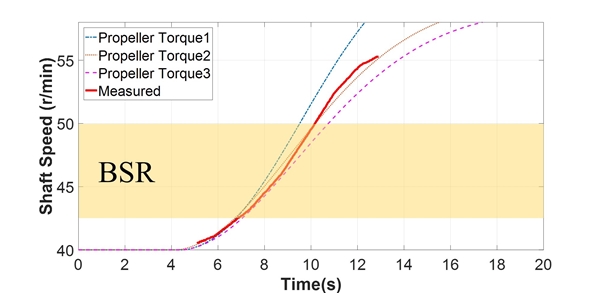
실제 선박의 시운전 시에는 해상 상황에 따라 DNVGL에서 정의한 프로펠러 토크와 다른 토크가 작용할 수 있다. 이를 관찰하기 위하여 LRM과 BPM을 조절하여 여러 가지 프로펠러 토크를 임의로 정의하여 그 때의 선박 증속 경향을 관찰해 보았다. Light running이란, 선박이 운항할 때 깨끗한 선체와 잔잔하고 깊은 바다에서 운항할 때의 상태를 말하며 sea trial condition이라고도 한다. 따라서 LRM 값이 클수록 프로펠러 토크의 크기는 작아진다. BPM은 LRM과 반대의 의미로서 이 값이 커질수록 프로펠러 토크의 값도 커진다. Propeller torque 1은 해석 코드 내에서 프로펠러 토크를 정의할 때 증속 전까지 LRM 7 %의 커브를 따르며 증속 시점부터 BPM 0 %, 즉 공칭 프로펠러 토크를 따라가도록 했을 때의 프로펠러 토크를 의미한다. 이는 증속 시점 전까지 파도가 없고 충분히 깊은 바다를 운항할 때의 프로펠러 토크에 대응된다고 알려져 있다. Propeller torque 2는 같은 방법으로 LRM 5 %, BPM 18.5 %를 적용한 결과이며, 이는 DNVGL에서 정의한 일반적인 증속 조건에서의 토크를 나타낸다. Propeller torque 3은 LRM 0 %, BPM 20 %를 적용한 결과로서 황천(荒天)조건일 때의 프로펠러 토크이다(7). 이 세 가지의 프로펠러 토크는 Fig. 7의 우측과 같이 1자유도계로 치환된 축계에 엔진 기진력과 반대 방향으로 작용한다. 계산 시 식 (3)의 우변 항에 적용된다. LRM, BPM에 따라 변화하는 프로펠러 토크를 Fig. 13에 나타내었으며, 이 때의 선박의 증속 패턴을 Fig. 14에 나타내었다. LRM이 크고 BPM이 작을수록 연속사용 금지범위의 통과시간이 짧아지는 것을 확인할 수 있다. LRM과 BPM을 적절히 조절하면 다양한 조건의 선박 운항 환경에 따른 프로펠러 저항을 모사할 수 있으며, 환경조건에 따른 연속사용 금지범위 통과시간을 추정할 수 있다.
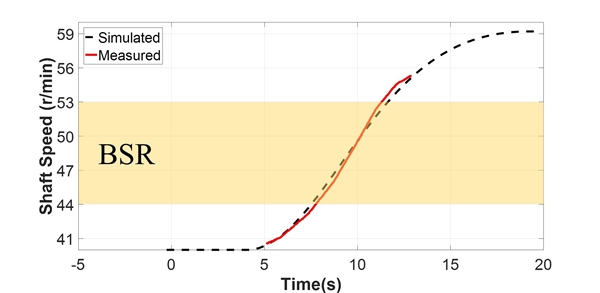
해석 대상 호선을 기준으로 작성된 해석 코드를 나머지 두 척의 호선에 적용하여 얻은 시뮬레이션 결과를 실제 계측 데이터와 비교하여 Fig. 15와 Fig. 16에 나타내었다. 연속사용 금지범위 통과시간 측면에서 다소 차이가 있으나, 전체적으로 유사한 증속 패턴을 보이고 있는 것을 확인하였다.
2.5 엔진 변동 기진력
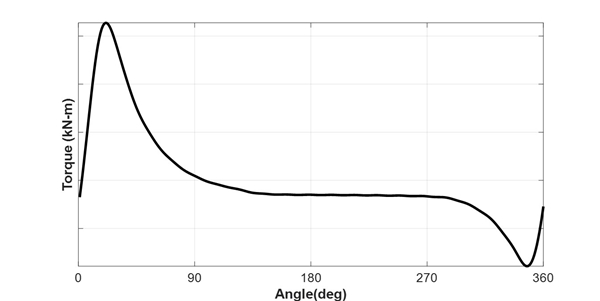
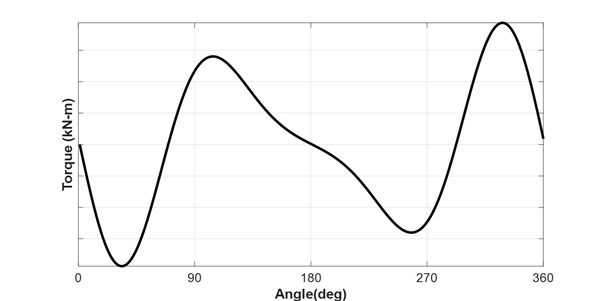
주 기관의 변동 기진력으로는 실린더 내부 폭발에 기인한 기진력과 관성에 의한 기진력을 고려한다. 두 기진력은 각각 식 (10)과 식 (11)에 나타내었으며 MCR에서 폭발 기진력과 관성 기진력을 각각 Fig. 17과 Fig. 18에 나타내었다.
| (10) |
| (11) |
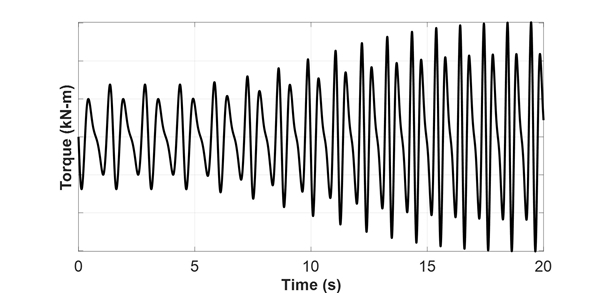
엔진 제작사에서는 엔진의 회전 속도에 따라 실린더 내의 평균유효압력(mean effective pressure)을 정의하였으며, 또 이에 대한 토크 하모닉스를 제공하였다. 이 논문에서는 엔진 제작사에서 제시한 토크 하모닉스를 토크로 변환하여 2.4절에서 시뮬레이션을 통해 얻은 엔진 회전수에 대하여 적용하였다. 또한 엔진의 기진력은 크랭크 1회전 당 1회 작용하므로 해석 코드 내에서 이를 적용하였고 결과를 Fig. 19와 Fig. 20에 각각 나타내었다.
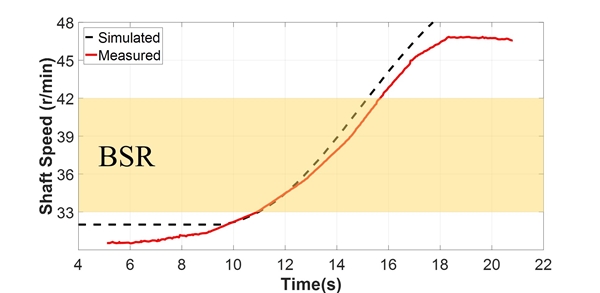
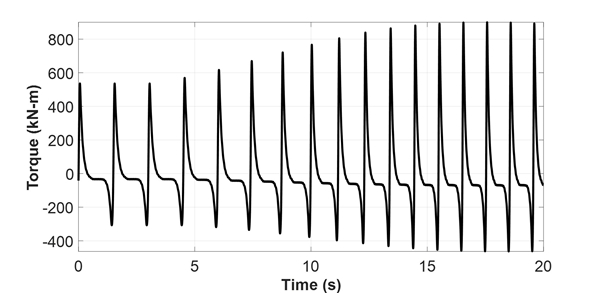
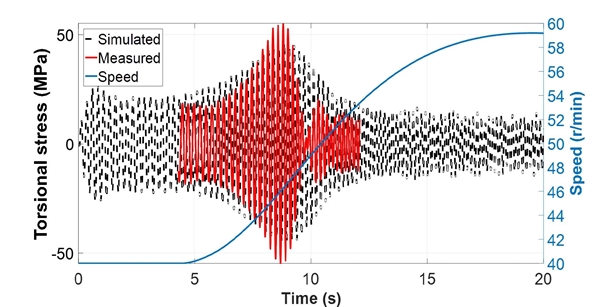
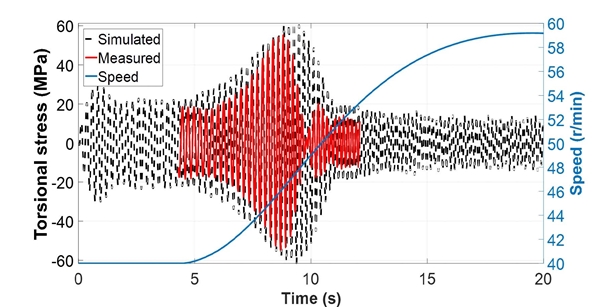
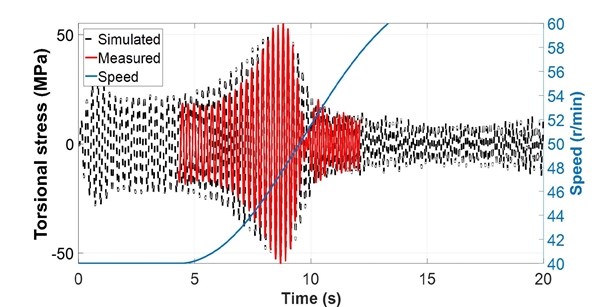
엔진의 변동 기진력 성분을 적용하여 과도 비틀림진동 해석을 수행한 결과를 Fig. 21에 나타내었고, 이를 이용하여 비틀림 변동 응력의 측면에서 관찰한 결과를 Fig. 22에 나타내었다. 실제 계측 결과보다 시뮬레이션 결과가 공진 영역에서 다소 낮은 비틀림 변동 응력을 나타내는 것을 확인하였다. 프로펠러의 감쇠에 대한 문헌에서 기존에 적용하는 감쇠비의 70 % ~ 80 %를 적용하는 것이 실제와 가장 유사한 결과를 나타낸다는 보고가 있으므로(8), 이를 적용하여 Fig. 23과 Fig. 24에 나타내었다. 결과를 살펴보면 해석 대상 호선에서는 기존 감쇠비(5.5 %)의 80 %인 4.4 %의 감쇠비를 적용했을 때 실제에 가까운 시뮬레이션 결과를 확인할 수 있었다.
비틀림 변동 응력에 미치는 엔진 기진력의 영향을 확인하기 위하여 Fig. 23과 같이 감쇠비를 4.4 %로 두고 프로펠러 토크에 따른 변화 양상을 살펴보았다. Fig. 25의 경우 propeller torque 1과 감쇠비 4.4 %를 적용했을 때의 결과이며, Fig. 26의 경우 감쇠비 4.4 %와 propeller torque 3을 적용했을 때의 결과이다.
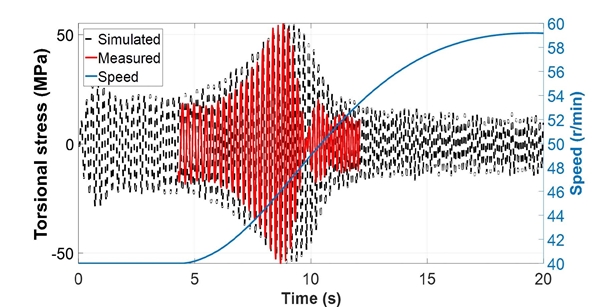
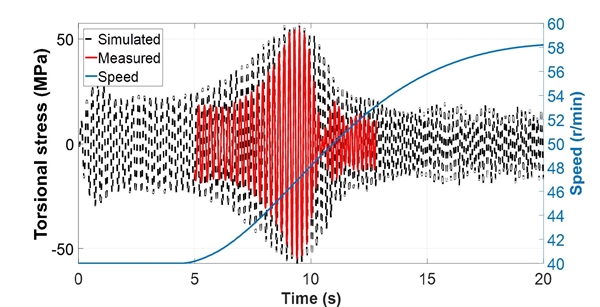
결과를 살펴보면 Fig. 25와 같이 기존 감쇠비의 80 %(damping ratio 4.4 %)를 적용하고, 부하가 가장 적을 때의 프로펠러 토크를 적용하였을 때가 실제 계측 결과와 유사한 것을 확인할 수 있다. 같은 조건으로 동종 엔진이 적용된 두 척의 선박에 대한 해석을 수행하고 그 결과를 Fig. 27과 Fig. 28에 나타내었다. 그 결과, 전반적인 경향은 일치하였으나 비틀림 변동 응력의 크기에서 다소 차이가 나는 것을 확인할 수 있다. 특히 공진점 전과 후보다 공진점 부근에서의 차이가 상대적으로 크게 나타났으며, 이는 감쇠의 영향이 지배적인 것으로 판단된다. 선박의 운항 중에 추진축계에 작용하는 감쇠는 선박의 크기와 모양, 비틀림 댐퍼의 유무, 시운전 시 해상상태 등에 따라 변화하는 부분이며 이에 대한 정확한 예측은 어렵다. 따라서 추후 다수의 실제 계측 결과를 확보하여 선박의 운항 시 운항 조건에 따른 감쇠비 적용에 대한 방법을 정립할 필요가 있다.
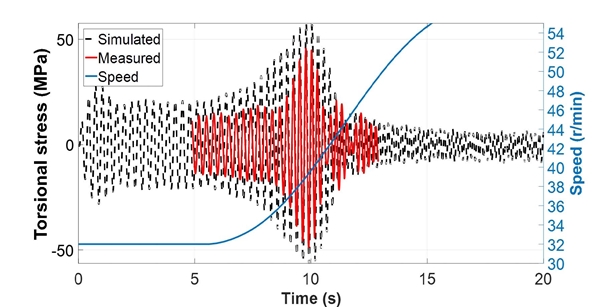
Simulation result of torsional stress (ship no. 2, propeller damping ratio 4.4 %, propeller torque 1)
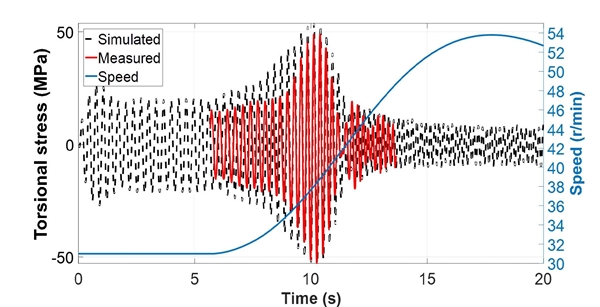
Simulation result of torsional stress (ship no. 3, propeller damping ratio 4.4 %, propeller torque 1)
해석 결과의 정확도를 알아보기 위하여 연속사용 금지범위를 통과할 때에 소요되는 시간과 비틀림 응력의 최대치를 비교하여 Table 3에 나타내었다. 각 수치는 선박1을 기준으로 튜닝된 해석코드를 사용하여 얻은 결과이다. 해석 결과 전반적인 경향은 일치하나, 선박에 따라 실제 계측결과와 다소 차이가 나는 것을 확인하였다. 이는 시운전 시의 환경조건을 각기 다르기 때문으로 추정되며, 보다 많은 계측자료가 축적된다면 개선이 가능할 것으로 생각된다.
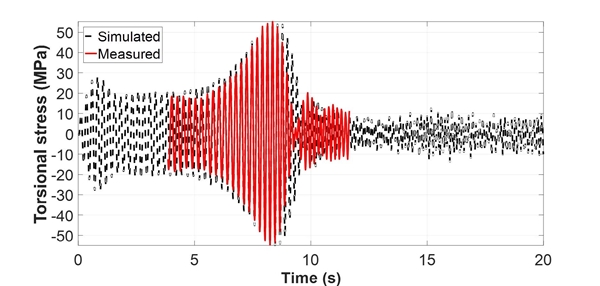
이 연구의 결과에서 해석 대상 선박의 경우 감쇠비 4.4 %, propeller torque 1을 적용했을 때가 가장 실제 계측 결과와 유사하였다. 여기서 시뮬레이션 결과와 실제 계측 결과 사이의 오차를 줄이기 위하여 임의로 감쇠비와 프로펠러 토크를 조절하여 결과를 관찰해 보았다. 그 결과를 Fig. 29에 나타내었으며, 이를 살펴보면 감쇠비 3.4 %에 LRM 40 %, BPM 5 %를 적용했을 때 실제와 거의 같은 시뮬레이션 결과를 도출할 수 있었다. 따라서 추후에 감쇠비와 프로펠러 토크를 선형에 따라 혹은 선박의 크기에 따라 설정하는 방법을 정립한다면 보다 정확한 시뮬레이션 결과를 얻을 수 있을 것으로 판단된다.
3. 결 론
이 연구에서는 MAN사의 G-type ME-C 엔진이 탑재된 선박의 연속사용 금지범위 통과 시 과도 비틀림 진동 해석을 수행하였다. 수치해석 모델로 11자유도 ~ 12자유도의 집중 질량 모델을 사용하였고 해석은 시간영역에서 이루어졌으며, 이 연구를 통해 얻은 결론은 아래와 같다.
- (1) G-type 엔진이 적용된 선박의 실제 시운전 시 얻은 계측 데이터를 바탕으로 동종 엔진이 적용된 선박은 연속사용 금지범위에서 동일한 증속 패턴을 가지는 것을 확인하였다.
- (2) 연속사용 금지범위를 통과하는 증속 과정을 예측하기 위하여 축의 회전속도를 제어하는 PI 제어기를 적용하였다. 제어기의 게인은 실측 데이터를 기준으로 튜닝하였다. 동일한 제어기를 사용하여 동종 엔진이 적용된 선박들의 증속 과정을 시뮬레이션한 결과 전반적인 경향이 실측치와 유사한 것을 확인하였다. 제어의 결과로 얻어진 엔진 평균 기진력을 이용하여 추진축계에 작용하는 기진력의 변동성분도 추정할 수 있었다.
- (3) 추정된 기진력 변동성분을 이용하여 다자유도 모델의 시간영역 과도해석을 수행하여 추진축계의 비틀림 변동 응력을 계산하였다. 연속사용 금지범위 통과시 비틀림 변동 응력의 변화와 최대 진폭은 프로펠러의 감쇠비와 프로펠러 토크에 큰 영향을 받는 것을 확인하였다. 감쇠비와 프로펠러 토크를 조정하여 실측치와 매우 유사한 해석 결과를 얻을 수 있었다.
Acknowledgments
A part of this paper was presented at the KSNVE 2018 Annual Autumn Conference.
이 연구는 울산대학교 중공업융합기술공학과 PBL(project based learning) 과제로서 ㈜현대중공업의 지원을 받아 수행하였습니다.
References
-
Brown, R. N., (1960), A Torsional Vibration Problem as Associated With Synchronous Motor Driven Machines, J. Eng. Power, 82(3), p215-219.
[https://doi.org/10.1115/1.3672768]

- Lee, D. C., Yu, J. D., and Jeon, H. J., (2002), Theoretical Analysis about Transient Torsional Vibration of Two Stroke Low Speed Diesel Engines, Proceedings of KSNVE Annual Spring Conference, p830-835.
-
Barro, R. D., Vuong, Q.-D., and Lee, D. C., (2018), Marine Intermediate Shaft Fatigue Strength and Lifetime during Barred Speed Range Passing, Transactions of the Korean Society for Noise and Vibration Engineering, 28(3), p259-263.
[https://doi.org/10.5050/ksnve.2018.28.3.259]

- Brodin, E., (2018), Class Rules – Passing Barred Speed Range, DNV GL.
-
Persson, S., (2015), Ice Impact Simulation for Propulsion Machinery, MTZ Industrial, 5(1), p34-40.
[https://doi.org/10.1007/s40353-015-0500-2]

- MAN Diesel & Turbo, (2013), Basic Principle of Ship Propulsion.
- MAN Diesel & Turbo, (2015), Market Update Note: Light Running Margin (LRM).
- Kim, Y. K., Hwang, S. J., and Kim, E. K., (2017), Damping Characteristics of High Efficiency Direct-coupled Propeller with 10MW Class, 2017, Journal of the Korean Society of Marine Engineering, 41(4), p310-315.

Hyoseong Lee finished his Bachelor Degree and Master Degree from University of Ulsan in 2017 and 2019 respectively. Presently, he is a researcher at the noise and vibration lab. of Hyundai-Heavy Industry.

Dojoong Kim received B.S. degree in Mechanical Engineering from Seoul National University in 1981, and MS degree from KAIST in 1983. He completed his Ph.D. degree in Mechanical Engineering from North Carolina State University in 1990. He is currently a Professor at the Department of Mechanical Engineering of University of Ulsan. His research interest is development of variable valve actuation system in internal combustion engines.

Okhyun Kang completed his Doctoral Degree in 2010 from KAIST Mechanical and Aerospace Engineering. He is currently a senior researcher at Hyundai Heavy Industry.