구멍 뚫린 강체 판의 차음 성능 향상을 위한 음향 메타물질 설계
© The Korean Society for Noise and Vibration Engineering
Abstract
In this work, we propose a new acoustic metamaterial panel to transmit fluid and attenuate noise in the frequency range of 300 Hz to 600 Hz. The acoustic metamaterial panel is filled with rectangular parallelepiped unit cells and each unit cell consists of a circular duct surrounded with arrayed annular cavities. While the fluid is passed through the duct, the noise in the frequency range of 300 Hz to 600 Hz is attenuated owing to the annular cavities. In each annular cavity, internal partitions are inserted and their locus is determined using the Archimedean spiral. The dispersion curve of the proposed acoustic metamaterial panel is calculated to understand its band gap. In addition, the effects of dimensions of the unit cell on the band gap are investigated and its final dimension for a given target frequency range is determined. The acoustic attenuation performance of the proposed acoustic metamaterial panel is experimentally validated.
Keywords:
Acoustic Metamaterial, Perforated Panel, Transmission Loss, Dispersion Curve, Transmission Coefficient키워드:
음향 메타물질, 다공성 패널, 투과 손실, 분산 곡선, 투과 계수1. 서 론
소음이 전달되는 경로에 방음 패널을 설치하여 패널에 도달한 음향 에너지를 흡수하거나 반사시켜서 패널의 반대쪽으로 투과되는 소음의 크기를 줄이는 소음 제어 방법이 널리 사용되고 있다. 현재 사용되고 있는 반사형 방음 패널의 차음 성능은 일반적으로 질량 법칙(mass law)(1)을 따르며, 차음 성능 향상을 위해 패널 양쪽의 유체 이동은 허락하지 않은 구조를 채택하고 있다. 그러나 기계 시스템의 외형을 구성하는 패널은 내부에서 발생하는 소음이 외부로 전달되는 것을 막으면서 내부에서 발생하는 열이 외부로 원활히 빠져나가게 설계되어야 한다. 즉, 구멍을 통해 유체는 통과시키면서 저주파 대역의 소음은 차단하는 새로운 형태의 패널이 필요하다.
최근 음향 메타물질 개념을 사용한 방음 패널 설계에 관한 연구가 활발히 진행되고 있다. 메타물질은 자연계에 존재하지 않는 특성을 갖도록 인공적으로 설계된 물질 또는 구조를 일컫는다(2~5). 메타 물질을 지나가는 파동의 주파수에 따라 변화하는 동적 물성치(6)는 해당 물질의 내부 구조에 의해 결정된다. 유효 매질 이론(effective medium theory)(7)에 의하면, 파동이 파장보다 작은 크기의 구조를 지나갈 때 해당 매질을 균질화된 매질(homogeneous medium)로 간주하고 동적 유효 물성치(dynamic effective property)로 그 매질의 파동 전파 특성을 설명할 수 있다고 한다. 음향 메타 물질에서는 주로 유효 질량 밀도(effective mass density)와 유효 체적 탄성 계수(effective bulk modulus)를 동적 유효 물성치로 사용한다(8~11). 국부 공진(local resonance)을 이용하여 목표 주파수 대역에서 유효 질량 밀도 또는 유효 체적 탄성 계수가 음의 값을 갖도록 설계하여 음파를 차단하는 음향 메타물질은 판(plate)(12,13), 막(membrane)(14~19) 또는 공명기(resonator)(20~27) 등을 주기적으로 배열한 구조를 갖는다. Oudich 등은(12) 판 구조에 스프링-질량 공명기(spring-mass resonator)를 부착한 메타물질을 설계하고, 평면파 전개 방법(plane wave expansion method)과 분산 곡선(dispersion curve)을 이용하여 소음 차단 주파수 대역을 계산하였다. Yang 등은(14) 막에 부착된 질량을 조절하여, 50 Hz ~ 1000 Hz의 주파수 대역에서 유효 질량 밀도가 음이 되게 하여 소음을 차단하는 구조를 제시하였다. 이외에도 분할 구형(split hollow sphere) 공명기(23,24), 깔때기 모양의 공명기(funnel-shaped resonator)(26), 환형 공동(annular cavity) 구조(27)를 갖는 메타물질 등이 연구되었다. Hao 등은(24) 분할 구형 공명기를 배열하여 유효 체적 탄성 계수가 목표 주파수 대역에서 음이 되도록 설계하였다. Cho 등과(26) Jung 등은(27) 유체 투과와 소음 차단이 동시에 가능한 방음 패널을 설계했다.
앞서 소개된 연구 결과는 음향 메타물질 패널로서 아주 우수한 소음 차단 결과를 보여주었지만, 저주파 대역에서 넓은 주파수 대역의 소음을 차단하기 위해서는 장착될 위치와 공간 등과 같은 추가 설계 조건에 맞게 적절히 개선되어야 한다. Oudich(12)와 Yang(14)이 제시한 음향 메타물질 패널은 저주파 대역의 소음을 효과적으로 차단하였으나 유체는 투과할 수 없는 구조이고, Hao(24)와 Cho(26)의 음향 메타물질 패널은 유체 투과와 소음 차단을 동시에 고려하였지만, 소음 차단 주파수 대역이 협소한 문제점이 있었다. 유체 투과를 고려하여 음향 메타물질을 설계한 Jung(27)의 구조는 비교적 넓은 주파수 대역의 소음을 차단하였으나 저주파 대역의 소음 차단을 위해서는 단위체의 크기가 지나치게 커지는 단점을 가지고 있다. 이 연구에서는 Jung(27)이 제시한 구조를 개선하여 유체는 투과시키고 저주파 대역에서 비교적 넓은 대역의 소음을 차단하는 음향 메타물질 패널 구조를 제시하고, 목표 주파수 대역에서 소음을 차단하는 패널을 설계할 것이다. 설계된 음향 메타물질 패널의 차음 성능은 등가 질량 패널의 차음 성능과 비교한다. 또한, 최종 설계된 음향 메타물질 패널을 제작하여 실험을 통해 소음 차단 성능을 검증한다.
2. 해석 모델과 음향 메타물질
2.1 해석 모델
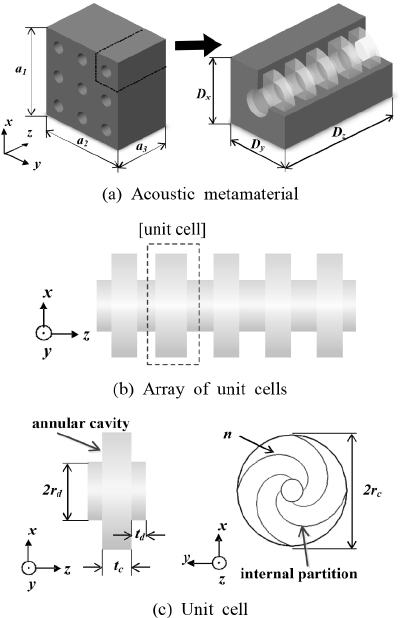
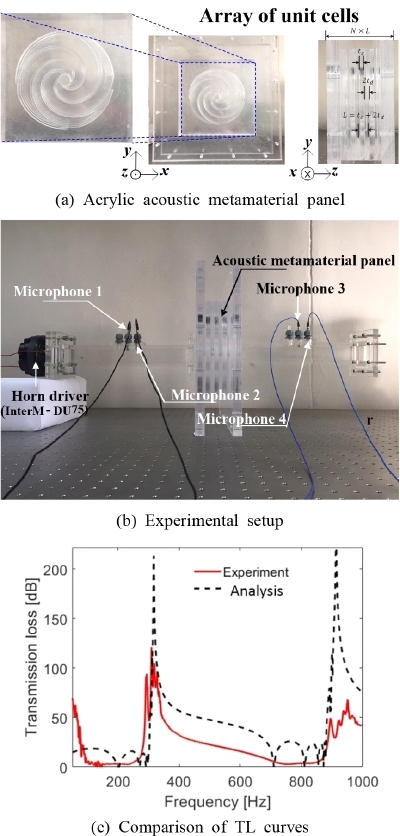
이 연구에서 제시할 음향 메타물질 패널은 Fig. 1(a)과 같이 x-y 평면상에 규칙적으로 구멍이 뚫려 있는 구조이고, 그 구멍은 원형 덕트와 그 덕트를 둘러싼 여러 개의 환형 공동(annular cavity)이 연결된 구조이다. Fig. 1(b)와 같이, 여러 개의 단위체를 z축을 따라 배열한 구조를 단위체 배열(array of unit cells: Dx×Dy×Dz)이라고 한다. 단위체 배열이 x-y 평면상에 M×M 형태로 배열되어 음향 메타물질 패널(acoustic metamaterial panel: a1×a2×a3)이 구성된다. Fig. 1(c)는 음향 메타물질의 단위체 구조를 보여주고 있는데, 환형 공동과 덕트 중심으로 연결된 입/출구로 구성되어 있고, 환형 공동 내부에는 곡률이 있는 내부 격벽 4개가 삽입되어 있다. 단위체를 구성하는 환형 공동의 직경(2rc)과 두께(tc), 입/출구단의 직경(2rd)과 두께(td), 내부 격벽의 기하학적 형상을 결정하는 회전율(n)이 설계 목적에 맞게 결정다. 환형 공동간 거리는 2td로 나타낼 수 있고, 내부 격벽의 곡률은 식 (1)의 아르키메데스 나선(archimedean spiral)식을 이용하여 결정하였다. 각 나선의 시작점들 사이의 각도 차이는 π/2이고, 시작점으로부터 회전 각도(θ)에 따른 각 나선의 (x, y)의 좌표는 각각 식 (1a)와 식 (1b)를 사용하여 결정한다.
| (1a) |
| (1b) |
| (1c) |
2.2 음향 메타물질의 음향 특성
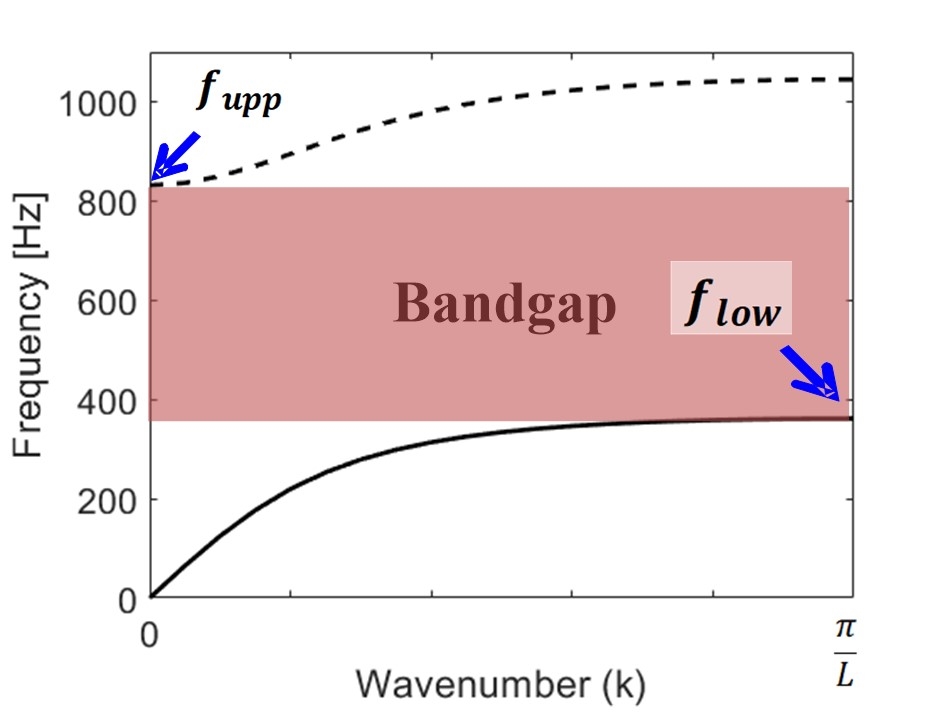
음향 메타물질의 음향 특성은 단위체에 대해 음향 해석을 수행하여 얻는 분산 곡선(dispersion curve)을 통해 알 수 있다. 분산 곡선은 파동의 주파수(frequency)와 파수(wavenumber, k)의 관계를 나타내는 곡선으로, 음향 모드가 존재하는 주파수 대역을 나타낸다. 음향 모드가 존재하지 않는 주파수 대역을 밴드갭(band gap)이라 하고, 밴드갭에서는 입사되는 음파의 진폭이 기하급수적으로 감소되어 음파가 차단된다.
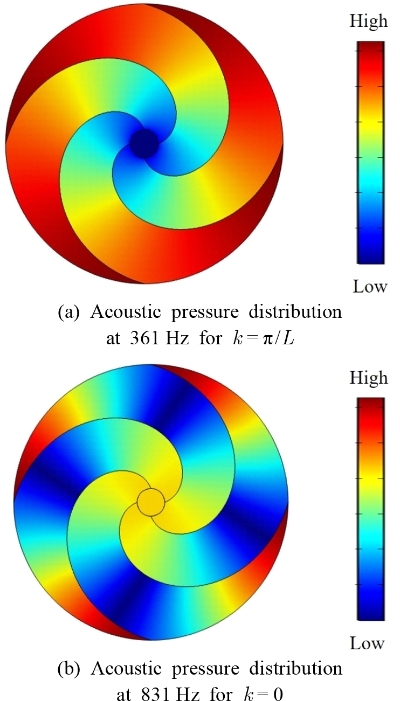
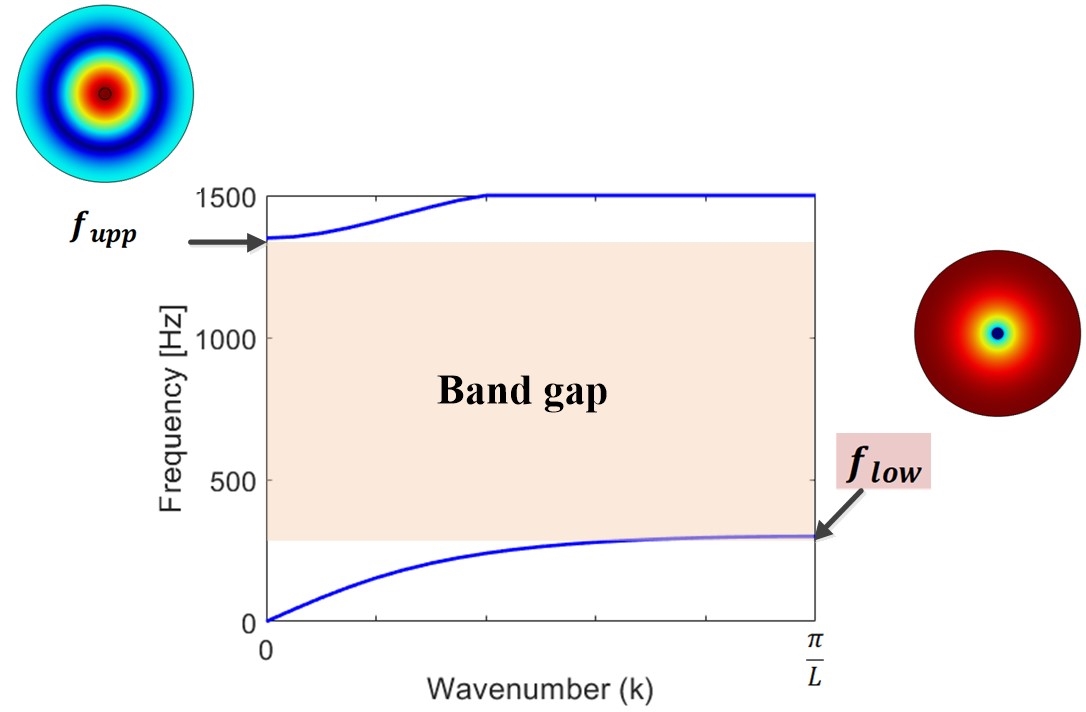
Fig. 2는 기준 단위체(reference unit cell: rc = 100 mm, rd = 10 mm, tc = 10 mm, td = 5 mm, n = 0.5)에 대해 상용 유한요소 프로그램인 COMSOL Multiphysics (Ver. 5.3)를 사용하여 얻은 분산 곡선을 나타낸다. 단위체의 입/출구단에 플로케 주기 조건(floquet periodic condition)을 부여하여 z축 방향으로 단위체가 무한히 배열된 구조로 가정하였다. “k = 0”을 기준으로 좌우가 대칭인 그래프이기에 k가 양인 구간만 나타낸다. 실선으로 표시된 첫 번째 음향 모드는 파수(k)가 π/L값을 가질 때, Fig. 3(a)와 같은 음압 분포를 갖는다. 점선으로 표시된 음향 모드는 파수(k)가 ‘0’일 때, Fig. 3(b)와 같은 음압 분포를 갖는다. 두 그림 모두 음압의 절대값을 나타내었다. 두 주파수 사이에도 음향 모드가 존재하지만, 수직 입사만 고려하면 덕트 중심부의 음향 가진에 의해 서로 상쇄되는 음압 분포를 가지기 때문에 분산 곡선에서 제외하였다. 즉, 위에서 언급한 두 음향 모드에 의해 이 음향 메타물질의 첫 번째 밴드갭이 형성되고, 이 밴드갭의 주파수 대역(flow ≤ f ≤ fupp)의 상한값과 하한값을 각각 fupp와 flow라고 표기한다
Fig. 3(a)의 첫 번째 음향 모드는 방사형 모드(radial mode)로 단극 공진(monopolar resonance)이라고 하는데, Li 등은(2) 단극 공진이 체적 탄성률 형태 응답(bulk modulus-type response)을 발생하여 음의 유효 체적 탄성계수를 갖는다고 설명하였다. 각 환형 공동들이 단극 공진할 때, 인접한 두 환형 공동안의 입자들은 서로 반대 위상(opposite phase)으로 진동하여 입사파가 점차 상쇄되어 사라진다(27). Fig. 3(b)는 두 번째 방사형 음향 모드로 나선형 격벽에 의해 분리된 각 공동의 중심에서 원주방향으로 음압 분포가 형성되었다.
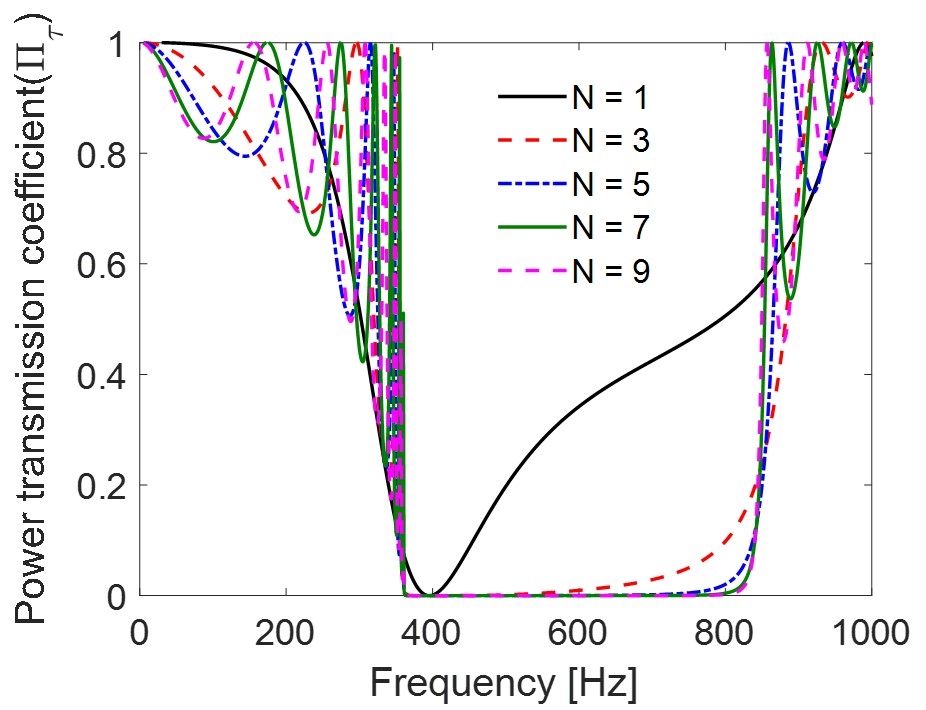
Fig. 4는 단위체 개수를 변화시키며 음향 메타물질의 파워 투과 계수를 나타낸다. 단위체 개수(N)가 많아질수록 음향 메타물질 패널의 소음 차단 구간이 밴드갭과 유사하지만, 패널이 지나치게 두꺼워질 수 있기 때문에, 이 연구에서는 단위체를 5개만 사용한다.
3. 음향 메타물질 패널 설계
3.1 설계 문제 정의
식 (2)와 같이 음향 메타물질 패널로 차단하고자 하는 목표 주파수 대역(target frequency range: ftupp ≤ f ≤ ftlow)이 밴드갭(ftlow ≤ f ≤ ftupp)에 포함되도록, 단위체의 구성 요소(rc, tc, rd, td, n)의 값을 결정하고자 한다. 그리고, 이런 구성 요소의 값은 식 (3)의 제한 조건을 만족해야 한다.
| (2a) |
| (2b) |
| (3a) |
| (3b) |
| (3c) |
3.2 설계 전략
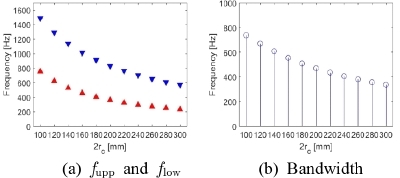
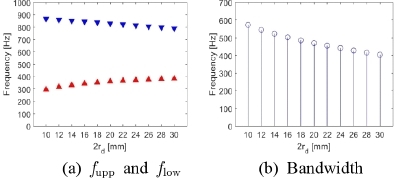
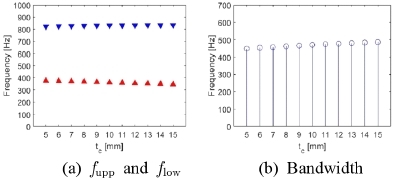
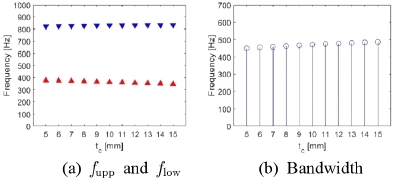
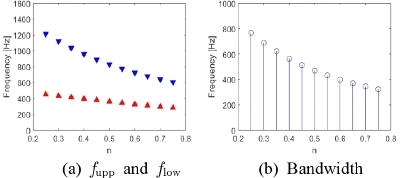
본격적인 설계에 앞서, 파라미터 스터디(parameter study)를 통해 각 구성 요소 변화(기준 값 ±50 %)에 따른 밴드갭의 변화를 살펴보고, 밴드갭 변화에 크게 영향을 미치는 구성 요소를 설계 변수로 결정한다. 밴드갭의 상/하한값(fupp / flow)과 대역폭(bandwidth: ∆f = fupp - flow)의 변화로 밴드갭의 변화 정도를 살펴본다. Case I에서는 환형 공동의 직경(2rc)을 100 mm에서 300 mm까지 20 mm 단위로 변경할 때 발생하는 밴드갭의 변화를 살펴보았고, 그 결과를 Fig. 5에 나타냈다. Case II에서는 원형 덕트의 직경(2rd)을 10 mm에서 30 mm까지 2 mm 단위로 변경할 때 발생하는 밴드갭의 변화를 살펴보았고, 그 결과를 Fig. 6에 나타냈다. Case III에서는 환형 공동의 두께(tc)를 5 mm에서 15 mm까지 1 mm 단위로 변경할 때 발생하는 밴드갭의 변화를 살펴보았고, 그 결과를 Fig. 7에 나타냈다. Case IV에서는 환형 공동간 거리(2td)를 5 mm에서 15 mm까지 1 mm 단위로 변경할 때 발생하는 밴드갭의 변화를 살펴보았고, 그 결과를 Fig. 8에 나타냈다. Case V에서는 내부 격벽의 회전율(n)을 0.25에서 0.75까지 0.05 간격으로 변경할 때 발생하는 밴드갭의 변화를 살펴보았고, 그 결과를 Fig. 9에 나타냈다.
환형 공동의 직경이 증가하면 상한/하한 주파수가 모두 감소하고 밴드갭의 대역폭 역시 감소한다. 이것은 환형 공동의 직경의 변화가 밴드갭을 결정하는 두 음향 모드 주파수에 변화를 가져오기 때문이다. 원형 덕트의 직경이 증가하면, 상한 주파수는 감소하지만, 하한 주파수는 증가한다. 환형 공동의 두께와 환형 공동간 거리가 증가하면 상한 주파수는 증가하고 하한 주파수는 감소하여 밴드갭의 폭은 증가한다. 내부 격벽의 회전율이 증가하면 상한/하한 주파수가 함께 감소하는데, 상한 주파수가 하한 주파수보다 크게 감소하여 밴드갭의 폭도 감소한다. 구성 요소의 변화가 밴드갭에 미치는 영향을 정량적으로 나타내기 위해 밴드갭 폭의 상대적 변화량(∆RBW = |∆f(+50%) - ∆f(-50%)| / ∆fref × 100)을 비교해 보았다. 이 계산식에서, ∆fref는 기준 단위체를 사용한 경우의 밴드갭의 폭이고, ∆f(+50%)는 각 구성 요소의 값을 기준 단위체의 50 % 증가된 값을 사용했을 때의 밴드갭의 폭이며, ∆f(-50%)는 각 구성 요소의 값을 기준 단위체의 50 % 감소된 값을 사용했을 때의 밴드갭의 폭이다. 계산 결과, 구성 요소 중 환형 공동의 직경(2rc)과 내부 격벽의 회전율(n)이 상대적 밴드갭 폭 변화량에 가장 크게 영향을 미쳤다. (∆RBW = 85.32 % for 2rc, 35.96 % for 2rd, 8.085 % for tc, 2.340 % for 2td, 94.47 % for n). 따라서, 설계 변수를 환형 공동의 직경(2rc)과 회전율(n)로 결정하였다.
3.3 단위체 설계
목표 주파수 대역은 300 Hz ~ 600 Hz, 음향 메타물질 패널의 두께(a3)는 100 mm, 패널 단면의 가로(a1)와 세로(a2)의 길이는 모두 300 mm, 배열되는 단위체의 개수(N)는 5로 설정한다. 5개의 구성 요소 중 환형 공동의 두께(tc), 원형 덕트의 직경(2rd)과 두께(td)는 기준 단위체의 값을 사용한다: tc = 10 mm, rd = 10 mm, td = 5 mm. 이 경우, 단위체의 두께(L)는 20 mm가 된다. 따라서, 식 (2)와 식 (3)을 만족하도록 환형 공동의 직경(2rc), 내부 격벽의 회전율(n)과 패널 단면에 존재하게 될 구멍의 개수(M)를 결정하면 된다.
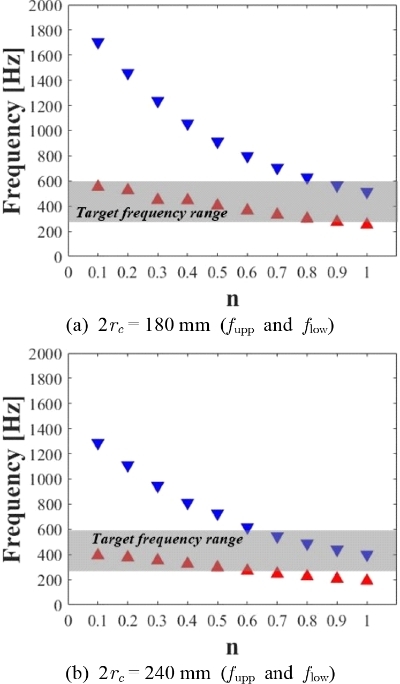
먼저, 환형 공동의 직경(2rc)이 가질 수 있는 값을 5개(160 mm, 180 mm, 200 mm, 220 mm, 240 mm), 내부 격벽의 회전율(n)이 가질 수 있는 값을 10개(0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0)를 선택하였다. 이렇게 구성된 50개의 조합에 대하여 분산 곡선을 그려서 밴드갭의 상한/하한 주파수를 얻었다. Fig. 10(a)는 환형 공동의 직경이 180 mm일 때, 내부 격벽의 회전율에 따른 밴드갭의 상한/하한 주파수를 나타낸 것이다. 목표 주파수 대역을 회색 상자로 나타냈다. Fig. 10(b)는 환형 공동의 직경이 240 mm일 때, 내부 격벽의 회전율에 따른 밴드갭의 상한/하한 주파수를 나타낸 것이다. 이렇게 50가지 경우에 대하여 밴드갭의 상한/하한 주파수를 얻었고, 식 (2)를 만족하는 경우가 다수 존재하였다. 즉, 환형 공동의 직경과 회전율만 변경하여 식 (2)을 만족하는 단위체를 설계할 수 있다는 것을 알 수 있었다. 그중에서 단위체의 부피를 줄이기 위해서, 환형 공동의 직경이 가장 작은 경우를 선택하였다: ∆ f = 329 Hz, fupp = 629 Hz, flow = 300 Hz, 2rc = 180 mm, 2rd = 20 mm, tc = 10 mm, 2td = 10 mm, n = 0.8.
3.4 단위체 배열과 음향 메타물질 패널
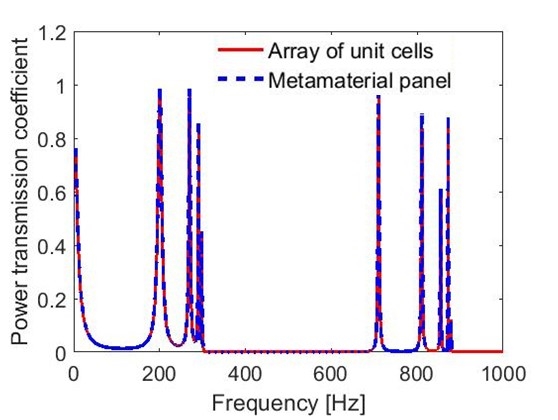
앞 장에서 선택한 단위체를 z축 방향으로 5번 반복 배열하여 “단위체 배열(array of unit cells)”을 구성하였고, 이 단위체 배열을 x-y 평면상에 2 × 2 형태로 배열하여 음향메타물질 패널을 구성하였다. Fig. 11은 단위체 배열과 음향 메타물질 패널의 파워 투과 계수 곡선을 계산하여 비교한 그림이다. 두 파워 투과 계수 곡선이 거의 일치하는 것으로 보아, 단위체 배열의 음향 특성이 음향 메타물질 패널의 음향 특성을 잘 나타내 주는 것을 알 수 있다. 따라서 특별한 언급이 없으면, 음향 메타물질 패널의 음향 특성은 단위체 배열에 대한 해석 결과로 나타낸다.
4. 설계 결과 검증
설계한 음향 메타물질 패널의 우수성을 세 가지 방법으로 살펴본다. 첫 번째로 등가 질량 패널과 음향 메타물질 패널의 음향 특성을 비교한다. 두 번째로, 음향 메타물질 패널에 대한 음향 실험을 수행하여 소음 차단 정도를 비교하였다. 해석과 실험의 편리를 위해 음향 메타물질 패널 대신 단위체 배열을 사용하여 설계 결과를 검증한다. 마지막으로 Jung이(27) 제시한 방법으로 설계된 음향 메타물질 패널과 비교한다.
4.1 등가 질량 패널과 음향 메타물질 패널
음향 메타물질 패널의 음향 특성을 구멍이 없는 등가 질량 패널과 비교하였다. 음향 메타물질 패널의 구멍과 환형 공동은 공기로 채워져 있고 나머지 부분은 고체 물질로 채워져 있다. 질량 법칙을 따르는 일반 패널의 음향 특성을 비교하여, 설계한 음향 메타물질 패널의 음향 특성을 살펴보고자 한다. 이를 위해 음향 메타물질 패널의 고체 물질을 아크릴로 가정하고, 비교할 일반 패널의 밀도는 식 (4)를 만족하는 등가 질량 밀도(equivalent mass density: ρeq)를 이용하여 계산하였다.
| (4a) |
| (4b) |
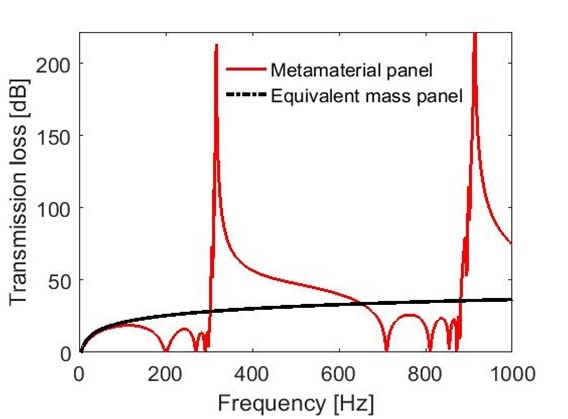
식 (4)에서 공기 밀도(ρair)와 아크릴 밀도(ρacryl)는 각각 1.21 kg/m3와 1190 kg/m3를 사용하였고, 공기의 음속(cair)과 아크릴의 음속(cacryl)은 각각 343 m/s와 2730 m/s를 사용하였다. 얻어진 등가 질량 밀도(ρeq)는 1019.9 kg/m3이다. 또한, Vair, Vacryl, Vtotal은 각각 1.3 × 10(-3) m3, 7.7 × 10(-3) m3, 9.0 × 10(-3) m3이다. Fig. 12는 음향 메타물질 패널과 등가 질량 패널의 투과 손실을 계산하여 비교한 그래프이다. 303 Hz ~ 652 Hz 대역에서 음향 메타물질 패널의 투과 손실이 구멍이 없는 등가 질량 패널의 투과 손실에 비해 상당히 높은 것을 알 수 있다.
4.2 음향 메타물질의 음향 특성 비교 실험
Fig. 13(a)에 보이는 것처럼, 설계한 음향 메타물질(단위체 배열)을 제작하고, Fig. 13(b)의 실험 장치를 이용하여 패널의 음향 특성을 실험적으로 검증한다. 덕트의 한쪽 끝에서 스피커(InterM DU-75)를 사용하여 전 주파수 대역에서 거의 동일한 크기를 갖는 음파를 패널에 수직으로 입사시키고, 입사되고 투과되는 음파를 양쪽 끝의 경계 조건에 관계 없이 정확히 분리하기 위해 4개의 마이크로폰(GRAS 46BE Microphone)을 사용하여 측정하였다. 실험에 필요한 신호 발생과 데이터 측정 및 후처리에는 LMS Testlab(Ver. 10a)을 사용하였다. Fig. 13(c)에서는 설계한 음향 메타물질 패널의 유한요소 해석과 음향 실험으로 구한 투과 손실 곡선을 비교한다. 두 그래프의 소음 차단 구간은 상당히 일치하는 것을 볼 수 있다. 이 소음 차단 구간에서, 측정한 투과 손실이 전체적으로 낮은 값을 갖는다. 이러한 차이의 원인은 유한요소 해석에서 사용한 강체 벽(rigid wall) 가정에서 기인한 것으로 추정된다. 해석에서 사용한 음향 모델은 강체벽으로 둘러싸여 있다고 가정하였지만, 제작한 음향 메타물질을 구성하는 아크릴 판의 일부가 진동하는 것을 인지할 수 있었다. 특히, 일렬로 배열된 인접한 두 환형 공동을 분리하는 아크릴 판은 입사파에 의한 진동을 피할 수가 없었다. 이를 감안하더라도 목표 주파수 대역인 300 Hz ~ 600 Hz에서 소음이 차단되는 것을 확인할 수 있다.
4.3 기존 연구와 비교
Jung(27)이 사용한 음향 메타물질을 이용하여 주어진 목표 주파수 대역(300 Hz ~ 600 Hz)이 밴드갭 영역에 포함되도록 음향 메타물질 패널을 설계하였다. 환형 공동의 두께(tc = 10 mm), 원형 덕트의 직경(2rd = 20 mm)과 두께(td = 5 mm)는 같은 값을 사용하였다. Jung(27)이 제안한 단위체는 내부에 격벽이 없는 구조의 환형 공동을 사용하는데, Fig. 14와 같은 분산 곡선 그래프를 얻었다(k가 양인 구간만 나타내었다). 그림에서 밴드갭의 하한과 상한 주파수를 결정하는 음향 모드는 각각 1차와 2차 방사형 음향 모드(radial acoustic mode)이다. 그 사이에 존재하는 방위각 음향 모드(azimuthal acoustic mode)는 평면파 입사 조건에서 가진되지 않으므로 나타내지 않았다. 설계 결과, 상한/하한 주파수는 300 Hz와 1349 Hz이고, 1049 Hz의 대역폭을 얻을 수 있었지만, 환형 공동의 직경이 306 mm에 달하였다. 이 연구에서 제안한 Fig. 1(c)의 단위체를 사용하여 얻은 음향 메타물질의 환형 공동 직경이 180 mm임을 고려할 때, Jung(27)이 제안한 단위체의 직경이 지나치게 큰 것을 알 수 있다. 즉, 이 연구에서 제안한 단위체 모델은 내부 격벽이 없는 구조에 비해 밴드갭의 대역폭은 줄어들었으나, 환형 공동의 직경이 작아져 실제 사용하기에 활용도가 높다고 할 수 있다. 나선형 내부 격벽에 의해서, 구멍 중심에서 환형 공동의 원주까지의 유효 길이가 길어져서 좀 더 짧은 외경으로도 저주파수대역의 밴드갭 형성이 가능한 것으로 추정된다.
5. 결 론
이 연구에서는 음향 메타물질을 이용하여 기계 시스템 내부에서 발생하는 열은 외부로 배출하고 내부 기계음이 외부로 방출되는 것을 막는 방음 패널을 설계하고자 하였다. 유체는 투과시키고 저주파 대역의 소음은 차단하는 음향 메타물질 패널 구조를 제시하고 목표 주파수 대역에서 소음을 차단하도록 패널을 설계했다. 저주파수 대역의 소음을 차단하기 위해, 환형 공동 내부에 곡률이 있는 내부 격벽을 삽입하였다. 제시된 음향 메타물질 구조에 대해 분산 곡선을 구하여 소음 차단 구간을 확인하였다. 분산 곡선의 밴드갭에 크게 영향을 미치는 구성 요소를 설계 변수로 선정하고, 파라미터 스터디를 통해 목표 주파수 대역에서 소음을 차단하는 음향 메타물질 패널 설계 방법을 제시했다. 이 방법을 통해 300 Hz ~ 600 Hz의 소음을 차단하는 음향 메타물질 패널을 구성하는 단위체의 사이즈를 결정하고, 유한요소 해석과 음향 실험을 통해 해당 주파수 대역에서 소음이 차단됨을 확인하였다. 향후에는 아르키메데스 나선형의 개수에 따른 설계나 다른 내부 구조를 이용하는 연구가 진행된다면 이 분야 연구 발전에 크게 기여할 것으로 기대된다.
기 호 설 명
| rc : | 환형 공동의 반지름 |
| tc : | 환형 공동의 두께 |
| rd : | 원형 덕트의 반지름 |
| 2td : | 환형 공동 간의 거리 |
| n : | 내부 격벽의 회전율 |
| a1, a2, a3 : | 패널의 가로/세로/두께 |
| fupp, flow : | 밴드갭의 상한/하한 주파수 |
| : | 목표주파수 대역의 상한/하한 주파수 |
| N : | 단위체의 개수 |
| L : | 단위체의 길이 |
| ΔRBW : | 밴드갭의 상대적 변화량 |
Acknowledgments
A part of this paper was presented at the KSNVE 2018 Annual Autumn Conference.
이 논문은 2016년도 정부(교육부)의 재원으로 한국연구재단의 지원을 받아 수행된 기초연구사업임(No. 2016R1D1A1B03932357).
References
-
Pierce, A. D., and Smith, P., (1981), Acoustics: An Introduction to Its Physical Principles and Applications, Physics Today, 34(12), p56-57.
[https://doi.org/10.1063/1.2914388]

-
Li, J., and Chan, C. T., (2004), Double-negative Acoustic Metamaterial, Physics Review E, 70(50), p055602.
[https://doi.org/10.1103/PhysRevE.70.055602]

- Haberman, M. R., and Guild, M. D., (2016), Acoustic Metamaterials, Physics Today, 69(6), p42-48.
-
Cummer, S. A., Christensen, J., and Alu, A., (2016), Controlling Sound with Acoustic Metamaterials, Nature Reviews Materials, 1(3), p16001.
[https://doi.org/10.1038/natrevmats.2016.1]

- Kim, S. Y., Park, J. H., Yang, J., Lee, H. R., Lee, J. S., Kang, Y. J., and Kim, Y. Y., (2017), Low-frequency Sound Transmission Reduction Using Slow Wave Based Acoustic Metamaterial Panels, Transactions of the Korean Society for Noise and Vibration Engineering, 2017(4), p387-381.
-
Fokin, V., Ambati, M., Sun, C., and Zhang, X., (2007), Method for Retrieving Effective Properties of Locally Resonant Acoustic Metamaterials, Physics Review B, 76(14), p144302.
[https://doi.org/10.1103/PhysRevB.76.144302]

- Aspne, D. E., (1982), Local-field Effects and Effective-medium Theory: A Microscopic Perspective, American Journal of Physics, 50(8), p704-709.
-
Huang, H. H., Sun, C. T., and Huang, G. L., (2009), On the Negative Effective Mass Density in Acoustic Metamaterials, International Journal of Engineering Science, 47(4), p610-617.
[https://doi.org/10.1016/j.ijengsci.2008.12.007]

-
Zigoneanu, L., Popa, B. I., Starr, A. F., and Cummer, S. A., (2011), Design and Measurements of a Broadband Two-dimensional Acoustic Metamaterial with Anisotropic Effective Mass Density, Journal of Applied Physics, 109(5), p054906.
[https://doi.org/10.1063/1.3552990]

-
Lee, S. H., Park, C. M., Seo, Y. M., Wang, Z. G., and Kim, C. K., (2009), Acoustic Metamaterial with Negative Density, Physics Letter A, 373(48), p4464-4469.
[https://doi.org/10.1016/j.physleta.2009.10.013]

- Lu, M. H., Feng, L., and Chen, Y. F., (2009), Phononic Crystals and Acoustic Metamaterials, Material Today, 12(12), p34-43.
-
Oudich, M., Zhou, X., and Badreddine, A. M., (2014), General Analytical Approach for Sound Transmission Loss Analysis through a Thick Metamaterial Plate, Journal of Applied Physics, 116(19), p193509.
[https://doi.org/10.1063/1.4901997]

-
Pennec, Y., Djafari-Rouhani, B., Larabi, H., Vasseur, J. O., and Hladky-Hennion, A. C., (2008), Low-frequency Gaps in a Phononic Crystal Constituted of Cylindrical Dots Deposited on a Thin Homogeneous Plate, Physics Review B, 78(10), p104105.
[https://doi.org/10.1103/PhysRevB.78.104105]

-
Yang, Z., Dai, H. M., Chan, N. H., Ma, G. C., and Sheng, P., (2010), Acoustic Metamaterial Panels for Sound Attenuation in the 50-1000Hz Regime, Applied Physics letters, 96(4), p041906.
[https://doi.org/10.1063/1.3299007]

-
Naify, C. J., Chang, C. M., McKnight, G., and Nutt, S., (2010), Transmission Loss and Dynamic Response of Membrane-type Locally Resonant Acoustic Metamaterials, Journal of Applied Physics, 108(11), p114905.
[https://doi.org/10.1063/1.3514082]

-
Chen, Y., Huang, G., Zhou, X., Hu, G., and Sun, C. T., (2014), Analytical Coupled Vibroacoustic Modeling of Membrane-type Acoustic Metamaterials: Plate Model, Journal of the Acoustical Society of America, 136(6), p2926-2934.
[https://doi.org/10.1121/1.4901706]

-
Huang, T. Y., Shen, C., and Jing, Y., (2016), Membrane- and Plate-type Acoustic Metamaterials, Journal of the Acoustical Society of America, 139(6), p3240-3250.
[https://doi.org/10.1121/1.4950751]

-
Wang, X., Zhao, H., Luo, X., and Huang, Z., (2016), Membrane-constrained Acoustic Metamaterials for Low Frequency Sound Insulation, Applied Physics Letters, 108(4), p041905.
[https://doi.org/10.1063/1.4940717]

-
Lu, K., Wu, J. H., Guan, D., Gao, N., and Jing, L., (2016), A Lightweight Low-frequency Sound Insulation Membrane-type Acoustic Metamaterials, AIP Advances, 6(2), p0255116.
[https://doi.org/10.1063/1.4942513]

-
Zhu, R., Huang, G. L., Huang, H. H., and Sun, C. T., (2011), Experimental and Numerical Study of Guided Wave Propagation in a Thin Metamaterial Plate, Physics Letter A, 375(30), p2863-2867.
[https://doi.org/10.1016/j.physleta.2011.06.006]

- Claeys, C., Deckers, E., Pluvmers, B., and Desmet, W., (2016), A Lightweight Vibro-acoustics Metamaterial Demonstrator: Numerical and Experimental Investigation, Mechanical Systems and Signal Processing, 70, p853-880.
-
Nateghi, A., Belle, L. V., Claves, C., Deckers, E., Pluvmes, B., and Desmet, W., (2017), Wave Propagation in Locally Resonant Cylindrically Curved Metamaterial Panels, International Journal of Mechanical Sciences, 127, p73-90.
[https://doi.org/10.1016/j.ijmecsci.2016.07.003]

-
Ding, C. L., and Zhao, X. P., (2011), Multi-band and Broadband Acoustic Metamaterial with Resonant Structures, Journal of Physics D: Applied physics, 44(21), p215402.
[https://doi.org/10.1088/0022-3727/44/21/215402]

-
Hao, L. M., Ding, C. L., and Zhao, X. P., (2012), Tunable Acoustic Metamaterial with Negative Modulus, Applied Physics A, 106(4), p807-811.
[https://doi.org/10.1007/s00339-011-6682-8]

-
Ye, Q., Liu, Y., Lin, H., Li, M., and Yang, H., (2012), Multi-band Metamaterial Absorber Made of Multi-gap SRRs structure, Applied Physics A, 107(1), p155-160.
[https://doi.org/10.1007/s00339-012-6796-7]

-
Cho, S. J., Kim, B. S., Min, D. K., and Park, J. H., (2015), Tunable Two-dimensional Acoustic Meta-structure Composed of Funnel-shaped Unit Cells with Multi-band Negative Acoustic Property, Journal of Applied Physics, 118(16), p163103.
[https://doi.org/10.1063/1.4934360]

-
Jung, J. W., Kim, J. E., and Lee, J. W., (2018), Acoustic Metamaterial Panel for Both Fluid Passage and Broadband Soundproofing in the Audible Frequency Range, Applied Physics Letters, 112(4), p041903.
[https://doi.org/10.1063/1.5004605]


Min Ho Kim received the B.S. and M.S. degrees in mechanical engineering from Ajou University in 2017 and 2019, respectively. During his stay at Ajou as a graduate student, he worked on NVH and acoustic metamaterial. He is now working as a research engineer at Hyundai Heavy Industries.

Jin Woo Lee has been a Professor of Mechanical Engineering at Ajou University since 2009. His research interests are in the area of vibrations, acoustics, acoustic and vibration metamaterial, topology optimization based design and fluid-structure interactions of microcantielvers for RF-MEMS and AFM. His Ph.D. is from the School of Mechanical and Aerospace Engineering from Seoul Notional University in South Korea in 2003. He worked with Samsung Electronics Company from 2003 to 2006 and studied as a post-doctoral research associate at Seoul National University from 2006 to 2007. From 2007 to 2009, he was a postdoctoral research associate of Mechanical Engineering at Purdue University, West Lafayette, IN, USA.