전기 자동차용 인휠 모터 시스템의 소음 저감
© The Korean Society for Noise and Vibration Engineering
Abstract
In this study, we identified the noise sources of an in-wheel motor system and proposed a low-noise design guideline through structural modification. To identify the noise sources, we not only measured the noise and vibration signals, but we also performed modal testing. Using waterfall plots for the frequency spectra of noise and vibration signals, we identified the vibration excitation frequencies owing to the gear mesh and the motor electromagnetic force of the motor. We obtained the natural frequencies of the in-wheel motor system from the modal test results. The results of the signal analysis and modal test showed that noise was generated by the resonance between the excitation and natural frequencies. To avoid this resonance, we proposed a design guideline for noise reduction in an in-wheel motor system by using a finite element simulation.
Keywords:
In-wheel Motor System, Gear Noise, Gear Mesh Frequency, Motor Noise, Noise Reduction키워드:
인휠 모터 시스템, 기어 소음, 기어물림주파수, 모터 소음, 소음 저감1. 서 론
오늘날 지구 환경의 오염과 석유 에너지 고갈에 대한 문제가 전 세계적으로 관심을 받아오고 있음에 따라 전력을 동력으로 대체하려는 연구가 활발히 진행되고 있다(1,2). 이 중에서도 인휠 모터 시스템은 모터와 제동 장치가 차량의 휠 안에 직접 장착되어 구동축이 없이 바퀴를 직접 구동시키는 방식으로 전기를 동력으로 사용한다(3). 인휠 모터 시스템은 기존의 차량과 비교하여 동력을 전달하는 경로와 구조가 간단하여 에너지 손실의 절감과 경량화를 기대할 수 있는 친환경 기술로서, 이에 관한 연구가 자동차 산업에서도 활발히 이루어지고 있다.
인휠 모터 시스템은 모터와 감속기의 조합으로 구성되어 있으며, 구동 중 하우징 내부의 모터와 기어들이 서로 맞물려 회전하면서 소음과 구조 진동을 발생시키게 된다. 이때 발생한 소음과 진동은 현가장치를 통해 차량의 내부로 전달되어 운전자에게 불쾌감을 유발하며 제품의 성능과 수명에도 악영향을 미친다. 일반적으로 감속기에서 발생하는 진동과 소음의 원인은 기어 치의 강성, 형상, 조립에 의한 오차나 백 래쉬 등에 의한 것으로 알려져 있다(4,5). 기어에서의 소음은 부하를 받는 상태의 와인 소음과 무부하 상태에서의 래틀 소음으로 나타나는데(6), 이러한 소음을 저감하기 위해서는 기어의 전달 오차 또는 기어물림주파수와 같은 소음과 진동의 발생원을 명확히 규명해야 한다. 선진 자동차 업계에서는 인휠 감속기의 저소음 설계를 위해 설계 단계에서부터 적용할 수 있도록 소음에 영향을 주는 인자들에 대해서 활발히 연구하고 있으나(7), 이에 반해 국내에서는 저소음 인휠 감속기에 관한 연구가 미흡한 실정이다.
이 연구에서는 인휠 감속기에서 발생하는 소음을 실험으로 규명하고 주요 가진주파수와 구조 공진 소음의 메커니즘을 규명하여 형상 설계를 통해 저소음 설계방안을 제시하였다. 먼저 인휠 감속기에서 발생하는 소음과 진동 신호를 실험으로 측정하고 이를 유발하는 주파수 영역을 분석하였다. 그리고 모드 실험을 통해 구조 공진을 유발하는 주요 모드를 파악하고 유한요소 해석 모델과 비교하여 검증하였다. 마지막으로 형상 설계를 통해 인휠 감속기의 저소음 설계를 위한 방안을 제시하였다.
2. 인휠 모터 시스템의 구조
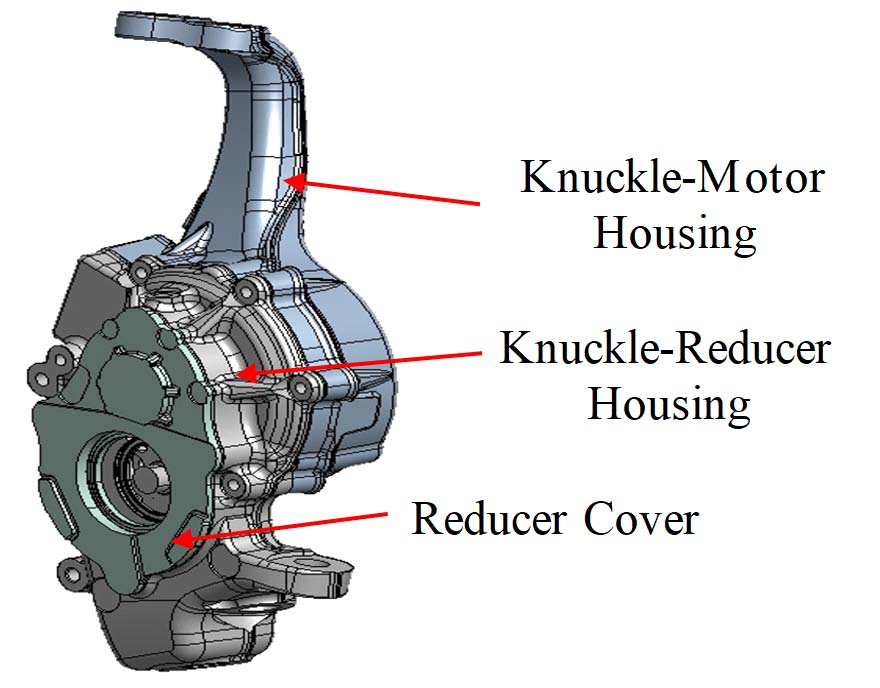
이 연구의 대상인 인휠 모터 시스템의 구조는 Fig. 1과 같다. 인휠 감속기의 외부는 모터를 감싸고 있는 너클-모터 하우징과 각 기어들로 구성된 감속기를 감싸고 있는 너클-감속기 하우징, 그리고 감속기의 위치에 부착어 감속기를 보호하는 감속기 커버로 구성된다. 상단의 너클은 서스펜션의 상부암(upper arm)과 체결되고 하단의 너클은 서스펜션의 하부암(lower arm)과 체결되어 고정된다.
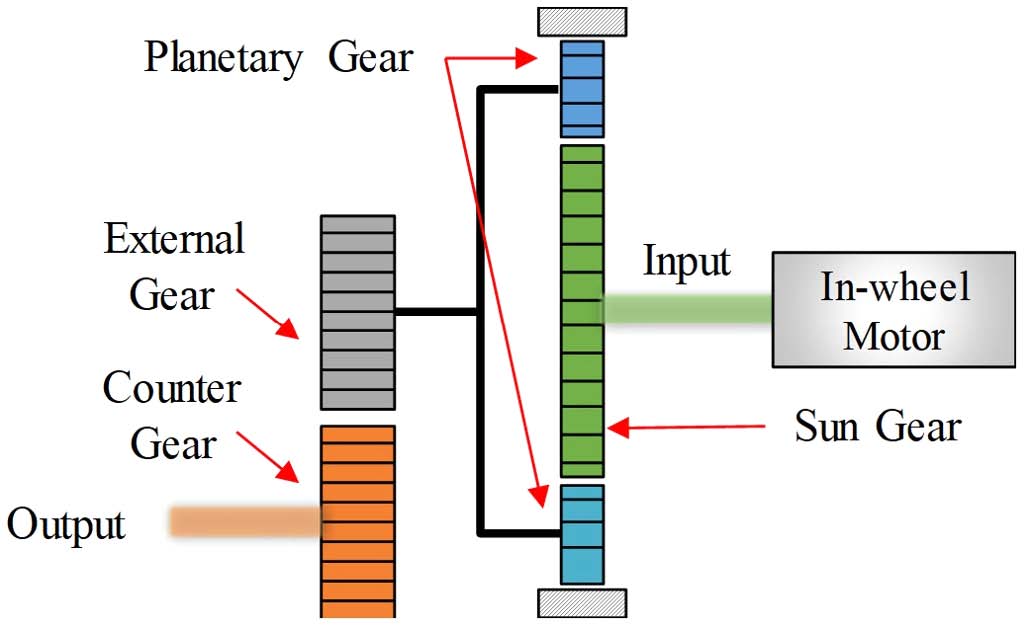
인휠 감속기는 유성기어와 외접기어 구조로 된 2단 감속기로, Fig. 2에 나타낸 것과 같다. 인휠 모터에서 토크를 발생시키며 이는 선기어로부터 1차 감속부인 3개의 유성기어를 통해 2차 감속부인 외접기어로 전달되며 카운터 기어로 최종 출력을 발생시키는 구조를 갖는다. 따라서, 모터로부터 전달된 동력은 감속기를 통해 휠 베어링, 브레이크 디스크와 함께 체결된 휠을 구동시켜 타이어를 회전시킨다.
3. 소음과 진동의 신호분석
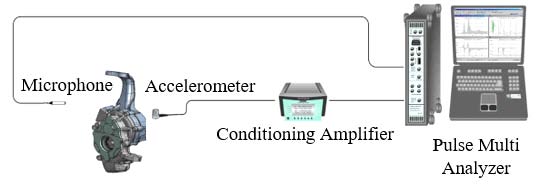
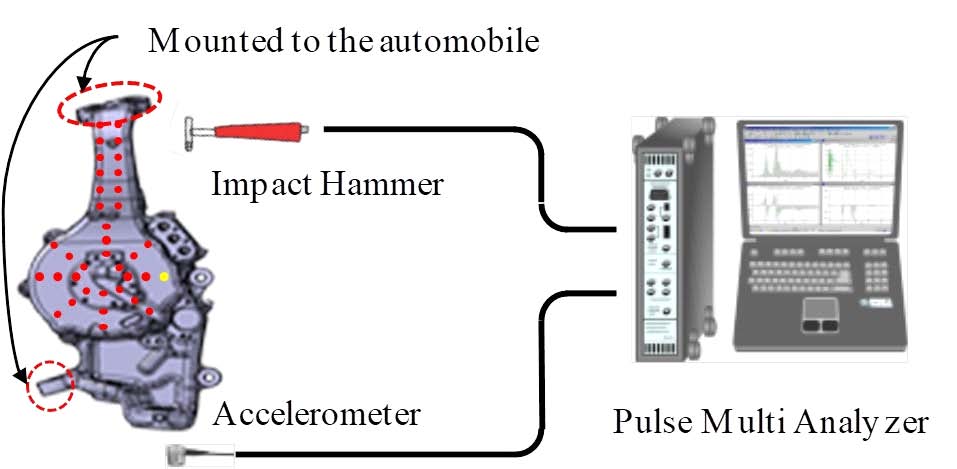
인휠 모터 시스템에서 발생하는 소음 소준을 파악하기 위하여 인휠 모터가 작동할 때 발생하는 소음과 진동 신호를 측정하였으며, 실험 장치는 Fig. 3와 같이 구축하였다. 일반적으로 소음은 진동에 의해 유발되므로 상대적으로 외부 환경에 영향을 덜 받는 진동 신호를 동시에 채집하였다. 회전속도에 대한 영향을 살펴보기 위하여 인휠 모터 시스템을 차량에 부착한 상태로 정지 상태부터 점점 가속하며 소음과 진동의 신호를 각각 측정하였다. 이 때, 마이크로폰(B&K 4190)은 인휠의 모터 상단에 장착하였으며, 단축 가속도계(B&K 4383)는 인휠 모듈의 감속기를 감싸고 있는 너클-감속기 하우징 위에 수직으로 부착하였다. 차량의 주행속도는 차량용 CAN 통신을 이용하여 ECU로부터 직접 모터의 회전수를 획득하였다. 가속도계와 마이크로폰으로부터 측정된 신호는 스펙트럼 분석기(B&K 3560C)를 통해 분석되었으며, 가속도계는 상태 증폭기(B&K Nexus)를 통해 진동 신호를 증폭시켰다.
소음과 진동에 영향을 주는 가진주파수를 파악하기 위하여 기어의 물림주파수(GMF, gear mesh frequency)를 정의해야 할 필요가 있다. GMF는 각 기어의 회전속도와 기어 잇 수와의 관계식으로 얻어진다. 먼저 1단 유성기어와 캐리어의 회전속도의 비를 계산해야 한다. 유성기어와 캐리어의 회전속도는 각각 다음과 같다.
| (1) |
| (2) |
여기서 선기어와 링기어의 잇 수는 각각 28개와 77개이다. 선회 모터의 회전속도를 X라 할 때, 선회 모터와 선기어의 회전속도는 동일하므로 위 식으로부터 유성기어와 캐리어의 속도는 각각 –0.5714X와 0.2667X로 계산된다. 또한, 유성기어의 기어물림주파수(GMFp)와 카운터 기어 감속기의 기어물림주파수(GMFct)는 각각 다음과 같이 구할 수 있다.
| (3) |
| (4) |
여기서 카운터 기어의 잇 수는 31개로 GMFp와 GMFct는 각각 20.53X와 8.27X로 계산된다.
모터에 의해 구동되는 시스템은 기어물림주파수와 함께 모터에 의한 전자기소음의 가진주파수도 함께 관찰된다. 전자기 소음의 가진주파수는 고정자 극 수와 회전자의 슬롯 수와 관련이 있으며, 반복적으로 변화하는 회전자와 고정자 사이의 인력과 척력에 의해 가진주파수가 발생한다. 고정자와 회전자의 상호작용으로 발생하는 고조파는 다음과 같이 계산된다.
| (5) |
여기서 n과 m은 임의의 정수이며, S는 회전자의 슬롯 수 그리고 P 고정자의 극 수로 각각 36개와 8개를 갖는다. 식 (5)로부터 계산된 구동 모터의 고조파는 8X의 배수로 계산된다.
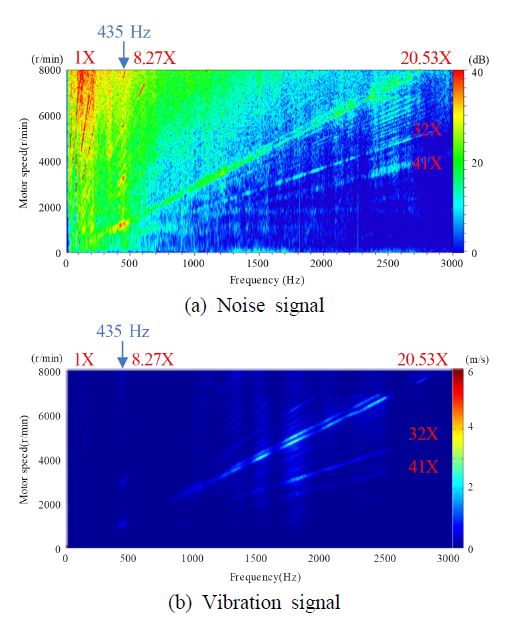
인휠 감속기 소음의 가진원을 파악하기 위해 인휠 모터 시스템 장착 차량의 주행속도 조건인 정지 상태부터 고속으로 가속하는 상태까지 소음과 진동의 신호를 측정하였다. 고속주행의 속도인 120km/h에 해당하는 모터의 회전속도는 8400r/min이며, 0r/min부터 8000r/min까지 20r/min 단위로 측정을 하였으며 주파수는 3000Hz까지 채집하였다. Fig. 4는 가속을 하며 획득한 소음과 진동의 신호이며, 구동 모터 속도의 변화에 따른 소음과 진동의 주파수 스펙트럼을 회전속도의 순서에 따라 그린 그래프이다. Fig. 4의 가로 좌표축은 주파수(Hz)를 의미하며 세로 좌표축은 모터의 회전속도(r/min)를 의미한다. 소음 신호인 Fig. 4(a)와 진동 신호인 Fig. 4(b)의 양상은 비슷하게 나타난다. 그래프에서 대각선 방향과 세로 방향의 선이 나타나는데 대각선 방향의 선은 기어와 모터의 가진성분과 관련이 있으며 세로 방향의 선은 인휠 모터 시스템의 고유진동수와 관련이 있다. 그리고 각 주파수 스펙트럼의 색상은 각 그래프의 우측에 나타난 신호의 크기를 의미한다.
그래프의 상단에 표기된 1X 성분은 회전축의 편심이나 회전체 지지단 취약에 의한 가진성분으로 나타나는 신호이다. 또한, 8.27X와 20.53X는 각각 앞에서 획득한 카운터 기어의 물림주파수와 유성기어의 물림주파수에 해당하는 가진성분으로 대각선으로 나타난다. 이들 가진주파수는 진동 신호보다는 소음 신호에서 더 도드라지며 소음은 카운터 기어보다 유성기어에 의한 영향이 더 크게 나타남을 확인할 수 있다. 유성기어의 물림주파수 아래로 32X와 41X의 성분이 확인된다. 32X는 식 (5)에서 확인한 구동 모터의 전자기 소음의 고조파에 의해 나타나는 신호이다. 41X의 신호는 유성기어의 물림주파수의 2배수 조화성분이다. Fig. 4(a)를 살펴보면 고주파수 영역보다 저주파수 영역, 저속 주행보다 고속주행에서 더 많은 소음이 발생하는 것을 확인할 수 있다. 또한, 4000r/min 이상의 고속 주행시 인휠 모터 시스템에서 발생하는 소음은 차량의 엔진이나 풍절음에 의해 사람이 거의 인지하지 못하므로 4000r/min 이하에서 발생하는 소음에 집중해야 할 필요가 있다. 4000r/min보다 낮은 주행속도에서 가장 소음이 크게 나타나는 주파수 영역은 435Hz인데 기어물림주파수나 고조파의 조화성분과 만나는 지점에서 소음이 커지는 것을 확인할 수 있다. 이는 인휠 모터 시스템이 435Hz에 해당하는 고유모드를 가지고 있으며, 이로 인해 공진 소음이 나타나는 것을 직접적으로 보여준다.
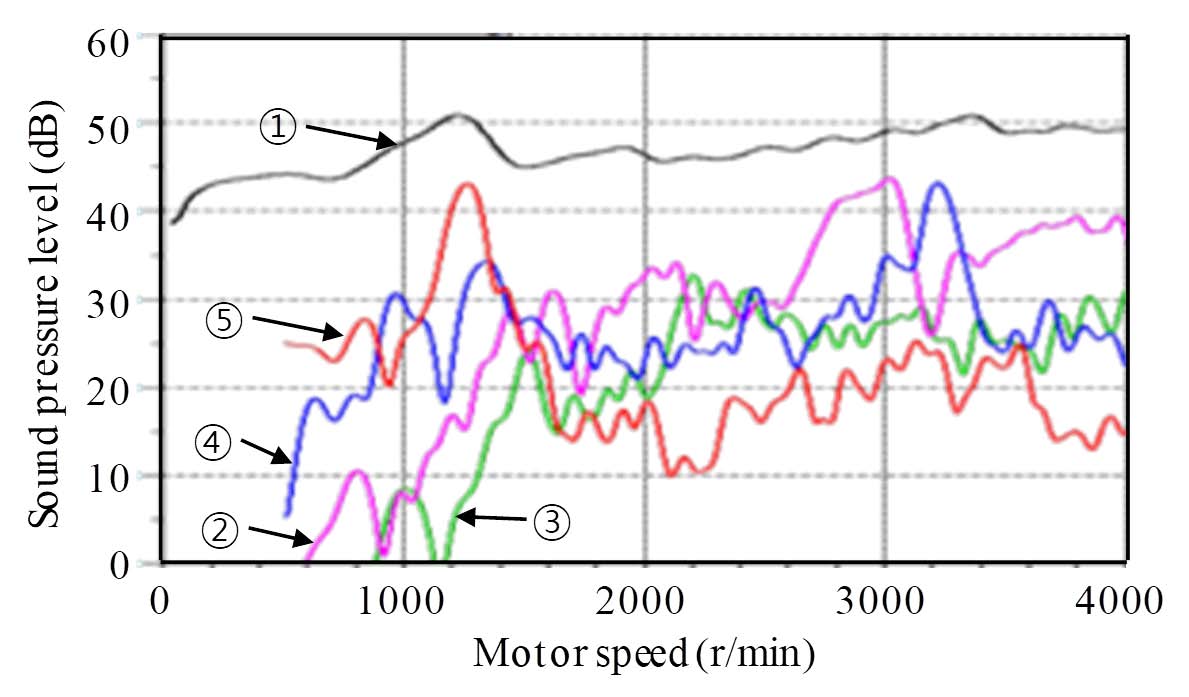
Fig. 5에 도시된 차수추적도(order tracking plot)를 분석하면 인휠 모터 시스템에 의해 발생하는 소음의 원인을 보다 구체적으로 규명할 수 있다. 다시 말해, 차수추적을 통해 모터와 기어의 성분이 소음의 발생에 기여하는 정도를 알 수 있다. 그림에서 볼 수 있듯이, 차량이 저속으로 주행하는 0r/min부터 4000r/min까지의 소음 수준은 40dB ~ 50dB이다. 일반적으로 자동차의 주행속도가 빨라질수록 전체 소음수준이 커지는데, Fig. 5는 1250r/min에서 일시적으로 큰 소음이 발생하는 것을 보여준다. 이 때 제일 큰 기여를 하는 성분이 유성기어의 기어물림주파수에 의한 것이며, 이 주파수는 Fig. 4에서 공진소음이 나타나는 주파수와 일치한다. 따라서, 인휠 모터 시스템에서 소음의 발생은 유성기어의 성분과 인휠 모터 시스템의 435Hz에 해당하는 고유진동수가 큰 영향을 미치는 것을 확인할 수 있다.
4. 공진 주파수 규명
조화성분과 공진을 일으키는 고유진동수를 규명하기 위하여 소음과 진동신호를 측정했던 것과 동일하게 차량에 부착된 상태에서 Fig. 6와 같이 모드 실험을 수행하였다. Fig. 6에 도시된 바와 같이 인휠 모터 시스템의 상단과 하단이 고정된 경계조건에 대해서 실험을 수행하였다. 모드실험은 소음이 방사되기 쉬운 구조를 갖는 너틀-모터 하우징을 대상으로 하였다. Fig. 6과 같이 모드실험 장치를 구성하였고 총 35개 점을 충격해머(B&K 4393)로 가진하고, 한 점에서 가속도계로 응답을 측정하였다. 이 때 충격 해머 팁의 재질은 스틸을 사용하였으며, 충격신호에 사각형창(rectangular window)를 적용하고 가속도계의 시간응답에는 지수창(exponential window)을 적용하였다.
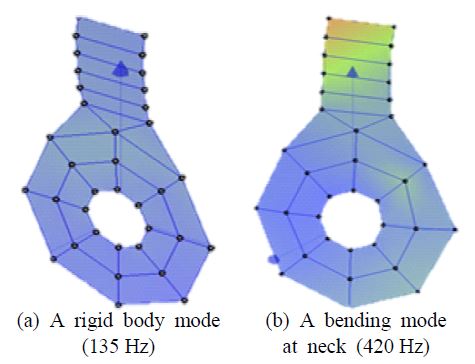
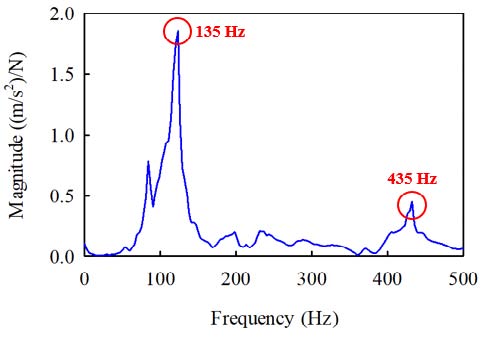
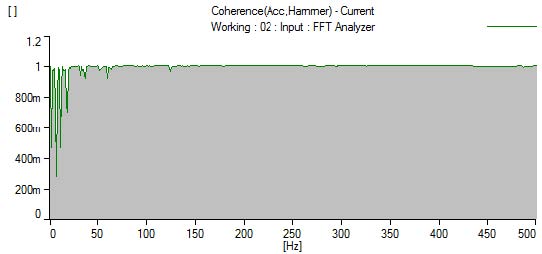
고유모드는 Fig. 7에서 보듯이 135Hz에서 시스템 전체가 같은 위상을 가지며 움직이는 모드가 존재한다. 이 모드는 인휠 모터가 부착된 현가장치 변형에 의해 발생된다. 435Hz에서 상부 너클과 감속기 사이를 이어주는 목부분에서 굽힘변형이 크게 나타나는 모습을 확인할 수 있다. Fig. 8의 주파수응답함수는 너클-모터 하우징의 고유진동수가 135Hz와 435Hz에 존재함을 보여준다. 그리고, 90Hz에 해당하는 주파수는 인휠 모터 시스템이 상하로 움직이는 현가장치 변형에 의한 모드이며 공진 주파수에 해당하지 않으므로 제외한다. 이 때 주파수 응답함수의 커브피팅은 Vibrant Technology사의 ME’scope에서 제공하는 Quick Fit을 사용하였으며 MIF(mode indicator function)은 기본으로 제공되는 CMIF를 사용하였다. 또한, Fig. 9에 도시된 간섭함수(coherence function)는 관심 주파수영역인 500Hz 내에서 3번의 반복 실험을 수행했을 때 50Hz 이상의 영역에서 1에 가까운 값을 갖는다. 따라서, 이 연구에서 수행한 모드실험은 충분히 신뢰할 만하다. 여러 실험결과를 살펴볼 때, 카운터 기어의 물림주파수와 유성기어의 물림주파수가 목부분의 변형모드의 고유진동수와 일치하여 발생하는 공진에 의해 소음이 증폭됨을 알 수 있다.
5. 저소음 설계 방안 도출
인휠 구동시에 발생하는 소음은 너클-모터 하우징의 목부분의 굽힘변형에 의해서 나타나는 것으로 규명되었다. 따라서, 저소음 설계를 위해 목부분의 굽힘변형을 줄이는 것이 필요하다. 실제 모델의 설계 변경은 많은 비용과 시간이 소요되기 때문에 이를 피하기 위해 유한요소 해석을 통한 시뮬레이션을 수행하였다. 이 연구에서는 실제 시스템에 대한 유한요소 해석 모델로 구축하고 이를 통해 형상 변경안을 도출하였다. 모델을 구축하고 해석하기 위하여 상용프로그램인 ANSYS ver 15.0.7을 이용하였다. 인휠 모터 시스템은 그 형상이 매우 두꺼우므로 솔리드 요소로 모델링하였으며, 사용된 메쉬의 크기는 5mm, 메쉬의 수는 307021개 그리고 노드의 수는 518539개를 사용하였다. 모드해석의 솔버는 ANSYS에서 자동으로 선정된 block lanczos 방법을 사용하였다. Block lanczos 방법은 원하는 주파수 영역 내에서 고유 주파수가 누락되지 않도록 추출하는 방법으로, 이 연구와 같이 해석 시간의 제약을 크게 받지 않는 비교적 단순한 모델의 모드 해석에 적합한 방법이다. 또한, 해석에 사용된 컴퓨터의 제원은 다음과 같다. CPU는 Intel i7-6700, GPU는 AMD W4300, RAM은 Samsung DDR4 16GB PC4-21300×2이다. 인휠 모터 시스템에 대한 유한요소 해석 모델은 비교적 단순하기 때문에 모드해석을 위해 1분 내외의 아주 짧은 시간이 소요되었다.
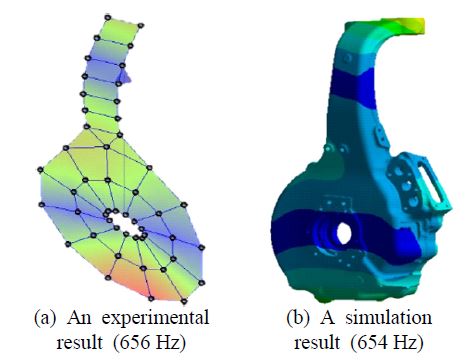
유한요소 해석 모델의 주요 물성치인 탄성계수를 구하기 위해서, 시스템의 단품에 대해 유한요소 해석과 실험을 비교 검증하는 방법을 채택하였다. 다시 말해, 인휠 모터 시스템을 구성하는 단품의 모드 실험의 결과와 해석 결과를 비교하여 모드 형상과 고유진동수가 일치하도록 물성치를 조절하여 획득하였다. 자유(free) 경계조건을 부과하기 위해서 인휠 모터 시스템의 상부암을 고무줄로 연결하여 기중기에 매달아 모드실험을 수행하였다. 단품들의 1차 고유진동수는 평균 0.7%의 오차 내로 계산되게 하였고, 실험을 통해 시뮬레이션에 사용될 물성치를 획득하였다. Fig. 10과 같이 너클-모터 하우징의 목부분 변형 모드이며 실험과 해석의 결과 값은 각각 656Hz와 654Hz로 약 0.3%의 오차를 보이므로 유한요소 모델이 문제없이 구축되었음을 확인할 수 있다. 각 물성치가 적용된 단품들을 모두 조립하여 최종 모델을 구축하였고, 모드실험과 해석의 결과 비교를 통해 유한요소 해석 모델이 충분히 시스템을 반영할 수 있음을 최종적으로 검증하였다.
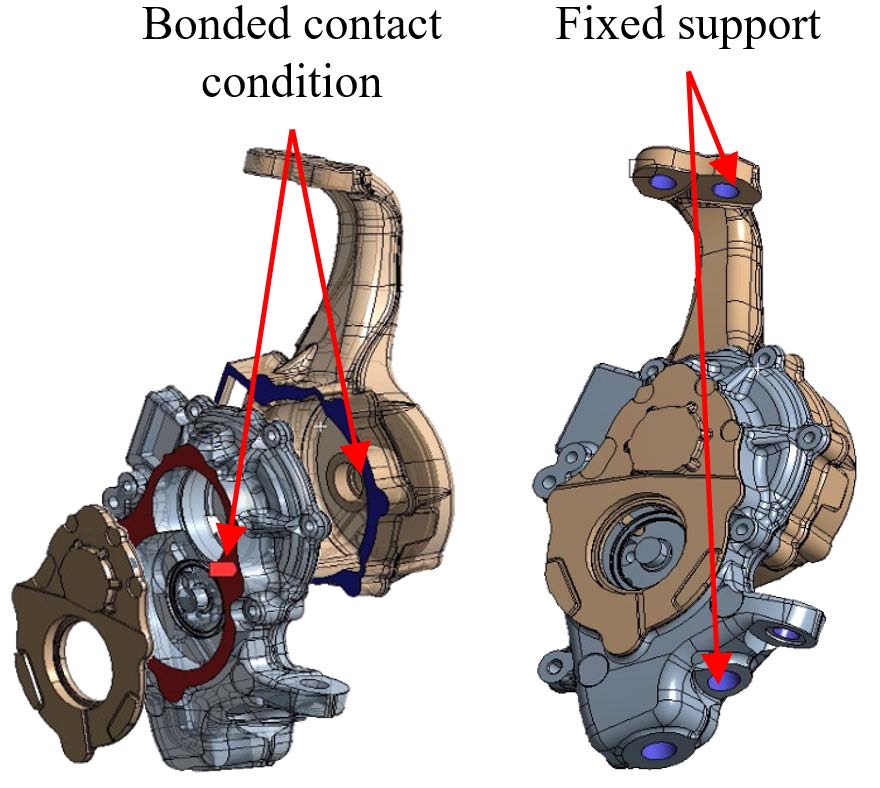
인휠 모터 시스템에서 소음을 유발하는 가장 취약한 부위는 너클-모터 하우징의 목부분이다. 저소음 설계를 위해 목부분의 강성을 부여하는 형상 설계를 수행하였고, 인휠 모터 시스템의 소음소준 저감을 위해 문제가 되는 모드의 고유진동수를 약 100Hz 증가시키는 것을 목표로 하였다. 유한요소 해석 모델의 경계조건은 실제 차량에 부착된 조건을 구현하기 위하여 Fig. 11과 같이 구성부품들 사이에 볼트로 조립되는 부위 간 구속조건을 적용하여 서로 만나는 지점을 결합(bonded)시켰으며 트림 공차는 2mm로 설정하였다. 그리고, 현가장치의 상부암과 하부암에 결속되는 하우징의 너클 상부와 하부에 구속조건을 적용하였다. 실제로는 차량의 현가장치와 구속이 되므로 경계조건에 스프링 요소를 추가하여야 하지만 공진을 일으키는 고유진동수가 면내외 방향으로 굽힘 운동을 하기 때문에 다소 간단한 구속조건을 적용하였다. 이와 같이 경계조건을 부여하였을 때 유한요소 해석 모델의 고유진동수는 430Hz로 실험의 결과인 435Hz와 비교하였을 때 단지 5Hz의 차이가 나므로 충분히 시스템을 반영한다고 할 수 있다.
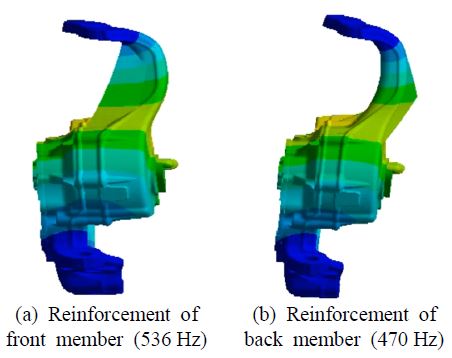
너클-모터 하우징의 목부분은 면내외 방향으로 굽힘 변형을 일으키므로 복부분에 부재를 보강하기 위하여 Fig. 12와 같이 목부분의 전면부와 후면부에 부재를 보강하는 2개의 설계방안을 도출하였다. 너클-모터 하우징의 구조상 전면부에 더 많은 공간이 있어 부재를 보강하기 용이한 반면 후면부는 부재를 보강하기에 충분한 공간이 존재하지 않아 충분한 굽힘 강성 증가 효과를 확인할 수 없었다. 결과적으로 너클-모터 하우징의 목부분 변형 모드에 대해 전면부와 후면부의 부재에 대하여 각각 536Hz와 470Hz의 결과를 나타내므로, 이는 각각 106Hz와 40Hz의 고유진동수가 증가하는 효과를 확인할 수 있었다. 이러한 방법으로 높아진 강성은 굽힘에 대한 저항을 증가시키며, 이에 따라 고유진동수 역시 그 값이 커지므로 기존에 발생하던 공진의 회피를 기대할 수 있다.
6. 결 론
이 연구에서는 인휠 모터 시스템의 감속기에서 발생하는 소음의 원인을 규명하고 소음 저감을 위한 방안을 제시하였다. 인휠 모터 시스템이 구동할 때의 소음과 진동 신호를 실험을 통해 측정하고, 회전속도에 따른 스펙트럼을 분석하여 기어물림주파수, 구동 모터의 고조파 그리고 고유진동수를 파악하였다. 소음을 유발하는 주요 요인은 너클-모터 하우징의 목부분이 변형하는 고유모드로서, 유성기어의 기어물림주파수와의 공진에 의해 소음이 발생하는 것으로 확인하였다. 또한, 공진이 발생하는 주파수 영역에서 고유진동수를 회피하는 방법을 사용하여 인휠 모터 시스템에서 발생하는 소음을 저감하기 위하여, 인휠 모터시스템의 너클-모터 하우징의 목부분에 부재를 보강하여 강성과 고유진동수를 증가시킴으로써 시스템의 강건성을 높이고 공진을 회피하는 방안을 제시하였다.
기 호 설 명
| Ns : | 선기어의 잇 수(개) |
| Nr : | 링기어의 잇 수(개) |
| Nct : | 카운터기어의 잇 수(개) |
| S : | 모터의 회전자 슬롯 수(개) |
| P : | 모터의 고정자 극 수(개) |
| X : | 모터의 회전 속도(r/min) |
| ωs : | 선기어의 회전 속도(r/min) |
| ωp : | 유성기어의 회전 속도(r/min) |
| ωc : | 캐리어의 회전 속도(r/min) |
| ωct : | 카운터기어의 회전 속도(r/min) |
Acknowledgments
이 논문은 2018년도 정부(교육부)의 재원으로 한국연구재단의 지원을 받아 수행된 기초연구사업임(No. 2018R1D1A1B07050187).
References
-
Brown, S., Pyke, D., and Steenhof, P., (2010), Electric Vehicles: The Role and Importance of Standards in an Emerging Market, Energy Policy, 38(7), p3797-3806.
[https://doi.org/10.1016/j.enpol.2010.02.059]

-
Nakada, T., Ishikawa, S., and Oki, S., (2014), Development of an Electric Motor for a Newly Developed Electric Vehicle, SAE Technical Paper 2014-01-1879.
[https://doi.org/10.4271/2014-01-1879]

- Itoh, Y., Sakai, K., and Makino, Y., (2011), In-wheel Motor System, NTN Technical Review, (79), p22-28.
- Kim, J. H., Sung, H. K., and Chung, J. K., (2001), An Investigation on Noise Quality of the Small Gear Reductioner Through Change of Gear Backlash, Proceedings of the KSME 2001 Annual Spring Conference, p635-640.
-
Seo, H. S., Park, S. P., and Chung, J. T., (2011), A Study on Noise Reduction for an Industrial Right-angled Reducer, Transactions of the Korean Society for Noise and Vibration Engineering, 21(6), p546-552.
[https://doi.org/10.5050/ksnve.2011.21.6.546]

- Niola, V., Avagliano, V., and Quaremba, G., (2011), The Gear Whine Noise, Proceedings of the 4th WSEAS (World Scientific and Engineering Academy and Society) International Conference on Energy and Development Environment-Biomedicine, p445-450.
- Kim, D. H., Shin, K. H, Lee, S. M., and Yeo, T. K., (2010), Development of In Wheel Motor System on Rear Wheels for Small Electric Vehicle, Proceedings of the KSAE 2010 Annual Autumn Conference, p1350-1354.

Jintai Chung received his B.S. and M.S. degrees in mechanical engineering from Seoul National University, Seoul, Korea in 1984 and 1986, respectively, and a Ph.D. degree in mechanical engineering from the University of Michigan, Ann Arbor, USA in 1992. He is now a professor in the Department of Mechanical Engineering, Hanyang University, Korea. His research fields are structural dynamics, vibration and noise.