2기1축 선박 추진시스템의 빙 충격 토크해석
© The Korean Society for Noise and Vibration Engineering
Abstract
The number of polar class vessels in the Arctic has been steadily increasing since the opening of the Arctic route. These vessels are designed for specific operations, and are classified using the established polar class (PC) rating system. The ratings, which range from PC1 to PC7, indicate those vessels that are the most useful (PC1) for year-round operation in polar waters to those that are the least useful (PC7) for summer/autumn operation. This study analyzed the ice impact torque in a 2-engine, 1-shaft propulsion system applied to a G/T 7765 vessel rated PC7, the lowest class, as well as the transient torsional vibration for the ice torque of a propeller and the excitation torque of a diesel engine. To conduct the analysis, a program was developed herein that complements the Newmark method using a numerical integration. The results showed that for a PC7 vessel, 2-engine, 1-shaft propeller operation mode can allow navigation through a frozen seaway because a large total equivalent inertia moment is achieved under an ice load, and the ice impact torque transmitted to the shaft is distributed to the generators and engines on both sides. However, in 1-engine, 1-shaft propeller operation mode, the vibratory torque of the generator’s flexible coupling exceeded the manufacturer’s guidelines because it was unable to split the small equivalent inertia moment transmitting the same excitation force.
Keywords:
Ice Torque, Transient Torsional Vibration키워드:
빙 토크, 과도비틀림진동1. 서 론
북극항로가 열리면서 일반화물선, 쇄빙선, 연구용 선박 그리고 어선까지 다양하게 빙해 운항 선박이 점차 늘어나고 있다. 이러한 선박은 선박의 사용 목적에 따라 설계의 기준도 달라진다.
이 연구는 대형 어선에 적용된 2기1축 추진시스템에서 빙 충격 토크와 디젤엔진의 기진력을 중심으로 과도비틀림진동 해석을 수행하여 이를 기준으로 하여 운항하고자 한다. 해석방법은 유한차분법의 하나인 Newmark 방법을 이용하였으며, 일반 사용자도 사용할 수 있도록 범용 목적으로 개발하였다.
2. 빙 토크와 진동계 요소 피로강도
대빙 선박에 관한 규정은 주로 스웨덴과 핀란드 선급에서 주도적인 역할을 해왔으며 계속 수정 보완하고 있다. 이 연구에서는 IACS(국제선급연합)(1)와 한국선급의 2018년 발행된 규정(2)을 중심으로 검토하고자 한다. Table 1은 대빙에 대한 등급별 빙 두께와 빙 강도 인덱스를 보인다. 이 연구에 적용된 선박은 PC7에 해당된다.
빙 토크에 대한 계산식은 D lim (= 1.81·Hice ) > D 일 때 식 (1)과 같으며, Dlim ≤ D 일 때는 식 (2)와 같다.
| (1) |
| (2) |
축계의 동역학 분석을 위한 프로펠러 빙 기진 토크는 날개에서 반 사인파로 일어나는 날개 충격을 순차적으로 나타내어야 한다. 프로펠러 회전각의 기능으로 단일 날개 빙 충격으로 인한 토크는 식 (3)과 식 (4)와 같다. 그리고 기진 토크를 위한 Cq, αi 는 Table 2와 같다.
| (3) |
| (4) |
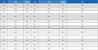
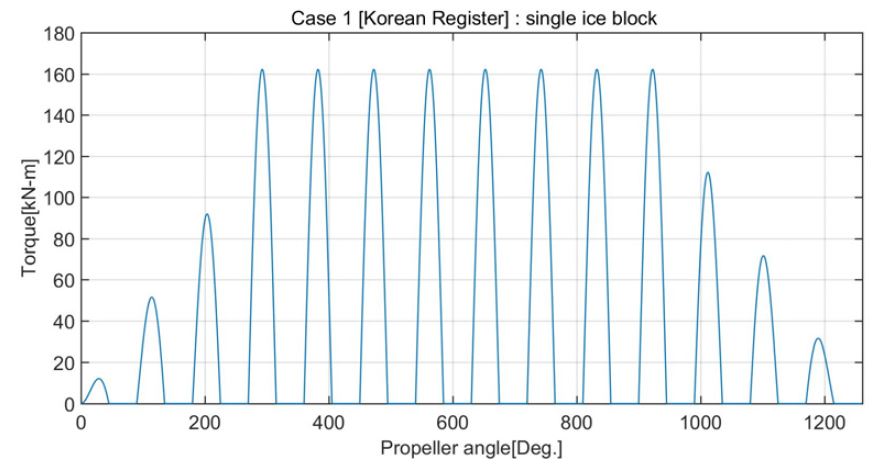
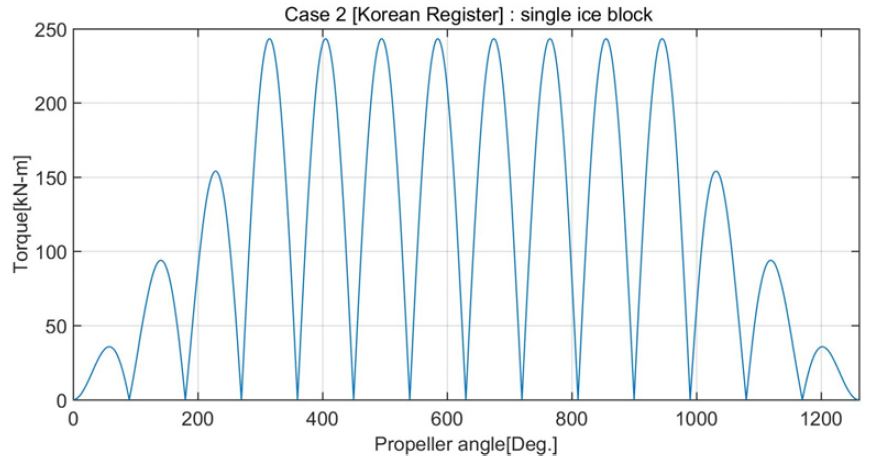
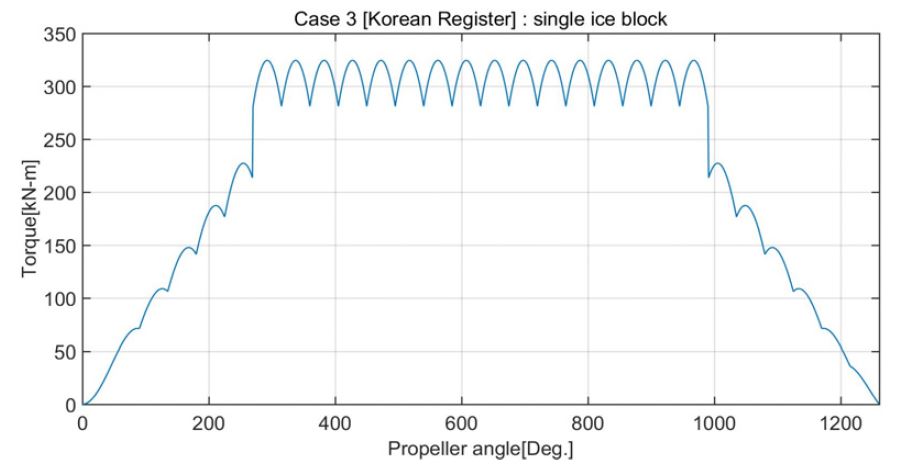
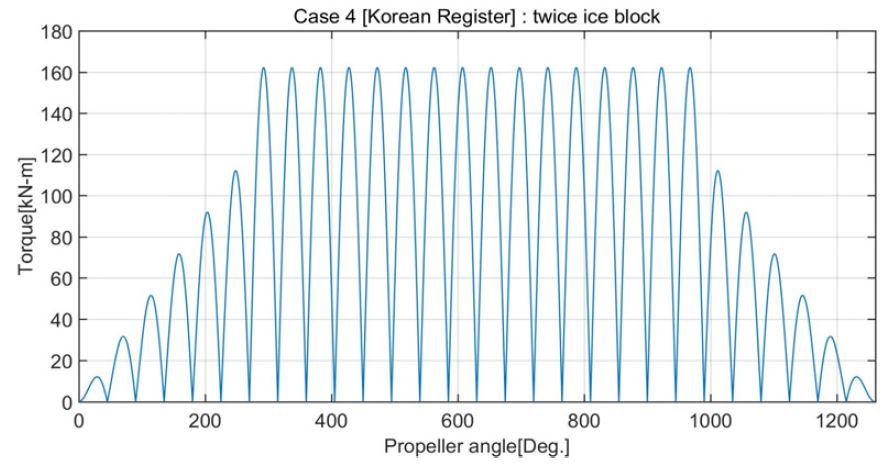
이 연구 선박의 프로펠러를 이용하여 Table 2의 각 경우 별 기진 토크를 계산한 결과를 Figs. 1 ~ 4에 보인다. 여기서 빙 충격 에너지 밀도는 case 3, case 2, case 4, case 1 순으로 진동계에서 실제 공진이 일어나지 않는다고 가정하면 이 순서대로 과도비틀림진동이 크게 된다.
축계 요소에 대한 피로강도는 DNV(노르웨이 선급)에서 추천한 Cassification Note 51·1(3)에서 광범위하게 언급하고 있다. 부분적으로 크랭크축은 IACS M53(4)으로 규정되어 있다.
중간축과 프로펠러축은 DNV에서 추천한 Cassification Note 41·4(5)와 IACS M68(6)을 중심으로 검토할 수 있으며 축경이 작은 중간축이 주 검토 대상이다. 기어는 IACS M56(7)을 이용할 수 있다. 유체 감쇠형인 Geislinger 커플링은 비교적 강재로 제작되어 검토 상 큰 문제가 없으나 고무 또는 최근 탄소섬유로 많이 제작된 커플링은 제작사의 가이드를 따르는 것이 바람직하다. 이러한 축계요소의 피로 누적은 빙해지역에서 선박의 운항시간과 계절을 고려하여 결정할 수 있다. 본선에 고무 탄성커플링을 제작 공급한 독일 Vulcan사(8)는 5×104 또는 106 사이클 중 하나를 택할 것을 추천하고 있다.
3. 과도비틀림진동 해석 S/W 개발
빙 토크를 적용할 수 있는 전문 S/W는 DNV를 비롯하여 일부 선급과 선박용 엔진설계사인 MAN ES에서 GTORSI를 개발하여 소개하고 있다(9). 그리고 선박용 디젤엔진 제작사인 기술제휴선은 이 프로그램을 주로 이용하고 있다. 주저자는 운전금지구역(BSR)에서 quick-passing의 순간적인 비틀림진동 응력평가를 위하여 과도비틀림진동 해석 프로그램을 개발하여 사용하여 왔으며, 해석방법으로는 직접 적분방법인 Newmark법을 이용하였다(10). 그러나 이 연구에서 복잡한 2기1축 시스템의 적용을 위하여 전반적으로 보완이 필요하였고, 누구나 손쉽게 사용할 수 있도록 범용성을 갖추도록 하였으며 본 선 해석에 이 수정된 프로그램을 이용하였다. 입력 자료는 기존 주파수 영역에서 해석할 수 있는 자체 전문 S/W를 이용할 수 있도록 하였다. 여기서 엔진기진력은 해당 엔진의 하모닉계수를 이용 합성된 기진력 파일을 자동적으로 생성하도록 하여 과도비틀림진동 해석 S/W에서는 이를 불러 사용하도록 하였다. 빙 충격 토크도 프로펠러를 중심으로 앞 장에서 소개한 4가지 경우 토크 계산을 하여 자동적으로 파일이 생성되도록 하였다. 동시에 진동계의 등가질량관성모멘트와 프로펠러의 부하곡선을 중심으로 토크마진율을 입력하여 빙 충격 토크에 의한 엔진 속도를 예측할 수 있도록 하였다. 다만 정확한 예측을 위해서는 엔진제작사에서 제공하는 엔진특성곡선과 과급기의 성능을 동시에 검토하여야 한다. 또한 빙 충격토크 대신에 클러치의 탈, 부착 시, 프로펠러의 외부 충돌 등 외부 기진력도 검토할 수 있도록 하였다. 이러한 기진력은 프로그램에서 계산하지 않고 별도로 작성된 외부파일을 불러서 처리하도록 하였다. 수치 적분 시 해석 시간 간격은 1 msec로 하였으며, 최대 480 sec까지 해석할 수 있도록 하였다. 그리고 일괄 처리된 해석결과는 Matlab을 이용 쉽게 그래픽처리를 하였다.
4. 실선해석
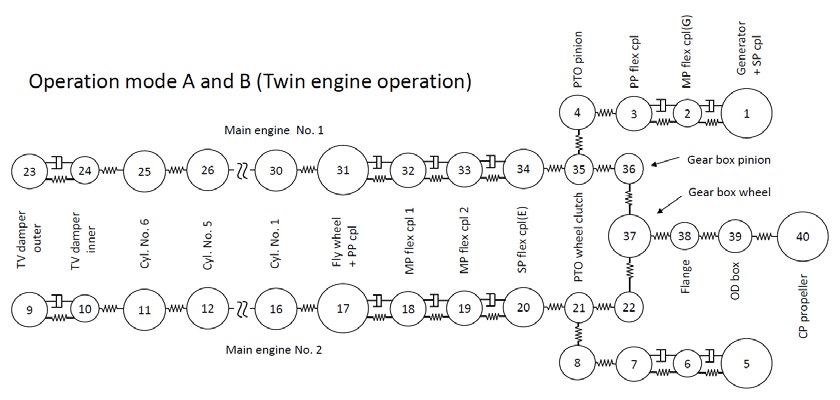
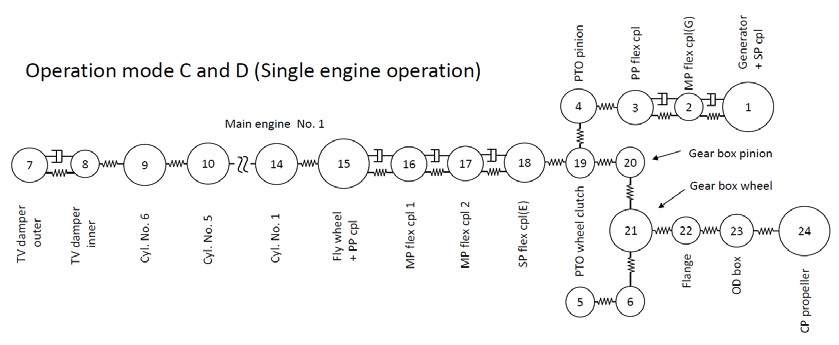
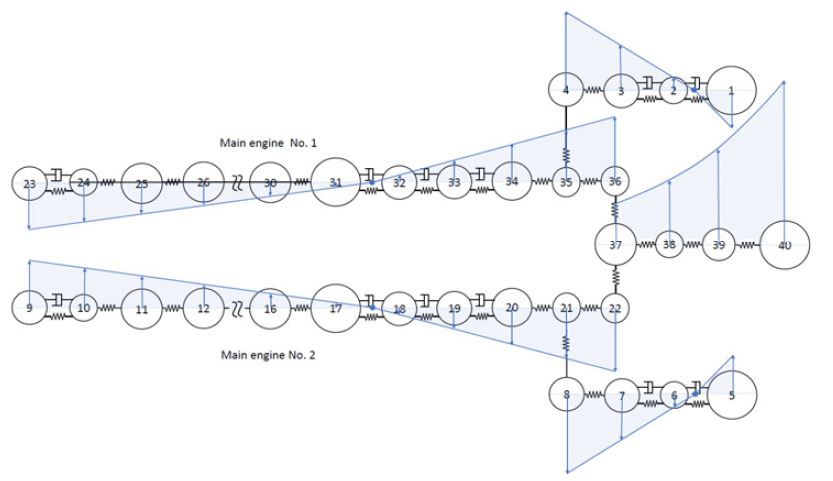
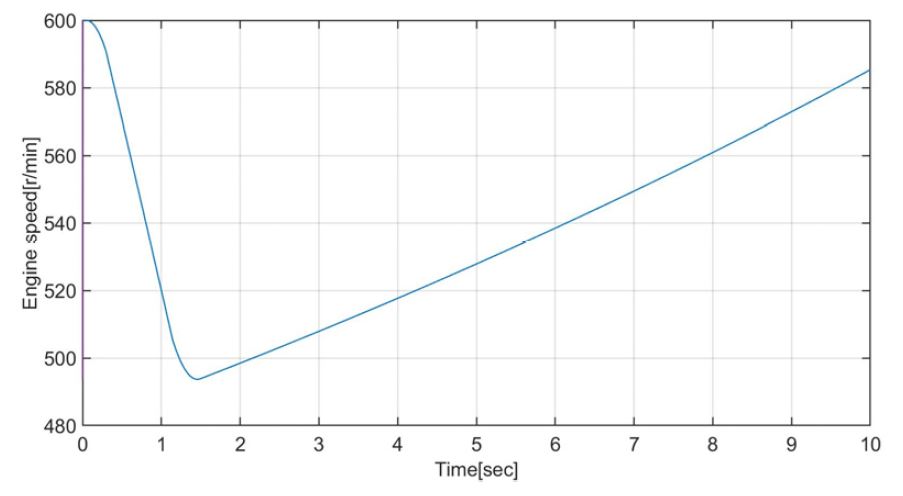
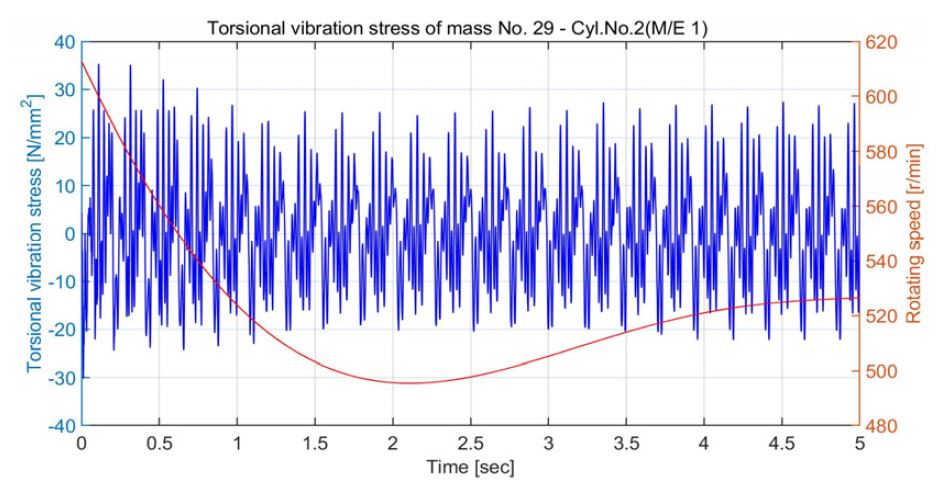
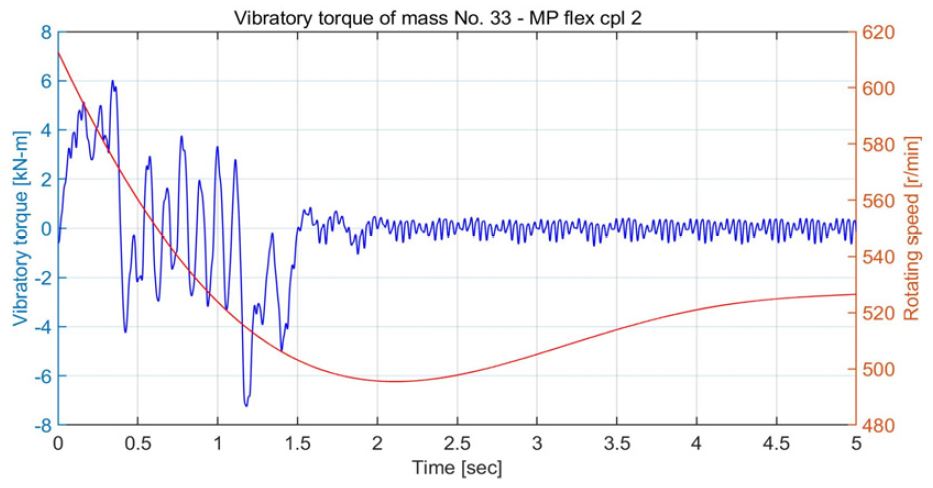
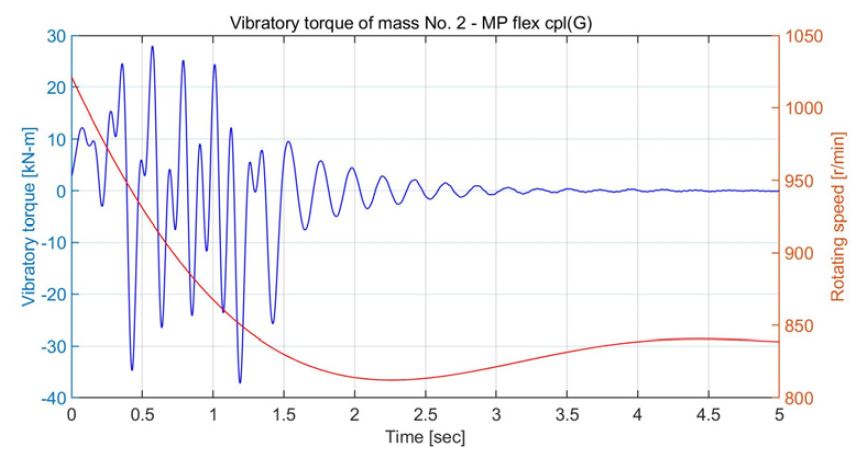
연구 대상 선박의 추진시스템의 요목은 Table 3과 같다. 운전 모드는 크게 2가지로 구분할 수 있으며, 2기1축 시스템의 질량-스프링 계는 Fig. 5와 같다. 여기서 질량번호 9번과 23번은 비틀림진동 댐퍼, 1번과 3번 사이, 5번과 7번 사이는 발전기 측에 설치된 고무 탄성커플링으로 Table 3의 발전기 탄성커플링 요목 2개가 직렬로 연결되어 있다. 17번과 20번 사이, 그리고 31번과 34번 사이는 엔진 측에 설치된 고무 탄성커플링으로 Table 3의 엔진 탄성커플링 요목에서 3개가 직렬로 연결되어 있다. 질량번호 38번과 39번 사이는 중간축이다. 그리고 편의상 전부하 상태의 프로펠러 피치를 운전 모드 A라 하고, 50 %부하의 프로펠러 피치를 운전 모드 B라 한다. 연구 대상 선박은 필요에 따라 1기1축으로 운항하는 경우가 있는데 이 경우 질량-스프링 계는 Fig. 6과 같다. 동일한 방법으로 전 부하의 운전모드를 C 그리고 50 % 부하의 운전 모드 D라고 한다. 비틀림진동 해석 S/W(주파수+시간영역)는 주 저자가 기업에 근무하면서 개발한 것으로 계속 개선하여 사용하고 있다. 주파수 영역의 해석은 전달매트릭스법을 그리고 시간영역은 직접적분방식의 하나로 Newmark 법을 이용하고 있다. 우선 충격하중에 영향을 주는 비틀림진동의 고유진동수를 계산한 결과를 Table 4에 보인다. 실제로 빙 토크에 영향이 가장 큰 고유진동수와 진동모드는 운전 모드 B에서 프로펠러의 상대진폭이 큰 4절 진동이며, 운전 모드 D에서는 2절 진동이다. Fig. 7은 운전모드 B에서 4절 진동의 진동모드를 보인다. 동일한 스케일을 적용하기가 어려워 프로펠러를 제외한 다른 부분은 상대진폭을 적용하였으며, 프로펠러는 축소된 스케일로 프로펠러인 질점 40번은 4번과 8번보다 상대진폭이 11배 크다. Fig. 8은 운전 모드 B에서 빙 토크 case 3(Fig. 3)의 빙 토크가 프로펠러에 가해질 때 엔진 속도의 예상 곡선이며, 빙 토크 에너지가 크기 때문에 하락속도가 상당히 크다. Fig. 9는 크랭크축의 비틀림진동 응력을 보이며 빙 토크의 영향력은 거의 없다. 즉 엔진 실린더에서 발생하는 연소가스와 피스톤의 관성력에 의해서 발생하는 비틀림진동이다. Fig. 10은 중간축의 비틀림진동 응력을 보이며 연속 운항은 아니더라도 5×104 ~ 106 사이클의 피로강도는 문제가 되지 않는다. Fig. 11은 발전기 탄성커플링의 진동토크로 Table 3의 ΔTm ax (5×104 사이클의 피로강도)를 만족하고 있다. Fig. 12는 엔진 탄성커플링의 진동토크로 1.5초 전에는 빙 토크의 영향으로 Table 3의 ΔTm ax 를 만족하며, 이후는 엔진 기진력에 의해서 발생하는 진동토크로 허용진동토크인 18.9 kN·m을 충분히 만족하고 있다. Fig. 13은 피니온 기어와 휠 사이의 진동토크로 피로강도의 검토 대상이나 본 논문에서는 관련 도면을 구하기가 힘들어 진동토크 계산으로 대체하였다.
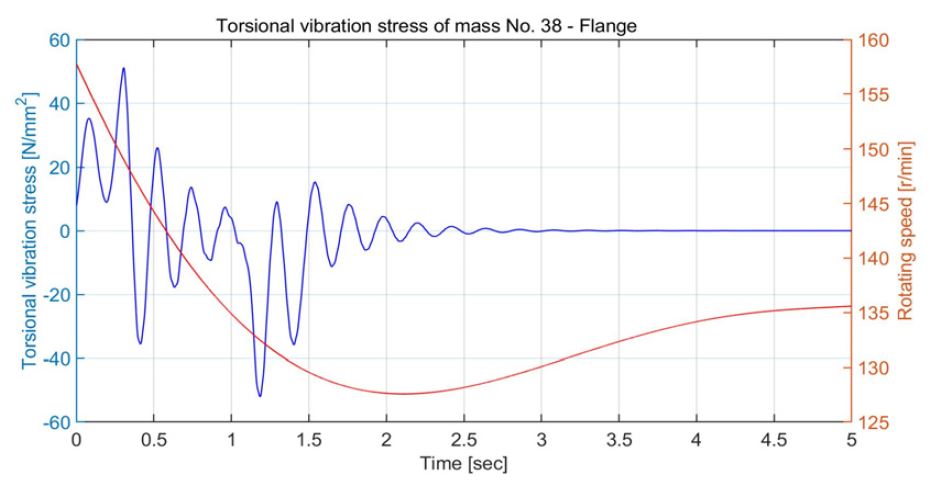
Torsional vibration stress of intermediate shaft in operation mode B due to case 3 torque excitation
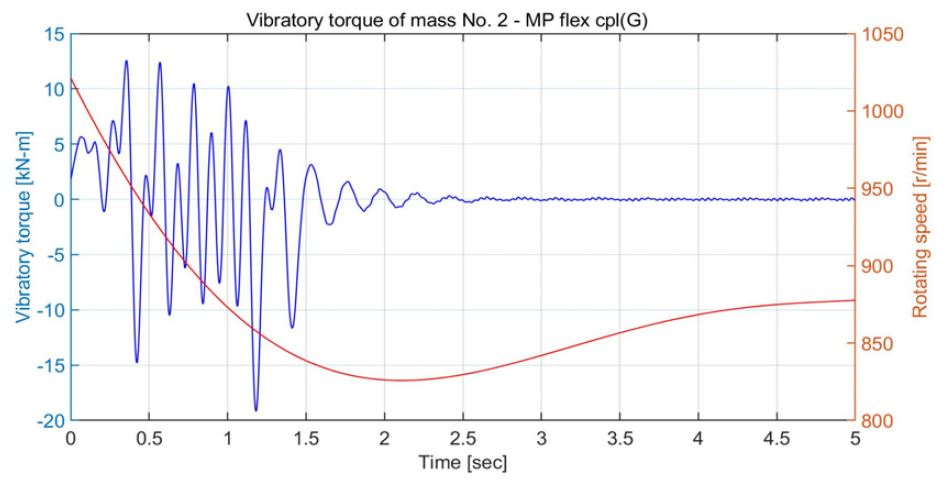
Vibratory torque of generator’s flexible coupling in operation mode B due to case 3 torque excitation
Vibratory torque between pinion gear and gear wheel in operation mode B due to case 3 torque excitation
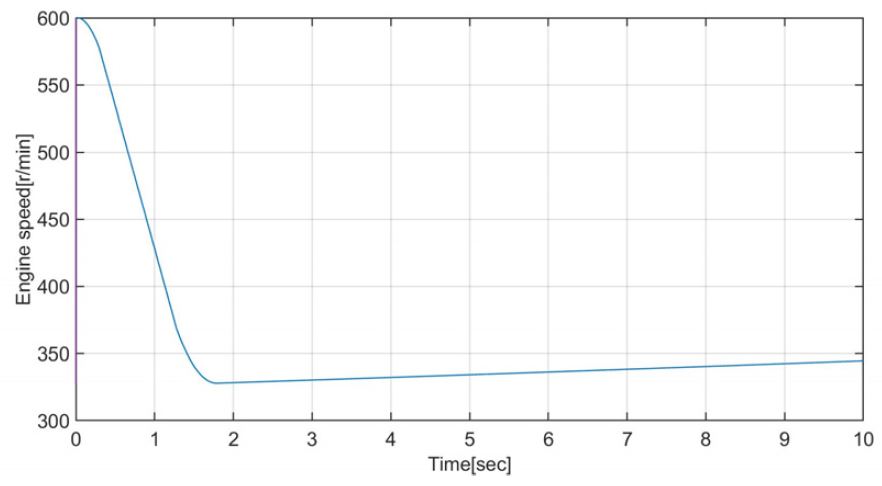
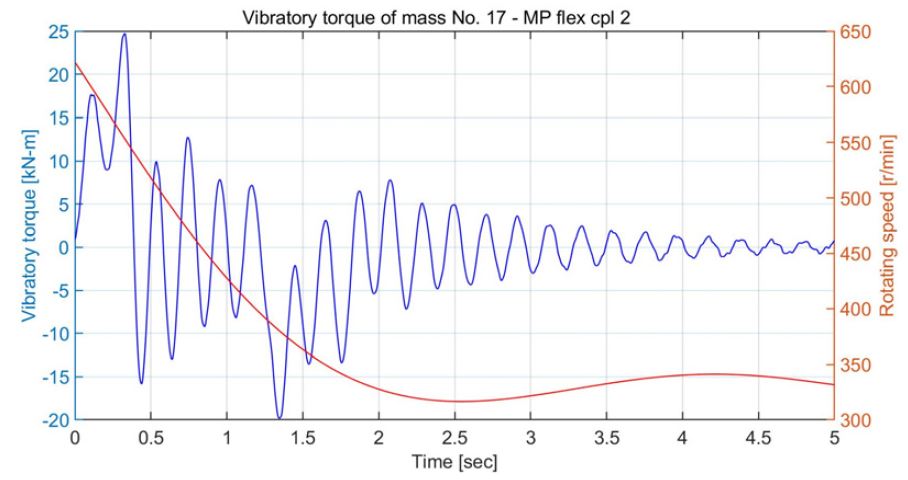
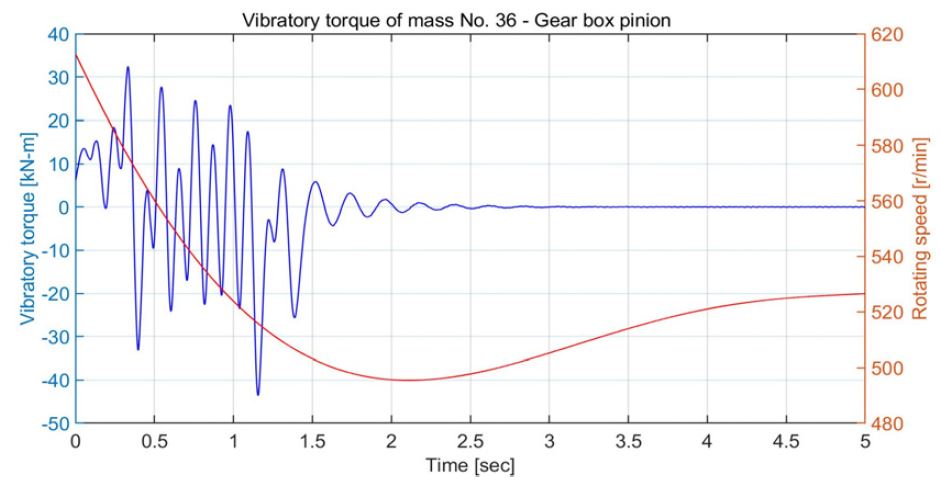
Fig. 14는 운전 모드 D에서 빙 토크 case 3(Fig. 3)이 프로펠러에 가해질 때 엔진의 속도 예측 곡선을 보이며, 엔진 및 발전기를 각각 한 대만을 사용하므로 Fig. 8과 비교하여 엔진의 하락속도가 더 크다. Fig. 15는 중간축의 비틀림진동 응력을 보이며 크기는 Fig. 10과 비교하여 큰 차이가 없으나 감쇠가 줄어들어 진동이 오래 동안 지속된다. Fig. 16은 발전기의 탄성커플링의 진동토크로 피로강도 ΔTm ax 을 만족하지 못하고 있다. Fig. 17은 엔진의 탄성커플링의 진동토크로 Table 3의 피로강도인 ΔTm ax 을 만족한다. Fig. 18은 피니온 기어와 휠 사이의 진동토크로 Fig. 13과 비교하여 약 3배 이상 증가하였다. 이들을 종합해 보면 운전 모드 D에서 case 3의 빙 토크가 가해질 때는 선박 운항이 어렵다. Fig. 19는 운전 모드 A에서 case 2의 빙 토크에 의해 가장 취약한 발전기 탄성커플링의 진동 토크로 제작사의 허용 값을 만족하여 운항에 지장이 없다. Fig. 20은 운전 모드 C에서 Fig. 19와 동일한 조건이지만 허용치를 초과한다. 결론적으로 이 추진시스템을 갖는 선박은 운전 모드 A, B로 빙해지역에서 운항이 가능하나 운전 모드 C, D는 유빙의 종류와 사용빈도수에 따라 결정할 수 있지만 발전기의 탄성 커플링을 보호하기 위하여 운항을 자제하는 것이 바람직하다. 동적인 응답으로 운전 모드 B의 경우 4절(4.78 Hz), 운전 모드 D에서는 2절 진동(4.74 Hz)이 지배적이다. 그리고 이 절들의 진동모드를 관찰해보며 발전기의 탄성커플링과 엔진의 탄성커플링에 모두 절점이 있어 프로펠러 날개수의 초기 가진주파수는 10.3 Hz로 상당히 떨어져 있는 ‘overcritical design’으로 빙 토크를 감소시키는데 적합하였다.
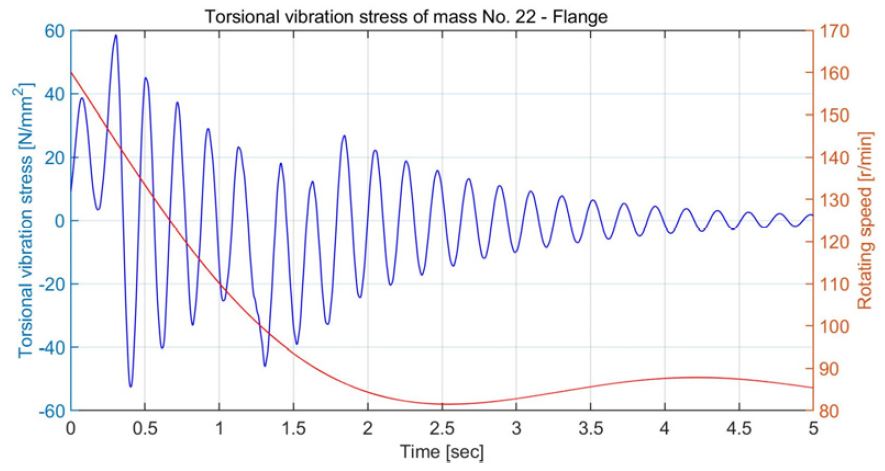
Torsional vibration stress of intermediate shaft in operation mode D due to case 3 torque excitation
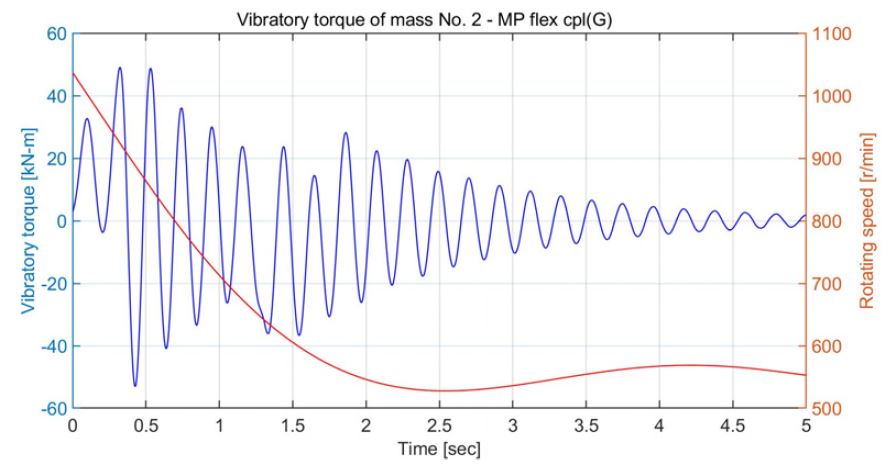
Vibratory torque of generator’s flexible coupling in operation mode D due to case 3 torque excitation
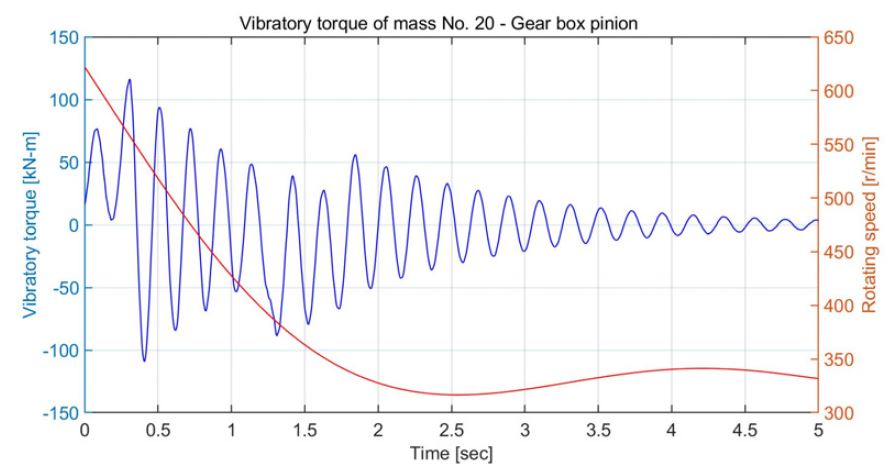
Vibratory torque between pinion gear and gear wheel in operation mode D due to case 3 torque excitation
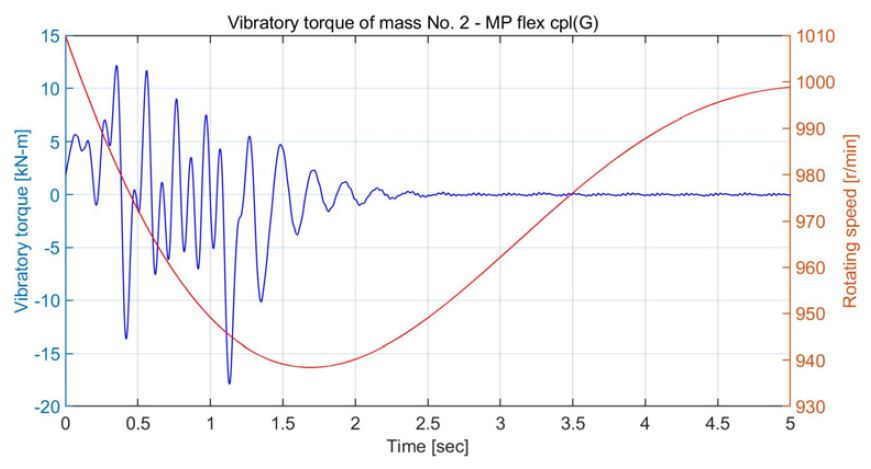
Vibratory torque of generator’s flexible coupling in operation mode A due to case 2 torque excitation
5. 결 론
선박용 2기1축 추진시스템의 빙 하중에 대한 동적 특정을 확인하였으며 이를 정리 요약하면 다음과 같다.
(1) 2기1축 시스템은 빙 하중을 받을 때 전체 등가관성모멘트가 크고 프로펠러축으로 전달된 빙 충격토크는 양쪽의 엔진과 발전기에 분산되어 1기1축으로 운전하는 것보다 안정적이었다.
(2) 빙 충격 토크는 진동계 요소 중에서 가까운 곳에 그리고 등가질량이 큰 곳에 집중적으로 전달된다. 따라서 1기1축 시스템에서 등가관성모멘트가 큰 발전기에 연결된 탄성커플링에 진동토크가 증가하여 가장 취약하였다.
(3) 빙 충격 토크에 의한 축계 요소들의 피로강도에 대한 기준은 현재 정착되어 가고 있는 중이다. 이중에서 중간축을 비롯하여 강철로 제작된 축계 요소들은 지금까지 경험 자료를 이용 판단이 가능하나, 고무와 탄소섬유와 같은 비철 재질로 제작된 축계요소들은 온도에 민감하고 피로시험을 통한 경험이 부족하여 신중하게 검토되어야 한다.
기 호 설 명
| D : | 프로펠러의 지름 |
| d : | 프로펠러 허브의 바깥지름(m) |
| EAR : | 날개의 전개 면적비 |
| Hice : | 강도설계를 위한 빙 두께(m) |
| n : | 프로펠러의 회전속도(rev./s) |
| P0.7 : | 반지름 0.7 R에서 프로펠러 피치(m) |
| Sice : | 날개 빙 힘의 빙 강도 인덱스 |
| Sqice : | 날개 빙 토크의 빙 강도 인덱스 |
| t0.7 : | 반지름 0.7 R에서 최대 날개 단면 두께 |
| Z : | 프로펠러의 날개 수 |
Acknowledgments
이 연구는 산업통상자원부 소관 산업융합기반구축사업의 “중소형 선박엔진 및 관련기자재 공인시험인증센터 구축” 사업의 지원(과제번호: N0001679)을 받아 수행되었습니다.
References
- International Association of Classification Societies, 2016, Requirements Concerning Polar Class, IACS I1, I2 and I3.
- Korean Register, 2018, Ice Class Ship Rules.
- Det Norske Veritas, 2011, Ice Strengthening of Propulsion Machinery, DNV Classification Note 51.1.
- International Association of Classification Societies, 2017, Calculations for I.C. Engine Crankshafts, IACS M 53(Rev3).
- Det Norske Veritas, 2002, Calculation of Shafts in Marine Applications, DNV Classification Note 41.4.
- International Association of Classification Societies, 2015, Dimensions of Propulsion Shafts and Their Permissible Torsional Vibration Stresses, IACS M 68(Rev2).
- International Association of Classification Societies, 2015, Marine Gears – Load Capacity of Involute Parallel Axis Spur and Helical Gears, IACS M 56(Rev3).
- Hilbk, D., Dylla, M. and Bauermester, R., 2017, Assessment of Ice Loads based on IACS/FSICR on the Highly Flexible Rubber Coupling, Proceedings of the 2nd Torsional Vibration Symposium, Salzburg, Austria, Paper No. 3B-2.
-
Persson, S., 2014, Ice Impact Simulation for Propulsion Machinery, Proceedings of the 1st Torsional Vibration Symposium, Salzburg, Austria, Paper No. 23.
[https://doi.org/10.1007/s40353-015-0500-2]

-
Barro, R. D., Eom, K. T. and Lee, D. C., 2015, Transient Torsional Vibration Response due to Ice Impact Torque Excitation on Marine Diesel Engine Propulsion Shafting, Transactions of the Korean Society for Noise and Vibration Engineering, Vol 25, No. 5, pp. 321~328.
[https://doi.org/10.5050/KSNVE.2015.25.5.321]


Don Chool Lee received his Dr. Eng. from Mechanical Engineering department at Korea Maritime University in 1995. He worked at Hyundai Heavy Industries from 1983 to 1999. He is now a professor of Mokpo National Maritime University.

Myeongho Song received his M. Eng. from Mokpo National Maritime University in 2008. He is now working Ship Repair Supporting Center. Also, he is Ph.D. candidate at Dynamics Lab. of Mokpo National Maritime University.

Quang Dao Vuong received his Ph.D. degree from Mokpo National Maritime University, South Korea. Now he is researcher at Dynamics Lab. of Mokpo National Maritime University.

Jae-ung Lee received Ph.D(2016) from Department of Marine System Engineering of Korea Maritime and Ocean University(KMOU). He worked at Korean Register (2007-2016) and Mokpo National Maritime University(2016-2019) and now a professor of KMOU.