소음 신호를 이용한 딥러닝 이용 파워 드라이빙 시스템의 건전성 감시
© The Korean Society for Noise and Vibration Engineering
Abstract
The power driving system (PDS) comprises parts such as the chain, sprocket, gear, bearing, and rotating shaft. The purpose of this study is to develop a condition-monitoring device that diagnoses component defects early by using a convolutional neural network to prevent complete damage due to component defects. For this study, eight types of defects are artificially manufactured in various parts and assembled to build a PDS. A convolutional neural network is developed to classify and diagnose the eight types of defects. A feature for faults is successfully extracted, and fault classification is achieved with 90 % accuracy.
Keywords:
Convolutional Neural Network, Continuous Wavelet Transform, Power Driving System키워드:
합성곱 신경망, 연속 웨이블렛 변환, 동력 구동 시스템1. 서 론
파워 드라이빙 시스템(이하 ‘PDS’라 한다.)은 큰 동력을 필요로 하는 공작기계, 자동차 엔진 타이밍 시스템 등 다양한 산업 분야에서 중요한 기계 시스템으로 적용되었다. 따라서 PDS에서 발생하는 결함을 조기에 발견하여 경제적 손실과 인명 피해를 미연에 방지하기 위해 여러 기법들이 연구되어오고 있다. 이 연구에 사용되는 PDS은 모터, 기어, 피니언, 베어링, 체인 등으로 구성되어 있다. 선행 연구에 의하면 PDS결함은 동력을 전달하는 샤프트와 기어를 지지하는 베어링의 결함 또는 체인의 파손(1~3)에 의해 발생한다. 결함을 조기에 발견하기 위해서 일반적으로 음향 진동 신호를 측정하여 측정된 신호로부터 결함의 특징을 추출하여 결함의 유무를 판단한다. 측정된 음향 진동 신호로부터 결함특징을 추출하기위해서 다양한 방법이 사용되어 왔다. 시간 평균법(4), 캡스트럼 분석(5), 스도-위그너-빌 분포(6) 웨이블렛 변환(7), 고차항 방법(8), 적응형 선 향상법(9), 경험적 모드 분해(10), 주기정상적 분석(10,11)과 같은 특징추출 방법이 사용되어 왔다. 이 방법들 중에 연속 웨이블렛(CWT: continuous wavelet transform) 분석방법은 비직교 웨이블렛 변환 방식이고 신호의 시간-주파수 영역에서 결함정보를 추출하는 장점이 있다. 따라서 CWT가 결함 신호의 시간-주파수 분석에 널리 사용되었다. 결함특징을 활용하여 결함의 종류를 분류하기 위해 최근접 이웃 알고리듬(12), 베이지안 분류기(13), 지지 벡터 기계(14), 그리고 인공신경망(15) 등이 사용되어오고 있다. 최근에는 인공지능학습 알고리듬의 개발로 특징추출 및 결함패턴을 분류하는 딥러닝 기술이 높은 정확도와 편리성을 갖고 적용되고 있다(16~23). 딥러닝 (deep learning) 기술을 활용한 회전 기계의 고장 진단과 관련된 논문은 대부분 베어링 마모 패턴(16,18~20), 기어 치열 패턴(17,21,22), 그리고 불균형 회전축(23)과 같은 특정 단일 부품 결함의 분류에 중점을 두고 있다. 따라서 이 연구에서는 베어링, 기어, 샤프트 등의 부품들이 결합된 경우 소음 신호를 측정하여 결함 유발 부품의 결함을 진단하고 결함의 패턴을 분류하는 딥러닝 기술을 개발하였다. 이 연구에 사용된 딥러닝 기술은 합성곱 신경망 (CNN: convolutional neural network)을 기초한 것이며, CNN는 입력데이터로 이미지를 요구함으로, 측정된 소음 신호에 CWT를 활용하여 이미지 데이터를 생성하여 CNN의 입력데이터로 사용하였다. 이 연구에서 개발된 CWT 및 CNN을 활용한 PDS의 결함진단 및 패턴 분류 기술은 90 %의 정확도를 나타냄을 확인하였다.
2. 이 론
2.1 연속 웨이브렛 이론
| (1) |
여기서, a는 주파수축으로 스케일링 요소이며, b는 시간축으로 이동값이며, ψ는 모 웨이블렛으로 시간과 주파수 영역에서 국부화된 고정함수이다. 함수 ψa,b는 시간 도메인에서 이동(b-tanslation)과 주파수 도메인에서 모웨이블렛으로 스케일링(a-dilation)을 적용한다. 이 연구에서 사용된 모 웨이블렛은 모아렛(morlet) 웨이블렛이며 식 (2)와 같이 정의된다.
| (2) |
w0모 웨이블렛이 주파수 도메인으로 변환될 때 모 웨이블렛의 중심 주파수이다. 이 연구에서는 측정된 소음신호를 CWT에 적용하여 시간-주파수 영역의 이미지 데이터를 생성하여 CNN의 입력데이터로 사용한다. CWT는 DWT 보다 시간-주파수 분해능이 우수하여 연산기간이 소요되나 결함에 대한 주파수 시간-주파수 정보를 잘 추출할 수가 있다.
2.2 합성곱 신경망 이론
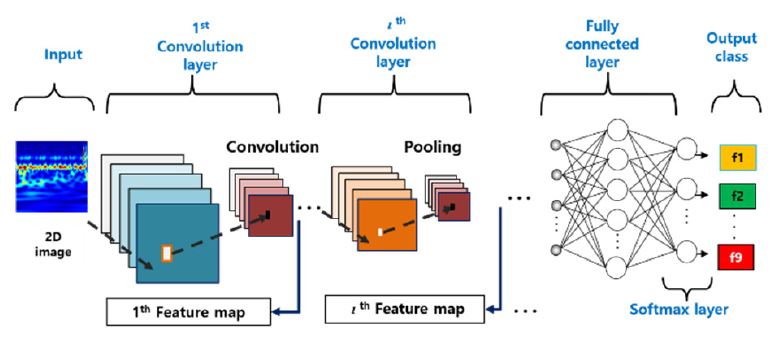
인공지능 기술은 인간의 뇌를 모사한 신경망기술을 적용하여 소음 및 진동 신호의 예측 및 분류에 널리 사용되었다(24~27). 심층신경망(DNN: deep neural network)이 도입되기 전에 얕은 신경망(SNN: shallow neural network) 구조를 가진 인공지능 신경망(ANN: artificial neural network)이 사용되었다. SNN은 신경망의 지도 학습을 위해 이미 알려진 특징벡터를 사용한다. 이 경우 동적 시스템의 결함 특징을 알고 있어야 한다. 그러나 결함 종류가 복잡하여 동적 시스템의 결함특성을 알 수 없는 경우 시스템의 결함에 대한 특징벡터의 추출이 어렵다. 이 경우는 DNN을 이용하여 특징을 추출하는 방법을 사용한다(28). 최근에 널리 사용되는 CNN은 DNN 구조 중 하나이며 데이터의 흐름도는 Fig. 1과 같다. Fig. 1은 전형적인 CNN 구조를 보여준다. CNN은 측정된 소음 신호에 CWT를 통하여 얻은 이미지데이터를 여러 개의 합성곱 층(layer) 및 풀링 층(pooling layer)을 통하여 이미지 데이터로부터 결함정보를 추출한다. CNN의 신경망은 여러 개의 합성곱층 및 풀링층의 단계로 이루어져 있으며, 각 합성곱 층에서 결함정보를 가진 특징지도(feature map)를 추출할 수 있다. l번째 합성곱 층에서 특징지도는 다음과 같이 식 (3)을 통하여 얻을 수 있다.
| (3) |
여기서 ∅은 비선형 활성화 함수이고 은 l번째 층의 스칼라(scalar) 바이어스(bias)이다. 는 번째 층에서 선택된 특징지도이다. ⊗는 이전 층의 활성화 함수를 합성곱하는 합성곱 연산자를 나타낸다. 는 2차원 필터(filter)이며 필터의 가중치는 특정한 특징을 감지하도록 학습된다. 따라서 새로운 입력 이미지의 정확한 분류를 위해 서로 다른 카테고리를 구별할 수 있는 연속적인 단계에서 효과적인 특징 선택이 필요하다. 이러한 이유로 풀링 층이 사용되며 번째 풀링 층 은 식 (4)와 같다.
| (4) |
χ는 에 의해 축소된 평균 또는 최대값 함수와 같은 축소 함수이다. 그리고 는 축소되기 위한 합성곱된 특징지도이다. CNN의 입력값이 연속적으로 합성곱 및 풀링 과정을 지나면서 네트워크는 모든 이미지를 효율적으로 특징을 추출하는 학습을 진행한다. 마지막 신경망 층의 출력값 yp는 식 (5)와 같이 주어진다.
| (5) |
는 출력 층의 바이어스이고, W는 완전히 연결된 층의 입력 층과 출력 층 사이의 가중치 행렬이며, f는 완전히 연결된 층의 특징을 나타내는 특징 벡터 (feature vector)를 나타내고, ψ는 결함을 분류하는 소프트 맥스(softmax) 함수이다(28). 학습매개변수 및 W는 학습 과정에서 최적화된 값이 결정된다. 실제 출력값과 원하는 목표값 간의 오차를 최소화하기 위해 확률적 경사하강법(SGD : stochastic gradient descent)를 통해 학습매개변수의 최적화가 이루어진다. 여기서 경사값은 역전파(back propagation) 방법을 통하여 계산된다(29).
3. 실 험
3.1 PDS 실험장치 및 결함 패턴
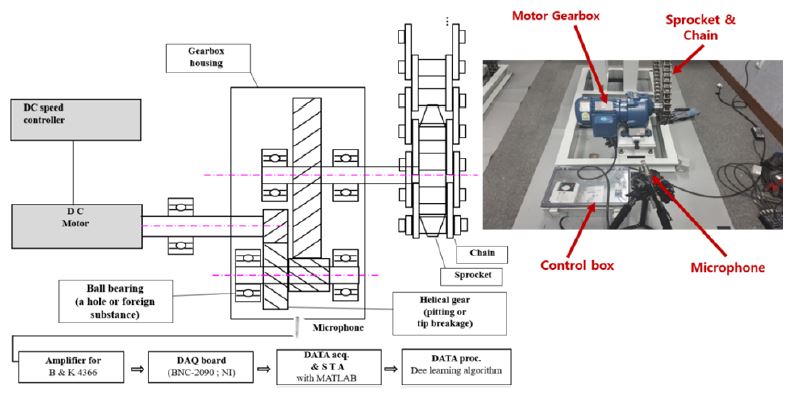
Fig. 2는 실험에 사용된 PDS 실험장치의 구성도 및 제어장치를 나타낸다. PDS는 동력전달의 구동을 위해서, 모터, 기어박스, 베어링, 체인시스템 등의 기계부품으로 구성되어 있다. 이 연구에서는 연구목적을 위하여 인위적으로 이들 기계부품들에 결함을 만들어 제작 결합하였다. PDS의 구동 중 기계부품들의 결함부터 발생하는 이상소음을 측정하고, 결함의 패턴을 분류하기 위해서, 소음 측정용 마이크로폰을 설치하였다. 측정된 소음 데이터는 계측장비를 통하여 디지털 데이터로 변화된 후 신호분석용 컴퓨터로 전송된다. 신호분석용 컴퓨터에서는 결함부품을 진단하고 결함의 패턴을 분류하는 작업을 시행한다.
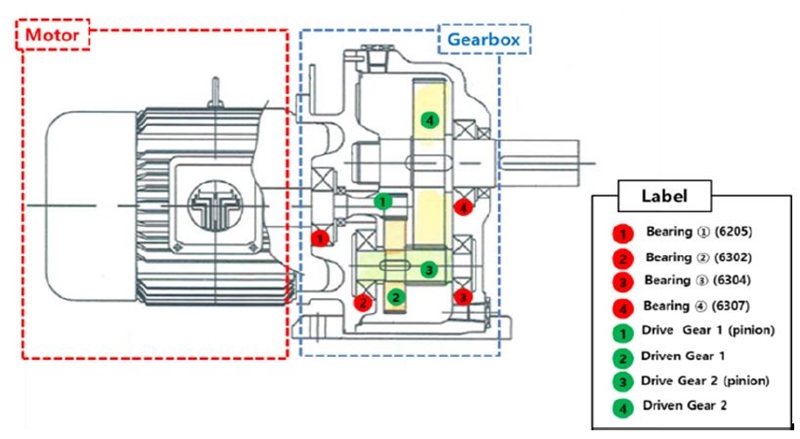
Fig. 3은 PDS에 적용된 베어링 및 기어 등에 대한 상세위치를 나타낸다. 실험용 PDS는 4개의 베어링, 4개의 기어, 1개의 체인, 2개의 스프라켓 및 1개의 모터로 구성되어 있다. 입력용 구동축의 회전 속도는 1800 r/min(30 Hz)이고 출력용 구동축의 회전 속도는 59.4 r/min(0.99 Hz)이다. 감속비는 30이다. 이 연구를 위한 인위적 결함은 모터 샤프트, 베어링, 기어에만 적용하였다. 스프라켓 및 체인에는 결함이 발생하면 완전 파손이 발생할 수 있음으로 인위적 결함을 적용하지 않았다. 각 인위적 결함 샘플은 2개 ~ 3개 제작하였으나 실제 사용된 것은 각각 1개의 샘플에 대한 실험데이터를 이용하였다.
이 연구에 적용된 인위적 결함의 패턴은 다음과 같다.
- ∙ 구동 기어 2의 치차 크랙 (결함 1)
- ∙ 구동 기어 2의 치차 절손 (결함 2)
- ∙ 모터에서 구동축의 편심(결함 3)
- ∙ 베어링 ①의 구멍으로 인한 외륜 결함 (결함 4)
- ∙ 베어링 ①의 이물질로 인한 내륜 결함 (결함 5)
- ∙ 모터의 구동축 편심 + 구동 기어 2의 치차 절손 (결함 6)
- ∙ 모터의 구동축 편심 + 구동 기어 2의 치차 절손 + 베어링 ①의 외륜 결함 (결함 7)
- ∙ 모터의 구동축 편심 + 구동 기어 2의 치차 절손 + 베어링 ①의 내륜 결함 (결함 8)
- ∙ 정상 상태 (정상)
3.2 실험측정 장비
PDS의 소음 데이터는 Fig. 2와 같이 방사 소음을 측정하기 위해 PDS에서 1 m 떨어진 위치에 마이크를 배치하였다. 1/2인치 free-field microphone (B & K 4189, 덴마크)를 사용하여 소음 데이터를 측정하였고 Data Acquisition System(NI 9233, USA)을 통해 컴퓨터로 전송했다. 이러한 설정으로 section 3.1에 나와있는 정상 및 결함 상태의 데이터를 획득하였다. 각각의 결함 조건에 대해 실험을 수행하였고 총 700번의 실험을 수행하였다. 각각의 테스트 구동시간은 5분이며, 마이크를 사용하여 마지막 30초의 소음 데이터를 획득하여 결함진단에 사용하였다.
4. 데이터 신호처리
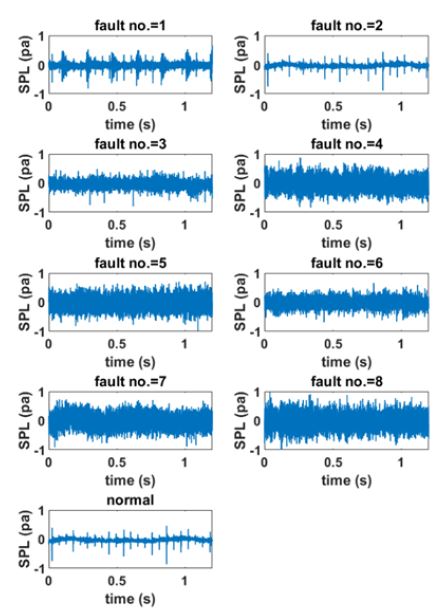
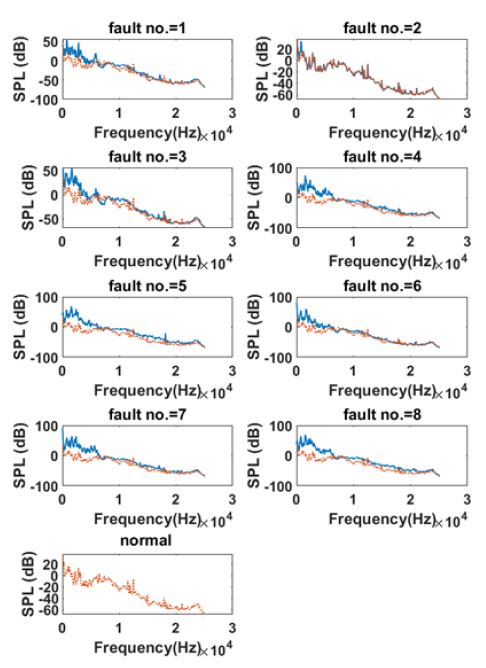
시간 영역에서 측정된 소음 데이터는 MATLAB (MathWorks, USA) 신호 처리 툴박스를 사용하여 주파수 및 CWT 분석을 시행하였다. Fig. 4는 마이크로폰으로 측정한 8개의 결함 및 1개의 정상 신호의 시간영역 데이터를 나타낸다.
Fig. 5는 정상 소음 신호와 8개의 고장 소음 신호의 파워 스펙트럼을 각각 비교한 것을 나타낸다. 8개의 고장 신호의 파워 스펙트럼은 정상 신호의 파워 스펙트럼의 형태와 차이가 난다. 회전 기계의 진동이론(30~33)에 따르면, PDS와 같은 회전기계의 경우, 기계의 진동 소음을 유발하는 여러 가진력이 존재하는데, 기어 맞물림으로 인한 가진력, 베어링의 구름 접촉으로 인한 접촉가진력, 그리고 모터의 샤프트의 가진력 및 스프라켓과 체인의 충격으로 인한 충격 가진력 등이 있다. 이들 가진력은 PDS의 정상적인 조건에서도 존재함으로 기본적으로 존재하는 소음 진동이다. PDS의 8개 결함으로 이들 가진력은 변화되며, 변화된 가진력은 소음신호에 주파수 스펙트럼의 변화를 일으킨다. 따라서 8개 고장 신호의 파워 스펙트럼은 정상 신호의 파워 스펙트럼의 형태와 차이가 나타난다.
5. 다중 결함 분류를 위한 CNN
5.1 CNN의 입력 데이터
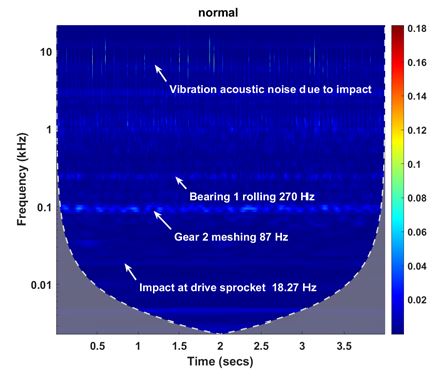
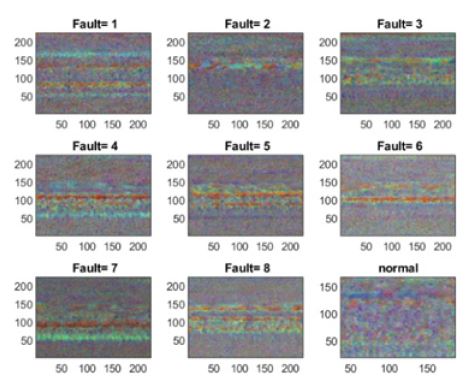
최근에 DNN을 기반으로 하는 비지도 학습의 분류 방법이 PDS의 결함진단을 위해 제안되었다(18~23). 특히 CNN을 활용한 기술이 다양한 분야에 적용되고 있다. PDS가 작동 중에 기어, 베어링, 샤프트 편심 등 여러 부품에서 결함이 존재하는 경우 특징 벡터를 추출하기가 어렵다. 이 경우 CNN과 같은 DNN을 사용하면 결함특징에 대한 정보가 자체적으로 추출된다. CNN은 결함정보를 갖는 이미지를 CNN의 입력 데이터로 사용한다. 이 연구에서는 마이크로폰으로 측정된 소음 신호에 CWT를 적용하여 이미지 데이터를 생성한다. CWT를 통하여 분석된 이미지 데이터는 Fig. 6에서 보여주는 바와 같이 PDS의 운전상태에 대한 정보를 제공한다. Fig. 6은 PDS의 정상 운전 조건에서 측정된 소음신호에 대한 CWT 결과이다. 이 결과에 따르면 정상조건에서 각종 부품의 가진력과 관련된 소음신호가 발생됨을 알 수 있다. 결함이 발생하는 경우 소음신호의 CWT는 변화하게 된다.
이 연구에서는 8개의 결함조건에서 30초마다 측정된 소음 데이터에 대해서 CWT를 적용하여 이미지를 구한 후 CNN의 입력데이터로 사용하였다. 각 결함 강 100개의 CWT 이미지를 구하고, 정상조건을 포함하여 총 900개의 이미지 데이터를 CNN의 입력 이미지 데이터로 사용하였다. 각 이미지의 데이터 크기는 244×244×3이다.
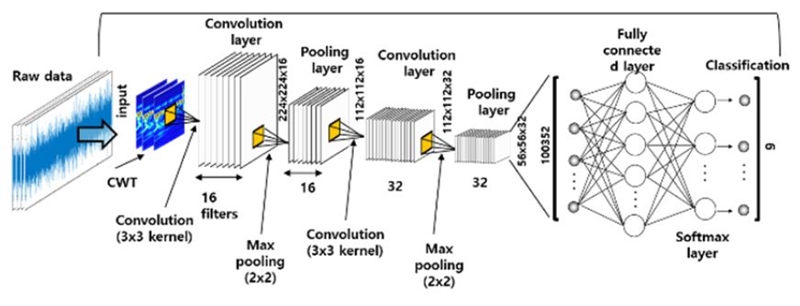
5.2 CNN의 구성과 학습
CWT 알고리즘은 MATLAB (MathWorks, USA)에서 제공한 CNN 툴박스가 사용되었다. CNN을 결함패턴 분류 및 결함특징 추출에 성공적으로 적용하기 위해서는 네트워크의 아키텍처 구성이 중요하다. 네트워크의 아키텍처 구성에 필요한 특별한 기술은 없으며 다양한 구성을 통하여 최적의 아키텍처 구성 찾는 것이다. 이 연구에 사용된 최적의 구성은 Fig. 7과 같다. 구성에 따르면 CWT 이미지가 입력되는 입력층과 입력층 다음에 위치하는 첫 번째 층은 필터 크기가 3×3인 16개의 특징지도가 있는 합성곱 층이다. 그다음은 크기가 2×2인 풀링 층이 있다. 그리고 그다음 층은 필터 크기가 3×3의 32개의 특징 지도와 2×2 사이즈의 풀링 층이 있는 합성곱 층이다.
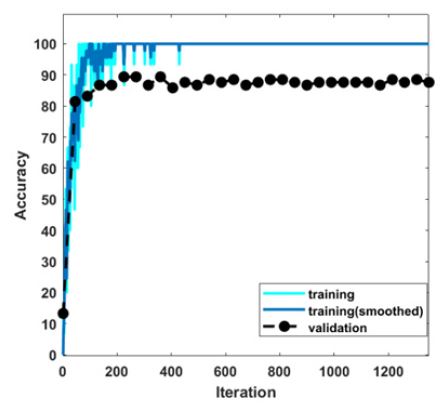
출력 층은 8개의 결함과 1개의 정상 조건에 대응하는 9개의 뉴런이 있다. 마지막의 최종 합성곱 층 (fully connected layer)에는 분류 함수로 softmax 함수가 적용되었다. SGD 학습 방법으로 최적화하고, 학습과정의 학습율은 0.001의 초기 학습 속도로 네트워크를 학습시키는 데 사용되었다. Batch 크기는 128로 취하였다. 학습은 1300회를 반복 (30 epoch)하여 수행되었다. 학습이 진행되는 동안 정확도는 Fig. 8에 나타나 있다.
최적의 가중치 값은 최소의 오차로 400회를 학습 후 얻어졌다. 학습을 위해 900개의 샘플 중 3/4 샘플은 학습에 사용되었고 1/4 샘플 중에 1/2은 네트워크 검증(validation)에 1/2은 테스트에 각각 사용되었다.
5.3 결과 분석
분류의 정확도는 총 테스트 샘플 수에서 정확하게 분류된 테스트 샘플 수의 비율이며 식 (6)과 같다(20).
| (6) |
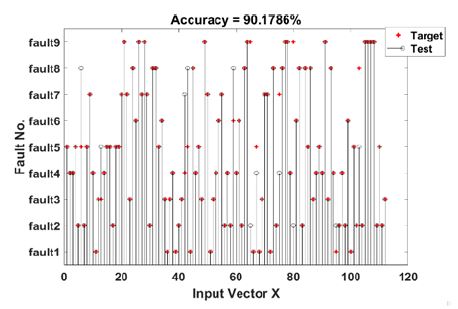
이번 실험에서 100개의 테스트 샘플 중 90개의 샘플이 Fig. 9와 같이 정확하게 분류되었다.
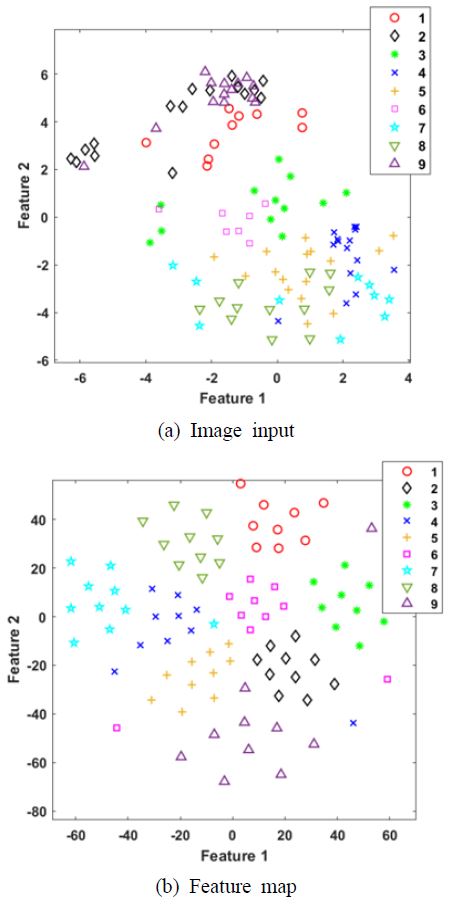
CNN의 학습결과 8개의 결함 및 1개의 정상 상태의 특징지도가 최종 합성곱 층에서 추출되었다. 특징지도는 Fig. 10과 같다. 이 결과에 의하면 각 결함에 대하여 다른 이미지를 나타냄을 알 수가 있다. 특징지도는 결함특징을 나타내는 숫자가 224 × 224 × 3으로 매우 많다. 이것을 2개의 특징 숫자로 변환하는 방법으로 t-확률적 임베딩(t-SNE: t-stochastic neighbor embedding)(34)을 활용하였다. 특징 지도를 방법을 이용하여 고차원 데이터를 2차원(2 dimension) 데이터로 변환하였다.
Fig. 11(a)는 CNN의 100개의 학습 전 입력 이미지에 대한 2차원 특징을 나타낸다. Fig. 11(b)는 CNN에 의해 학습된 10개의 특징지도에 대한 2차원의 특징을 보여준다. 입력 이미지의 2차원 특징은 무작위로 흩어지기 때문에 결함과 정상 상태의 분류를 어렵게 만든다. 그러나 학습된 특징지도에 대한 2차원 특징은 결함에 대한 그룹화가 선명하다. 즉 초기 학습하기 전의 이미지는 분류가 어려우나, 학습 후 나타난 Feature(Fig. 10) 이미지의 경우 분류가 명확하게 나타납니다. 따라서 학습된 CNN은 결함상태와 정상상태를 분류할 수 있음을 알 수 있다.
6. 결 론
이 논문에서는 CWT와 CNN을 결합하여 PDS에 대한 새로운 건전성 감시 방법을 제안하였다. 실험을 위해 8개의 단일 결함 및 다중 결함과 1개의 정상 상태가 인위적으로 제작되었다. 소음 데이터는 PDS에서 1 m 거리에서 마이크를 사용하여 측정하였다. 시간 영역에서의 1차원 소음 신호를 CWT를 적용하여 시간 스케일 이미지로 변환하였다. 이러한 이미지는 CNN으로 분류되고 결함 유형과 밀접한 관련이 있는 이미지에 포함된 특징을 추출하였다. 네트워크 분류 정확도에 영향을 미치는 중요한 요소로서 필터 크기와 필터 개수는 CNN 구조의 컨벌루션 및 풀링 층에서 최적화되었다. CWT를 적용하여 획득된 입력 이미지 및 CNN에 의해 추출된 특징지도는 고차원 데이터이다. 따라서, t-SNE는 고차원 데이터를 저차원 데이터로 변환하여 시각화에 사용되었다. 2차원 특징을 통해 8개의 결함과 1개의 정상 상태를 명확하게 분류할 수 있었다. CWT와 CNN를 결합하여 PDS에 대한 건전성 감시 방법이 탁월한 분류 방법이라는 것을 검증하였다.
Acknowledgments
이 연구는 2020년도 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(No. 2019R1A2B5B02069400). 또한 이 연구는 2020년도 정부(중소기업청)의 재원으로 한국콘베어주식회사의 위탁과제 지원을 받아 수행된 연구임(No. S2938505).
References
-
Papadopoulou, S., Pressas I., Vazdirvanidis, A. and Pantazopoulos, G., 2019, Fatigue Failure Analysis of Roll Steel Pins from a Chain Assembly: Fracture Mechanism and Numerical Modeling, Engineering Failure Analysis, Vol. 101, pp. 320~328.
[https://doi.org/10.1016/j.engfailanal.2019.03.030]

-
Amarnath, M. and Lee, S. K., 2015, Assessment of Surface Contact Fatigue Failure in a Spur Geared System based on the Tribological and Vibration Parameter Analysis, Measurement, Vol. 76, pp. 32~44.
[https://doi.org/10.1016/j.measurement.2015.08.020]

-
Arakere, N. K., 2016, Gigacycle Rolling Contact Fatigue of Bearing Steels: A Review, International Journal of Fatigue, Vol. 93, pp. 238~249.
[https://doi.org/10.1016/j.ijfatigue.2016.06.034]

-
McFadden, P. D., 1987, Examination of a Technique for the Early Detection of Failure in Gears by Signal Processing of the Time Domain Average of the Meshing Vibration, Mechanical Systems and Signal Processing, Vol. 1, No. 2, pp. 173~183.
[https://doi.org/10.1016/0888-3270(87)90069-0]

- Randall, R., 1982, Cepstrum Analysis and Gearbox Fault Detection, Technical Report, pp. 13~150.
-
Wang, W. J. and McFadden P. D., 1993, Early Detection of Gear Failure by Vibration Analysis i. Calculation of the Time-frequency Distribution, Mechanical Systems and Signal Processing, Vol. 7, No. 3, pp. 193~203.
[https://doi.org/10.1006/mssp.1993.1008]

-
Wang, W. J. and McFadden P. D., 1995, Application of Orthogonal Wavelets to Early Gear Damage Detection, Mechanical Systems and Signal Processing, Vol. 9, No. 5, pp. 497~507.
[https://doi.org/10.1006/mssp.1995.0038]

-
Lee, S. K. and White, P. R., 1997, Higher-order Time-frequency Analysis and Its Application to Fault Detection in Rotating Machinery, Mechanical Systems and Signal Processing, Vol. 11, No. 4, pp. 637~650.
[https://doi.org/10.1006/mssp.1997.0098]

-
Lee, S. K. and White, P. R., 1998, The Enhancement of Impulsive Noise and Vibration Signals for Fault Detection in Rotating and Reciprocating Machinery, Journal of Sound and Vibration, Vol. 217, No. 3, pp. 485~505.
[https://doi.org/10.1006/jsvi.1998.1767]

-
Kim, J. S. and Lee, S. K., 2018, Identification of Tooth Fault in a Gearbox based on Cyclostationarity and Empirical Mode Decomposition, Structural Health Monitoring, Vol. 17, No. 3, pp. 494~513.
[https://doi.org/10.1177/1475921717704384]

-
Capdessus, C., Sidahmed M. and Lacoume, J. L., 2000, Cyclostationary Processes: Application in Gear Faults Early Diagnosis, Mechanical Systems and Signal Processing, Vol. 14, No. 3, pp. 371~385.
[https://doi.org/10.1006/mssp.1999.1260]

-
Wang, D., 2016, K-nearest Neighbors based Methods for Identification of Different Gear Crack Levels under Different Motor Speeds and Loads: Revisited, Mechanical Systems and Signal Processing, Vol. 70, pp. 201~208.
[https://doi.org/10.1016/j.ymssp.2015.10.007]

-
Baraldi, P., Podofillini, L., Mkrtchyan L., Zio E. and Dang, V. N., 2015, Comparing the Treatment of Uncertainty in Bayesian Networks and Fuzzy Expert Systems Used for a Human Reliability Analysis Application, Reliability Engineering & System Safety, Vol. 138, pp. 176~193.
[https://doi.org/10.1016/j.ress.2015.01.016]

- Vapnik, V., 2013, The Nature of Statistical Learning Theory, Springer Science & Business Media, Berlin, Germany.
-
Liu, R., Yang, B., Zio, E. and Chen, X., 2018, Artificial Intelligence for Fault Diagnosis of Rotating Machinery: A Review, Mechanical Systems and Signal Processing, Vol. 108, pp. 33~47.
[https://doi.org/10.1016/j.ymssp.2018.02.016]

-
Gan, M., Wang, C. and Zhu, C., 2016, Construction of Hierarchical Diagnosis Network based on Deep Learning and Its Application in the Fault Pattern Recognition of Rolling Element Bearings, Mechanical Systems and Signal Processing, Vol. 72-73, pp. 92~104.
[https://doi.org/10.1016/j.ymssp.2015.11.014]

-
Janssens, O., Slavkovikj, V., Vervisch, B., Stockman, K., Loccufier, M., Verstockt, S., Van de Walle, R. and Van Hoecke, S., 2016, Convolutional Neural Network based Fault Detection for Rotating Machinery, Journal of Sound and Vibration, Vol. 377, pp. 331~345.
[https://doi.org/10.1016/j.jsv.2016.05.027]

-
Chen, Z., Deng, S., Chen, X., Li, C., Sanchez, R. V. and Qin, H., 2017, Deep Neural Networks-based Rolling Bearing Fault Diagnosis, Microelectronics Reliability, Vol. 75, pp. 327~333.
[https://doi.org/10.1016/j.microrel.2017.03.006]

-
Lu, C., Wang, Z. Y., Qin, W. L. and Ma, J., 2017, Fault Diagnosis of Rotary Machinery Components Using a Stacked Denoising Autoencoder-based Health State Identification, Signal Processing, Vol. 130, pp. 377~388.
[https://doi.org/10.1016/j.sigpro.2016.07.028]

-
Lu, C., Wang, Z. and Zhou, B., 2017, Intelligent Fault Diagnosis of Rolling Bearing Using Hierarchical Convolutional Network based Health State Classification, Advanced Engineering Informatics, Vol. 32, pp. 139~151.
[https://doi.org/10.1016/j.aei.2017.02.005]

-
Du, Yan., Wang, A., Wang, S., He, B. and Meng, G., 2020, Fault Diagnosis under Variable Working Conditions based on STFT and Transfer Deep Residual Network, Shock and Vibration, Vol. 2020, pp. 1~18.
[https://doi.org/10.1155/2020/1274380]

-
Cabrera, D., Sancho, F., Li, C., Cerrada, M., Sancez, R. V., Pacheco, F. and de Oliveira, J. V., 2017, Automatic Feature Extraction of Time-series Applied to Fault Severity Assessment of Helical Gearbox in Stationary and Non-stationary Speed Operation, Applied Soft Computing, Vol. 58, pp. 53~64.
[https://doi.org/10.1016/j.asoc.2017.04.016]

-
Arakere, N. K., 2016, Gigacycle Rolling Contact Fatigue of Bearing Steels: A Review, International Journal of Fatigue, Vol. 93, pp. 238~249.
[https://doi.org/10.1016/j.ijfatigue.2016.06.034]

-
Back, J., Kim, S. W., Lee, S. K. and Lee, C., 2020, Conditioning Monitoring in Chain Sprocket Drive Unit System Based on Artificial Neural Network, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 30, No. 3, pp. 286~293.
[https://doi.org/10.5050/KSNVE.2020.30.3.286]

-
Kim, E. Y., Lee, Y. J. and Lee, S. K., 2012, Heath Monitoring of a Glass Transfer Robot in the Mass Production Line of Liquid Crystal Display Using Abnormal Operating Sounds Based on Wavelet Packet Transform and Artificial Neural Network, Journal of Sound and Vibration, Vol. 331, No. 14, pp. 3412~3427.
[https://doi.org/10.1016/j.jsv.2012.03.007]

-
Samanta, B., 2004, Gear Fault Detection Using Artificial Neural Networks and Support Vector Machines with Genetic Algorithms, Mechanical Systems and Signal Processing, Vol. 18, No. 3, pp. 625~644.
[https://doi.org/10.1016/S0888-3270(03)00020-7]

-
LeCun, Y., Bengio, Y. and Hinton, G., 2015, Deep Learning, Nature, Vol. 521, No. 7553, pp. 436~444.
[https://doi.org/10.1038/nature14539]

-
Lee, S., Back, J., An, K., Kim, S., Lee, C. and Kim, P., 2020, Condition Monitoring of Chain Sprocket Drive System Based on IoT Device and Convolutional Neural Network, Cambridge University Press, Shock and Vibration, Vol. 2020, pp. 1~17.
[https://doi.org/10.1155/2020/8826507]

-
LeCun, Y., Bottou, L., Bengio, Y. and Haffner, P., 1998, Gradient-based Learning Applied to Document Recognition, Proceedings of the IEEE, Vol. 86, No. 11, pp. 2278~2324.
[https://doi.org/10.1109/5.726791]

-
Liu, X., Wang, W., Sun, W., Wu, T., Liu, J. and Liu, J., 2012, Design and Experimental Analyse of Low Noise Double-pitch Silent Chain for Conveyor, Procedia Engineering, Vol. 29, pp. 2146~2150.
[https://doi.org/10.1016/j.proeng.2012.01.277]

-
Lefebvre, L. and Laville, F., 2008, Noise Source Identification for Mechanical Systems Generating Periodic Impacts, Applied Acoustics, Vol. 69, No. 9, pp. 812~823.
[https://doi.org/10.1016/j.apacoust.2007.03.007]

-
Zheng, H. Y., Wang, Y. G., Liu R., Lam, K. Y., Quek, K. P., Ito, T. and Noguchi, Y., 2001, Efficient Modelling and Prediction of Meshing Noise from Chain Drives, Journal of Sound and Vibration, Vol. 245, No. 1, pp. 133~150.
[https://doi.org/10.1006/jsvi.2000.3545]

-
Fuglede, N. and Thomsen, J. J., 2016, Kinematic and Dynamic Modeling and Approximate Analysis of a Roller Chain Drive, Journal of Sound and Vibration, Vol. 366, pp. 447~470.
[https://doi.org/10.1016/j.jsv.2015.12.028]

- Van der Maaten, L. and Hinton, G., 2008, Visualizing High-dimensional Data Using t-SNE, Journal of Machine Learning Research, Vol. 9, pp. 2579~2605.

Seon-Won Kim is a graduate student in Department of Mechanical Engineering at Inha University. He has studied for the application of signal processing to the ride quality analysis of a vehicle and the health monitoring of mechanical system.

Jiseon Back is a graduate student in Department of Mechanical Engineering at Inha University. He has studied for the application of signal processing to automotive sound quality and active noise control.

Sang-Kwon Lee studied in the Department of Mechanical Engineering at the Pusan National University, Pusan, Korea for B.S. In 1998, he received a Ph.D. degree in signal processing at the ISVR (Institute of Sound and Vibration Research) of the University of Southampton in U.K. He has continued the sound and vibration research in the department of mechanical engineering inha University since 1999. He worked in Hyundai Motor Company between 1984 and 1994 and researched Samsung Motor Company on 1998.