선체 진동신호의 DEMON 분석 단순화 및 Cross Entropy를 이용한 함정 CIS 판정 지표 연구
© The Korean Society for Noise and Vibration Engineering
Abstract
The Detection of Envelope Modulation on Noise (DEMON) method is widely used to detect the propeller cavitation noise signals of naval surface ships. In the DEMON method, the accuracy of analysis strongly tends to rely on the user skill and experiences because noise signals must be investigated visually and qualitatively. This study suggests a quantitative indicator that detects the cavitation noise signal to improve the accuracy of signal analysis. The cross entropy concept of information theory was applied to derive the quantified indicator.
Keywords:
Cavitation Inception Speed, Detection of Envelop Modulation on Noise, Information Entropy, Cross Entropy, Kullback-Leibler Divergence키워드:
CIS, 캐비테이션 초생 속도, DEMON, 데몬 분석, 정보엔트로피, 교차엔트로피, 쿨백-라이블러 발산1. 서 론
수중방사소음에는 함정을 탐지 및 식별할 수 있는 중요 정보들이 담겨있다. 특히 수상함에서 발생하는 수중방사소음은 적 잠수함에게 탐지되어 아군의 생존성에 큰 위협을 초래할 수 있으므로 매우 엄격하게 관리해야 한다. 함정의 수중방사소음 발생원인은 함정에 탑재된 기계류에 의한 소음(machinery noise), 유동에 의한 소음(hydrodynamic noise), 프로펠러에 의한 소음(propeller noise)으로 분류된다(1). 특히 고속 항해 시 프로펠러에 의한 소음은 수중방사소음의 가장 지배적인 소음원으로 발전하는데, 이는 프로펠러의 고속회전에 따른 캐비테이션 발생이 주요 원인인 것으로 알려져 있다(2). 따라서 함정에서는 프로펠러의 캐비테이션 발생이 시작되는 항해 속도를 캐비테이션 초생 속도(CIS, cavitation inception speed)로 정의하고 대잠전 등 작전 시 특별한 주의를 기울이고 있다.
함정의 CIS는 고정된 값이 아니라 함정의 운용방식, 해상상태, 프로펠러에 부착된 수중생물 등에 영향을 받아 매순간 변동하는 값이므로, 함 운용자 입장에서는 자함의 CIS를 실시간으로 모니터링하는 것이 중요하다. 그러나 현재는 함정 인도 전후에 청음선 및 하이드로폰 배열을 활용한 계측시험을 수행하여 수중방사소음을 정의하고 있으며, 수년에 한번씩 CIS 계측시험을 재수행하여 자함의 변동된 CIS 값을 획득하고 있다.
이런 문제점을 개선하기 위해 최근에는 프로펠러 상부 선체의 진동신호를 계측하여 프로펠러 캐비테이션 소음 및 CIS를 실시간으로 예측하는 연구가 활발히 진행되고 있다. 미국조선학회(SNAME)는 상선에 대하여 캐비테이션 발생 시 프로펠러 상부 선체구조의 진동레벨로부터 프로펠러 소음을 추정할 수 있는 실험식을 제공하고 있다(3). Han 등(4)은 함정에 대하여 선체부착 가속도계를 통해 계측한 선체 진동 신호로부터 수중방사소음레벨을 예측하는 연구를 수행하여 자함 수중방사소음의 실시간 모니터링 가능성을 확인하였다.
선체 진동신호로부터 프로펠러 캐비테이션 소음의 특징 주파수를 탐지하고 CIS를 판정하기 위해 대표적으로 DEMON(detection of envelop modulation on noise) 기법이 사용된다. DEMON 분석은 주로 등고선 선도(contour diagram)에 나타난 프로펠러 회전 주파수(SR, shaft rate) 및 프로펠러 날개 통과 주파수(BR, blade rate) 성분을 시각적으로 검토하여 판정하기 때문에 분석자의 주관과 경험에 의존하여 분석될 수 있다. 특히 신호 대 잡음비가 낮아 SR 및 BR 성분이 모호하게 관찰될 때는 DEMON 판독 및 CIS 판단이 제한된다. 이러한 문제점들을 해결하기 위하여 DEMON 처리기법 개선 및 CIS의 정량적 판단 지표 개발을 통하여 결과분석의 신뢰도를 높이는 연구들이 활발히 진행되고 있다. Kim 등(5)은 DEMON 분석 시 자체 토널 소음에 의한 혼란을 배제할 수 있도록 토널 신호 간섭을 제거한 DEMON 처리 기법을 제안하였다. Lee 등(6)은 캐비테이션 발생 유무 및 CIS를 판단하기 위하여 DEMON 분석 전 연속 웨이브렛(wavelet) 변환을 수행하여 분석 정확도를 높이는 연구를 수행하였다. Han 등(7)은 선체 진동신호의 DEMON 스펙트럼의 첨도(kurtosis)값을 활용하여 CIS의 정량적 판단 지표를 제안하였다. Kim 등(8)은 DEMON 처리된 신호의 CIS 전/후 데이터 군집을 형성하여 마할라노비스 거리 비교를 통해 정량적 CIS 판단 가능성을 확인하였다.
이 연구에서는 프로펠러 캐비테이션이 발생하였을 때 변동압력의 영향으로 발생하는 프로펠러 직상부 선체 진동신호를 활용하여 프로펠러 캐비테이션 소음의 특징 주파수 판독 및 CIS를 판정하기 위한 정량적 방법을 제안하였다. 이를 위하여 먼저 DEMON 분석 신호에 대한 단순화 및 정량화 처리를 수행하였고, 정보이론의 교차엔트로피(cross entropy) 계산을 통해 CIS 도달 여부를 정량적으로 판정할 수 있는 지표를 제시하였다.
2. 이론적 배경
2.1 DEMON 신호처리 기법
수중에서 프로펠러 캐비테이션 현상이 발생하면 공동(cavity)의 생성, 부피변화, 붕괴 과정이 반복되면서 광대역에 걸쳐 큰 소음이 발생한다. 이때 캐비테이션에 의해 발생된 광대역 고주파소음은 수면과 회전하는 프로펠러 날개 끝의 거리 변화에 따라 발생하는 압력변화 때문에 달라지며, SR 및 BR에 강하게 동조되어 수중으로 전파된다(9). 방사된 소음을 계측하여 복조(demodulation) 처리하면 SR 및 BR 주파수 성분들을 추출할 수 있고, 캐비테이션 발생 여부를 판단할 수 있다. 이 과정에서 주로 DEMON 기법을 사용한다(10).
DEMON 기법은 변조 처리된 시간영역 소음신호에 힐버트 변환(Hilbert transform)을 적용하여 포락선(envelop)을 추출하는 방법이다. 변조된 시간영역 소음신호 계측값은 식 (1)을 통해 힐버트 변환할 수 있고, 식 (2)와 같이 복소수 차원의 해석적 신호로 표현한 뒤, 식 (3)을 통해 복조된 포락선 신호를 얻을 수 있다. 식 (3)의 포락선 시간신호를 푸리에변환(fast Fourier transform)을 통해 주파수 신호로 변환하면 프로펠러에서 캐비테이션이 발생할 때 프로펠러의 SR 및 BR 주파수 성분들을 추출할 수 있다(7,11).
| (1) |
| (2) |
| (3) |
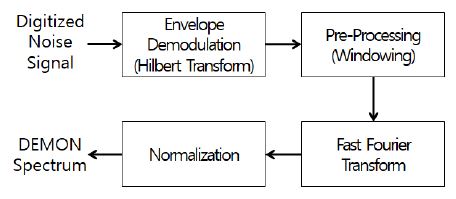
여기서 a(t)은 캐비테이션 소음에 의해 변조된 시간영역 소음신호, 는 소음신호의 힐버트 변환된 신호, 는 힐버트 변환을 포함하여 복소 차원으로 나타낸 해석적 소음신호를 의미한다. Fig. 1은 힐버트 변환에 의한 포락선 복조과정 및 FFT를 포함한 일반적인 DEMON 처리과정을 보여준다(12).
2.2 정보엔트로피와 교차엔트로피
어떤 사건이 일어날 확률이 낮을 때 통계적으로 불확실성(uncertainty)이 높다고 표현한다. 정보이론에서는 확률변수의 불확실성에 대한 정량적 척도로 정보엔트로피(information entropy) 개념을 사용한다. 특정 확률변수(X)에 대한 정보엔트로피(H(X))는 그 확률변수 자체의 평균 정보량을 의미하며 식 (4)와 같이 정의한다(13).
| (4) |
여기서 p(x)는 확률분포, log p(x)는 확률분포의 정보량을 의미한다. 정보엔트로피가 클수록 불확실성이 크며, 정보량이 많고, 발생 확률은 낮은 상태라고 할 수 있다.
하나의 확률변수에 대한 2개의 서로 다른 확률분포가 있을 때, 정보이론에서는 두 분포의 상대적 차이를 교차엔트로피(CE, cross entropy) 개념으로 설명한다. 확률변수 X에 대한 2개의 확률분포 중 목표값(target)의 분포를 p(x), 그와 차이를 보이는 예측값(forecasting)의 분포를 q(x)라고 지정하면, p(x)를 기준으로 삼았을 때 q(x)가 갖는 상대적 불확실성을 교차엔트로피 CE(X)라고 하며 식 (5)와 같이 정의한다. 어떤 분포의 교차엔트로피가 크다면 목표로 삼은 분포와의 차이가 큰 상태라고 할 수 있다.
| (5) |
교차엔트로피를 사용하여 두 확률분포 간의 상대적 차이를 거리(distance) 개념으로 나타낸 것을 쿨백-라이블러 발산(Kullback-Leibler divergence) 또는 상대엔트로피(relative entropy)라고 하며, 식 (6)과 같이 D(p||q)라고 표현하며, 교차엔트로피에서 정보엔트로피를 뺀 값으로 정의한다. 두 분포간의 상대적 차이를 정량적으로 표현한다는 관점에서 쿨백-라이블러 발산과 교차엔트로피가 의미하는 바는 서로 같다.
| (6) |
프로펠러에서 발생하는 소음의 DEMON 스펙트럼 값을 일종의 확률변수로 가정하면, DEMON 스펙트럼상에서 캐비테이션이 발생하지 않았을 때의 소음과 캐비테이션이 발생했을 때의 소음을 각각 서로 다른 2개의 확률분포로 지정해 볼 수 있다. 이 연구에서는 이러한 가정으로부터 교차엔트로피를 적용하여 캐비테이션 발생 전/후 차이를 정량적으로 표현하는 지표를 제시하였고, 관련된 사항을 4장에 서술하였다. 정보엔트로피 개념을 활용하기 위해서는 DEMON 스펙트럼상에 나타나는 값들을 확률값으로 변환할 필요가 있으며, 캐비테이션 전/후의 엔트로피가 명확히 대비될 수 있도록 적절한 작업을 수행해야 한다. 관련된 사항을 3장에서 설명하였다.
3. DEMON 신호의 단순화 및 정량화 처리
3.1 DEMON 신호 단순화 처리
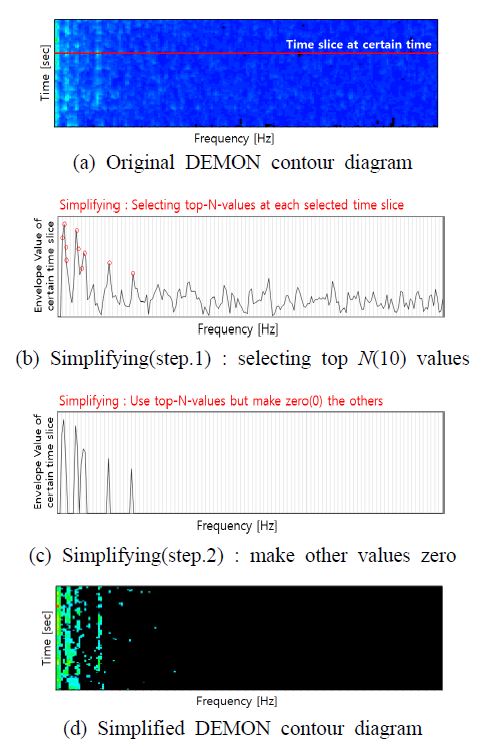
CIS 판정을 목적으로 DEMON 스펙트럼 신호를 분석하는 경우, 관심 주파수는 SR 및 BR 성분과 같은 프로펠러의 특징 주파수들에 국한된다. 특히 CIS 이후에는 프로펠러 특징 주파수들이 캐비테이션 소음에 강하게 변조되어 DEMON 스펙트럼 상에서 피크 형상으로 나타나며, 분석자는 주로 이 피크의 강도 및 지속시간을 시각적으로 관찰한다. 따라서 DEMON 스펙트럼 상 피크 형상을 나타내는 주파수 신호만 선택적으로 사용하고 그 외의 신호들은 폐기 또는 배제 처리하더라도 프로펠러의 특징 주파수 관찰 및 분석이 가능하다고 할 수 있다. 이 연구에서는 DEMON 스펙트럼에서 신호크기 순으로 상위 N개 신호만 선택하고 그 외 신호는 배제(0, Zero) 처리하는 방식으로 피크 신호 식별 및 신호 단순화 처리를 수행하였다. Fig. 2(a)는 기존 방식을 사용하여 나타낸 프로펠러 상부 선체의 진동 가속도신호에 대한 특정 속도에서의 DEMON 스펙트럼 등고선 선도이다. Fig. 2(a)의 특정 시점에서의 DEMON 스펙트럼은 Fig. 2(b)와 같다. 여기서 DEMON 신호를 단순화 처리하기 위해 상위 N개 값만을 선택하고 나머지는 배제 처리하여 Fig. 2(c)와 같이 만들 수 있다. 이와 같은 방법을 매 샘플링 시간마다 적용하면 Fig. 2(d)와 같이 단순화된 DEMON 스펙트럼 등고선 선도를 도시할 수 있다.
Fig. 3은 특정 함정의 프로펠러 상부 선체 구조에서 계측한 진동 가속도 신호에 대해 각 속력별 DEMON 스펙트럼 등고선 선도를 나타낸 것이다. Fig. 3(a)는 기존 방식의 DEMON 스펙트럼 등고선 선도이며, Fig. 3(b)는 이 연구에서 제시한 방법을 사용하여 단순화 처리한 DEMON 스펙트럼 등고선 선도이다. Fig. 3(b)의 경우 프로펠러 특징 주파수 분석에 유용하지 않은 잡음 신호들이 배제되어 시각적 명료성이 개선됨을 확인할 수 있다. 특히 speed no. 5 ~ 6 구간에서 SR 및 BR 성분이 검출되기 시작함에 따라 캐비테이션이 발생되었음을 알 수 있는데, 이러한 현상도 Fig. 3(a)보다 Fig. 3(b)에서 더 명료하게 관찰할 수 있다.
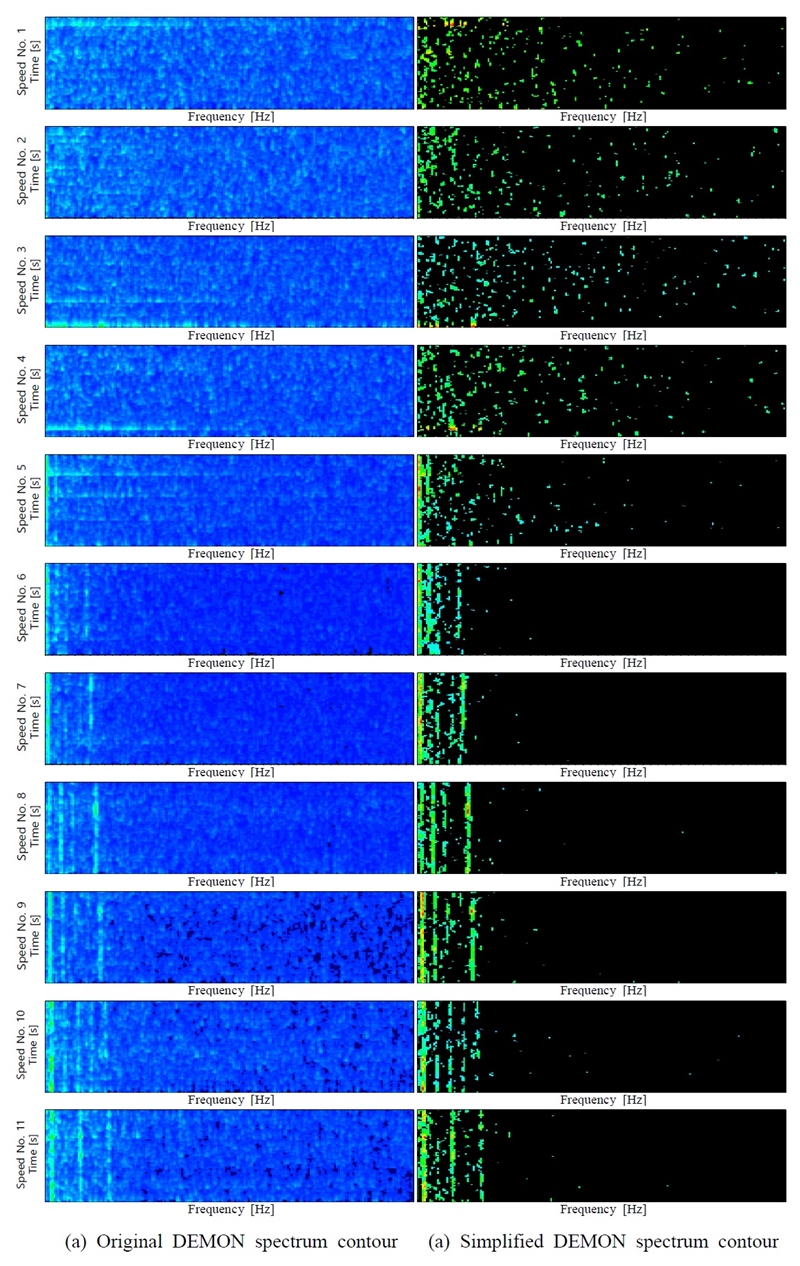
Comparison between original and simplified DEMON spectrum contour(source: vibration level measured on hull structure located directly above propeller)
이 연구에서는 단순화 처리 시 N=10을 적용하여 신호의 크기순으로 상위 10개 값을 선택하고 그 외 신호는 배제 처리하는 방법을 기준으로 삼았다. 일반적으로 DEMON 스펙트럼 신호의 크기는 저주파 대역에서 가장 크고 중-고주파 대역에서는 현저히 작아지는 양상을 보이기 때문에 상위 10개 신호를 선택하면 대부분 저주파 대역에서 선택된다. 저주파 영역에서 SR 및 BR 등의 프로펠러 특징 주파수들이 저주파 잡음 등에 의해 음폐되는 문제를 예방하기 위해 주파수 분해능을 0.25 Hz로 설정하였고, 상위 10개 신호를 선택하여 0 Hz ~ 50 Hz 정도의 저주파 영역에서 프로펠러 특징 주파수 성분들을 명료하게 추출할 수 있음을 확인하였다. 또한, 이 연구에서 사용한 프로펠러 상부 선체 진동 신호에는 기계류 토널 성분은 거의 관찰되지 않았는데, 주요 기계류 설치위치로부터 계측지점까지의 거리가 상당히 멀고, 캐비테이션 발생 시 기계류 소음보다 프로펠러 소음이 지배적으로 발전하기 때문에 기계류 진동 신호의 영향이 미미한 것으로 추정된다. 그러나 각 함정마다 계측된 신호 및 CIS가 상이할 수 있으므로, N값은 각 함정에 맞게 조정할 필요성이 있다.
3.2 DEMON 신호 정량화 처리
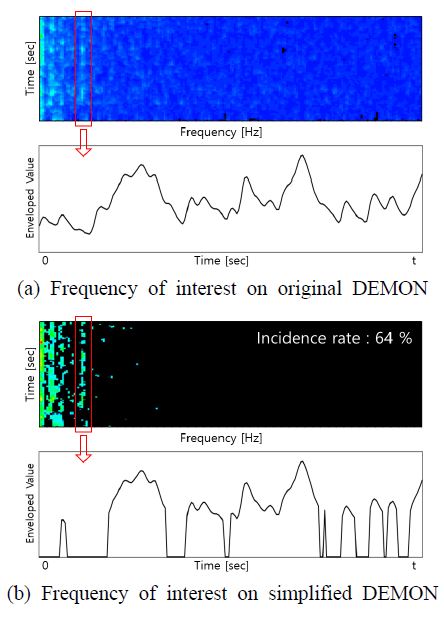
단순화된 DEMON 스펙트럼을 사용하면 관심 주파수에 대한 신호 발생빈도를 정량화할 수 있다. Fig. 4는 특정 함정의 프로펠러 상부 선체 구조에서 계측한 진동 가속도 신호에 대해 CIS의 징후로 주로 관측되는 BR 1차 주파수에 대한 DEMON 스펙트럼 정량화 과정이다. Fig. 4(a)는 기존 DEMON 스펙트럼의 BR 1차 주파수 신호 크기의 변화를 시간에 따라 나타낸 그래프이다. Fig. 4(b)는 단순화 처리된 DEMON 스펙트럼의 BR 1차 주파수 신호 크기의 변화를 나타낸다. 신호의 크기순으로 상위 10개 값만 선택되고 나머지 값은 배제처리 하였기 때문에 부분적으로 신호의 크기가 0인 구간이 존재하며, 신호의 크기가 0이 아닌 구간을 합하여 전체 계측시간 t초에 대한 비율을 계산함으로써 관심 주파수에 대한 신호 발생빈도를 정량적으로 표시할 수 있다.
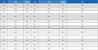
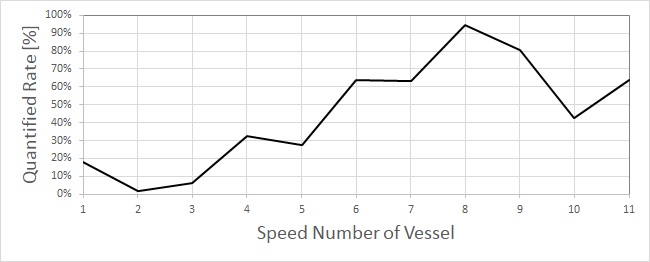
정량화된 BR 1차 주파수 신호가 함정의 전 속력구간에 대해 어떠한 양상으로 나타내는지 확인하기 위하여 특정 함정의 최저속력에서부터 최고속력까지의 BR 1차 주파수를 정량화 처리하여 Table 1 및 Fig. 5 에 나타냈다. 사용된 신호는 특정 함정의 프로펠러 상부 선체 구조에서 계측한 진동 가속도 신호이며, speed no.가 큰 값일수록 함정의 항해 속력이 빠름을 의미한다. 점검결과 항해 속력이 빨라질수록 정량화 처리된 BR 1차 신호의 발생빈도 역시 증가함을 확인할 수 있으며, 특히 speed no. 5에서 speed no. 6 구간을 지날 때 BR 1차 신호 발생빈도가 큰 폭으로 증가함에 따라 캐비테이션 발생 가능성이 상당히 높아졌음을 짐작할 수 있다. 이 절에서 제시한 DEMON 신호 단순화 및 정량화 방법을 사용하여 프로펠러 특징 주파수들의 발생빈도를 정량적으로 점검할 수 있음을 확인하였고, CIS 판단 시 보조 지표로서 활용 가능할 것으로 판단된다.
4. Cross Entropy를 활용한 CIS 판정 지표
4.1 Information Entropy를 활용한 지표
단순화된 DEMON 스펙트럼상에서 발생하는 신호들을 확률변수로 정의하고, 각 speed no.에서 나타나는 신호들의 분포형태를 확률분포로 가정하면, 신호분포의 정보량 및 불확실성을 정보엔트로피로 나타낼 수 있다. Fig. 3(b)의 단순화된 DEMON 스펙트럼 선도를 보면 신호분포의 차이를 확인할 수 있다. Speed no.가 낮을수록 신호들이 무질서하게 분포된 형태를 보이고 있으며, speed no.가 높을수록 캐비테이션 소음이 발생함에 따라 신호들이 SR 및 BR 주파수 성분으로 집중되는 형태를 보이고 있다.
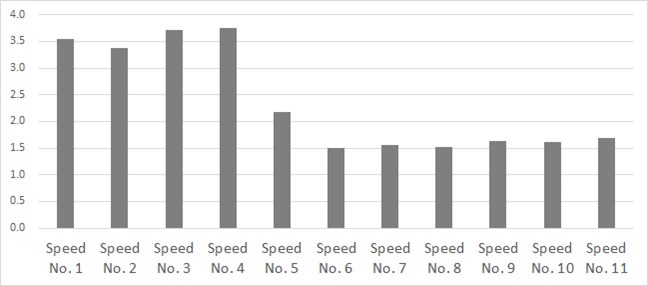
신호의 분포상태를 정보엔트로피 개념에 적용해보면, 신호들이 무질서하게 분포될수록 불확실성이 높아 정보엔트로피가 클 것이고, 신호들이 집중될수록 불확실성이 낮아 정보엔트로피가 작을 것이라 예상할 수 있다. Fig. 3(b)의 각 speed no. 마다 단순화 처리된 DEMON 스펙트럼에 대하여 식 (4)에 따른 정보엔트로피를 계산하면 Fig. 6과 같다. 정보엔트로피는 각 speed no. 별 전체 계측시간 t초 동안 발생한 신호를 주파수별로 평균하여 계산하였다. Speed no. 1 ~ 4 구간과 같이 신호들이 무질서한 형태로 분포될수록 정보엔트로피는 높게 나타났으며, 항해속력이 빨라져 캐비테이션이 발생함에 따라 신호들이 SR 및 BR 성분에 집중될수록 정보엔트로피가 낮아지는 것을 확인할 수 있다. 따라서 정보엔트로피를 사용하여 캐비테이션 발생 전/후의 변화를 정량적으로 정의하여 비교할 수 있다.
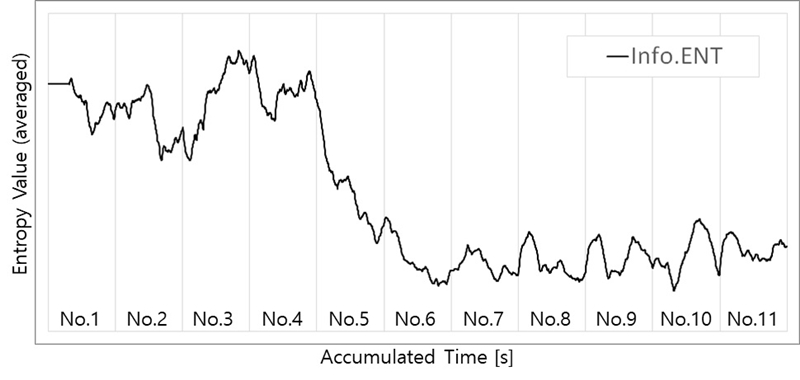
함 속력이 speed no. 1에서부터 11까지 증가할 때 시간에 따른 정보엔트로피 변화를 확인하기 위하여, Fig. 3(b)의 프로펠러 상부 선체구조에서 수집한 진동 가속도의 DEMON 스펙트럼 신호들로부터 매 샘플링 시간마다 정보엔트로피를 계산하여 Fig. 7과 같이 나타냈다. Fig. 7의 그래프는 매 샘플링 시간마다 발생하는 포락선 값의 직전 t초까지의 데이터를 실시간 평균하여 정보엔트로피를 계산한 결과이다. 그래프의 요동(fluctuation)을 감소시키기 위해 매 t초 동안의 포락선 데이터를 평균하여 도시하였으며, 이 연구에서는 t=30초를 적용하였으나 필요시 t값은 각 함정에 맞게 조정할 수 있다. Fig. 7의 speed no. 1 ~ 4까지는 정보엔트로피가 높은 수준을 유지하다가 speed no. 5부터는 현저하게 낮아지는 현상을 볼 수 있다. 이는 Fig. 3(b)에 나타난 바와 같이, 무질서하게 흩어져있던 상위 10개 신호들이 캐비테이션 발생에 따라 SR 및 BR 주파수 성분으로 집중되었기 때문인 것으로 판단된다.
정보엔트로피를 CIS 판정용 지표로 활용하기 위해서는 함정의 항해속력이 빨라질수록 엔트로피의 값도 증가하는 형태로 나타나는 것이 직관적이고 효과적이다. 캐비테이션 발생 전/후의 신호분포 간 정보엔트로피의 상대적 차이를 나타내는 교차엔트로피 개념을 적용하면 항해속력이 빨라질수록 엔트로피값도 증가하는 방향으로 표현되는 지표를 도출할 수 있다.
4.2 Cross Entorpy를 활용한 지표
두 신호분포간 엔트로피의 상대적 차이를 식 (5)를 통해 교차엔트로피로 계산할 수 있는데, 이를 활용하기 위해서는 먼저 비교의 기준이 되는 신호분포 정의가 필요하다. 이 연구에서는 Fig. 3(b)의 speed no. 1 ~ 4와 같이 캐비테이션이 발생하지 않았을 때의 가속도에 대한 DEMON 스펙트럼 신호분포를 모사하여, 전 주파수에서 피크 성분이 발생하지 않는 평탄한 형태의 신호분포를 기준으로 설정하였다.
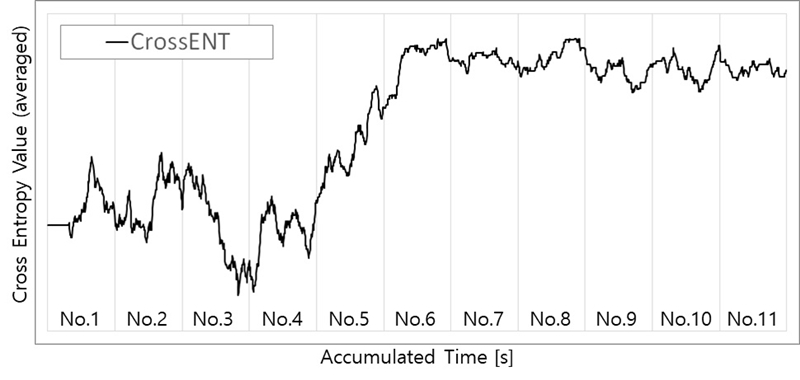
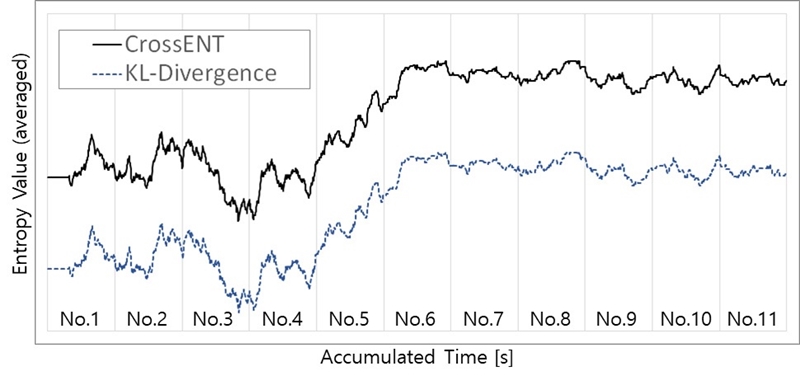
기준 신호분포와 비슷한 speed no. 1 ~ 4의 신호분포는 교차엔트로피가 작고, speed no.가 빨라질수록 교차엔트로피가 증가할 것으로 예상할 수 있다. Fig. 3(b)에 나타낸 신호들의 시간에 대한 교차엔트로피의 변화를 Fig. 8에 나타냈다. Fig. 8의 그래프는 매 샘플링 시간마다 발생하는 포락선 값의 직전 t초까지의 데이터를 실시간 평균하여 교차엔트로피를 계산한 결과이며, t=30초를 적용하였다. Fig. 3과 Fig. 8을 비교 검토하면 DEMON 스펙트럼 등고선 선도의 SR 및 BR과 성분의 발생여부에 따라 교차엔트로피 지표가 증감함을 확인할 수 있다.
Speed no. 1 ~ 4 구간에서는 전반적으로 교차엔트로피가 낮으므로 캐비테이션이 발생하지 않은 상태임을 의미하고, speed no. 5 ~ 6에서는 교차엔트로피가 큰 폭으로 증가하였으므로 이 구간에서 캐비테이션 발생이 시작되었음을 의미한다. Speed no. 7 ~ 11 구간에서는 교차엔트로피가 높은 값을 유지하고 있으므로 지속적으로 캐비테이션에 의한 소음이 발생하고 있음을 알 수 있다. 단순화된 DEMON 신호에 교차엔트로피를 적용하여 캐비테이션 발생 전/후의 차이를 정량적으로 나타낼 수 있고, 함 속력의 증가 및 캐비테이션 발생 정도에 따라 증가하는 특징을 나타내므로, 교차엔트로피를 함정의 CIS를 판정하는 지표로 활용할 수 있을 것으로 판단된다.
한편, 식 (6)을 사용하면 정보엔트로피와 교차엔트로피의 차이를 계산하여 Fig. 9와 같이 쿨백-라이블러 발산값을 사용하여 Fig. 3의 신호에 대해 CIS 판정 지표를 표현할 수 있다. 쿨백-라이블러 발산은 실시간으로 변동하는 교차엔트로피 값과 하나의 기준 정보엔트로피 값의 차이를 산술적으로 계산한 값으로, 결과적으로 교차엔트로피와 동일한 트렌드를 나타낸다. 교차엔트로피 또는 쿨백-라이블러 발산 모두 CIS 판정 지표로 활용할 수 있지만, 이 연구에서는 교차엔트로피를 활용한 CIS 판정 지표만 제시하였다.
4.3 제한사항 및 발전사항
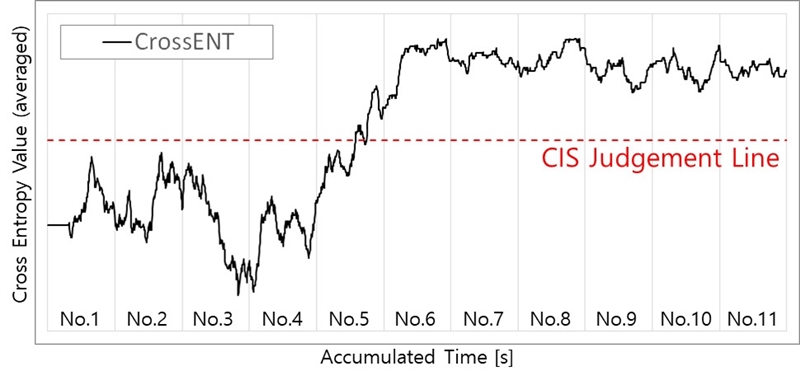
교차엔트로피를 활용하면 함정 프로펠러 캐비테이션 발생 전/후의 징후를 정량적으로 구별할 수 있다는 점을 확인할 수 있었다. 향후 이 지표를 활용하여 정확하게 CIS를 판정하기 위해서는 지표의 변화율, 방사소음의 크기, 각 함정별로 계측된 공식 CIS 값 등을 종합적으로 고려하여 지표의 정밀도를 향상시켜, Fig. 10에 표시한 CIS 판정기준선을 마련해야 할 것으로 판단된다. 또한, 함정별 프로펠러 상부 선체구조의 구성이 상이하여 진동 가속도 계측 지점에 따라 계측신호의 질이 달라질 수 있으므로, 교차엔트로피를 사용한 CIS 판정 지표 역시 각 함정의 특성에 맞도록 미세한 조정이 요구될 수 있다.
5. 결 론
함정의 CIS는 환경에 따라 달라질 수 있으므로 이를 실시간으로 모니터링 하는 것이 중요하다. 이 연구에서는 프로펠러 상부 선체 구조에서 계측한 진동신호의 DEMON 분석 단순화와 교차엔트로피 개념을 적용한 정량적 실시간 CIS 판정 지표를 제시하였다.
기존 DEMON 스펙트럼 등고선 선도의 매 샘플링 시간마다 스펙트럼 신호의 상위 N개 값만 선택하여 분석에 사용하고 나머지는 배제 처리하는 방식으로 단순화를 수행하였다. 단순화된 DEMON 스펙트럼을 활용하여 관심 주파수 별 포락선 발생빈도를 정량화 할 수 있었고, 또한 정보엔트로피 및 교차엔트로피를 계산하여 캐비테이션 발생 전후 차이를 정량적으로 표현하는 지표를 도출할 수 있었다. 이 지표를 실선 측정 결과에 적용하고 기존 DEMON 스펙트럼과 비교한 결과, 캐비테이션 발생 속력에서 교차엔트로피 값이 크게 증가하여, 교차엔트로피 지표를 활용한 함정 CIS의 정량적 판단 가능성을 확인할 수 있었다.
추가적으로, 이 연구에서 제안한 방법에 각 함정별 공식 CIS 기록을 연동하면 정확성 높은 CIS 판정 기준선을 설정할 수 있을 것으로 판단된다.
Acknowledgments
이 연구는 방위사업청과 방위산업기술지원센터의 지원(사업명: 선체 부착 센서를 이용한 함정추진기 CIS 모니터링 기술, 계약번호: UC200001D)하에, LIG넥스원 위탁연구(계약번호: LIGNEX1-2020-0937(00))로 진행되었습니다.
References
- Marage, J. P. and Mori, Y., 2010, Sonar and Underwater Acoustics, ISTE Ltd, UK.
- Ross, D. P., 1973, Mechanics of Underwater Noise, Pergamon Press, New Work.
- Fischer, R. W. and Boroditsky, L., 2001, Supplement to the Design Guide for Shipboard Airborne Noise Control, Technical and Research Bulletin 3-37 (Supplement), The Society of Naval Architects and Marine Engineers, New Jersey.
-
Han, H. S., Jeon, S. H., Lee, C. W. and Kim, Y. H., 2019, Study for Estimation of Propeller Cavitation Sound using Underwater Radiated Sound from the Hull Estimating with Hull Vibration, Transactions of the Korean Society for Noise and Vibration Engineering. Vol. 29, No. 6, pp. 705~713.
[https://doi.org/10.5050/KSNVE.2019.29.6.705]

-
Kim, J. S., Hwang, S. B. and Lee, C. M., 2012, A DEMON Processing Robust to Interference of Tonals, Transactions of the Journal of the Acoustical Society of Korea, Vol. 31, No. 6, pp. 384~390.
[https://doi.org/10.7776/ASK.2012.31.6.384]

- Lee, H. C., Kim, T. H., Sohn, K. and Lee, P. H., 2017, Cavitation Noise Detection Method using Continuous Wavelet Transform and DEMON Signal Processing, Transactions of the Journal of the KIMST, Vol. 20, No. 4, pp. 505~513.
-
Han, H. S., Lee, C. N., Jeon, S. H., Lee, K. H. and Park, S. H., 2018, Development of an Evaluation Method to Determine Cavitation Inception Speed with Aft Hull Vibration Using Kurtosis of the DEMON Spectrum, Ocean Engineering, Vol. 152, pp. 167~180.
[https://doi.org/10.1016/j.oceaneng.2018.01.075]

-
Kim, S. Y., Lee, H. C., Choi, J. Y. and Oh, J. S., 2017, Study on the Analysis of Cavitation Inception Speed Using Hull Vibration, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 27, No. 5, pp. 602~607.
[https://doi.org/10.5050/KSNVE.2017.27.5.602]

- Ross, D., 1976, Mechanics of Underwater Noise, Pergamon Press, New York.
- Waite, A. D., 2002, Sonar for Practising Engineers, John Wiley & Sons, LTD, Chichester.
- Randall, R. B., 1987, Frequency Analysis, Bruel & Kjaer, Denmark.
-
Kummert, A., 1993, Fuzzy Technology Implemented in Sonar Systems, IEEE Journal of Oceanic Engineering, Vol. 18, No. 4, pp. 483~490.
[https://doi.org/10.1109/48.262298]

- Thomas, M. C. and Joy, A. T., 2006, Elements of Information Theory, John Wiley & Sons, New Jersey.

Yonghoon Kim received a B.S. in Mechanical Engineering from Pusan National University in 2009. Mr. Kim is currently a Researcher at Defence Agency for Technology and Quality, Daejeon, Korea.

Hyungsuk Han received a B.S. in Production and Mechanical Engineering from Pusan National University in 1996. He then went on to receive his M.S. and Ph.D. degrees in Mechanical Engineering from Pusan National University in 1998 and 2007, respectively. Dr. Han is currently a Principal Researcher at Defense Agency for Technology and Quality, Daejeon, Korea.

Soohong Jeon received a B.S. in Production and Mechanical Engineering from Pusan National University in 2007. He then went on to receive his M.S. and Ph.D. degrees in Mechanical Engineering from Pusan National University in 2009 and 2014, respectively. Dr. Jeon is currently a Senior Researcher at Defense Agency for Technology and Quality, Daejeon, Korea.

Cheongwon Lee received a B.S. in Mechanical Engineering from Dong-A University in 2007. Mr. Lee is currently a Senior Researcher at Defence Agency for Technology and Quality, Daejeon, Korea.

Dong-Nyok Lee received a B.S. in Aerospace Engineering from Inha University in 2005 and in Biology from Inha University in 2008. He is Ph.D. candidate in Aerospace Engineering from Inha University. Mr. Lee is currently Lee is currently a Senior Researcher at Defence Agency for Technology and Quality, Daejeon, Korea.

Sock-Kyu Lee received his B.S. and M.S. degrees from Pusan University in 1995 and 1997. He is a research engineer at Mechanical Engineering R&D Lab, LIG Nex1. His research interests are design and analysis about military equipment endured at vibration, shock and noise environments.