소노부이 수중 진동 예측을 위한 동유체력 반영 집중소자 모델

1. 서 론

소노부이(sonobuoy)는 음파탐지기를 뜻하는 소나(sound navigation and ranging, SONAR)와 부표를 뜻하는 부이(buoy)의 혼성어로, 해군 대잠전(anti-submarine warfare)시 잠수함 소음 탐지를 목적으로 사용되는 음파 탐지용 부표이다. 소노부이는 항공기를 이용하여 해상에 다량으로 투하되고, 해상에 부유하면서 수중음향센서(hydrophone)를 이용하여 잠수함이 방사하는 수중 음파를 탐지한다. 탐지된 신호들은 부이에 부착되어 있는 신호 송수신 조립체를 통해 무선 주파수(radio frequency, RF) 신호를 이용하여 항공기로 전달된다. 소노부이의 기본적인 구조는 해수면을 부유하는 부이, 케이블이 감겨있는 케이블 팩(cable pack), 소노부이의 움직임을 억제하는 제동기(drogue), 수중 음파를 탐지하는 음향센서로 구성되어 있고, 각각의 구성 요소들이 탄성 케이블로 연결되어 있다.

해수면을 부유하는 부이에는 해면파에 의해 수직 방향의 진동이 발생하며, 이는 탄성 케이블을 통해 하부에 위치한 음향센서에 전달된다. 전달된 진동은 음향센서의 수직 진동을 유발하고, 이는 음향센서의 전기 신호를 발생시킴에 따라 신호 대 잡음비(signal-to-noise ratio, SNR)를 저하시켜 음파 탐지에 어려움을 야기한다. 이러한 음향센서의 진동을 저감하기 위해 케이블과 음향센서로만 이루어져 있던 소노부이에 탄성 케이블, 다양한 형태의 제동기, 보조 질량 등이 추가되어 왔으며⁽¹⁾, 최근에는 이들을 포함한 소노부이의 진동을 저감하기 위한 최적 설계가 요구되고 있다. 이를 위해서는 부이 진동에 따른 음향센서의 진동을 해석 및 예측할 수 있는 소노부이 수중 진동 모델 개발이 필수적이다. 소노부이는 여러 수중 구조물과 같이 주변 유체에 의해 영향을 받기 때문에, 소노부이 수중 진동 모델은 소노부이 각 구성 요소에 작용하는 동유체력(hydrodynamic force)으로 항력(drag force)과 부가질량(added mass)을 반드시 반영해야 한다^(2,3).

소노부이의 복잡한 형상과 동유체력을 연계하여 해석해야 하는 특성으로 인해, 유한요소법(finite element method, FEM)을 소노부이 모델링에 적용하기에는 어려움이 있다⁽³⁾. 이에 따라, 기존의 소노부이 진동 모델들은 소노부이의 수중 진동을 수학적으로 해석 및 예측하기 위해 집중소자 모델(lumped-element model)을 제시해 왔다^(3~6). 이는 소노부이의 각 구성 요소를 진동계의 기본 요소인 질량(mass, m), 강성(stiffness, k), 감쇠(damping, c)로 나타내는 것으로⁽⁷⁾, 유한요소법에 비해 낮은 계산 비용으로 소노부이 음향센서 잡음의 주요 원인인 수직 방향의 진동을 예측할 수 있다⁽⁸⁾. Din 등은⁽⁴⁾ 소노부이를 2자유도계 집중소자 모델로 구축하여, 부이 진동에 의한 음향센서의 진동을 해석하였다. 하지만 수중 진동에서 중요한 요소인 동유체력이 고려되지 않아, 주변 유체에 의해 동유체력이 작용하는 실제 소노부이에 적용하기 어려운 한계가 있다. Huang 등은^(5,6) 소노부이를 1자유도계 집중소자 모델로 구축하고, 물에 잠겨 있는 구성 요소의 항력을 반영하여 수중 진동을 예측하였다. 그들의 모델은 동유체력으로 항력을 반영하였으나, 수중 부가질량에 의한 힘을 반영하지 않아 부가질량이 크게 작용하는 형상을 가진 소노부이 모델의 경우에는 해당 진동 모델의 예측 정확도가 낮아질 수 있다. Guan 등은⁽³⁾ 원판(damping disk)을 질량 요소로 하여 소노부이 1자유도계 집중소자 모델을 구축하고, 원판의 수중 진동을 해석 및 예측하였다. 원판의 항력계수와 관성계수를 이용해 원판에 작용하는 동유체력을 고려하였고, 부가질량이 소노부이 수중 진동 예측에 있어 주요한 요소임을 확인하였다. 그러나 원판과 같이 잘 알려진 항력계수와 관성계수를 그대로 사용하는 것은 수중 진동 예측 정확도가 낮아 계수들의 미세 조정(fine-tuning)이 요구된다. 또한, 위 계수들은 실제 소노부이의 제동기와 같이 복잡한 형상에 적용이 어렵다는 한계가 있다.

이 논문에서는 소노부이 수중 진동 예측을 위해, 동유체력 측정 및 3자유도계 집중소자 모델에 기반한 동유체력 반영 집중소자 모델을 제시한다. 이 모델은 우선적으로 소노부이 각 구성 요소에 작용하는 동유체력을 실험적으로 측정하여, 항력과 부가질량을 도출한다. 그리고 이들을 집중소자 모델의 입력값으로 사용하여 낮은 계산 비용과 높은 정확도로 음향센서의 수직 진동 주파수 응답을 예측한다. 이 모델은 소노부이의 형상 및 모델에 제약 없이 적용할 수 있어 기존 소노부이 진동 모델들에 비해 높은 범용성을 가질 것으로 기대된다. 논문의 구성은 다음과 같다. 2장에서는 동유체력 반영 집중소자 모델에 대해 기술하고, 3장에서는 소노부이 수중 진동 예측을 위한 동유체력 측정 및 주파수 응답 예측에 대해 기술한다. 4장에서는 동유체력 반영 집중소자 모델의 물리적 정합성 검증을 위한 수중 진동 실험 및 이 모델을 이용한 실제 해상에서의 해면파에 의한 음향센서 진동 예측에 대해 기술한다. 끝으로 5장에서는 요약 및 향후 계획으로 결론을 맺는다.

2. 동유체력 반영 집중소자 모델

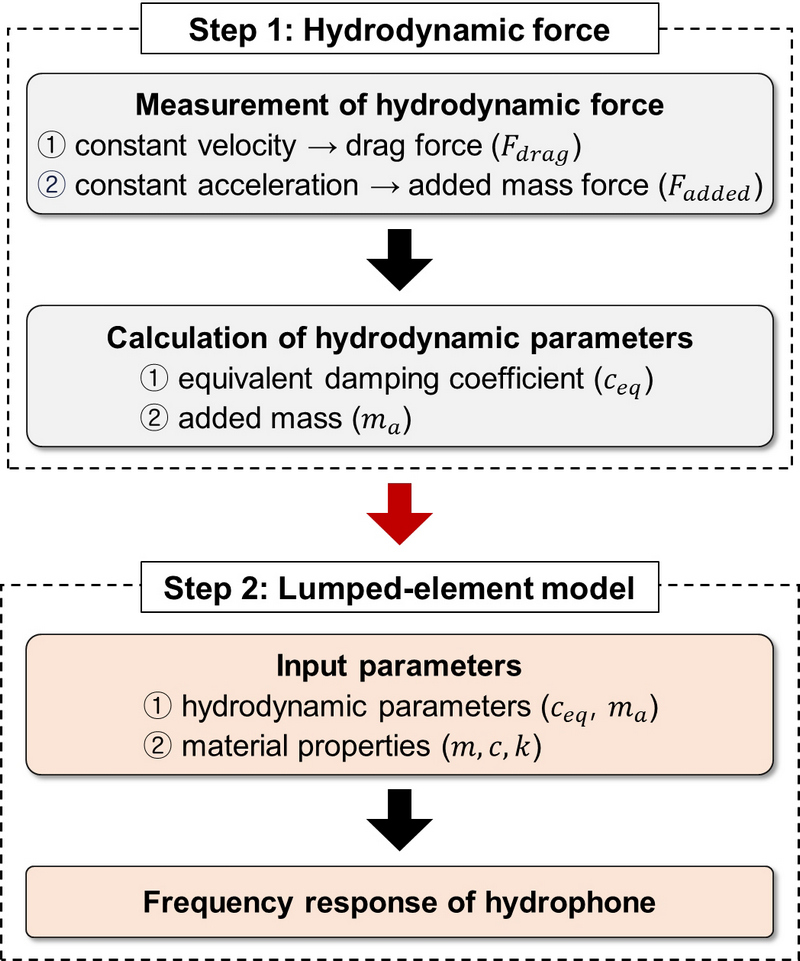
동유체력 반영 집중소자 모델은 Fig. 1에 나타나 있는 것처럼 2단계로 구성되어 있다. 먼저 1단계는 소노부이 각 구성 요소에 작용하는 동유체력에 관한 것이다. 실험을 통해 항력(F_drag)과 부가질량에 의한 힘(F_added)을 측정하고, 최종적으로 각 구성 요소의 동유체력 매개변수인 등가 감쇠계수(c_eq)와 부가질량(m_a)을 산출한다. 그 다음 단계로, 앞서 산출한 각 구성 요소의 동유체력 매개변수와 질량 등의 물성치를 소노부이 집중소자 모델에 입력한다. 이를 통해 이 연구에서 목적으로 하는 해면파에 기인한 음향센서의 주파수 응답을 예측한다.

Fig. 1

Schematic of lumped-element model with consideration of hydrodynamic force

2.1 동유체력

동유체력은 수중에서 진동하는 구조물에 작용하는 힘으로 항력과 부가질량에 의한 힘이 있다⁽⁹⁾. 항력은 구조물이 유체 내에서 운동 시 운동 방향의 반대 방향으로 작용하는 힘이고, 부가질량은 구조물이 유체 내에서 가속 시 주변 유체의 가속으로 인해 발생하는 질량이다. 일반적으로 부가질량은 주파수 및 모드에 따라 그 크기가 달라지기 때문에 편차가 존재한다. 이 논문에서는 부가질량을 집중소자 모델에 반영하기 위한 값으로 활용하기 위해, 부가질량을 실험적으로 측정한 후 그 평균을 도출하여 부가질량을 상수(constant)로 모델링 하였다. 항력과 부가질량은 형상과 관련된 함수로, 제동기와 같이 형상이 복잡한 구조물의 경우 값을 정의하는 데 어려움이 있어 실험적으로 측정하는 과정이 필요하다⁽¹⁰⁾.

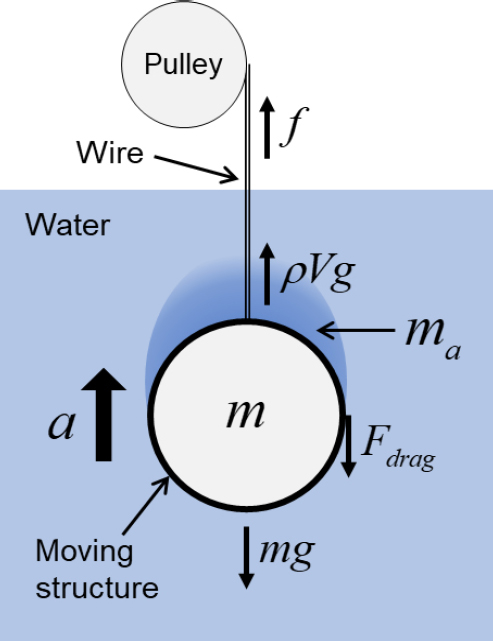
동유체력 측정 이론을 서술하기 위해 먼저, Fig. 2와 같이 수중에서 와이어에 의해 수직 운동하는 구조물의 운동방정식을 식 (1)과 같이 기술할 수 있다(위쪽 방향을 양의 부호로 설정)⁽¹¹⁾.

$\[ \sum F=f+\rho Vg-mg-F_{\mathrm{d}\mathrm{r}\mathrm{a}\mathrm{g}}=\left(m+m_a\right)a, \]$

(1)

Fig. 2

Free-body diagram of underwater structure

여기서 ΣF는 구조물에 작용하는 합력(net force), f는 구조물이 당겨지는 힘, ρ는 유체의 밀도, V는 구조물의 부피, g는 중력 가속도, m은 구조물의 질량, F_drag는 구조물에 작용하는 항력, m_a는 구조물의 부가질량, a는 구조물의 가속도이다. 이와 같이 수중에서 운동하는 구조물은 구조물 운동에 의한 힘, 부력, 중력 이외에도 동유체력인 항력과 부가질량에 의한 힘이 추가적으로 발생한다.

항력과 부가질량에 의한 힘은 식 (1)의 운동방정식에 기반하여 측정할 수 있다. 먼저 항력의 측정은 수중에서 구조물을 등속도(a = 0)로 운동하게 함으로써 수행할 수 있다. 이 경우 구조물의 운동방정식은 구조물이 당겨지는 힘, 부력, 중력, 그리고 항력에 대한 식만 나타나, 식 (2)와 같이 항력에 관한 식으로 기술할 수 있다.

$\[ F_{\mathrm{d}\mathrm{r}\mathrm{a}\mathrm{g}}=f+\rho Vg-mg. \]$

(2)

그리고 항력을 집중소자 모델에 반영하기 위한 선형 댐퍼(linear damper)로 모델링 하기 위해, 식 (3)과 같이 등가 감쇠계수를 산출한다.

$\[ F_{\mathrm{d}\mathrm{r}\mathrm{a}\mathrm{g}}=c_{eq}v, \]$

(3)

여기서 v는 구조물의 속도이다. 등가 감쇠계수는 속도에 따른 항력을 실험으로 측정 후, 선형 회귀(linear regression) 분석을 통해 얻은 직선의 기울기로 계산할 수 있다.

부가질량의 측정은 수중에서 구조물을 등가속도(a = constant)로 운동하게 함으로써 수행할 수 있다. 이 경우 구조물의 부가질량은 식 (4)와 같이 기술할 수 있으며, 이 때 항력은 식 (2)에서 측정한 값을 이용한다.

$\[ m_a=\frac{f+\rho Vg-mg-F_{\mathrm{d}\mathrm{r}\mathrm{a}\mathrm{g}}-ma}{a}. \]$

(4)

2.2 집중소자 모델

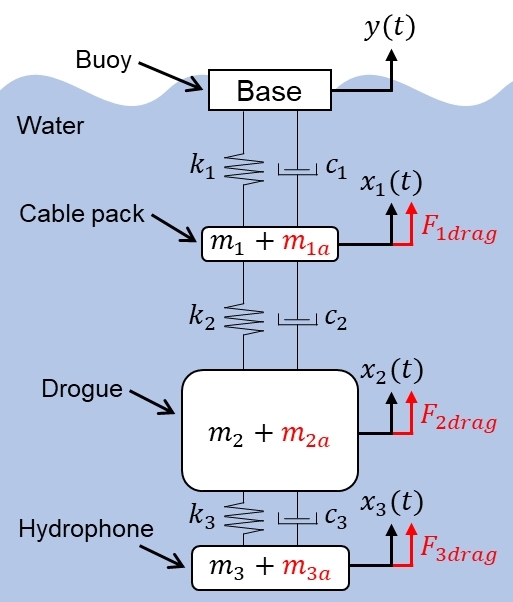
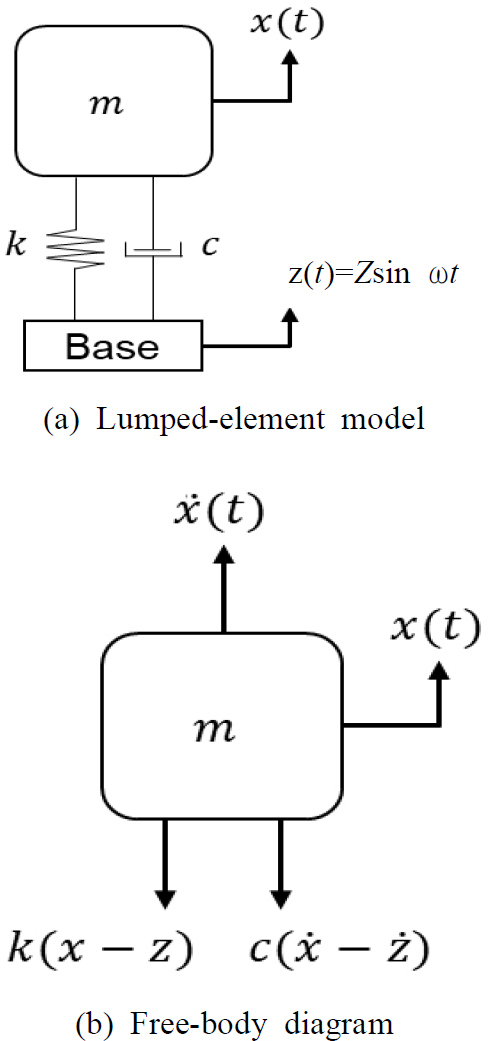
집중소자 모델은 구조물의 각 구성 요소를 진동계의 기본 요소인 질량, 강성, 감쇠로 나타낸 것이다. 각 구성 요소들은 각각의 질량으로, 탄성 케이블은 강성과 감쇠로 나타낸다. 서론에서 언급한 부이, 케이블 팩, 제동기, 음향센서로 이루어진 소노부이는 Fig. 3과 같이 3자유도계 집중소자 모델로 구축될 수 있고, 각 질량 요소에 작용하는 동유체력으로 부가질량과 항력을 나타낼 수 있다. 또한, 해면파에 의해 진동하는 부이는 질량이 아닌 기초 가진(base excitation)으로 모델링 할 수 있다. 기초 가진은 Fig. 4(a)와 같이 집중소자 모델의 기초가 조화운동을 하는 경우로써, 기초와 질량 요소 간의 상대 변위 및 상대 속도를 이용해 Fig. 4(b)와 같이 자유물체도를 나타낼 수 있다⁽¹²⁾. 동유체력을 반영한 집중소자 모델을 통해 부이 진동에 따른 소노부이 수중 강제진동 운동방정식을 식 (5)와 같이 기술할 수 있다.

$\[ \begin{array}{c}\left[M\right]\ddot{\overrightarrow{\mathbf{x}}}+\left[C\right]\dot{\overrightarrow{\mathbf{x}}}+\left[K\right]\overrightarrow{\mathbf{x}}+{\overrightarrow{\mathbf{f}}}_{\mathrm{a}\mathrm{d}\mathrm{d}\mathrm{e}\mathrm{d}}={\overrightarrow{\mathbf{f}}}_{\mathrm{e}\mathrm{x}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{n}\mathrm{a}\mathrm{l}}+{\overrightarrow{\mathbf{f}}}_{\mathrm{d}\mathrm{r}\mathrm{a}\mathrm{g}}\\ \left[M\right]=\left[\begin{array}{ccc}{m}_1& 0& 0\\ 0& m_2& 0\\ 0& 0& m_3\end{array}\right]\\ \left[C\right]=\left[\begin{array}{ccc}\left(c_1+c_2\right)& -c_2& 0\\ -c_2& \left(c_2+c_3\right)& -c_3\\ 0& -c_3& c_3\end{array}\right]\\ \left[K\right]=\left[\begin{array}{ccc}\left(k_1+k_2\right)& -k_2& 0\\ -k_2& \left(k_2+k_3\right)& -k_3\\ 0& -k_3& k_3\end{array}\right]\end{array} \]$

(5)

Fig. 3

Lumped-element model of sonobuoy with consideration of hydrodynamic force

Fig. 4

Base excitation

여기서 [M], [C], [K]는 각각 소노부이의 질량행렬, 감쇠행렬, 강성행렬이며, $$ \overrightarrow{\mathbf{x}}, \dot{\overrightarrow{\mathbf{x}}},\mathit{ }\ddot{\overrightarrow{\mathbf{x}}}$$는 각각 소노부이의 변위벡터, 속도벡터, 가속도벡터이다. $$ {\overrightarrow{\mathbf{f}}}_{\mathrm{a}\mathrm{d}\mathrm{d}\mathrm{e}\mathrm{d}}$$와 $$ {\overrightarrow{\mathbf{f}}}_{\mathrm{d}\mathrm{r}\mathrm{a}\mathrm{g}}$$는 각각 소노부이의 부가질량에 의한 힘과 항력을 나타내는 힘벡터이며, $$ {\overrightarrow{\mathbf{f}}}_{\mathrm{e}\mathrm{x}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{n}\mathrm{a}\mathrm{l}}$$는 해면파에 의해 소노부이에 가해지는 힘벡터로 식 (6)과 같이 기술할 수 있다.

$\[ {\overrightarrow{\mathbf{f}}}_{\mathrm{e}\mathrm{x}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{n}\mathrm{a}\mathrm{l}}=\left\{\begin{array}{c}{c}_1\dot{y}\left(t\right)+k_{1}y\left(t\right)\\ 0\\ 0\end{array}\right\} \]$

(6)

여기서 $$ y\left(t\right),\dot{y}\left(t\right)$$는 각각 부이의 진동 변위, 진동 속도이다. 그리고 소노부이에 작용하는 부가질량에 의한 힘과 항력은 식 (5)의 질량행렬과 감쇠행렬에 반영해 식 (7)과 같이 기술할 수 있다.

$\[ \left[M+M_a\right]\ddot{\overrightarrow{\mathbf{x}}}+\left[C+C_{eq}\right]\dot{\overrightarrow{\mathbf{x}}}+\left[K\right]\overrightarrow{\mathbf{x}}={\overrightarrow{\mathbf{f}}}_{\mathrm{e}\mathrm{x}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{n}\mathrm{a}\mathrm{l}} \]$

(7)

여기서 [M_a]는 부가질량 행렬, [C_eq]는 항력에 의한 등가 감쇠행렬로서, 식 (8)과 같이 기술할 수 있다.

$\[ \left[M_a\right]=\left[\begin{array}{ccc}{m}_{1a}& 0& 0\\ 0& m_{2a}& 0\\ 0& 0& m_{3a}\end{array}\right],\left[C_{eq}\right]=\left[\begin{array}{ccc}{c}_{1eq}& 0& 0\\ 0& c_{2eq}& 0\\ 0& 0& c_{3eq}\end{array}\right] \]$

(8)

여기서 m_na는 소노부이 n번째 구성 요소의 부가질량, c_neq는 소노부이 n번째 구성 요소에 작용하는 항력을 나타내는 등가 감쇠계수이다. 항력은 구성 요소 간의 상대 속도가 아닌 구성 요소의 절대 속도에 의해 작용하므로, 등가 감쇠행렬은 식 (8)과 같이 대각 행렬로 나타나게 된다.

이 연구에서 목표로 하는 해면파 가진에 의한 음향센서의 주파수 응답을 구하는 과정은 다음과 같다. 시간 영역의 식 (7)을 푸리에 변환을 이용하여 주파수 영역으로 변환 후 식 (9)와 같이 기술할 수 있다.

$\[ \begin{array}{c}\overrightarrow{H}\left(j\omega \right)={\left(-{\omega }^2\left[M+M_a\right]+j\omega \left[C+C_{eq}\right]+\left[K\right]\right)}^{-1}\\ \times \left[\begin{array}{c}j\omega c_1+k_1\\ 0\\ 0\end{array}\right]\end{array} \]$

(9)

여기서 $$ \overrightarrow{H}\left(j\omega \right)$$는 부이 진동에 따른 소노부이 각 구성 요소의 진동을 나타내는 주파수 응답 함수이며, w는 각주파수, j는 허수를 나타낸다. 소노부이 3번째 구성 요소인 음향센서의 주파수 응답은 주파수 응답 함수의 (3, 1) 성분을 도출함으로써 이론적으로 예측할 수 있다.

3. 소노부이 수중 진동 예측

앞서 설명한 동유체력 반영 집중소자 모델을 Fig. 5와 같이강철, 제동기, 음향센서 및 탄성 케이블로 이루어진 총 길이 5.22 m의 소노부이에 적용하여, 음향센서의 주파수 응답을 예측하였다. 소노부이는 일반적으로 10 m 이상의 길이를 가지고 있어, 긴 길이로 인해 향후 모델 검증 실험에 어려움이 있을 수 있다. 따라서, 이 연구에서는 Fig. 5(a)와 같이 상용 소노부이와 유사한 구조를 가지며, 전체 길이는 검증 실험에 용이할 수 있도록 조정하였다. Fig. 5(b)의 제동기는 지름 0.44 m의 두 원판이 0.96 m의 거리를 두고 연결되어 있는 형태를 가지고 있다. 두 원판 사이의 약 146 L의 물은 제동기의 부가질량을 발생시키고, 이는 진동 감쇠 효과를 갖게 된다. Fig. 5(c)의 강철은 케이블 팩을 대체하는 시편으로, 케이블 팩과 동일한 질량을 가지며, 탄성 케이블 연결이 용이하도록 제작하였다.

Fig. 5

Schematic and photograph of the sonobuoy

3.1 동유체력 측정

동유체력 반영 집중소자 모델의 첫 번째 단계는 각 구성 요소의 동유체력을 실험적으로 측정하고, 등가 감쇠계수와 부가질량을 각각 산출하는 것이다. 제동기는 다른 구성 요소들에 비해 상대적으로 큰 단면적과 부피를 가지고 있어, 동유체력이 크게 작용할 것으로 예상된다. 따라서, 제동기의 역학적 성격을 규명하는 것이 가장 중요하다고 사료되는 바, 이 장에서는 제동기의 동유체력 측정 및 동유체력 매개변수 산출에 대해 자세히 서술한다.

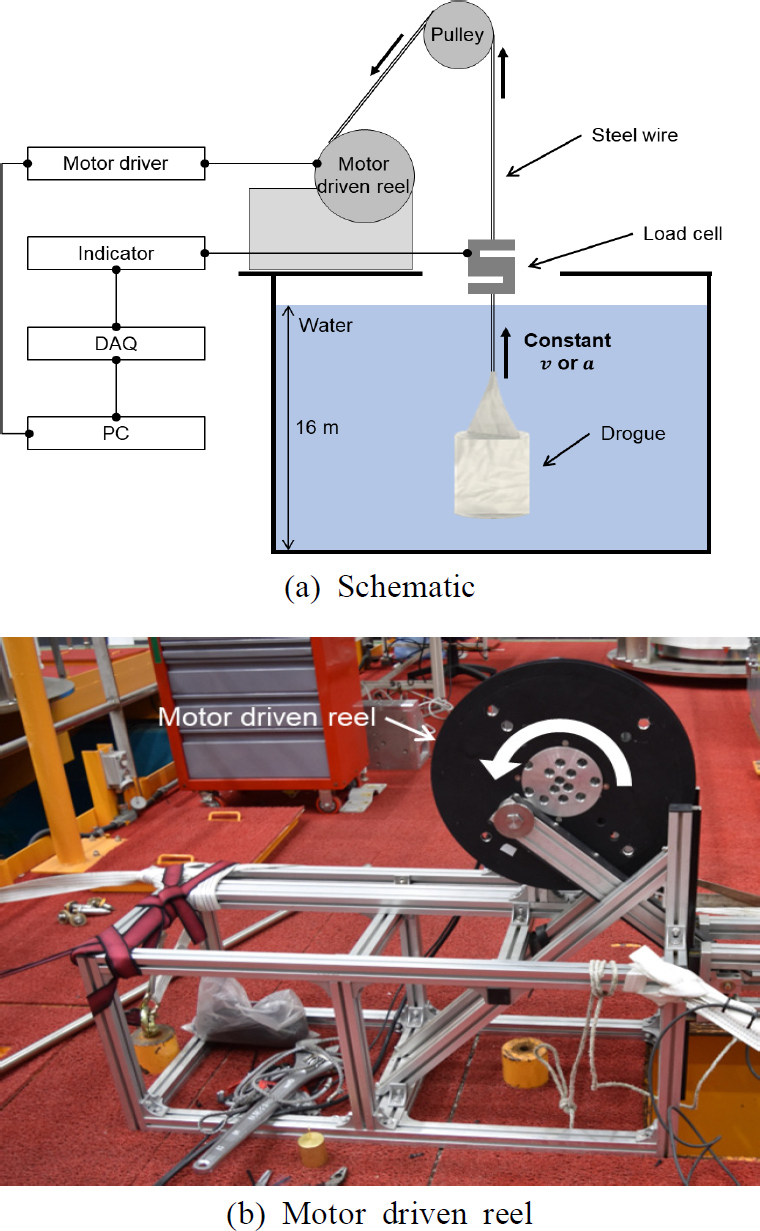
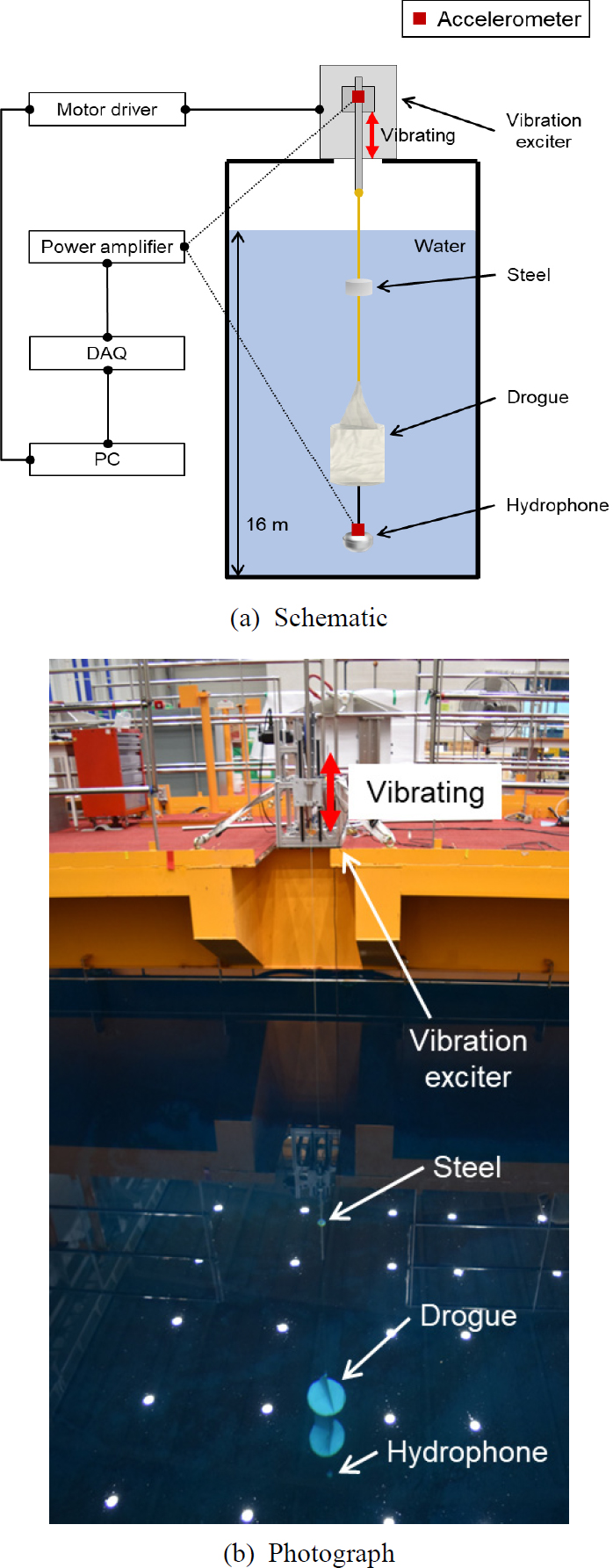
제동기의 동유체력은 제동기의 식 (2)의 등속도와 식 (4)의 등가속도 운동을 통해 측정할 수 있다. 동유체력 측정 실험은 Fig. 6(a)와 같이 대형 수조 시험장(24 m × 15 m × 16 m)에서 실험 환경을 구성하여 수행되었다. 제동기는 등속도 및 등가속도로 운동하는 모터 구동 릴(motor driven reel)과 연결되어 있으며, 그 사이에 힘을 측정하는 로드 셀(Zemic, 모델 H3-C3-25kg-3B)이 위치하고 있다. Fig. 6(b)와 같이 모터 구동 릴은 제동기의 수직 운동을 위해 제작된 것으로, 도르래(pulley)를 이용하여 모터의 회전 운동을 수직 운동으로 변환하였다. 그리고 모터 드라이버(motor driver)를 이용하여 모터 구동 릴의 속도와 가속도를 제어하였으며, 속도와 가속도의 범위는 제동기의 형상이 왜곡되지 않는 범위로 지정하였다. 로드 셀은 제동기가 당겨지는 힘을 측정하고, 측정값은 인디케이터(DACELL, 모델 SM-10)에 실시간으로 표시되었으며, 동시에 데이터 수집 장치(National instruments, 모델 cDAQ-9178, NI-9234)를 통해 PC에 저장되었다.

Fig. 6

Experimental setup

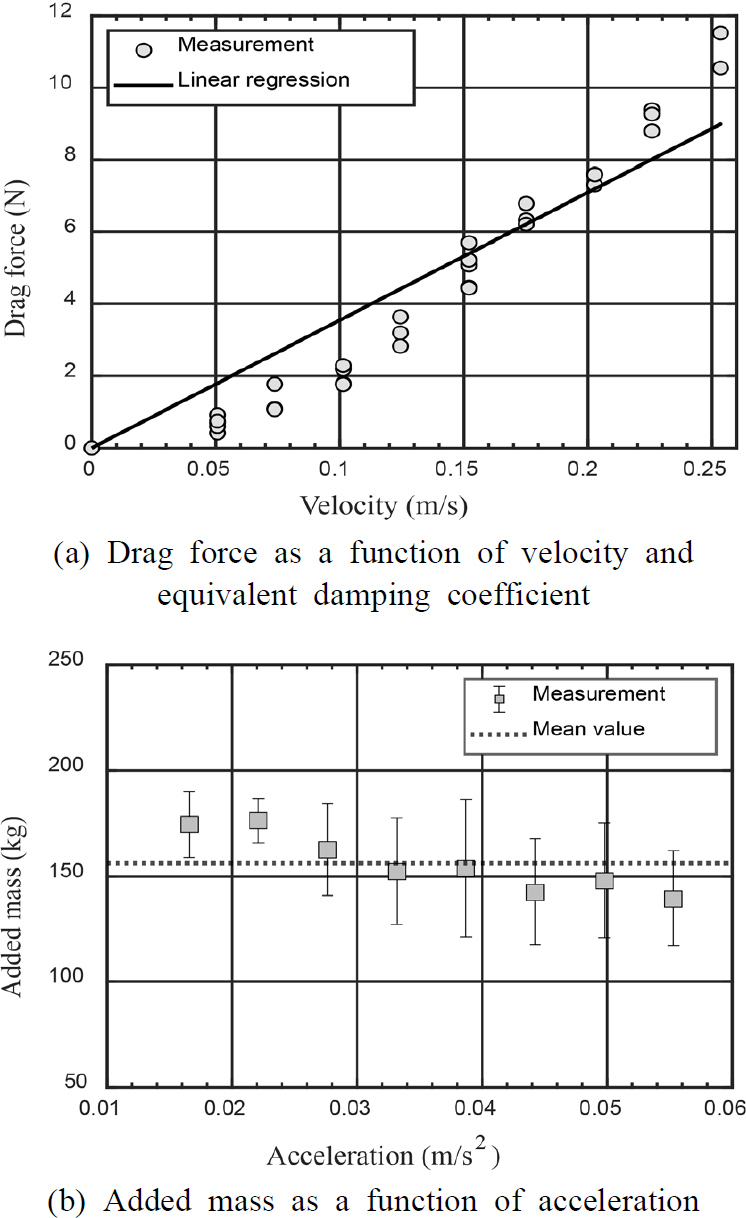
Fig. 7은 제동기의 항력과 부가질량을 측정한 결과를 나타낸 것이다. 먼저 Fig. 7(a)는 등속도에 따라 측정된 항력을 나타낸 것이다. 총 32회의 측정값을 표시하였으며, 선형 회귀 분석을 통해 속도와 항력의 관계를 나타내고, 등가 감쇠계수를 도출하였다. 선형 회귀 분석은 제동기가 정지 상태일 때, 항력이 없다는 전제를 충족하기 위해 원점을 포함하여 수행하였다. 그 결과, 등가 감쇠계수는 선형 회귀 분석을 통해 얻은 직선의 기울기 값인 35.48 Ns/m를 도출하였다. 해당 선형 회귀 모델의 적합도는 결정계수(R²) 0.87로 적합한 회귀 모델로 판단하였다⁽¹³⁾.

Fig. 7

Experimental results

그 다음으로 Fig. 7(b)는 등가속도에 따라 산출된 부가질량을 나타낸 것이다. 앞서 측정한 항력과 식 (4)를 이용해 부가질량을 계산하여 155.69 kg(±13.861 kg)을 도출하였다. 이는 공기 중에서의 제동기 질량(0.18 kg)과 큰 차이를 보이며, 제동기 부가질량은 제동기가 수중에 전개되었을 때, 그 안에 차있는 물의 부피인 146 L의 질량과 유사함을 확인하였다. 부가질량의 편차는 측정 간 제동기의 형상이 일정하게 유지되지 않아 발생하는 것으로 예상되며, 또한 계산 과정에 반영되는 항력의 비선형성에 의한 영향도 있을 것으로 예상된다.

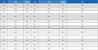
제동기 외에 소노부이의 구성 요소인 강철 및 음향센서의 동유체력으로 등가 감쇠계수와 부가질량은 마찬가지로 앞서 기술한 것과 동일한 방법으로 측정을 수행하였고, 그 중 부가질량은 측정 결과 크기가 매우 작아 무시하였다. Table 1은 소노부이 각 구성 요소의 동유체력 매개변수 산출 결과를 정리하여 나타낸 것으로, 이로써 동유체력 반영 집중소자 모델의 첫 번째 단계가 완료되었다.

Table 1

Hydrodynamic parameters of sonobuoy

3.2 주파수 응답 예측

동유체력 반영 집중소자 모델의 두 번째 단계는 Table 1과 같이 3.1장에서 산출한 각 구성 요소의 동유체력 매개변수와 물성치를 집중소자 모델에 입력하여 음향센서의 주파수 응답을 산출하는 것이다. 소노부이 각 구성 요소의 물성치인 질량, 강성, 감쇠는 각각 전자저울, 인장시험(Instron, 모델 3382), Table 2와 같이 감쇠 자유진동 실험을⁽¹⁴⁾ 통해 측정하였다. 이후 Fig. 3과 같이 소노부이의 동유체력을 반영한 3자유도계 집중소자 모델에 Table 1과 Table 2의 값들을 입력하고, 식 (9)를 이용해 음향센서의 주파수 응답을 계산하였다.

Table 2

Material properties of sonobuoy

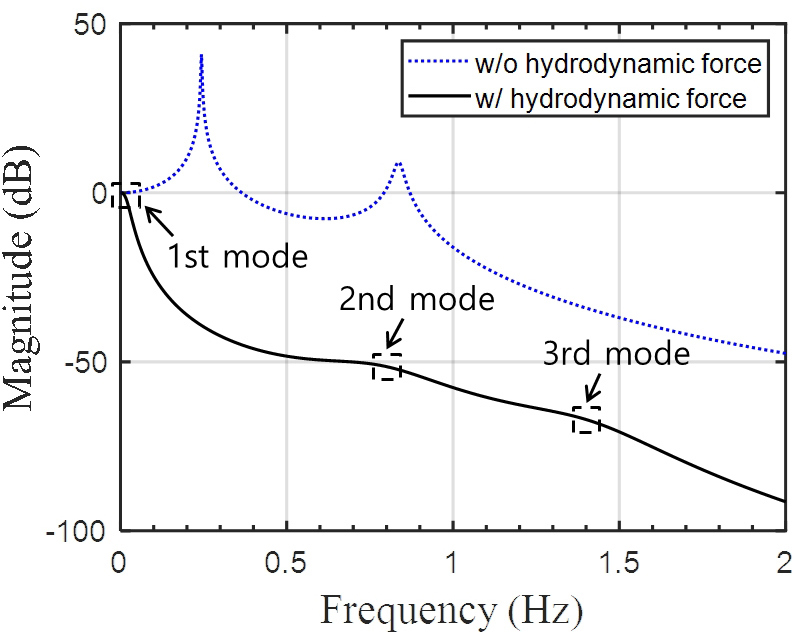
부이 진동에 따른 음향센서의 주파수 응답 산출 결과는 Fig. 8과 같다. 청색 점선은 소노부이의 동유체력을 반영하지 않았을 경우, 흑색 실선은 반영했을 경우의 예측값이다. 두 예측값 비교를 통해 저주파 대역(~ 5 Hz)에 소노부이 공진 주파수가 분포함과, 동유체력 영향에 의해 주파수 응답 크기, 공진 주파수, 공진 피크 유무에 있어 큰 차이가 보임을 확인하였다. 이를 통해 동유체력이 수중 진동 해석 및 예측에 있어 유효하게 작용함을 확인하였으며, 동유체력이 진동 저감에 영향을 주는 주요한 요소임을 확인하였다. 그리고 각 모드에서의 주파수는 고유치 문제(eigenvalue problem)의 해를 구함으로써 알 수 있다. 이 논문에서와 같이 3자유도계 모델의 경우 세 개의 해를 구할 수 있고, 각 해는 각 모드에서의 고유진동수를 의미한다. 동유체력을 반영했을 경우의 예측값에서 1차 모드 주파수(0.024 Hz)에서의 음향센서 주파수 응답의 공진 피크는 제동기의 항력으로 인해 매우 작게 나타남을 확인할 수 있다. 따라서, 다음 4장의 수중 진동 실험을 통한 모델 검증에서는 관심 주파수로 2차 모드 주파수(0.809 Hz)와 3차 모드 주파수(1.432 Hz)를 포함하여 실험을 수행하였다.

Fig. 8

Comparison of the frequency responses of hydrophone with(black solid line) and without hydrodynamic force(blue dotted line)

4. 수중 진동 실험을 통한 모델 검증

이 연구에서 구축한 동유체력 반영 집중소자 모델을 통해 산출한 음향센서 주파수 응답 예측값의 물리적 정합성을 검증하기 위해 소노부이 수중 진동 실험을 수행하였다.

4.1 실험 환경

Fig. 9는 소노부이 수중 진동 실험의 개요도와 사진을 나타낸 것이다. 가진기(vibration exciter)는 해면파에 의한 부이 진동을 모사하기 위해 제작된 것으로, 소노부이를 매달아 적색 화살표와 같이 수직으로 진동할 수 있도록 하였다. 그리고 모터 드라이버를 이용하여 가진기의 가진 주파수를 제어하였다. 가진 주파수의 범위는 음향센서의 진동 모드와 가진기 작동 범위를 고려하여 0.15 Hz ~ 1.65 Hz로 지정하였다. 그리고 음향센서 주파수 응답 산출을 위해 부이 진동을 나타내는 가진기와 진동이 전해지는 음향센서에 각각 수중 가속도계(CTC, 모델 AC194-2D)를 부착하여 신호를 측정하였다. 측정된 2채널의 가속도 신호는 컨디셔닝 앰프(Dytran instruments, 모델 E4114B1)에 입력되어 증폭된 후, 데이터 수집 장치(National instruments, 모델 cDAQ-9178, NI-9234)를 통해 샘플링 주파수 51.2 kHz로 샘플링 후 PC에 저장되었다.

Fig. 9

Experimental setup

4.2 실험 결과

측정된 음향센서의 주파수 응답을 3.2장에서 산출한 예측값과 비교하였다. Fig. 10은 3.2장에서 산출한 동유체력 반영 유무에 따른 음향센서의 주파수 응답 예측값과 실험을 통해 측정한 주파수 응답을 함께 도시한 그래프이다. 해당 값들의 비교는 각 예측값을 정규화하지 않은 절대 비교를 나타낸다. 적색 원은 실험값을 나타내며, 0.05 Hz의 간격을 두고 측정을 수행하였다. 동유체력을 반영하지 않았을 경우 예측값과 실험값이 평균적으로 37.5 dB의 큰 오차를 가짐을 확인함으로써 수중 진동 예측의 정확도를 높이기 위해서는 동유체력이 반드시 반영되어야 함을 알 수 있다. 그리고 동유체력을 반영한 경우 예측값과 실험값의 비교를 통해 평균 4.3 dB의 오차를 확인하였다. 이는 모델의 경제성 및 동유체력의 비선형성을 감안했을 때 작은 값으로 사료된다. 그리고 2차, 3차 진동 모드 및 주파수 응답의 감소 추세가 유사함을 통해 동유체력 반영 집중소자 모델의 물리적 정합성을 검증하였다.

Fig. 10

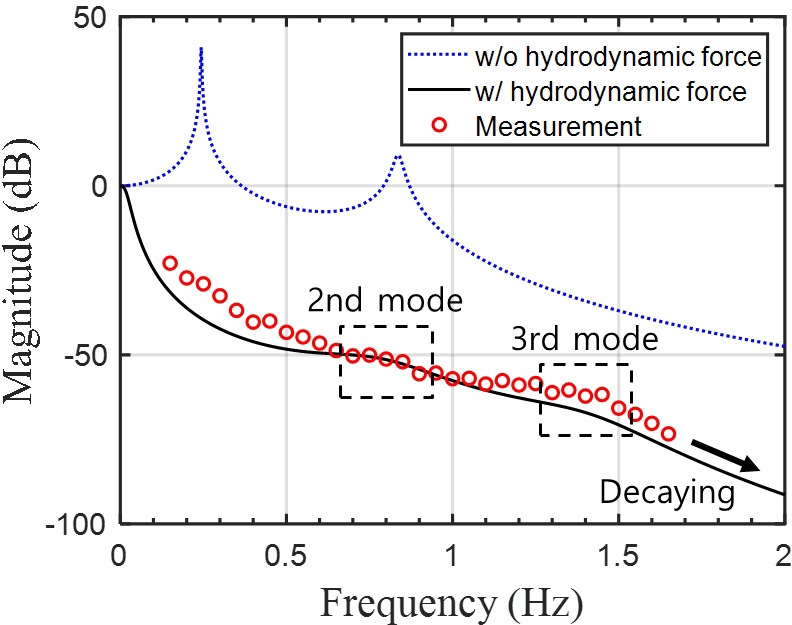
Comparison of the experimental result(red circles) and predicted frequency response of hydrophone with(black solid line), without hydrodynamic force(blue dotted line)

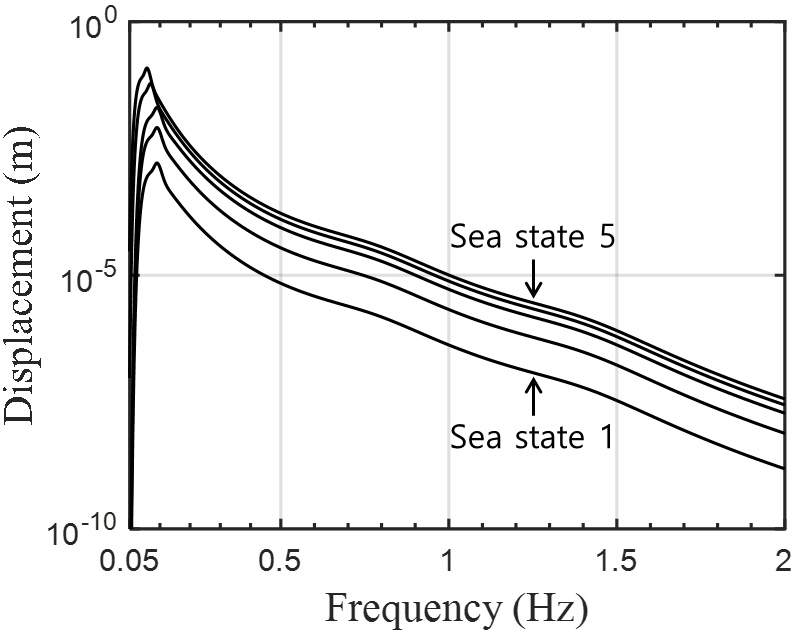
그 다음으로, 이 모델을 통해 산출한 주파수 응답을 이용하여 실제 해상에서의 해면파에 의한 음향센서의 진동을 예측하였다. 이 연구에서는 해면파 조건으로 일반적으로 널리 사용되는 JONSWAP(joint north sea wave project) 파도 스펙트럼을 이용하였다⁽¹⁵⁾. 파도 스펙트럼은 해상상태(sea state) 1부터 5까지를 기준으로 선정하여, 파도 스펙트럼을 계산하였다. 해당 파도 스펙트럼은 0.1 Hz에서 가장 큰 값을 나타내고, 주파수가 커질수록 그 크기가 점차 감소하는 경향을 보이는 특성을 가지고 있다. 계산한 파도 스펙트럼을 통해 주파수 별 파고를 산출하고, 이를 음향센서의 주파수 응답과 곱하여 음향센서의 진동을 계산할 수 있다. Fig. 11은 해상상태(1 ~ 5)에 따른 음향센서의 진동을 나타낸 그래프로서, 해상상태 등급이 높아질수록 음향센서의 진동이 커짐을 알 수 있다. 추가적으로 음향센서 진동 시 출력되는 전기 신호의 민감도를 알고 있을 경우, 동유체력 반영 집중소자 모델을 이용하여 해면파에 의하여 음향센서에서 출력되는 잡음 신호의 크기 또한 예측할 수 있다.

Fig. 11

Predicted vibration of hydrophone induced by surface waves in sea state 1~5

5. 결 론

이 논문에서는 해면파에 기인한 소노부이 음향센서의 수중 진동을 해석 및 예측하기 위한 소노부이 수중 진동 모델로 동유체력 반영 집중소자 모델을 제시하였다. 이 모델은 실험적으로 도출한 동유체력을 집중소자 모델에 반영한 모델로, 이를 이용해 음향센서의 수중 진동을 해석 및 예측하였다. 그리고 소노부이 수중 진동 실험을 통해 해당 모델의 물리적 정합성을 검증하였다. 향후에는 보다 다양한 소노부이 모델을 대상으로 동유체력 반영 집중소자 모델을 적용하여 수중 진동을 예측하고, 나아가 이 모델에 기반하여 음향센서 진동 저감을 위한 최적화를 수행할 예정이다.

그리고 이 논문에서 수행한 것과 같이 동유체력을 실험적으로 측정하는 것이 제한되는 경우, 수치해석적으로 동유체력을 예측하는 방법의 적용도 고려할 수 있다. 또한, 해면파에 의한 소노부이의 진동 외에도 탄성 케이블에서 발생하는 와류진동 등 음향센서의 신호 대 잡음비를 저하시키는 다양한 요인을 개선하기 위한 연구가 수행된다면 소노부이 성능 향상에 기여할 수 있을 것으로 예상된다.

Acknowledgments

이 연구는 LIG Nex1의 지원[수동음파탐지부표 연구개발용역(21H085-I)]으로 수행되었습니다.

References

• Holler, R. A., 2012, The Evolution Of The Sonobuoy from World War II to the Cold War, U.S. Navy Journal of Underwater Acoustics, Vol. 62, No. 2, pp. 322~346.
• Joe, B.-J., Hong, S.-Y., Song, J.-H. and Kwon, H.-W., 2020, Natural Vibrations of Hydrofoils Considering Added Stiffness Effects, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 30, No. 5, pp. 454~463. [https://doi.org/10.5050/KSNVE.2020.30.5.454]
• Guan, G., Geng, J. and Wang, L., 2020, Dynamic Calculation for Sonobuoy Suspension Heave Reduction System with Experimental Correction, Ocean Engineering, Vol. 201, 107141. [https://doi.org/10.1016/j.oceaneng.2020.107141]
• Din, N. A., Ali, S., Farid, M. and Cheema, Z. A., 2018, Mathematical Modeling for the Vertical Damping Analysis of Sonobuoy Lumped Suspension System, Proceedings of the 15th International Bhurban Conference on Applied Sciences and Technology (IBCAST), pp. 729~737. [https://doi.org/10.1109/IBCAST.2018.8312303]
• Huang, C., Yang, K., Ma, Y. and Sun, Q., 2018, Flow Noise Calculation and Suppression for Sonobuoy, Proceedings of OCEANS - MTS/IEEE Kobe Techno-oceans (OTO), pp. 1~4. [https://doi.org/10.1109/OCEANSKOBE.2018.8559090]
• Huang, C., Yang, K., Yang, Q., Li, H. and Ma, Y., 2021, Sinusoidal Vertical Motion Suppression and Flow Noise Calculation for a Sonobuoy, Journal of Marine Science and Application, Vol. 20, No. 3, pp. 546~557. [https://doi.org/10.1007/s11804-021-00220-3]
• Rao, S. S., 2011, Mechanical Vibrations, 5th Edition, Prentice Hall, Upper Saddle River, Chapter 1, Fundamentals of Vibration, pp. 1~123.
• Huang, C., Yang, Q., Yang, K., Liu, H. and Ma, Y., 2021, Numerical and Experimental Study on Spectrum and Temporal Coherence Analyses of Flow Noise Caused by Sinusoidal Vertical Motion of Sonobuoy, Ocean Engineering, Vol. 234, 109241. [https://doi.org/10.1016/j.oceaneng.2021.109241]
• Journée, J. M. J., Massie, W. W. and Huijsmans, R. H. M., 2015, Offshore Hydromechanics, 3rd Edition, TU Delft, Delft, Netherlands, Chapter 6, Rigid Body Dynamics, pp. 1~44.
• Chan, W. L. and Kang, T., 2011, Simultaneous Determination of Drag Coefficient and Added Mass, IEEE Journal of Oceanic Engineering, Vol. 36, No. 3, pp. 422~430. [https://doi.org/10.1109/JOE.2011.2151370]
• Lin, C.-C., Chen, R.-C. and Li, T.-L., 1999, Experimental Determination of the Hydrodynamic Coefficients of an Underwater Manipulator, Journal of Robotic Systems, Vol. 16, No. 6, pp. 329~338. [https://doi.org/10.1002/(SICI)1097-4563(199906)16:6<329::AID-ROB2>3.3.CO;2-X]
• Rao, S. S., 2011, Mechanical Vibrations, 5th Edition, Prentice Hall, Upper Saddle River, Chapter 3.6, Response of a Damped System Under the Harmonic Motion of the Base, pp. 281~283.
• Harel, O., 2009, The Estimation of R² and Adjusted R² in Incomplete Data Sets Using Multiple Imputation, Journal of Applied Statistics, Vol. 36, No. 10, pp. 1109~1118. [https://doi.org/10.1080/02664760802553000]
• Rao, S. S., 2011, Mechanical Vibrations, 5th Edition, Prentice Hall, Upper Saddle River, Chapter 2.6.3, Logarithmic Decrement, pp. 164~166.
• Journée, J. M. J., Massie, W. W. and Huijsmans, R. H. M., 2015, Offshore Hydromechanics, 3rd Edition, TU Delft, Delft, Netherlands, Chapter 5, Ocean Surface Waves, pp. 1~56.