동특성 기반 유체-구조 연성의 부가 질량 효과 분석을 위한 변수 선정에 관한 연구
© The Korean Society for Noise and Vibration Engineering
Abstract
In this research, we derive equations related to the fluid-structure interaction of pressure vessels containing fluids from previous research. Moreover, we analyze the changes in the dynamic characteristics based on parameters specified through the dimensions and material properties of the pressure vessel. A fluid is composed of acoustic elements that are adaptable in the frequency domain, and changes in the dynamic characteristics are examined through mode analysis based on the selected parameters. Specifically, the variables selected include the thickness of the fluid compared to the structure, the density, and the stiffness of the pressure vessel. These are selected as the upper and lower limits of the various arrangements of each cylinder and the variation of the material property’s value. In conclusion, the smaller the ratio of the thickness of the fluid to the structure, the more noticeable the natural frequency reduction effect (or added mass effect), and it is also confirmed that the change in Young's modulus of the pressure vessel does not contribute to the change in the dynamic characteristics in terms of reducing natural frequencies.
Keywords:
Fluid-structure Interaction, Finite Element Analysis, Modal Analysis, Added Mass Effect, Pressure Vessel키워드:
유체-구조 상호작용, 유한요소해석, 모드 해석, 부가질량효과, 압력용기1. 서 론
압력용기 내부 유체의 포함 여부에 따라 기기에 나타나는 동특성의 차이가 발생하며, 이는 내부 유체 자체의 질량 및 구조적인 강성의 변화에 기인한다(1). 따라서 이러한 유체를 반영함으로써 실제 작동 및 설치 환경에 대한 동적인 응답을 정확하게 예측할 수 있다. 따라서 압력용기와 내부 유체가 직접적으로 맞닿는 경계면에서의 거동을 반영하는 것이 중요하다. 구체적으로 유체-구조 상호작용은 유체역학과 구조 역학을 나타내는 법칙 간의 다 물리계를 대상으로 한다. 동특성을 기반으로 경계면에서의 거동은 유체의 압력 및 점성효과로 인해 구조의 변형을 일으키고, 이는 유체의 변형으로 다시 이어지기 때문에 동특성의 변화가 두드러지게 된다. 이에 따라 유체가 포함된 구조물은 유체-구조 연성 효과로 인해 고유진동수 감소 및 모드 역전 현상이 발생하기도 한다(2~6). 또한, Au-Yang은 이론적으로 동축 실린더의 고유진동수 분석을 하였지만, 원주 방향으로의 거동만을 대상으로 제한함으로써 결과를 도출하였다(7). 각 기능을 담당하는 여러 원통형 구조물이 결합된 동축 실린더 형상의 압력 용기에 대한 원전 및 다양한 산업 분야에서의 활용도가 높으며, 특히 이러한 동축 실린더 형상의 용기의 경우 각 용기 간의 거리가 매우 가깝게 설치되는 경우가 빈번하다. 해당 조건은 유체 관점에서 유체의 두께를 감소시키고, 이에 따라 경계면 간의 거리가 짧아짐에 따라 유체-구조 상호작용의 효과가 더욱 커지는 것을 앞선 선행연구에서 검증하였다(8,9). 이러한 현상은 비교적 큰 간극의 유체 대비 얇은 간극을 갖는 유체가 구조물의 부가 질량 효과로 기술된다.
따라서 이 연구에서는 유체가 포함된 압력용기의 유체-구조 상호작용과 관련된 지배 방정식에 대해 파악하고, 유한요소해석을 통해 지정한 파라미터를 기반으로 동특성의 변화에 대한 경향성을 분석하고자 한다. 이를 위해 주파수 도메인에서의 활용도가 큰 acoustic 요소를 통해 유체를 모델을 구축하였으며, 선정 파라미터를 기반으로 모드 분석을 통해 동특성 변화를 고찰하고자 한다. 이때 변수는 구조 대비 유체의 두께, 구조물의 밀도 및 강성을 변수를 선정하였다. 해당 변수는 동축 실린더의 형상 변화나 활용도가 높은 재료 물성을 상하한으로 선정하였다.
2. 본 론
2.1 유체-구조 상호작용
이전 연구에는 유체를 대상으로 구조와 같은 요소를 적용하여, 유한요소 모델을 구축하였으며(10), 다물리계로의 유체-구조 연성 효과를 이 연구에서는 적용하고자 한다. 접수된 구조물의 유체-구조 연성 효과는 수력 하중과 유체에 의한 점성 효과의 반영이 필요하다. 구조물의 관점에서 지배 방정식을 표현하면 식 (1)과 같은 2차 미분방정식의 형태로 표현할 수 있다.
| (1) |
여기서 [M], [K]는 구조물의 질량 및 강성의 행렬식을 나타내며, , {u}는 가속도와 변위 벡터를, 그리고 유체에 의해 구조물이 받는 수력은 {Fp}이다. 유체 내부 압력장에 대한 압축성 유체의 파동방정식은 식 (2)와 같다. 구체적으로 경계면에서의 수력하중은 구조 벽면의 변형을 발생시키며, 또한 이러한 구조 벽면에서의 변형은 유체의 압력장에 가하게 된다.
| (2) |
여기서 c는 유체의 음속, P, t는 각각 압력과 시간을 나타낸다.
식 (1)에서의 우변에 나타난 수력 하중은 유체-구조 경계면에 대하여 압력장의 변화로 발생하는 힘이며, 경계면 S에 작용하는 수력 하중은 식 (3)과 같다.
| (3) |
이때, {Nu}는 적분점 기준으로 나타난 변위 행렬인 {u}를 요소 단위 연속적인 물리량으로 근사화한 요소의 형상 함수를 나타낸다. 또한 우변의 P{n}은 경계면에 수직한 방향으로의 압력 성분을 나타낸다. 구체적으로 식 (2)의 압력 P를 유한요소로 나타내기 위해서는 식 (4)와 같이 기술된다.
| (4) |
여기서 {Np}T는 {Pe}를 근사화 하기위한 요소 형상 함수를 나타내며, 식 (4)를 식 (3)에 대입하면 식 (5)와 같다. 여기서 식 (5)의 각 요소의 형상함수를 통해 식 (6)과 같이 [B]를 정의할 수 있다. 이는 압력장의 단위 벡터와 구조의 변위 벡터를 수력하중의 형태와 coupling mass로 표현하는 경계면에서의 유체 행렬이다. 식 (5)를 식 (1)에 대입하면 아래와 같이 구조 관점에서의 유한요소 기반의 지배방정식을 식 (7)과 같이 나타낼 수 있다.
| (5) |
| (6) |
| (7) |
또한 식 (2)의 유체의 파동방정식을 요소 관점에서 이산화 하면 식 (8)과 같다(12).
| (8) |
여기서 [Q], [H]는 식 (9)와 식 (10)과 같다. 이때 [Q]는 유체의 질량효과, 그리고 [H] 유체의 강성효과를 대표한다.
| (9) |
| (10) |
따라서 유체-구조 사이의 경계면에서 발생하는 변형 중, 경계면에 수직한 성분은 동일하므로 식 (11)과 같이 나타낼 수 있다.
| (11) |
최종적인 유체 영역에서의 유한요소 기반 지배 방정식은 식 (11)을 식 (8)에 대입하여 식 (12)와 같이 나타낼 수 있다.
| (12) |
결과적으로 앞서 구했던 구조물의 행렬식 (7)과 식 (12)를 연성하여 행렬식으로 나타내면 식 (13)과 같다.
| (13) |
식 (13)과 같이 유체와 구조물의 경계면에서의 유체-구조 연성효과를 나타내는 행렬식을 도출하였으며, 비대칭적인 질량행렬과 강성행렬을 가진다. 따라서 3차원 해석에서 이론적으로 유체-구조 연성효과를 반영한 고유치를 도출하는 것은 제한적이며, 경계면의 수직 성분인 원통형 구조물의 원주 방향 성분만을 고려한 분석을 수행하기도 했다. 이 연구에서는 유한요소를 활용하여 수치적으로 지배방정식을 반영하고자 한다. 이 연구에서는 ANSYS workbench 기준으로 앞선 유체의 연성효과를 반영하기에 적절한 acoustic 요소를 활용하였다. 또한 유체-구조 연성효과를 반영하는 3차원 해석에 적합한 유체 요소를 활용하였으며, 이때 활용 가능한 유체요소는 Fluid220, Fluid221 그리고 Fluid130을 선택할 수 있다. 위 유체 요소의 차이는 요소의 order의 차이로 이 연구에서는 육면체 요소로 구성되며 20개의 적분점으로 구성되는 2차 요소인 Fluid220을 이용하여 유체 요소를 구성하였다. 구조물의 경우에도 마찬가지로 육면체 2차요소인 Solid186을 이용하여 모델을 구축하였다.
2.2 유한요소 모델의 구축
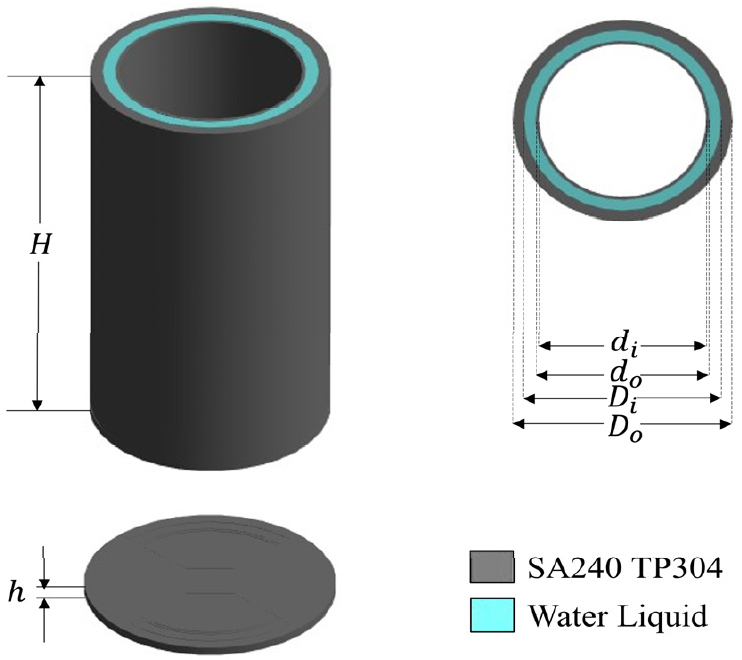
유체-구조 간의 연성효과를 파악하기 위해 냉각재에 접수된 소형 원자로 모듈의 압력용기에 대한 단순화된 유한요소 해석 모델을 Fig. 1과 같이 구축하였다. 압력용기는 내부 실린더, 외부 실린더 및 하부 판으로 구성되어 있는 동축 실린더 형상의 기기이며 제원 및 물성치는 Table 1과 같다. 구조물에 대해서는 단순한 문제 구성을 위해 SA240 TP304의 탄성 물성만을 입력하였다(11). 유체의 경우 물의 압축성 효과 및 질량 효과를 반영하기 위하여 각각 음속 및 밀도를 입력하였다.
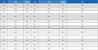
이 연구에서는 Fig. 2와 같이 유체와 구조 간의 모든 적분점을 공유시킬 수 있도록 격자망을 구성하였다. 압력장에 의한 하중 전달 방향인 두께에 대한 요소 개수는 유체 그리고 구조 모두 3개 이상으로 분할하였으며, 다시 말해 두께 방향으로는 최소 적분점의 개수는 7개 이상으로 구성하였다. 더불어 요소 질의 저하를 막기위해 압력 용기의 두께 방향으로의 aspect ratio가 5 이하가 되도록 격자망을 구축하였다.
압력용기의 동특성 변화에 대한 경향성 파악을 위해 3가지의 변수선정을 하였다. 변수 선정은 기하학적인 관점과 재료 성질의 관점에서 고려하였으며, 이에 대한 수치는 Table 2에 명시 되어있다. 각 변수는 case original을 기준으로 선정하였다.
첫 번째로 고려된 점은 식 (14)와 같이 외부 실린더의 두께 대비 유체의 두께비다. 여기서 Tf/s는 각각 내부 유체, 외부 실린더의 두께이다.
이때, 유체의 두께 조정에 따른 내/외부 실린더의 두께 변화로 인한 동특성 변화를 고려하지 않기 위하여 내/외부 실린더의 두께 및 형상은 일정하게 유지하며 유체의 간극을 조정하였다. 두께의 경우 상세 모델의 유체 간극인 270 mm 부터 5 mm의 매우 좁은 간극을 갖는 범위까지 총 8개의 case로 구성하였다.
| (14) |
두 번째 및 세 번째로 선정한 변수는 구조물의 영률및 밀도이다. 식 (15)와 같이 일반화된 영률 E를 나타내었다. 여기서 Emax는 SA240 TP304의 영률을 나타내며, Emin은 aluminum의 영률을 나타낸다. Ei는 각 case에 해당한다. 마찬가지로 식 (16)과 같이 일반화된 밀도를 나타내었다.
| (15) |
| (16) |
상세모델에서 채택한 SA240 TP304의 재료물성은 고강성 및 고밀도를 갖는 재료이다. 따라서 고강성부터 저강성, 고밀도부터 저밀도까지의 물성을 갖는 구조의 연성효과를 파악하기 위해 반영을 하였다. 이를 위해 ASME BPVC code case를(11) 참고하여 상온에서의 aluminum alloy 6061의 재료 밀도 및 영률을 반영하였다. 따라서 이 연구에서 좁은 유체 간극, 그리고 압력 용기의 재료 물성 변화에 따른 동특성 변화를 고찰하기 위해 선정된 케이스는 Table 2와 같다.
2.3 변수 변경에 따른 동특성 변화 분석
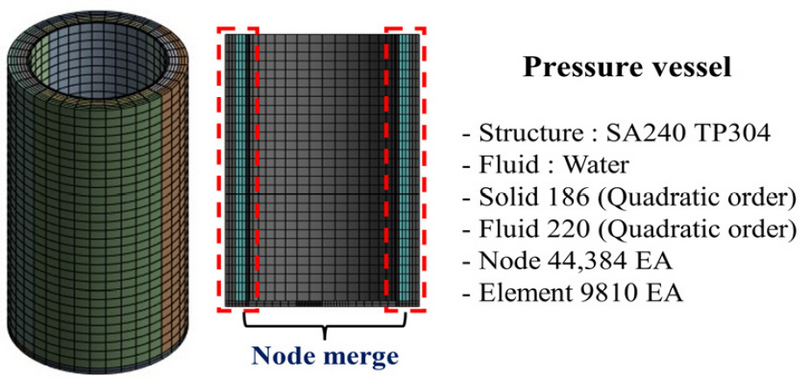
압력용기의 보다 정확한 동적 거동 및 변수에 따른 경향성 분석을 위해 상용 소프트웨어인 Ansys 2022 R2 프로그램을 이용해 유한요소해석을 진행하였다. 유한요소해석 모델의 유체와 구조의 연성 효과로 인한 동특성을 파악하기 위해 앞서 선정한 변수에 대한 모드해석을 진행하였다. 대조군으로 구조 모델과 유체요소가 포함된 모델(FSI)로 구분하였다. 선정한 3개의 변수의 공통적인 기준에 해당하는 case original 모델의 고유진동수와 모드 형상은 Table 3 및 Fig. 3과 같다. 이때 (n,m)에서 n은 원주방향을 m은 축 방향으로의 모드 형상을 기준으로 하였으며 굽힘 모드에 해당할 경우 B로 표기하였다. Case original 모델의 모드해석 결과를 보면 알 수 있듯이 유체의 존재 유/무로 인해 고유진동수가 급격히 감소하는 것을 확인할 수 있다. 특히, 내부 실린더의 경우 그 감소폭이 매우 큰 것을 확인할 수 있다. 반면에 내부 실린더의 (1,1)B 즉 1차 bending 모드에 해당하는 결과에서는 고유진동수가 감소하지 않고 증가하는 양상을 띄게 되는데, 이는 내/외부 실린더가 유체로 인해 연성 되어 in-phase 거동을 하며, 이로 인해 계의 등가강성이 증가하고, 유체 요소의 변형이 작아져 added mass effect가 작아지기 때문에 나타나는 현상이라고 판단된다. 이에 따라 구조 모델과 다르게 FSI 모델에서의 1차 굽힘 모드에 해당하는 경우 유체와 구조 모두 연성된 유사 모드로 도출됨을 확인하였다. 또한, 감소폭이 가장 큰 내부 실린더의 (2,1) 모드는 비교적 저주파 대역의 고유진동수를 나타냄을 확인하였으며, 외부 실린더와는 연성이 되지 않는 거동을 보임을 모드 형상을 통해 확인하였다.
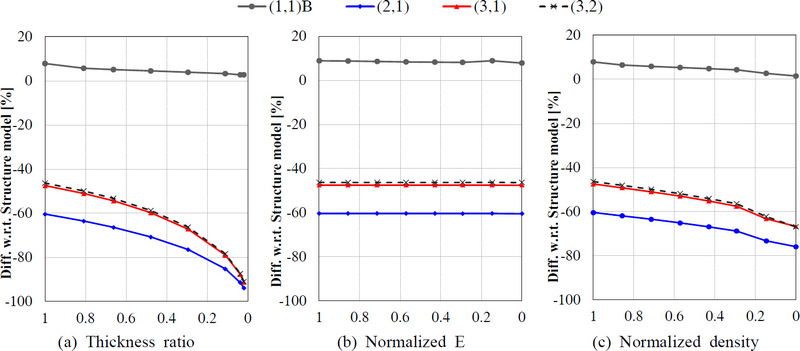
유체의 두께 비에 따른 내부 실린더의 모드해석 결과는 Fig. 4(a)와 같다. 이는 FSI와 structure 모델의 각 선정변수 및 case에 따른 고유진동수 감소폭 변화를 나타낸 그래프이다. 구체적으로 그래프에서 x축으로부터 오른쪽으로 갈수록 각 변수에 해당하는 물리량이 작아지게 된다. 결론적으로 유체의 두께 비가 구조 대비 작아질 수록, 유체-구조 연성 효과로 인한 고유진동수 감소폭이 구조 대비 최대 90 % 이상 발생하는 것을 확인하였다. 내/외부 실린더 모두 구조물의 1차 bending에 있어서는 크게 감소폭의 변화의 수준이 나타나지 않는 것을 확인하였다. 또한, 외부 실린더의 동적 연성에 의한 고유진동수 감소폭 변화 및 모드 역전 현상은 1차 bending과 마찬가지로 내부 실린더와의 동적 연성으로 인해 in-phase 거동을 하므로 최대 2 % 이하의 미미한 수준의 고유진동수 변화폭 감소가 나타나는 것을 확인하였다. 반면에 내부 실린더의 경우 외부 실린더와의 동적 연성이 되지 않고, 유체와의 연성 효과만 고려된 상태로 나타남에 따라 고유진동수 감소폭 변화와 모드 역전 현상이 두드러지게 나타나게 된다. 다시 말해 외부 실린더는 유체와 내부 실린더 모두 동적 연성이 되기 때문에 유체 요소의 변형이 작아지게 된다. 이로 인해 유체가 포함되지 않은 구조 대비 added mass effect로 인한 연성효과가 두드러지게 변화되지 않게 된다. 내부 실린더의 경우 외부 실린더와의 동적 연성의 부재로 인해 유체와의 연성만이 고려되기 때문에 상대적으로 유체 요소의 변형이 크며, added mass effect가 커지게 되어 고유진동수 감소폭 변화가 커지게 된다. 특히 이러한 변화는 case 3부터 case 7까지 급격하게 증가된다. 이때 case 3은 구조 두께 대비 유체의 두께가 약 0.5배에 해당하는 값이다.
영률(E)은 구조물의 강성을 결정 짓는 변수 중 하나이다. Fig. 4(b)와 같이, 영률의 변화에 따른 8개의 case를 분석해 보았을 때 case original 모델 대비 case 7에서 최대 1 % 미만의 미미한 변화 수준이 발생함을 확인하였다. 이는 구조물의 강성 변화가 유체가 포함된 구조물의 등가 강성 변화에 크게 영향을 미치지 않아 유체-구조 연성효과가 두드러지게 변화되지 않음을 의미한다.
구조물의 밀도 변화는 구조물의 질량 변화를 의미하는 변수이다. Fig. 4(c)와 같이 구조물의 밀도 변화에 따라 내부 실린더의 고유진동수 감소폭 변화가 최대 20 %가 발생하게 된다. 이는 case original 대비 상대적으로 감소한 질량으로 인해 FSI모델의 대조군인 구조 모델의 고유진동수 저감에 따른 효과 및 유체의 변형량에 따른 added mass effect에 기인한 것으로 판단된다. 특히, 유체에 의한 부가 질량 효과 보다 구조 모델의 고유진동수 감소폭의 증가의 원인이 더욱 큰 요인으로 작용되는 것을 확인했다.
3가지의 변수에 따른 유체-구조 상호작용의 영향을 파악해 보았을 때, 가장 연성효과가 두드러지게 나타나는 변수는 차례대로 두께 비, 밀도, 강성 변화의 순이다. 특히, 구조 대비 유체의 두께 비 변화에 따른 고유진동수 감소폭은 매우 큰 수준으로 나타남을 확인하였으며, 밀도의 경우에도 마찬가지로 내부 실린더의 원주방향 모드에서 고유진동수 감소폭이 급격히 증가하는 것을 확인하였으며, 이는 구조물의 질량 감소로 인해 구조 모델의 고유진동수 저감 폭의 증가에 해당되는 요인이다. 또한, 구조물의 강성 변화는 상대적으로 매우 큰 구조물인 압력용기의 각 모드에 해당하는 등가강성의 큰 변화를 야기시키지 못하여 강성 변화에 따른 고유진동수 감소폭 변화가 미미한 것으로 판단된다. 결론적으로 접수된 압력용기에 대하여 압력용기 자체의 강성변화는 고유진동수 저감 효과에 미치는 영향이 거의 나타나지 않으며, 압력 용기 자체의 질량 변화는 동특성 변화에 미치는 영향이 두드러진다.
3. 결 론
이 연구를 통해 선정 파라미터 case에 따른 압력용기의 유체-구조 상호작용의 경향성을 분석하였다. 유체가 포함된 구조물은 동특성이 두드러지게 변화되기 때문에 이에 대한 이해와 정확한 해석 설정이 필요하다. 따라서 이 연구에서는 유체가 존재하는 구조물의 지배방정식을 파악하였으며, 유한요소해석 진행을 위한 요소 및 적분점 선정 관련 사항을 고찰하였다. 더불어 각 변수에서 가장 동특성이 두드러지게 변화하는 변수를 정의하였고, 각 인자에 대해 내/외부 실린더와 유체와의 연성 유/무에 따른 동특성 차이를 모드 형상을 기준으로 분석하였다. 따라서 이 연구에서 고찰한 내용은 다음과 같다.
1) 유체-구조 간의 연성효과를 반영하기 위하여 경계면에서의 지배방정식을 검토하였으며, 이러한 지배방정식에 적합한 유체요소 및 경계조건을 검토하였다.
2) 외부 실린더 두께를 기준으로, 동축 실린더 사이 간극에 해당하는 유체 두께의 두께비를 동특성 변화 분석의 변수로 활용하였다. 두께비가 감소할수록 유체를 고려하지 않은 구조 대비 고유진동수 감소 효과가 두드러진다. 더불어 구조물의 두께 대비 유체 두께비가 0.5 이하일 때 고유진동수 감소폭의 변화가 더욱 두드러지는 것을 확인하였다.
3) 산업계에 활용도가 높을 것으로 예상되는 재료 물성에 대해, 강성을 대표하는 영률을 변수로 설정하였다. 그 결과 영률 변경에 따른 구조 대비의 FSI 모델에 대한 고유진동수 저감효과는 미미한 것으로 나타났다. 다른 thickness ratio를 적용했을 때도 이러한 효과가 동일하게 발생한다. 이는 해당 모드 형상에 대해서 등가 강성을 저하시키는 원인이 아닌 것으로 판단한다. 다시 말해 영률의 변화는 구조 대비의 감소 효과에 미치는 영향이 작다.
4) 질량 효과를 대표하는 밀도를 변수로 FSI 모델의 고유진동수 저감 효과를 분석하였다. 기존 스테인리스강 재질의 밀도에서 알루미늄 재질로 변경할 때 고유진동수 감소폭이 줄어든 것을 확인하였다. 이를 통해 압력 용기의 밀도 변화는 고유진동수 저감 효과에 미치는 영향이 두드러지는 것을 검증하였다.
기 호 설 명
| c : | 유체의 음속 |
| D : | 밀도 |
| E : | 영률(Young’s modulus) |
| Fp : | 유체와 구조면에서의 압력 하중 |
| H : | 유체 요소의 강성 행렬 |
| K : | 구조물의 강성 행렬 |
| M : | 구조물의 질량 행렬 |
| n : | 수직 방향 벡터 |
| Np : | 요소의 형상 함수 |
| Nu : | 요소의 형상 함수 |
| P : | 유체의 압력 |
| Pe : | 적분점 압력장의 단위 벡터 |
| Q : | 유체의 질량 행렬 |
| Tf, Ts : | 내부 유체 및 외부 실린더의 두께 |
| : | 가속도, 변위 벡터 |
| : | 구조 및 유체 요소의 변위 |
| ρ : | 유체의 밀도 |
| : | 구조 요소의 응력 텐서 |
Acknowledgments
이 연구는 2019년도 산업통상자원부의 재원으로 한국에너지기술평가원(KETEP)의 지원을 받아 수행 한 연구과제입니다(No. 20193110100020, 해외 내 진분석 기술기준을 적용한 표준형 원전 설계초과지진 대응 기술개발).
References
-
Lee, C. K., Lee, S. J., Lee, E. H. and Park, N.-C., 2020, Methodology for Time History Analysis of Piping System Contains Internal Fluid Including Natural Frequency Separation Effect, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 30, No. 2, pp. 112~118.
[https://doi.org/10.5050/KSNVE.2020.30.2.112]

-
Horvay, G. and Bowers, G., 1975, Influence of Entrained Water Mass on the Vibration Modes of a Shell, Journal of Fluids Engineering, Vol. 97, No. 2, pp. 211~216.
[https://doi.org/10.1115/1.3447253]

-
Au-Yang, M. K., 1977, Generalized Hydrodynamic Mass for Beam Mode Vibration of Cylinders Coupled by Fluid Gap, Journal of Applied Mechanics, Vol. 44, No. 1, pp. 172~173.
[https://doi.org/10.1115/1.3423989]

-
Krajcinovic, D., 1974, Vibrations of Two Coaxial Cylindrical Shells Containing Fluid, Nuclear Engineering and Design, Vol. 30, No. 2, pp. 242~248.
[https://doi.org/10.1016/0029-5493(74)90169-1]

-
Chen, S. S., 1981, Fluid Damping for Circular Cylindrical Structures, Nuclear Engineering and Design, Vol. 63, No. 1, pp. 81~100.
[https://doi.org/10.1016/0029-5493(81)90018-2]

-
Brown, S. J., 1982, A Survey of Studies into the Hydrodynamic Response of Fluid‐coupled Circular Cylinders, Journal of Pressure Vessel Technology, Vol. 104, No. 1, pp. 2~19.
[https://doi.org/10.1115/1.3264181]

-
Au-Yang, M. K., 1976, Free Vibration of Fluid-coupled Coaxial Cylindrical Shells of Different Lengths, Journal of Applied Mechanics, Vol. 43, No. 3, pp. 480~484.
[https://doi.org/10.1115/1.3423895]

-
Choi, Y., Park, J., Park, N.-C., Park, Y.-P., Park, K.-S. and Jeong, K.-H., 2015, Application of Seismic Analysis Methodology to Small Modular Integral Reactor Internals, Journal of Nuclear Science and Technology, Vol. 52, No. 2, pp. 228~240.
[https://doi.org/10.1080/00223131.2014.945506]

-
Choi, Y., Lim, S., Ko, B.-H., Park, K.-S. and Park, N.-C., et al., 2013, Dynamic Characteristics Identification of Reactor Internals in SMART Considering Fluid-structure Interaction, Nuclear Engineering and Design, Vol. 255, pp. 202~211.
[https://doi.org/10.1016/j.nucengdes.2012.10.010]

-
Ji, M., Inaba, K. and Triawan, F., 2019, Vibration Characteristics of Cylindrical Shells Filled with Fluid Based on First-order Shell Theory, Journal of Fluids and Structures, Vol. 85, pp. 275~291.
[https://doi.org/10.1016/j.jfluidstructs.2019.01.017]

- ASME Boiler and Pressure Vessel Committee on Materials, 2015 ASME Boiler and Pressure Vessel Code, Section II: Materials, Part D: Properties (Customary), The American Society of Mechanical Engineers, New York, United States, pp. 788~791.
- Zienkiewicz, O. C. and Newton, R. E., 1969, Coupled Vibrations of a Structure Submerged in a Compressible Fluid, Proceedings of the Symposium on Finite Element Techniques. No. C/R/101/69

Jeonghyun Kim is a graduate school student in mechanical engineering at Yonsei University. His research interests include structural vibration, fluid-structure interaction especially in research reactor assembly.

Chiwoong Ra is a graduate school student in mechanical engineering at Yonsei University. His research interests include structural vibration, non-linear finite element analysis especially in NPP piping systems.

Hyungyu Roh is a graduate school student in mechanical engineering at Yonsei University. His research interests include impact, non-linear finite element analysis especially in canister containing spent nuclear fuel.

No-cheol Park serves as a professor in mechanical engineering at Yonsei University. His research interests include vibration, optics.