배후 공기층이 적용된 단일 미세 타공판에 대한 유전알고리즘 기반 소음저감계수 최적화
© The Korean Society for Noise and Vibration Engineering
Abstract
In this paper, we search for the optimal combination of main shape variables that can maximize the noise reduction coefficient of a sound absorption system using a single micro-perforated panel backed by a cavity. A genetic algorithm is selected as the optimization method, and an orthogonal array table of the design of experiments is introduced to improve the efficiency of the algorithm. Experiments and analysis for the optimization results are performed, and the results are compared. It is confirmed that the trends of the sound absorption coefficient across the frequency band are similar and the noise reduction coefficient has an error of approximately 3.2 %.
Keywords:
Micro-perforated Panel, Genetic Algorithm, Noise Reduction Coefficient, Optimal Design키워드:
미세 타공판, 유전알고리즘, 소음저감계수, 최적설계1. 서 론
소음은 대다수의 경우 사람에게 부정적인 영향을 미치는 요인으로 작용한다. 소음의 발생을 차단하거나 이미 발생된 소음을 저감하는 등에 관한 연구는 과거부터 현재에 이르기까지 소음 관련 학문의 주요 주제로 다뤄지고 있다. 소음저감 즉, 소음 제어는 크게 차음(sound insulation)과 흡음(sound absorption)의 관점에서 다뤄질 수 있다. 흡음은 다공성 물질로써 구현하는 것이 일반적으로, 이 물질을 구성하는 프레임과 유체 간 상대운동에 의한 점성마찰과 공기의 팽창/수축에 의한 열전도로써 음향 에너지를 소산시키는 것으로 알려져 있다(1~3). 상대적 저주파수 대역에서 흡음 효율이 떨어지는 것으로 알려진 다공성 물질의 흡음 계수(sound absorption coefficient)는 일반적으로 주파수가 상승함에 따라 첫 번째 피크(peak)에 도달하고 이후 부드럽게 변동하는 형태를 지니며 첫 번째 피크가 나타나는 주파수는 다공성 물질의 두께에 반비례한다(4). 즉, 상대적 저주파수 대역에서 흡음 계수를 향상시키기 위해 두께를 늘려야 하므로 비용 상승 및 공간 효율 저하를 초래하는 요소로 작용할 수 있다. 또한, 다공성 물질은 일반적으로 폴리에스터(polyester), 폴리우레탄(polyurethane)과 같은 수지(resin)로 제작되어 열과 같은 환경요소에 취약하다는 단점이 있다.
현재까지 소음제어를 목적을 고전적 다공성 물질 외에 국부 공진 시스템의 주기적인 배열(5), 음향 양자결정(acoustic phononic crystal) 등을(6) 활용하여 밴드갭(band gap)을 형성, 특정 주파수에서 파동 전달을 차단하는 것과 같이 자연에서 쉽게 발견되지 않는 특성을 활용하는 음향 메타물질(acoustic meta-material)과 직경 1 mm 이하의 미세한 홀이 주기적으로 타공된 판재와 배후 공기층이 결합된 흡음 시스템 등(7)이 개발된 바 있으며 적절한 소재를 사용할 경우 우수한 내환경성(environmental resistance)을 갖출 수 있어 다공성 물질의 대안이 될 수 있다. 최근, 합성곱 신경망(convolutional neural network, CNN)을 활용한 흡음 계수 추정(8), 기계학습에 의한 메타물질 단위 낱칸(unit cell) 설계 기술 등과(9) 같이 인공지능 기법을 활용하여 다공성 물질과 음향 메타물질의 자체 성능이나 활용효율을 향상시키려는 연구도 활발히 진행되고 있다.
이들 중 미세 타공판은 관 내 공진주파수에서 유체와 고체 간 점성마찰로써 흡음 효과를 구현하며 다공성 물질에 비해 흡음 주파수 대역이 좁고 그 레벨이 비교적 낮은 것이 특징이다. 하지만, 미세 타공판은 다공성 물질로써 흡음을 구현하기 어려운 비교적 낮은 주파수 대역 소음 제어에 좋은 대안으로써 기계, 항공, 조선해양, 건축 등 다양한 분야에 활용될 수 있다.
미세 타공판에 관한 이론은 Maa에(7) 의해 정립된 것으로 평가된다. 이에 따르면 배후 공기층이 결합된 미세 타공판은 공명기와 같은 형태로 거동하며, 기하학적 형상을 적절히 제어하여 원하는 주파수 대역 소음 제어가 가능하다. 하지만, 기능적 한계에 의해 흡음이 가능한 대역은 하나 또는 두 개의 옥타브 밴드에 국한되는 점은(10) 미세 타공판의 활용성을 저하시키는 요소라 할 수 있다. 이는 곧 미세 타공판-배후 공기층 시스템에 의한 소음제어를 위해 매우 정교한 설계가 요구됨을 의미한다. 다양한 소재에 대한 적용성 검토 등을 목적으로 미세 타공판의 진동이 흡음 특성에 미치는 연구 또한 진행된 바 있으며, 플라스틱과 같은 상대적으로 저밀도 물질의 경우 판재의 음압 가진에 의해 흡음 계수가 약 0.1 미만 가량 떨어질 수 있음이 보고된 바 있다(11).
이후 연구는 흡음 대역의 확장을 중심으로 건축(11), 항공우주 등(12) 다양한 분야에 대한 응용이 주를 이루는 것으로 평가되며 최적화 기법을 적용한 연구도 일부 확인된다. 미세 타공판에 의한 흡음 시스템은 흡음의 관점에서 다변수, 단일 목적함수 문제로 다뤄질 수 있다. 즉, 비교적 단순한 형태의 최적화 문제로써 정식화 될 수 있는 것이다. 하지만, 각 변수의 목적함수에 대한 기여가 불분명하고 최적해 탐색 영역이 비교적 넓으며 각 변수의 최적해 탐색 범위 또한 상이한 특징을 지니므로 최적화 알고리즘을 구성하는 과정에서 이와 같은 특징들이 적절히 고려될 수 있도록 제어변수에 대한 동시 탐색 등의 장치가 적절히 구현되어야 한다.
Ruiz et al(13)은 다중층 미세 타공판-배후 공기층 시스템에 대해 담금질 기법(simulated annealing method)을 적용하여 주요 설계변수에 대한 최적해를 성공적으로 탐색한 바 있으며, Yan et al(14)은 벌집형(honeycomb-type) 미세 타공판에 대해 입자 군집 최적화 기법(particle swarm optimization method)을 적용하여 배후 공기층의 두께에 대한 최적해 탐색을 수행한 바 있다. 하지만, 유전알고리즘에 기반한 최적화 사례는 드물다.
Holland에(15) 의해 정립된 것으로 평가받는 유전알고리즘은 목적함수의 제어변수 변화에 대한 기울기 정보가 필요치 않고 기존의 기울기 기반 최적화 방법에 비해 넓은 구간에서 여러 설계변수를 동시에 탐색할 수 있다. 또한, 변이 연산(mutation operation)을 통해 국소 수렴 문제를 비교적 쉽게 해결할 수 있다는 장점이 있다(16). 앞서 언급한 특성을 갖는 미세 타공판에 의한 흡음 시스템의 최적화 문제에 대해유전알고리즘을 최적화 기법으로 선택하는 것이 합리적이라 판단된다.
전술한 바를 종합하여 이 논문에서는 고전적 다공성 물질 대비 우수한 내환경성을 갖는 단일 미세 타공판-배후 공기에 의합 흡음 시스템의 주요 설계변수를 최적화 하는 것을 목적으로 한다. 이를 위해 미세 타공판-배후 공기층 흡음 시스템을 최적화 문제로 정식화하고 유전알고리즘으로써 이를 최적화 하였다. 최적화 결과는 잔향실을 이용한 무작위 입사조건에서의 흡음계수 측정결과와 해석결과를 상호 비교하여 그 신뢰성을 검증하였다.
2. 미세 타공판-배후 공기층 시스템의 흡음계수 해석
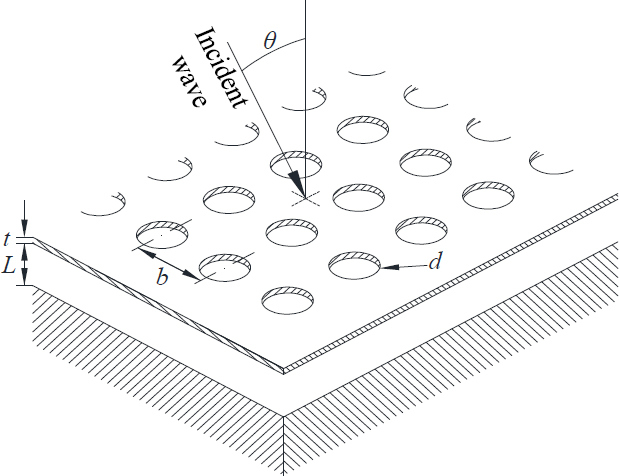
미세 타공판에 의한 흡음 시스템은 통상 Fig. 1과 같이 직경 1 mm 이하의 홀이 주기적으로 배열된 판재가 배후에 공기층을 갖는 형태로 구성된다. Maa는(7) Crandall에 의해(17) 제안된 mm 단위 이상의 직경을 갖는 실린더에 대한 간략화된 식을 직경 1 mm 이하로 확장하여 식 (1)과 같이 정규화된 비 음향 임피던스(normalized specific acoustic impedance) 경험식을 제안하였다(7,18).
| (1) |
여기서, w는 각주파수, j는 허수, r은 비 음향 레지스턴스(specific acoustic resistance), m은 비 음향 리엑턴스(specific acoustic reactance)로 각각 식 (2)와 식 (3)과 같이 정의된다.
| (2) |
| (3) |
여기서, d는 홀 직경, ϕ는 표면 공극률, t는 판 두께, g1, g2는 금속/비금속 소재에 대한 상수로 금속의 경우 g1 = 0.335, g2 = 0.21이고 비금속의 경우 g1 = 0.147, g2 = 0.316 이다(7). 이며, f는 주파수이다. 배후 공기층의 미세 타공판 표면에서 비 음향 임피던스는 식 (4)와 같이 정의 될 수 있다.
| (4) |
여기서, c는 음속(speed of sound), L은 배후공기층의 두께이다. 미세 타공판 표면에서 이 흡음 시스템의 비 음향 임피던스는 미세 타공판과 배후공기층의 그것과의 합으로써 식 (5)와 같이 정의될 수 있다.
| (5) |
음파가 미세 타공판 면과 수직한 축에 대해 어떤 각 θ로 입사할 경우 미세 타공판에 의한 흡음 시스템의 비 음향 임피던스는 최종적으로 식 (6)과 같이 정의될 수 있다.
| (6) |
이상과 같이 유도된 Maa의 경험식은 홀 직경 1 mm 이하, 입사파의 파장보다 짧은 홀 간 거리, 적절한 두께의 배후공기층 등의 조건에 유효한 것으로, 판재 자체가 진동함에 따른 소음 방사, 홀과 홀 사이 부분에서의 반사파 등은 고려하지 않는다(7). 식 (6)을 바탕으로 특정 입사각에 대한 흡음계수는 식 (7)과 같이 계산 가능하다.
| (7) |
여기서, Re과 Im은 대상 복소수의 실수부와 허수부를 각각 의미한다. 다루고자 하는 모든 입사각에 대한 이 시스템의 평균 흡음 계수는 식 (8)과 같이 계산 가능하다.(19)
| (8) |
여기서, 하첨자 min은 최소 입사각을, max는 최대 입사각을 의미한다. 매우 높은 입사각에서 음파는 전반사에 근접할 것이므로 이 논문에서는 θmin을 0˚, θmax을 88˚로 각각 정의하였으며 θmin부터 θmax까지 2˚의 등 간격으로 구분하여 무작위 입사 조건을 구현하였다.
3. 소음저감계수 최적화
3.1 문제 정식화
이 논문에서 다루는 시스템의 경우 최적 설계의 기준이 되는 목적함수는 흡음 및 차음의 관점에서 정의될 수 있다. Maa의 경험식에 따르면 배후 공기층이 적용된 단일 미세 타공판은 일종의 흡음재(absorber)이므로 흡음 관점에서 목적함수를 정의하는 것이 합리적이라 판단된다. 흡음 성능을 표현하는 다양한 방법이 존재하나, 건축음향, 조선, 항공 등 분야에서 부재의 흡음성능을 정량적으로 표현하는 방법인 소음저감계수(noise reduction coefficient, NRC)를 목적함수 정의 기준으로 정하였다. 소음저감계수는 1/3 옥타브 밴드 대역에서 측정한 흡음계수 중 중심주파수 250 Hz, 500 Hz, 1 kHz, 그리고 2 kHz에서 흡음 계수를 산술적으로 평균한 것으로 1에 가까울수록 우수한 흡음성능을 지닌다.
임의의 입사각에 대해 배후 공기층을 갖는 미세 타공판의 흡음계수는 식 (8)을 활용하여 계산할 수 있다. 이때, 미세 타공판의 소재가 특정되었을 경우, 제어 가능한 변수는 홀 직경(d), 홀 피치(b), 패널 두께(t), 그리고 배후 공기층 두께(L)와 같은 형상변수로 한정된다. 홀 피치가 홀 직경보다 커야 한다는 제한조건이 존재하나, 이 제약조건이 만족된다는 조건 하에 네가지 형상변수는 서로 독립이다. 이상을 고려하여 전술한 네가지 형상변수를 제어변수로써 정의하였다.
이 논문에서는 ‘최적’의 의미를 ‘가능한 높은 수준의 흡음성능’으로 정의하였다. 소음저감계수가 1이라는 물리적 상한을 가지므로 목적함수를 특정 값에 근접할수록 좋은 망목 특성(nominal-is-best characteristics)의 관점에서 정의할 수 있으나, 목적함수를 정의하기 위해 최적값에 대한 오차함수 등의 수학적 장치가 추가적으로 요구된다. 하지만, 소음저감계수가 1에 도달하는 것은 현실적으로 어려움을 감안하여 최적에 이르는 조건을 망대 특성(larger-is-better characteristics) 관점에서 목적함수를 식 (9)와 같이 소음저감계수로써 정의하였다.
| (9) |
여기서, 하첨자 250, 500, 1000, 2000은 1/3 옥타브밴드에서 중심주파수이다.
최적설계 문제 정식화를 위해 요구되는 마지막 요소는 구속조건이다. 구속조건은 다음 두 가지 사항에 기준하여 정의하였다. 첫째, 구속조건은 추후 최적화 결과에 대한 실험적 검증을 위해 현실적으로 제작 가능한 수준으로 정의되어야 한다. 둘째, 구속조건은 유전알고리즘의 성능에 지배적인 요소로 작용하는 보다 구체적인 구속조건을 정의하기에 앞서 재료 특성에 관한 선택이 선행되어야 한다. 이 논문에서는 자체 강성, 부식에 대한 저항성 등을 고려하여 스테인레스를 판재 소재로 정의하였다. 금속 판재의 두께가 지나치게 두꺼울 경우 가공성이 떨어질 수 있고 지나치게 얇을 경우 자체 구조강성이 부족하여 형상 유지에 어려움이 있을 수 있다. 스테인레스 판재 0.35 T부터 상기 조건을 만족하며 0.7 T를 초과할 경우 가공성이 매우 떨어짐을 고려하여 하한을 0.35 T, 상한을 0.7 T로 구속 조건을 비교적 짧게 정의하였다.
홀 직경은 이번 논문에서 다루는 바와 같은 단일 미세 타공판-배후 공기층 문제에 대한 사전 실험/해석적 검토 결과를 바탕으로 0.1 mm ~ 0.2 mm 부근에서 최대가 됨을 고려하여 이 구간을 포함하며, 초기 해집단의 다양성이 적절히 확보될 수 있도록 하한을 0.05 mm 상한을 0.22 mm로 정의하였다.
홀 피치는 짧을수록 높은 소음저감계수를 보이는 파라미터로 미세 타공판의 정의가 홀 직경 1 mm 이하인 것과 홀 직경의 구속조건을 고려하여 하한을 1 mm로 정의하였다. 10 mm 이상인 경우 소음저감계수가 0.1 수준의 값을 지니는 점을 고려하여 상한을 30 mm로 정의하였다.
배후 공기층 두께는, 미세 타공판-배후 공기층 흡음 시스템의 매커니즘에 의해 주요 흡음 주파수 대역이 두께에 반비례함을 고려하여 비교적 낮은 주파수 대역인 250 Hz와 500 Hz가 적절히 포함 되는 100 mm를 하한으로 정의하였다. 상한은 현실적인 제작 가능성을 고려하여 700 mm 이하로 설정하였다. 구속조건에 관한 이상의 사항을 정리하면 Table 1과 같다.
전술한 바를 종합하면 배후 공기층을 갖는 단일 미세 타공판의 형상변수 최적설계 문제는 흡음의 관점에서 다음과 같이 정식화 될 수 있다.
Find v= [d, b, t, L] Maximize J(v)Subject to0.05 mm ≤ d ≤ 0.22 mm1 mm ≤ b ≤ 30 mm0.35 mm ≤ t ≤ 0.7 mm100 mm ≤ L ≤ 700 mm
3.2 유전알고리즘기반 최적화
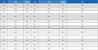
유전알고리즘은 통상 Fig. 2에 도시한 바와 같이 구성되어 세대를 거듭하며 적합도를 검토해 나가는 것을 기본 구조로 한다(15). 이를 위해 제어변수를 염색체(chromosome)로 변환한 뒤 교차(crossover), 변이(mutation) 등의 연산을 수행하게 된다. 이때, 염색체는 이진수(binary number), 16진수(hexadecimal number) 등으로 표현 가능하며 현재 이진수 형태의 표현 방법이 구현의 간결함 등을 사유로 가장 널리 활용되고 있다. 전술한 바를 고려하여 이 논문에서는 유전알고리즘 중 염색체를 이진수로 표현하는 이진유전알고리즘(binary coded genetic algorithm)을 활용하였다.
유전알고리즘에 의한 효과적 최적해 탐색을 위해 해집단의 다양성은 적정 수준으로 유지되어야 하며, 이는 알고리즘의 성능이 지배적인 영향을 미치는 요소 중 하나라 할 수 있다. 이 논문에서 다루는 비교적 단순한 최적설계 문제에 대한 해집단 크기는 100 ~ 200 정도로 알려져 있다(20). 이를 고려하여 해집단 크기를 150으로 정의하였다. 각 설계변수의 제한조건 내에서 중복을 허용하지 않고 150 개체를 무작위로 선택하여 내림차순으로 정렬한 뒤 하나의 벡터로써 정의하였다. 모든 설계변수에 대한 초기 해 벡터를 병렬적으로 배치하여 행렬화하고 이를 초기 해집단으로써 정의하였다. 이때, 초기 해집단에서 한 행은 하나의 해 그룹으로 간주된다.
주어진 환경에 대한 적합도를 표현하는 적합도 함수는 최적화 문제에서의 목적함수에 해당하는 것으로 식 (9)와 동일하게 정의하였다.
종료조건은 세대 변화에 대한 해집단의 최고(또는 평균) 적합도 변화율이 특정 값 이하일 때와 같은 현상 해석적 방법 또는 기타의 방법으로 정의될 수 있다. 이 논문에서는 종료조건을 설정하지 않고 해집단의 적합도 성장 양상을 평가한 뒤 연산시간, 결과의 유효성 등을 종합적으로 고려하여 최적화 과정이 1000번째 세대까지 수행되도록 종료조건을 정의하였다.
선택 연산은 해집단에서 교배를 위한 한쌍의 부모해를 선택하는 과정으로 정의될 수 있다. 현재까지 비례 룰렛-휠 선택(ratio roulette wheel selection)(15) 과 순위 기반 선택(rank based selection)(21) 그리고 토너먼트 선택(tournament selection) 등의(22) 방법이 제안되어 활용되고 있다. 이 중 토너먼트 선택은 유전알고리즘에서 가장 널리 사용되는 선택 방식 중 하나로 개체 n개를 무작위 선정한 뒤 개체 간 1:1로 적합도를 비교하여 높은 확률로 우수한 개체가 상위 라운드로 진행하여 최종 승자가 부모해로써 활용된다. 선택 과정에서 별도의 수학적 장치가 요구되지 않아 여타 방식보다 시간 복잡도 측면에서 유리하다고 할 수 있으며, 토너먼트 참가 개체수를 제어함으로써 손쉽게 선택 압력을 제어할 수 있다는 것이 장점이다(21~23).
하나의 부모해를 선택에 적절한 토너먼트 참가 개체 수는 2개 ~ 5개인 것으로 알려져 있다. 이 논문에서는 해집단에서 23 개체를 중복을 허용하지 않고 선택한 후 토너먼트에 참가시켰으며 최종 2개체를 부모해로 선정하였다. 이때, 각 라운드의 우성개체(dominant individual) 승리 확률은 70 %로 Fig. 3과 같이 정의하였다.
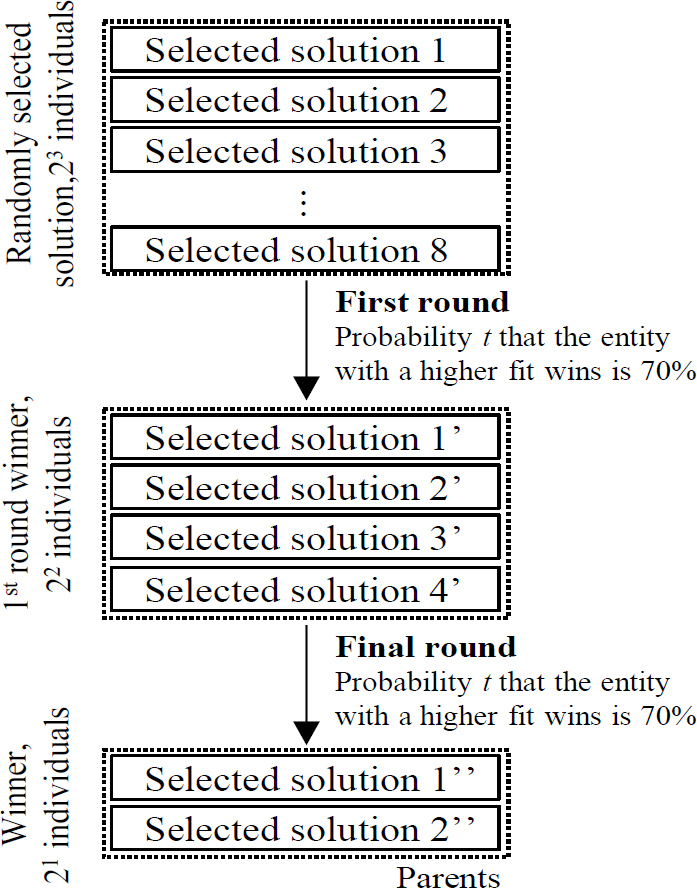
Tournament selection scheme diagram. Initial number of individuals is 23, winning probability for dominant individuals is 70 %.
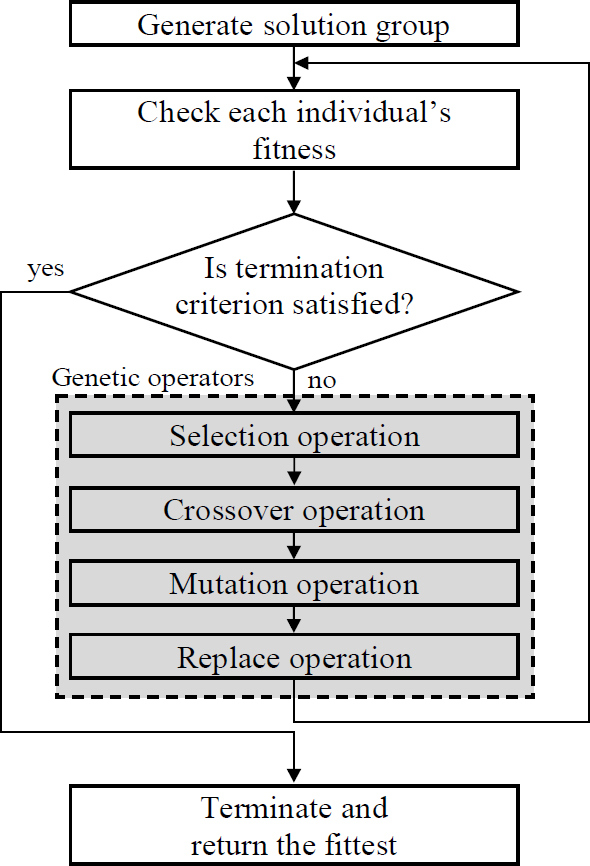
선택된 부모해는 이후 교배를 위해 Fig. 4와 같이 이진수(binary number)로 인코딩한 뒤 이를 유전 연산을 위한 염색체(chromosome)로써 정의하였다. 이때, 각 제어변수의 구속조건을 고려하여 염색체의 길이는 홀 직경 8 bit, 홀 피치 9 bit, 패널 두께 10 bit, 그리고 공기층 두께 10 bit로 각각 정의하였다.
교차 연산은 부모해를 교배하여 자식해를 생성하는 과정으로 정의될 수 있다. 교차 연산으로 한 지점 또는 다수 지점을 분할하는 것이 일반적이나, 다점 교차의 경우 세대 간 유전 정보 전달의 일관성 확보에 어려움이 발생할 수 있으므로 이 논문에서는 Fig. 5에 도시한 바와 같이 1점 교차 방식을 활용하였다.
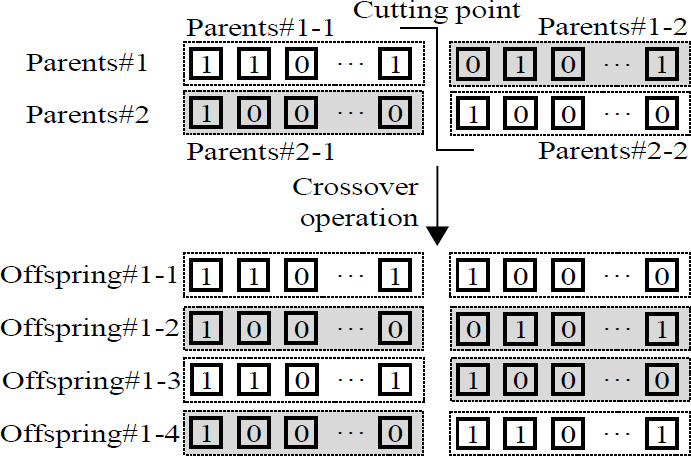
Crossover operation scheme. Number of child solutions that can be generated from a pair of parent solutions
염색체를 구성하는 4개의 해들은 비록 하나의 해 그룹으로써 취급되나 상호 독립적이므로 교차 연산은 각 해에 대해 개별적으로 수행되어야 한다. Fig. 5에 도시한 바와 같이, 각 해에 대한 교차 연산 후 생성 가능한 자식해의 경우의 수는 4개로 각 해가 서로 독립적임을 고려하면, 부모해 즉, 한 쌍의 염색체를 교배함으로써 생성 가능한 자식해의 경우의 수는 44개가 된다.
모든 경우의 수를 고려할 경우 시간복잡도 측면 등에서 최적화 알고리즘의 효율이 저하될 것으로 판단하여 효과적인 실험 수행을 위해 활용되는 실험계획법(design of experiment)을 도입하였다(24~26).
실험 계획의 관점에서 제어변수는 실험변수(experiment variable)로, 각 해별 생성 가능한 자식해의 개수는 제어 수준(control level)으로 각각 간주될 수 있다. 제어 수준이 4임을 감안하여 Table 2와 같이 제어수준 4, 제어변수 5개 이하의 실험에 주로 활용되는 L16 직교배열표를 도입하여 생성 가능한 자식해의 경우의 수를 16개로 축약하였다.
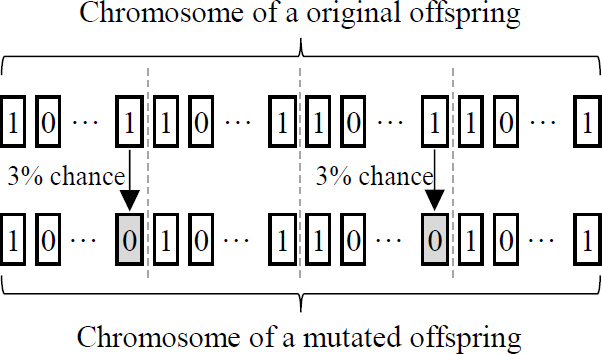
변이 연산은 일종의 국소 수렴 탈출 장치로 간주될 수 있다. 일반적으로 자식해 염색체에서 하나의 유전자 또는 다수를 임의 선택하고 일정 확률로 이를 강제 변경하는 방식으로 작동한다. 변이확률을 지나치게 높게 설정하거나 2개 이상의 유전자를 변이 대상으로 정의할 경우 최적해 탐색 영역을 세대가 지남에 따라 좁혀가지 못하는 임의 탐색(random search) 문제로 변질될 수 있다. 현재, 적정 변이확률은 현재 2 % ~ 3 %, 적정 유전자 변이 개수는 1개로 각각 알려져 있으므로 이 논문에서는 매 교차연산 후 3 %의 확률로 1개의 유전자를 임의 선택하여 0인 경우 1로, 1인 경우 0으로 강제 조정하는 방식으로 Fig. 6과 같이 변이 연산을 구현하였다.
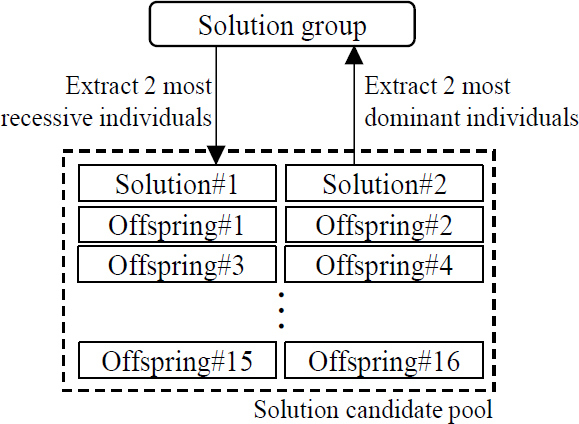
대치 연산은 한 세대가 지난 후 해집단에서 가장 열성인 개체와 교차, 변이 연산 결과 생성된 자식해 집단에서 가장 우성인 개체의 적합도를 비교하여 우성인 개체를 해집단에 편입(또는 잔류)시키는 연산으로, 이 논문에서는 Fig. 7에 도시한 바와 같이 해집단에서 2개의 열성 개체를 추출하여 자식해 집단에 편입시켜 해집단 편입 후보 풀(pool)을 구성하고, 여기서 우성인 개체 2개를 추출하여 해집단에 편입시키는 방식으로 대치연산을 구현하였다.
3.3 최적화 결과 및 유효성 검토
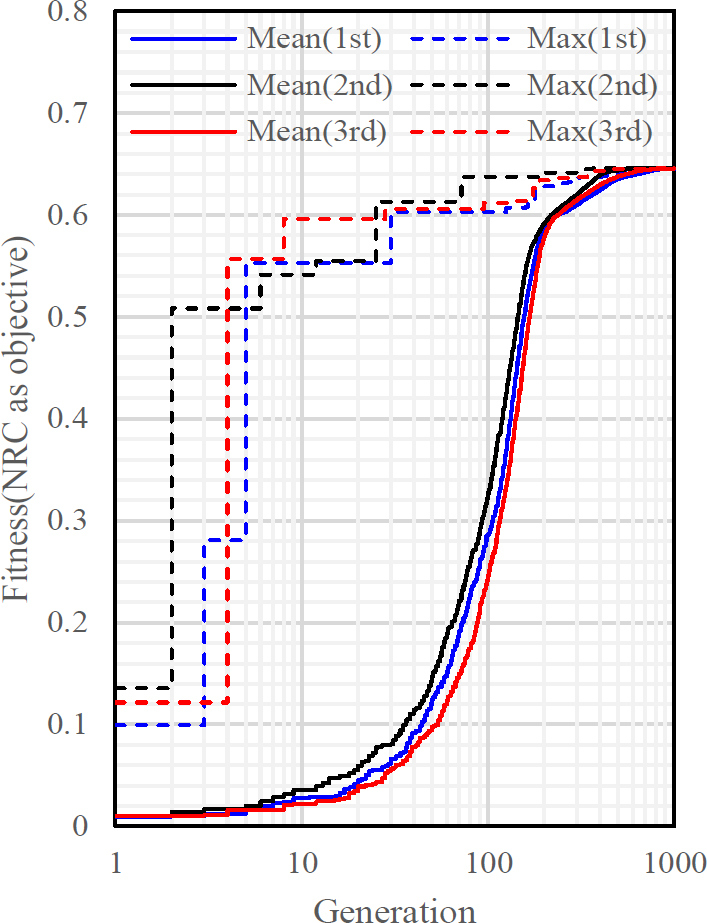
유전알고리즘에 의한 최적화 결과 3회의 시행 모두 Fig. 8에 도시한 바와 같이 약 250세대까지 해집단의 평균 적합도(mean fitness)가 급격히 상승하는 경향을 보였으며 이후부터 종료 기준인 1000세대까지 비교적 완만하게 최적해로 수렴하는 경향을 보였다. 이때 소요 시간은 Intel i7-7700 CPU, 8 GB RAM 환경에서 약 43초 정도로 기록되었다. 적합도는 해집단의 최 우성 개체의 그것이 평균에 비해 비교적 빠르게 수렴하여 약 400세대 부근에서 사실상 최적해에 수렴하는 것으로 확인되었다. 이때의 최적해는 Table 3과 같이 얻어졌다.
최적화 결과의 유효성 검토를 위해 실험체를 제작하고 흡음계수를 측정하였다. 흡음계수의 측정에는 여러 방법 중 무작위 입사(random incident) 조건 구현이 용이한 잔향실법(reverberation chamber method)을 사용하였으며, 이와 관련한 구체적 사항은 국내 표준 KS F 2805:2014에 준해 수행하였다.
실험에는 Table 4의 설비를 활용하였다. 실험체의 홀 직경은 0.14 mm, 홀 피치는 1.1 mm, 패널 두께 0.4 mm로 제작하였으며 배후 공기층 두께는 305 mm로 설정하였다. 면적은 10.9 m2가 되도록 하였다. 시험체 측면부는 테이프를 통해 외기소통을 차단하였다. 마이크로폰은 Fig. 9에 나타낸 바와 같이 실험체 상면으로부터 수직상방 1.2 m 이내 거리 6개소에 배치하였다. 음원위치는 잔향실 모서리부 2개소로 정의하였으며, 백색소음을 음원으로 활용하였다. 주파수 측정 대역은 1/3 옥타브 밴드 기준, 100 Hz에서 5 kHz로 정의하였다. 음원중단법(interrupted noise method)을 이용하여 실험체 설치/제거 상태에서 잔향시간을 측정하고 다음의 식 (10)에 따라 주파수별 흡음계수를 산출하였다.
| (10) |

Sound absorption coefficient measurement setup using the reverberation chamber method. Blue arrow(solid line): microphone, red arrow(dotted line): tweeter, yellow arrow(dashed line): woofer, red circle(dotted line): noise source position, black circle (dashed line): side sealing
여기서, V는 잔향실 체적, T는 잔향시간, λ는 ISO 9613-1에 준해 계산되는 파워감쇠계수, 하첨자 1은 공실, 2는 실험체 설치 조건, K는 실내 온도다.
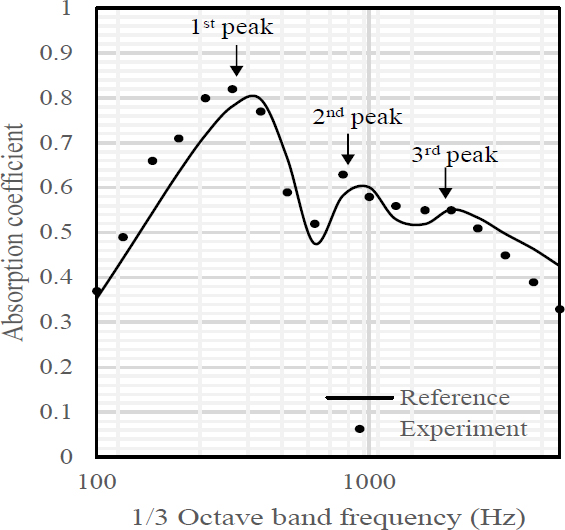
실험체에 대한 흡음계수 측정 결과와 최적화 결과에 대한 흡음계수 해석 결과를 Fig. 10과 같이 도시하였다. 실험결과의 첫 번째 및 두 번째 피크가 해석결과에 비해 낮은 주파수 대역으로 이동되고 흡음계수가 약 0.01 수준 차이 나는 것으로 확인되었다. 주파수 대역에 대한 흡음계수 변화 추이는 상호 유사한 것으로 나타났다.
4. 결 론
이 논문에서는 배후 공기층이 적용된 단일 미세 타공판에 대한 주요 형상변수를 유전알고리즘을 활용하여 소음저감계수에 대해 최적화 하였다. 효과적인 최적해 탐색을 위해 유전알고리즘의 주요 연산 중 교차 연산에 실험계획법을 적용하였으며 최적해 탐색결과를 바탕으로 제작된 실험체에 대한 흡음률을 측정하고 해석결과와 상호 비교하였다. 검토 결과, Fig. 10을 기준으로, 첫 번째와 두 번째 피크 주파수가 서로 상이한 것으로 확인되었으며 이는 다음과 같은 두 가지 측면에 기인한 것으로 판단된다.
첫 번째 측면은 실험과 해석 간 형상변수의 차이다. 실험체를 제작/설치 등의 한계로 최적화 결과가 있는 그대로 구현되지 못하였다. 특히, 첫 번째 피크가 상이한 이유는 배후 공기층 두께 차에 의한 시스템의 공진주파수 불일치로 판단된다.
두 번째 측면은 실험과 해석간 미세 타공판의 물리적 규모에 관한 차이에 기인한 것으로 판단된다. Maa의 경험식은 기존 실린더에 대한 이론에 기반 하여 실험적으로 보완한 것으로써 측방으로 무한한 즉, 무한평판(infinite plate)을 가정하나, 실험은 10.9 m2의 유한한 면적에 한정된다. 하지만, 전체적인 경향이 상호 유사하고, 소음저감계수 또한 해석과 실험간 오차율이 3.2 % 수준으로 확인되어 이 논문에서 제시한 배후공기층을 갖는 단일 미세 타공판에 대한 형상변수 최적화 방법론의 공학적 유용성이 충분한 것으로 판단된다. 무한-유한평판간 차이 보정에 관한 문제는 이후 후속연구를 통해 규명되어야 할 것으로 판단된다.
추가로, 이번 논문은 단일 미세 타공판-배후 공기층에 대한 비교적 단순한 경우만을 다루고 있으므로 보다 복잡한 구조에 대한 최적화 연구와 흡음과 차음을 동시에 고려하는 다목적(multi-objective) 최적화에 대한 연구도 수행되어야 할 것으로 판단된다.
Acknowledgments
이 논문은 2023년도 중소벤처기업부 기술개발사업[과제번호: RS-2023- 00224887]의 지원을 받아 수행된 연구임.
References
-
Biot, M. A., 1956, Theory of Propagation of Elastic Waves in a Fluid-saturated Porous Solid, The Journal of the Acoustical Society of America, Vol. 28, No. 2, pp. 168~191.
[https://doi.org/10.1121/1.1908239]

-
Johnson, D. L., Koplik, J. and Dashen, R., 1987, Theory of Dynamic Permeability and Tortuosity in Fluid-saturated Porous Media, Journal of Fluid Mechanics, Vol. 176, pp. 379~402.
[https://doi.org/10.1017/S0022112087000727]

-
Champoux, Y. and Allard, J.-F., 1991, Dynamic Tortuosity and Bulk Modulus in Air-saturated Porous Media, Journal of Applied Physics, Vol. 70, No. 4, pp. 1975~1979.
[https://doi.org/10.1063/1.349482]

- Atalla, Y. and Panneton, R., 2005, Inverse Acoustical Characterization of Open Cell Porous Media Using Impedance Tube Measurements, Canadian Acoustics, Vol. 33, No. 1, pp. 11~24.
-
Liu, Z., Zhang, X., Mao, Y., Zhu, Y. Y. and Yang, Z., et al., 2000, Locally Resonant Sonic Materials, Science, Vol. 289, No. 5485, pp. 1734~1736.
[https://doi.org/10.1126/science.289.5485.1734]

-
Wu, F., Hou, Z., Liu, Z. and Liu, Y., 2002, Acoustic Band Gaps in Two-dimensional Rectangular Arrays of Liquid Cylinders, Solid State Communications, Vol. 123, No. 5, pp. 239~242.
[https://doi.org/10.1016/S0038-1098(02)00203-X]

- Maa, D. Y., 1975, Theory and Design of Microperforated Panel Sound-absorbing Constructions, Scientia Sinica, Vol. 18, No. 1, pp. 55~71.
-
Yang, H., Zhang, H., Wang, Y., Zhao, H., Yu, D. and Wen, J., 2022, Prediction of Sound Absorption Coefficient for Metaporous Materials with Convolutional Neural Networks, Applied Acoustics, Vol. 200, 109052.
[https://doi.org/10.1016/j.apacoust.2022.109052]

-
Wu, L., Liu, L., Wang, Y., Zhai, Z. and Zhuang, H., et al., 2020, A Machine Learning-based Method to Design Modular Metamaterials, Extreme Mechanics Letters, Vol. 36, 100657.
[https://doi.org/10.1016/j.eml.2020.100657]

-
Maa, D.-Y., 1987, Microperforated-panel Wideband Absorbers, Noise Control Engineering Journal, Vol. 29, No. 3, pp. 77~84.
[https://doi.org/10.3397/1.2827694]

-
Sakagami, K., Morimoto, M. and Yairi, M., 2009, A Note on the Relationship between the Sound Absorption by Microperforated Panels and Panel/Membrane-type Absorbers, Applied Acoustics, Vol. 70, No. 8, pp. 1131~1136.
[https://doi.org/10.1016/j.apacoust.2009.03.003]

-
Park, S.-H., Seo, S.-H. and Jang, Y.-S., 2010, Design of a Micro-perforated Panel Absorber at High Incident Sound Pressure, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 20, No. 10, pp. 983~990.
[https://doi.org/10.5050/KSNVE.2010.20.10.983]

-
Ruiz, H., Cobo, P. and Jacobsen, F., 2011, Optimization of Multiple-layer Microperforated Panels by Simulated Annealing, Applied Acoustics, Vol. 72, No. 10, pp. 772~776.
[https://doi.org/10.1016/j.apacoust.2011.04.010]

-
Yan, S., Wu, J., Chen, J., Xiong, Y., Mao, Q. and Zhang, X., 2022, Optimization Design and Analysis of Honeycomb Micro-perforated Plate Broadband Sound Absorber, Applied Acoustics, Vol. 186, 108487.
[https://doi.org/10.1016/j.apacoust.2021.108487]

-
Holland, J. H., 1992, Adaptation in Natural and Artificial Systems, The MIT Press, Cambridge, MA. United States.
[https://doi.org/10.7551/mitpress/1090.001.0001]

-
Yang, J. and Soh, C. K., 1997, Structural Optimization by Genetic Algorithms with Tournament Selection, Journal of Computing in Civil Engineering, Vol. 11, No. 3, pp. 195~200.
[https://doi.org/10.1061/(ASCE)0887-3801(1997)11:3(195)]

- Crandall, I. B., 1926, Theory of Vibrating Systems and Sound, D. Van Nostrand Company, NY, United States. pp. 229~241.
-
Kang, J. and Brocklesby, M. W., 2005, Feasibility of Applying Micro-perforated Absorbers in Acoustic Window Systems, Applied Acoustics, Vol. 66, No. 6, pp. 669~689.
[https://doi.org/10.1016/j.apacoust.2004.06.011]

-
Allard, J. F. and Atalla, N., 2009, Propagation of Sound in Porous Media: Modelling Sound Absorbing Materials, 2nd Edition, Wiley, Chichester, UK.
[https://doi.org/10.1002/9780470747339]

- Roeva, O., Fidanova, S. and Paprzycki, M., 2013, Influence of the Population Size on the Genetic Algorithm Performance in Case of Cultivation Process Modelling, Proceedings of Federated Conference on Computer Science and Information Systems, pp. 371~376.
- Whitley, D., 1989, The GENITOR Algorithm and Selection Pressure: Why Rank-based Allocation of Reproductive Trials is Best, Proceedings of the 3rd International Conference on Genetic Algorithms, pp. 116~121.
- Miller, B. L. and Goldberg, D. E., 1995, Genetic Algorithms, Tournament Selection and the Effects of Noise, Complex Systems, Vol. 9, No. 3, pp. 193~212.
-
Shukla, A., Pandey, H. M. and Mehrotra, D., 2015, Comparative Review of Selection Techniques in Genetic Algorithm, Proceedings of International Conference on Futuristic Trends on Computational Analysis and Knowledge Management(ABLAZE), pp. 515~519.
[https://doi.org/10.1109/ABLAZE.2015.7154916]

-
Lee, I.-S. and Park, Y.-H., 2022, Non-acoustic Parameter Estimation for Multilayer System with Porous Material by Genetic Algorithm, International Journal of Naval Architecture and Ocean Engineering, Vol. 14, 100469.
[https://doi.org/10.1016/j.ijnaoe.2022.100469]

-
Kacker, R. N., Lagergren, E. S. and Filliben, J. J., 1991, Taguchi’s Orthogonal Arrays are Classical Designs of Experiments, Journal of Research of the National Institute of Standards and Technology, Vol. 96, No. 5, pp. 577~591.
[https://doi.org/10.6028/jres.096.034]

-
Ryu, S.-P., Yoon, K.-S., Park, C.-W. and Lee, I.-S., 2022, Study on the Optimization of CI Engine Simulation Using Taguchi Method, Transaction of KSAE, Vol. 30, No. 3, pp. 231~240.
[https://doi.org/10.7467/KSAE.2022.30.3.231]


In-seok Lee received his M.S. degree in Naval Architecture and Ocean Engineering at Changwon National University. He is currently working at Korea Marine Equipment Research Institute as a senior researcher.

Young-ho Park received his Ph.D. degree in Naval Architecture and Ocean Engineering at Seoul National University. He currently works as a professor in the Department of Naval Architecture and Marine Engineering at Changwon National University.