프롭 로터 천이비행 조건 전달행렬 생성을 위한 매개변수 연구

2.1 개별 블레이드 조절 적용 운용조건 분석

한국항공우주연구원에서 연구 중인 5인승급 UAM용 프롭 로터는 지름이 2.6 m이고 5개의 블레이드로 구성되며 순항속도는 250 km/h를 목표로 한다. 이를 위한 프롭 로터의 추력 조건 및 운영 조건은 비행 조건에 따라 달라진다. 정지비행(hover) 조건에서는 헬리콥터처럼 프롭 로터의 추력만으로 항공기의 중량을 이겨내며 상공에 떠 있어야 한다. 따라서 블레이드가 실속이 발생하지 않는 받음각 조건에서 각 프롭 로터에 할당된 항공기 중량에 해당하는 추력을 발생시켜야 한다. 그에 반해 전진비행(forward flight) 조건에서는 항공기의 전진비행시 발생하는 유입류를 고려해야 하므로 정지비행 조건 대비 높은 블레이드 피치각을 형성해야 하며, 항공기 날개에서 양력을 발생시킬 수 있도록 전진속도를 발생시켜야 하므로 정지비행 조건 대비 낮은 추력이 요구되며 이로 인해 프롭 로터의 회전 속도는 낮아지게 된다.

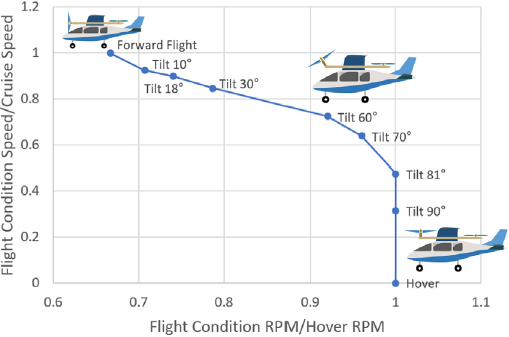
또한 프롭 로터의 천이비행 조건은 정지비행 상태에서 전진비행 상태로 전환하는 과정에 발생하는 비행 조건이다. 따라서 각 전환 단계에서 항공기가 비행 안전성을 유지할 수 있도록 프롭 로터의 기울임 각도 별 전진 속도에 따른 항공기 날개에서 발생하는 양력을 고려한 운용 조건을 산출해야 한다. 다음의 Fig. 2는 각 비행단계 별 항공기의 전진 속도 비, 프롭 로터의 기울임 각도 및 회전 속도 비를 나타내고 있다⁽⁸⁾.

Fig. 2

Prop-rotor operating frequency & forward speed of flight condition

2.2 개별 블레이드 조절 적용 프롭 로터 시스템 해석 모델 구성

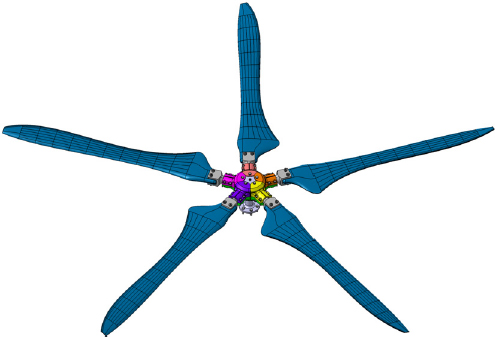
먼저 5인승급 UAM 적용을 목표로 하는 프롭 로터 시스템을 설계하였다. 프롭 로터 운용 시 낮은 수준의 소음을 발생시킬 수 있도록 5엽 블레이드 형태를 구성하였으며, 제자리비행 FM(figure of merit) 최대화, 전진비행 동력 최소화, 제자리비행 소음 OASPL(overall sound pressure level) 최소화, 전진비행 소음 OASPL 최소화를 목표로하는 블레이드 최적 설계를 수행하여 블레이드 OML(outer mold line)을 도출하였다. 허브는 기계식 힌지/베어링이 적용된 전관절형 허브 형태를 적용하였다. 다음의 Fig. 3은 5엽 프롭로터 형태를 보여주고 있다.

Fig. 3

Configuration of 5-blade prop-rotor

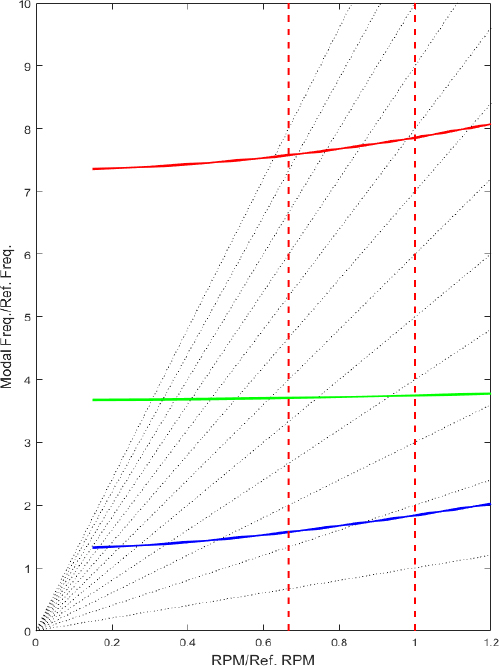
블레이드 단면 설계는 블레이드의 구조 건전성 요구도 만족과 동시에 블레이드 단면 무게중심을 최대한 앞전 영역에 위치시키기 위하여 C스파와 D스파를 동시에 적용하였다. 다만, 블레이드 끝단은 블레이드 전체 중량을 고려하여 C스파만 적용하였다. 또한 전진비행 조건과 정지비행 조건에서 공진이 발생하지 않도록 프롭 로터 운용 주파수와 프롭 로터 블레이드의 고유진동수가 15 % 이상 이격되도록 동특성 근사모델을 활용한 최적설계를 통해 스팬 방향 단면 사이징을 수행하였다⁽⁹⁾. 다음의 Fig. 4는 프롭 로터 블레이드 운용 조건에 따른 고유진동수를 나타내는 팬 플롯(fan plot)을 보여주고 있다.

Fig. 4

Prop-rotor fan plot

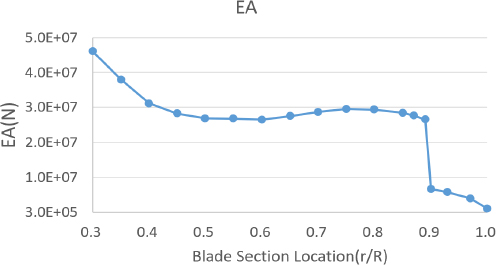
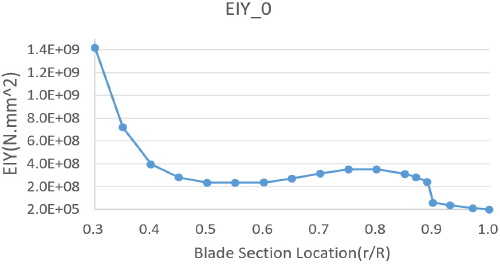
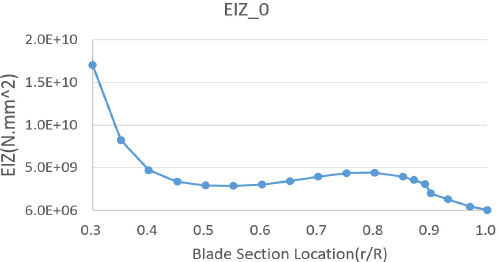
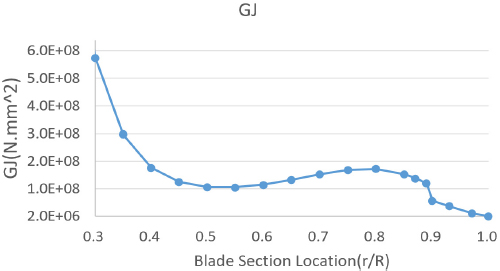
5엽 프롭 로터 시스템의 하중해석 수행을 위해 헬리콥터 로터 통합 해석 프로그램인 CAMRAD II를 활용하였다⁽¹⁰⁾. 허브/블레이드 모델링을 위해 Euler-bernoulli 비선형 보 모델을 사용하였다. 또한 프롭 로터의 성능/하중 해석을 위해 후류와 프롭 로터간 유동간섭이 미미한 것을 고려하여 해석 시간이 상대적으로 짧은 uniform inflow 모델을 사용하였다. 그리고 고조화 조종 입력을 위해 rotating frame의 pitch angle control HHC 입력 모델을 사용하였다. 이 때 최대 입력 하모닉은 블레이드 개수를 고려하여 6을 적용하였다. Fig. 5 ~ Fig. 8은 CAMRAD II 입력에 사용된 블레이드 인장 강성, 플랩/래그 굽힘 강성, 뒤틀림 강성을 나타내고 있다.

Fig. 5

Blade tension stiffness distribution

Fig. 6

Blade flap bending stiffness distribution

Fig. 7

Blade lag bending stiffness distribution

Fig. 8

Blade torsion stiffness distribution

2.3 개별 블레이드 조절 매개변수 연구 조건 선정

개별 블레이드 조절에 의한 고조화 조종은 다음의 식 (1)로 나타낼 수 있다.

5엽 블레이드 프롭 로터 시스템에서 5/rev 고조화 조종 입력에 따른 목적값을 허브 수직 하중(F_z)이라고 가정할 경우 고조화 조종 입력과 허브 수직 하중과의 관계는 식 (2) ~ 식 (4)와 같이 이득 행렬(gain matrix)과의 관계로 나타낼 수 있다.

이를 통해 허브 하중은 고조화 조종 입력과 전달 행렬(transfer matrix)의 관계로 나타낼 수 있으며, 프롭 로터에 고조화 조종 입력을 적용함에 따른 허브 하중은 다음의 식 (5)로 나타낼 수 있게 된다.

여기서 최소화 하고자 하는 허브 하중 요소의 개수$$ \left(\overrightarrow{z}\right)$$와 적용하고자 하는 고조화 조종 입력의 회전속도 정수배 주파수의 개수$$ \left(\overrightarrow{\theta }\right)$$에 따라 전달 행렬의 크기(T)가 결정되게 된다. 따라서 개별 블레이드 조절 매개변수 연구 조건은 다음과 같이 선정하였다.

κ개의 블레이드를 가지는 프롭 로터 허브 하중은 κ/rev 하중이 가장 높게 나타나며, 프롭 로터 허브 κ/rev 하중에 큰 영향을 주는 블레이드 하중은 κ ± 1/rev 하중이므로 3/rev, 4/rev, 5/rev 주파수를 고조화 조종 입력 주파수로 선정하였다. 그리고 2/rev의 영향성 확인을 위해 고조화 조종 입력 주파수로 추가하였다. 그리고 개별 블레이드 조절을 통한 고조화 조종 입력 크기는 너무 작으면 프롭 로터 허브 하중에 영향이 미미할 것이고, 너무 크면 프롭 로터 성능에 영향을 줄 수 있으므로 이 두 가지 사항을 고려하여 1°를 선정하였으며, 고조화 조종 입력 크기의 변화에 따른 특성 변화를 확인하기 위해 2°도 선정하였다. 그리고 고조화 조종 입력의 위상각에 따라 달라지는 프롭 로터 허브 하중의 변화를 분석하기 위해 0°에서 345°까지 15°간격으로 위상각을 변화하였다. 그리고 이러한 고조화 조종 매개변수 연구를 앞서 2.1장에 설명한 총 7개 천이비행 조건에 대해 수행함으로써 각 조건에 대한 전달함수를 획득할 수 있도록 구성하였다. Table 1은 개별 블레이드 조절 고조화 조종 입력에 대한 전달행렬을 생성할 수 있는 매개변수 연구 조건을 나타내고 있다.

Table 1

Parametric study condition for IBC input

2.4 개별 블레이드 조절 매개변수 연구 수행 결과

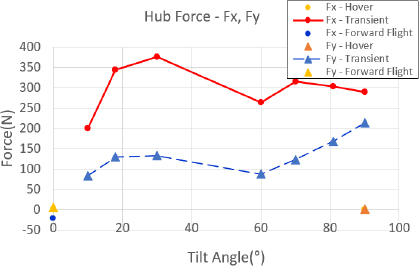
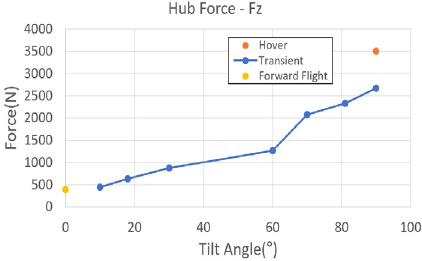
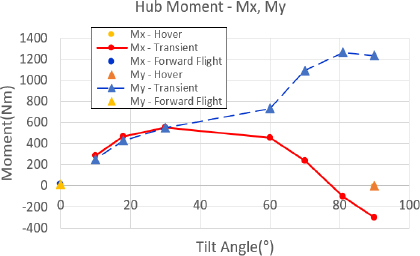
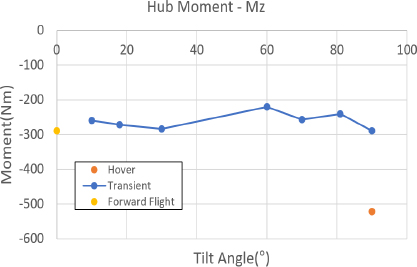
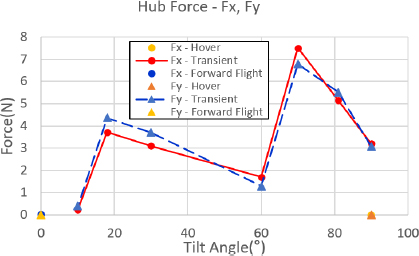
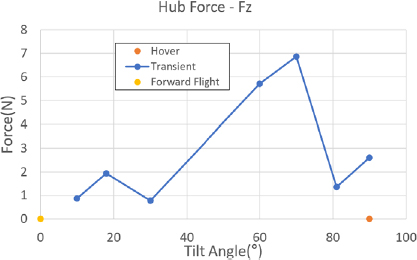
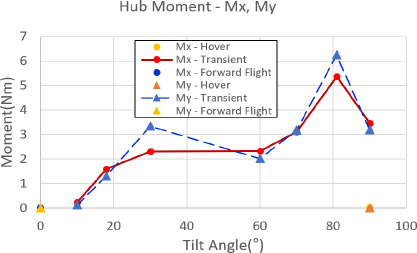
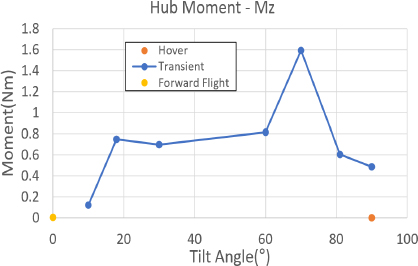
먼저 개별 블레이드 조절 고조화 조종 입력을 하지 않은 상태에서 각 비행 조건 별 허브 하중을 분석하였다. 허브 하중은 정하중과 동하중으로 구분하여 분석하였다. 정하중의 경우, 전진 비행과 정지 비행 조건에서 Fx, Fy, Mx, My 하중은 0에 가까운 값을 가지며, 전진 속도를 가지는 틸트 프롭 기울임각 90°를 포함한 천이 비행 조건에서는 높은 수준의 하중이 발생함을 알 수 있다. Fz와 Mz의 경우는 프롭 로터의 추력과 토크를 의미하므로 틸트 프롭 기울임 각 조건에 맞는 크기의 하중이 발생함을 알 수 있다. Fig. 9 ~ Fig. 12는 각 비행 조건 별 허브 정하중의 크기를 나타내고 있다.

Fig. 9

Static hub load according to flight condition - Fx and Fy

Fig. 10

Static hub load according to flight condition - Fz

Fig. 11

Static hub moment according to flight condition - Mx and My

Fig. 12

Static hub moment according to flight condition - Mz

동하중의 경우는 전진비행과 정지비행 조건에서 모든 하중 요소는 0에 가까운 값을 가진다. 하지만 천이비행 조건으로 들어가면서 모든 하중 요소에 대해 동하중이 발생함을 알 수 있다. Fig. 13 ~ Fig. 16은 각 비행 조건 별 허브 동하중의 크기를 나타내고 있다.

Fig. 13

Dynamic hub load according to flight condition - Fx and Fy

Fig. 14

Dynamic hub load according to flight condition - Fz

Fig. 15

Dynamic hub moment according to flight condition - Mx and My

Fig. 16

Dynamic hub moment according to flight condition - Mz

다음은 천이비행 조건 별 개별 블레이드 조절 고조화 조종 입력 매개변수 변화에 따른 허브 동하중 변화 추세를 분석하였다. Fig. 17 ~ Fig. 19는 프롭로터 기울임각 90° 천이 비행 조건에서 고조화 조종 입력 각도를 1°로 설정하였을 때 고조화 조종 입력 주파수 별 위상각 변화에 따른 Fz 허브 동하중의 변화를 보여주고 있다. 이 결과를 통해 2/rev 입력 주파수는 이 천이비행 조건에서 Fz 허브 동하중에 큰 영향을 미치지 않으며 위상각 변화에 따른 Fz 허브 동하중 변화의 경향성이 비선형성을 나타냄을 알 수 있다. 이에 반해 5/rev 입력 주파수는 다른 입력 주파수에 비해 Fz 허브 동하중에 큰 영향을 미치며 위상각 변화에 따른 Fz 허브 동하중 변화의 경향성도 선형성을 나타냄을 알 수 있다. 그리고 4/rev과 6/rev은 Fz 허브 동하중에 미치는 영향성이 비슷하며 위상각 변화에 따른 Fz 허브 동하중 변화의 경향성도 선형성을 나타냄을 알 수 있다.

Fig. 17

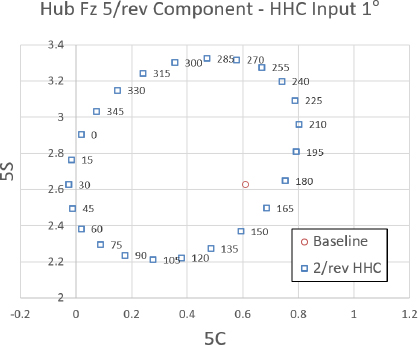
Tilt angle 90° transient condition tilt-prop hub Fz 5/rev component variation - HHC input angle 1° 2/rev frequency

Fig. 18

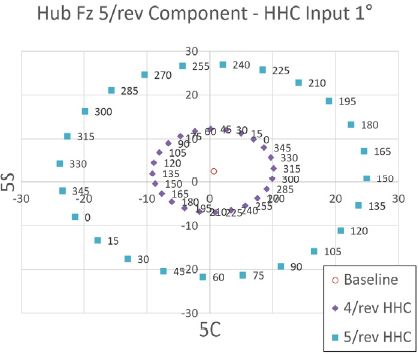
Tilt angle 90° transient condition tilt-prop hub Fz 5/rev component variation - HHC input angle 1° 4/rev & 5/rev frequency

Fig. 19

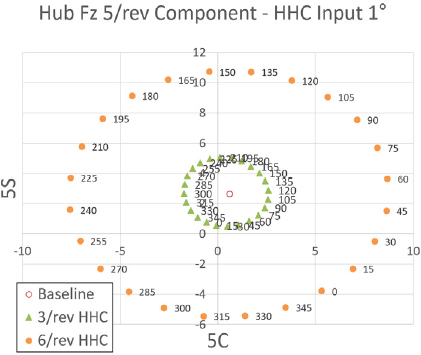
Tilt angle 90° transient condition tilt-prop hub Fz 5/rev component variation - HHC input angle 1° 3/rev & 6/rev frequency

Fig. 20 ~ Fig. 22는 프롭로터 기울임각 90° 천이 비행 조건에서 고조화 조종 입력 각도를 2°로 설정하였을 때 고조화 조종 입력 주파수 별 위상각 변화에 따른 Fz 허브 동하중의 변화를 보여주고 있다. 이 결과를 통해 동일 조건에서 고조화 조종 입력 각도를 1°에서 2°로 변화시켜도 위상각 변화에 따른 Fz 허브 동하중 변화에 대한 경향성은 유사하게 나타남을 알 수 있다. 그리고 앞선 해석 결과와의 비교를 통해 고조화 조종 입력 각도를 증가시킴에 따라 Fz 허브 동하중의 크기는 비례해서 커짐을 확인할 수 있다.

Fig. 20

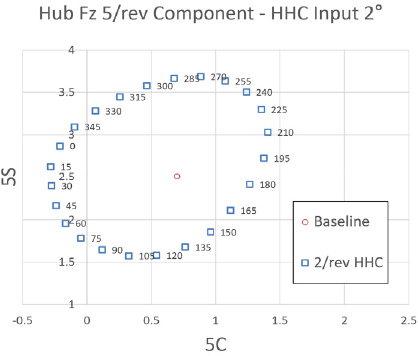
Tilt angle 90° transient condition tilt-prop hub Fz 5/rev component variation - HHC input angle 2° 2/rev frequency

Fig. 21

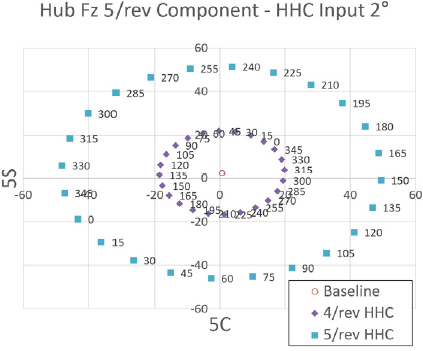
Tilt angle 90° transient condition tilt-prop hub Fz 5/rev component variation - HHC input angle 1° 4/rev & 5/rev frequency

Fig. 22

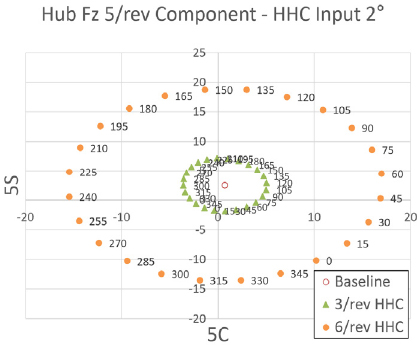
Tilt angle 90° transient condition tilt-prop hub Fz 5/rev component variation - HHC input angle 2° 3/rev & 6/rev frequency

Fig. 23 ~ Fig. 25는 프롭로터 기울임각 81° 조건에서 고조화 조종 입력 각도를 2°로 설정하였을 때 고조화 조종 입력 주파수 별 위상각 변화에 따른 Fz 허브 동하중 요소의 변화를 보여주고 있다. 이 결과를 통해 5/rev 입력 주파수 조건은 앞선 기울임각 90° 조건과 유사한 수준으로 Fz 허브 동하중에 가장 큰 영향을 미치는 것을 알 수 있다. 그에 반해 3/rev, 4/rev, 6/rev 입력 주파수 조건은 앞선 조건에서 보다는 낮은 수준으로 Fz 허브동하중에 영향을 미치는 것을 알 수 있다. 2/rev 입력 주파수 조건은 앞선 조건과 마찬가지로 Fz 허브 동하중에 가장 낮고 미미한 영향을 미치는 것을 알 수 있다. 다만, 위상각 변화에 따른 Fz 허브 동하중 변화의 경향성은 앞서와는 다르게 모든 입력 주파수 조건에서 약간의 비선형성을 나타내고 있다.

Fig. 23

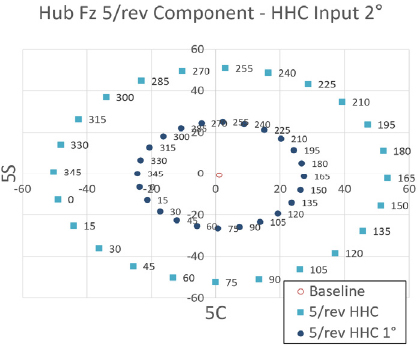
Tilt angle 81° transient condition tilt-prop hub Fz 5/rev component variation - HHC input angle 1° & 2° 5/rev frequency

Fig. 24

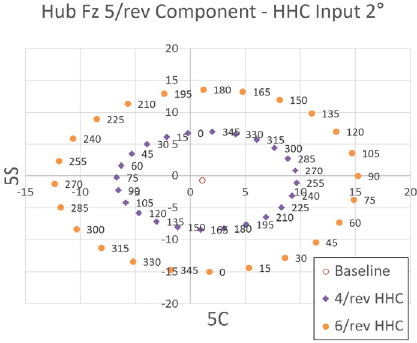
Tilt angle 81° transient condition tilt-prop hub Fz 5/rev component variation - HHC input angle 2° 4/rev & 6/rev frequency

Fig. 25

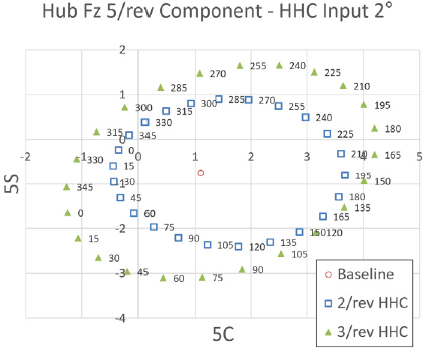
Tilt angle 81° transient condition tilt-prop hub Fz 5/rev component variation - HHC input angle 2° 2/rev & 3/rev frequency

그리고 Fig. 23에서는 5/rev 입력 주파수에 대한 고조화 조종 입력 각도 1°에 대한 결과도 보여주 고 있다. 이 결과를 통해 고조화 조종 입력 각도가 1°에서 2°로 증가함에 따라 위상각 변화에 따른 Fz 허브 동하중 변화의 경향성은 유사하며 Fz 허브 동하중의 크기는 선형적으로 증가함을 알 수 있다.

Fig. 26 ~ Fig. 28은 프롭로터 기울임각 70° 조건에서 고조화 조종 입력 각도를 2°로 설정하였을 때 고조화 조종 입력 주파수 별 위상각 변화에 따른 Fz 허브 동하중 요소의 변화를 보여주고 있다. 이 결과를 통해 5/rev 입력 주파수 조건은 앞선 두 조건과 유사한 수준으로 Fz 허브 동하중에 가장 큰 영향을 미치는 것을 알 수 있다. 그리고 3/rev, 4/rev, 6/rev 입력 주파수 조건 역시 앞선 두 조건과 유사하거나 약간 낮은 수준으로 Fz 허브 동하중에 영향을 미치는 것을 알 수 있다. 2/rev 입력 주파수 조건은 앞선 조건과 마찬가지로 Fz 허브 동하중에 가장 낮고 미미한 영향을 미치는 것을 알 수 있다. 하지만 위상각 변화에 따른 Fz 허브 동하중 변화의 경향성은 앞선 두 조건보다 비선형성이 좀 더 크게 나타남을 알 수 있다.

Fig. 26

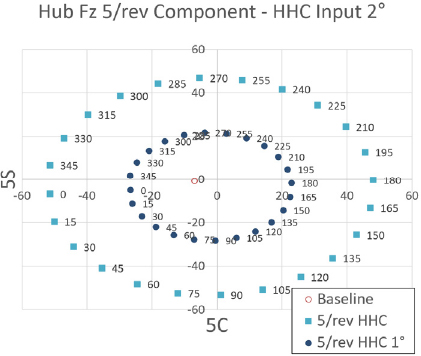
Tilt angle 70° transient condition tilt-prop hub Fz 5/rev component variation - HHC input angle 1° & 2° 5/rev frequency

Fig. 27

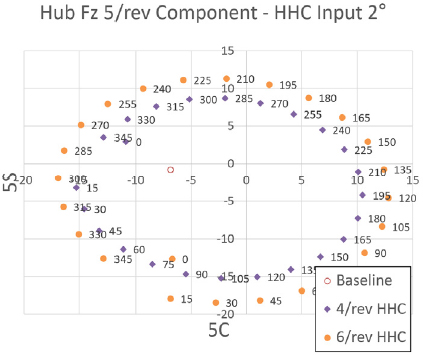
Tilt angle 70° transient condition tilt-prop hub Fz 5/rev component variation - HHC input angle 2° 4/rev & 6/rev frequency

Fig. 28

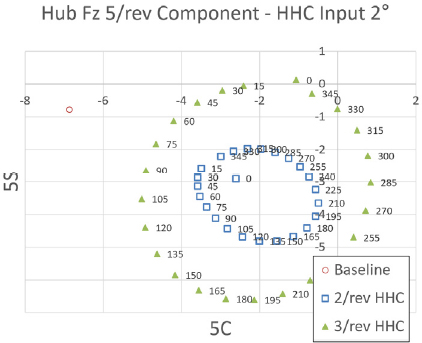
Tilt angle 70° transient condition tilt-prop hub Fz 5/rev component variation - HHC input angle 2° 2/rev & 3/rev frequency

그리고 Fig. 26에서는 5/rev 입력 주파수에 대한 고조화 조종 입력 각도 1°에 대한 결과도 보여주고 있다. 이 결과는 앞선 해석 결과들과 유사한 결과를 보여주고 있다.

Fig. 29 ~ Fig. 31은 프롭로터 기울임각 60° 조건에서 고조화 조종 입력 각도를 2°로 설정하였을 때 고조화 조종 입력 주파수 별 위상각 변화에 따른 Fz 허브 동하중 요소의 변화를 보여주고 있다. 이 결과를 통해 5/rev 입력 주파수 조건은 앞선 조건들보다 더 큰 수준으로 Fz 허브 동하중에 가장 큰 영향을 미치는 것을 알 수 있다. 그리고 3/rev, 4/rev, 6/rev 입력 주파수 조건 역시 앞선 조건들보다 더 큰 수준으로 Fz 허브 동하중에 영향을 미치는 것을 알 수 있다. 그에 반해 2/rev 입력 주파수 조건은 Fz 허브 동하중에 미치는 영향도 매우 작지만, 위상각 변화에 따른 Fz 허브 동하중 변화의 경향성이 과도한 비선형성을 나타내고 있다. 2/rev 입력 주파수를 제외한 나머지 입력 주파수 조건에서는 위상각 변화에 따른 Fz 허브 동하중 변화의 경향성은 앞선 조건들에 비해 선형성이 매우 크게 나타남을 알 수 있다.

Fig. 29

Tilt angle 60° transient condition tilt-prop hub Fz 5/rev component variation - HHC input angle 1° & 2° 5/rev frequency

Fig. 30

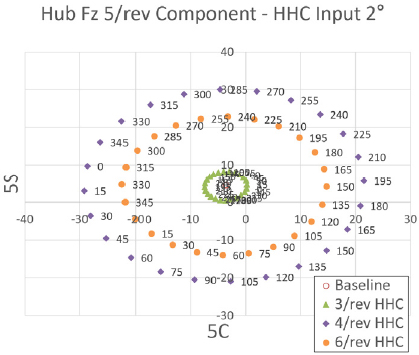
Tilt angle 60° transient condition tilt-prop hub Fz 5/rev component variation - HHC input angle 2° 3/rev & 4/rev & 6/rev frequency

Fig. 31

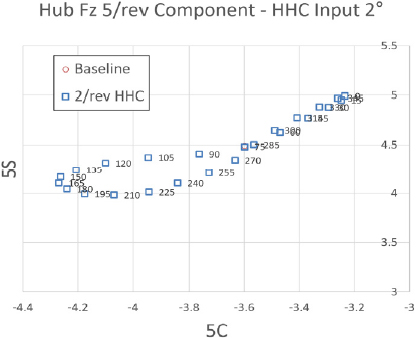
Tilt angle 60° transient condition tilt-prop hub Fz 5/rev component variation - HHC input angle 2° 2/rev frequency

그리고 Fig. 29에서는 앞서와 마찬가지로 5/rev 입력 주파수에 대한 고조화 조종 입력 각도 1°에 대한 결과도 보여주고 있다. 이 결과는 앞선 해석 결과들과 유사하게 고조화 조종 입력 각도가 증가함에 따라 Fz 허브 동하중에 대한 영향력이 선형적으로 증가하는 결과를 보여주고 있다.

Fig. 32 ~ Fig. 34는 프롭로터 기울임각 30° 조건에서 고조화 조종 입력 각도를 2°로 설정하였을 때 고조화 조종 입력 주파수 별 위상각 변화에 따른 Fz 허브 동하중 요소의 변화를 보여주고 있다. 이 결과를 통해 전체적으로 앞선 프롭로터 기울임각 60° 조건보다 절반 또는 그 이하의 수준으로 Fz 허브 동하중에 영향을 미치는 것을 알 수 있다. 하지만 가장 큰 영향력을 미치는 입력 주파 수는 앞선 결과들과 마찬가지로 5/rev 조건임을 알 수 있다. 위상각 변화에 따른 Fz 허브 동하중변화의 경향성은 전반적으로 선형성을 나타내고 있으나, 2/rev 입력 주파수의 경우는 약간의 비선형성이 나타내고 있다.

Fig. 32

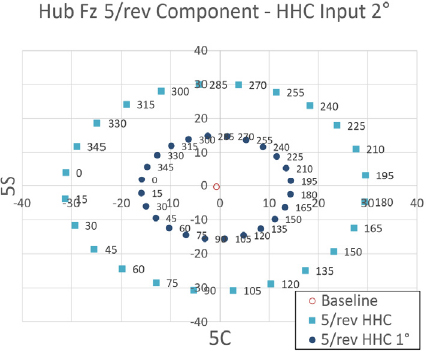
Tilt angle 30° transient condition tilt-prop hub Fz 5/rev component variation - HHC input angle 1° & 2° 5/rev frequency

Fig. 33

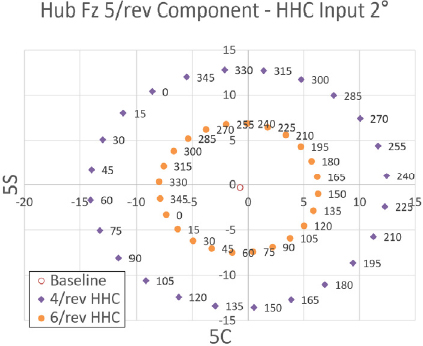
Tilt angle 30° transient condition tilt-prop hub Fz 5/rev component variation - HHC input angle 2° 4/rev & 6/rev frequency

Fig. 34

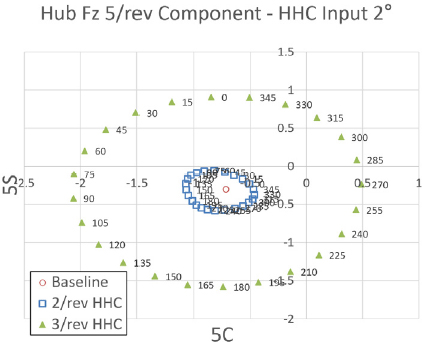
Tilt angle 30° transient condition tilt-prop hub Fz 5/rev component variation - HHC input angle 2° 2/rev & 3/rev frequency

그리고 Fig. 32에서는 앞서와 마찬가지로 5/rev 입력 주파수에 대한 고조화 조종 입력 각도 1°에 대한 결과도 보여주고 있다. 이 결과는 앞선 해석 결과들과 유사하게 고조화 조종 입력 각도가 증가함에 따라 Fz 허브 동하중에 대한 영향력이 선형적으로 증가하는 결과를 보여주고 있다.

Fig. 35 ~ Fig. 37은 프롭로터 기울임각 18° 조건에서 고조화 조종 입력 각도를 2°로 설정하였을 때 고조화 조종 입력 주파수 별 위상각 변화에 따른 Fz 허브 동하중의 변화를 보여주고 있다. 이 결과를 통해 프롭로터 기울임각 18° 조건에서는 전체적으로 앞선 결과들 중 Fz 허브 동하중에 대한 영향력이 가장 낮았던 프롭로터 기울임각 30° 조건보다도 낮은 수준으로 Fz 허브 동하중에 영향을 미치는 것을 알 수 있다. 그럼에도 여전히 Fz 허브 동하중에 가장 큰 영향력을 미치는 입력 주파수는 5/rev 조건임을 알 수 있다. 위상각 변화에 따른 Fz 허브 동하중 변화의 경향성은 앞선 프롭로터 기울임각 30° 조건과 유사한 결과를 보여주고 있다.

Fig. 35

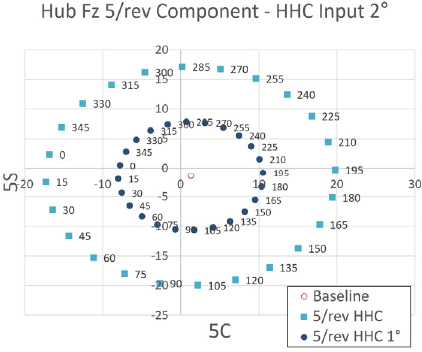
Tilt angle 18° transient condition tilt-prop hub Fz 5/rev component variation - HHC input angle 1° & 2° 5/rev frequency

Fig. 36

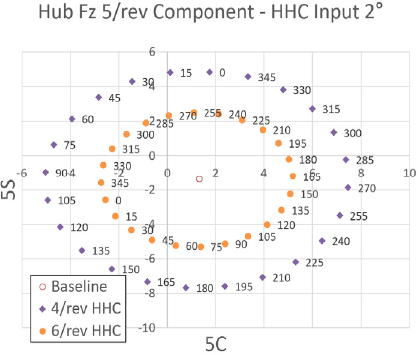
Tilt angle 18° transient condition tilt-prop hub Fz 5/rev component variation - HHC input angle 2° 4/rev & 6/rev frequency

Fig. 37

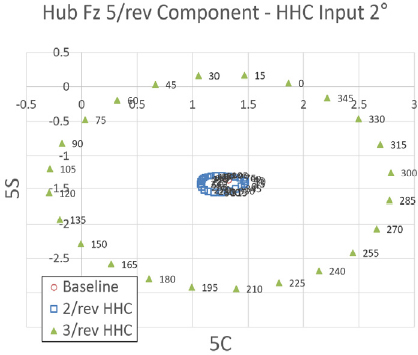
Tilt angle 18° transient condition tilt-prop hub Fz 5/rev component variation - HHC input angle 2° 2/rev & 3/rev frequency

그리고 Fig. 35에서는 앞서와 마찬가지로 5/rev 입력 주파수에 대한 고조화 조종 입력 각도 1°에 대한 결과도 보여주고 있다. 이 결과는 앞선 해석 결과들과 유사하게 고조화 조종 입력 각도가 증가함에 따라 Fz 허브 동하중에 대한 영향력이 선형적으로 증가하는 결과를 보여주고 있다.

Fig. 38 ~ Fig. 40은 프롭로터 기울임각 10° 조건에서 고조화 조종 입력 각도를 2°로 설정하였을 때 고조화 조종 입력 주파수 별 위상각 변화에 따른 Fz 허브 동하중의 변화를 보여주고 있다. 이 결과를 통해 프롭로터 기울임각 10° 조건에서는 전체적으로 모든 입력 주파수 조건에 대해 Fz 허브 동하중에 대한 영향력이 매우 낮은 것을 알 수있다. 또한 Fz 허브 동하중에 가장 큰 영향을 미치는 입력 주파수는 앞선 해석 결과와는 다르게 4/rev 조건임을 알 수 있다. 위상각 변화에 따른 Fz 허브 동하중 변화의 경향성은 다른 모든 조건은 선형성을 나타내고 있으나, 2/rev 입력 주파수 조건에서는 비선형성이 매우 크게 나타나고 있다.

Fig. 38

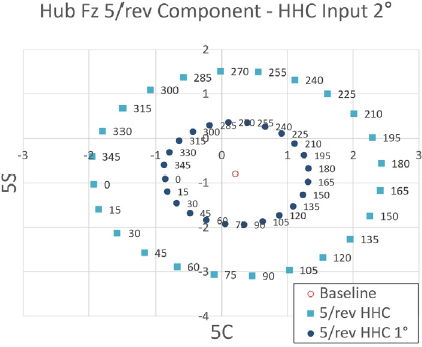
Tilt angle 10° transient condition tilt-prop hub Fz 5/rev component variation - HHC input angle 1° & 2° 5/rev frequency

Fig. 39

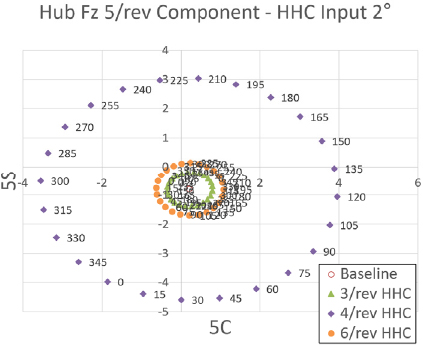
Tilt angle 10° transient condition tilt-prop hub Fz 5/rev component variation - HHC input angle 2° 3/rev & 4/rev & 6/rev frequency

Fig. 40

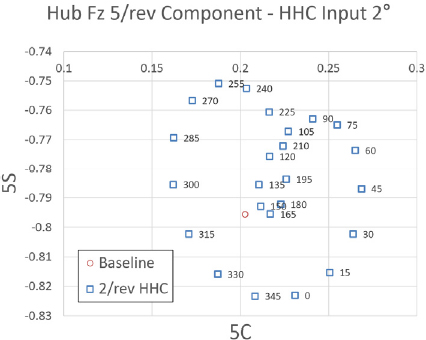
Tilt angle 10° transient condition tilt-prop hub Fz 5/rev component variation - HHC input angle 2° 2/rev frequency

그리고 Fig. 38에서는 앞서와 마찬가지로 5/rev 입력 주파수에 대한 고조화 조종 입력 각도 1°에 대한 결과도 보여주고 있다. 이 결과는 앞선 해석 결과들과 유사하게 고조화 조종 입력 각도가 증가함에 따라 Fz 허브 동하중에 대한 영향력이 선형적으로 증가하는 결과를 보여주고 있다.