[ Article ]

Transactions of the Korean Society for Noise and Vibration Engineering - Vol. 34, No. 4, pp.393-401

ISSN: 1598-2785 (Print) 2287-5476 (Online)

Print publication date 20 Aug 2024

Received 22 Feb 2024 Revised 16 Jun 2024 Accepted 17 Jun 2024

DOI: https://doi.org/10.5050/KSNVE.2024.34.4.393

다중 오토인코더를 이용한 반도체 핸들러 결함탐지

이원섭^* ; 강연준^†

Fault Diagnosis of Semiconductor Handlers using Multiple Autoencoders

Won-Sup Lee^* ; Yeon-June Kang^†

*Member, School of Mechanical Engineering/Institute of Advanced Machines and Design, Seoul National University, Student

Correspondence to: ^†Member, School of Mechanical Engineering/ institute of Advanced Machines and Design, Seoul National University, Professor E-mail : yeonjune@snu.ac.kr # A part of this paper was presented at the KSNVE 2023 Annual Autumn Conference‡ Recommended by Editor Jong Moon, Ha

Abstract

This paper introduces a denoising autoencoder designed to distinguish between normal vibration data and various types of fault vibration data generated in semiconductor handlers. Unlike previous studies that windowed all time-series data based on fixed intervals, this study proposes a method of windowing data at the unit of action, using semiconductor handler time stamps for initial segmentation. The data are then uniformly standardized via linear interpolation. Additionally, to simplify the time-series vibration data patterns, the Hilbert transform and Butterworth low-pass filter are applied. The deep-learning model is structured with parallel components with both time and frequency domains, facilitating detection across various fault scenarios. In contrast to studies processing time-series data into fixed sizes, this approach demonstrates strong performance despite employing a relatively simple deep-learning model.

Keywords:

Fault Detection, Machine Learning, Deep Learning, Unsupervised Learning, Feature Extraction

키워드:

고장탐지, 머신 러닝, 딥러닝, 비지도 학습, 특징 추출

1. 서 론

반도체 산업은 빠르게 발전하고 있으며, 그 과정에서 제품의 품질과 신뢰성을 확보하는 것이 점점 더 중요해지고 있다. 특히, 시스템 반도체 생산라인의 규모가 증가함에 따라 고장진단과 품질 관리의 중요성이 대두되고 있다. 이러한 배경 하에, 이 연구는 시스템 반도체 테스트 장비 내부의 핸들러 장비에 딥러닝을 적용한 실시간 고장진단 시스템의 개발에 초점을 맞추고 있다. 고장진단은 반도체 제조 과정에서 발생할 수 있는 다양한 결함을 탐지하고 분석하는 과정으로, 제품의 신뢰성을 보장하고 생산 효율성을 향상시키는 데 핵심적인 역할을 한다⁽¹⁾. 전통적인 고장진단 방법은 주로 사람의 경험과 규칙 기반의 알고리즘에 의존했으나, 이러한 방식은 새로운 유형의 결함이나 복잡한 패턴을 탐지하는 데 한계가 있었다.

딥러닝은 이러한 한계를 극복할 수 있는 유망한 기술로 부상하고 있다. 특히, 합성곱 신경망과 같은 딥러닝 모델들은 이미지 인식과 패턴 분석 분야에서 뛰어난 성능을 보여주고 있으며⁽²⁾, 이는 반도체 고장진단에도 효과적으로 적용될 수 있다.

이 연구에서는 반도체 핸들러 장비의 작동 시 발생하는 진동 데이터를 기반으로 핸들러 장비의 고장유무를 검출하는 모델을 제안한다. 핸들러의 다양한 동작 중 반도체 디바이스를 집는 피킹(picking) 동작 단위로 시계열 진동데이터를 전처리 하였고, 힐버트 변환(Hilbert transform)과 버터워스 저역통과 필터(butterworth low pass filter)를 이용하여 시계열 데이터를 단순화시켰다. 데이터 구축 단계에서는 다양한 고장 데이터를 얻기에 실질적인 한계가 존재하였다. 이러한 학습 데이터의 한계를 극복하기 위해, 비지도 학습 방법 중 하나인 오토인코더(autoencoder)를 이용하였다. 특히 모델의 강건성을 높이기 위해, 학습과정 중 입력 데이터에 노이즈를 첨가하여 학습시키는 방법인 잡음제거 오토인코더(denoising autoencoder) 기법을 이용하였다^(3,4). 한가지의 고장 케이스와 정상 데이터에 대해서 학습된 모델이 잘 분류를 시키는지 확인하였고, 추가적으로 실제로 발생 가능한 고장 데이터를 생성하여 이를 검출할 수 있는지 확인하였다. 이전 연구에서는 고장을 검출하기 위해 시계열 데이터를 일정한 크기로 분할하는 방법이 주로 사용되었다. 그러나 이 연구에서는 핸들러 장비 데이터를 기반으로 동작별로 시계열 데이터를 처리하여, 상대적으로 간단한 모델을 채택함에도 높은 정확도를 달성하였다.

2. 잡음 제거 오토인코더

2.1 오토인코더

오토인코더는 인공신경망의 한 종류로, 주로 비지도 학습 방식으로 사용된다. 오토인코더는 입력 데이터를 압축하고, 압축된 데이터를 다시 원래의 형태로 복원한다. 이 과정에서 데이터의 중요한 특징들을 학습하게 된다. 이러한 특징에 의해 오토인코더는 데이터의 차원축소⁽⁵⁾, 잡음 제거⁽⁶⁾, 이상치 탐지⁽⁷⁾ 등 다양한 응용분야에서 활용된다.

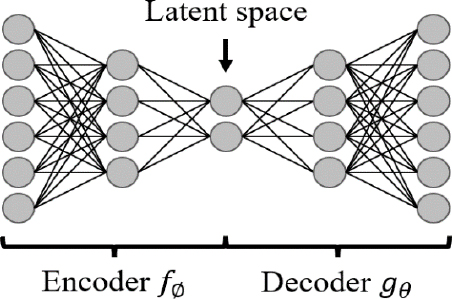
오토인코더는 Fig. 1과 같이 크게 세 부분으로 구성된다.

Fig. 1

Structure of autoencoder

(1) 인코더(encoder)

인코더는 입력 데이터를 저차원의 특징 벡터로 압축하는 역할을 한다. 이 과정에서 데이터의 복잡성이 줄어들고, 중요한 정보만을 압축된 형태로 표현하게 된다.

(2) 잠재 공간(latent space)

잠재 공간은 인코더에 의해 생성된 압축된 데이터의 표현공간이다. 잠재 공간의 차원은 원본 데이터의 차원보다 보통 작게 구성된다. 이를 통해 데이터의 중요한 특징만을 담게 된다.

(3) 디코더(decoder)

디코더는 잠재 공간의 벡터를 사용하여 원본 데이터와 같은 차원의 출력을 생성하는 역할을 한다. 디코더는 잠재 공간의 벡터를 원본 데이터와 최대한 유사한 출력으로 변환하는 것이다. 이 변환된 출력과 원본 데이터 사이의 차이를 최소화하는 방향으로 학습된다.

2.2 잡음 제거 기법

인위적으로 학습 데이터에 잡음을 추가하여 학습을 시키는 기법들은 오래전부터 사용되어 왔다. 학습 데이터에 작은 노이즈를 첨가함으로써 과적합을 방지하는데 쓰일 수 있고⁽³⁾, 학습 모델이 더욱 강건해지는데 도움을 줄 수 있음이 이전 연구를 통해 밝혀졌다⁽⁴⁾. 노이즈를 이용해 학습을 할 경우에는, 학습 데이터에 임의의, 또는 어떠한 확률 분포를 가지는 노이즈를 추가를 해서 학습을 한다. 다만, 추론 단계에서는 노이즈를 추가하지 않은 데이터를 이용한다.

2.3 오토인코더 이상치 탐지

오토인코더의 많은 응용분야 중 이상치 탐지는 오토인코더의 핵심적인 특징 중 하나인 재구성 오차(reconstruction error)를 이용한다. 재구성 오차는 오토인코더가 입력 데이터를 압축한 후 복원하여 얻은 출력과 원래의 입력 데이터의 차이를 나타내는 값이다. 이는 오토인코더가 데이터의 특징을 얼마나 잘 학습했는지를 나타내는 지표로 사용된다.

이상치 탐지에서의 핵심 아이디어는 다음과 같다. 먼저, 학습과정에서 정상 데이터에 대해서만 학습된다. 학습 과정에서, 오토인코더는 정상 데이터의 패턴과 구조를 학습하게 되고, 입력 데이터와 비슷한 출력을 내도록 학습된다. 그 결과 정상 데이터는 낮은 재구성 오차를 가지게 된다. 반면에, 정상 데이터와 다른 특징을 가진 비정상 데이터의 경우, 오토인코더가 학습하지 않은 패턴을 가지므로, 재구성할 때 높은 재구성 오차를 가지게 된다. 따라서 재구성 오차가 특정 임계값보다 크면 해당 데이터 포인트를 이상치로 판단할 수 있다.

오토인코더를 이용한 이상치 탐지 기법은 비지도학습의 일종으로서, 다른 머신러닝 모델에 비해서 높은 정확도를 가지는 것이 장점이다. 특히 연산량이 크지 않은 것이 특징이며, 이상치 탐지기법과 같이 사용될 시 principal component analysis(PCA)에 비해서 더 높은 정확도와, 비선형데이터에 적용 가능하다는 특징이 있다⁽⁸⁾.

3. 데이터 취득

3.1 센서 부착

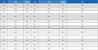
진동 데이터 취득을 위해 피커(picker) 뒤편에 Fig. 2와 같이 가속도 센서를 설치하였다. 사용한 가속도 센서의 주요 스펙은 Table 1과 같다.

Fig. 2

Sensor value of each state

Table 1

Accelerometer specifications

올바른 방법으로 가속도 센서를 부착하는 것은 측정 데이터의 질적인 측면에서 매우 중요하다. 테스트 장비에 가속도 센서를 부착하는 방법은 볼트체결, 자석부착, 시멘트 고정, 왁스 고정 등 여러가지 방법이 있다⁽⁷⁾. 각각의 방법은 주파수 제한 범위가 존재한다. 이 연구에서는 피커의 빠른 동작 속도와, 결함탐지에 사용할 데이터의 주파수 범위를 고려하여 볼트 고정 방식을 채택하여 Fig. 3과 같이 설치하였다.

Fig. 3

Accelerometer attachment

3.2 고장 데이터

핸들러 장비내 피커는 복잡한 구조를 가지고 있어, 이로 인해 다양한 고장 원인과 증상이 발생할 수 있다. 하지만 다양한 고장 증상에 대한 데이터 수집은 현실적으로 어려웠다. 따라서 이 연구에서는 수집 가능한 고장 증상 중 하나를 선정하여 그에 따른 진동 데이터와 정상 데이터만을 수집하였다. 데이터 수집에 이용된 고장 상태는 피커 설정 오류로 인해 피킹 동작 시 하강 속도가 비정상 적으로 빠르게 설정되어, 반도체 디바이스 피킹시 피커와 디바이스가 충돌하면서 특정한 소음과 진동을 발생시키는 상태이다. 이 상태로 계속해서 피킹을 진행한다면, 반도체 디바이스가 손상될 수 있고, 피커 또는 핸들러 장비 전체에 무리가 발생할 수 있다.

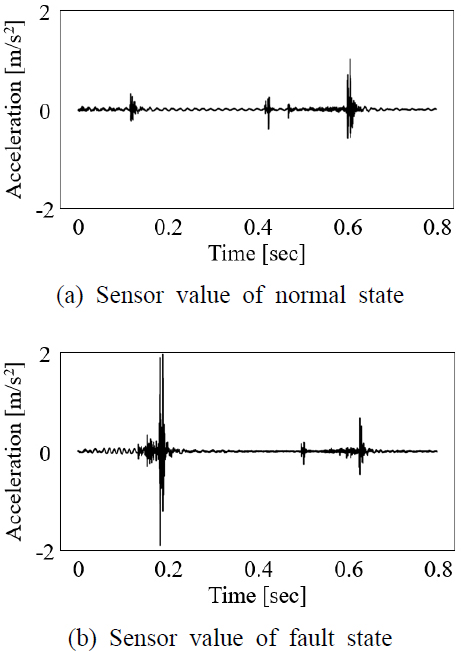
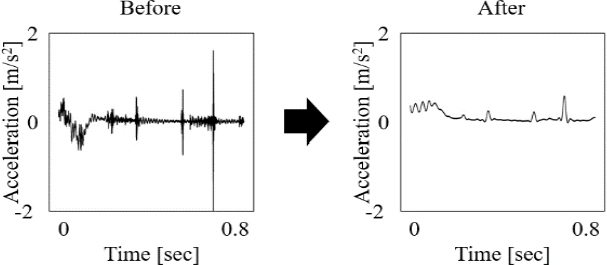
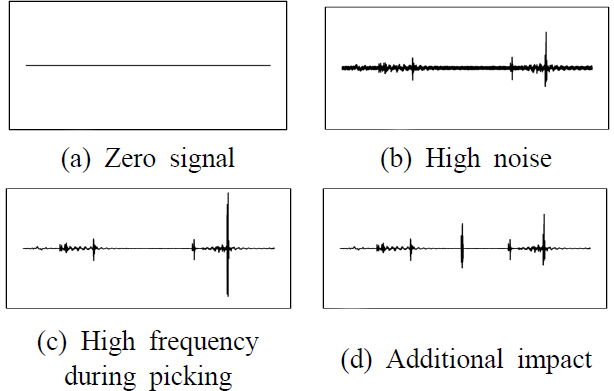
정상 상태와 고장 상태의 센서값은 Fig. 2와 같다. 여기서 고장 상태에 해당하는 Fig. 2(b)에서는 0.2초 부근에서 피커의 하강 시 충격에 의해 큰 가속도 값을 가지는 것을 확인할 수 있다.

3.3 데이터 취득

장착된 가속도 센서를 통해 20 480 Hz의 샘플링 속도로 시계열 데이터를 얻었고, 이를 4.1에 소개될 방법으로 전처리를 진행하며 데이터셋을 취득하였다.

핸들러 장비에 실제 반도체 디바이스와 유사한 형태인 더미 디바이스를 4개 두고, 핸들러 내부의 트레이에 디바이스를 옮겨가며 진동을 측정하였다. 정상 데이터의 경우 핸들러에 정상상태의 피커를 4개 설치하여 총 3520개의 데이터를 얻었다. 고장 데이터의 경우 고장상태의 피커를 핸들러 장비에 설치하고, 정상데이터 측정과 동일한 방법으로 측정을 진행하였다. 데이터의 다양성을 늘리기 위해서 고장피커 위치를 바꿔가며 진행을 하였고, 고장데이터 측정 시 정상 피커가 작동한 시점의 데이터는 정상데이터로 처리하였다. 총 480개의 고장 데이터를 취득하였다.

4. 결함탐지 알고리즘

4.1 진동신호 전처리

(1) 데이터 윈도우 기법

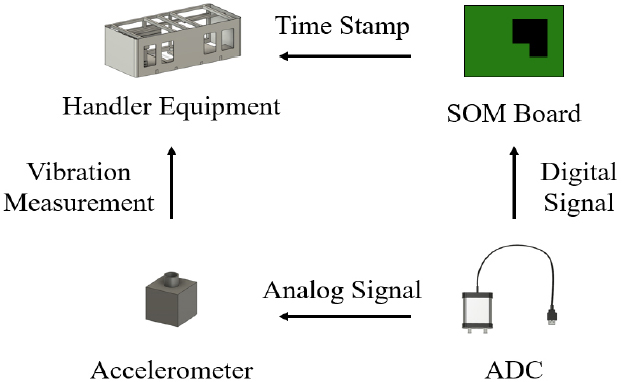
진동 데이터를 딥러닝 모델에 학습시키기 위해서는, 센서에서 만들어진 시계열 데이터를 일정한 크기의 각각의 데이터로 만들어야 한다. 핸들러 장비는 반도체 디바이스를 테스트 베드에 옮기기 위해서 ‘피킹 → 이동 → 배치 → 이동’을 반복하게 된다. 이 연구에서는 핸들러 장비의 피킹 동작과 배치 동작을 기준으로 시계열 데이터를 각 시간단위로 잘랐다. 핸들러 장비에서는 각 동작의 명령을 내릴 때 마다 시간 데이터와 같이 저장을 하게 된다. 이 중 피킹 또는 배치를 시작하는 명령어와, 끝내는 명령어에 해당하는 시간데이터를 보드로 전송하고, 이 시간데이터를 기준으로 전체 시계열 데이터를 자른다. 이를 그림으로 나타내면 Fig. 4와 같다.

Fig. 4

Timestamp and signal transmission structure

피킹과 배치는 대략 0.7초 ~ 1초 가량 소요가 된다. 따라서 피킹과 배치 동작을 기준으로 잘라진 각각의 데이터를 같은 크기로 맞춰주기 위해 선형 보간법을 이용하여(14 000)크기의 벡터로 만들었다. 이 연구에서는 선형 보간법 대신 제로 패딩을 이용한 정규화 방법도 적용해 보았다. 피킹 과정은 일반적으로 0.7초에서 1초 정도 소요되는데, 이를 제로 패딩을 이용하여 정규화하면 짧은 피킹 과정에서는 많은 0의 값이 포함되어 모델을 이용한 재구성 시 큰 노이즈가 발생함을 확인하였다. 또한, 학습에 이용된 데이터보다 짧거나 긴 시간 동안 피킹이 이루어지는 경우, 정상 데이터를 고장 데이터로 잘못 판단하는 현상도 발견되었다. 따라서 진동 데이터의 본질적인 패턴을 더 정확히 학습시키기 위해 선형 보간법을 이용하여 정규화하였다.

(2) 특징 추출 - 힐버트 변환

윈도우 기법이 적용된 데이터를 오토인코더 모델에 학습시키기 위해서, 복잡한 시계열 진동 데이터를 간단하게 변환시킬 필요가 있다. 따라서 진동신호의 단순화를 위해 먼저 힐버트 변환을 이용하였다. 힐버트 변환은 선형 변환 중 하나로, 신호의 진폭은 유지하면서 위상만 이동시키는 변환이다. 음의 주파수에서는 +π/2 만큼 이동시키고, 양의 주파수에서는 -π/2 만큼 이동시킨다. 이를 식으로 나타내면 식 (1)과 같다. 또한, 식 (1)을 이용하여 시간 영역에서 x(t)를 힐버트 변환한 y(t)는 식 (2)와 같이 나타낼 수 있다.

H t = ∫ - ∞ ∞ - j ⋅ sgn ⁡ f e j 2 π f t d f = 1 π t

(1)

y t = ∫ - ∞ ∞ x t h t - τ d τ = 1 π p ⋅ v ⋅ ∫ - ∞ ∞ x t t - τ d τ

(2)

여기서 p.v.는 코시 주요값(Cauchy principal value)을 의미한다. 식 (3)을 이용하여 신호의 포락선을 얻을 수 있다. 힐버트 변환을 사용하면 다른 방법에 비해 시계열 데이터의 패턴을 훨씬 간결하게 단순화할 수 있었으며, 이는 모델 학습 단계에서 확인하였다.

env ⁡ t = x t 2 + y t 2

(3)

(3) 특징추출 - 저주파 통과 필터

힐버트 변환을 이용해 얻은 진동신호의 포락선을 단순화시키기 위해, 버터워스 저주파 통과필터를 추가로 이용하였다. 버터워스 필터는 평평한 주파수 응답으로 널리 사용되는 필터이다. 이 특성은 필터의 패스밴드에서 리플이 발생하지 않는다는 장점이 있다⁽⁹⁾. 버터워스 필터의 전달함수는 식 (4)와 같이 주어진다.

H j ω 2 = 1 1 + ω / w c 2 N

(4)

여기서 ω_c는 차단 주파수로, 이는 필터의 주파수 응답이 -3 dB로 떨어지는 주파수를 나타낸다. 필터의 차수를 나타낸다. 차수가 커질수록 필터를 통과하지 못하는 정지대역의 기울기가 가팔라진다. 이 연구에서는 차단 주파수로 40 Hz, 필터의 차수는 5를 이용하였다.

식 (2)와 식 (3)의 과정을 통해 신호를 Fig. 5와 같이 변경할 수 있고, 기존 진동 신호의 패턴은 유지한 채 훨씬 단순한 형태의 시계열 데이터를 얻을 수 있다.

Fig. 5

Feature extraction before/after

4.2 오토인코더 모델 구성

측정 데이터중 정상 데이터 3520개의 60 %에 해당하는 2112개를 모델 학습에 이용하였고, 그 중 20 %에 해당하는 데이터를 검증용, 나머지 20 %와 측정한 고장데이터 480개의 데이터를 더한 1183개의 데이터를 테스트용으로 사용하였다.

(1) 딥러닝 모델 구성

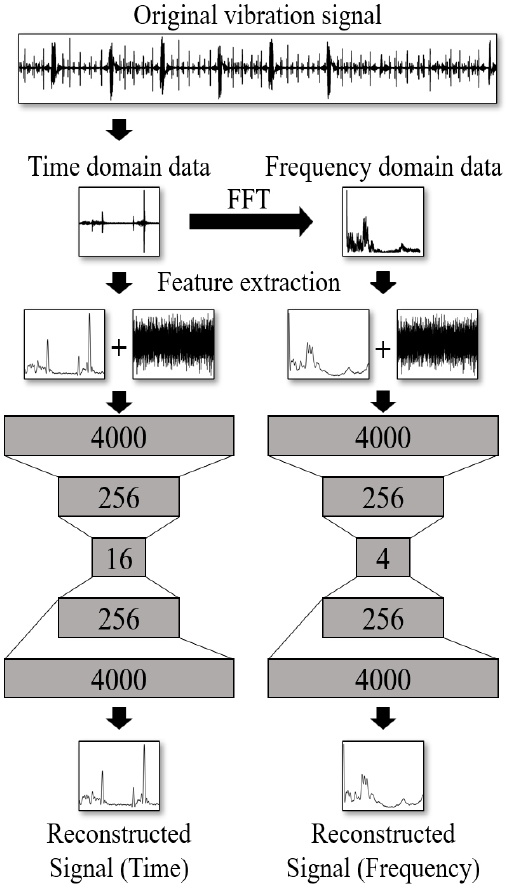
Fig. 6과 같이 모델을 구성하여 모델을 학습하였다. 이 연구에서는 총 2개의 오토인코더를 사용하여 구성을 하였다. 하나는 시간 영역의 데이터의 비정상을 검출하는 알고리즘이고, 다른 하나는 주파수 영역의 데이터의 비정상을 검출하는 알고리즘이다. 두 오토인코더 모두에서 정상데이터라고 판단을 해야, 최종적으로 모델은 입력 데이터를 정상데이터라고 판단을 한다. 이렇게 전체 알고리즘을 구성함으로써, 시간 영역상에 뚜렷하게 나타나지 않는 고장 경우에 대해서도 알고리즘이 검출할 수 있다.

Fig. 6

Structure of fault detection model(training)

두 오토인코더 모델은 완전 연결 계층으로 이루어져 있으며, 5개의 층으로 이루어져 있다. 잠재 공간은 각각 16개와 4개로 선택하였다. 층의 개수와 각 층의 노드의 개수는 실험적으로 반복하여 정상 데이터를 잘 복구하고, 정상 패턴과 다른 데이터가 주어졌을 때 잘 복구하지 못하는 특징을 가지도록 선택하였다.

(2) 모델 학습

모델 학습 단계에서는 추출된 피처에 각각의 데이터에 의도적으로 노이즈를 추가한 후, 이 노이즈가 추가된 데이터를 원본 데이터로 복원할 수 있도록 오토인코더를 학습시켰다. 오토인코더의 입력 값으로는 노이즈가 더해진 신호를 이용하고, 모델의 출력 값과, 노이즈가 더해지기 전의 신호의 차이를 계산한 값을 손실함수로 이용하였다. 이 과정에서 피처와 크기가 동일하고, 평균이 0인 정규분포를 따르는 랜덤 노이즈를 사용하였다.

(3) 재구성 오차

제안한 모델에서 재구성 오차를 계산하는 전통적인 방식인 평균 제곱 오차와는 약간 다른 방식 식 (5)와 같은 방법을 사용하였다.

R E = ∑ i = 1 N y pred, i - y true, i 2 ∑ i = 1 N y pred, i 2 + ∑ i = 1 N y true, i 2

(5)

다음과 같은 방법으로 계산을 하면 데이터의 스케일에 덜 민감하다. 해당 방법의 경우 입력과 출력의 평균 크기로 평균 제곱 오차를 정규화 하는 과정이 포함되어 있다. 가속도 센서의 오류 등의 이유로 센서 값 자체가 작게 측정되는 경우에, 오토인코더에 의해 재구성된 신호도 작을 것이다. 따라서 전체 재구성 오류가 작아서 정상상태로 분류할 가능성이 있는데 이를 방지할 수 있다. 다시 말하자면, 오차의 절대 크기보다 오차의 상대적 크기를 계산하기 위하여 사용된 계산방법이다.

(4) 임계값 설정

오토인코더 모델에서 데이터의 정상과 비정상을 판단하는 임계값를 설정하는 것은 매우 중요하다. 임계값을 너무 낮게 설정되면 거짓양성(false positive)가 증가하게 되고, 너무 높게 설정되면 거짓 음성(false negative)가 증가하게 된다. 즉 모델 성능에 임계값은 매우 중요한 역할을 한다.

임계값을 설정하는 방법에는 여러가지 방법이 있는데, 흔히 사용하는 방법으로는 정밀도-재현율 곡선(precision-recall curve)를 이용하는 방법, ROC 곡선(receiver operating characteristic curve)를 이용하는 방법, 통계적 방법 등이 있다⁽¹⁰⁾.

이 연구에서 사용한 데이터의 경우, 수많은 고장 데이터 중 단 한가지만의 고장 데이터만 측정이 가능하였기 때문에, 측정하였던 고장 데이터에 대해서 모델이 과적합이 발생하는 것을 방지하기 위해서 정상 데이터만을 이용하는 통계적 기법을 이용하였다.

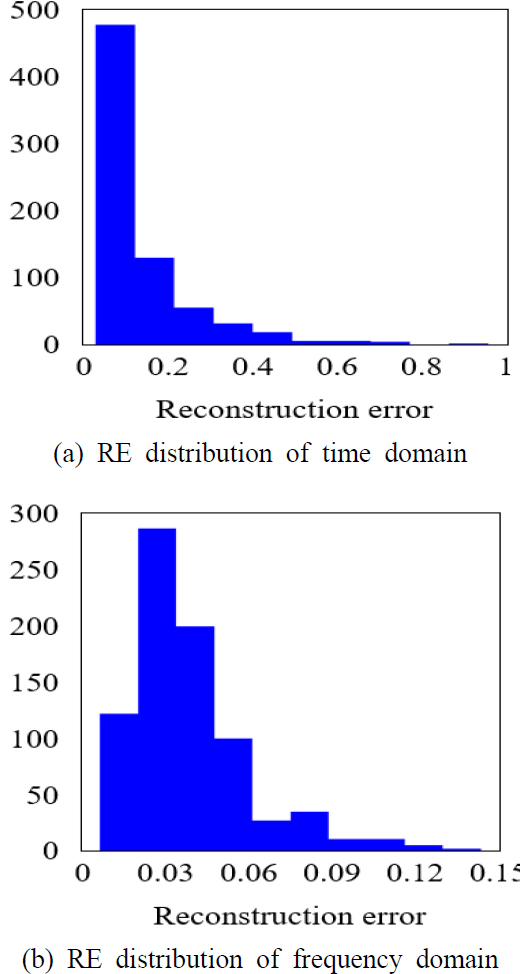
각각의 오토인코더에서, 정상 데이터에 해당하는 검증용 데이터셋의 재구성 오차의 상위 1 %값을 임계값으로 설정하였다. 시간 영역의 모델과 주파수 영역의 모델의 재구성 오차의 분포는 Fig. 7과 같다. 해당 분포에 따라 시계열 모델의 임계값은 0.6786, 스펙트럼 모델의 임계값은 0.1184로 설정하였다.

Fig. 7

Distribution of reconstruction error

이 방법을 사용할 경우, 정상인 상황이나 재구성 오차 값이 크게 계산되어 고장이라고 인식하는 제1종 오류의 수준을 쉽게 결정할 수 있다. 실제로 1종오류의 경우 불필요한 비용 발생 등 여러가지 악영향을 끼칠 수 있기 때문에 해당 방법을 통해 1종 오류를 제어하는 것이 바람직한 방법이라고 사료된다.

4.3 모델 학습 결과

학습한 모델을 평가하기 위해서, 두가지 방법을 사용하였다. 먼저, 측정한 고장 데이터가 포함된 테스트 데이터셋을 이용하였다. 추가적인 검증을 위해, 이전에 핸들러 장비에서 발생한 고장 사례를 참고하여 실제로 발생할 가능성이 큰 고장 데이터를 모방하여, 모델이 이를 검출할 수 있는지 확인하였다.

(1) 테스트 데이터셋 결과

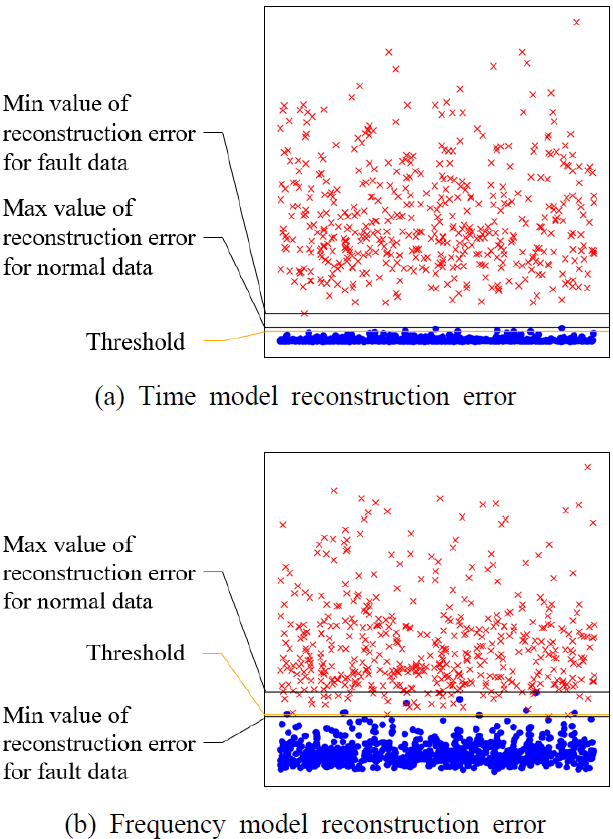
테스트 데이터셋을 이용하였을 때 재구성오차는 Fig. 8과 같다. 그림에서 o로 표시된 항목은 정상 데이터의 재구성오차를 나타내며, x로 표시된 항목은 고장 데이터의 재구성오차를 나타낸다. 그림에서, 대부분의 정상 데이터는 대부분의 고장데이터보다 작게 나타남을 확인할 수 있다. 또한 시계열 모델에서는 정상 데이터의 재구성 오차의 최댓값이 고장 데이터의 최솟값 보다 작은 값을 가진다 는 사실을 확인할 수 있다. Fig. 8(a)에서 확인할 수 있듯이, 측정한 테스트 데이터셋을 이용하였을 때에는, 시계열 모델 하나를 이용하여 완벽히 분류가 가능하다. 또한 Fig. 8(b)에서 스펙트럼 모델을 이용할 경우, 모델의 성능이 오히려 떨어짐을 확인할 수 있다. 시계열 모델과 스펙트럼 모델을 연립하여 더 복잡한 모델을 사용 한 이유는, 아래의 모방 고장 데이터를 이용한 결과로 확인 할 수 있다.

Fig. 8

Reconstruction error distribution

(2) 모방 고장 데이터

테스트 데이터셋에 포함된 고장 데이터의 경우, 측정 당시 구현할 수 있는 유일한 고장 케이스이다. 이 연구의 목표는 측정을 진행하였던 고장 케이스 이외의 발생 가능한 다양한 고장 케이스에 대해서 대응할 수 있는 모델을 구축하는 것이 목표이다.

따라서 실제로 발상했던 고장을 기반으로, 고장 데이터를 생성후, 이를 모델이 올바르게 고장으로 판단하는지 검증하는 단계를 추가하였다. Fig. 6에서도 확인할 수 있듯이, 전체 고장탐지 모델은 두개의 오토인코더를 구성하여, 두 오토인코더 모델에서 모두 정상으로 판단해야 최종적으로 입력 데이터를 정상이라고 판단을 하게 된다. 임의로 생성한 데이터는 Fig. 9와 같다.

Fig. 9

Generated fault signal

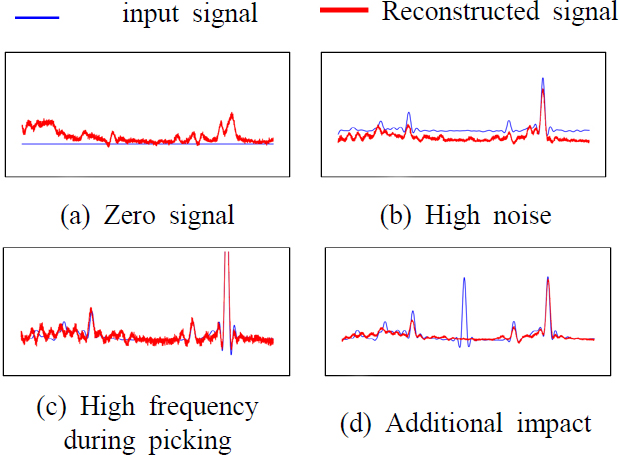
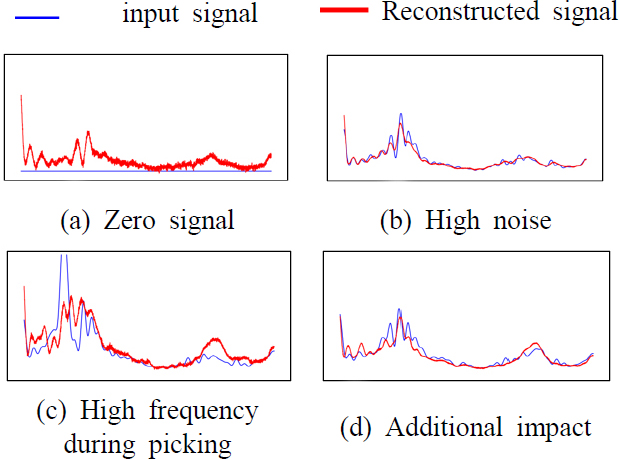
Fig. 10은 Fig. 9의 고장 데이터들을 전처리 후 시계열 모델을 통과시켰을 때의 입력 값과 출력 값을 나타낸 것이다. 4가지 고장 생성데이터 모두 복원을 잘 하지 못하는 모습을 보인다. Fig. 11의 경우 생성된 고장 데이터들을 FFT와 전처리를 거친 후 입력값과 출력 값을 나타낸 것이다. Fig. 11(b), Fig. 11(d)와 같은 고장 신호에서는 큰 차이를 나타내지는 못하지만, Fig. 11(a), Fig. 11(c)는 입력데이터를 복원하지 못하는 것을 확인할 수 있다.

Fig. 10

Input and output in time domain

Fig. 11

Input and output in frequency domain

Table 2는 Fig. 9 4개의 고장 데이터들을 시계열 모델과 스펙트럼 모델에 넣고 결과값을 나타낸 것이다. 각 모델이 정상이라고 판단한 경우에 N, 고장이라고 판단한 경우에 F라고 표시하였다. 시계열 모델이나 스펙트럼 모델을 각각 단독으로 사용했을 때는 고장 데이터를 정상으로 분류하는 경우가 있다. 그러나 두 모델을 함께 사용하여 판단한 경우, 모든 4가지 케이스에서 올바르게 고장으로 판단됨을 확인할 수 있다.

Table 2

Result of generated signal

5. 결 론

이 논문에서 반도체 핸들러 장비의 결함 탐지를 위한 오토인코더 기반의 모델을 제안하였다. 제안한 모델에서는 시계열 진동 데이터를 입력데이터로 사용하였다. 센서에서 얻은 시계열 진동 데이터를 데이터의 학습과 추론을 위하여, 핸들러 장비의 타임스탬프를 이용하여 전처리를 하였다. 데이터를 추가적으로 힐버트 변환과 버터워스 필터를 이용하여 추가적인 단순화 과정을 거처 오토인코더를 학습하였다. 학습결과, 정상 데이터의 경우 입력 데이터와 비슷한 패턴으로 복원이 되었고, 고장 데이터의 경우에는 그렇지 않았다. 다양한 고장 케이스에 대한 모델의 강건성을 높히기 위하여, 학습과정에 입력 데이터에 임의로 노이즈를 첨가하여 학습을 하였고, 다양한 고장 케이스를 검출할 수 있는 모델을 만들기 위하여, 시간 영역의 데이터와 주파수 영역의 데이터에 대해 각각 오토인코더 모델을 구성하였다. 각각의 오토인코더 모델은 재구성 오차로 정규화 된 평균 제곱 오차를 이용하였고, 정상 데이터로 이루어진 별도의 데이터셋에서 상위 1 %의 값을 임계값으로 사용하였다. 그 결과, 실제로 측정한 1건의 고장 케이스 및 정상 데이터로 이루어진 데이터셋에서, f1스코어 0.9877의 높은 성능을 보였으며, 추가적인 고장 케이스에 대해 확인하기 위하여 만들어진 4 종류의 데이터에 대해서도 성공적으로 대응할 수 있음을 확인하였다.

해당 연구에서는 핸들러 장비의 운영환경이 변경되면 기존의 학습된 모델을 완전히 교체해야 한다는 제약이 있으며, 학습된 패턴과 다른 정상 데이터가 입력되면 이를 고장으로 판단할 수 있는 한계점이 존재한다. 이러한 한계를 극복하기 위해 전이 학습과 같은 방법을 도입하여 해결 할 수 있을 것이라 판단된다.

Acknowledgments

이 연구는 2023년도 중소벤처기업부의 기술개발사업 지원에 의한 연구임 [1425172552].

References

Venkatasubramanian, V., Rengaswamy, R., Yin, K. and Kavuri, S. N., 2003, A Review of Process Fault Detection and Diagnosis: Part I: Quantitative Modelbased Methods, Computers & Chemical Engineering, Vol. 27, No. 3, pp. 293~311. [https://doi.org/10.1016/S0098-1354(02)00160-6]
Kim, S., Park, S., Lim, D. and Han, J.-H., 2023, Deep-learning-based Prediction of Qualitative Evaluation Grade for Abnormal Noise in Commercial Vehicles using Convolution Neural Network, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 33, No. 1, pp. 58~66. [https://doi.org/10.5050/KSNVE.2023.33.1.058]
Bishop, C. M., 1995, Training with Noise Is Equivalent to Tikhonov Regularization, Neural Computation, Vol. 7, No. 1, pp. 108~116. [https://doi.org/10.1162/neco.1995.7.1.108]
Balcan, D. and Lewicki, M., 2005, A Theoretical Analysis of Robust Coding over Noisy Overcomplete Channels, Advances in Neural Information Processing Systems 18.
Wang, Y., Yao, H. and Zhao, S., 2016, Auto-encoder based Dimensionality Reduction, Neurocomputing, Vol. 184, pp. 232~242. [https://doi.org/10.1016/j.neucom.2015.08.104]
Chiang, H.-T., Hsieh, Y.-Y., Fu, S.-W., Hung, K.-H. and Tsao, Y. et al., 2019, Noise Reduction in ECG Signals using Fully Convolutional Denoising Autoencoders, IEEE Access, Vol. 7, pp. 60806~60813. [https://doi.org/10.1109/ACCESS.2019.2912036]
Ewins, D. J., 2009, Modal Testing: Theory, Practice and Application, 2nd Edition, John Wiley & Sons.
Chen, Z., Yeo, C. K., Lee, B. S. and Lau, C. T., 2018, Autoencoder-based Network Anomaly Detection, Proceedings of Wireless Telecommunications Symposium(WTS), pp. 1~5. [https://doi.org/10.1109/WTS.2018.8363930]
Butterworth, S., 1930, On the Theory of Filter Amplifiers, Wireless Engineer, Vol. 7, No. 6, pp. 536~541.
Saito, T. and Rehmsmeier, M., 2015, The Precision-recall Plot Is More Informative than the ROC Plot when Evaluating Binary Classifiers on Imbalanced Datasets, PLOS One, Vol. 10, No. 3, e0118432. [https://doi.org/10.1371/journal.pone.0118432]

Won-Sup Lee received a B.S. degree from Inha University in 2022. He is currently M.S. candidate in Acoustic and Vibration Lab. at Seoul National University. His research interest include vibration and deep learning applications in fault detection.

Yeon-June Kang received a B.S. and M.S. degrees from Seoul National University in 1988, 1990. He then received his Ph.D. degree from Purdue University in 1994. He is currently a professor at the department of mechanical engineering at Seoul National University, South Korea, since 1997. His research interests include acoustical materials and automotive NVH.

Model	HS 13A231
Number of measuring axis	1
Sensitivity(±10 %)	10.2 mV/(m/s²)
Measurement range	±490 m/s² pk
Frequency range(±10 %)	0.5 to 10 000 Hz
Overload limit(shock)	±19 600 m/s² pk
Size - height	19 mm
Size - width	14.5 mm
Weight	15.5 gm

	(a)	(b)	(c)	(d)
Time	F	N	N	F
Freq	F	F	F	N
Total	F	F	F	F