압축 차주파수 빔형성 기법을 이용한 도래각 추정
© The Korean Society for Noise and Vibration Engineering
Abstract
Frequency-difference beamforming offers an alternative method for estimating direction-of-arrival (DOA) with a sparse receiving array. However, it suffers from reduced spatial resolution due to forming the beam at a low frequency, known as the difference frequency. Consequently, this unconventional beamforming approach can hinder the discrimination of closely spaced targets. This study proposes a simple yet effective method to enhance the spatial resolution of frequency-difference beamforming. Drawing inspiration from the compressive sensing employed in conventional beamforming, we introduce a sparsity-promoting constraint in the formulation of frequency differences. This enhancement, termed compressive frequency-difference beamforming, enables sharp estimation of the spatial DOA spectrum. Under conditions where the signal-to-noise ratio remains sufficiently high, the proposed method exhibits superior separation performance compared to traditional frequency-difference beamforming. Experimental validation using real sea data supports the validity of our approach.
Keywords:
Frequency-difference, Beamforming, Direction of Arrival, Compressive Sensing키워드:
차주파수, 빔형성, 도래각, 압축센싱1. 서 론
도래각(direction of arrival, DOA)은 음향/전자기 소스의 입사 각도를 의미하며, 센서 배열신호를 이용한 도래각 추정은 신호처리에서 활발히 연구되고 있는 분야이다. 지연합(delay & sum)을 이용한 기존 빔형성 방법(conventional beamforming, CBF)은 낮은 공간 해상도와 높은 부엽(sidelobe) 수준에도 불구하고 가장 간단하고 널리 사용되는 DOA 추정 방법이다(1). CBF의 한계를 극복하기 위해 MVDR(minimum variance distortionless response), MUSIC(multiple signal classification)등 여러 방법이 제안된 바 있다(2). 그러나, 적응형 기법은 낮은 배경 잡음, 비상관 음원(incoherent source), 다중 스냅샷(multi snapshot) 등 몇 가지 까다로운 조건을 요구하다는 제약이 있다. 상기의 모든 빔형성 기법은 측정된 신호의 대역폭 내에서 처리된다. 주어진 배열이 공간 나이키스트(nyquist) 주파수 이상의 고주파수 신호를 다룰 경우, 참 DOA 외 앨리에이싱(aliasing)된 DOA가 나타나 빔형성 결과를 악화시킨다. 또한, 고주파수 대역 신호처리는 사용된 음장 모형의 오류가 발생할 가능성이 높아 권장되지 않는다. 특히, 해상 실험환경에서는 밀도 높은 센서배열을 구성하기 어려움에 따라 공간 앨리에이싱 관련 문제가 중요이슈로 부각된다(3,4).
공간 나이키스트 주파수 이상 대역에서 DOA 추정을 위해, 차주파수 빔형성(frequency-difference beamforming, FD) 기법이 최근 소개된 바 있다(3,4). 이 방법은 신호의 광대역성을 가정한다. 구체적으로는 고주파 및 저주파 두 주파수 배열 데이터에 대한 하다마드(Hadamard) 곱을 구성하여 FD를 얻는다. 하다마드 곱은 이를 구성하는 데 사용된 두 주파수 사이의 차이인 차주파수, 즉 낮은 주파수의 음장을 모방하는 것으로 알려져 있다.
처리 주파수를 낮추면 공간 앨리에이싱(spatial aliasing)과 가정된 음원모형 오류에 대한 강인성이 높아져, 기존 대역내 처리기법이 다루지 못하는 고주파 신호에 대한 DOA 추정이 가능하다는 장점이 있다. 그러나, 처리 주파수 감소는 주엽(mainlobe) 폭을 증가시켜, 서로 인접한 DOA를 구분하기가 어렵게 된다. Xie et al.은 디컨볼루션(deconvolution)을 기법을 사용하여 FD의 해상도를 개선하고자 하였다(5). 그러나 이 방법은 비상관 음원 및 균일간격선배열(uniform linear array)을 전제한다는 단점이 있다.
이 연구에서는 압축 센싱(compressive sensing, CS)으로 알려진 희소 처리법을 사용하여 다른 접근 방식을 취한다. CS는 l1-norm 희소화 구속조건을 이용한 최소자승오차 문제, 즉, LASSO(the least absolute shrinkage and selection operator)를 바탕으로 수신 신호의 DOA를 추정한다(6~8). CS는 상관음원(coherent source) 및 단일 스냅샷(single-snapshot) 등 까다로운 조건에서도 일관된 좋은 성능을 보인다. 무엇보다, l1-norm 구속 조건에 의해 고해상도 빔형성 스펙트럼을 구현할 수 있는 장점이 있다.
압축 차주파수 빔형성(compressive frequency-difference beamforming, CFD)으로 지칭되는 제안 기법에서는, CS의 측정 벡터를 하다마드 곱으로 대체하고, 차주파수에서 산출한 측정행렬(sensing matrix)을 이용한다. CS가 CBF에 대응하는 개념이라면 CFD는 FD에 대응하는 개념으로 볼 수 있다. CFD는 CS의 장점을 계승하므로 음원 특성(상관 또는 비상관 여부)이나 센서 간격에 대한 제한이 없다. 따라서, 이 연구는 FD의 해상도를 개선하기 위한 실용적 방법을 제시한다는 측면에서 의의를 찾을 수 있다.
2. 차주파수 및 압축 차주파수 빔형성 기법
간격이 d인 M개의 센서로 구성된 균일선형배열(uniform linear array, ULA)에 입사하는 평면파를 고려하자. 또한, 강도 xk∈ℂ 및 DOA θk∈[-90°, 90°]로 정의되는 k(=1,…, K)번째 음원은 fL ~ fU 대역폭을 가진다고 가정한다(0°는 배열의 전방을 가리키며, f[Hz]는 주파수를 의미함). 참고로, Fig. 1은 d = 3.75 m, M = 16, K = 2인 시뮬레이션 상황에 대해 보이고 있다. 각 센서로부터 k번째 음원까지의 위상 지연은 식 (1)과 같은 조향벡터(steering vector) a(θk)로 묘사된다.
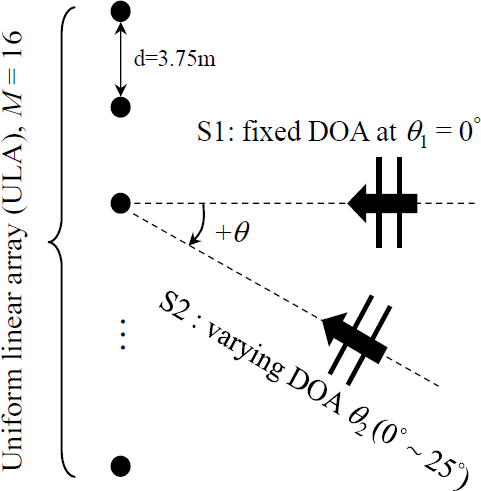
Two DOAs simulation environment with M= 16 uniform linear array(ULA). Sensor spacing d is 3.75 m; One DOA θ1 is fixed at 0°, while another DOA θ2 is varied from 0° to 25°.
| (1) |
여기서, c는 음속, 상첨자 T는 전치(transpose)를 의미하고 이다. 빔형성 결과가 M과 무관하도록 으로 정규화하였다. 측정벡터 y∈ℂM(M차원 복소벡터)에 대한 주파수 영역 표현은 식 (2)와 같고, K는 음원의 개수, n∈ℂM은 잡음벡터를 의미한다.
| (2) |
2.1 차주파수 빔형성기법(FD)
하다마드 곱(z∈ℂM)은 식 (3)과 같이 fl과 fu(fl < fu) 두 주파수 성분에 대한 요소별 곱(elementwise)으로 정의된다(3,9).
| (3) |
기호 ‘◦’는 벡터 성분에 대한 요소별 곱을, ‘*’는 켤레 복소화(complex conjugation)을 의미한다. 두 주파수 fu와 fl은 신호 대역폭 내에 속해야 하며(fL ≤ fl < fu ≤ fU), 중심 주파수 fc = (fu + fl)/2 및 차주파수 ∆f=fu-fl를 이용한 등가표현은 fL + ∆f/2 ≤ fc ≤ fU - ∆f/2, 0 ≤ ∆f ≤ fU-fL과 같다.
하다마드 곱은 차주파수에서 음향 헬름홀츠 방정식의 해를 모방(mimic)한다(9). 이는 진폭 x(f)를 갖는 평면파 y(f,r) = x(f)exp(j2πfesㆍr)를 이용하여 증명 가능하다(es는 파 진행방향 단위벡터, r은 위치벡터를 의미함). 하다마드 곱은 y(fu,r)y*(fl,r) = x(fu)x*(fl)exp(j2πfesㆍr)와 같은데, 진폭 x(fu)x*(fl), 주파수 ∆f를 가지는 평면파와 같다. 부연하면, 하다마드 곱은 그것이 의도하는 음장과 단위/진폭 측면에서 다르더라도, 여전히 저 주파수인 ∆f에서의 평면파를 묘사하고 있는 것이다(이에 상기에서 ‘모방’이라는 용어를 사용하였다).
따라서, CBF가 조향벡터 a(θ,f)와 측정벡터 y사이의 유사성을 평가하듯이, FD의 빔파워(BFD)를 산출하기 위한 자연스러운 선택은 식 (4)처럼 y대신 z를, f 대신 ∆f에서의 조향벡터 a(θ,∆f)를 사용하는 것이다.
| (4) |
여기서, 상첨자 ‘H’는 허미시안(hermitian) 전치이다. BFD는 조향각도(look angle) θ가 음원의 DOA와 일치할 때 최대화된다. ∆f가 신호의 주파수 대역보다 훨씬 낮기 때문에, 해당 파장 ∆λ(=c/∆f)이 공간 앨리에이싱 방지조건인 d < ∆λ/2를 충족하는 범위에서 ∆f를 선택한다. 저 주파수 영역 신호처리는 CBF가 취급하기 어려운 희박 배열에 대한 접근을 가능하게 할 뿐만이 아니라, 사용된 음원 모형에 대한 오류를 저감시키는 장점을 제공한다.
하다마드 곱의 특징 중 하나는 참 DOA 외에도 유령(ghost) DOA로 귀결되는 교차항(cross-term)이 발생한다는 것이다(9). 이 유령 DOA θg는 공간 나이키스트(nyquist) 기준을 위배하여 발생하는 앨리에이싱 DOA와 구별된다. K개 음원에 대해 식 (3)의 하다마드 곱은 K2개의 항을 생성하는데, 이 중 K개의 자기항(auto-term)은 참 DOA에, 나머지 K(K-1)개의 교차항은 유령 DOA에 해당한다. 참 DOA와 달리 유령 DOA는 주파수 의존성을 가지므로(10), 식 (4)에 대한 주파수 평균을 통해 유령 DOA의 영향을 억제할 수 있다. 즉, 식 (4)에 대한 광대역 표현은 식 (5)와 같다.
| (5) |
〈 〉fc,∆f는 두 주파수 fc,∆f에 대한 이중 평균을 의미하며, 식 (4)와 구분하기 위해 막대기호 ‘-’를 사용하였다. 상기 설명한 FD 기법은 단일 스냅샷(L=1)에 대한 것이다. 신호 대역폭이 넓은 경우(충분한 주파수 평균이 가능하므로), 단일 스냅샷 상황에서도 유령 DOA의 억제가 가능하다. 다중 스냅샷(L>1)의 경우, 스냅샷 평균화를 통해 빔형성 결과의 안정성을 더욱 향상시킬 수 있다.
한편, FD는 처리 주파수 감소에 따라 주엽폭이 넓어져, 서로 인접한 DOA의 식별이 어렵다. 다음절에서는 FD의 해상도 한계를 개선하기 위한 방법인 압축 차주파수 빔형성 기법(CFD)에 대해 논의한다.
2.2 압축 차주파수 빔형성기법(CFD)
압축센싱(compressive sensing, CS)은 정보통신 분야에서 제안된 이론으로서, 해가 희소한 경우 부정 문제(underdetermined problem)를 풀이할 수는 방법이다. 음원(해)은 공간 내에서 작은 범위를 차지하므로, CS를 DOA 추정에 적용할 수 있다. 압축 빔형성 기법으로(6,8) 알려진 해당 방법은 l1-norm 기반 최적화 문제(7), 즉, LASSO를 풀이하여 DOA를 추정한다. 식 (2)의 신호모형에 대한 LASSO 문제는 식 (6)과 같이 정식화된다.
| (6) |
여기서, 는 lp-norm을 의미한다. 측정행렬 A(f)=[a(θ1,f)a(θ2,f)...a(θN,f)]∈ℂM×N는 주파수 f에서 모든 조향각도에 대한 조향벡터를 수집하여 구성된다. 정규화인자 μ(>0)는 모형오차항(식 (6)의 우변 첫째항)와 미지수 x = [x1(f)x2(f) … xN(f)]T∈ℂN의 희소성(식 (6)의 우변 둘째항) 사이의 상대적인 기여도를 조정한다. μ를 증가시키면 해 xcs의 희소성을 촉진하고, 반대의 경우 모형적합성을 지향하여 xcs에서 비영요소(nonzero element)의 수가 증가한다. 따라서, 적절히 선정된 μ에 대해, xCS가 생성하는 DOA 스펙트럼은 초해상도(super-resolution) 특성을 가지게 된다.
이 연구에서 제안하는 CFD에서는, CS(식 (6))에서 배열데이터 y를 하다마드 곱 z로 대체하고, 차주파수에서 측정행렬을 산출한다, A(∆f) = [a(θ1,∆f) a(θ2,∆f) ... a(θN,∆f)]. 즉, 식 (7)과 같다.
| (7) |
CFD는 CS와 달리 2차 오더(order) 하다마드 곱을 사용하여 정의되므로 1차 오더 x와 구분하기 위해 2차 오더 미지수 기호 q를 사용한다. CS가 CBF의 희소화 표현인 것과 마찬가지로, CFD는 FD의 희소화 표현으로 간주할 수 있다. 식 (6)과 식 (7)을 비교하면, 측정벡터와 산출주파수만이 변경됨을 알 수 있다. 이로써 CFD는 CS의 장점을 계승하여 우수한 공간 해상도 뿐만 아니라 상관음원/단일 스냅샷 상황에도 적용가능하다는 장점을 갖는다. 그러나, 기저 불일치(basis mismatch) 및 상관기저(coherent basis)와 관련된 CS의 단점은(8) CFD 역시 회피할 수 없다.
식 (7)은 컨벡스(convex) 최적화 문제로서, 공개 소프트웨어인 CVX(11) 또는 l1-magic 등을 이용하여 풀이할 수 있다(12). 충분히 수렴한 경우, 해 qCFD는 K2개의 비영요소를 가지며(K2≪N), 나머지 N-K2개 요소들은 0 또는 0에 가까운 값을 가진다.
CFD의 빔형성 파워는 qCFD의 제곱으로 표현되며(BCFD(θ)=|qCFD|2), 식 (4)의 BFD와 견줄 수 있다. CFD 역시 교차항이 유발하는 유령 DOA를 억제하기 위해 주파수 평균을 수행해야하며, 이에 식 (5)에 상응하는 CFD 표현은 식 (8)과 같다.
| (8) |
FD와 동일하게, 식 (8)은 단일 스냅샷에 대한 결과이다. 당연히, 다중 스냅샷에 대해서는 추가적인 스냅샷 평균을 수행하여 추정결과의 안정성을 향상시킬 수 있다.
3. 유효성 검증
3.1 시뮬레이션
Fig. 1은 FD 및 CFD의 성능비교를 위한 환경설정을 보이고 있다. 자유 수중 공간내(c = 1510 m/s) M = 16개의 센서를 d = 3.75 m 간격으로 배치하였다. 이 배열에 대해, 공간 앨리에이싱을 회피하기 위한 공간 나이키스트 주파수는 fN(=c/(2d)) = 200 Hz이다. 두 개 평면파 음원 θ1, θ2를 가정하되, θ1은 0°에 고정되어 있으며 θ2는 0° ~ 25° 범위에서 변화시키며 제안기법의 음원분리능력을 평가하고자 한다. 음원의 주파수 대역은 [fL, fU] = [10, 20] kHz이며, 해당 범위에서 d/λ는 25 ~ 50로써 기존방법(CBF, CS)을 DOA 추정에 적용하기는 어렵다. L = 20개 스냅샷을 식 (2)를 이용하여 생성하였으며, 신호대 잡음비(signal-to-noise ratio, SNR = )는 30 dB로 설정하였다.
조향각도 탐색범위 및 간격은 각각 θ∈[-90°, 90°], 0.1°이다(N = 1801). 공간 앨리에이싱을 회피함과 동시에 FD 주엽폭을 가급적 줄이기 위해 배열의 공간 나이키스트 주파수(fN = 200 Hz)를 차주파수 ∆f로 사용한다. ∆f를 일정하게 유지함에 따라, 중심주파수 fc에 대해서만 평균화를 수행하며(식 (5), 식 (8)), 식 (9)와 같은 겹침(overlapping) 규칙을 이용하여 fc(=(fl + fu)/2)를 변화시켰다.
| (9) |
식 (9)에서, F=1+(fU-fL-∆f)/[(1-q)∆f]는 (fl, fu) 주파수 쌍 개수를 의미하며, 겹침비율 q를 75 %로 설정함에 따라 F = 197, 즉 197회의 주파수 평균을 취하게 된다. 이 이상의 평균은 결과에 큰 영향을 주지 않음을 확인하였다.
식 (7)의 컨벡스 최적화 문제 풀이를 위해 CVX를 이용하였으며(11), L-curve 방법을 이용하여 정규화인자 μ를 0.1로 선정하였다(13). 엄밀하게는, 각 주파수 쌍 마다 μ를 세밀히 조율해야 하지만, 편의상 그 값을 일정하게 유지하였다. 선정치 기준 수십 % 범위에서 변화시키더라도, 아래 설명할 시뮬레이션 결과와 양상이 크게 다르지 않다.
첫 시뮬레이션에서는 비상관 음원을 다룬다. 즉, 두 음원간 상대위상은 균일분포 ∪[0, 2π]을 따른다. Fig. 2는 세가지 대표적인 경우에 대한 FD와 CFD의 비교를 보이고 있다. 왼쪽 패널은 스냅샷에 대해 평균한 빔형성 파워 B를 중심주파수 fc 및 조향각도 θ에 대해 표현한 2D 결과이다. FD의 경우 fc에 대해 일정하게 나타나는 참 DOA의 주변에서, 동적으로 변화하는 유령 DOA를 볼 수 있다. 중간 및 오른쪽 패널에서 보듯, fc축 주파수 평균을 통해 얻은 DOA 스펙트럼은 유령 DOA를 억제하여 참 DOA 성분만 남긴다. CFD에서는 2D 결과의 희소성이 향상됨에 따라, DOA 스펙트럼이 높은 해상도를 갖는 것을 확인할 수 있다.
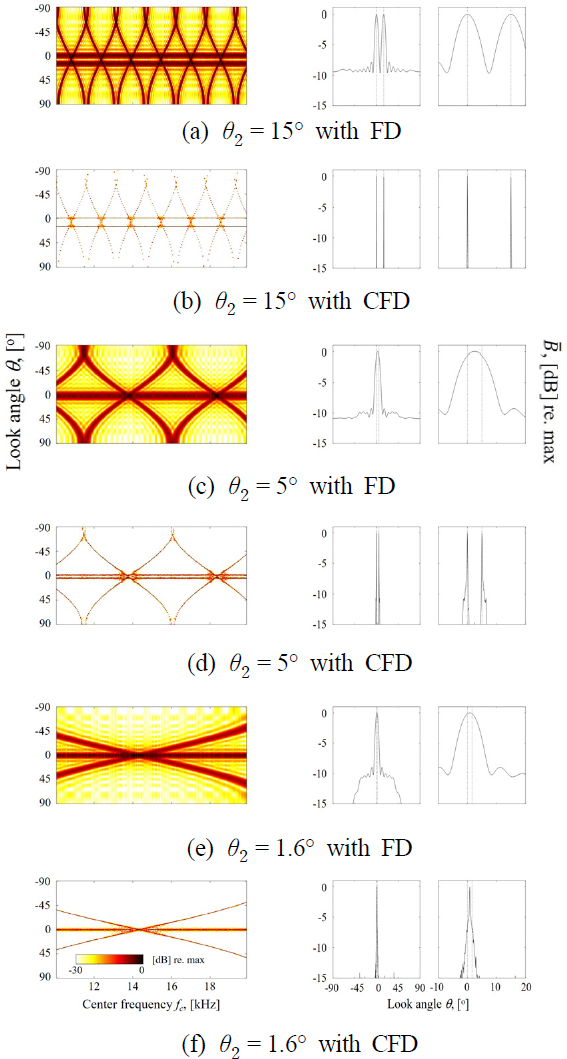
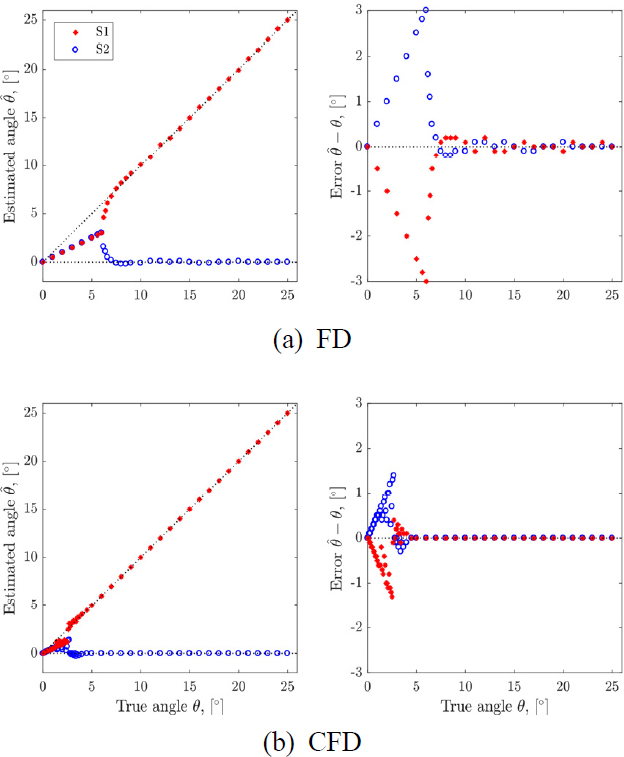
Comparison of FD and CFD for DOA differences between two sources. θ1 is at 0°, while another changes(left: beampower B using Eq. (4) for FD and BCFD(θ) = |qCFD|2 for CFD as a function of the look angle θ and center frequency fc, mid: frequency averaged-beampower B using Eq. (5) for FD and Eq. (8) for CFD, right: detailed view for the region [-10°, 20°] in the mid. True DOAs are represented by dotted lines).
FD에 대한 rayleigh 해상도 한계는 ∆θFD = sin-1(∆λ/Md) = 7.2°로서(2), 두 음원이 이 각도 이상 분리되어야 음원식별이 가능함을 의미한다. Fig. 2(a)와 Fig. 2(b)는 분리각도가 rayleigh 한계보다 큰 경우, Fig. 2(c) ~ Fig. 2(f)는 반대 경우에 속한다. 넓은 분리간격에서는 FD, CFD 두 방법 모두 DOA를 정확하게 추정하는데, CFD가 FD 보다 고해상도 추정결과를 제공함을 알 수 있다. 분리각도가 ∆θFD이하(Fig. 2(c))이면 FD의 두 주엽이 합쳐져 마치 하나의 음원만이 존재하는 것으로 해석될 수 있는 오해를 야기한다. 반면, Fig. 2(d)에서 볼 수 있듯이, CFD에서는 두 DOA를 정확하게 식별할 수 있음을 알 수 있는데, 이는 제안 기법의 우수성을 입증하고 있다.
그러나, 분리각도가 매우 작은 경우, FD 뿐만이 아니라 CFD도 DOA 분리가 어렵다(Fig. 2(e), Fig. 2(f)). Fig. 3은 시뮬레이션에서 고려된 모든 DOA에 대한 추정오차를 보이고 있다. FD는 분리각도가 ∆θFD = 7.2°보다 커야 두 음원을 구별하기 시작하지만, CFD는 구분 가능한 최소분리각도(분해능)가 2.2°로서 FD보다 우수한 성능을 보인다.
물론, CFD의 분해능 ∆θCFD는 FD와는 달리 SNR에 대해 의존적인 특성을 보이며, 이에 추가 시뮬레이션을 통해 SNR에 따른 ∆θCFD를 조사하였다. Fig. 4에 도시한 바와 같이, SNR이 감소함에 따라 CFD의 분해능도 감소하는 경향을 볼 수 있는데, 이는 잡음이 커질수록 참 DOA에 해당하는 조향벡터 식별이 모호해지는 상관기저 특성과 관련이 깊다(8). CFD의 분해능은 FD보다 SNR = 4 dB 이하에서 열등하지만, 그 이상의 SNR 조건에서는 CFD의 분해능이 우수함을 강조할 수 있다.
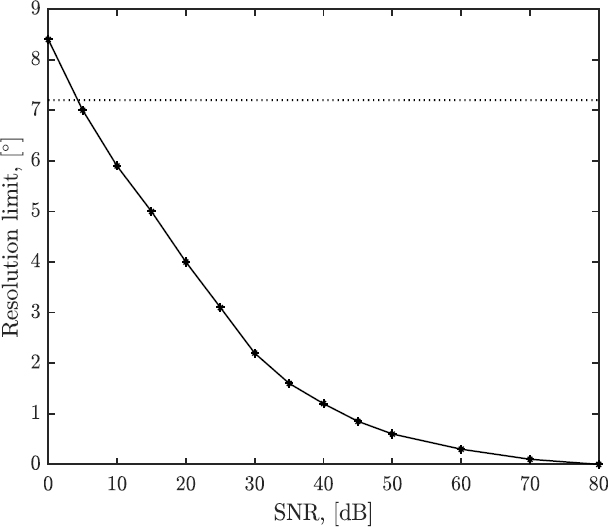
Analysis of CFD resolution limit(∆θCFD) with increasing SNR. Dotted line represents the rayleigh resolution limit
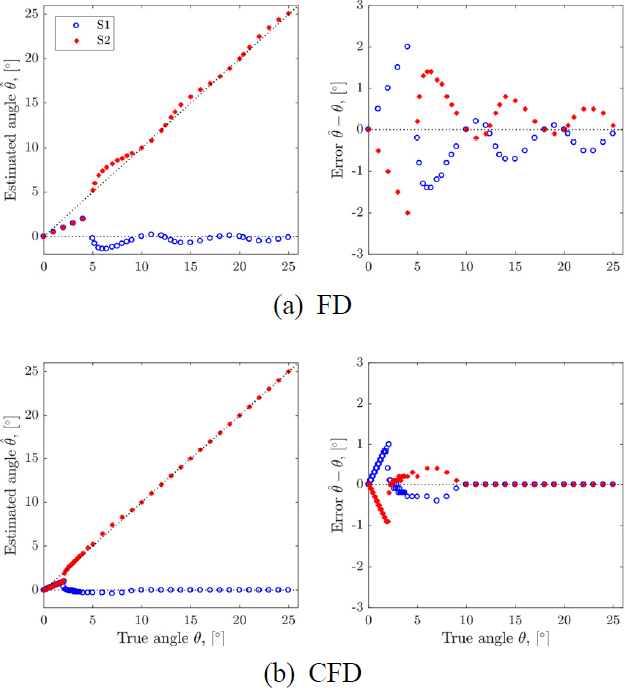
다음 시뮬레이션은 다중경로(multi-path) 상황에서 발생할 수 있는 상관음원에 대한 것으로서, 음원간 상대 위상을 0°로 설정하였다. 음원 간 완벽한 상관관계는 분리각도에 따라 두 주엽의 주기적인 상쇄/보강 간섭을 유발한다. 보강간섭의 경우, FD의 두 주엽이 서로를 밀어내어 추정된 DOA가 참 DOA 외부에 위치하고, 상쇄간섭의 경우에는 그 반대가 발생한다. 따라서, FD의 추정오차는 주기적으로 진동하는 거동을 보인다(Fig. 5(a)). CFD의 해상도 한계는 음원의 상관관계와 관련이 없다. 따라서 CFD의 추정오차는 진동을 보이지 않으며, 분리각도 ∆θCFD 이상 영역에서 FD 대비 추정도가 향상된다(Fig. 5(b)).
3.2 FAF06 실험
CFD의 성능을 실험적으로 검증하기 위해, FAF06(focused acoustic field 06)로(14) 지칭되는 수심 100 m 가량 실해역에서 측정한 데이터를 이용한다. 이 실험은 시뮬레이션과 동일한 형태의 수직 ULA를 사용한다. 총 길이 56.25 m인 배열의 중심은 수면으로부터 깊이 52.8 m에 있고, 수면에 가까운 몇 센서를 제외하고는 모두 음속 c = 1510 m/s로 간주할 수 있는 등음속(iso-soundspeed) 깊이 범위내에 있다. 신호 샘플링 주기는 1/50 000 s(= 50 kHz)이다.
FAF06 실험의 주 목적은 배열로부터 멀리 떨어진 음향 프로젝터에서 송출된 신호를 기록하는 것이다. 그러나, 의도된 송출신호가 아닌 수중생물의 먹이활동 또는 배열 케이블과 고정용 부이 간 마찰에서 기인한 충격성 잡음이 자주 포착된다. 이 연구에서는 그 충격 사건들을 합성하여 두 가지 경우를 시연하고자 한다.
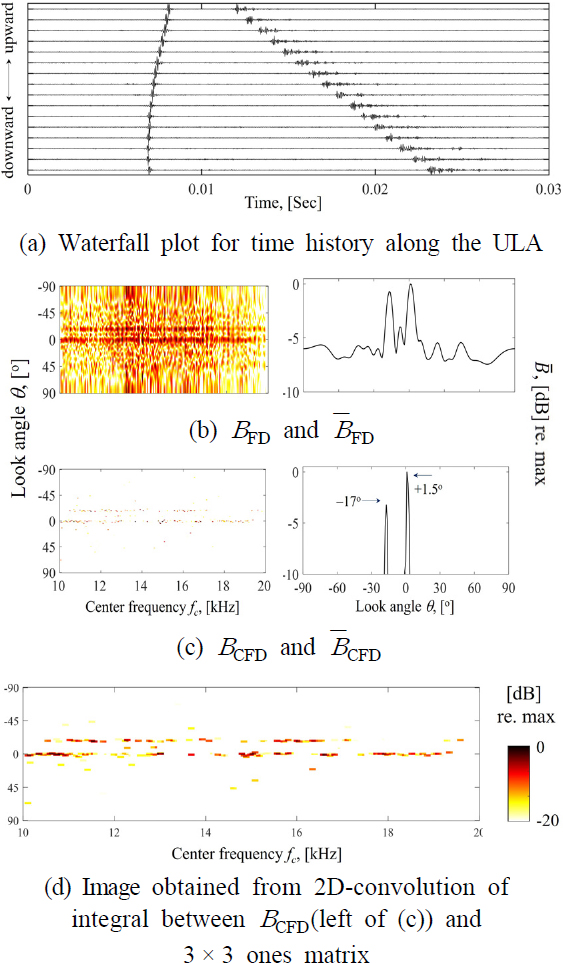
Fig. 6(a)에는 첫 시연을 위해 합성된 신호를 보였다. 충격신호 형태를 부각시키기 위해 9 kHz의 고역통과필터(high-pass filter)를 적용하였다. 구형파면(spherical wavefront)을 닮은 선행신호는 겉보기 DOA +1.1° ~ +3.3°를, 후속 평면파 신호는 겉보기 DOA -17°를 가진다. 따라서, 첫 시연은 넓은 분리각도(약 20°)에 대한 것으로 볼 수 있다. 참고로, 별도의 빔형성기법을 거치지 않고 Fig. 6(a)와 같은 워터폴 플롯(waterfall plot)만으로도 DOA 추정이 가능하다. 따라서, 합성된 시계열 데이터(Fig. 6(a) 및 Fig. 7(a))는 FD와 CFD의 성능을 비교하기 위한 용도로만 사용되어야 함에 유의해야 한다.
시계열 신호에 대한 2048개 FFT를 통해 주파수 대역 신호를 마련하였고, 조향각도 간격을 제외하고(θ = [-90° : 0.5 : 90°], N = 361) 나머지 해석 설정은 시뮬레이션과 동일하다.
Fig. 6(b)의 FD의 2D 결과에서, fc를 따라 두 개 일정한 DOA 성분이 나타남을 볼 수 있다. 그 두 성분은 오른쪽의 주파수 평균 결과에 나타난 것처럼 겉보기 DOA와 일치한다. Fig. 6(b)의 CFD의 2D 결과 역시 희소화 처리에 의해 가느다란 두 개의 줄기를 보이며, Fig. 6(c)와 같이 해당 DOA 스펙트럼은 부엽수준을 억제함과 동시에 두 개의 피크만을 보인다. 참고로, 희소결과의 가시성 향상을 위해 Fig. 6(c) 왼쪽의 BCFD와 3×3- ‘1’ 행렬(3 × 3 ones matrix)의 합성곱 적분(convolution integral) 결과를 Fig. 6(d)에 나타내었다.
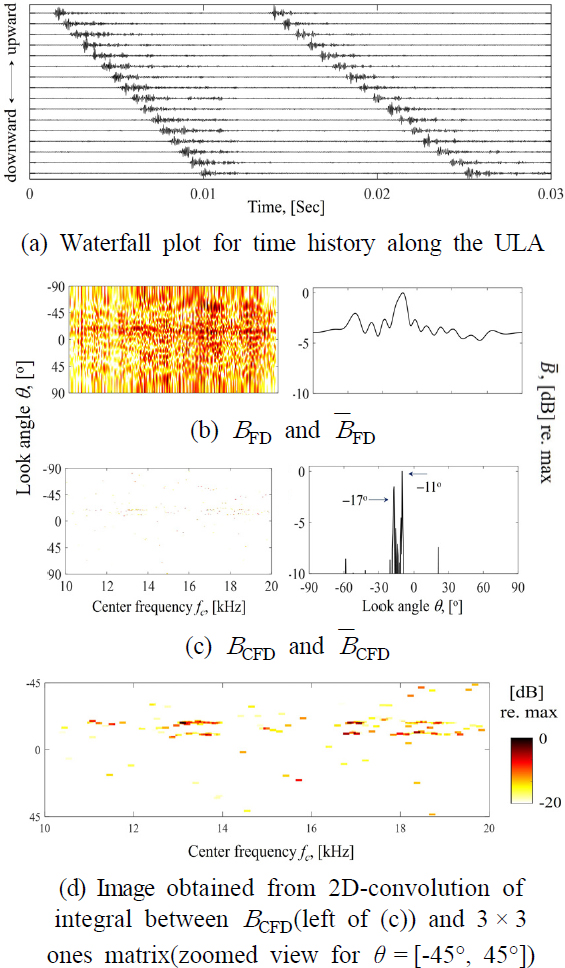
두 번째 시연의 겉보기 DOA는 Fig. 7(a)와 같이 -12°, -17°로서 분리각도가 작은 상황을 다룬다. Fig. 7(b)에서 보듯, FD의 2D 결과는 Fig. 6(b) 대비 유의미한 특징이 없다. 작은 분리각도로 인해 주엽들이 서로 무작위로 보강/상쇄 간섭을 반복하고 있으며, 이에 FD의 DOA 스펙트럼은 -13° 주변 하나의 넓은 주엽을 형성하며 동시에 높은 부엽도 생성한다. 이에 비해, CFD는 개선된 추정결과를 보인다. Fig. 7(c)와 Fig. 7(d)와 같이 fc를 따라 겉보기 DOA에 해당하는 두 개의 미세한 줄기를 생성하고 있으며, 결국 CFD의 DOA 스펙트럼은 서로 인접한 두 DOA 성분을 구분하게 된다.
4. 결 론
차주파수 빔형성(FD)은 상대적으로 낮은 주파수인 차주파수 ∆f에서 빔형성 파워를 산출하므로 서로 인접한 DOA의 분리가 어렵다. 본 연구에서는 LASSO 기법을 활용, FD에 대한 희소화 처리를 적용함으로써 압축 차주파수 빔형성(CFD) 기법을 제안하였다. 시뮬레이션 분석 결과, SNR이 너무 낮지 않은 한 CFD가 FD보다 분해능 측면에서 우수한 성능을 보임을 확인할 수 있었으며, 해상실험 데이터를 통해서도 유효성을 검증할 수 있었다. 따라서, FD의 분해능 개선법을 제안한 측면에서 본 연구의 의미를 찾을 수 있으며, CFD는 FD 적용이 어려운 상황에서 적용가능한 대안이 될 것으로 사료된다.
Acknowledgments
This research was supported by Changwon National University in 2023~2024.
References
-
Kim, Y., Seol, H., Lee, J. and Jeong, H., 2021, Estimation of Propeller Cavitation Source Level based on Beamforming Method for Prediction of Underwater Radiated Noise, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 31, No. 2, pp. 133~141.
[https://doi.org/10.5050/KSNVE.2021.31.2.133]

-
Van Trees, H. L., 2002, Arrays and Spatial Filters, Optimum Array Processing(part IV of detection, estimation, and modulation theory), John Wiley & Sons, NY, United States, pp. 17~89.
[https://doi.org/10.1002/0471221104.ch2]

-
Abadi, S. H., Song, H. C. and Dowling, D. R., 2012, Broadband Sparse-array Blind Deconvolution using Frequency-difference Beamforming, Journal of the Acoustical Society of America, Vol. 132, No. 5, pp. 3018~3029.
[https://doi.org/10.1121/1.4756920]

- Kim, S. M. and Byun, S. H., 2017, Performance Analysis for the DOA Estimation of Acoustic Sources with a Circular Array using Frequency-difference Beamforming Methods, Proceedings of the Joint Conference by KSNVE, ASK and KSME(DC).
-
Xie, L., Sun, C. and Tian, J., 2020, Deconvolved Frequency-difference Beamforming for a Linear Array, Journal of the Acoustical Society of America, Vol. 148, No. 6, pp. EL440~EL446.
[https://doi.org/10.1121/10.0002927]

-
Gerstoft, P., Xenaki, A. and Mecklenbräuker, C. F., 2015, Multiple and Single Snapshot Compressive Beamforming, Journal of the Acoustical Society of America, Vol. 138, No. 4, pp. 2003~2014.
[https://doi.org/10.1121/1.4929941]

-
Tibshirani, R., 1996, Regression Shrinkage and Selection via the Lasso, Journal of the Royal Statistical Society: Series B(methodological), Vol. 58, No. 1, pp. 267~288.
[https://doi.org/10.1111/j.2517-6161.1996.tb02080.x]

-
Xenaki, A., Gerstoft, P. and Mosegaard, K., 2014, Compressive Beamforming, Journal of the Acoustical Society of America, Vol. 136, No. 1, pp. 260~271.
[https://doi.org/10.1121/1.4883360]

-
Worthmann, B. M. and Dowling, D. R., 2017, The Frequency-difference and Frequency-sum Acousticfield Autoproducts, Journal of the Acoustical Society of America, Vol. 141, No. 6, pp. 4579~4590.
[https://doi.org/10.1121/1.4985440]

-
Park, Y., Gerstoft, P. and Lee, J.-H., 2022, Difference-frequency MUSIC for DOAs, IEEE Signal Processing Letters, Vol. 29, pp. 2612~2616.
[https://doi.org/10.1109/LSP.2022.3230365]

- Grant, M. and Boyd, S., 2014(date of access; 2024), CVX: Matlab Software for Disciplined Convex Programming, CVX Research, Inc., Version 2.1, TX, United States.
- Candes, E. and Romberg, J., 2005(date of access; 2024), A Collection of MATLAB Routines for Solving the Convex Optimization Programs, Posted on ℓ1-MAGIC, Code.
-
Kim, Y. and Nelson, P. A., 2004, Optimal Regularisation for Acoustic Source Reconstruction by Inverse Methods, Journal of Sound and Vibration, Vol. 275, No. 3-5, pp. 463~487.
[https://doi.org/10.1016/j.jsv.2003.06.031]

-
Song, H. C., Hodgkiss, W. S., Kuperman, W. A., Akal, T. and Stevenson, M., 2009, High-frequency Acoustic Communications Achieving High Bandwidth Efficiency, Journal of the Acoustical Society of America, Vol. 126, No. 2, pp. 561~563.
[https://doi.org/10.1121/1.3160284]


Jeung-Hoon Lee received B.S. degree in mechanical engineering from Hanyang Univ. in 2001, followed by M.S. and Ph.D. degrees from KAIST in 2002 and 2007, respectively. After industrial experiences in SSMB of Samsung Heavy Industries Co. Ltd. for 9 years, he in 2016 joined the department of mechanical engineering of Changwon National Univ. as associate professor. Since 2023, he has held the position of full professor at the same university. His research interest includes several fields such as signal processing, acoustic cavitation and etc.