회전축의 정적/진동 특성 향상을 위한 중공축의 단면 설계

1. 서 론

최근 높은 공정 생산성을 요구하는 반도체 생산 공정에 투입되는 장비의 경량화와 고속화에 대한 필요성이 높아지고 있다. 특히, 반도체 수율 향상을 위하여 요구되는 택 타임(tack time) 감소를 위해 장비에서의 동력 전달은 고속으로 진행되어야 한다. 그러나, 장비의 경량화는 강성 저하와 고유 주파수의 하강을 초래할 수 있다. 회전체 시스템의 부족한 강성으로 인하여 발생하는 비틀림 변형은 정밀도에 영향을 줄 수 있다⁽¹⁾. 그리고, 높은 구동 주파수가 낮아진 고유 주파수에 일치한다면 전체 시스템에 공진 현상이 발생할 수 있다. 따라서, 고속으로 회전하는 회전축의 정격 속도가 위험 속도에 가깝지 않도록 설계되어야 하고, 충분한 횡 방향 강성과 비틀림 강성을 갖도록 설계하여야 한다.

일반적으로 회전 시스템에서의 질량 중심은 회전체 자중으로 인한 처짐(lateral deflection) 혹은 추가적인 기계 요소의 무게로 인하여 회전축 중심과 일치할 수 없다. 이러한 이유로 축의 회전 속도가 증가할수록 질량 중심에 작용하는 원심력이 축을 더 휘게 만든다. 또한, 증가된 변형은 더 큰 편심을 일으켜 원심력을 증가시킨다. 경량화로 인한 강성 저하로 인하여 위험 속도와 구동 속도가 일치하는 문제를 해결하기 위하여 일반적으로 중공축을 고려한다⁽²⁾.

중공축에 대한 연구는 다양한 측면에서 진행되어 왔다. 동일한 면적 조건에서 다양한 단면을 갖는 중공축을 설계하여 큰 하중을 지지시 축의 안정성을 파악하는 연구^(3~6), 중공 크랭크축의 비틀림 진동을 해석 및 측정하는 연구^(7,8), 경량화를 위한 중공 조향축을 설계하여 구조 해석을 진행한 연구 등이 존재한다⁽⁹⁾. 그러나, 동적 특성과 진동 특성을 함께 고려하여 중공축의 단면을 설계하는 연구는 그리 활발히 진행되고 있지 않다.

과거 중공축 설계는 단순히 중실축의 중심에 구멍을 내고 직경을 변화시키는 수준이었다. 이는 단면 가공 기술의 한계에 제한을 받은 것이었다. 그러나, 최근에서는 3차원 프린팅 기술과⁽¹⁰⁾ 같은 가공 기술의 발전으로 인하여^(11,12), 다양한 중공축 단면을 고려할 수 있게 되었다. 설계한 결과가 당장 제작으로 옮겨지지 못하더라도 정적/동적 특성을 개선할 수 있는 단면의 제시는 회전축 설계 분야에 크게 기여할 수 있을 것으로 예상한다.

따라서, 이 연구에서는 단순 중공축이 아닌 다양한 형태의 중공축 단면 형상에 대한 정적/동적 해석을 수행하여, 두 특성을 개선할 수 있는 단면을 선택하는 방법과 그에 따른 결과를 보여주고자 한다. 이를 위해, 중공축 주변에 규칙적인 사다리꼴을 생성하여 그 사다리꼴의 개수와 치수가 정적/동적 특성에 미치는 영향을 파악하고, 그 경우에 중공축의 직경 변화가 전체 특성에 미치는 영향도 파악해 본다.

2. 해석 모델과 단면 형상

2.1 해석 모델

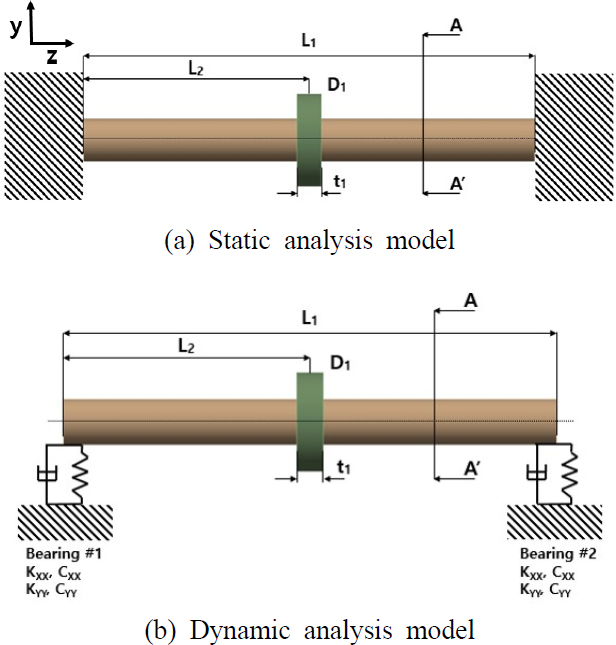
Lalanne’s model을⁽¹³⁾ 참고 모델로 선정하여 동적 해석 모델과 정석 해석 모델을 Fig. 1과 같이 구성하였다. 두 모델은 균일한 외경을 갖는 회전축의 가운데에 베어링이나 기어가 연결될 수 있는 회전자로 구성되어 있다. 정적 해석을 위해서는 양쪽 끝이 고정(clamped boundary condition)되어 있는 것으로 가정하였고, 동적 해석을 위해서는 양쪽 끝이 용수철과 점성 감쇠기에 연결되었다고 가정하였다. 축의 길이(L₁)는 2 m, 좌측 끝에서 회전자의 중심까지의 거리(L₂)는 1 m, 회전자의 지름(D₁), 두께(t₁), 질량은 각각 0.4 m, 0.1 m, 85 kg으로 정하였다. 동적 해석의 경우 모델의 좌우 양단을 지지하는 베어링 요소의 강성 및 감쇠 값은 Lalanne’s model에서의⁽¹³⁾ 강성 및 감쇠 값을 사용하여 각각 K_xx = 5 × 10⁷ N/m, C_xx = 7 × 10² kg/s, K_yy = 5 × 10⁷ N/m, C_yy = 7 × 10² kg/s를 부여하고, 회전축의 정격 속도는 40 000 r/min으로 설정하였다⁽¹⁴⁾. 이 연구에서는 실제 작업 환경을 고려하여 개연성 있는 해석 모델, 경계 조건과 작동 조건 등을 사용하였다.

Fig. 1

Analysis models

2.2 단면 형상

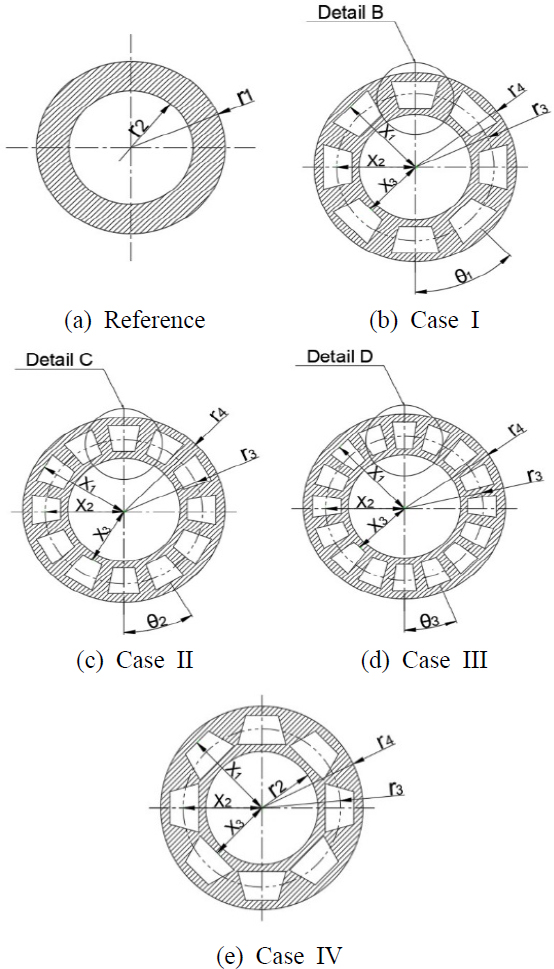
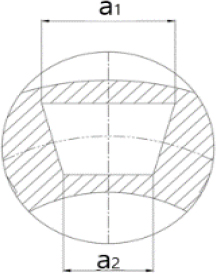
Fig. 2에서와 같이, 단순 중공축을 기준 모델(reference model)로 설정하고, 단순 중공축의 내경(inner diameter)과 단면적(cross-sectional area)이 동일한 3개의 비교 모델(Case I, II, III)과 단순 중공축의 외경(outer diameter)과 동일한 1개의 비교 모델(Case IV)을 구성하였다. 단순 중공축의 바깥쪽 반경(r₁)과 안쪽 반경(r₂)은 각각 75.9 mm와 50 mm이다. Cases Ⅰ ~ Ⅲ의 축 단면적과 바깥쪽 반경(r₄ = 90 mm)은 동일하게 유지하면서, 사다리꼴의 단면의 치수를 조절하였다. 중공축 주변에 8개의 사다리꼴을 갖는 Case I의 두 사다리꼴의 중심축 사이의 각도(θ₁)는 45도, 12개의 사다리꼴을 갖는 Case II의 두 사다리꼴 중심축 사이의 각도는(θ₂)는 30도, 16개의 사다리꼴을 갖는 Case III의 두 사다리꼴의 중심축 사이의 각도(θ₃)는 22.5도이다. 축의 중심에서 사다리꼴의 밑변과 윗변까지의 거리(X₁, X₃)는 각각 83 mm와 57 mm이고, 축의 중심에서 사다리꼴의 중심까지의 거리(X₂)는 70 mm이다. Fig. 3은 각 경우(Case)의 단면을 구성하는 한 개의 사다리꼴을 확대하여 보여주고 있다. 단면적을 일정하게 유지하면서, 윗변과 아래 변의 길이를 변화시켰다. Case Ⅳ에서는 a₁을 29 mm로 a₂를 43 mm로 고정하고, 안쪽 반경만 50 mm에서 1.25 mm씩 점차적으로 증가시켰다.

Fig. 2

Cross section of a shaft

Fig. 3

Cross section of trapezoid in each case

각 경우에, 윗변과 아래 변의 길이를 조절하여 좀 더 다양한 경우의 단면 형상을 생성해 보았다. 이렇게 생성된 단면 형상을 구성하는 사다리꼴의 윗변과 아래 변의 길이를 Table 1 ~ Table 3에 정리하였다. Table 4는 Case IV에서 변화되는 안쪽 반경을 정리하였다.

Table 1

Dimensions of detail B(Case I)

Table 2

Dimensions of detail C(Case II)

Table 3

Dimensions of detail D(Case III)

Table 4

Radius of Case Ⅳ

3. 단면 형상에 따른 해석 결과

ANSYS mechanical 모듈을 사용하여 정적 해석과 진동 해석을 진행하였고, 해석에는 사용된 재료의 밀도, 영계수, 전단 계수, 푸아송비는 각각 7850 kg/m³, 210 GPa, 77 GPa, 0.3으로 설정하였다. 정적 해석에서는 자중에 의한 처짐과 비틀림에 의한 변형을 살펴보았고, 진동 해석에서는 고유값 해석을 통해 얻은 고유 주파수 변화를 살펴보았다.

3.1 비틀림 구조 해석 결과

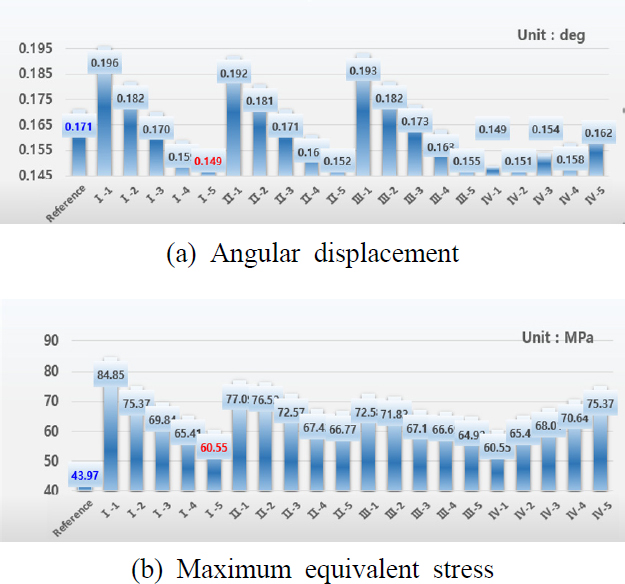
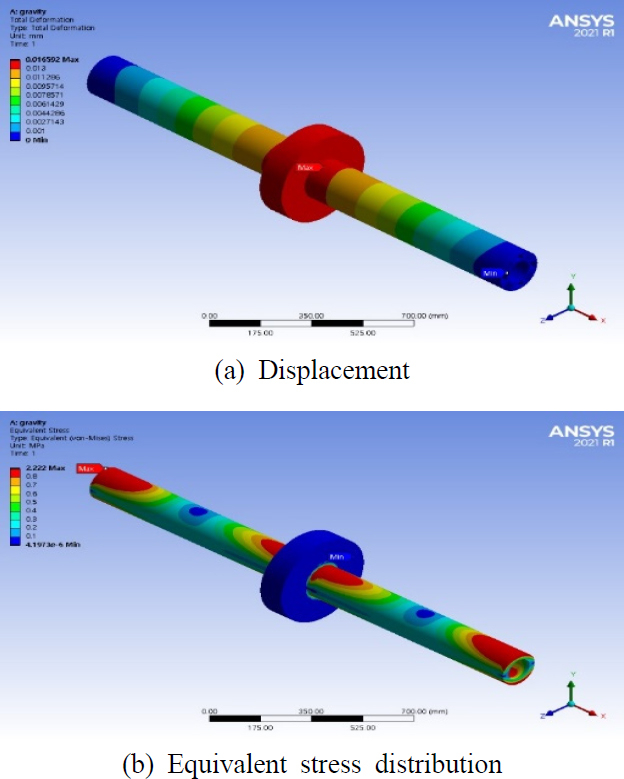
비틀림 정적 해석을 위해서 Fig. 1(a)의 회전자에 1350 Nm의 토크를⁽¹⁵⁾ 부여하였다. Fig. 4는 기준 모델의 비틀림 변형과 등가 응력 분포를 보여주고 있다. 기준 모델은 육면체 유한 요소를 사용하여 만들었고, 사용된 요소의 수는 139 397개이다. 기준 모델의 최대 변형각과 최대 등가 응력은 각각 0.171도와 43.97 MPa였다. Case I ~ Case IV의 최대 변형각과 최대 등가 응력을 Fig. 5에 정리하였다.

Fig. 4

Torsional static analysis results for a reference model

Fig. 5

Comparison of torsional static analysis results

최대 회전 각변위는 단면적이 동일하더라도 단면의 모양에 따라 다양하게 변화하였고, 최대 회전 각변위가 가장 낮은 경우(Case I-5)는 기준 모델에 비하여 12.6 % 감소하였다. 그러나, 기준 모델에 비하여 모든 경우의 최대 등가 응력은 증가하였다. 그 중에서도 증가량이 가장 작은 경우는 Case I-5였다. 따라서, 중공축(Case I, II, III, IV)을 사용하면 단면의 형상으로 인한 중공축 내부의 노치 부분에서 응력 증대로 최대 등가 응력의 상승은 피할 수 없지만, 단면적 조절로 회전 강성의 증가를 기대할 수 있다고 할 수 있다. 노치로 인한 응력 증가는 모따기(chamfer)나 모깍기(fillet) 등으로 어느 정도 감소시킬 수 있다.

3.2 자중에 의한 처짐 구조 해석 결과

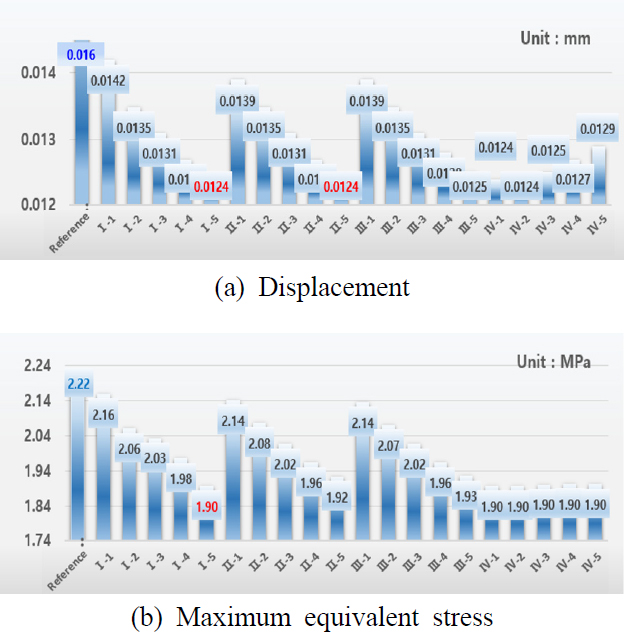
Fig. 6은 자중에 의한 기준 모델의 처짐과 등가 응력 분포를 보여주고 있고, Fig. 7은 자중에 의한 정적 해석을 수행하여 얻은 결과를 비교하고 있다. 기준 모델의 최대 처짐값과 최대 등가 응력값은 0.016 m와 2.22 MPa이었다. 모든 중공축의 최대 등가 응력값과 최대 처짐값이 모두 기준 모델(중실축)보다 작았다. 이 결과는 원형 단면 보의 처짐이 축 외경의 네제곱에 반비례하다는 사실을 그대로 보여주고 있다. 최대 처짐값 측면에서는 Case I-5와 Case II-5가 우수(24.28 % 개선)하였으며, 최대 등가 응력값 측면에서는 Case I-5가 가장 우수(14.6 % 개선)하였다.

Fig. 6

Static analysis results for a reference model

Fig. 7

Comparison of static analysis results

3.3 진동 해석 결과

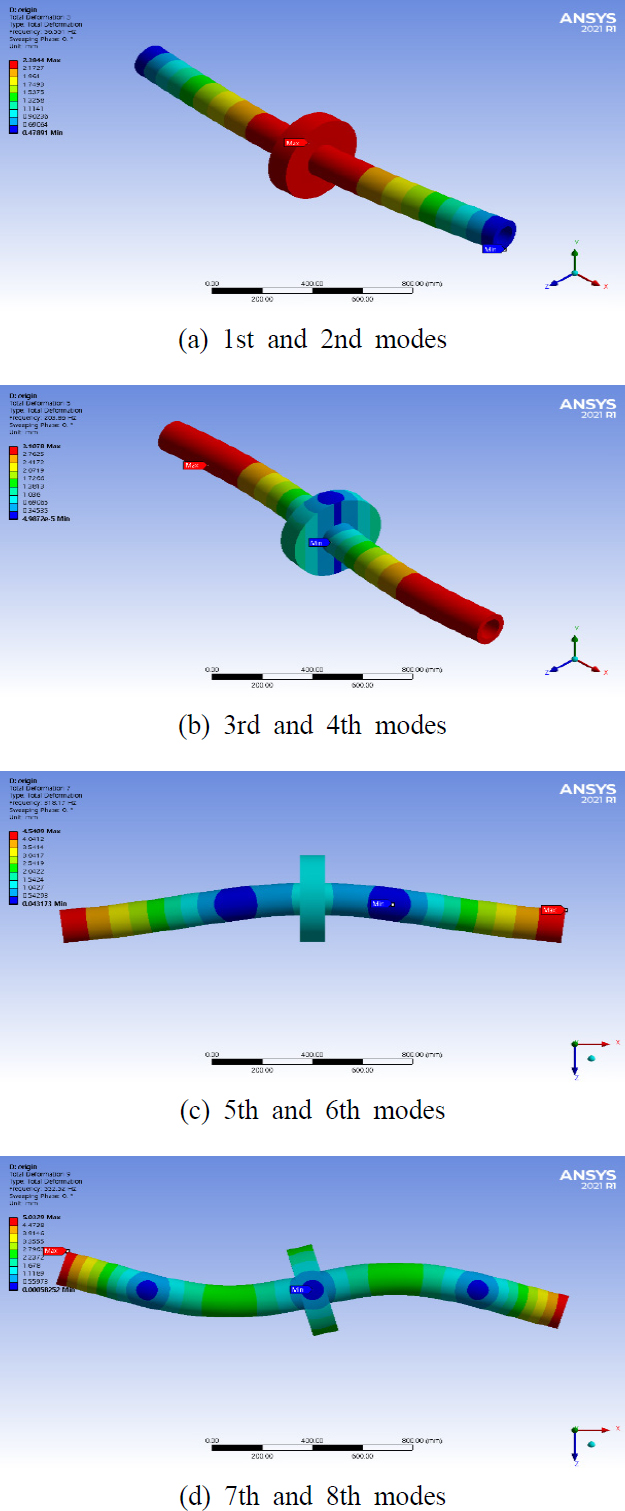
Table 5와 Fig. 8은 기준 모델에 대한 고유값 문제를 ANSYS에서 ‘rotordynamic control’ 옵션을 알맞게 사용하여 구한 결과(고유 주파수와 고유 모드)를 보여주고 있다. 근접한 주파수에서 같은 형상의 고유 모드가 2개씩 쌍으로 존재하였다. 축의 회전 속도의 증가에 따라 고유 모드 주파수 중 한 개는 증가하고 나머지 한 개는 감소한다. 따라서, 정지해 있는 회전축의 고유 주파수뿐만 아니라 정격 회전 속도에서 증가 또는 감소된 고유 주파수를 살펴보는 것이 중요하다. 이는 campbell diagram을 통하여 회전 속도에 의한 가진 주파수와 고유 모드 주파수의 근접도 여부를 파악하여 확인할 수 있다⁽¹⁶⁾.

Table 5

Natural frequencies of the reference model[unit: Hz]

Fig. 8

Natural modes of the reference model

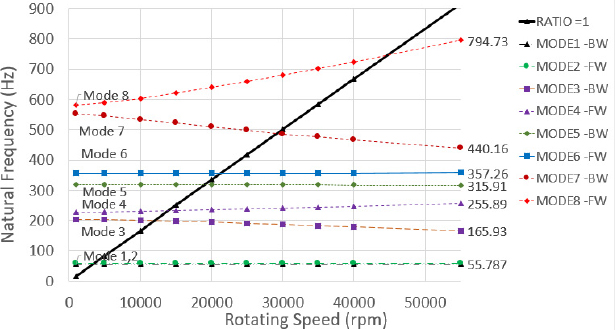
Fig. 9는 0 r/min ~ 55 000 r/min의 범위에서 회전 축의속도에 따른 기준 모델의 고유 주파수 변화를 나타내는 campbell diagram을 보여주고 있다. 앞서 회전축의 정격 속도를 40 000 r/min으로 설정했다는 것을 참고하면, 8 번째 고유 모드 주파수와 정격 속도에 의한 가진 주파수의 근접도를 살펴보는 것이 중요하다는 것을 알 수 있다. 기준 모델의 경우, 해당 고유 주파수를 r/min으로 변경한 위험 속도가 44 731 r/min으로 약 4731 r/min 정도의 여유(40 000 r/min의 정격 속도를 기준으로 할 경우 11.8 %)를 가지고 있다.

Fig. 9

Campbell diagram of reference model

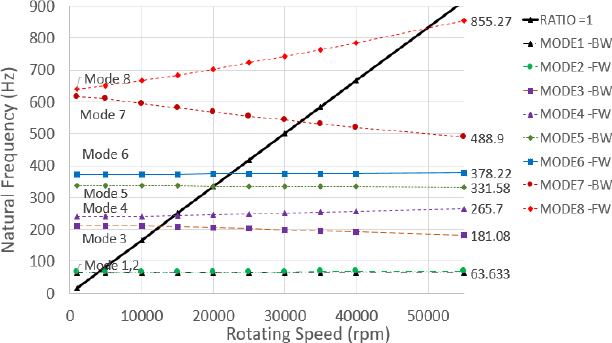
Table 6은 각 단면의 8차 고유 모드 주파수에 해당하는 위험 속도를 정리한 것이다. 기준 모델에 비하여 전반적으로 위험 속도가 증가하였음을 알 수 있고, Case IV-5에서 최대 분리 여유(31.6 %)를 갖는 것을 알 수 있었다. 같은 단면적을 갖는 Cases I ~ III에서는 case I-5가 가장 큰 분리 여유(24.7 %)를 가지는 것을 알 수 있다. Fig. 10은 case I-5의 campbell diagram을 보여주고 있다.

Table 6

Critical speed of shaft(8th natural mode)[unit: r/min]

Fig. 10

Campbell diagram of Case Ⅰ-5

4. 고 찰

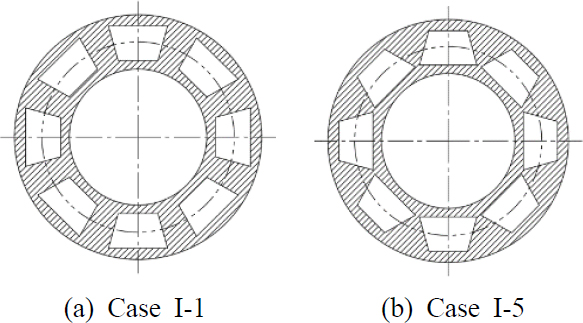
Fig. 11은 동일한 단면적을 갖지만 단면을 구성하는 사다리꼴의 윗변과 아랫변이 정반대인 두 경우(Cases I-1과 I-5)를 비교한다. 자중으로 인한 정적 해석 결과를 살펴보면, 단순 중공축에 비하여 Case I-5(Fig. 11(b)참조)와 같이, 축 단면의 외곽에 질량이 상대적으로 몰려 있을 때, 응력과 변형량이 모두 개선되는 효과를 확인할 수 있었다. 단순 중공축인 기준 모델 대비 응력은 14.6 %, 변형량의 경우 24.8 % 개선되었다.

Fig. 11

Comparison of cross sections of Cases I-1 and I-5

중앙 회전자에 토크를 입력하여 수행한 비틀림 정적 해석에서는 단순 중공축에 비하여, 최대 응력 측면에서 모든 단면이 악화되는 것을 확인하였다. 이는 급격한 단면 형상 변화로 인해 발생한 노치가 원인으로 판단된다. 하지만 Case I-5의 비틀림 변위는 기준 모델에 비하여 12.8 % 개선되었음을 확인하였다.

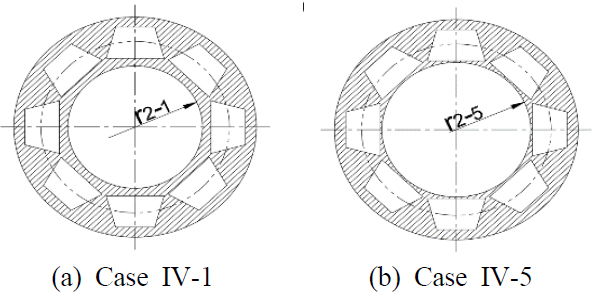
진동 해석을 수행하여 얻은 campbell diagram으로부터 파악한 모든 경우의 8 차 진동 모드의 위험 속도는 이 연구 모델의 정격 회전 속도(40 000 r/min)에 일치하지 않았지만, 경우에 따라 분리 여유에는 차이가 발생하였다. 기준 모델의 경우 11.8 %의 분리 여유를 가지고 있었고, 경량화를 위하여 외경을 고정한 채 내경을 증가시킨 Case Ⅳ-5는 31.6 % 가장 우수하였다. 또한, Case IV보다 내경이 작은 경우에는 Case I-5가 분리 여유 측면에서 가장 우수하였다. 즉, 경량화를 위하여 비틀림에 비교적 영향이 작은 내경을 증가시킨 Case Ⅳ(Fig. 12 참조)의 경우, 내경이 증가하여 경량화 될수록 정격 속도에서의 분리여유는 증가함을 보였다. 반면 비틀림이나 중력에 의한 단순 처짐량 크기는 증가함을 보였다.

Fig. 12

Comparison of cross sections of Cases IV-1 and IV-5

동일한 단면적일 경우에, Case Ⅰ-5의 경우가 다른 경우에 비하여 강성 측면에서 우수한 결과를 나타냈었다. 또한, 선정한 정격 회전 속도(40 000 r/min)를 기준으로 20 % 이상의 충분한 분리 여유를 가졌다. Case Ⅰ, Case Ⅱ, Case Ⅲ의 경우 정적 해석 및 동적 해석 결과에서 미소하지만 Case Ⅰ이 조금 더 우수한 결과를 보인다. 하지만 결과 값의 차이가 워낙 작아 수치해석에서의 오차로 판단된다. 그리고, 구멍 개수가 동일할 때는 사다리꼴의 윗변보다 밑변이 길 때 우수한 특성을 보였다.

5. 결 론

이 논문에서는 상용 유한요소 프로그램을 활용하여 다양한 중공축 단면에 대한 회전축의 정적/동적 특성 변화를 살펴보았다. Lalanne’s 모델과 유도전동기 회전자 형상을 참조하여 축 시스템을 구성하였으며, 일반적인 중공축 단면의 중심 구멍 주변에 사다리꼴 구멍을 생성하여 중공축 단면을 형성하였다. 자중에 의한 처짐과 응력, 토크 입력 시 비틀림 응력을 계산하였고, 동특성 파악을 위하여 캠벨선도(campbell diagram)를 얻어서 각 단면에 따라 계산된 위험 속도를 정격 속도와 비교하여 분리 여유를 계산하였다. 비록 이 연구가 가공 가능성은 배제한 채 중공축의 단면 설계를 진행하였기에, 현재의 가공 기술로 실제 제작까지 어려울 수도 있다. 그러나, 미래에 가공기술이 발전한다면 현재의 연구 결과가 이 논문에서 고려한 중공축 단면이외에도 다양한 단면 형상을 고려한 중공축 설계 기술 발전에 크게 기여할 것으로 기대한다.

Acknowledgments

이 성과는 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(No. RS-2024-00345634).

References

• Rim, K.-H., An, C.-H., Oh, J.-B., Lee, H. and Roh, J.-H., 2008, Vibration Analysis of Inspection Equipment for a Semiconductor, Proceedings of the KSNVE Annual Spring Conference, pp. 559~654.
• Kim, G.-B., 2014, A Study on the Structure and Rotor Analysis of a High Speed Motor Generator, M.S. Thesis, Dong-A University, Busan, pp. 7~8.
• Kim, C. K., 2016, Finite Element Analysis on the Displacement Behavior Safety of Hollow Shafts with Equivalent Volume, Journal of the Korean Institute of Gas, Vol. 20, No. 3, pp. 73~77. [https://doi.org/10.7842/kigas.2016.20.3.73]
• Kim, C. K., 2014, A Study on the Displacement Behavior Safety of Cylindrical Hollow Rollers, Journal of the Korean Institute of Gas, Vol. 18, No. 1, pp. 41~45. [https://doi.org/10.7842/kigas.2014.18.1.41]
• Kim, C. K., 2014, A Study on the Displacement and Stress Analysis of Hollow Rollers for a Wire Saw Machine, Journal of the Korean Institute of Gas, Vol. 18, No. 2, pp. 10~15. [https://doi.org/10.7842/kigas.2014.18.2.10]
• Kim, C. K., 2015, Finite Element Analysis of Stress and Deformation Behaviors in Cylindrical Hollow Rollers, Journal of the Korean Institute of Gas, Vol. 19, No. 1, pp. 23~27. [https://doi.org/10.7842/kigas.2015.19.1.23]
• Kim, Y. and Park, J., 2023, Crack Growth Life Prediction of Hollow Shaft with Circumferential through Type Crack by Torsion, Journal of Aerospace System Engineering, Vol. 17, No. 2, pp. 1~8.
• Kim, G. J., Mun, H. J. and Lee, B. N., 1995, Torsional Vibration Analysis and Measurement of Hollow Crankshaft, Proceedings of KSAE Annual Autumn Conference, pp. 377~383.
• Lim, J.-H., Lee, B. I., Song, Y.-J., Kim, S.-D., Roh, C.-I. and Song, C. K., 2023, Structural Analysis of a Hollow Intermediate Shaft for Mass Reduction, Journal of the Korean Society of Manufacturing Process Engineers, Vol. 22, No. 1, pp. 8~15. [https://doi.org/10.14775/ksmpe.2023.22.01.008]
• Kang, M.-C., Ye, D.-H. and Go, G.-H., 2016, International Development Trend and Technical Issues of Metal Additive Manufacturing, Journal of Welding and Joining, Vol. 34, No. 4, pp. 9~16. [https://doi.org/10.5781/JWJ.2016.34.4.9]
• Son, H. J., 2023, A Study on the Fabrication of Inconel 625 Alloy Impeller through Wire Arc Additive Manufacturing, M.S. Thesis, Changwon National University, Changwon.
• Lee, Y. S., Lee, M. K., Sung, J. H., Hong, M. P., Son, Y. et al., 2021, A Study on the Method and Application of Shaft Repair using Directed Energy Deposition Process, Journal of the Korean Society of Manufacturing Process Engineers, Vol. 20, No. 9, pp. 1~10. [https://doi.org/10.14775/ksmpe.2021.20.09.001]
• Lalanne, M. and Ferraris, G., 1998, Rotordynamics Prediction in Engineering, 2nd Edition, John Wiley & Sons, Chichester, UK.
• Ki, W., Lee, J., Lee, H., Roh, T.-S. and Huh, H., 2020, Overseas Research Trends of an Electric-pump Cycle for Application in Upper-stage Propulsion Systems, Journal of the Korean Society of Propulsion Engineers, Vol. 24, No. 1, pp. 64~77. [https://doi.org/10.6108/KSPE.2020.24.1.064]
• Lee, J.-H., 2017, Study on a Reliability Test of Power Transmission Shafts for High Speed Transportation System, Doctoral Dissertation, Chungbuk National University, Cheongju.
• Yoon, T.-H., Park, Y.-H. and Jeon, S.-D., 2019, Rotordynamic Analysis and Radiation Noise Analysis for 2.5 MW Steam Turbine Generator, Journal of the Korean Society of Marine Engineering, Vol. 43, No. 3, pp. 157~162. [https://doi.org/10.5916/jkosme.2019.43.3.157]