적응 제어 알고리즘을 이용한 자동차 능동 현가장치 제어 특성

1. 서 론

자동차 현가장치는 바퀴로부터 차체를 물리적으로 분리하는 메커니즘으로, 주행 중 발생하는 수직 가속도를 최소화하여 승차감 및 주행 안정성을 향상시키는데 중요한 역할을 수행한다⁽¹⁾. 현가장치는 제어 입력에 따라 수동, 능동, 반능동 세 가지 시스템으로 분류된다. 일반적인 차량에 적용되는 수동 현가장치 시스템은 스프링과 댐퍼로 구성되어 있으며 고정되어 있는 특성으로 인하여 추가적인 제어가 불가능하다. 이러한 특성으로 인해 다양한 도로 입력에 대한 진동을 차단하는 데 한계가 있다⁽²⁾. 이러한 문제를 해결하기 위해 외부에서 조정이 가능한 반능동 또는 능동 현가장치에 대한 연구가 집중되고 있다. 반능동 현가장치는 댐퍼의 감쇠 계수를 변화시켜 차체의 진동을 억제한다. 별도의 동력원을 사용하지 않고 외부에서 발생한 진동에 의해 작동되기 때문에 능동 현가장치에 비해 기능이나 자유도가 떨어진다는 단점이 있다. 이러한 단점을 해결하기 위해 다양한 도로 환경 조건에 신속하게 적응하며, 보다 성능이 뛰어난 능동 현가장치 제어에 관한 연구가 더욱 조명되고 있다. 능동 현가장치는 기존 수동 현가장치 시스템에 액츄에이터가 추가된 형태로 가속도와 같은 파라미터들을 센서로 모니터링하며, 측정된 신호를 제어기에서 액츄에이터로 적절한 피드백을 제공한다. 최근 차량의 주행 안정성과 승차감을 향상시키기 위해 능동 현가장치의 효과적인 제어와 관련해 많은 연구가 진행되고 있다⁽³⁾. Hac et al.은 1/4 차량 모델을 사용한 능동 차량 현가장치의 예측 제어 문제를 도출하고 예측 정보를 사용하여 현가장치 성능을 향상시킬 수 있음을 보여주었다⁽⁴⁾. Kumar et al.은 linear quadratic regulator (LQR) 제어 방법을 사용하여 수동 현가장치에 비해 능동 현가장치 시스템이 승차감과 도로 접지력 면에서 더 우수함을 확인하였다⁽⁵⁾. Unger et al.은 LQR 기반 반능동 및 컨트롤러 개념에 대한 실험적 성능 평가를 조사하였다⁽⁶⁾. Ulsoy et al.은 LQR과 linear quadratic gaussian(LQG) 제어기를 비교하여 칼만 필터를 사용한 LQG 제어기의 도입이 필요함을 강조했다⁽⁷⁾. Yuk et al.은 강화학습의 deep deterministic policy gradient(DDPG) 알고리즘을 통하여 학습에 사용되지 않는 다양한 노면 조건에서 현가장치를 효과적으로 제어할 수 있음을 확인하였다^(8,9). Papadimitrakis and Alexondridis는 노면 모델 예측 제어 알고리즘을 적용하여 능동 서스펜션을 제어하는 연구를 제안하였다⁽¹⁰⁾. Ahmed et al.은 실제 시스템 적용이 용이한 비례-적분-미분(proportional-integral-derivative, PID) 제어기를 사용하여 능동 현가장치가 수동 현가장치에 비해 더 나은 승차감과 자동차의 주행 안정성을 향상시킬 수 있음을 확인하였다⁽¹¹⁾. 이와 같은 제어기들로도 충분히 좋은 성능을 얻을 수 있으나 고정된 제어 이득을 사용하기 때문에 다양한 도로 조건이나 외부 환경 변화에 신속하게 대응하기 어렵다는 단점이 있다. 이러한 문제점을 해결하기 위하여 적응 제어 알고리즘을 이용하여 능동 현가장치를 제어하는 연구가 진행되고 있다⁽¹²⁾. Fuzzy 알고리즘과 같은 적응 제어를 이용하여 현가장치를 능동 제어한다면 다양한 도로 입력에 실시간으로 대응하여 동작을 조정할 수 있다⁽¹³⁾.

이 연구에서는 대표적인 노면 모델인 범프 노면과 랜덤 노면 입력에 대하여 적절한 제어 이득을 발생시킬 수 있는 적응 제어 알고리즘의 하나인 fuzzy 알고리즘을 이용하여 자동차 능동 현가장치의 제어 성능을 확인한다. 1/4 자동차 현가장치 모델을 고려하고, 충분한 성능을 가지는 능동 액추에이터가 있는 것으로 가정한다. 제안된 fuzzy 알고리즘의 우수성을 확인하기 위하여 능동 현가장치 시스템에 대하여 Ziegler- Nichols 방법을 적용하여 일반적인 비례적분미분 제어기의 이득을 결정한다. Fuzzy 규칙과 멤버쉽 함수를 결정하여 PID 제어기의 이득이 연속적으로 변하고 적응 제어를 구현할 수 있는 fuzzy-PID 제어기를 설계한다. 범프 노면과 랜덤 노면에 대하여 일반적인 PID 제어기와 제안된 fuzzy-PID 제어기의 성능을 비교하여 제안된 적응 제어기의 우수성을 검증한다.

2. 시스템 모델링

2.1 1/4 서스펜션 모델

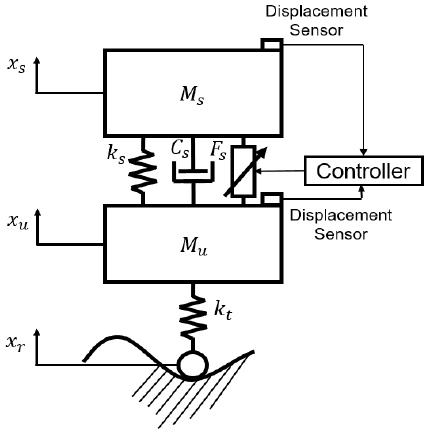
이 연구에 사용된 1/4 차량 모델은 Fig. 1에 나타내었고, 사용된 파라미터는 Table 1과 같다. 모델로부터 시스템 방정식을 도출할 수 있으며, 서스펜션 시스템의 운동 방정식은 뉴턴의 법칙을 사용하여 식 (1)과 식 (2)와 같이 주어지게 된다.

$\[ M_s{\ddot{x}}_s=k_s\left(x_u-x_s\right)+C_s\left({\dot{x}}_u-{\dot{x}}_s\right)+F_s \]$

(1)

$\[ M_u{\ddot{x}}_u\begin{array}{l}=k_t\left(x_r-x_u\right)-k_s\left(x_u-x_s\right)\\ -C_s\left({\dot{x}}_u-{\dot{x}}_s\right)-F_s\end{array} \]$

(2)

Fig. 1

Quarter vehicle active suspension model

Table 1

Parameters for quarter vehicle suspension

식 (2)에서 x_u는 바퀴의 변위, x_s은 차체의 변위, x_r은 도로의 외란, F_s는 액추에이터의 힘을 의미한다. 제안된 서스펜션 모델의 고유진동수는 1.25 Hz, 11.6 Hz로 확인되었다. 일반적인 자동차의 첫 번째 모드가 1 Hz ~ 2 Hz 사이에 있으므로 제안된 모델의 파라미터는 적절한 것으로 판단된다.

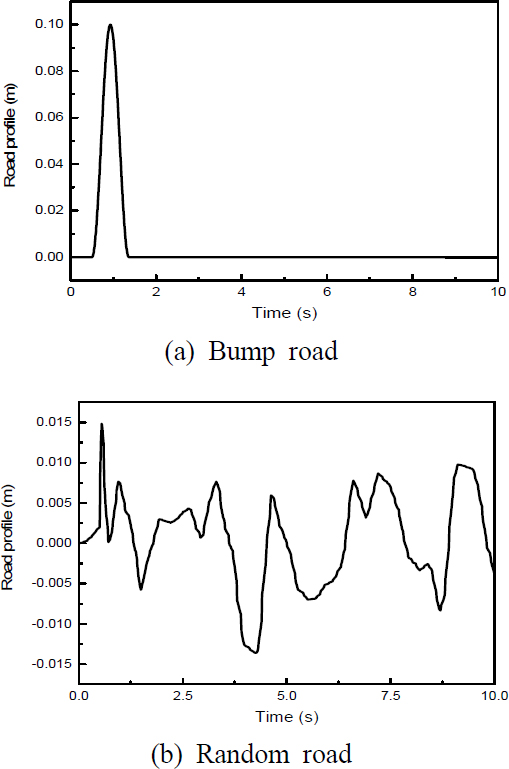
이 연구에 사용된 도로 모델의 종류는 총 2가지로 Fig. 2에 사용되는 노면 그래프를 나타내었다. Fig. 2(a) 범프 노면 모델의 식 (3)은 다음과 같다.

$\[ x_b\left(t\right)=\left\{\begin{array}{cc}\frac{h}{2}\left(1-\mathrm{c}\mathrm{o}\mathrm{s}\left(\frac{2\pi vt}{L}\right)\right),& 0\le t\le \frac{L}{v}\\ 0& \mathrm{O}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}\end{array}\right. \]$

(3)

Fig. 2

Road input profile

여기서 h는 범프의 높이, v는 차량 속도, L은 폭의 길이이다. 파라미터는 국토교통부가 정한 규격으로 높이는 0.1 m 그리고 폭은 3.6 m로 설정되었다⁽¹⁴⁾. Fig. 2(b)에 나타낸 랜덤 노면 모델은 식 (4)에서 나타낸 것과 같이 ISO 8608에 기반하여 시계열 영역으로 표현된 식 (4)를 이용하였다⁽¹⁵⁾.

$\[ {\dot{x}}_r\left(t\right)=-2\pi f_0{x}_r\left(t\right)+2\pi n_0\sqrt{G_p\left(n_0\right)v_0}\omega \left(t\right) \]$

(4)

여기서 f₀는 저차 컷오프 시간-주파수, n₀는 표준 공간 주파수, G_p(n0)는 도로 거칠기 상수, v₀는 차량 속도 그리고 w(t)는 2σ²ρv의 강도를 가진 단위 백색 소음 신호이다. σ²는 노면 불규칙성의 공분산, ρ는 노면 거칠기 매개변수이다. 포장된 도로 상태를 고려하여 선택되었다⁽¹⁶⁾. 범프 노면의 제어 결과 비교는 차량의 속도가 15 km/h, 30 km/h일 때, 랜덤 노면은 20 km/h, 60 km/h, 100 km/h일 때로 진행하였다.

2.2 제어기 설계

PID 제어기는 가장 일반적인 제어기로 원하는 설정 값과 측정된 변수 간의 오차 값을 계산하여 최소화 시킨다. 제어기의 전달 함수는 식 (5)와 같이 주어진다.

$\[ f_2\begin{array}{l}=K_p\left(1+\frac{1}{T_i}\int edt+T_d\frac{de}{dt}\right)\\ =K_p+K_i\int edt+K_d\frac{de}{dt}\end{array} \]$

(5)

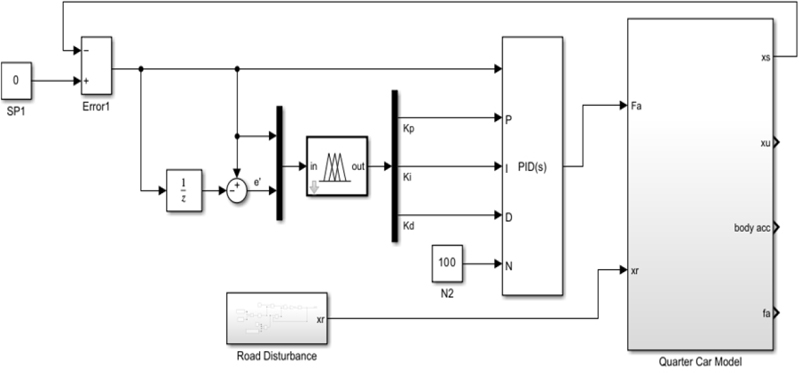
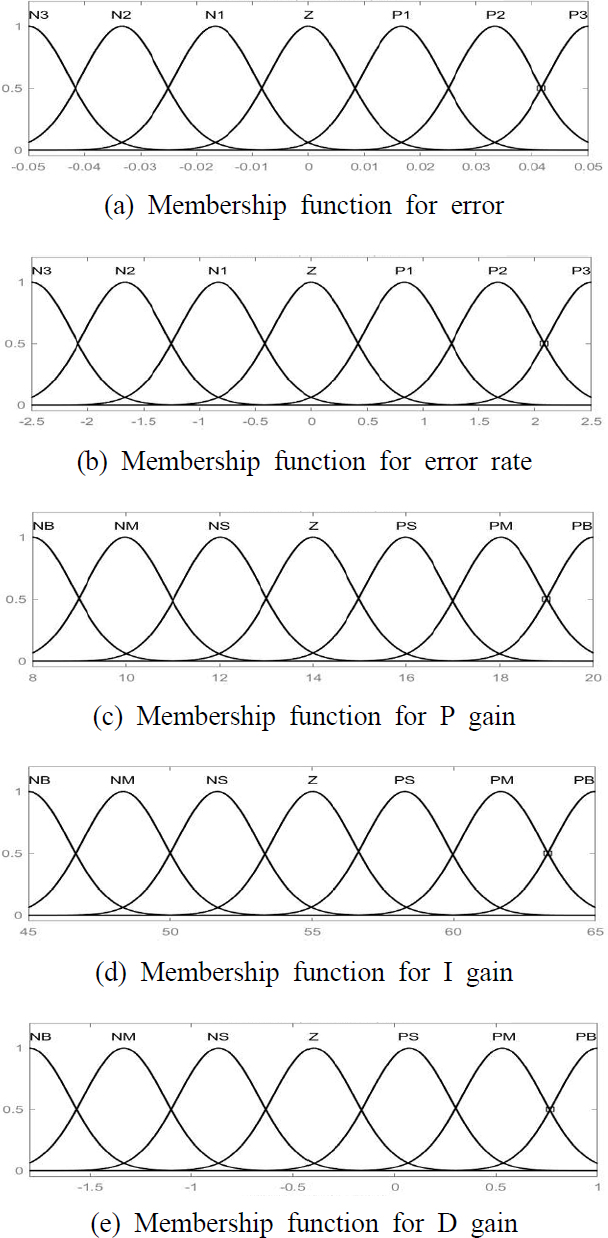
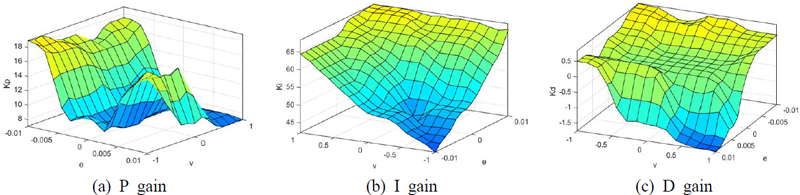
식 (5)를 바탕으로 Ziegler-Nichols 방법을 사용하여 PID 제어기의 이득 값을 조정한다. PID만을 사용하여 서스펜션을 제어하는 것은 다양한 도로 상황에 대상의 비선형성과 외란 등으로 인해 어려움이 따른다. 이러한 문제를 해결하기 위해 퍼지 알고리즘을 사용하여 능동 현가장치를 제어하였다. Lotfi Zadeh가 1965년에 소개한 퍼지 제어 이론은 사람의 지식을 바탕으로 제어 규칙을 정하여 제어 수순을 정의하는 방법이다⁽¹⁷⁾. 일반적인 퍼지 제어 시스템은 크게 3개의 요소로 구성되며 퍼지 논리를 이용하여 값을 도출해 내는 과정이다. 이를 퍼지 추론 과정(fuzzy inference process)이라 하며 Fig. 3에 진행되는 순서를 나타내었다. 먼저 명확한 입력 값이 퍼지화(fuzzification)라는 프로세스에서 퍼지 변수로 변환된다. 퍼지 변수는 퍼지 논리 규칙에 적용되어 새로운 퍼지 변수를 생성하게 되고, 이러한 퍼지 값들은 역퍼지화(defuzzification)라는 프로세스를 통해 다시 명확한 출력 값으로 변환된다. 이 연구에서는 MATLAB Simulink를 이용하여 두 종류의 노면 상태에 대해 퍼지 논리를 사용하여 제어하는 실험을 진행하였다. 최종적으로 사용된 시뮬레이션 모델은 Fig. 4에 나타내었다. 능동 현가장치의 제어에 사용되는 퍼지 제어기의 입력 변수로는 차체의 변위와 변위에 대한 변화율로 설정해 주었고, 출력 변수로는 PID의 이득 값 K_p, K_i, K_d로 설정해 주었다. 퍼지 논리 제어기를 설계하기 위해 입력 변수와 현가장치 시스템의 출력을 퍼지화 하기 위해 각 변수에 대해 멤버십 함수를 정의한다. 각 입출력 변수의 멤버쉽 함수는 가장 자연스러운 응답을 제공하는 가우시안 함수를 사용하였다. Fig. 5에 입력과 출력의 멤버십 함수를 나타냈다. Fig. 5(a), Fig. 5(b)는 입력 변수인 차체 변위와 변화율이고 Fig. 5(c) ~ Fig. 5(e)는 PID의 이득 값이며 이러한 퍼지 집합에 할당된 언어 변수는 NB, NM, NS, Z, PS, PM, PB 총 7가지로 설정해 주었다. 3개의 출력 변수에 대한 49개의 규칙이 만들어지며 Mamdani 추론 방법과 중심 값 방법을 사용하였다. 규칙을 통해 얻은 변수들은 퍼지 집합의 중심 값을 계산하며 최종 출력 변수인 PID 이득 값을 출력한다. 퍼지 제어 규칙은 Table 2 ~ Table 4와 같이 설정해 주었고, 규칙에 대한 퍼지 제어 표면은 Fig. 6과 같다.

Fig. 3

Fuzzy inference process

Fig. 4

Simulink model for quarter vehicle suspension with adaptive fuzzy-PID controller

Fig. 5

Fuzzy membership functions

Table 2

Fuzzy rules based for Kp

Table 3

Fuzzy rules based for Ki

Table 4

Fuzzy rules based for Kd

Fig. 6

Fuzzy control surfaces

3. 결과 및 분석

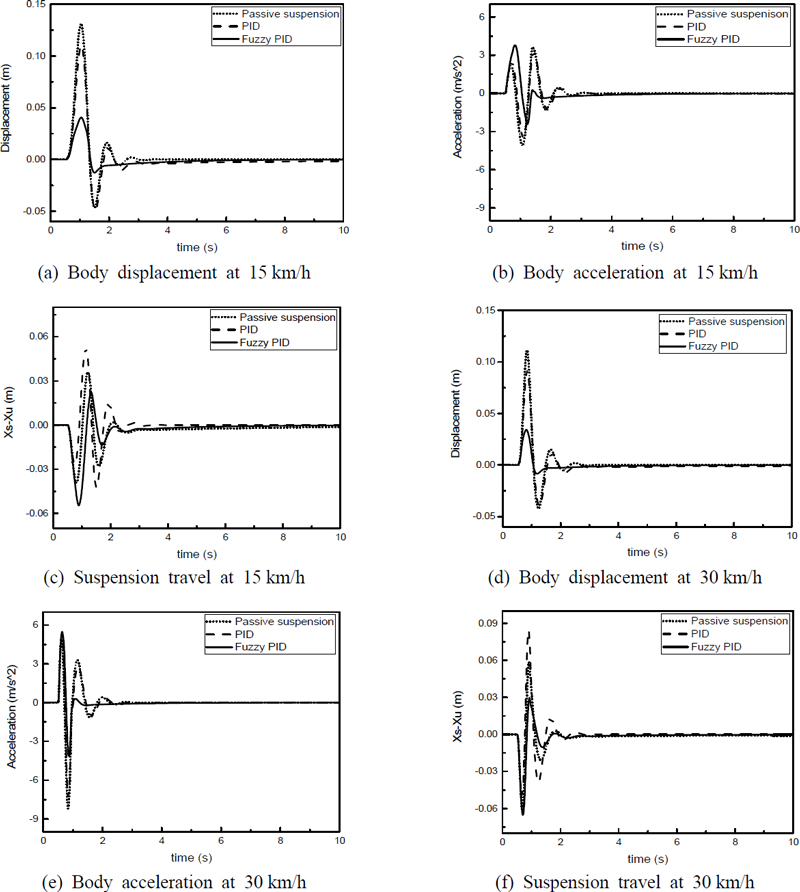
시뮬레이션 결과는 노면 종류에 따라 2가지의 결과로 도출되었다. 첫 번째 범프 노면 모델의 제어 결과는 Fig. 7에서 차체 질량의 변위와 가속도에 대한 그래프로 나타내었다. 차량 속도가 15 km/h인 경우에 대한 제어 결과는 Fig. 7(a)와 (b)에 나타내었다. 제안된 fuzzy-PID 제어를 적용한 경우 차체의 변위와 가속도가 기존 PID 제어를 적용한 경우보다 더 크게 감소하는 것을 확인할 수 있다. 차량 속도가 30 km/h인 경우에 대한 제어 결과는 Fig. 7(d)와 (e)에 나타내었다. 차량 속도 15 km/h 경우와 동일하게 제안된 fuzzy- PID 제어기가 기존 PID 제어기보다 우수한 성능을 갖는 것을 확인할 수 있다. 각 속도 조건에서 제안된 서스펜션의 변위를 Fig. 7(c)와 (f)에 나타내었다. fuzzy-PID 제어기를 적용한 경우 서스펜션 변위가 기존 PID 제어를 적용한 경우보다 더 크게 발생하면서 차체 변위가 작게 발생되도록 하여 향상된 승차감을 갖게 되는 것을 확인할 수 있다. Ziegler-Nichols 방법을 사용하여 결정된 PID 제어기의 비례, 적분, 미분 이득은 각각 8, 40, 0.3으로 고정된 값이지만, fuzzy-PID 제어기의 제어이득은 Fig. 8과 같이 상태 변화에 따라 연속적으로 변하기 때문에 기존 PID 제어기보다 더 우수한 제어 결과를 나타내는 것을 확인할 수 있다.

Fig. 7

Bump road results

Fig. 8

Control gains for bump road excitation

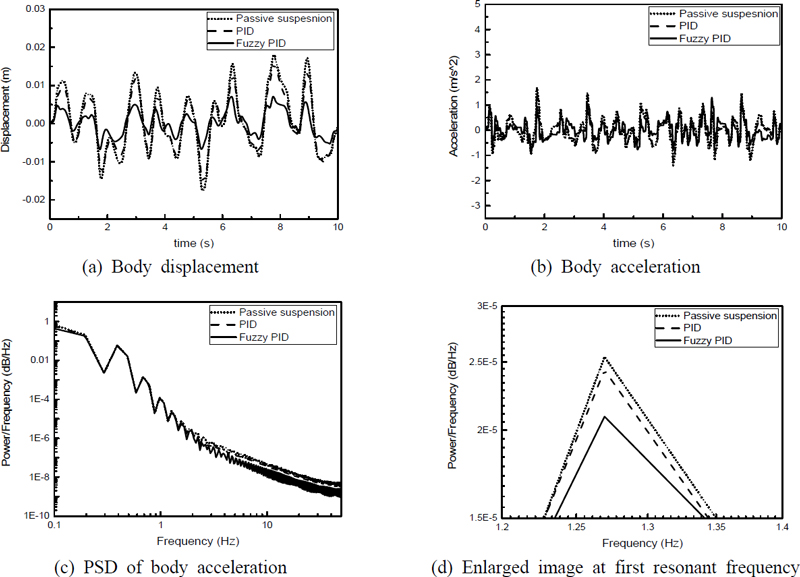
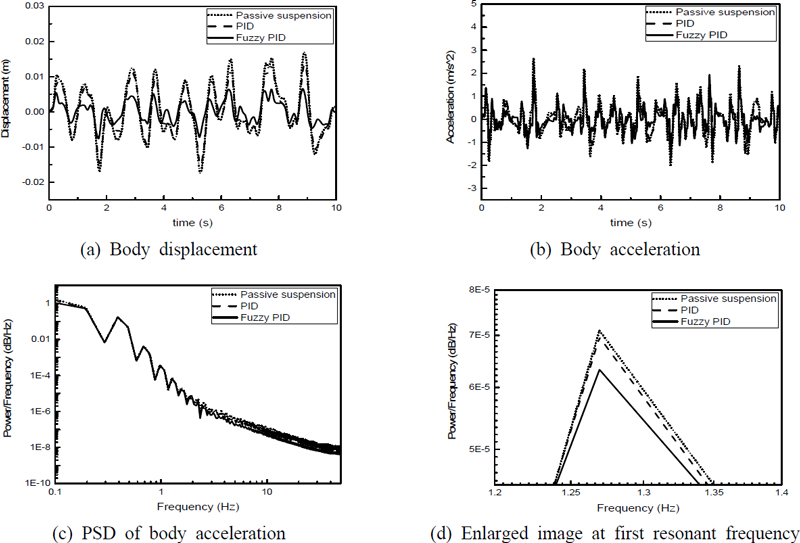
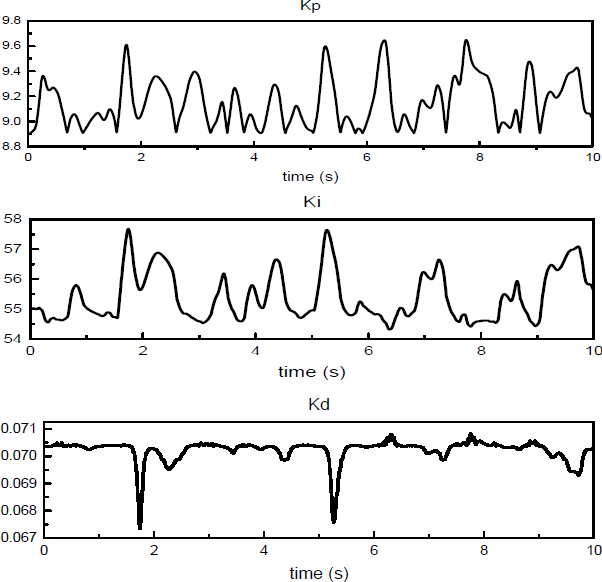
두 번째로 랜덤 노면 모델에 대한 결과는 차체 변위와 차체 가속도 그리고 차체 가속도에 대한 PSD (power spectrum density) 그래프를 차량의 속도에 따라 Fig. 9 ~ Fig. 11에 나타내었다. 차량 속도가 20 km/h인 경우의 랜덤 노면 가진 모델의 제어 결과를 Fig. 9에 나타내었다. Fig. 9(a)에 나타난 바와 같이 차체 변위는 제안된 fuzzy-PID 제어기를 적용한 경우 변위량이 더 크게 감소한 것을 확인할 수 있다. Fig. 9(b)에 나타낸 차체 가속도의 경우 제시된 그래프 만으로는 성능 비교가 어려워 Fig. 9(c)와 같이 차체 가속도의 PSD 그래프를 나타내었으며, 제안된 fuzzy- PID 제어기를 적용한 경우에 차체 가속도가 더 크게 감소한 것을 확인할 수 있다. Fig. 9(d)에 나타난 바와 같이 공진 영역에서 기존 PID 제어기를 적용한 경우보다 제안된 제어기를 통해 20 %의 가속도가 더 감소한 것을 확인할 수 있다. Fig. 12에는 Fig. 9 결과에서 얻어진 fuzzy-PID 제어기의 제어이득을 나타내었고, 노면 가진 변화에 따라 제어 이득이 연속적으로 변하면서 더 우수한 제어 성능을 가질 수 있는 것을 확인할 수 있다.

Fig. 9

Random road results at 20 km/h

Fig. 10

Random road results at 60 km/h

Fig. 11

Random road results at 100 km/h

Fig. 12

Control gains for random road excitation at 20 km/h

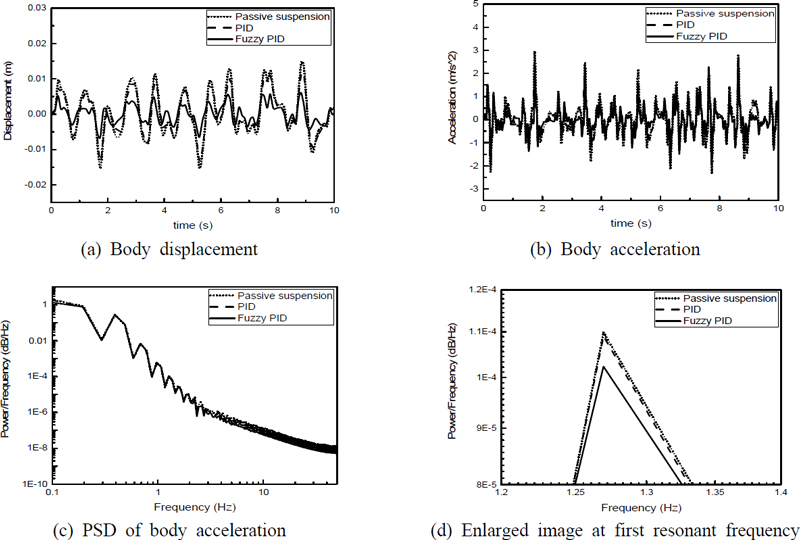
Fig. 10과 Fig. 11에는 차량 속도가 60 km/h와 100 km/h인 경우에 대한 시뮬레이션 결과를 각각 나타내었으며, Fig. 9의 결과와 동일하게 fuzzy-PID 제어기를 적용한 경우 더 우수한 제어 성능을 갖는 것을 확인할 수 있다. Fig. 10(d)와 Fig. 11(d)에 확대하여 나타낸 시스템 고유 진동수 영역에서도 제안된 제어기를 적용한 경우 기존 PID 제어기를 적용한 경우보다 15 %, 10 % 이상 가속도가 감소하여 제어 성능이 향상된 것을 확인할 수 있다. Fig. 9 ~ Fig. 11에 나타난 바와 같이 차량의 속도가 증가하는 경우, 차체 변위는 큰 변화가 없으나 차체 가속도의 크기는 증가하는 것을 확인할 수 있다. 또한, PSD의 결과를 보면 차체 속도가 증가함에 따라 제어 성능이 다소 감소하지만, 기존 PID 제어 결과보다는 더 우수한 진동 제어 성능을 가지는 것을 확인할 수 있다.

Fig. 9 ~ Fig. 11에 나타낸 차체 변위와 가속도에 대한 RMS 감소율과 PSD 감소율을 Table 5와 Table 6에 각각 나타내었다. Table 5와 Table 6에서 나타난 바와 같이 차체 변위와 가속도에 대한 RMS와 PSD 감소율이 fuzzy-PID를 적용하여 제어한 결과가 기존 PID 제어기를 적용한 경우보다 더 높게 나온 것을 확인하였다. 차량 속도가 20 km/h에서 100 km/h까지 증가하여도 RMS 감소율과 PSD 감소율은 크게 변동되지 않았으며, 모든 차량 속도에서 제안된 fuzzy- PID 제어기를 적용한 경우에 기존 PID 제어기를 적용한 경우보다 더욱 우수한 제어 성능을 갖는 것을 확인할 수 있다. 기존 PID 제어기는 제어 이득이 고정되어 있으므로 다양한 도로 상황과 차량 속도에 대해 능동적으로 대응하기 어렵다는 단점이 있으나 퍼지 논리를 사용하여 PID 제어기의 제어 이득을 연속적으로 결정하는 fuzzy-PID 제어기의 경우 다양한 도로 조건에 대응하여 이득 값을 스스로 조정할 수 있어 더욱 향상된 제어 성능을 가질 수 있는 것으로 판단된다.

Table 5

RMS reduction percentage for random road

Table 6

PSD reduction percentage for random road

4. 결과

이 연구에서는 자동차 현가장치의 능동적인 적응 제어를 위하여 fuzzy 알고리즘을 기반으로 제어 이득을 연속적으로 결정하는 fuzzy-PID 제어기를 제안하고 제어 성능을 확인하였다. 1/4 자동차 현가장치 모델에 대하여 fuzzy 규칙과 멤버쉽 함수를 결정하여 PID 제어기의 제어 이득이 연속적으로 변하고 적응 제어를 구현할 수 있는 fuzzy-PID 제어기를 설계하였다. 제안된 제어기의 우수성을 확인하기 위하여 Ziegler- Nichols 방법을 적용하여 일반적인 PID 제어기를 설계하고 제어 성능을 비교하였다. 범프 노면과 랜덤 노면에 가진에 대하여 기존 방식의 PID 제어기를 적용한 경우보다 제안된 fuzzy-PID 제어기를 적용한 경우 향상된 제어 성능을 가질 수 있음을 확인하였고, 제안된 적응 제어기의 우수성을 확인하였다. 다음 단계 연구에서는 작동기 특성을 포함하는 전체 차량 모델에 제안된 적응 제어기를 이용하여 다양한 노면 상태에서도 우수한 제어 성능을 가지는 것을 확인할 예정이다.

Acknowledgments

이 성과는 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(No. 2023R1A2C1007973).

References

• Hrovat, D., 1997, Survey of Advanced Suspension Developments and Related Optimal Control Applications, Automatica, Vol. 33, No. 10, pp. 1781~1817. [https://doi.org/10.1016/S0005-1098(97)00101-5]
• Rosli, R., Mailah, M. and Priyandoko, G., 2014, Active Suspension System for Passenger Vehicle using Active Force Control with Iterative Learning Algorithm, WSEAS Transactions on Systems and Control, Vol. 9, No. 2, pp. 120~129.
• Cao, J., Liu, H., Li, P. and Brown, D. J., 2008, State of the Art in Vehicle Active Suspension Adaptive Control Systems based on Intelligent Methodologies, IEEE Transactions on Intelligent Transportation Systems, Vol. 9, No. 3, pp. 392~405. [https://doi.org/10.1109/TITS.2008.928244]
• Hać, A., 1992, Optimal Linear Preview Control of Active Vehicle Suspension, Vehicle System Dynamics, Vol. 21, No. 1, pp. 167~195. [https://doi.org/10.1080/00423119208969008]
• Kumar, M. S. and Vijayarangan, S., 2006, Design of LQR Controller for Active Suspension System, Indian Journal of Engineering & Materials Sciences, Vol. 13, No. 3, pp. 173~179.
• Unger, A., Schimmack, F., Lohmann, B. and Schwarz, R., 2013, Application of LQ-based Semi-active Suspension Control in a Vehicle, Control Engineering Practice, Vol. 21, No. 12, pp. 1841~1850. [https://doi.org/10.1016/j.conengprac.2013.06.006]
• Ulsoy, A. G., Hrovat, D. and Tseng, T., 1994, Stability Robustness of LQ and LQG Active Suspensions, Journal of Dynamic Systems, Measurement and Control, Vol. 116, No. 1, pp. 123~131. [https://doi.org/10.1115/1.2900666]
• Yuk, D.-G. and Sohn, J. W., 2024, Active Suspension Control using Reinforcement Learning, Journal of the Korean Society for Precision Engineering, Vol. 41, No. 3, pp. 223~230. [https://doi.org/10.7736/JKSPE.023.141]
• Kim, Y.-J., Hong, S. and Oh, J.-S., 2022, Design of Control Algorithm for Micro Electric Vehicle Suspension System using Reinforcement Learning Algorithm, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 32, No. 2, pp. 124~132. [https://doi.org/10.5050/KSNVE.2022.32.2.124]
• Papadimitrakis, M. and Alexandridis, A., 2022, Active Vehicle Suspension Control using Road Preview Model Predictive Control and Radial Basis Function Networks, Applied Soft Computing, Vol. 120, 108646. [https://doi.org/10.1016/j.asoc.2022.108646]
• Ahmed, A. E.-N. S., Ali, A. S., Ghazaly, N. M. and Abd el-Jaber, G. T., 2015, PID Controller of Active Suspension System for a Quarter Car Model, International Journal of Advances in Engineering & Technology, Vol. 8, No. 6, pp. 899~909.
• Han, S.-Y., Dong, J.-F., Zhou, J. and Chen, Y.-H., 2022, Adaptive Fuzzy PID Control Strategy for Vehicle Active Suspension based on Road Evaluation, Electronics, Vol. 11, No. 6, 921. [https://doi.org/10.3390/electronics11060921]
• Gang, H. G., Choi, S.-B. and Sohn, J. W., 2017, Torque Tracking Control of MR Brake using a Fuzzy-PID Control Algorithm, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 27, No. 4, pp. 444~450. [https://doi.org/10.5050/KSNVE.2017.27.4.444]
• Ministry of Land Infrastructure and Transport, 2022, Guideline No. 681, Ministry of Land Infrastructure and Transport, Sejong-si, Korea.
• ISO, 2016, Mechanical Vibration - Road Surface Profiles - Reporting of Measured Data. International Organization for Standardization, Edition 2, ISO 8608: 2016.
• Choi, S. B., Choi, Y. T. and Park, D. W., 2000, A Sliding Mode Control of a Full-car Electrorheological Suspension System via Hardware In-the-loop Simulation, Journal of Dynamic Systems, Measurement and Control, Vol. 122, No. 1, pp. 114~121. [https://doi.org/10.1115/1.482435]
• Zadeh, L. A., 1965, Fuzzy Sets, Information and Control, Vol. 8, No. 3, pp. 338~353. [https://doi.org/10.1016/S0019-9958(65)90241-X]