헬리콥터 주로터 소음 저감 설계를 위한 와류법과 FW-H 음향상사법 기반의 공력 소음 예측 코드 개발

1. 서 론

고정익 항공기와 달리 제자리 비행과 수직이착륙이 용이하다는 점에서 큰 차별성을 가지는 헬리콥터는 군사적인 목적뿐만 아니라 소방 및 여객을 위한 민간용으로도 활발하게 활용되고 있다. 하지만 상대적으로 저고도로 비행하는 특성으로 인해 공항 주변 지역뿐만 아니라 도심과 주거지역 인근 주민들에게 환경 소음을 유발하고 있다. 최근 국내에서는 군용비행장 인근 주민들의 소음 피해가 심각하다는 사실이 인정되어 2019년에 군용비행장ㆍ군사격장 소음 방지 및 피해 보상에 관한 법률이 제정되었다⁽¹⁾. 특히 군용 헬리콥터는 소음으로 인해 적에게 감지될 위험이 있으므로 생존성을 높이고 성공적으로 임무를 수행하기 위해서는 저소음 설계가 요구된다.

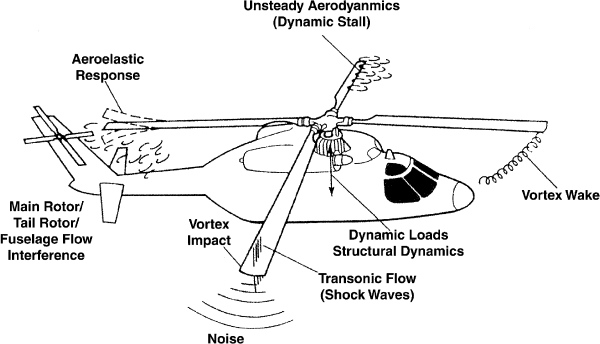
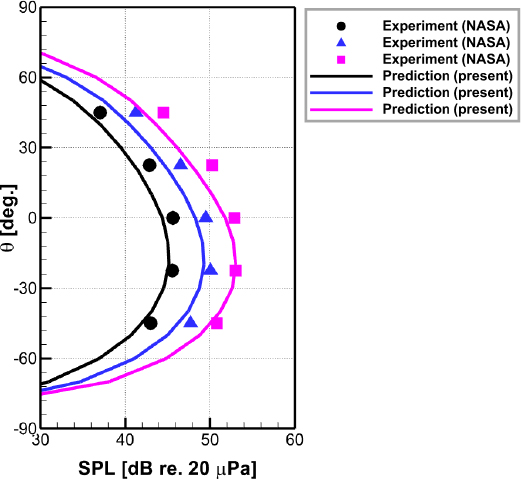
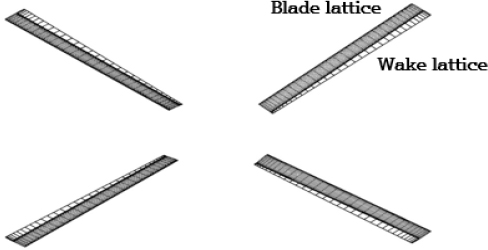
헬리콥터 소음은 Fig. 1과 같이 회전하는 로터 시스템에서 발생하는 복잡한 유동현상들로 인해 자동차나 철도와 같은 다른 교통수단에 비해 상대적으로 소음을 예측하고 분석하는 것이 어렵다⁽²⁾. 특히, 발생하는 소음의 주파수 특성을 살펴보면 주 로터에 의해 발생하는 소음이 전체 헬리콥터에서 발생하는 소음에 지배적인 영향을 미치는 것을 알 수 있다⁽³⁾. 따라서, 헬리콥터의 전체적인 소음 수준을 저감하기 위해서는 로터 블레이드에서 발생하는 소음을 낮출 수 있는 저소음 설계가 필요하다. 이를 위해서는 효율적이면서 정확한 소음 해석이 기본적으로 선행되어야 하며, 전 세계적으로 독자적인 소음 예측 프로그램의 개발 및 검증을 위한 연구가 활발히 이루어져 왔다. Brentner et al.과 Bres et al.은 헬리콥터 로터 블레이드에서 발생하는 공력소음을 예측하기 위해 Farassat’s 1A 식 기반의 PSU-WOPWOP 코드를 개발하였고, 현재 다양한 회전익기 공력소음 해석 연구에 널리 활용되고 있다^(4,5). Yücekayalı et al.은 in-house 코드인 Turkish aerospace acoustic code(TACO)를 이용하여 HART-II 로터 블레이드의 blade vortex interaction(BVI) 소음을 예측하였고, PSU-WOPWOP 결과와 비교함으로써 개발 코드의 예측 정확성을 검증하였다⁽⁶⁾. 이외에도 프랑스의 ONERA, 독일의 German aerospace center (DLR), 영국의 GKN Westland에서 각각 PARIS^(7,8), AKUROT^(9,10), DEAF⁽¹¹⁾ 소음 예측 코드를 자체적으로 개발하였다. 이에 따라, 이 연구에서는 독자적인 저소음 로터 블레이드 플랜폼 형상 설계 프레임워크 구축 연구의 일환으로 로터 공력소음을 예측할 수 있는 소음해석 코드를 개발하고 검증하였다. 특히 플랜폼 설계 과정에서 요구되는 반복적인 목적함수 평가에 대응하기 위해 효율적으로 공력 하중을 예측할 수 있는 와류법 기반의 공력해석자와 연계된 소음해석자를 개발하였다. 이미 이전 연구에서 로터 간의 상호 간섭이 제자리 비행중인 멀티콥터형 무인비행체의 공력성능 및 소음 특성에 미치는 영향을 분석하고 소음해석자에 대한 검증을 수행한 바 있으며, 이는 Fig. 2에 나타내었다^(12,13). 하지만 이는 상대적으로 크기가 작은 드론 프로펠러에 적용했던 사례이므로 이 연구에서 초점을 두고 있는 헬리콥터와는 소음 특성에서 상당한 차이가 있다. 추가적으로 이 연구에서는 제자리 비행뿐만 아니라 전진 비행 조건에 대해 로터 공력소음 해석을 수행하고 예측값을 실험 결과와 비교 검증하였다.

Fig. 1

A schematic of the complicated aeromechanical environment

Fig. 2

Comparison of the first BPF directivity at different rotating speed(black: 4800 r/min, blue: 5400 r/min, magenta: 6000 r/min)

2. 수치해석 기법

3. 제자리 비행 소음해석

3.1 Caradonna-Tung 로터 블레이드 모델

제자리 비행 중인 로터 블레이드의 소음해석을 수행하기 위해 Caradonna-Tung 로터 블레이드 모델을 이용하였다. Caradonna-Tung 로터 모델은 비틀림각이 없고 시위 길이 분포가 일정한 직사각형의 플랜폼 형상을 갖고 있으며, 단면은 NACA0012 에어포일로 구성되어있다. 로터 블레이드에 대한 자세한 제원과 해석 조건은 각각 Table 1, Table 2에 정리하였다. 소음해석을 위한 공력 데이터 확보를 위해 로터 블레이드는 시위 방향으로 21개, 반경 방향으로 31개의 와류 격자 요소로 이산화하였고, 피치각 5°, 8°, 12° 조건에서 해석을 수행하였다.

Table 1

Blade geometry of Caradonna-Tung rotor

Table 2

Simulation conditions

3.2 제자리 비행 중인 로터 소음해석 결과

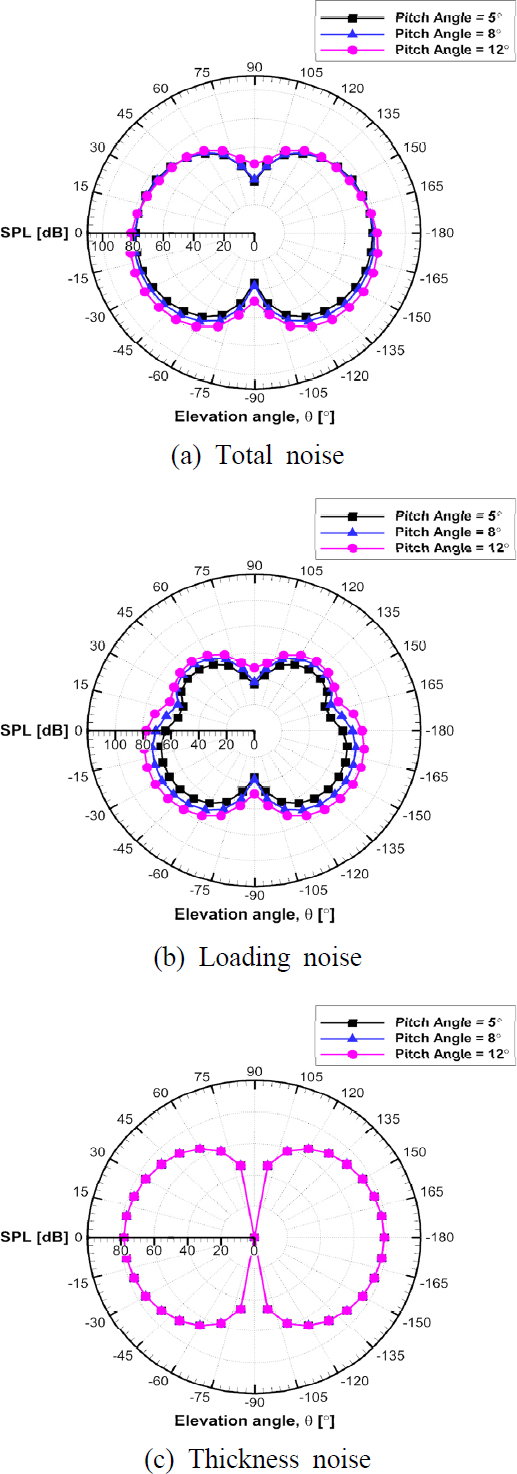
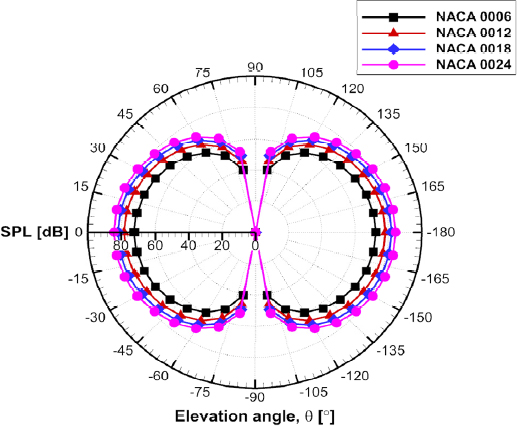
제자리 비행 중인 Cardonna-Tung 로터 모델에 대한 공력해석 검증은 이전 연구에서 수행되었고⁽¹⁴⁾, 비선형 와류 격자법이 피치각도에 따른 추력계수, 양력계수 분포, 끝단 와류 궤적을 실험값과 유사하게 예측할 수 있었다. 로터 소음의 방사특성을 확인하기 위해 로터 회전축을 중심으로 약 15R(30 m) 거리에 고도각 10° 간격으로 수음자를 배치하였다. Fig. 3은 블레이드의 피치각에 따른 overall sound pressure noise(OASPL)의 크기를 보여주고 있다. Fig. 3(a)에서는 하중 및 두께 소음을 포함한 로터 소음 결과를 나타내었으며, 개별 소음원이 전체 소음 발생에 미치는 기여도를 분석하기 위해 하중 소음과 두께 소음을 각각 Fig. 3(b)와 Fig. 3(c)에 나타내었다. Fig. 3(a)에서 피치각이 증가함에 따라 전체 로터 소음이 증가하는 것을 관찰하였고 이는 Fig. 3(b)에서 확인할 수 있듯이 하중 소음 증가가 주요 요인인 것으로 보인다. 피치각이 증가함에 따라 모든 마이크로폰 위치에서 소음의 크기가 점진적으로 증가하며, 이는 피치각이 증가함에 따라 추력이 증가하는 경향성과 일치한다. 블레이드에서 생성하는 추력이 증가할수록 블레이드에 작용하는 하중이 증가해 하중소음이 증가하기 때문이다. 특히, 소음 방사의 지향성은 사선 방향임을 확인할 수 있는데, 단일로터가 제자리 비행 조건에서는 비정상 하중보다는 정상 하중이 대부분 작용하여 이러한 결과가 도출되었다. Fig. 3(c)에서는 피치각에 따른 두께소음을 나타내며, 피치 각도의 변화에 따라 두께소음이 변화했지만 유의미한 큰 차이는 관찰되지 않았다. 하지만, 비교적 큰 반경과 코드 길이를 가지는 헬리콥터는 하중소음뿐만 아니라 두께소음도 높은 tip mach number로 인해 소음 기여도가 있음을 보여준다. Fig. 4에서는 Caradonna-Tung 로터 블레이드 해석만으로는 판단하기 어려웠던 소음 예측 코드의 두께 소음 예측 타당성을 추가로 확인하기 위해 로터 블레이드의 제원은 모두 동일하게 유지하되, 임의로 에어포일의 두께만 달리한 추가 해석을 진행하였다. 에어포일의 두께가 증가할수록 로터 회전면에 평행한 방향으로의 두께소음이 증가하는 것을 관찰하였고, 이로써 소음 예측 코드가 두께소음 또한 잘 예측하는 것을 확인하였다.

Fig. 3

OASPL comparison of Caradonna-Tung rotor depending on the pitch angles

Fig. 4

OASPL comparison of Caradonna-Tung rotor with different airfoils

4. 전진 비행 소음 해석

4.1 HART-Ⅱ 로터 블레이드 모델

전진 비행 중인 로터 블레이드의 공력소음 예측 정확도를 검증하기 위해 HART II(higher-harmonic aeroacoustic rotor test) 실험에 사용된 로터 모델을 이용하였다. HART II 실험은 higher harmonic control (HHC) 제어기법 적용에 따라 로터 공력 특성, blade vortex interaction(BVI) 소음 등을 분석하기 위해 2001년에 실시된 국제 공동 연구 프로그램이다⁽²¹⁾. HART II 로터는 BO105 무힌지 로터의 40 % mach scaled 축소 로터이며 Fig. 5와 같이 이 연구에서는 HHC 기법을 적용하지 않은 기준 조건(baseline)에 대해 해석을 수행하였다. 로터의 회전직경(D)은 2 m, 블레이드 시위길이는 0.121 m, 비틀림각 변화율은 -8°로 정의되며 형상에 대한 자세한 정보는 Table 3에 정리하였다. 또한 이 연구에서 고려한 해석 조건은 Table 4와 같다.

Fig. 5

Geometry of HART II rotor blade

Table 3

Blade geometry of HART II rotor

Table 4

Simulation conditions

4.2 전진 비행 중인 로터 공력해석 결과

전진비행하는 로터 블레이드는 회전운동에 따른 원심력 뿐만 아니라 방위각에 따른 양력 불균형으로 인해 주기적인 플랩핑 및 피칭 운동이 동반된다. 따라서, 실험에서 측정한 추력계수와 동일하게 일치시키고 로터의 회전축 이외의 다른 축에서 발생하는 공력 모멘트를 최소화하기 위해서는 전진 비행 시 수치적 트림 절차가 수행되어야 한다. 이 연구에서는 테일로터 및 전기체의 다른 요소는 제외하고 메인로터만 고려했으며, 이 경우에는 로터의 추력 F_z을 목표 추력으로 정하고 모멘트 M_x, M_y를 0이 되도록 하는 정상상태 수평 전진비행 트림이 일반적이다. M_z는 테일로터에 의해, F_x와 F_y는 로터 회전면의 기울기와 항공기 자세에 의해 트림 상태가 되기 때문이다. 그러므로 이 연구에서는 주어진 주 로터 추력과 허브에서의 모멘트를 이용하여 주 로터의 collective 피치각과 cyclic 피치각만을 계산하는 주 로터 트림을 수행하였다. 블레이드의 피칭 움직임은 식 (12)와 같이 표현할 수 있다.

$\[ \theta \left(\psi \right)={\theta }_0+{\theta }_{1c}\mathrm{c}\mathrm{o}\mathrm{s}\left(\psi \right)+{\theta }_{1s}\mathrm{s}\mathrm{i}\mathrm{n}\left(\psi \right) \]$

(12)

여기서 θ₀, θ_1c, θ_1s는 각각 collective 피치각, 종방향 및 횡방향에 따른 cyclic 피치각을 의미하며, Ψ는 블레이드가 회전하는 방위각을 뜻한다. θ₀는 추력의 크기를 결정하고, θ_1c와 θ_1s는 각각 롤링 모멘트와 피칭 모멘트를 제어한다. 또한, 특정한 속도로 전진 비행하는 로터의 추력 및 모멘트 계수는 식 (13)과 같이 피치각으로 표현된다.

$\[ \begin{array}{c}{C}_T=C_T\left({\theta }_0,{\theta }_{1c},{\theta }_{1s}\right)\\ C_{Mx}=C_{Mc}\left({\theta }_0,{\theta }_{1c},{\theta }_{1s}\right)\\ C_{My}=C_{My}\left({\theta }_0,{\theta }_{1c},{\theta }_{1s}\right)\end{array} \]$

(13)

여기서 C_T는 추력계수를 의미하고, C_Mx와 C_My는 각각 롤링과 피칭 모멘트를 나타낸다. 식 (13)의 비선형 방정식의 해를 구하기 위해 식 (14)의 Newton-Raphson 반복법을 적용하였으며⁽²²⁾, 피치각 계수 θ₀, θ_1c, θ_1s에 대한 C_T, C_Mx, C_My의 변화율은 유한차분 형태로 계산하였다.

$\[ \left(\begin{array}{c}\mathrm{\Delta }{\theta }_0\\ \mathrm{\Delta }{\theta }_{1c}\\ \mathrm{\Delta }{\theta }_{1s}\end{array}\right)={\left(\begin{array}{c}\frac{\partial C_T}{\partial {\theta }_0}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\frac{\partial C_T}{\partial {\theta }_{1c}}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\frac{\partial C_T}{\partial {\theta }_{1s}}\\ \frac{\partial C_{My}}{\partial {\theta }_0}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\frac{\partial C_{My}}{\partial {\theta }_{1c}}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\frac{\partial C_{My}}{\partial {\theta }_{1s}}\\ \frac{\partial C_{Mz}}{\partial {\theta }_0}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\frac{\partial C_{Mz}}{\partial {\theta }_{1c}}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\frac{\partial C_{Mz}}{\partial {\theta }_{1s}}\end{array}\right)}^{-1}\times \left(\begin{array}{c}{C}_T^{\mathrm{d}\mathrm{e}\mathrm{s}\mathrm{i}\mathrm{r}\mathrm{e}\mathrm{d} }-C_T\\ -C_{My}\\ -C_{Mz}\end{array}\right) \]$

(14)

이 연구에서는 로터의 피칭/롤링 모멘트 평형 및 풍동 실험과 동일한 추력계수를 얻기 위한 로터 트림해석을 수행하였다, HART II 실험을 대상으로 식 (14)에 있는 $$ C_T^{\mathrm{d}\mathrm{e}\mathrm{s}\mathrm{i}\mathrm{r}\mathrm{e}\mathrm{d} }$$의 값을 적용하였으며 초기 트림 계산에는 실험에 사용한 각을 적용하였다. 수치적인 트림 해석을 통해 도출된 collective, cyclic 피치각도는 Table 5에 정리하였다.

Table 5

Trim solution

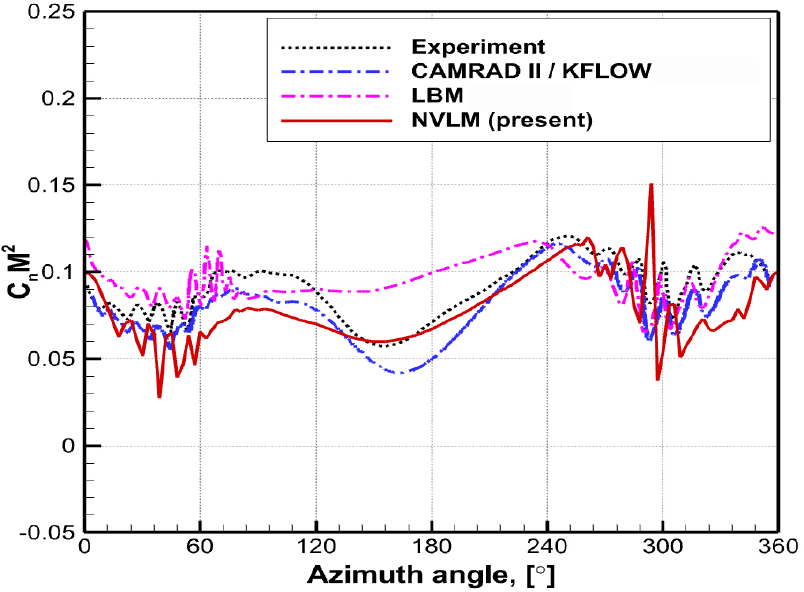
Fig. 6에서는 비선형 와류 격자법 통해 예측한 로터 블레이드 87 % 지점에서의 수직력 변화를 타 전산해석 결과, 실험 결과와 함께 비교하였다. 방위각 300° 부근에서는 과도한 수직력 변화가 발생하여 실험값과 잘 맞지 않는 경향성이 있지만 지배적인 소음원인 BVI 현상을 비교적 잘 예측할 수 있음을 확인하였다. 블레이드의 탄성을 고려한 CFD/CSD 연계해석 결과는 탄성을 고려하지 않은 비선형 와류 격자법 결과에 비해 실험치에 더욱 근접한 결과를 보여주고 있지만⁽²⁰⁾, 타 CFD 결과에 비해 회전 방위각에 따른 공기력 변화를 잘 예측하는 것을 확인하였다⁽²¹⁾.

Fig. 6

Comparison of section normal forces at the radial station of 87 %

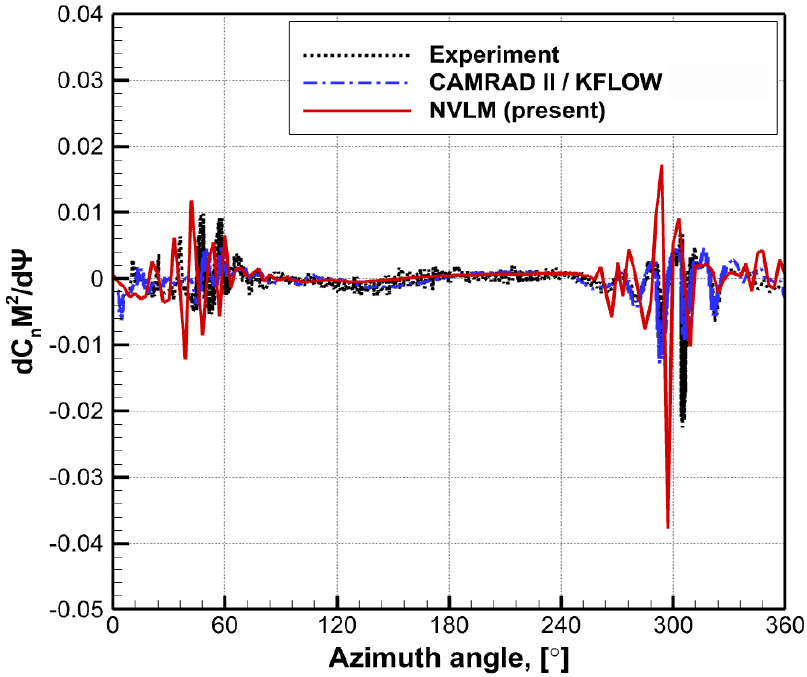
Fig. 7에는 방위각에 따른 단면 수직력의 변화를 나타내었다. 단면 수직력의 변화율은 소음의 특성을 이해하는 데에 유용하게 사용되며, 특히 BVI 소음의 물리적인 현상은 시간에 따른 단면 수직력의 변화율에 기인한다^(22,23). 첫 번째 peak는 전진면의 Ψ=60° 부근에서 관찰되며 실험값과 비교하였을 때 위상각 차이 없이 BVI 현상을 정확히 잘 예측하는 것을 볼 수 있다. 두 번째 peak는 후퇴면의 Ψ=300° 부근에서 관찰되며 실험값과 위상각 차이는 크게 발생하지 않지만 진폭이 크게 발생하는 것을 볼 수 있는데, 이는 앞선 Fig. 6의 4사분면 결과에서 비선형 와류 격자법 해석자가 수직력을 과도하게 예측한 것이 원인이다.

Fig. 7

Comparison of gradient of section normal force at radial station of 87 %

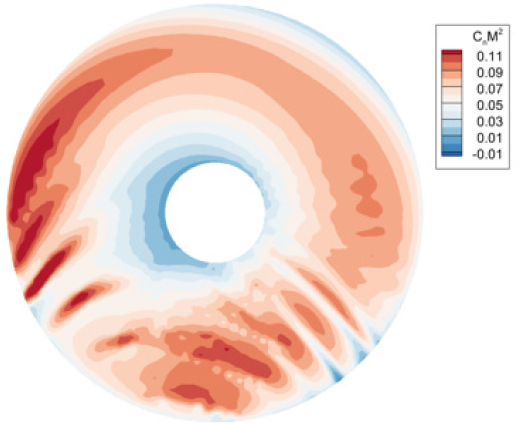
Fig. 8은 블레이드가 한 바퀴 회전하는 동안 블레이드에서 발생한 수직력 분포를 디스크 형태로 나타낸 것이다. HART II 실험에서는 블레이드 스팬 방향에 따른 단면 양력계수 데이터가 제공되지 않아 실험값과의 정량적인 비교는 수행할 수 없다⁽²⁴⁾. 하지만 로터의 전진면과 후퇴면에서 발생하는 BVI 모두를 잘 포착하는 것을 볼 수 있으며, 비선형 와류 격자법이 전진 비행 소음 해석을 위한 공력 해석자로 사용하기에 적합함을 확인하였다.

Fig. 8

Section normal force distribution

4.3 전진 비행 중인 로터 소음해석 결과

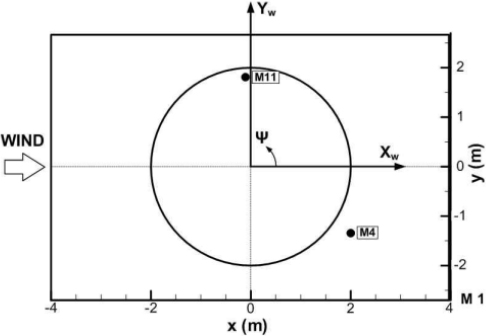
전진 비행 조건에서 로터 소음해석 결과를 검증하기 위해 이전의 블레이드 스팬방향의 공기력 변화를 이용하여 소음 해석한 결과는 Fig. 9에서 볼 수 있다. 실험에서 가장 큰 소음이 측정된 위치인 전진면의 11번 마이크 위치와 후퇴면의 4번 마이크 위치에 대해서 측정된 소음압을 블레이드 1회전 시간에 대해서 소음해석자 결과와 비교하였으며⁽¹⁸⁾, 실험에 사용된 마이크의 위치 좌표계는 Fig. 10에 나타내었다. 측정 결과에서 BVI 소음압 신호의 peak to peak 크기가 블레이드에 따라서 차이가 발생하는 것에서 볼 수 있는데 이는 블레이드의 비균질성 등으로 인한 실험 오차로 판단된다^(19,20). 실험 결과와 해석 결과 모두 BVI에 의한 4/rev의 주기적인 음압 변화가 관찰되며 특히 블레이드가 전진면에 위치하는 ψ=90°에서 크게 발생하게 된다. 해당 위치에서 실험값보다 다소 음압폭을 크게 예측하긴 하지만, 전반적인 경향성은 잘 포착하고 있으며 후퇴면 또한 실험값과 상당히 유사한 결과를 도출하였다.

Fig. 9

Comparison of acoustic pressure of HART II rotor

Fig. 10

Acoustic array and coordinate system of HART II test

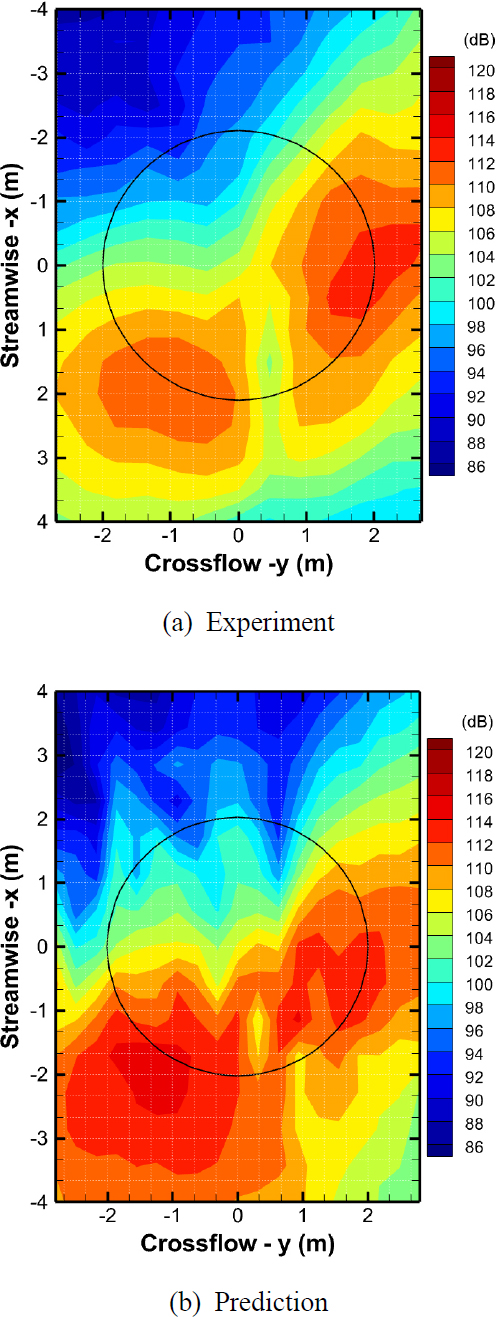
BVI 소음은 일반적으로 전체 소음 신호의 6 BPF ~ 40 BPF 대역의 주파수로 구성된다⁽²⁰⁾. 정확한 BVI 소음의 비교를 위해 모든 관측점의 소음압에 대해 FFT를 수행하여 6 BPF ~ 40 BPF 주파수 대역의 소음압 수준을 구하고, 로터 허브 기준 2.2 m 아래에 BVI 소음 방사 지도를 Fig. 11에 나타내었다. HART II 기준 비행 조건에서 측정된 BVI 소음 방사 지도와 해석 결과를 비교하였고, BVI 소음의 dB 수준 분포와 소음의 방향성을 살펴보았다. 실험 결과와 같이 소음 세기가 가장 높게 나타나는 두 lobe 지점은 잘 예측하는 모습을 보인다. 하지만, 실험값과 3 dB 내외의 오차 수준을 보이며 lobe 영역의 크기와 형태에 있어서도 약간의 차이가 발생하는데 이는 이 연구에서 헬리콥터의 동체와 블레이드의 탄성을 고려하지 않은 것으로 판단된다^(21,25). Romani and Casalino가 수행한 연구에서는 탄성변형을 반영한 로터 모델링이 전반적인 소음의 방향성과 전진면에서의 소음 lobe를 잘 포착하였으며⁽²¹⁾, BVI 소음 예측의 정확도 또한 향상시킨다는 결과를 제시하였다. 또한 Bernardini et al. 연구에서는 탄성 효과를 고려한 로터 블레이드 모델에 비해 semi-rigid 모델이 소음 수준과 방사 형태를 다소 부정확하게 예측하였다⁽²⁵⁾.

Fig. 11

Comparison of noise footprint between experiment and prediction

5. 결 론

이 연구에서는 저소음 로터 블레이드 플랜폼 설계를 위해 FW-H 방정식 기반의 소음 해석 코드를 개발하고 실험 결과와 비교하였다. 로터 블레이드 공력소음 해석을 위해 필요한 공력데이터는 비선형 와류격자법을 이용하여 예측하였고, 제자리 비행 중인 Caradonna-Tung 단일 로터와 전진 비행 중인 HART-II 단일 로터를 이용하여 개발된 소음 해석자에 대한 검증 연구를 수행하였다.

제자리 비행 중인 로터의 소음해석 결과는 하중소음과 두께소음, 전체소음으로 나누어 분석하였다. 블레이드의 피치각이 증가함에 따라 모든 마이크로폰 위치에서 하중 소음의 크기가 점진적으로 증가하였으나 두께소음에 미치는 영향은 미미하였다. 하지만, 비교적 큰 반경과 코드 길이를 가지는 헬리콥터는 하중소음 뿐만 아니라 두께소음도 지배적인 소음원으로 작용함을 확인하였다. 전진비행 중인 로터의 공력해석 검증을 위해 블레이드 span 87 % 지점의 공력하중과 시간에 따른 단면수직력 변화를 해석한 결과, 실험값과 굉장히 유사한 경향성이 도출되었으며 1사분면과 4사분면의 BVI 현상을 잘 예측하는 것을 확인하였다. 블레이드 스팬 방향의 공기력 변화를 이용하여 1회전 시간에 대한 전진면과 후퇴면에서의 BVI 소음압 신호의 peak-to-peak 크기를 실험값과 비교한 결과, 음압 진폭의 크기는 다소 실험값과 차이가 있지만 전반적인 경향성은 잘 포착하였다. 소음 방사 지도 작성 결과 또한 최대 BVI 소음이 발생하는 위치를 실험 결과와 거의 유사하게 예측하였다.

이 연구에서는 비투과면 기반의 FW-H 방정식을 이용하여 제자리 및 전진 비행 공력소음 예측 연구를 수행하였다. 하지만 투과면 기법까지 고려하게 된다면 CFD가 제공하는 데이터의 양이나 질에 따라 소음 해석코드를 범용적으로 사용할 수 있을 것으로 예상된다. 또한, 로터-로터, 로터-기체, 로터-동체 등 상호작용으로 인해 발생하는 난류 소음 성분을 추가로 예측할 수 있으며, 이는 전기체 헬리콥터 형상에서 발생하는 소음이나 다양한 형태의 로터 추진 시스템을 가진 도심항공모빌리티(urban air mobility)에도 널리 활용할 수 있을 것으로 기대된다. 따라서 향후 연구에는 투과면 기반의 FW-H 음향상사법도 추가로 고려하여 코드를 확장시킬 것이며, 궁극적으로 이 논문의 소음 해석 기법을 통해서 향후 저소음 블레이드 제작 시 초기 설계 단계에서부터 로터 블레이드의 소음을 빠르게 예측할 수 있는 기술을 개발하는 것이 최종 목표이다. 이는 로터 블레이드 형상 설계 연구와 저소음 블레이드 소음 특성 분석 연구에 널리 활용될 것으로 기대된다.

Acknowledgments

이 연구는 정부(방위사업청)의 재원으로 국방기술진흥연구소의 핵심기술 과제인 ‘저소음 블레이드 플랜폼 설계 기술’ 과제의 일환으로 수행되었습니다. 지원에 감사드립니다(No. 18-202-805-051).

References

• Green Korea, 2008, Reports on the Impact of the Noise from Military Airfields and Shooting Ranges on Affected Residents, Green Korea, Seoul, Korea.
• Brentner, K. S. and Farassat, F., 2003, Modeling Aerodynamically Generated Sound of Helicopter Rotors, Progress in Aerospace Sciences, Vol. 39, No. 2~3, pp. 83~120. [https://doi.org/10.1016/S0376-0421(02)00068-4]
• Edwards, B., Cox, C. and Booth, E. R. Jr., 2002, Revolutionary Concepts for Helicopter Noise Reduction: SILENT Program, NASA Langley Research Center, Report No. Rept-699-099-529, VA, United States.
• Brentner, K. S., Bres, G. A., Perez, G. and Jones, H. E., 2002, Maneuvering Rotorcraft Noise Prediction: A New Code for a New Problem, AHS Aerodynamics, Acoustics and Test Evaluation Specialist Meeting, CA, United States.
• Brès, G. A., Brentner, K. S., Perez, G. and Jones, H. E., 2004, Maneuvering Rotorcraft Noise Prediction, Journal of Sound and Vibration, Vol. 275, No. 3-5, pp. 719~738. [https://doi.org/10.1016/j.jsv.2003.07.005]
• Yücekayalı, A., Şenipek, M., Ortakaya, Y. and Özyörük, Y., 2018, TACO: Helicopter Noise Predictions, The 7th Asian/Australian Rotorcraft Forum, Jeju, Korea.
• Spiegel, P. and Rahier, G., 1991, Theoretical Study and Prediction of BVI Noise Including Close Interactions, AHS International Specialists’ Meeting on Rotorcraft Acoustics and Fluid Dynamics, PA, United States.
• Polacsek, C., Zibi, J. and Costes, M., 1993, Helicopter Rotor Noise Predictions using 3D Computed Aerodynamic Data for Different Blade Geometries, Proceedings of the 19th European Rotorcraft Forum, Paper No. B3, Cernobbio, Italy.
• Schultz, K.-J. and Splettstoesser, W. R., 1987, Prediction of Helicopter Rotor Impulsive Noise using Measured Blade Pressures, Proceedings of the 43rd Annual Forum of the AHS, MO, United States. pp. 405~420.
• Schultz, K. J. and Splettstoesser, W. R., 1987, Measured and Predicted Impulsive Noise Directivity Characteristics, The 13th European Rotorcraft Forum, Arles, France.
• Hwang, C. and Joo, G., 2003, Parametric Study for the Low BVI Noise Rotor Blade Design, KSAS International Journal, Vol. 4, No. 1, pp. 88~98. [https://doi.org/10.5139/IJASS.2003.4.1.088]
• Lee, H. and Lee, D.-J., 2019, Prediction of Aerodynamic Noise Radiated from a Small Multicopter Unmanned Aerial Vehicle using Acoustic Analogy, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 29, No. 4, pp. 518~526. [https://doi.org/10.5050/KSNVE.2019.29.4.518]
• Lee, H. and Lee, D.-J., 2020, Rotor Interactional Effects on Aerodynamic and Noise Characteristics of a Small Multirotor Unmanned Aerial Vehicle, Physics of Fluids, Vol. 32, No. 4, 047107. [https://doi.org/10.1063/5.0003992]
• Lee, H., Sengupta, B., Araghizadeh, M. S. and Myong, R. S., 2022, Review of Vortex Methods for Rotor Aerodynamics and Wake Dynamics, Advances in Aerodynamics, Vol. 4, No. 20. [https://doi.org/10.1186/s42774-022-00111-3]
• Katz, J. and Plotkin, A., 2001, Low-speed Aerodynamics, Second Edition, Cambridge University Press, Cambridge, United Kingdom. [https://doi.org/10.1017/CBO9780511810329]
• Lee, S.-L., Jeong, I., Cho, H., Kang, W.-R. and Lee, H., 2024, Development of Aeroelastic Analysis Code for Rotor Blade using Coupled Nonlinear Vortex Lattice Method and Geometrically Exact Beam Theory, Journal of the Korean Society for Aeronautical and Space Sciences, Vol. 52, No. 1, pp. 25~35. [https://doi.org/10.5139/JKSAS.2024.52.1.25]
• Chung, K., Hwang, C. and Lee, D. J., 2006, Helicopter BVI Noise Prediction using Acoustic Analogy and High Resolution Airloads of Time Marching Free Wake Method, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 16, No. 3, pp. 291~297. [https://doi.org/10.5050/KSNVN.2006.16.3.291]
• van der Wall, B. G. and Burley, C. L., 2005, 2nd HHC Aeroacoustic Rotor Test(HART II) Part II: Representative Results, German Aerospace Center, DLR-IB 111-2005/03, Köln, Germany.
• Chung, K., Hwang, C., Park, Y., Jeon, W. and Lee, D., 2005, Numerical Predictions of Rotorcraft Unsteady Air-loadings and BVI Noise by using a Time-marching Free-wake and Acoustic Analogy, Proceedings of the KSAS Annual Autumn Conference, pp. 1071~1075.
• You, Y. and Jung, S. N., 2015, Validation of Rotor Aeroacoustic Noise in Hovering and Low Speed Descent Flight, Journal of the Korean Society for Aeronautical and Space Sciences, Vol. 43, No. 6, pp. 516~525. [https://doi.org/10.5139/JKSAS.2015.43.6.516]
• Romani, G. and Casalino, D., 2019, Rotorcraft Blade-vortex Interaction Noise Prediction using the Lattice-Boltzmann Method, Aerospace Science and Technology, Vol. 88, pp. 147~157. [https://doi.org/10.1016/j.ast.2019.03.029]
• Jung, S. N., Sa, J. H., You, Y. H., Park, J. S. and Park, S. H., 2013, Loose Fluid-structure Coupled Approach for a Rotor in Descent Incorporating Fuselage Effects, Journal of Aircraft, Vol. 50, No. 4, pp. 1016~1026. [https://doi.org/10.2514/1.C031826]
• Schneider, O. and van der Wall, B. G., 2007, Comparison of Simple and Conditional Averaging Methodology based on Results of the HART II Wind Tunnel Test, The 1st International Forum on Rotorcraft Multidisciplinary Technology, Seoul, Korea.
• van der Wall, B. G. and Yin, J., 2013, A Semi-empirical Approach to Simulate the Effects of Higher Harmonic Rotor Blade Control using Prescribed Wake, Advances in Applied Acoustics, Vol. 2, No. 2, pp. 45~60.
• Bernardini, G., Serafini, J., Lanniello, S. and Gennaretti, M., 2007, Assessment of Computational Models for the Effect of Aeroelasticity on BVI Noise Prediction, International Journal of Aeroacoustics, Vol. 6, No. 3, pp. 199~222. [https://doi.org/10.1260/147547207782419570]