완전 압축 상태의 코일 스프링 완충기의 비선형 특성 해석
Ⓒ The Korean Society for Noise and Vibration Engineering
Abstract
This study analyzed the nonlinear dynamic behavior of a cylindrical coil spring under full compression. While previous research has primarily focused on the linear characteristics of springs, this study considers the nonlinear response arising from interwire friction and contact. To achieve this, the Rayleigh energy method is applied to theoretically derive the dynamic characteristics of a spring-mass system, and the results are validated through experimental analysis. The experiments include stiffness measurement using a universal testing machine and dynamic response analysis employing a laser Doppler vibrometer and accelerometers. Time-frequency analysis is conducted under single and multiple impact conditions using short-time and fast Fourier transform to quantitatively evaluate the dynamic behavior of the spring. The findings of this study are expected to contribute to the design of spring-based isolators in defense applications and the evaluation of operational characteristics in extreme environments.
Keywords:
Nonlinear Dynamics, Coil Spring, Time-frequency Analysis, Contact Mechanics, Vibration Isolator키워드:
비선형 동역학, 코일 스프링, 시간-주파수 분석, 접촉 역학, 진동 아이솔레이터1. 서 론
원통형 코일(coil) 스프링은 소형 모터에서부터 대형 차량 등, 여러 산업분야에서 널리 사용되는 중요한 기계적 구성 부품이고, 특히 국방분야에서는 진동을 줄이기 위해 아이솔레이터(isolator)로써 많은 부분에 적용되는 기본 기계부품이다(1). 이러한 스프링의 동적 특성 및 진동특성은 구조적 설계와 더불어 외부적 압력에 영향을 받는다. 기존 연구에서는 스프링의 선형적 변화 또는 압축률에 따른 특성 분석 등 만을 고려하였다(2). 선형 스프링 시스템의 기계적 특성을 구하기 위해 후크(hook)의 법칙과 월(Wahl)의 스프링 이론을 통해 일반적인 코일 스프링의 매개변수와 기계적 특성을 공식화했다(3). 그러나 코일 스프링은 정적 하중 조건 외에도 급격한 충격이나 고주파와 동적 조건에 종종 노출되는데, 이런 조건들에 노출될 시, 기존 후크의 법칙에서 벗어나 비선형적 특성이 나타나게 된다(4,5). 이로 인해 높은 값의 응력변화를 수반해 균열과 스프링 내 파손으로 이뤄진다(6~9). 이렇듯 완전 압축된 코일 스프링의 동적 응답은 기존의 선형 스프링 해석 및 분석으로는 파악이 어렵다. 이는 이 영역이 실제 운영 중에 발생하는 구간이 아닌 사고성으로 발생되기 때문이다. 그러나 국방 분야의 경우 거친 환경에서 다양한 기계 시스템이 운영되기 때문에 이러한 완전 압축단계를 넘어서는 경우도 발생하곤 한다.
실제 스프링의 거동은 불균일한 스프링의 끝단, 가변 스프링 피치 및 스프링이 완전히 압축되는 상황일 시 와이어간 접촉 마찰로 인해 비선형적 거동이 발생한다(10). 특히 스프링이 완전히 압축되는 경우 코일 간 접촉으로 인한 응력 증가가 발생하는 현상이 나타나며, 주기적 하중이 가해질 경우 반복적인 접촉과 비접촉이 발생해 동적 거동에 중요한 영향을 끼친다. 그러므로, 코일 스프링을 완전 압축현상에서 정밀하게 분석하기 위해서는 비선형적인 힘-변위 관계 및 시간적 변화에 따른 특성변화를 포함한 새로운 분석 방법이 필요하다. 스프링의 와이어간 충돌로 발생하는 동적 응답을 분석하여 단순 강성 계수 기반 설계이 아닌 시간에 따른 동적 특성을 포함한 실질적인 코일 스프링의 동적 거동을 설계할 필요가 있다.
이에 이 연구에서는 기존 연구에서 분석한 코일 스프링의 축하중에 따른 선형적 변화가 아닌 완전압축시 마찰에 의해 발생하는 비선형적 특성에서 진동특성 해석을 수행한다. 이를 위해 일반적인 국방 환경과 같은 저주파 입력특성에 대한 코일 스프링의 변위 및 압축 특성을 확인할 수 있는 실험 셋업을 구축한다. 또한 기본 예압 크기에 따른 완전 압축 코일 스프링의 비선형 특성 변화분석을 수행하고자 한다.
2. 스프링 시스템 설계
2.1 스프링 주파수 설계
에너지 보존법칙을 기반으로 한 Rayleigh energy 방법론을 통해서 식 (1)과 같이 미소영역에서 스프링 -질량(spring-mass) 시스템의 총 에너지는 전체 질량에 의한 운동 에너지와 스프링의 운동에 의한 운동 에너지로 나뉜다. 스프링의 전체 높이를 l, 스프링 질량을 ms, 스프링-질량시스템의 총 질량을 m, 단위 길이당 질량은 ms/l이다. 위치 x에서의 변위를 y라 정의하면 스프링의 운동에너지 미소질량은 식 (1)과 같다(10).
| (1) |
스프링의 각 부분은 고정된 끝을 기준으로 진동하므로 길이 y에 대한 요소의 속도는 식 (2)와 같다.
| (2) |
따라서 해당 미소 요소의 운동에너지는 식 (3)과 같다.
| (3) |
이를 y에 대해 적분하면
| (4) |
정적분을 수행 시 스프링의 운동에너지는 식 (5)와 같다.
| (5) |
시스템의 총 에너지는 스프링-질량 시스템의 총 질량 m에 의한 운동 에너지과 스프링 운동에너지의 합으로 표현된다.
| (6) |
이를 등가질량 meq으로 정의할 시 스프링-질량 시스템의 총 질량과 스프링 질량의 1/3의 합으로 표현된다. 이를 스프링의 물리적 특성에 대입하면, 코일 스프링 시스템의 진동수는 식 (7)과 같이 표현할 수 있다(11,12).
| (7) |
여기서 d는 와이어의 직경, R은 스프링 반경, N은 코일의 감은 수, G는 전단계수, g는 중력 가속도이며 ρ는 재료의 밀도를 나타낸다. 식 (7)은 재료 특성과 기하학적 파라미터를 통해 스프링의 고유진동수를 효율적으로 예측할 수 있다(13,14).
3. 실 험
3.1 스프링 강성 실험
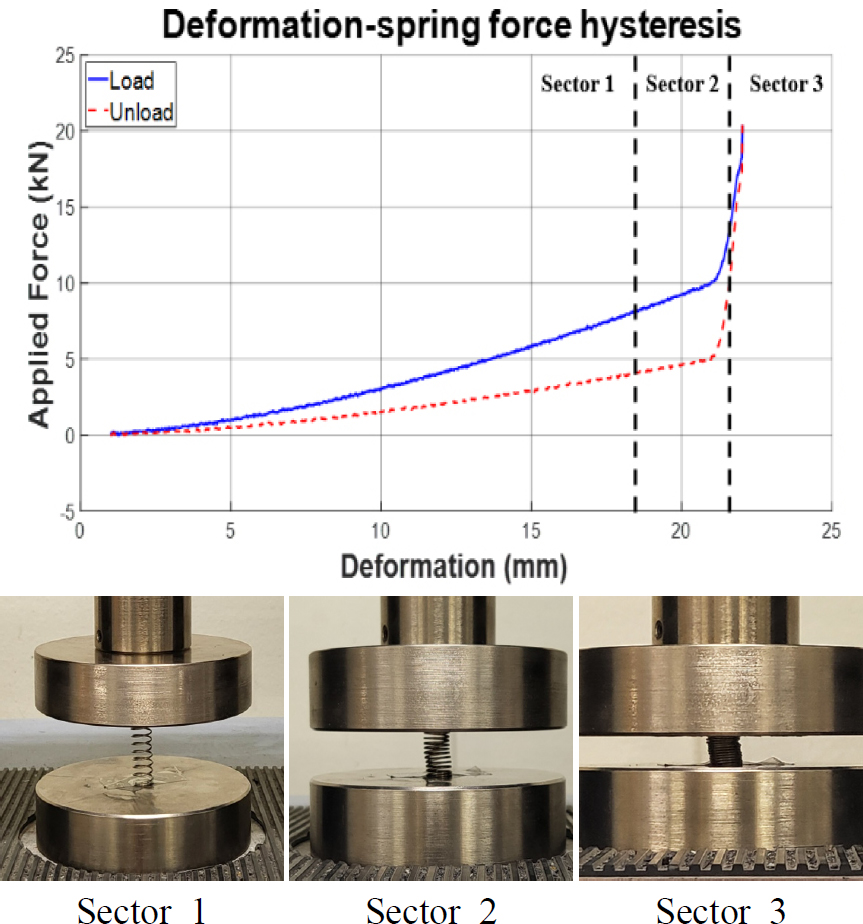
스프링의 강성 k를 측정하기 위해 Fig. 1과 같은 universal testing machine을 사용하여 스프링 압축실험을 수행하였다. 실험에서 사용된 스프링은 강철 d=1 mm인 강철 와이어로 만들어졌으며 압축 전 자유 높이는 H=38 mm, 감긴 코일 수 N=10으로 스프링 질량 ms=1.6 g이다.
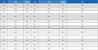
스프링 압축 길이당 필요한 압력을 분석하여 스프링 강성을 계산하였다. Fig. 2와 Table 1은 스프링 압축 시 각 sector 별 스프링 압축 길이와 압력 간의 관계를 나타낸다. Sector 1에서는 스프링이 완전 압축에 도달하기 전 상태로, 이 구간의 평균 스프링 강성 k는 452 N/m로 일정한 값을 유지하며 압축 길이와 압력 간 관계는 선형적인 비례관계로 관측되었다. Sector 2는 스프링이 완전압축되기 시작해 와이어간 접촉이 시작되어 이때 와이어간 거리 h가 0에 가까워지는 상태이다. 스프링 내부에서 와이어간 접촉 마찰력에 의해 저항력이 발생하여 강성 그래프는 비선형적 형태로 변형되었다. 이로 인해 스프링 강성은 1733 N/m로 크게 증가하였다. Sector 3은 스프링에 완전 압축에 필요한 압력 이상의 힘을 가해 좌굴 상태에 도달하는 구간으로, 이 시점에서 스프링의 기하학적 특성 변화로 인해 비선형적 거동이 더욱 두드러지게 나타나, 스프링의 강성은 12 276 N/m로 크게 증가하는 형태를 보인다.
3.2 스프링 압축 실험
하단의 Fig. 3과 Fig. 4는 스프링의 동적 특성 및 압축 거동을 분석하기 위한 실험장치와 거동방식을 나타낸다. 하부 프레임을 통해 스프링 하단을 고정시켰고, 양 옆의 알루미늄 가이드 레일은 알루미늄 판과 철제 리니어 가이드를 사용하였고, 두 개의 가이드 레일과 가이드 블록을 통해 스프링의 거동을 수직으로 제한하였다. 스프링 상부에는 블록 고정부와 센서 부착부 및 충격 전달을 위한 충격판을 설계하여 고정하였다. 특별히 설계된 충격판이 레일을 따라 거동하여 스프링이 수직 축으로 압축시키게 하여 안정적인 압축이 가능케 하였다. 스프링의 압축 특성을 파악하기 위해 각 0 N, 4.9 N, 9.8 N의 사전 하중을 적용하고 솔레노이드 액추에이터를 통해 충격을 적용했다. 솔레노이드와 충격판간 높이를 각각 2 mm, 6 mm, 12 mm로 조정하여 스프링에 가해지는 힘의 적용시간을 제어해 응답 과정을 분석하고 충격이 가해질 시 스프링의 진동 및 변형 특성을 파악했다. 정확한 스프링의 진동특성을 얻기 위해 레이저 도플러 속도계(LDV)와 고속 카메라, 가속도 센서를 활용하였다. Polytec OFV-534와 NLV-2500 컨트롤러를 사용하여 레이저를 통해 속도-시간 데이터를 측정 하고 스프링의 동적 응답을 정밀하게 분석했다. 또한 고속카메라인 Phantom VEO 410L을 사용하여 스프링의 빠른 변형 및 진동을 시각적으로 분석 및 실험 시 발생하는 모든 동적 현상을 측정하였다. 또한 스프링 진동 특성을 정확하게 파악하기 위해 PCB 356B21 3축 가속도계를 사용했다. 스프링 진동을 3차원으로 측정해 스프링의 진폭을 각 축간 독립적으로 기록해 스프링의 동적 특성을 종합적으로 분석하였다. 측정한 데이터를 기반으로 주파수 응답함수를 계산하여 동적 특성을 분석하였다(15).
실험은 단일 충격을 가한 상태에서 스프링의 압축에 따른 동적 분석을 진행하였다. 솔레노이드 높이를 제어하여 이를 통해 50 % 압축(12 mm offset), 99 % 압축(6 mm offset) 좌굴 상태(2 mm offset)을 분석하였다. 또한 동일 조건에서 다중 입력을 가해 단시간 푸리에 변환(STFT)을 이용한 시간-주파수 분석을 통해 동적 거동을 상세히 분석하였다. STFT의 수식 표현은 식 (8)과 같다.
| (8) |
여기서 t, f, T, τ, H, ω는 각 변환 후 시간 인덱스, 변환 후 주파수 인덱스, 변환 전 시간 인덱스, 센서신호, 윈도우 이동 간격 및 윈도우 함수이다. 시간 -주파수 영역의 스펙트럼을 측정할 시 정확한 신호 탐지와 파라미터 값의 추정을 위해 시간 및 주파수 해상도가 중요한 역할을 한다(16). 따라서 측정시간에서 지배적으로 나타내는 주파수 성분을 분석하는 FFT(고속 푸리에 변환)와 동시에 시간에 따른 주파수 성분을 실시간으로 분석하고 각 시간-주파수 영역에서 동적 거동을 세밀하게 파악할 수 있는 STFT를 사용하여 각 시간에 따른 주파수 변화를 분석하지 못하는 FFT를 보완하였다(17). STFT를 통해 윈도우 길이를 최적화하여 급격한 변화가 포함된 신호에서 순간적인 주파수 성분을 정확하게 파악 가능하다. 실험 후, FFT(고속 푸리에 변환)를 통해 동적 해석을 수행하여 전체적인 스프링 응답을 주파수 도메인에서 확인하였다(18,19).
4. 결 과
4.1 충격 단일 입력 결과
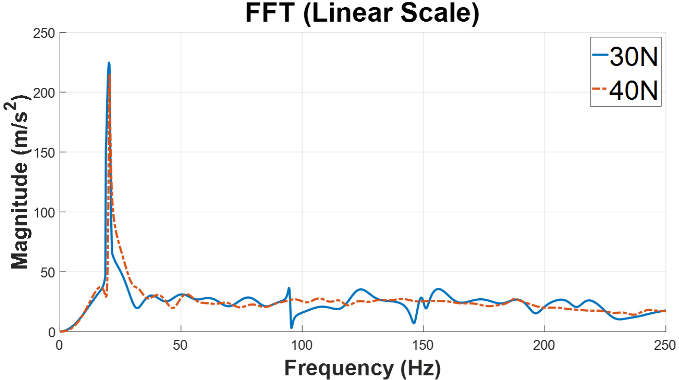
스프링 예압에 따른 주파수 변화에 대한 실험은 3축 가속도 센서가 부착된 충격판에 임팩트 해머를 통해 충격을 가하고 데이터를 측정함으로써 수행되었 다. 사용된 스프링 시스템과 스프링의 제원은 다음과 같다. 시스템의 전체 질량은 27 g, 스프링 질량은 1.6 g, 스프링 전체 길이는 38 mm이며 스프링의 외경은 10.0 mm, 와이어의 지름은 1.0 mm이다. 스프링의 선형 강성은 452 N/m로 측정하였다. 예압이 없는 상태에서의 스프링의 동적 응답을 측정한 후, 일정한 충격을 가해 고유주파수 변화를 관찰하였다. Fig. 4는 각 30 N, 40 N의 단일 충격을 가한 후, 가속도 센서를 통해 진폭을 측정하여 FFT를 통해 고유주파수를 측정하였다. 이를 통해 단일 충격 입력 시 힘의 크기에 상관없이 스프링의 완전 압축으로 인해 비선 형적 거동이 발생하지 않는 이상 거의 동일한 고유주파수를 관측가능한 사실을 확인할 수 있다.
이는 비선형적 거동 없이 선형 영역에서 작동하여 스프링 강성의 변화가 거의 발생하지 않았음으로 해석된다. 실험 결과 스프링의 고유주파수는 20.25 Hz 로 이론 값인 20.4 Hz와 결과간 차이가 1 % 미만으로 나타났다. 이는 이 연구의 측정 시스템과 해석 방법이 정밀하게 작동했음을 알 수 있다.
4.2 충격 다중 입력 STFT 측정 결과
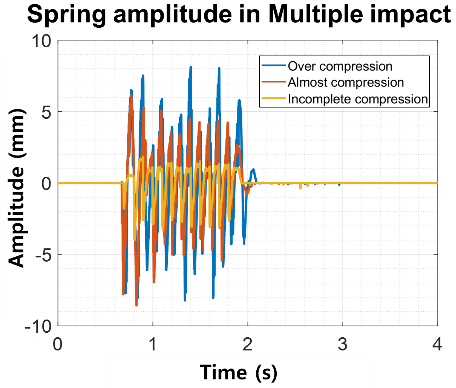
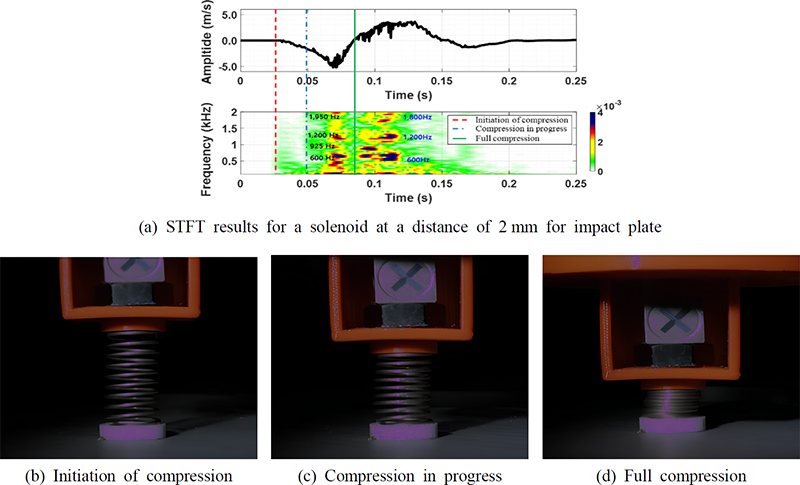
스프링에 다중 충격을 가할 시, 스프링은 Fig. 5와 같이 진동한다. Fig. 6 ~ Fig. 8은 레이저 도플러 속도 계(LDV)를 이용하여 측정한 데이터를 STFT로 분석한 결과를 나타낸다. 이 실험에서는 솔레노이드 액추에이터를 통해 30 N의 일정한 충격을 가했다. 또한 사전 예압 대신 impact plate와 액추에이터 간 거리를 각 2 mm(over compression), 6 mm(almost compression), 12 mm(incomplete compression)로 조정하여 스프링의 압축 변위를 조정하였다.
Fig. 6은 충격판과 솔레노이드 액추에이터 간 거리를 2 mm로 설정하여 스프링의 와이어간 거리 h=0에 도달하는 완전압축에서 추가로 압력을 가해 좌굴이 발생하도록 조절하였다. 이 실험에서는 과도한 압력으로 인한 스프링의 와이어간 마찰과 스프링의 좌굴이 발생하여 변위 진폭이 증가하고, 비선형적 강성 증가로 인해 주파수 응답이 변화했다. 스프링이 완전 압축되는 0.05 s 구간에서 1960 Hz로 고주파수 응답이 관찰되었다. 또한 0.1 s구간은 와이어간 마찰이 스프링 상부에서부터 발생하면서 600 Hz ~ 1800 Hz으로 주파수 증답이 증가하였다. 이로써 와이어간 비선형적 스프링 좌굴 현상으로 인한 비선형적 거동이 주파수 응답에 큰 영향을 미친 것을 확인 할 수 있다.
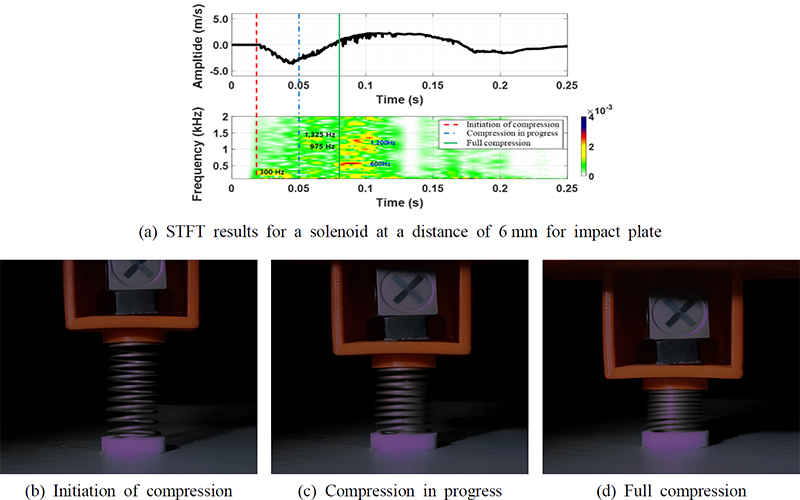
Fig. 7은 충격판과 솔레노이드 액추에이터간 거리를 6 mm로 설정하여 스프링이 99 % 압축하도록 조정하였다. 충격이 가해지는 0.02 s ~ 0.03 s 구간에서 충격으로 인한 주파수 성분이 발생했으며, 스프링이 충격에 의한 압축이 종료되는 0.1 s 구간에서는 상단부에서 와이어간 접촉으로 인한 마찰이 발생해 주파수 성분이 600 Hz에서 1325 Hz로 확장한 것을 확인할 수 있다.
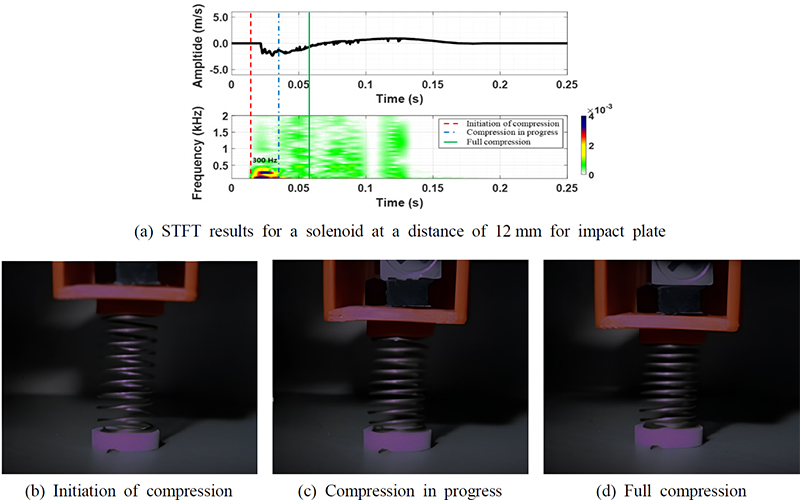
Fig. 8은 충격판과 솔레노이드 액추에이터 간 거리 를 12 mm로 설정하여 스프링이 50 % 압축하도록 조정하였다. 충격이 가해지는 0.02 s ~ 0.03 s 구간에서 충격으로 인한 주파수 성분이 발생했지만, 와이어간 접촉이 발생하지 않아 이후 주파수 응답은 전반적으로 안정적인 선형적 특성을 일정하게 유지하였다.
5. 결 론
이 논문에서는 코일 스프링에 충격이 적용되었을 때의 진동 특성과 동적 특성을 해석함으로써 스프링의 비선형 거동을 분석하는 데 주안점을 두었다. 특히, 스프링 주파수 설계를 기반으로 한 이론적 접근, FRF와 FFT를 활용한 실험적 접근을 통해 스프링의 고유진동수를 계산하고, 이를 비교함으로써 각 방법론의 정확성을 검증하였다. 특히, 실험값인 이론적 공식으로 도출한 값의 오차율이 1 % 미만으로 높은 일치로 스프링의 기계적 거동을 정확히 반영하여 실험에 충분한 설계를 구축하였다. 실험적 접근은 예압 상태에서의 코일 스프링의 고유진동수 및 동적 응답과 스프링 압축 상태에 따른 동적 응답을 분석하는 데 중점을 두었다. FRF와 FFT를 활용하여 스프링이 다양한 압축 조건에서 나타내는 응답을 정량적으로 측정하였으며, 실험 결과는 이론적 계산과 잘 부합하였다. 특히, 스프링이 압축되어 와이어간 접촉이 발생하는 것을 넘어 과도한 압력을 받아 좌굴이 발생하여 급격한 구조적 변형과 충돌로 인한 비선형 응력 변화에 기인하여 고주파수 진동 성분이 뚜렷하게 나타났다. 이를 시간-주파수 분석(time-frequency analysis)을 통해 정밀하게 분석해 기존 스프링의 고유진동수가 비선형적으로 변화하는 특정 조건에서의 동적 특성을 이해하는데 중요한 역할을 하였다. 스프링의 압축 정도에 따른 동적 특성을 분석하기 위해 경미한 압축 상태, 거의 압축된 상태, 좌굴 상태를 포함한 세 가지 조건에서 실험을 수행하였다. 이 과정에서 단일 입력 및 다중 입력을 적용하여 스프링의 동적 응답을 측정하였으며, STFT(short-time Fourier transform)를 통해 시간 데이터에 기반한 주파수 분석을 수행해 스프링의 압축 정도에 따른 스프링의 진동 특성이 어떻게 변하는지를 구체적으로 보여주었다. 이런 고주파수 진동은 좌굴하면서 발생하는 급격한 기하학적 변형과 와이어들 간 충돌 및 마찰 현상에 의해 유발되며 기존 선형 모델로는 설명할 수 없는 비선형 동적 거동의 중요한 특징을 확인할 수 있었다. 이를 통해 스프링의 동적 응답에 내재한 비선형성을 보다 심도 있게 규명할 수 있었다.
결론적으로, 이 논문에서는 스프링의 동적 및 진동 특성을 이해하는 데 있어 이론적 접근과 실험 적 접근법의 상호 보완적 가치를 입증했다. 이번 결과는 스프링 설계 및 분석에 있어 예압 상태에서의 비선형 거동과 진동수 변화를 정량적으로 이해하는데 기여할 것으로 기대된다.
Acknowledgments
이 연구는 LIG 넥스원 지원을 받아 수행된 연구임(202207470001).
References
- Lee, J., Kim, S., Heo, S.-J. and Thompson, D. J., 2000, Vibration Analysis of a Coil Spring by using Dynamic Stiffness Method, Proceedings of the KSNVE Annual Conference, pp. 1933~1938.
-
Hamza, A., Ayadi, S. and Hadj-Taïeb, E., 2013, The Natural Frequencies of Waves in Helical Springs, Comptes Rendus Mécanique, Vol. 341, No. 9-10, pp. 672~686.
[https://doi.org/10.1016/j.crme.2013.09.006]

-
Zhao, J., Gu, Z., Yang, Q., Shao, J. and Hou, X., 2023, Dynamic Finite Element Model based on Timoshenko Beam Theory for Simulating High-speed Nonlinear Helical Springs, Sensors, Vol. 23, No. 7, 3737.
[https://doi.org/10.3390/s23073737]

-
Kato, H. and Suzuki, H., 2021, Nonlinear Deflection Analysis of Helical Spring in Elastic-perfect Plastic Material: Application to the Plastic Extension of Piano Wire Spring, Mechanics of Materials, Vol. 160, 103971.
[https://doi.org/10.1016/j.mechmat.2021.103971]

-
Frikha, A., Treyssède, F. and Cartraud, P., 2011, Effect of Axial Load on the Propagation of Elastic Waves in Helical Beams, Wave Motion, Vol. 48, No. 1, pp. 83~92.
[https://doi.org/10.1016/j.wavemoti.2010.08.001]

-
Gu, Z., Hou, X., Keating, E. and Ye, J., 2020, Non-linear Finite Element Model for Dynamic Analysis of High-speed Valve Train and Coil Collisions, International Journal of Mechanical Sciences, Vol. 173, 105476.
[https://doi.org/10.1016/j.ijmecsci.2020.105476]

-
Gu, Z., Hou, X. and Ye, J., 2021, Advanced Static and Dynamic Analysis Method for Helical Springs of Non-linear Geometries, Journal of Sound and Vibration, Vol. 513, 116414.
[https://doi.org/10.1016/j.jsv.2021.116414]

-
Arslan, E. and Genel, K., 2023, Failure Analysis of Automotive Helical Spring, Engineering Failure Analysis, Vol. 153, 107569.
[https://doi.org/10.1016/j.engfailanal.2023.107569]

-
Kobelev, V., 2018, Durability of Springs, 1st Edition, Ch. 9, Failure Probability of Helical Spring, Springer, Cham, Switzerland, pp. 215~227.
[https://doi.org/10.1007/978-3-319-58478-2_9]

-
Burns, S. J., 2011, The Relation between Helical Spring Compliances with Free and Fixed End Rotations, Journal of Applied Mechanics, Vol. 78, No. 6, 061005.
[https://doi.org/10.1115/1.4003739]

-
Ruby, L., 2000, Equivalent Mass of a Coil Spring, The Physics Teacher, Vol. 38, No. 3, pp. 140~141.
[https://doi.org/10.1119/1.880475]

-
Yang, C. J., Zhang, W. H., Ren, G. X. and Lin, X. Y., 2014, Modeling and Dynamics Analysis of Helical Spring under Compression using a Curved Beam Element with Consideration on Contact between its Coils, Meccanica, Vol. 49, No. 4, pp. 907~917.
[https://doi.org/10.1007/s11012-013-9837-1]

- Kalpakjian, S., 1991, Manufacturing Processes for Engineering Materials, 2nd Edition, Addison-Wesley, MA, United States.
-
Huber, R., Clauberg, J. and Ulbrich, H., 2010, An Efficient Spring Model based on a Curved Beam with Non-smooth Contact Mechanics for Valve Train Simulations, SAE International Journal of Engines, Vol. 3, No. 1, pp. 28~34.
[https://doi.org/10.4271/2010-01-1057]

- Yıldırım, V., 2009, Numerical Buckling Analysis of Cylindrical Helical Coil Springs in a Dynamic Manner, International Journal of Engineering and Applied Sciences, Vol. 1, No. 1, pp. 20~32.
-
Niranjan, N. and Tarun, K. S., 2020, Static and Modal Analysis of Diaphragm Spring used in Micro Depth Sensing Indenting Machine, Materials Today: Proceedings, Vol. 20, Part 2, pp. 161~166.
[https://doi.org/10.1016/j.matpr.2019.10.098]

-
Triana, C. A. and Fajardo, F., 2013, Experimental Study of Simple Harmonic Motion of a Spring-mass System as a Function of Spring Diameter, Revista Brasileira de Ensino de Física, Vol. 35, No. 4, 4305.
[https://doi.org/10.1590/S1806-11172013000400005]

-
Kim, J.-W., Lee, J.-H., Shin, D.-J., Choi, S.-H., Shin, H.-S. et al., 2024, Robust Convolutional Neural Network Resistant to Overfitting for Classifying Bearing Fault Modes, Transactions of the Korean Society of Mechanical Engineers A, Vol. 48, No. 11, pp. 735~741.
[https://doi.org/10.3795/KSME-A.2024.48.11.735]

-
Kim, N. and Oh, S., 2017, Performance Improvement of Blind Detection and Estimation for Frequency Hopping Signals using Short-time Fourier Transform, Journal of Korean Institute of Communications and Information Sciences, Vol. 42, No. 12, pp. 2276~2278.
[https://doi.org/10.7840/kics.2017.42.12.2276]