가우스-마르코프 프로세스 기반 랜덤 도로 조도 측정

1. 서론

차량이 주행하는 동안 타이어와 노면(road surface)과의 상호작용으로 인해 차량은 마찰력, 회전 저항(rolling resistance), 도로 가진(road excitation) 등의 영향을 받게 된다. 이러한 상호작용은 차량의 주행성능과 안정성, 승차감을 결정하는 요소이며, 특성을 파악하기 위해 타이어와 상호 작용하는 노면의 특성을 파악할 필요가 있다. 노면의 특성을 파악하는 방법은 여러 가지가 있지만 그 중에서 가장 중요한 것은 노면의 형상을 나타내는 노면 프로파일(road profile)에 대해 알아내는 것이다. 노면 프로파일은 타이어의 마모, 타이어와 노면사이의 소음 및 마찰력, 타이어의 회전 저항 그리고 차량의 승차감과 같은 다양한 요소들에 영향을 주기 때문에 이를 측정하고 모델링하는 것은 차량의 거동에 대해 이해하는데 중요하다고 할 수 있다.

차량의 현가 장치는 차체(body)와 섀시(chassis) 사이에 위치하여 차체의 하중을 지탱하고 노면으로부터 들어오는 도로 가진(road excitation)을 흡수하여 차량의 승차감과 주행 안정성을 향상시키는 역할을 한다⁽¹⁾. 이러한 현가 장치에서 도로 가진은 시스템의 입력으로 작용하기 때문에 현가장치를 설계하고 해석하는데 중요한 요소라고 할 수 있다. 특히 도로 가진은 노면의 불규칙한 변화인 도로 조도(road roughness)에 의해 결정되기 때문에 측정 등을 통해 특성을 분석할 필요가 있다. 특히 도로 조도는 노면 프로파일의 특정 파장 영역을 의미하기 때문에 노면 프로파일을 측정하면 현가 장치를 장착한 차량의 승차감 및 안정성 해석에 활용이 가능하다.

노면 프로파일을 측정하는 방법은 Table 1과 같이 크게 3가지로 분류할 수 있다. 먼저, 직접 측정(direct measurement) 방식은 레이저 센서나 초음파 센서와 같은 거리 센서를 이용하여 노면 프로파일을 측정하는 방법이다^(2,3). 이 방식은 사용하는 거리 센서의 정밀도에 따라 정밀한 측정이 가능하지만 정밀한 거리 센서는 가격이 비싸고 센서를 차량에 안정적으로 장착하는 것이 쉽지 않다는 단점이 있다. 3D 이미지 기반(3D image based) 측정 방식은 카메라나 LiDAR와 같은 3D 이미지를 측정할 수 있는 센서를 통해 노면 프로파일의 3D 형상을 측정한다^(4,5). 특히 LiDAR를 이용하면 3D 노면 프로파일 형상을 정밀하게 측정을 할 수 있지만 LiDAR는 가격이 비싸기 때문에 측정하는데 많은 비용이 들어가고 카메라를 통한 노면 프로파일 측정은 복잡한 영상처리 알고리즘이 필요하다는 단점이 존재한다. 응답형(response type) 측정방식은 주로 가속도계나 LVDT와 같은 센서를 현가장치에 장착하고 이를 통해 노면 프로파일을 역으로 추정하는 측정방법이다^(6,7). 이 방법은 앞에서 언급한 두 가지 방법에 비해 가격이 저렴하고 적용하기 쉽다는 것이 장점이다. 하지만 현가장치의 도로 가진에 대한 응답을 통해 노면 프로파일을 추정하기 때문에 현가 장치에 영향을 주는 파장 영역만 측정이 가능하므로 정밀한 측정은 어려운 단점이 존재한다.

Table 1

Methods of road profile measurement

이 논문에서는 노면 프로파일의 정밀한 측정을 위해 레이저 센서를 기반으로 한 직접 측정 방식을 이용하여 노면 프로파일을 측정하고 이를 통해 대역통과필터(band pass filter)를 사용하여 현가 장치에 영향을 주는 파장 영역인 도로 조도를 측정하였다. 2장에서는 파장에 따라 노면 프로파일을 분류하고 노면 프로파일의 일부 영역인 도로 조도를 모델링하는 방법에 대해 소개한다. 3장에서는 도로 조도를 측정하기 위한 측정 장치와 필터를 설계하는 방법에 대해 알아보고 4장에서 측정 결과를 제시한다.

2. 도로 조도

2.1 파장에 따른 노면 프로파일 분류

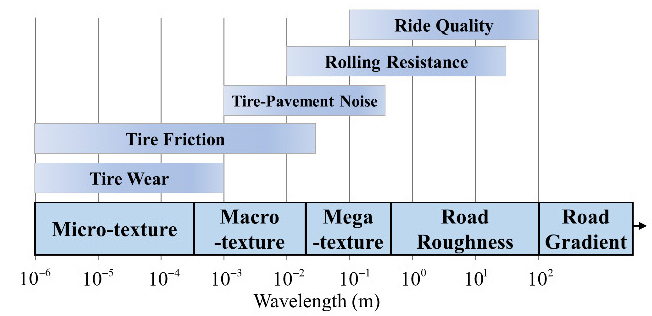
Fig. 1에 나타난 바와 같이 노면 프로파일은 파장 영역에 따라 차량에 각각 다른 형태로 영향을 주기 때문에 이를 각 파장 영역별로 이를 구분해야 할 필요가 있다. 파장이 0.5 mm 이하인 영역을 microtexture라고 하고 이 영역에서 노면은 타이어 트레드(tread)의 마모와 타이어의 마찰력에 큰 영향을 끼친다⁽⁸⁾. 노면의 파장이 0.5 mm에서 50 mm까지의 영역은 macrotexture라고 부르고 이 영역은 타이어와 노면사이에서 발생하는 마찰력과 소음에 주로 영향을 끼치게 된다^(8,9). Megatexture 영역은 파장이 50 mm에서 0.5 m인 영역의 노면을 의미하며 이 영역의 노면은 타이어의 회전 저항과 타이어와 노면사이에서 발생하는 소음에 영향을 준다^(10,11). 노면 프로파일의 파장이 0.5 m에서 100 m인 영역을 도로 조도(road roughness)라고 부르며 이 영역에서 도로 조도는 차량의 수직방향 힘으로 작용하는 도로 가진의 형태로 차량에 영향을 주기 때문에 이 영역에서 노면 프로파일은 차량의 승차감에 주된 영향을 준다. 그리고 노면 프로파일의 파장이 100 m 이상이면 노면 프로파일의 거리에 따른 높낮이의 변화가 아주 적다는 것을 의미하고 이를 도로 구배(road gradient)라고 정의한다. 따라서 현가장치를 보다 정밀하게 해석하기 위해서는 도로 조도의 특성에 대한 연구가 필요하다.

Fig. 1

Classification of a road profile by its wavelength

3. 도로 조도 측정 방법

3.1 측정 장비 구성 및 측정 방법

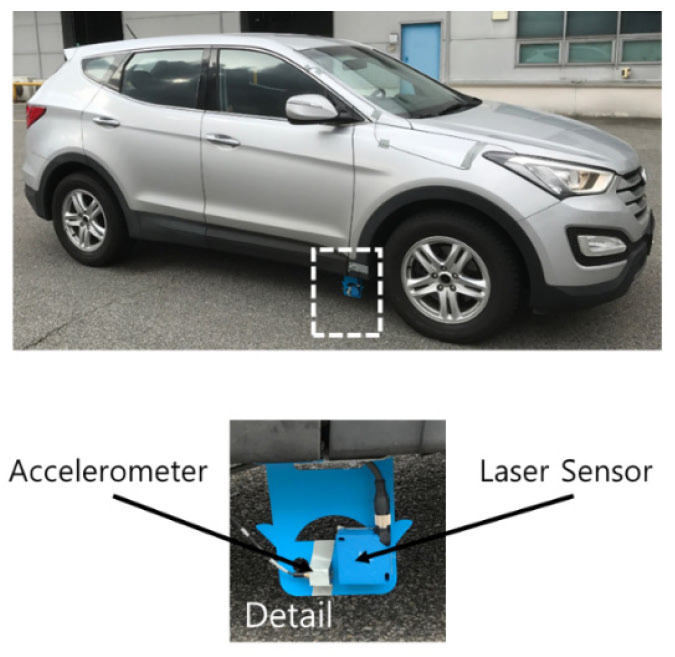
Fig. 2는 도로 조도 측정을 위한 실험장비의 구성을 나타낸다. 실험은 중형 SUV 차량(현대자동차, 뉴 싼타페2)에 레이저 센서(Wenglor, CP08MHT80)을 장착하여 도로 조도 측정을 위한 노면 프로파일을 측정하였다. 또한 노면 프로파일을 측정하는 과정에서 차량의 수직방향 진동으로 인해 오차가 발생하는데 이를 보정해주기 위해서 가속도계(Brüel & Kjær, DeltaTron Type 4506)를 레이저 센서와 함께 장착하였다. 또한 가속도계로 측정한 가속도로부터 차량의 수직방향 진동 오차를 보정하기 위해 측정된 가속도 신호를 적분하여 변위를 계산해야 한다. 가속도계에서 측정한 신호를 적분할 때 드리프트 오차(drift error)가 발생하기 때문에 이를 제거해주기 위해 고역통과필터(high pass filter)를 사용해야 한다. 이에 대한 내용은 3.2절에서 언급한다.

Fig. 2

Photograph of sensor setup for road profile measurement

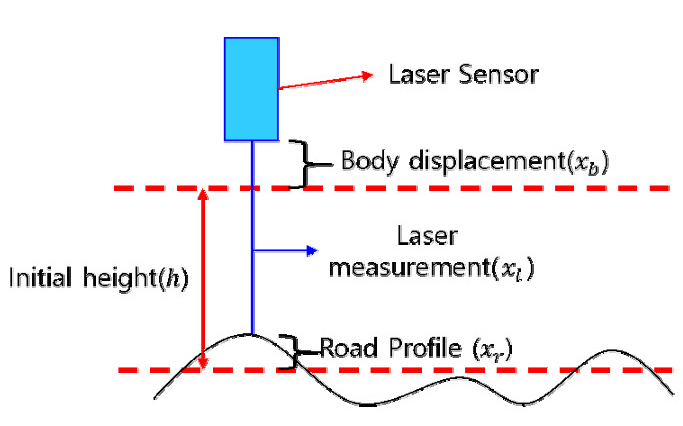
Fig. 2의 측정 장비를 이용하여 도로 조도를 측정하는 방법은 Fig. 3과 같다. 앞서 언급한 바와 같이 레이저 센서의 측정치(x_l)는 차량의 수직방향 진동으로 인해 차체의 변위(x_b)만큼의 오차를 포함하게 된다. 따라서 가속도계를 이용하여 차체의 변위(x_b)를 계산하여 오차를 보정해주면 노면 프로파일 (x_r)은 다음과 같이 계산할 수 있다.

$\[ x_r=h+x_b-x_l \]$

(11)

Fig. 3

Schematic of road roughness measurement method

3.2 도로 조도 계산을 위한 신호처리

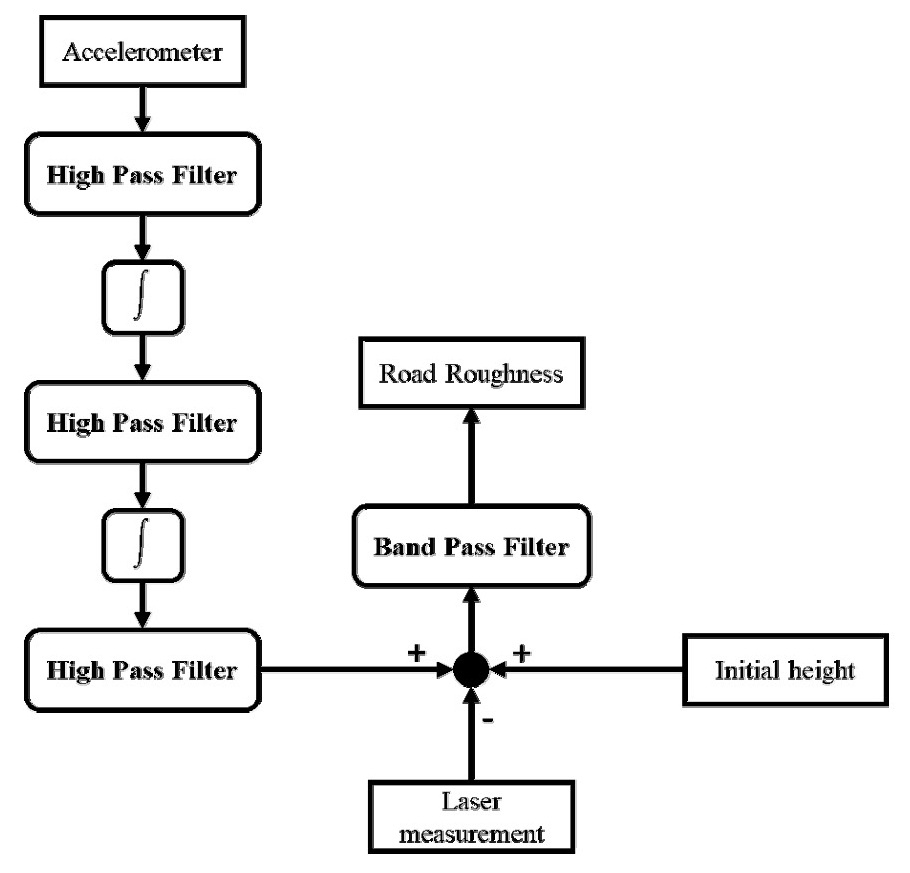
식 (11)로부터 노면 프로파일(x_r)을 계산하기 위해서는 가속도계의 신호를 적분하여 차체 변위(x_b)를 구해야 한다. 일반적으로 가속도계와 같은 관성센서는 지구의 자전으로 인한 코리올리 효과(Coriolis effect)로 인해 편향 오차(bias error)를 가지는 것으로 알려져 있고 이로 인해 가속도계를 적분하면 적분 값이 발산하게 된다⁽¹³⁾. 가속도계에서 발생하는 편향 오차는 주로 저주파 성분으로 이루어져 있기 때문에 고역통과필터를 사용하여 이를 제거해줄 필요가 있다. 현가장치의 대역폭이 0.5 Hz에서 15 Hz까지로 알려져 있기 때문에 가속도계 적분을 위한 고역통과필터의 차단 주파수(cut-off frequency)를 0.5 Hz로 정하였다. MATLAB Signal Processing Toolbox를 사용하여 차단 주파수가 0.5 Hz인 1차 디지털 버터워스(butterworth) 필터를 설계하면 다음과 같다.

$\[ H_1\left(z\right)=\frac{0.999877\left(1-z^{-1}\right)}{1-0.999756z^{-1}} \]$

(12)

식 (12)에서 분자에 (1-z^-1)는 디지털 적분기의 분모에 존재하는 (1-z^-1)과 서로 상쇄되기 때문에 고역통과필터는 적분기의 불안정한 극점(pole)을 제거해서 적분되는 신호가 발산하지 않도록 방지해주는 역할을 한다. 위와 같이 설계된 고역통과필터는 Fig. 4와 같이 적분기의 앞뒤에 연결한다.

Fig. 4

Schematic of signal processing to calculate the road roughness

식 (11)과 같이 계산된 노면 프로파일(x_r)에서 도로 조도를 얻어내기 위해 도로 조도에 해당하는 파장 영역으로 필터링할 필요가 있다. 도로 조도는 0.5 m에서 100 m사이의 파장을 가지기 때문에 도로 조도의 주파수 영역은 식 (4)에 의해 다음과 같이 결정된다.

$\[ \frac{v}{100}\le f\le \frac{v}{0.5} \]$

(13)

• where v: vehicle speed, f: bandwidth of bandpass filter

따라서 식 (11)로부터 얻은 노면 프로파일(x_r)을 식 (13)에 해당하는 대역폭을 가지는 대역통과필터(band pass filter)를 사용하여 필터링 해줄 필요가 있다. 대역통과필터는 MATLAB Signal Processing Toolbox를 사용하여 식 (13)의 대역폭을 가지는 2차 디지털 버터워스 필터를 설계된다. 이와 같이 설계된 대역통과필터를 사용하여 Fig. 4와 같이 적용하면 도로 조도를 측정할 수 있다.

4. 도로 조도 측정 결과

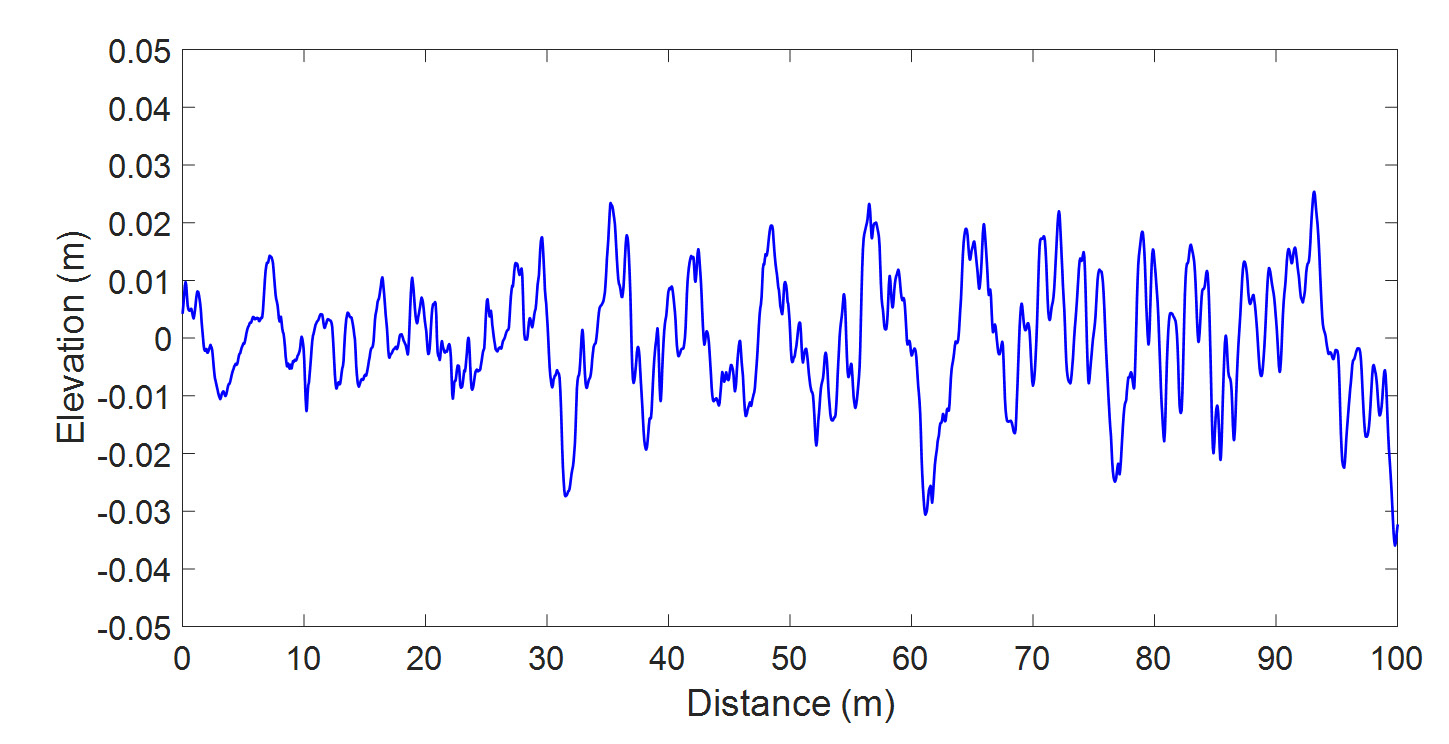
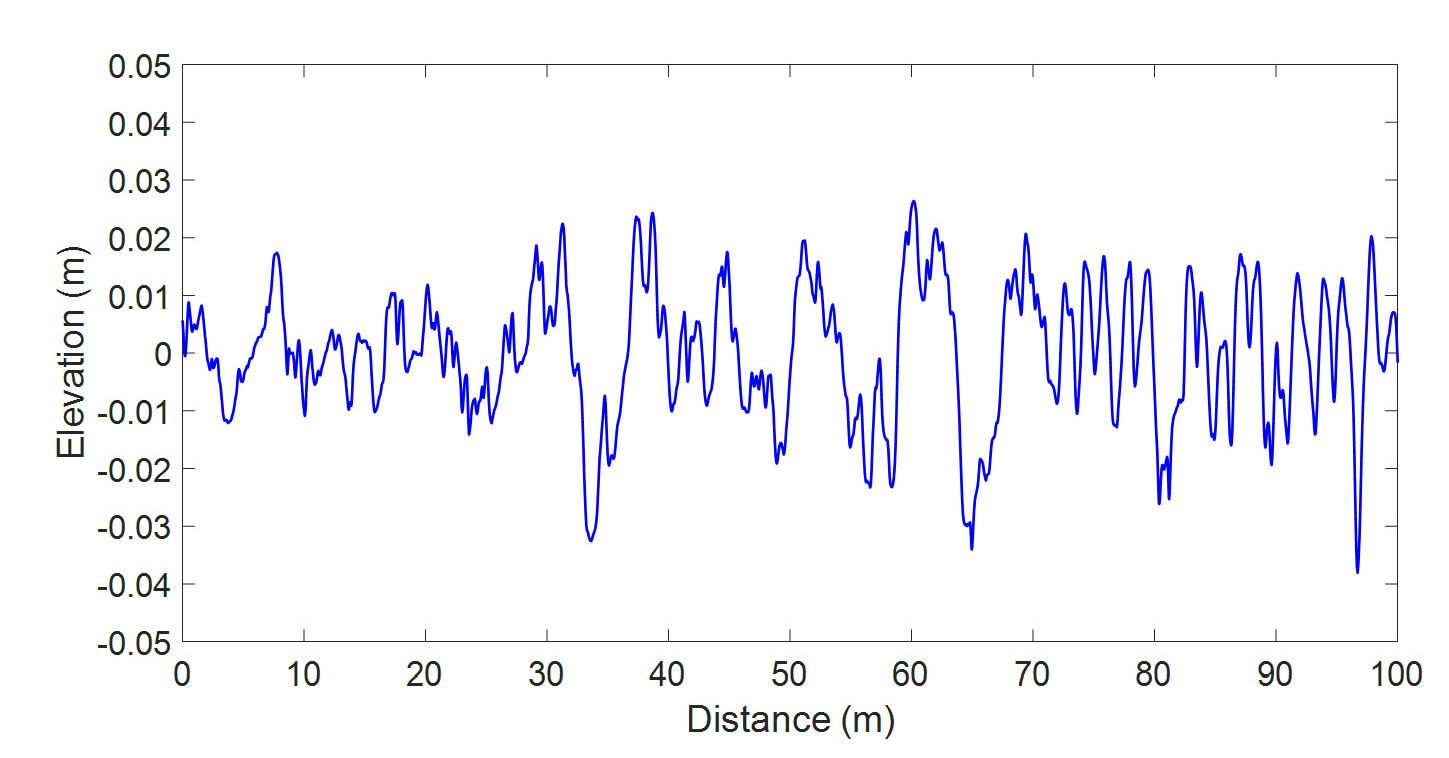
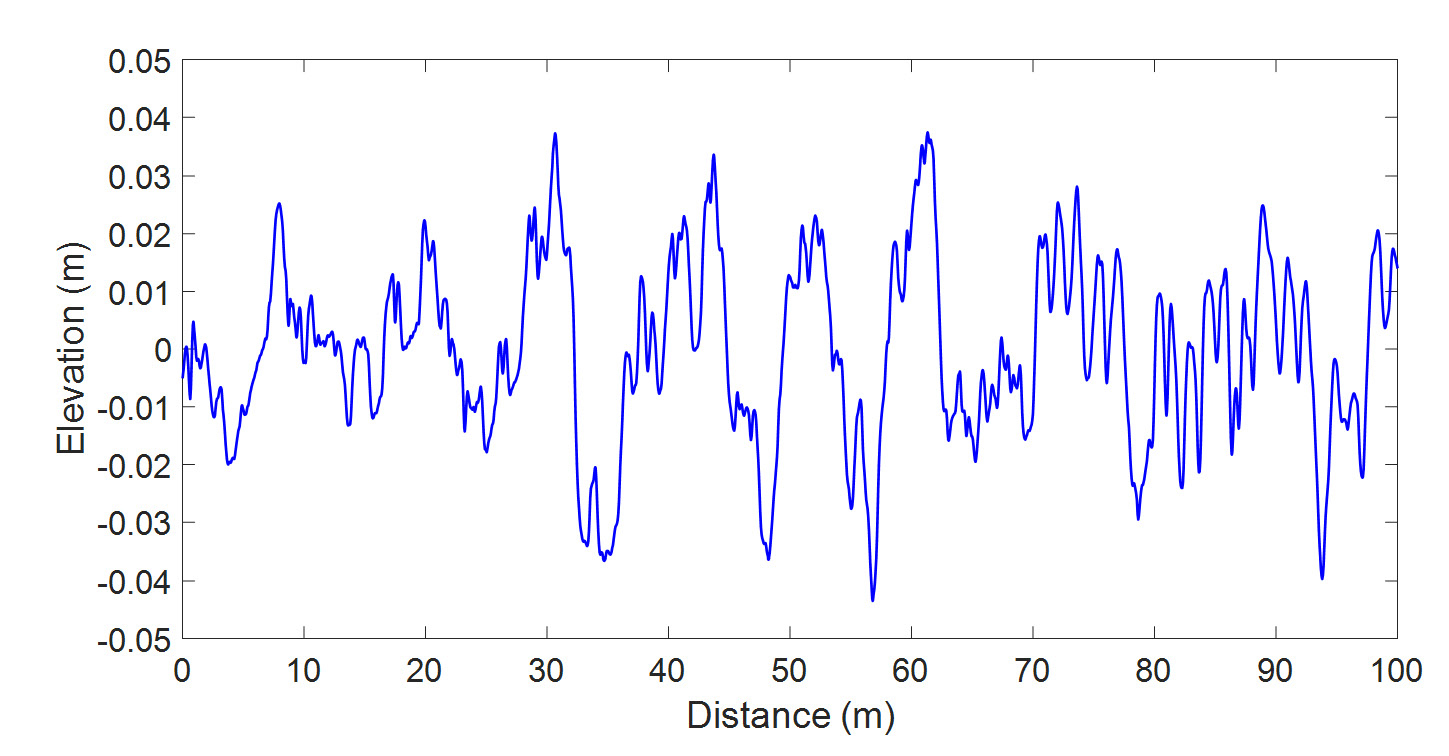
도로 조도는 한국타이어의 P/G(proving ground)를 측정하였고 측정 시 차량 속력은 40 km/h, 50 km/h, 60 km/h로 총 3가지의 경우에 대해 측정하였다. 또한 도로 조도 측정 후 신호처리를 위해 대역통과필터를 설계해야 하는데 대역통과필터의 대역폭은 식 (13)에 주어진 것과 같이 차량 속력에 따라 다르다. 따라서 차량 속력에 따라 각각 다른 대역폭을 갖는 대역통과필터를 설계해야 하는데 이때의 대역폭은 Table 2와 같다. 이를 이용하여 도로 조도를 측정한 결과는 Fig. 5부터 Fig. 7과 같다.

Table 2

Bandwidth of band-pass filter for each speed of the test vehicle

Fig. 5

Measurement of road roughness at vehicle speed of 40 km/h

Fig. 6

Measurement of road roughness at vehicle speed of 50 km/h

Fig. 7

Measurement of road roughness at vehicle speed of 60 km/h

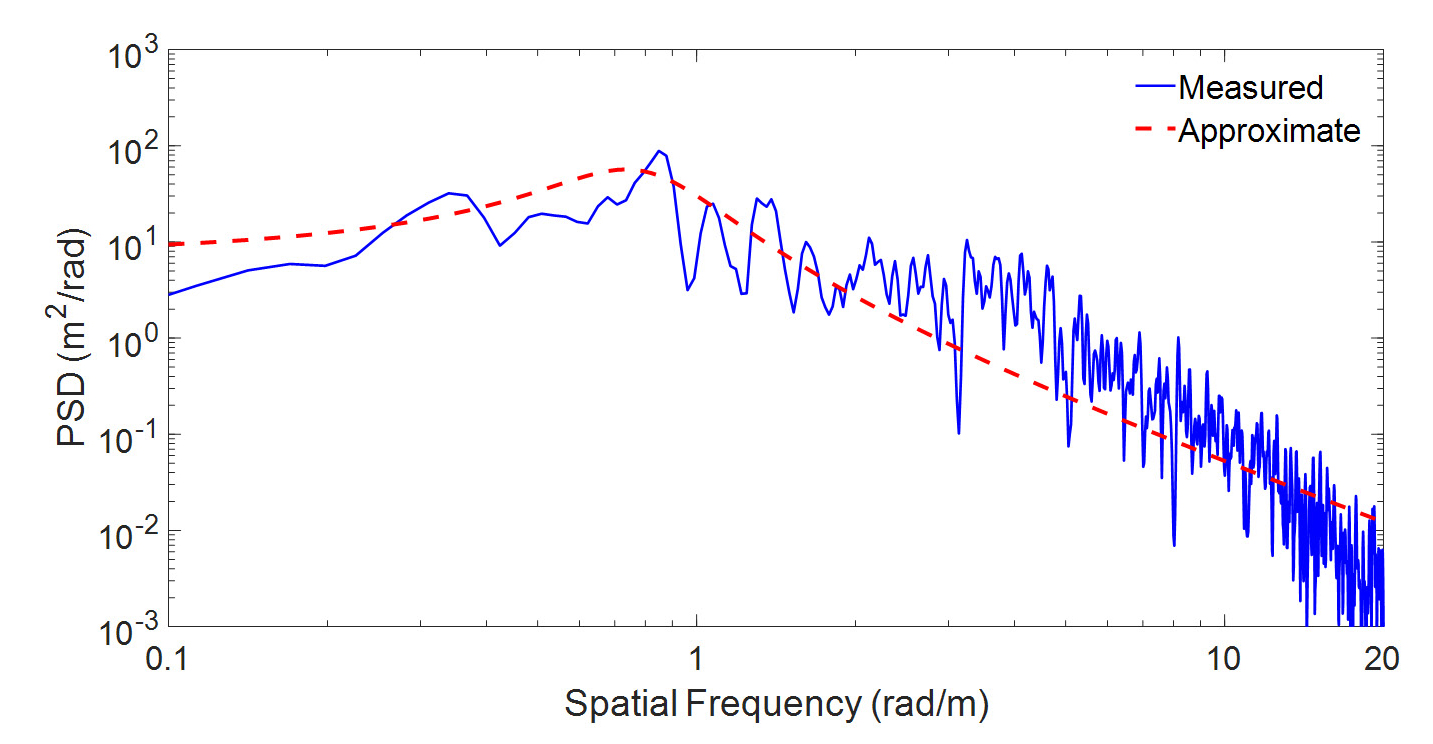
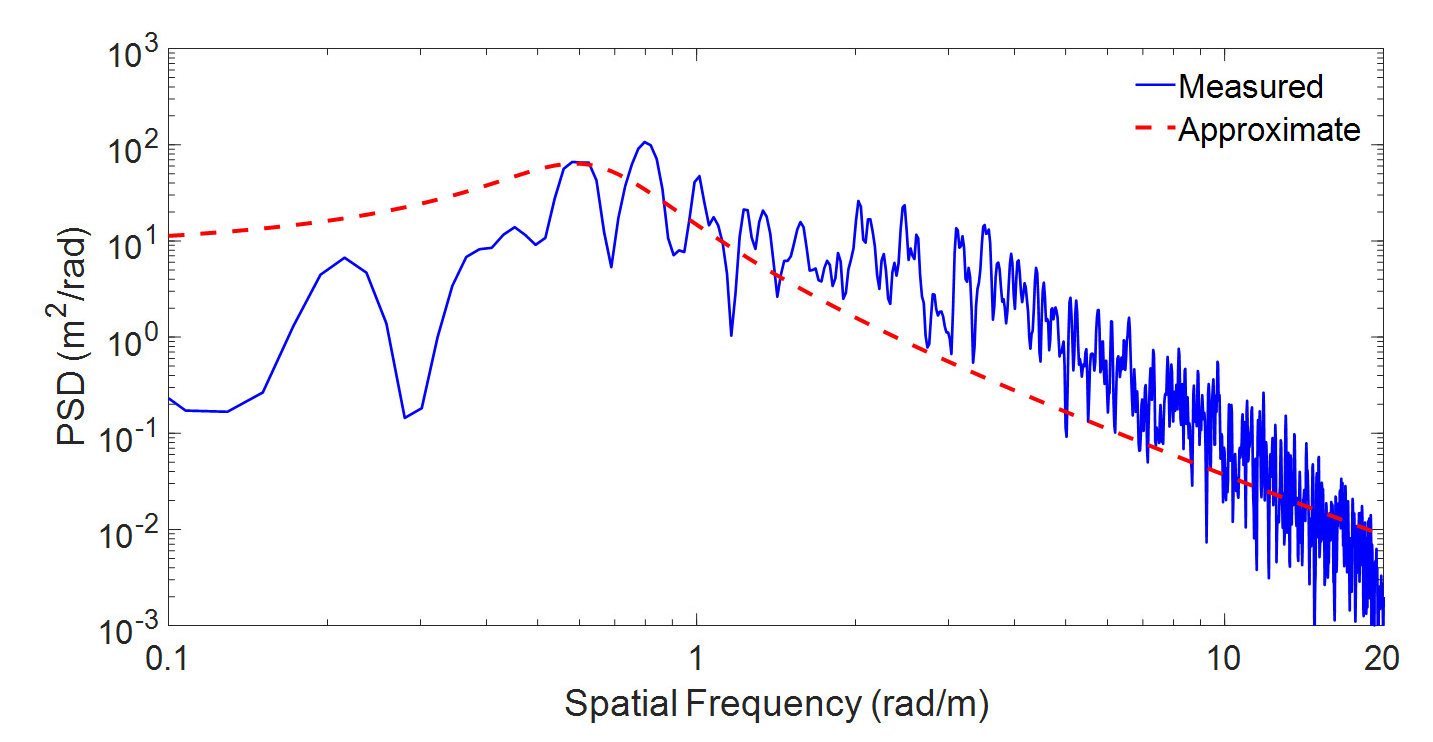
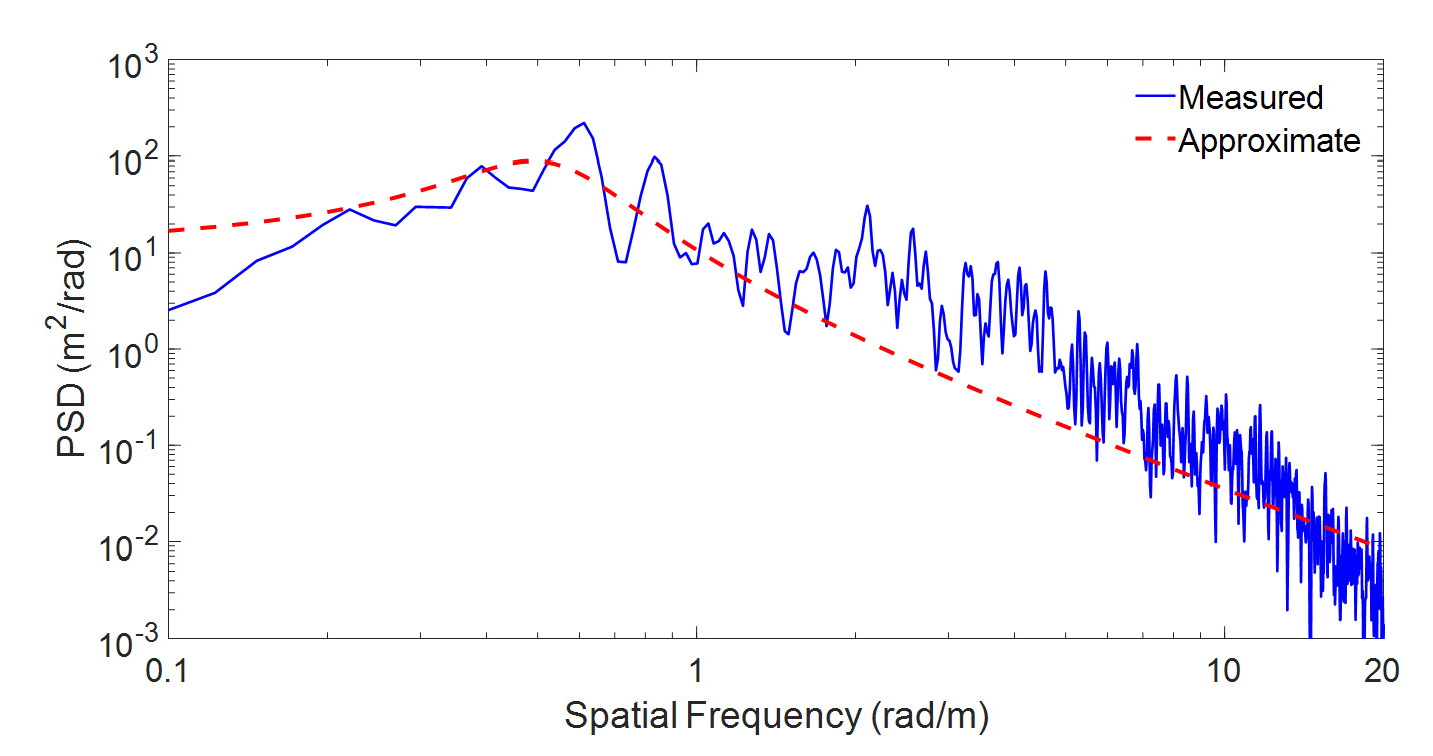
Fig. 5부터 7까지는 각각 차량의 속력이 40 km/h, 50 km/h, 60 km/h에서 같은 노면을 주행하였을 때 도로 조도를 측정한 결과이다. 또한 이 결과에 대한 공간주파수 영역에서의 PSD 함수는 Fig. 8부터 10까지와 같다. Fig. 8에서 10까지의 PSD 함수는 y축을 로그 스케일로 하여 그래프를 그렸다. 또한 Fig. 8에서 10까지에서 점선으로 표시된 부분은 Gauss-Markov 모델을 이용하여 도로 조도의 PSD 함수를 근사화한 것이다. 보다 정확한 근사를 위해 식 (8)을 다음과 같이 변형한 모델을 적용하였다.

Fig. 8

PSD function of measured road roughness at vehicle speed of 40 km/h

Fig. 9

PSD function of measured road roughness at vehicle speed of 50 km/h

Fig. 10

PSD function of measured road roughness at vehicle speed of 60 km/h

여기서 Ω₀는 식 (8) 모델을 공간주파수 영역에서 평행이동 시켜주는 상수이다. 식 (14)에서 표준편차 σ는 도로 조도의 표준편차를 사용하였고 β=0.5이다. Fig. 8에서 10의 그래프에서 보이는 바와 같이 저주파수 부분에서는 식 (14)를 통해 구한 PSD가 일정한 값을 가지지만 측정치를 구한 PSD는 감소하는 경향을 보이는데 이는 Fig. 4에서 대역통과필터를 사용했기 때문이다. 하지만 저주파 대역은 Fig. 1에서 언급한 road gradient 영역을 나타내고 이 논문의 목표는 상대적으로 주파수가 큰 도로 조도를 측정하는 것이기 때문에 저주파 대역의 오차를 크게 고려하지 않아도 무방하다. 따라서 도로 조도는 식 (14)의 Gauss-Markov 모델로 비교적 잘 맞는다고 결론을 내릴 수 있다.

5. 결론

이 논문에서는 Gauss-Markov 모델을 이용하여 도로 조도를 모델링하고 실측한 도로 조도를 통해 모델의 유효성을 알아보았다. Gauss-Markov 모델은 수학적으로 처리하기 용이하기 때문에 이 모델을 활용하면 현가장치의 몬테 카를로 시뮬레이션(Monte- Carlo simulation)을 수행할 수 있다. 또한 현가장치에 칼만 필터(Kalman filter)를 적용하기 위해서는 도로 조도의 확률론적 모델이 필요하게 되는데 이 논문에서 제시한 모델을 활용하면 현가장치에서 칼만 필터를 설계할 때 도움이 될 것으로 예상된다.

Acknowledgments

이 연구는 한국타이어의 산학위탁연구과제(2018) 지원에 의하여 연구되었음.

References

• Sung, K., and Choi, S., (2013), Ride Comfort Evaluation of Electronic Control Suspension Using a Magneto-Rheological Damper, Transactions of the Korean Society for Noise and Vibration Engineering, 23(5), p463-471. [https://doi.org/10.5050/KSNVE.2013.23.5.463]
• Kook, H., Kim, H., Nam, K., and Ih, K., (2017), Correlation of Road Noise with Road Roughness, Transactions of the Korean Society for Noise and Vibration Engineering, 27(7), p870-876. [https://doi.org/10.5050/KSNVE.2017.27.7.870]
• Cai, Y., (2017), Kalman Filtering-based Real-time Inertial Profiler, Journal of Surveying Engineering, 143(4), p04017017.
• Lee, J., Lee, S., Kang, D., Na, S., and Yoo, W., (2017), Development of a 3D Road Profile Measuring System for Unpaved Road Severity Analysis, International Journal of Precision Engineering and Manufacturing, 18(2), p155-162.
• Han, J., Chen, A., and Lin, Y., (2015), Image-based Approach for Road Profile Analyses, Journal of Surveying Engineering, 142(1), p06015003.
• Rath, J. J., Veluvolu, K. C., and Defoort, M., (2015), Simultaneous Estimation of Road Profile and Tire Road Friction for Automotive Vehicle, IEEE Transactions on Vehicular Technology, 64(10), p4461-4471.
• Fauriat, W., Mattrand, C., Gayton, N., Beakou, A., and Cembrzynski, T., (2016), Estimation of Road Profile Variability from Measured Vehicle Responses, Vehicle System Dynamics, 54(5), p585-605. [https://doi.org/10.1080/00423114.2016.1145243]
• Gunaratne, M., Bandara, N., Medzorian, J., Chawla, M., and Ulrich, P., (2000), Correlation of Tire Wear and Friction to Texture of Concrete Pavements, Journal of Materials in Civil Engineering, 12(1), p46-54. [https://doi.org/10.1061/(ASCE)0899-1561(2000)12:1(46)]
• Hong, S. J., Park, S. W., and Lee, S. W., (2015), The Effect of Texture Wavelength on the Tire-pavement Noise in Asphalt Concrete Pavement, International Journal of Highway Engineering, 17(1), p1-6. [https://doi.org/10.7855/IJHE.2015.17.1.001]
• Sakhaeifar, M., Banihashemrad, A., Liao, G., and Waller, B., (2017), Tyre–pavement Interaction Noise Levels Related to Pavement Surface Characteristics, Road Materials and Pavement Design, p1-13.
• Boere, S., Arteaga, I. L., Kuijpers, A., and Nijmeijer, H., (2014), Tyre/Road Interaction Model for the Prediction of Road Texture Influence on Rolling Resistance, International Journal of Vehicle Design, 65(2-3), p202-221. [https://doi.org/10.1504/IJVD.2014.060815]
• Tyan, F., Hong, Y., Tu, S., and Jeng, W. S., (2009), Generation of Random Road Profiles, Journal of Advanced Engineering, 4(2), p1373-1378.
• Farrell, J., and Barth, M., (1999), The Global Positioning System and Inertial Navigation, MaGraw-Hill, USA.