점탄성 재료 기반 진동저감장치의 수학적 모델링
ⓒ The Korean Society for Noise and Vibration Engineering
초록
In this paper, a vibration isolator using a viscoelastic material is proposed for reducing the micro-vibration in satellite platforms. In order to describe the vibration isolator, a mathematical model is derived in six degrees of freedom: three translational and three rotational motions. Then, the mathematical expressions of the force and moment transmissibility, which can evaluate the amount of reduction in micro-vibration through the vibration isolator, are established. The proposed mathematical model for vibration isolator is verified by comparing the transmissibility plots obtained from the mathematical model and the ANSYS results. Finally, the effect of the design parameters on the isolation performance is investigated using the mathematical model.
Keywords:
Viscoelastic Material, Passive Vibration Isolation, Micro-vibration, Jitter키워드:
점탄성 물질, 수동 진동 절연, 미소 진동, 지터1. 서론
위성체의 다양한 임무 장비와 구성품은 인공위성의 자세 제어를 위해 사용되는 반작용휠(reaction wheel), 제어 모멘트 자이로(control moment gyroscope), 극저온 냉각을 위한 냉각기(cryocooler)와 같은 지속적인 진동원에 노출되어있다(1). 비록 진동원에서 발생하는 진동의 크기가 매우 작다고 하더라도, 우주공간에는 별도의 감쇠 요인이 없기 때문에 위성체의 임무 장비에는 지속적인 미소 진동(micro-vibration)이 발생할 수 있다. 이러한 미소 진동은 지터(jitter)라고도 불리우며, 위성체에 탑재된 다양한 장비들의 성능 저하에 직접적으로 관여한다. 따라서 위성체의 고성능과 고정밀화를 만족시키기 위해서는 진동원으로부터 발생하는 진동이 임무 장비로 전달되지 않도록 진동이 전달되는 경로에 진동 절연 장치를 도입하는 기술이 필요하다.
진동을 줄이는 기법은 제어기(controller), 센서(sensor), 작동기(actuator)의 유무에 따라 수동(passive), 능동(active), 반능동(semi-active)의 형태로 나눌 수 있다(2,3). 수동 진동 절연 장치의 경우 시스템의 고유 파라미터(parameter)가 고정되어 있기 때문에 위성 탑재체의 무게, 주파수 특성 및 위성체 내 배치 등에 따라 절연 장치의 형태 및 특성이 달라져야 하므로 새로운 위성 시스템 개발 시마다 설계 변경이 필요하다. 하지만 능동, 반능동 기법보다 비용이 저렴하고 시스템의 안정화와 신뢰도 측면에서 유리하기 때문에 현재까지 많은 임무수행에 적용되었다. 대표적인 예로써, 허블 우주관측 망원경(Hubble space telescope)의 관측 성능 향상을 위해 Honeywell사가 개발한 수동 진동 절연 장치가 있다. 이는 허블 우주관측 망원경의 자세제어에 사용되는 반작용휠의 미소 진동을 차단할 목적으로 개발된 절연기로서, 점성 유체를 사용하는 댐퍼와 금속 스프링을 이용한다(4). 또한 허블 우주관측 망원경에 장착된 태양전지판과 위성체의 동적 간섭을 줄이기 위해 티타늄과 점탄성 물질이 사용된다(5). Chandra X-선 우주망원경을 위한 수동 진동 절연 장치도 수동 진동 절연 장치의 또 다른 예이다. 반작용휠로부터 발생된 미소 진동이 반사경 지지 구조물 모드를 가진하는 것을 차단하기 위해 6개의 반작용휠 각각에 절연 장치가 적용되었다. 이 절연 장치는 티타늄 스프링과 점탄성 재질의 부재가 나란히 연결된 형태로 구성된 6개의 댐퍼가 헥사포드(hexapod)의 형상으로 배치되어있다(6). 천리안위성은 태양 전지판이 위성의 한쪽에만 장착된 비대칭 형상을 가지기 때문에 외란으로 인한 토크 발생이 크다. 이를 제어하기 위해 대용량의 모멘텀휠이 적용되었다. 모멘텀휠로 인한 미세 진동을 최소화할 목적으로 모멘텀 휠의 하단에 진동 절연 장치가 도입되었으며 이 진동 절연 장치는 탄성중합체(elastomer) 블록을 이용하여 휠이 발생시키는 진동 전달을 저하시킨다(7).
이 연구에서는 위성체의 제어 모멘트 자이로 등에서 발생하는 미소 진동을 저감시키기 위해 수동 진동 절연 장치 기법 중의 하나인 점탄성 물질을 이용한다. 진동 저감 장치의 성능을 분석하기 위해 3개의 병진 운동과 3개의 회전운동을 포함한 총 6자유도 운동방정식을 세우고, 힘/모멘트 전달률 식을 유도한다. 앞서 세운 수학적 모델은 ANSYS 결과와 비교함으로써 검증되었다. 마지막으로, 검증된 수학적 모델을 이용해 설계 변수에 따른 진동 저감 장치의 성능을 분석한다.
2. 점탄성 물질
2.1 점탄성 물질의 특성
점탄성 물질은 시간에 무관하게 즉각적으로 반응하는 탄성거동과 하중이 가해짐에 따라 변형이 지연되는 시간에 의존하는 점성거동이 동시에 나타나는 물질로서 내부 마찰이 크며 경제성, 성형 용이성 등 장점으로 인하여 충격, 진동 및 소음의 차단과 제어에 널리 이용된다(8~10).
정현파(sinusoidal) 응력(stress)이 가해질 경우, 탄성 특성에 의한 변형률(strain)은 응력과 같은 위상을 가지는 반면 점성 특성에 의한 변형율은 응력과 π/2의 위상차를 갖는다. 따라서 탄성과 점성의 특성을 함께 가지고 있는 점탄성 물질의 경우, 정현파 응력이 가해질 경우 점성을 가지고 있는 정도에 따라 0과 π/2 사이의 위상차를 갖게 된다. 이러한 점탄성 물질의 특성 때문에 점탄성 물질의 재료 계수(modulus)는 복소수를 사용하여 식 (1)로 간편하게 표현할 수 있다.
| (1) |
식 (1)에서 M은 인장탄성계수(Young’s modulus) 또는 전단탄성계수(shear modulus)이며 M*을 복소탄성계수(complex modulus), 복소수의 실수부인 M’을 저장탄성계수(storage modulus), 복소수의 허수부인 M’’을 손실탄성계수(loss modulus), η는 손실계수(loss factor)라 한다. 저장탄성계수는 점탄성 재료에 저장된 에너지(탄성 거동)를 의미하고 손실탄성계수는 손실된 에너지(점성 거동)를 의미한다. 손실 계수는 동적 하중을 받는 점탄성 재료가 한 주기 동안 저장할 수 있는 최대 변형률 에너지 중에서 감쇠에 의해 한 주기 동안 손실되는 에너지량의 상대적인 비율로 정의된다.
식 (1)에 표현된 ω와 T는 각각 주파수와 온도이며, 점탄성 물질의 특성은 온도와 주파수에 의해 많은 영향을 받는 것으로 알려져 있다(11). 따라서 점탄성 물질을 사용하여 진동 절연 장치를 설계할 경우 온도와 주파수에 따른 재료의 특성 변화가 반영되어야 더욱 효과적이고 정확한 설계가 가능하다. 이 연구에서는 진동 저감 장치의 온도가 비교적 일정하다고 가정하여 온도 변화에 따른 점탄성 재료의 특성 변화보다 주파수 변화에 따른 물성치 변화를 중점적으로 살펴보았다.
3. 수학적 모델 수립
3.1 진동 저감장치 모델
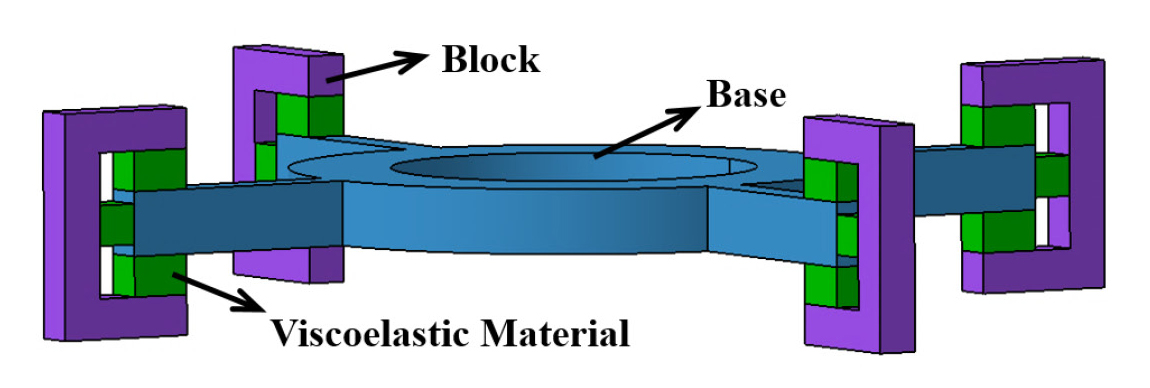
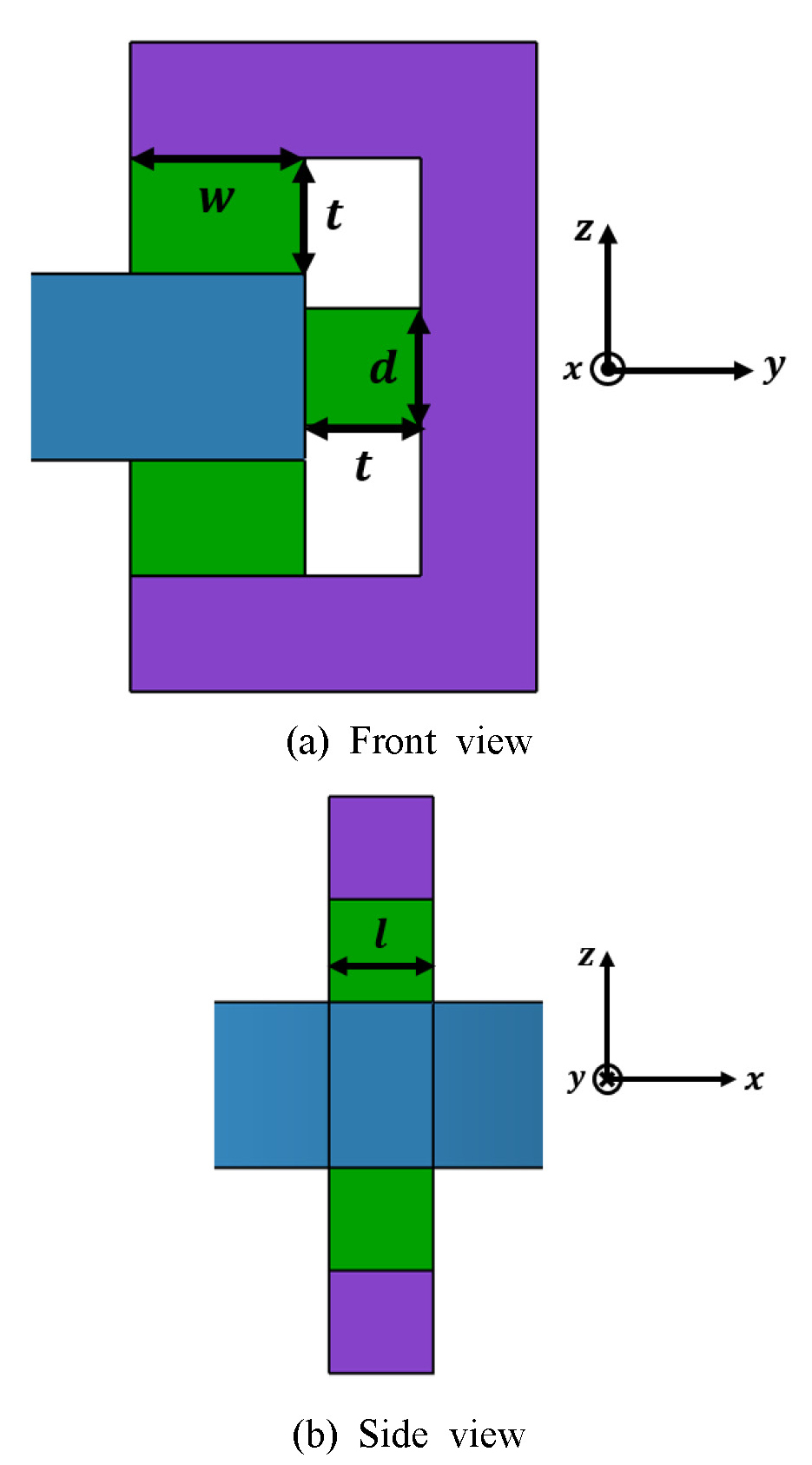
이 연구는 위성체의 미소진동을 저감시키기 위해 점탄성 재료를 삽입한 진동 저감장치를 설계하였으며 진동 저감장치 모델의 형상은 천리안 위성에 사용된 절연 장치(7)를 참고하였다.
이 진동 절연 시스템은 Fig. 1과 같이 제어 모멘트 자이로 등 진동원이 장착되는 알루미늄 재질의 base와 base 주변에 90° 간격으로 배치된 4개의 세트로 구성된다. 각 세트는 진동원으로부터 발생된 미소 진동을 저감시킬 점탄성 물질, 그리고 위성체와 연결되며 점탄성 물질을 둘러싸고 있는 ㄷ자형의 block으로 구성된다.
3.2 유효압축계수
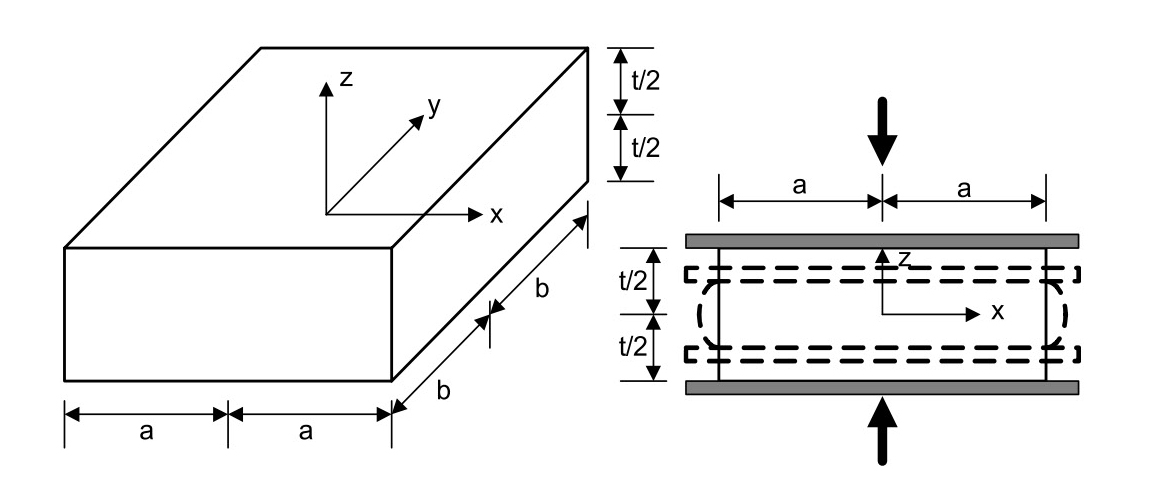
Fig. 2와 같이 탄성 층이 두개의 강성 판 사이에 결합 될 때(12), 강성 판은 탄성 층이 옆으로(lateral) 팽창하는 것을 제한하기 때문에 두 개의 강성 판 사이에 결합된 탄성 층은 결합되기 전보다 높은 압축 강성을 갖게 된다. 이 효과를 고려한 인장 탄성 계수를 유효 압축 계수(effective compression modulus)라고 하며 인장 탄성 계수와 식 (2)와 같은 관계를 갖게 된다(12).
| (2) |
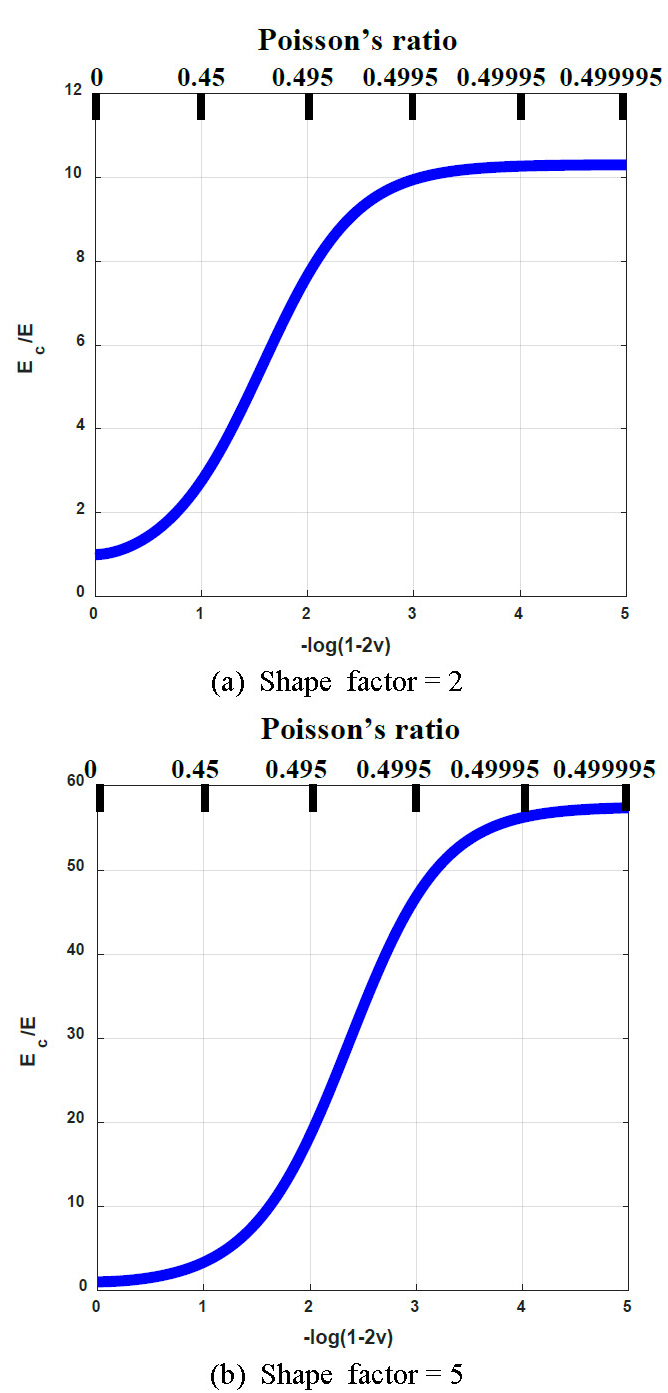
Fig. 3은 푸아송 비(Poisson’s ratio)와 힘을 받는 면적과 힘을 받지 않는 면적의 비를 나타내는 형상 계수(shape factor) 변화가 탄성 층의 유효 압축 계수에 미치는 영향을 보여준다. 형상 계수는 식 (3)과 같이 나타낼 수 있다.
| (3) |
Fig. 3으로부터 알 수 있듯이 푸아송 비가 0.5에 가까워질수록 유효 압축 계수와 인장탄성계수의 비가 증가하며, 형상 계수가 클수록 푸아송 비의 효과가 커진다. 따라서 점탄성 물질이 block과 base 사이에 삽입되어 있고, 점탄성 물질의 푸아송 비가 0.5에 가깝다는 것을 고려하여 유효 압축 계수의 개념을 수학 모델에 적용하였다.
3.3 진동 저감 장치의 강성
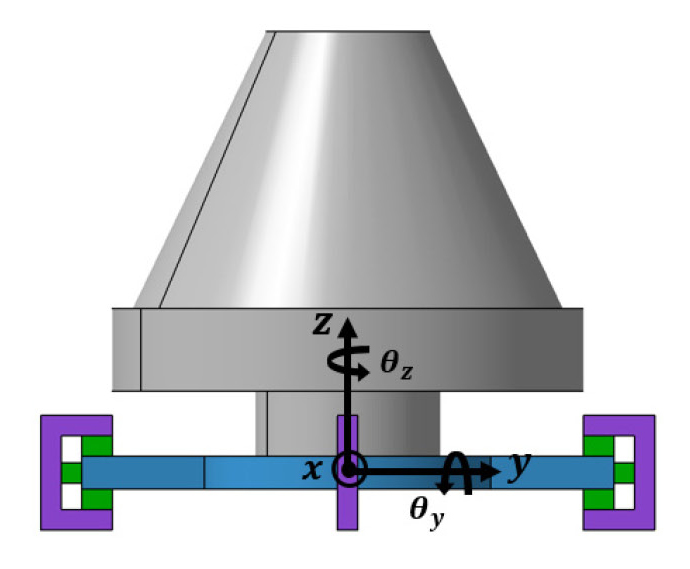
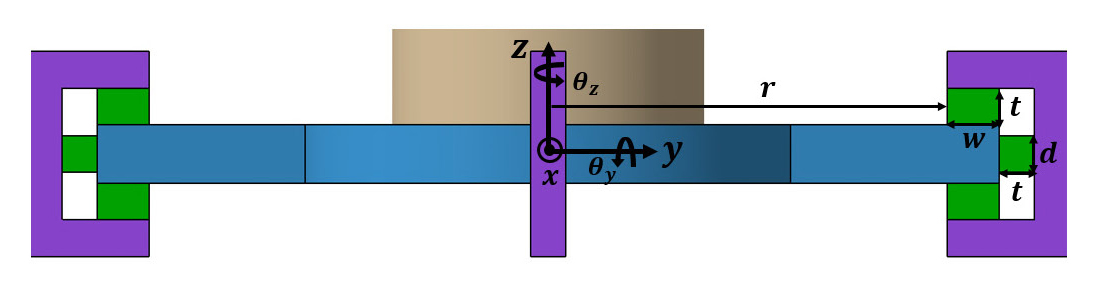
운동방정식을 세우기 위해 이 연구에서 세운 가정은 다음과 같다. 좌표축의 원점은 Fig. 4에서 보이는 것과 같이 base의 중심으로 정의하였으며 base와 진동원은 하나의 강체로 운동한다고 가정하였다. 진동원이 발생시키는 미소진동으로 인해 진동 저감 장치의 base는 x, y, z축에 대해 병진 및 회전운동을 한다. 따라서 진동 저감 장치는 총 6자유도를 가지며, 진동원이 발생시키는 교란력과 교란 토크의 크기가 작기 때문에 각 자유도는 decouple되어 있다고 가정하였다. 따라서 진동 저감 장치의 각 자유도에 대한 운동방정식은 식 (4) ~ (9)와 같이 표현할 수 있다.
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
진동 저감 장치의 성능을 분석하기 위해 이 연구에서는 진동 저감 장치의 각 축 방향에 대한 강성 (stiffness)을 유도하였다.
Base가 x, y 및 z축을 따라 움직일 때 점탄성 물질이 받는 응력을 고려하여 병진 강성(translational stiffness)을 유도하였다. 예를 들어 base가 x축으로 움직일 때 x축을 따라 놓여있는 block에 삽입되어 있는 위, 아래의 점탄성 물질은 전단 응력을 받게 되고, 옆에 삽입되어 있는 점탄성 물질은 압축 또는 인장 응력을 받는다. 식 (10) ~ (12)는 각 축에 대한 진동 저감 장치의 병진 강성이며, 식에서 표현된 첨자 ω는 주파수에 따라 점탄성 물질의 물성치가 변하는 것을 뜻한다.
| (10) |
| (11) |
| (12) |
각 축 방향에 대한 회전 강성(rotational stiffness)을 유도하기 위해 각 회전축에 대해 운동 방정식을 수립하였다. Figs. 5, 6에 이후 운동방정식에 사용될 주요 치수 기호들이 정의되어 있다.
먼저 base가 x축에 대해 회전하게 되면 x축을 따라 놓여있는 2개의 block에 삽입된 점탄성 재료들의 변형은 거의 미미하다고 보기 때문에 무시하고, y축을 따라 놓여있는 block에 삽입된 점탄성 재료들의 변형만 고려한다. 이 때 위아래로 삽입된 점탄성 물질은 압축 응력을 받게 되는데 base 중심에서의 거리에 따라 점탄성 물질의 변형률이 다른 것을 고려하기 위해 강성을 구하는 과정에서 적분을 수행하였다. 따라서 base가 x축에 대해 θx만큼 회전할 경우, 운동방정식은 식 (13)과 같다. 진동 저감 장치는 y-z평면, x-z평면에 대해 대칭이기 때문에, base가 y축에 대해 θy만큼 회전할 경우의 운동방정식은 x축에 대해 회전한 경우와 동일한 방식으로 유도한다. base가 z축에 대해 θz만큼 회전하게 되면 4개의 block에 삽입된 모든 점탄성 재료들은 전단 응력을 받게 된다. 이 때 위 아래에 삽입된 점탄성 물질은 base 중심에서의 거리에 따라 점탄성 물질의 변형률이 다른 것을 고려하기 위해 강성을 구하는 과정에서 식 (15)와 같이 적분을 수행하였다.
| (13) |
| (14) |
| (15) |
식 (13) ~ (15)의 운동방정식을 정리하면 식 (16) ~ (18)과 같이 각 축에 대한 회전 강성을 유도할 수 있다.
| (16) |
| (17) |
| (18) |
3.4 힘/모멘트 전달률
정상상태의 조화 진동에 대한 진동 저감 장치의 성능은 가진력의 크기와 전달력의 크기의 비를 나타내는 전달률을 사용해 정의된다. 이 연구에서는 설계한 진동 저감 장치의 성능을 분석하기 위해 가진력과 전달력의 비인 힘 전달률(force transmissibility)과 가진 모멘트와 전달 모멘트의 비인 모멘트 전달률(moment transmissibility)을 유도하였으며 3.3절에서 구한 진동 저감 장치의 강성을 대입함으로써 전달률을 구할 수 있었다. 식 (19)과 식 (20)은 각각 힘 전달률과 모멘트 전달률의 크기를 의미하며, 식 (21)과 식 (22)는 각각 가진력과 전달력의 위상차, 가진 모멘트와 전달 모멘트의 위상차를 의미한다.
| (19) |
| (20) |
| (21) |
| (22) |
4. 수학적 모델 검증
4.1 전처리 및 가정
수학적 모델로부터 얻은 각 축 방향에 대한 전달률을 상용 유한요소 해석 소프트웨어 ANSYS의 결과와 비교 검증하였다. ANSYS로 해석 수행 시, 각 축 방향에 대한 개별적인 분석을 위해 해당 자유도를 제외한 모든 자유도는 구속시켰다. 예를 들어 Base가 x축으로 병진 운동을 할 경우, x축 외에는 해석 모델이 움직이지 않도록 구속 조건을 주었다.
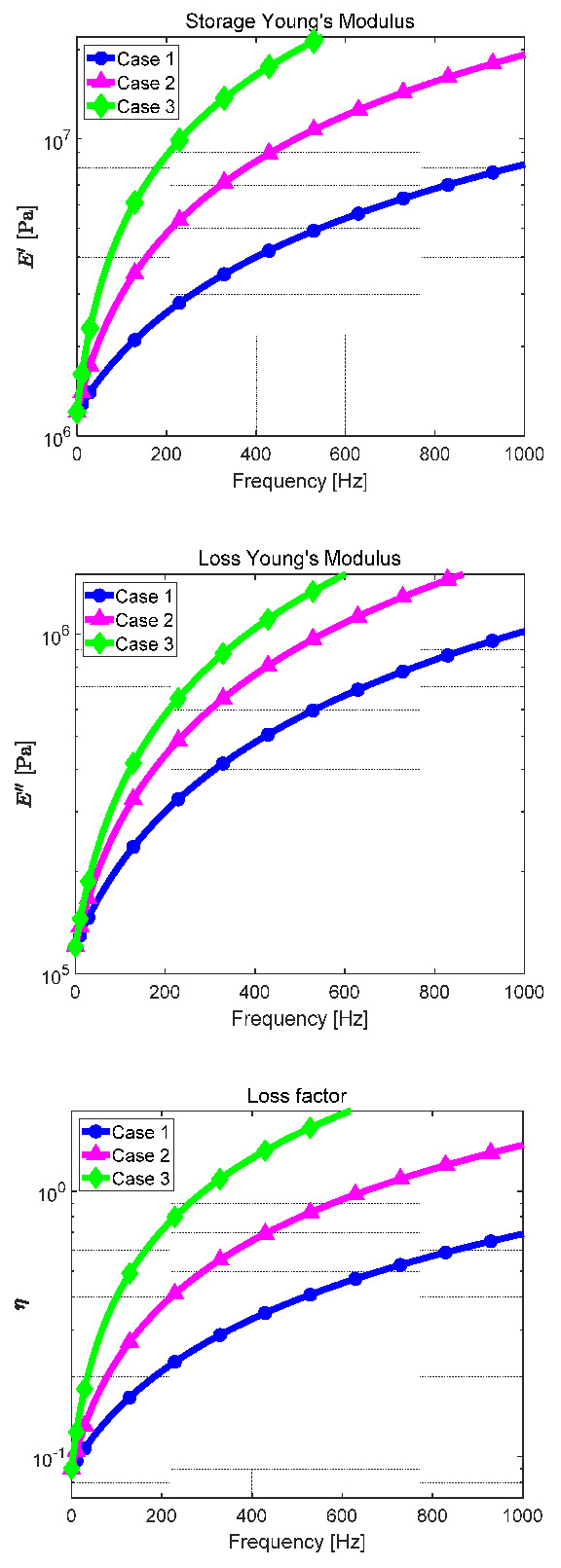
ANSYS Workbench 내에서 TB, ELASTIC, SDAMP Command을 사용하여 주파수에 따라 변하는 점탄성 물질의 물성치를 ASNYS에 적용하였다. 점탄성 물질의 물성치는 주파수에 따라 선형으로 증가하고, 0 Hz에서 1.2 MPa, 500 Hz에서 4.7 MPa의 인장탄성계수를 가지며, 0 Hz에서 0.09 Hz, 500 Hz에서 0.39의 손실 계수를 갖는다고 가정하였다(적용된 물성치는 이소프렌고무(IR)의 물성치를 참고하였다).
4.2 수학 모델과 ANSYS 해석 비교
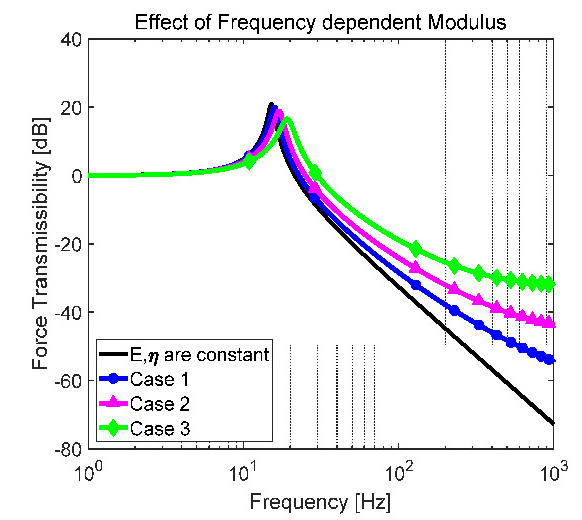
Figs. 7, 8은 ANSYS로 해석한 결과와 수학적 모델로 얻어낸 각 축에 대한 전달률의 크기와 위상차 결과이다. 고주파수에서 ANSYS 해석 결과에 피크가 생기는 현상은 수학식에는 포함되지 않는 2차 모드에 의한 영향으로 보여진다. 그래프에서 파란색 선은 수학 모델로부터, 분홍색 선은 ANSYS 해석으로부터 구한 결과이며 점선은 점탄성 물질의 물성치가 주파수에 의존하지 않고 일정할 때, 실선은 물성치가 주파수에 따라 변할 때를 나타낸다. 유도된 수학 모델의 타당성은 수학 모델과 ANSYS 결과로부터 얻은 공진주파수와 Roll-off rate가 거의 동일하다는 것을 보임으로써 입증하였다. Fig. 7로부터 주파수 변화에 따른 점탄성 물질의 물성치를 고려할 경우 공진주파수가 높아지며 고주파수 대역에서의 절연 성능이 악화되는 것을 확인할 수 있다.
5. 전달률 변화 분석
5.1 물성치 변화에 따른 전달률 변화
이 연구에서는 관심있는 주파수의 범위가 넓기 때문에 주파수에 따른 점탄성 재료의 물성 변화가 고려되어야 하며 물성 변화에 따라 설계한 진동 저감 장치의 성능이 어떻게 변화하는지 분석하는 일은 중요하다. 따라서 Fig. 9와 같이 주파수에 따라 물성 변화율이 다른 3가지 경우에 대해 전달률 변화를 살펴보았다.
Fig. 10은 주파수에 따라 물성 변화율이 다른 3가지 경우에 대해 전달률 변화를 나타낸다. Fig. 10에서 볼 수 있듯이 물성 변화율이 클수록 진동 저감 장치의 고유진동수는 커지고 고주파수에서의 절연 성능이 악화되는 것을 확인할 수 있다.
5.2 치수 변화에 따른 전달률 변화
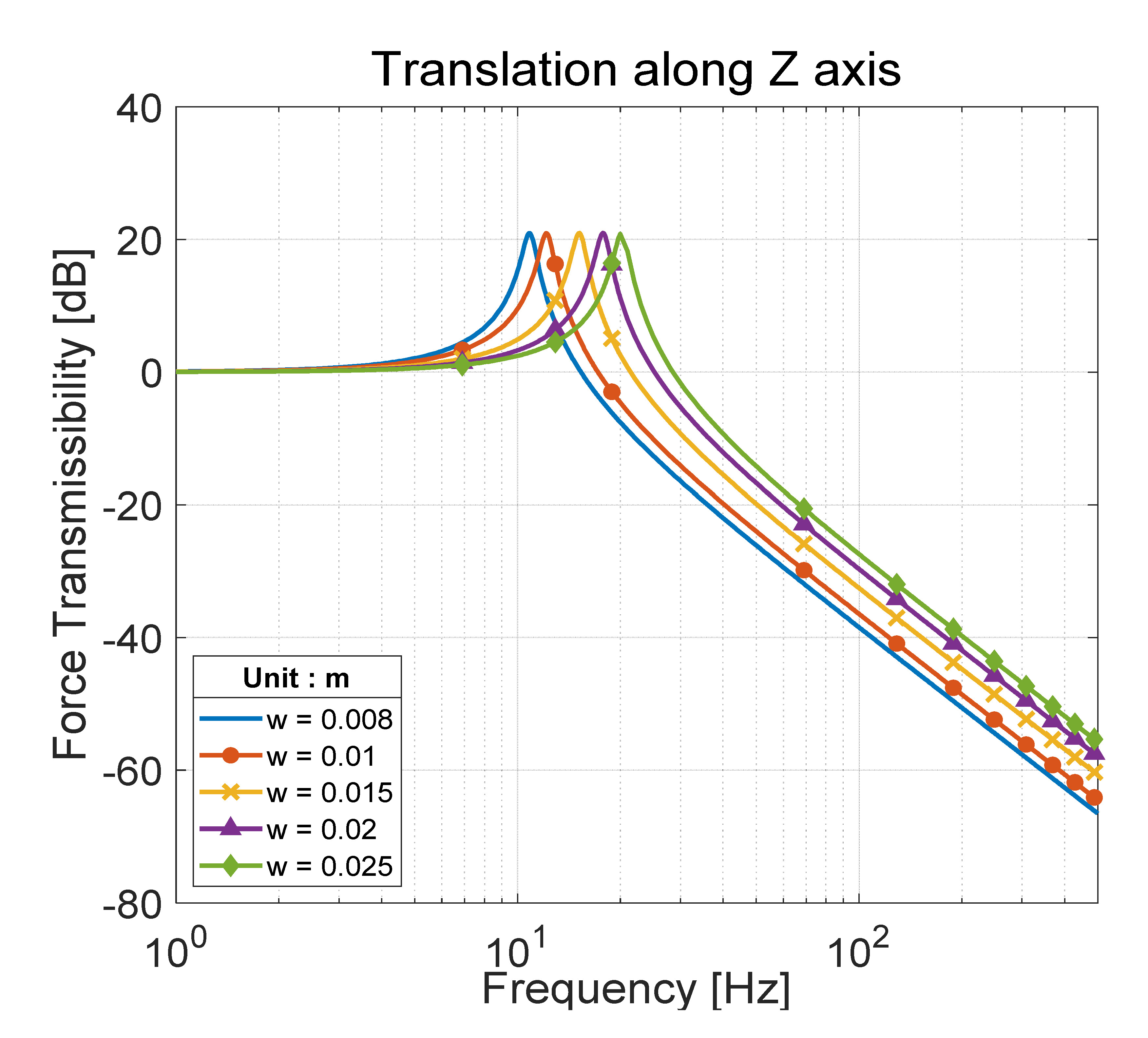
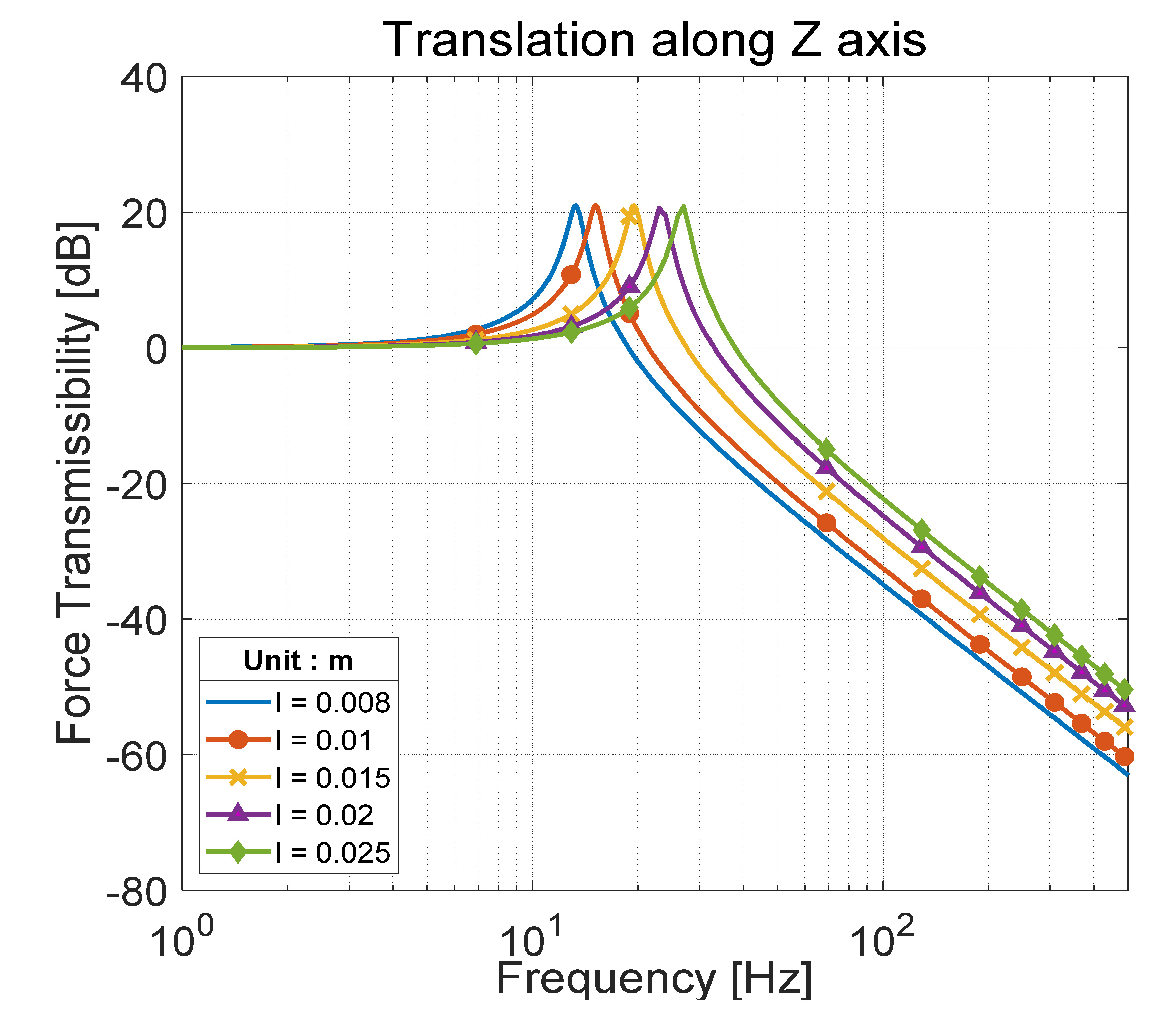
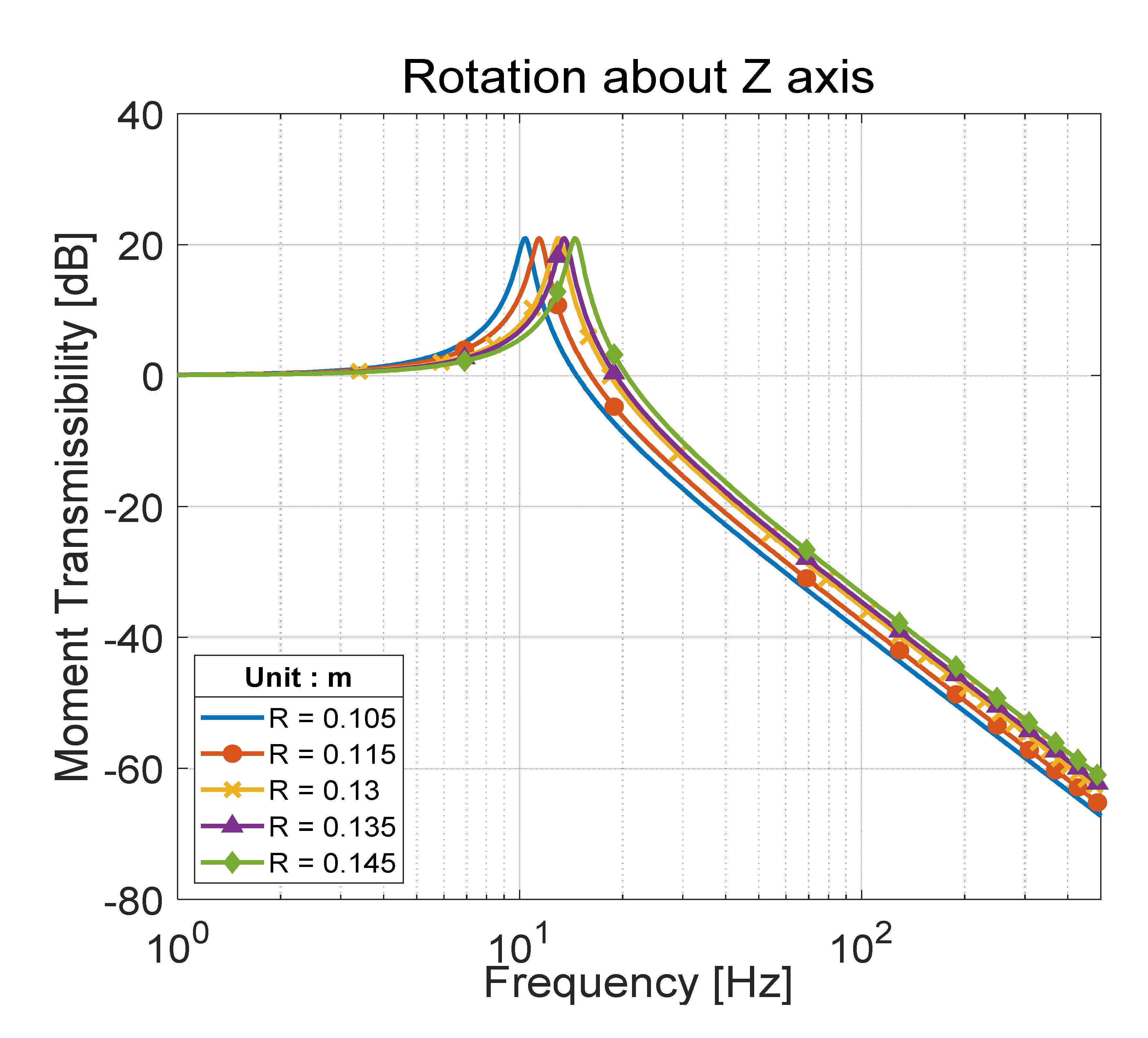
이 연구에서는 미소 진동을 저감시킬 점탄성 물질의 치수와 base 다리의 길이가 진동 저감 장치의 성능에 미치는 영향을 분석하였다. Figs. 11 ~ 13은 각각 점탄성 물질의 두께(t), 폭(w), 길이(l)에 따른 전달률 변화를 나타내며 Fig. 14는 base의 다리 길이(R)에 따른 전달률 변화를 보여준다. Figs. 11 ~ 13에서 볼 수 있듯이 진동 저감 장치의 고유진동수는 점탄성 물질의 두께가 증가함에 따라 감소하며, 폭과 길이가 증가함에 따라 증가한다. 모멘트 전달률의 경우, base의 다리가 길어질수록 고유진동수는 증가한다. 따라서 형상 설계 변수는 진동 저감 장치의 고유진동수만을 변화시키고, 고주파수에서의 roll-off rate는 –40 dB/decade로 일정하게 유지시킨다는 것을 알 수 있다.
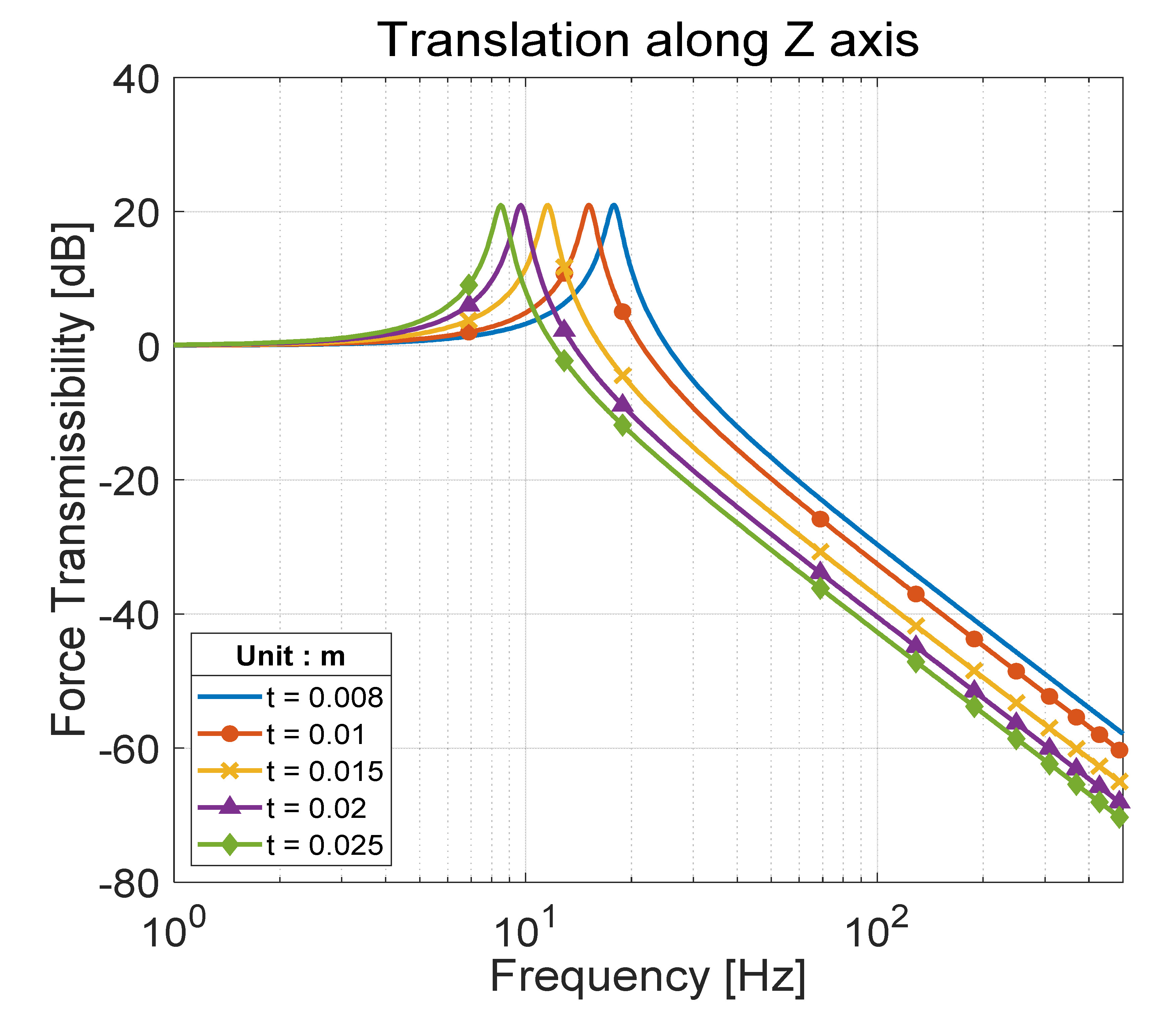
Comparison of transmissibility for several different values of the viscoelastic material’s thickness
6. 결론
이 연구에서는 위성체에서 제어 모멘트 자이로 등이 발생시키는 미소 진동을 저감시키기 위해 점탄성 물질을 삽입한 진동 저감 장치를 설계하였으며 저감 장치의 성능을 분석하기 위해 6자유도 운동방정식을 구하였다. 점탄성 물질의 특징을 고려하기 위해 유효 압축 계수의 개념과 주파수에 따라 물성치가 변하는 점탄성 물질의 특성을 수학적 모델에 반영하였다. 수학적 모델은 ANSYS로 수행한 해석 결과와 전달률의 크기와 위상차를 비교함으로써 검증하였다. 마지막으로 설계 변수에 따른 전달률 그래프의 변화를 비교 분석하였다.
이 논문에서 제안한 수학적 모델은 특정 설계 요구조건을 만족하는 점탄성 재료를 이용한 진동 저감 장치의 성능 평가 및 설계 변경에 유용하게 활용될 수 있을 것으로 기대된다.
기 호 설 명
| Ec : | 유효압축계수(effective compression modulus) |
| E* : | 복소탄성계수(complex Young’s modulus) |
| E : | 인장탄성계수(Young’s modulus) |
| G : | 전단탄성계수(shear modulus) |
| η : | 손실계수(loss factor) |
| v : | 푸아송 비(Poisson’s ratio) |
| m : | 진동원과 base의 질량 |
| t : | 점탄성 재료의 두께 |
| w : | 점탄성 재료의 폭 |
| d : | 점탄성 재료의 높이 |
| l : | 점탄성 재료의 길이 |
| R : | Base 다리의 길이 |
| : | 진동원을 포함한 진동 저감 장치의 질량중심에 대한 진동원과 base의 관성 모멘트 |
| Ix, Iy, Iz : | Base의 중심에 대한 진동원과 base의 관성 모멘트 |
| h : | 좌표축의 원점으로부터 진동원과 base의 질량중심까지의 거리 |
| Fd,x, Fd,y, Fd,z : | 진동원이 발생시키는 x,y,z축에 대한 가진력 |
| Ftr,x, Ftr,y, Ftr,z : | 진동저감장치를 지나 위성체에 전달되는 힘 |
| Md,x, Md,y, Md,z : | 진동원이 발생시키는 x,y,z축에 대한 가진 모멘트 |
| Mtr,x, Mtr,y, Mtr,z : | 진동저감장치를 지나 위성체에 전달되는 모멘트 |
References
-
Park, G., Lee, D., Yoon, J., and Han, J., (2014), Analytical & Experimental Study on Microvibration Effects of Satellite, Transactions of the Korean Society for Noise and Vibration Engineering, 25(1), p5-13.
[https://doi.org/10.5050/KSNVE.2014.24.1.005]

-
Jeong, H., Lee, J., Han, J., and Wereley, N. M., (2016), Design of Frequency-tunable Mesh Washer Isolators Using Shape Memory Alloy Actuators, Journal of Intelligent Material Systems and Structures, 27(9), p1265-1280.
[https://doi.org/10.1177/1045389X15588629]

-
Kim, B., Han, C., and Choi, S., (2018), Design and Analysis of MR Damper for Airplane Landing Gear, Transactions of the Korean Society for Noise and Vibration Engineering, 28(1), p102-109.
[https://doi.org/10.5050/KSNVE.2018.28.1.102]

- Wilson, J. F., and Davis, L. P., (1987), Viscous Damped Space Structure for Reduced Jitter, Proceedings of the 58th Shock and Vibration Symposium, p233-243.
- Maly, J. R., Pendleton, S. C., Salmanoff, J., Blount, G. J., and Mathews, J., (1999), Hubble Space Telescope Solar Array Damper, Proceedings the SPIE, Smart Structures and Materials: Passive Damping and Isolation, Newport Beach, CA, p186-197.
- Bronowicki, A. J., (2008), Forensic Investigation of Reaction Wheel Nutation on Isolator, 49th AIAA/ASMS/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Schaumburg, p1-11.
- Park, J. S., and Yang, K., (2010), Trends of the Vibration Isolation System for Spacecrafts, Current Industrial and Technological Trends in Aerospace, 8(2), p54-64.
-
Kim, S., (2017), RDVM Topology Optimization for Optimal Damping Treatment, Transactions of the Korean Society for Noise and Vibration Engineering, 27(1), p72-79.
[https://doi.org/10.5050/KSNVE.2017.27.1.072]

-
Rao, M. D., (2003), Recent Applications of Viscoelastic Damping for Noise Control in Auto-mobiles and Commercial Airplanes, Journal of Sound and Vibration, 262(3), p457-474.
[https://doi.org/10.1016/S0022-460X(03)00106-8]

-
Rashid, A., and Nicolescu, C, M., (2008), Design and Implementation of Tuned Viscoelastic Dampers for Vibration Control in Milling, International Journal of Machine Tools and Manufacture, 48(9), p1036-1053.
[https://doi.org/10.1016/j.ijmachtools.2007.12.013]

- Snowdon, J. C., (1968), Vibration and Shock in Damped Mechanical Systems, John Wiley & Sons, Inc, New York.
-
Tsai, H. C., (2005), Compression Analysis of Rectangular Elastic Layers Bonded between Rigid Plates, International Journal of Solids and Structures, 42(11-12), p3395-3410.
[https://doi.org/10.1016/j.ijsolstr.2004.10.015]


Do-hee Yoon received B.S. degree in mechanical engineering from Inha Univ. in 2017. She is currently a M.S. candidate in aerospace engineering at KAIST. Her research interests are structural dynamics and vibration isolation.

Jong-Eun Suh received B.S. degree in mechanical engineering from KAIST in 2015. He received M.S. degree in aerospace engineering at KAIST. He is currently a Ph. D candidate in aerospace engineering at KAIST. His research interests are structural dynamics and deployable structures.

Jae-Hung Han received a B.S. degree in aerospace engineering from KAIST in 1991. He then received M.S. and Ph.D. degree from KAIST in 1993 and 1998, respectively. Dr. Han is currently a professor and department head of the department of aerospace engineering at KAIST in Daejeon, Korea. His research interests are in the area of smart materials, structures and systems.

Joongbo Seo received the B.S. degree in electronic engineering from Korea Advanced Institute of Science and Technology, Daejeon, South Korea, in 2006, and the M.S. and Ph.D. degrees in mechanical and aerospace engineering from Seoul National University, Seoul, South Korea, in 2008 and 2014, respectively. He joined the Defense Industry Technology Center, Agency for Defense Development in 2015. His research interests concern guidance and control, formation flight of unmanned aerial vehicles, aircraft, and satellite attitude control.

Deok Ki Song received the B.S. degree in mechanical engineering from Han Yang Univ. in 1999. He then received M.S. degree in precision mechanical engineering from Han Yang Univ. in 2001. He joined the LIG Nex1 Co., Ltd in 2001. He is currently a research engineer. His research interests dynamics of many gimbal application for aerospace and satellite attitude control.