초음파 센서의 진동분포에 따른 음향 특성

1. 서론

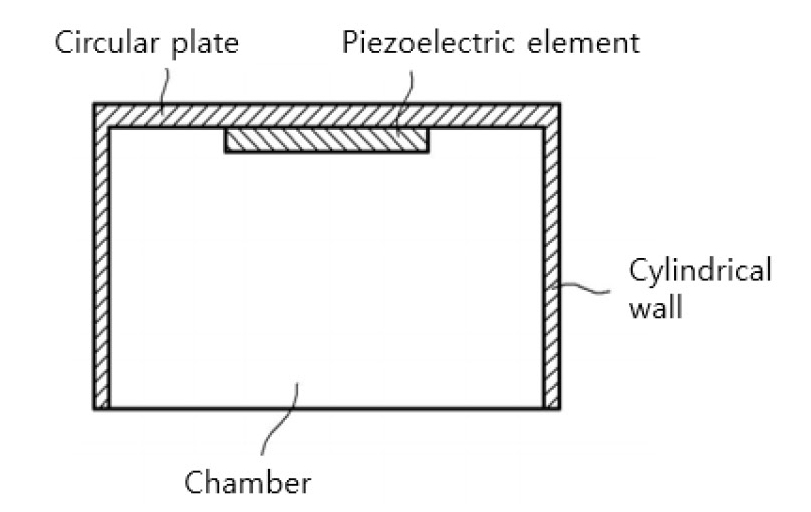
거리측정용 초음파 센서는 자동차 또는 드론에서 장애물 탐지에 사용되거나^(1,2) 산업 및 농업용 수위 측정에 사용된다⁽³⁾. 자동차에서는 Fig. 1에 보인 바와 같이 뒤 범퍼에 설치되어 후진 때 후방 장애물 감지에 주로 사용되고 있고, 주차 보조 시스템에서 전/후/측방 장애물 감지에도 사용된다⁽⁴⁾. 이는 자연계에서 박쥐가 초음파를 사용하여 동굴벽을 감지하는 원리와 같다⁽⁵⁾.

Fig. 1

Ultrasonic sensors on a bumper

자동차용 초음파 센서는 Fig. 2에 보인 바와 같이 압전 소자와 원판 및 원통벽으로 구성된다⁽⁶⁾. 원판과 원통 벽의 결합체를 하우징이라 부른다. 압전 소자의 가진에 의해 하우징 원판이 진동하여 초음파가 발생된다. 방사된 초음파가 전파하다가 반사면에서 되돌아와 센서에서 수신된다. 측정되는 전파시간과 음속의 곱으로 전파거리가 구해진다. 초음파 센서의 측정 가능한 거리 범위에 영향을 주는 인자 중 하나는 음향 지향성이다. 지향성은 음향파워를 원하는 방향으로 집중시키는 정도를 의미한다⁽⁷⁾. 초음파 센서의 지향성은 하우징 원판의 진동 속도분포 또는 변위분포에 따라 다르다⁽⁸⁾. 따라서 지향성을 향상시키기 위해서는 진동변위분포와 지향성의 상관관계를 파악할 필요가 있다.

Fig. 2

Cross-sectional view of an ultrasonic sensor

원판의 고유진동 모드형상과 조화가진 응답분포는 경계조건에 따라 베셀함수의 조합으로 표현된다⁽⁹⁾. 원판의 둘레가 단순지지 되거나 고정되어 있는 경우에 기본 모드형상을 단순화하여 2차 함수 또는 4차 함수로 표현하고 음향 해석을 한 사례도 있다⁽⁸⁾. 한편, Umchid는 의료용 초음파 센서로 사용되는 트랜스듀서의 지향성 패턴을 측정하였다⁽¹⁰⁾. Manthey 등은 배열된 미소 초음파 트랜스듀서를 사용하여 원하는 빔 패턴을 구현하고자 하였으며, 사각지대를 회피하는 방법에 적용하였다⁽¹¹⁾.

이 논문은 거리측정용 초음파 센서 원판의 균일 진동분포와 실제 진동분포에 따른 초음파 음향 지향성을 다룬다. 진동변위분포가 균일한 경우에 지향성을 이론적 음향 해석으로 구하고 유한요소 해석으로도 구하여 비교하였다. 실제 초음파 센서의 진동변위분포와 음향 지향성을 유한요소 해석으로 파악하였다. 이 연구를 통해 지향성을 향상시키는 진동변위분포를 찾고 하우징 구조를 개선하고자 한다.

2. 이론적 음향 해석

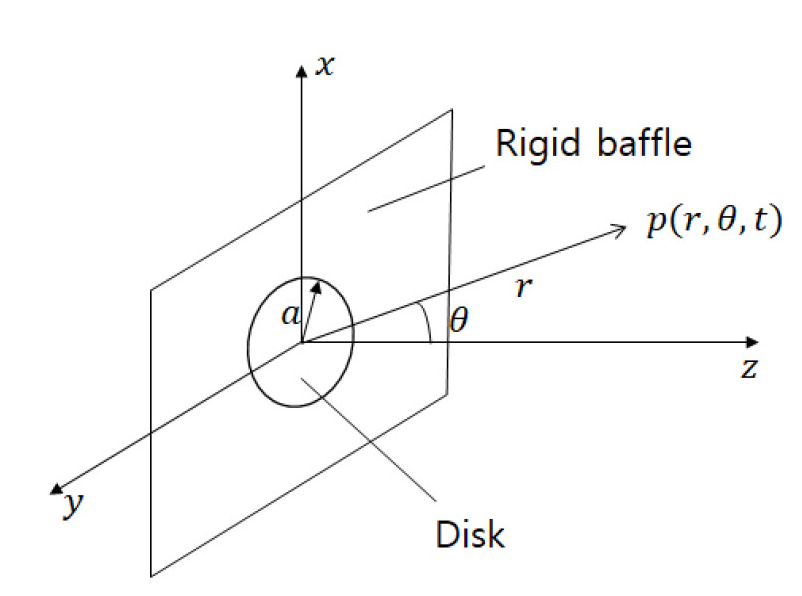
축 대칭 초음파 센서의 원판 진동에 의해 방사되는 초음파의 음향 특성을 이론적으로 해석한다. 원판형 음향 방사면의 진동이 균일하면 기존 이론⁽⁷⁾을 적용할 수 있다. Fig. 3과 같이 반지름이 a인 진동 원판으로부터 방사되어 전파하는 음파의 음압 p(r,θ,t)는 다음 식으로 표현된다⁽⁷⁾.

Fig. 3

Geometry used in deriving the acoustic field

여기서 ω는 가진주파수이고, k(=ω/c)는 파동수이며, c는 음속이다. 식 (1)에서 P(r,θ)는 음압 크기로서 다음과 같다.

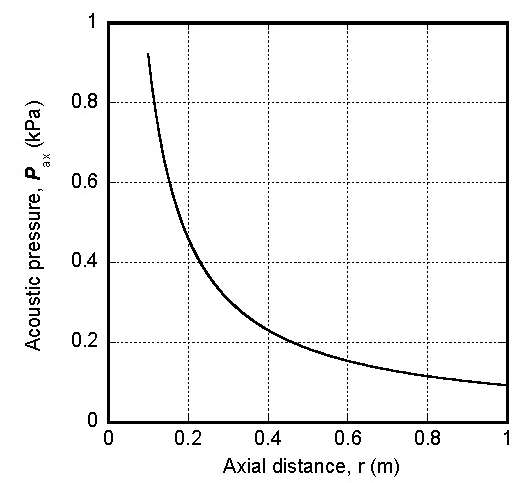
여기서 θ는 원판에 수직인 중심 축으로부터 벗어난 각도이고, H(θ)는 지향성 인자(directivity factor) 이며, P_ax(r)은 원판 중심에서 축 방향으로 거리 r만큼 떨어진 지점의 음압 크기이다. 원거리 음장(r/a ≫ ka)에서 P_ax(r)이 다음과 같이 표현된다⁽⁷⁾.

여기서 ρ는 공기의 밀도이고, U는 원판의 수직방향 속도 진폭이다. 식 (3)은 원거리 음장의 음압 크기가 거리 r에 반비례함을 의미한다.

지향성 인자 H(θ)는 다음과 같이 표현된다⁽⁷⁾.

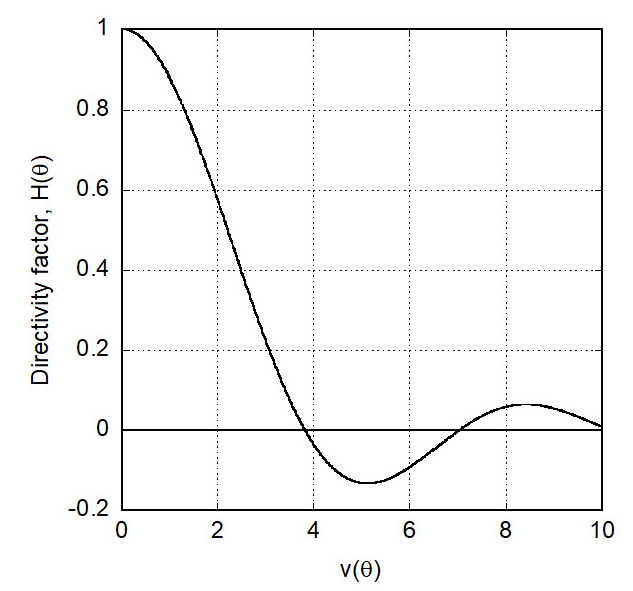
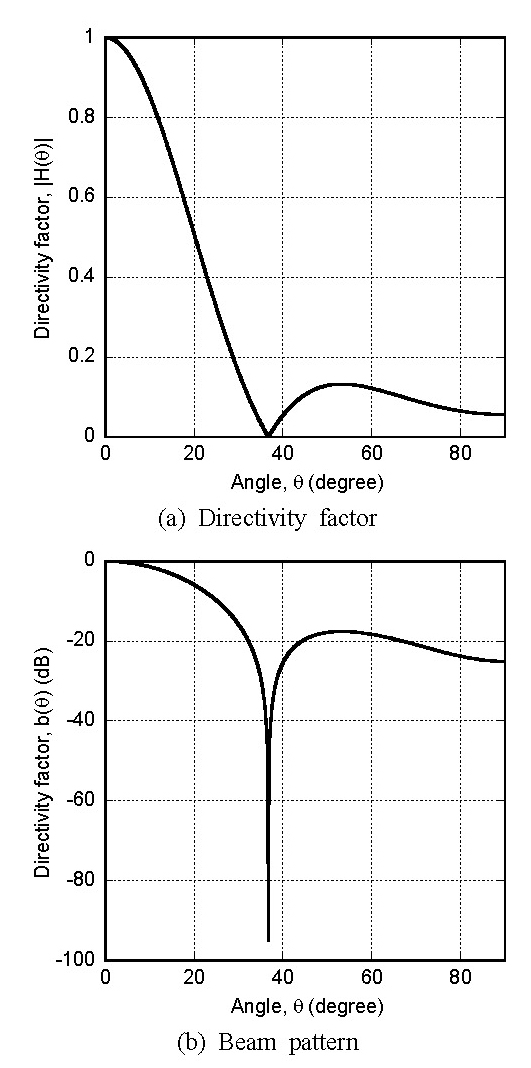
여기서 v(θ)=kasinθ이고 J₁은 1종 베셀 함수이다. 지향성 인자는 방향 각도 θ의 함수이고, 파동수 k와 원판 반지름 a에 따라서도 다르다. 원판 반지름 a가 7 mm이고 주파수 범위가 20 kHz ~ 100 kHz이면, ka의 범위는 2.6 ~ 12.9이므로 v(θ)는 12.9 이하이다. 지향성 인자 함수의 양상을 Fig. 4에 나타내었다. 지향성 인자를 dB 단위로 환산하여 방향에 따라 표현하면 다음과 같고, 이를 빔 패턴(beam pattern)이라 한다⁽⁷⁾.

Fig. 4

Functional behavior of the directivity factor H(θ)

음향 지향성 D는 음향강도(acoustic intensity)의 비로 정의되며 다음 식으로 표현된다.

여기서 I_s(r)과 P_s(r)은 음파를 발생시키는 점 음원의 중심에서 거리 r만큼 떨어진 위치의 음향강도와 음압이고, I_ax(r)은 원판 음원의 중심에서 축 방향으로 거리 r만큼 떨어진 위치의 음향강도이다. 음향파워(acoustic power)로부터 유도한 결과 지향성 D가 다음과 같다.⁽⁷⁾

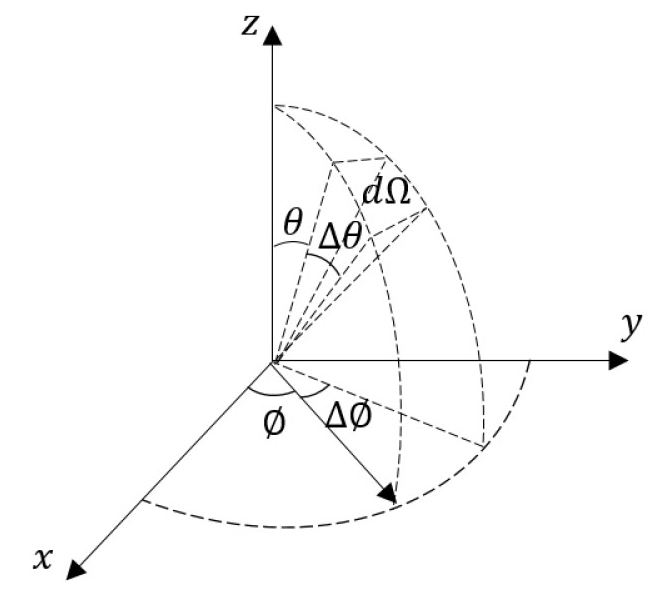
여기서 적분구간 4π는 구의 입체각 범위를 의미한다. Fig. 5와 같이 구의 표면에서 미소 면적을 입체각 dΩ(=2πsinθdθ)로 표현하고 적분할 수 있다.

Fig. 5

Geometry used in deriving the 3-dimensional angle dΩ

적분 범위 Θ는 구면에서 π인데 배플(baffle)된 반 구면에서는 π/2이다.

식 (8)의 분모를 이산(discrete)표현으로 대체하면 다음과 같다.

이 표현은 유한요소 해석 결과로부터 지향성을 계산할 때 사용된다.

한편 식 (8)은 다음과 같이 근사화된다⁽⁷⁾.

초음파 센서 원판의 진동 분포가 균일한 경우 지향성 D는 파동수와 원판의 반지름의 곱 ka에 주로 달려있다.

Table 1에 제시된 바와 같이 대기압 상온(20 ˚C) 조건에 공기 물성치는 밀도가 1.2 kg/m³이고 음속이 343 m/s이다. 원판은 반지름이 7 mm이고 구동주파수가 50 kHz이며 속도 진폭이 10 m/s이다. 이를 식 (3)에 적용하여 거리별 음압 크기 P_ax(r)을 계산하여 Fig. 6에 나타내었다.

Table 1

Air properties and disk specification

Fig. 6

Acoustic pressure magnitude along the axial distance

식 (4)에 표현된 지향성 인자를 계산하고 절대값을 취하여 방향별로 나타낸 결과를 Fig. 7(a)에 제시하였다. 또한 식 (5)로부터 빔 패턴을 계산한 결과는 Fig. 7(b)이다. Fig. 7(a)에서 음압이 0이 되는 각도가 Fig. 7(b)에서 노드면을 나타낸다.

Fig. 7

Calculated directivity factor and beam pattern

3. 진동분포 유한요소 해석

2절의 이론적 음향 해석에서, 센서 하우징 원판의 진동분포가 균일한 경우의 초음파 음향 지향성을 계산하였다. 실제 초음파 센서의 하우징 원판의 진동분포는 균일하지 않다. Fig. 2에 보인 바와 같이, 센서의 하우징은 원판과 원통 벽의 결합체여서 원판 둘레가 고정되어 있다. 둘레가 고정된 원판의 진동은 중심에서 가장 크고 가장자리로 갈수록 작다. 원판의 진동분포를 [1-(r/R)²]²으로 단순화하여 방사 초음파의 음향 지향성을 살펴본 사례가 있다⁽⁶⁾. 이 논문에서는 유한요소 해석으로 실제 초음파 센서의 원판 진동분포를 구하여, 단순화 식과 비교하고 음향해석에 사용한다.

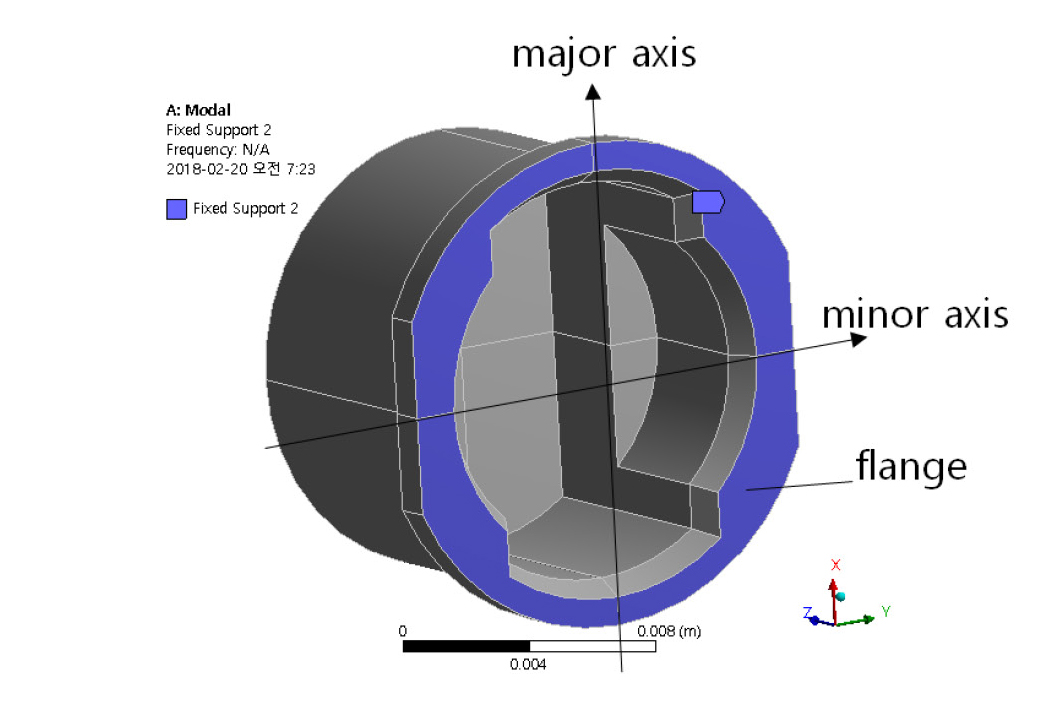
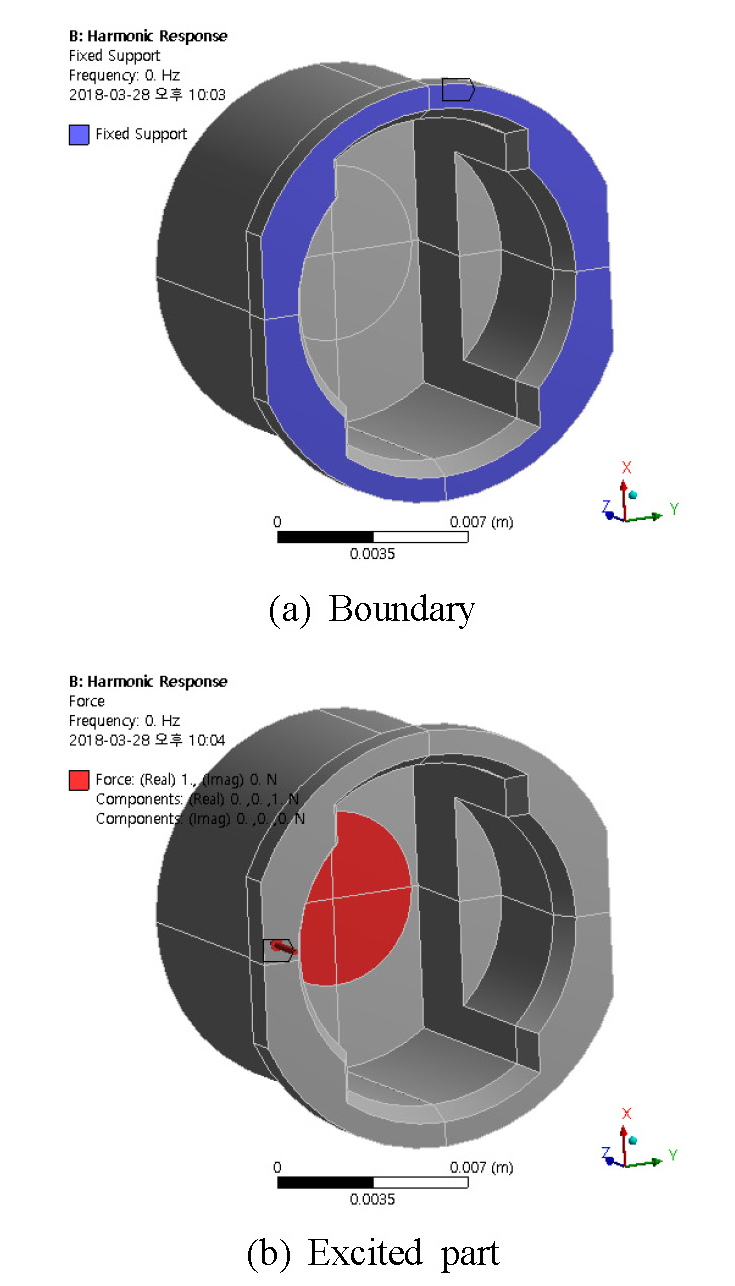
원판이 결합된 원통 벽의 반대쪽에 플랜지가 있는 초음파 센서 하우징에 대해, 상용 프로그램인 SolidWorks를 사용하여 Fig. 8과 같이 해석 모델을 만들었다. 수직방향은 장축, 수평방향은 단축에 해당된다. 하우징의 재질은 알루미늄 합금이고, 하우징 원판의 지름은 14 mm이다. 원판의 두께방향 진동분포를 찾아내고자 상용 프로그램인 ANSYS를 사용하였다. 유한요소는 사면체 형태(SOLID72)이며, 요소 크기는 0.5 mm이고, 요소 개수는 약 13000이다. Fig. 8에 보인 모델에서 하우징의 플랜지에 고정(fixed)경계조건을 설정하고, 모드해석과 조화가진 응답 해석을 하였다.

Fig. 8

Model of an ultrasonic sensor housing

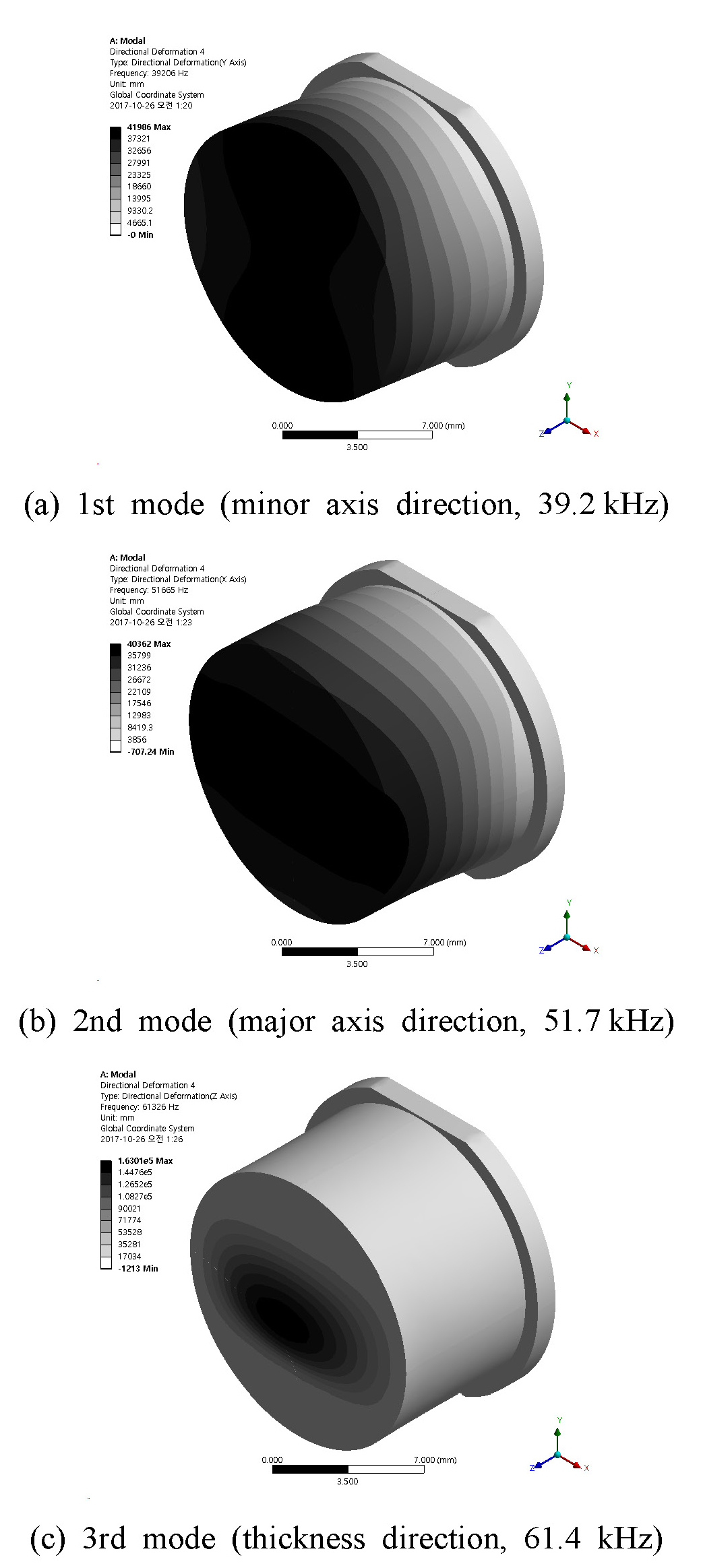
초음파 센서 하우징을 대상으로 모드 해석한 결과를 Fig. 9에 보였다. Fig. 9의 (a)와 (b)에 각각 보인 1차 모드와 2차 모드는 원통벽의 진동이다. 3차 모드에서 원판에 두께방향 진동이 나타났다. Fig. 9의 (c)에 보인 3차 모드는 진동 원판의 표면에서 두께방향 진동 분포가 2면 대칭 형태이며 종(bell) 모양을 이루고 있다. 장축과 단축의 진동분포를 비교하면 종 모양의 폭이 다르다.

Fig. 9

Modal analysis result for the housing of an ultrasonic sensor

압전 소자의 가진에 따른 하우징 원판의 두께방향 진동변위분포를 확인하고자 조화가진 응답 해석을 하였다. Fig. 10에 보인 해석 모델에서 (a)에는 고정 경계조건이 설정되는 플랜지 부분을 표시하였고, (b)에는 원판 중앙의 가진부를 표시하였다. 가진부는 원판의 내부 표면에서 지름 6.5 mm인 원이고, 1 N 크기와 61 kHz 진동수의 조화 가진 힘이 두께방향으로 가해진다. 가진 진동수는 모드해석에서 얻은 두께방향 고유진동수이다.

Fig. 10

Boundary and excited part of an ultrasonic sensor model for harmonic analysis

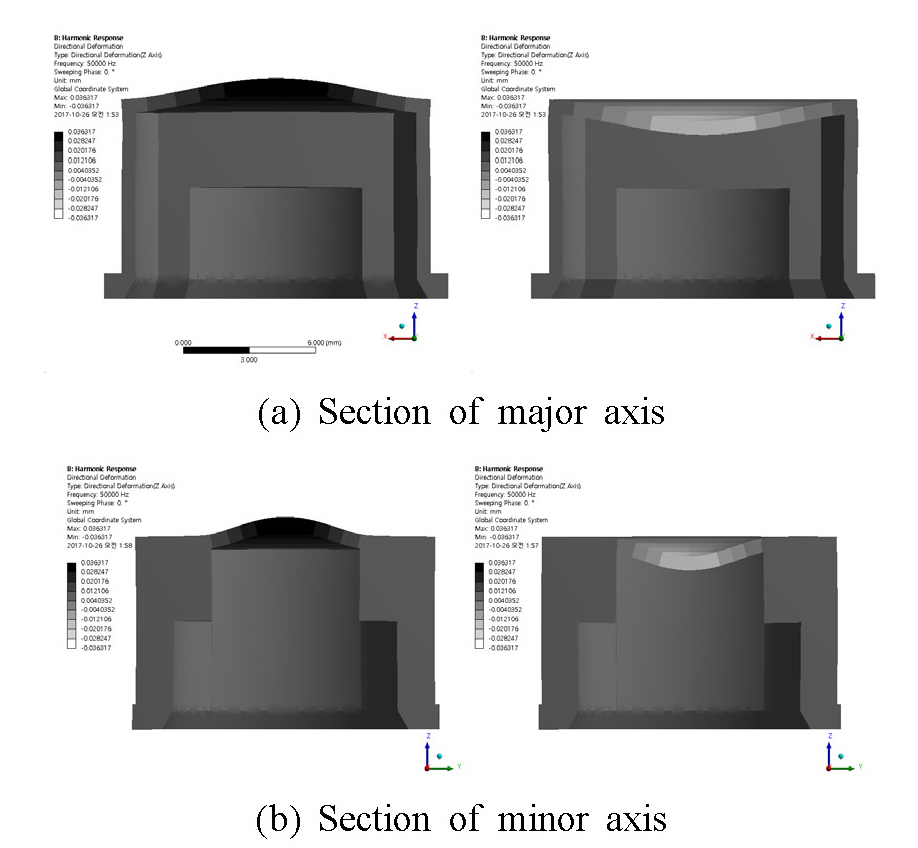
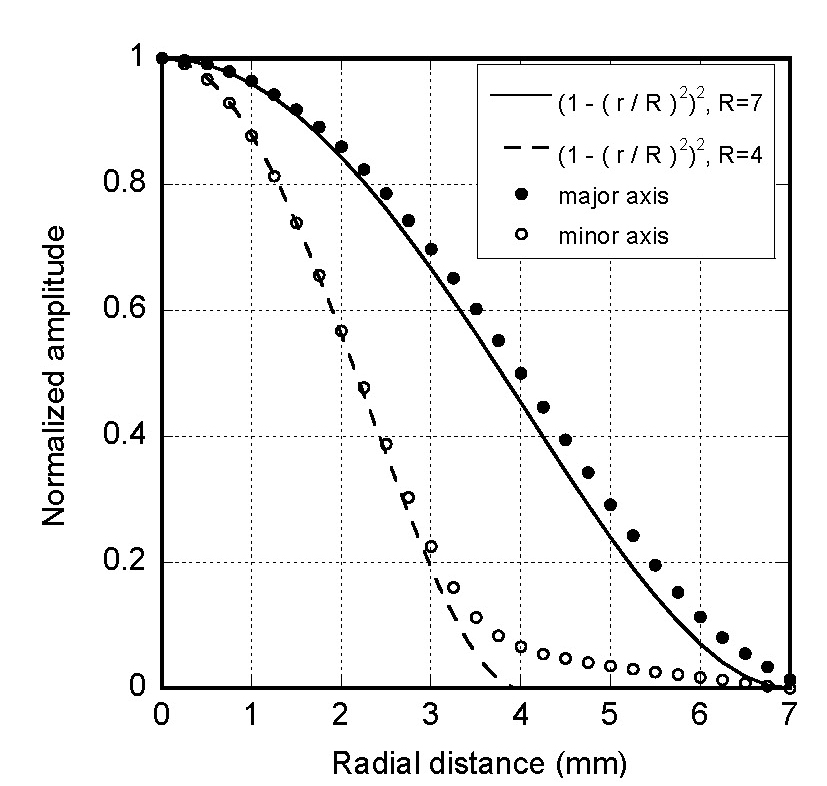
Fig. 11은 조화가진 응답 해석 결과 중 두께방향 진동분포이며, 종 모양을 띠고 있다. (a)는 장축 단면에서 두께방향 진동 변위의 결과이며, (b)는 단축 단면에서의 결과이다. Fig. 11에 제시된 원판의 진동 분포를 정규화하여 Fig. 12의 그래프에 점으로 표현하였다. 조화가진 응답 해석의 결과에서 두께방향 진동 변위는 모드 해석을 통한 3차 모드 형상의 진동 분포와 유사한 형태를 보인다. 이는 가진부의 가진 방향이 모드형상에서 나타난 진동방향과 일치하기 때문이다. 장축과 단축 단면에서 진동분포가 다른 것은 하우징이 2면 대칭 구조이기 때문이다.

Fig. 11

Harmonic analysis result for the housing of an ultrasonic sensor

함수형태 진동변위분포를 Fig. 12에 선으로 나타내어 해석 결과의 진동분포와 비교하였다. 유한요소 해석 결과가 함수형태의 진동분포와 유사한 경향을 갖는다.

Fig. 12

Vibration distribution on the plate of two-sided housing

4. 음향특성 유한요소 해석

초음파 센서의 하우징 원판의 진동에 의해 방사되는 초음파의 음향 특성을 파악하기 위해 음향 유한요소 해석을 하였다. 3절에서 구한 종 모양 분포의 진동에 의한 초음파의 음향 특성을 해석하고, 2절에서 이론적으로 해석한 결과와 비교하였다.

4.1 해석모델 및 가진 조건

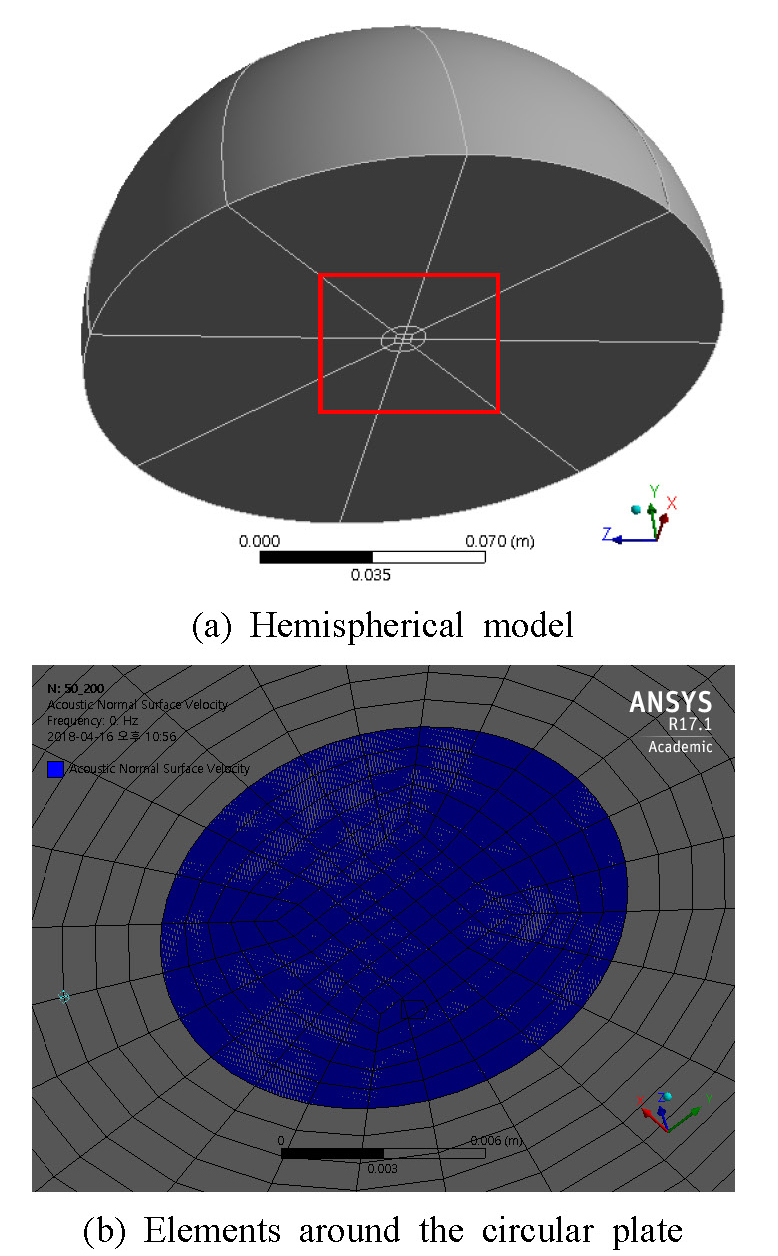
배플(baffle)된 원판의 진동으로부터 방사되는 초음파가 전파하는 영역의 음향 해석 모델을 반구 형태로 설정하였다. ANSYS에서 작성한 음향 해석모델을 Fig. 13에 제시하였는데, (a)는 전체 모델이고 (b)는 원판 부근 확대도이다. 가진 원판은 반구의 바닥면 중심에서 지름 14 mm인 원이고, 가진주파수는 50 kHz이다. 반구의 지름은 200 mm이며, 크기가 1 mm 이하인 육면체 요소(FLUID30) 약 540 000개이다. 반구의 반경방향 구면에 방사(radiation) 경계조건을 적용하였고, 바닥면에서 가진 원판을 제외한 나머지 부분에는 수직방향 변위가 0인 경계조건을 설정하였다.

Fig. 13

Acoustic analysis model

균일분포 가진은 가진 원의 수직방향으로 모두 균일한 변위분포를 가지며, 속도의 크기는 10 m/s이다. 종 모양 불균일분포의 가진은 변위분포를 10(1-(r/R)²)² m/s 형태로 입력한 것이다. 여기서 r은 반경방향 위치이고, R은 원판의 반지름 크기이다.

실제 초음파 센서의 가진부 원판의 진동분포는 3절에서 구한 바와 같이 종 모양으로 불균일하다. 2절에서는 이론적 음향해석을 위해 균일분포의 진동을 대상으로 하였지만, 이 절에서는 실제에 가까운 진동분포를 대상으로 하였다.

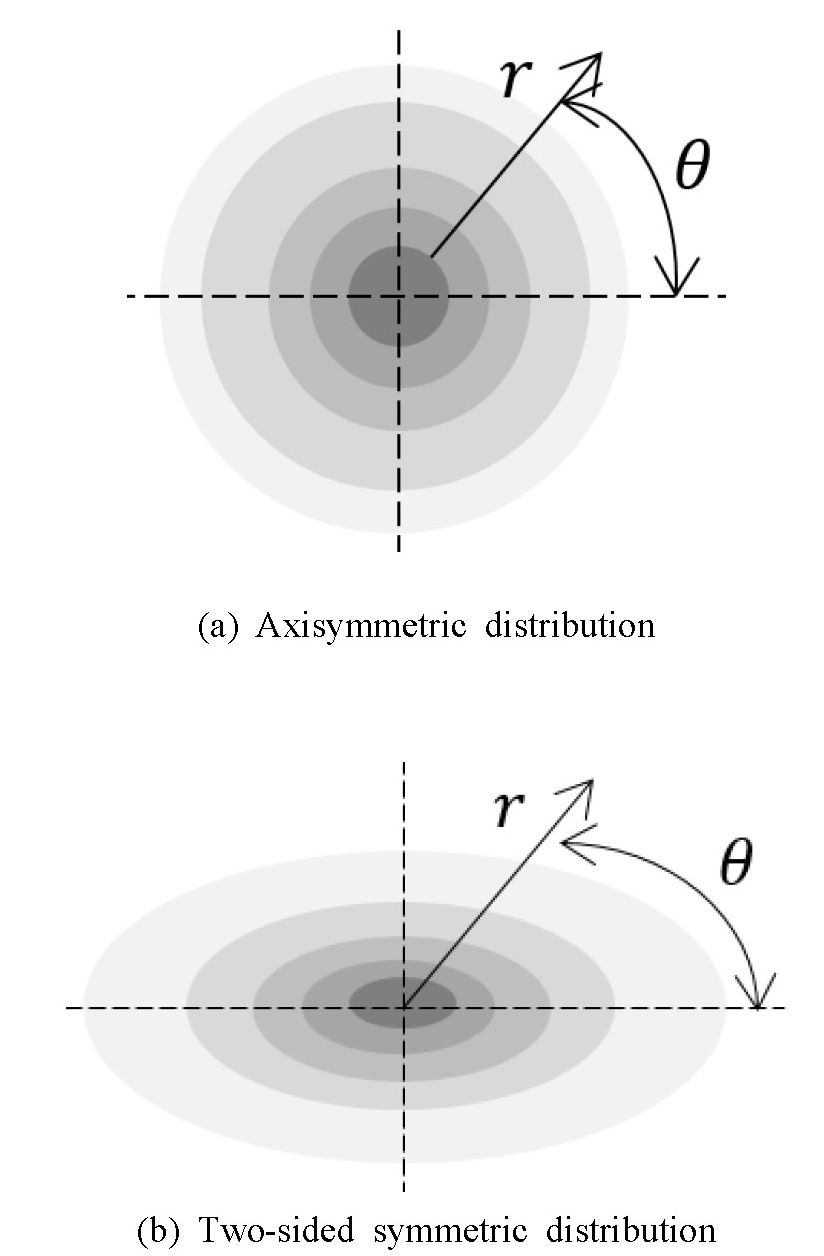
종 모양 분포는 Fig. 12에 보인 바와 같이 원판 중심에서 반경방향으로 갈수록 속도 진폭이 작아지는 형태이다. 또한 종 모양 진동분포에서는 축 대칭인 경우와 2면 대칭인 경우가 있다. Fig. 14는 진동분포가 종 모양인 2가지 경우를 나타낸다. (a)는 축 대칭인 경우이고 (b)는 2면 대칭인 경우이다. 축대칭 분포는 원형의 등고선으로 표현되고, 2면 대칭 분포는 타원의 등고선으로 표현된다.

Fig. 14

Non-uniform distribution of plate vibration

4.2 해석 결과

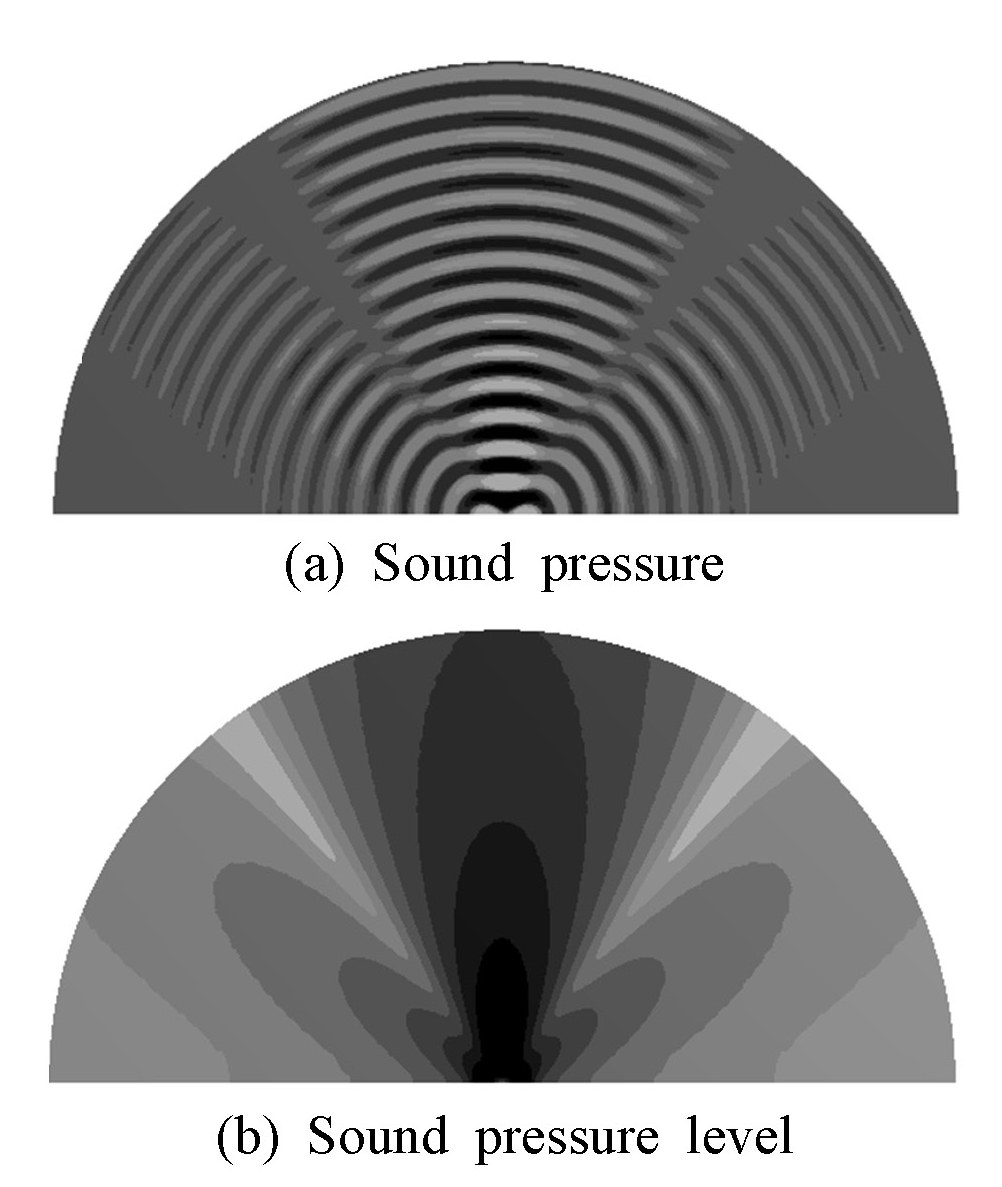
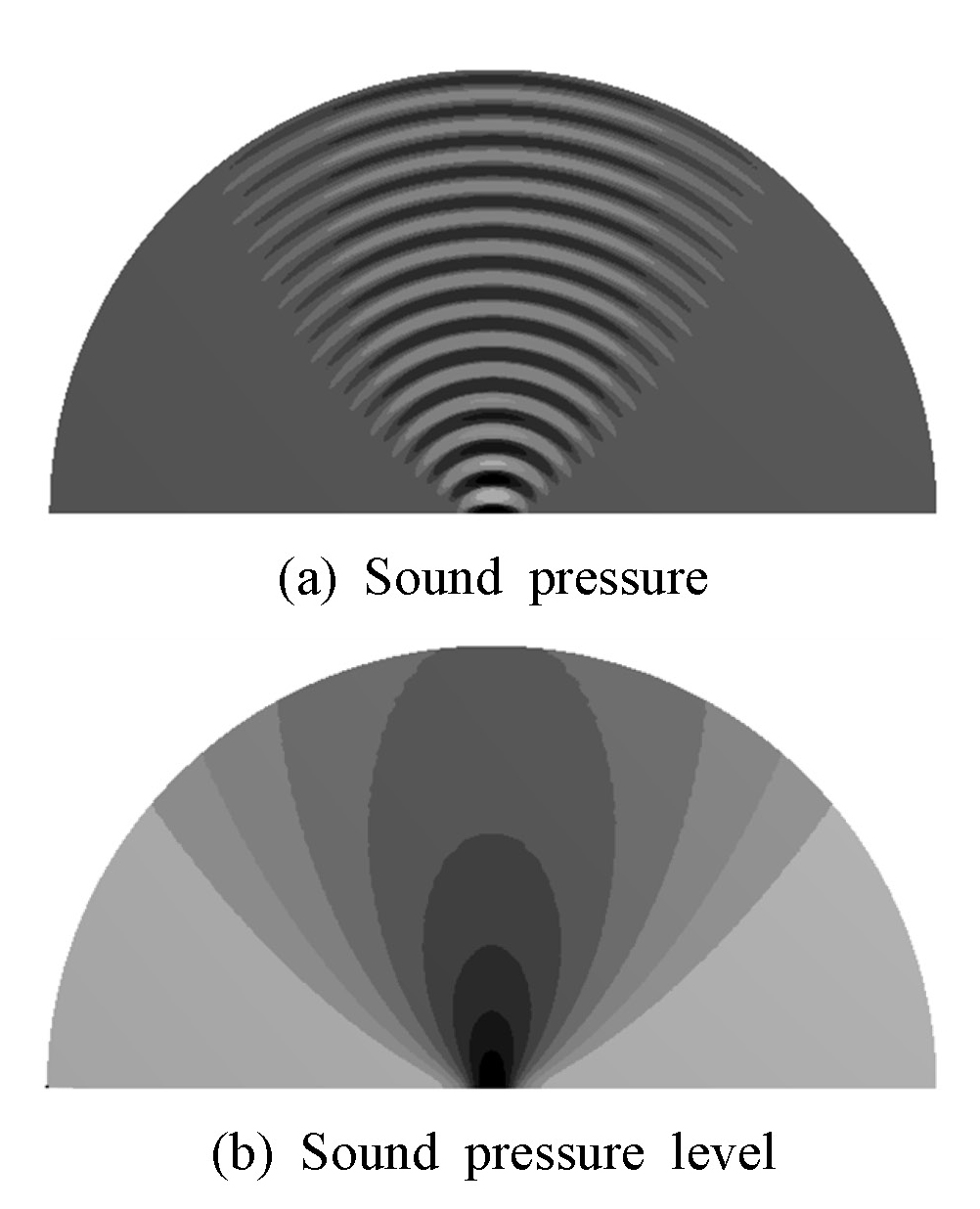
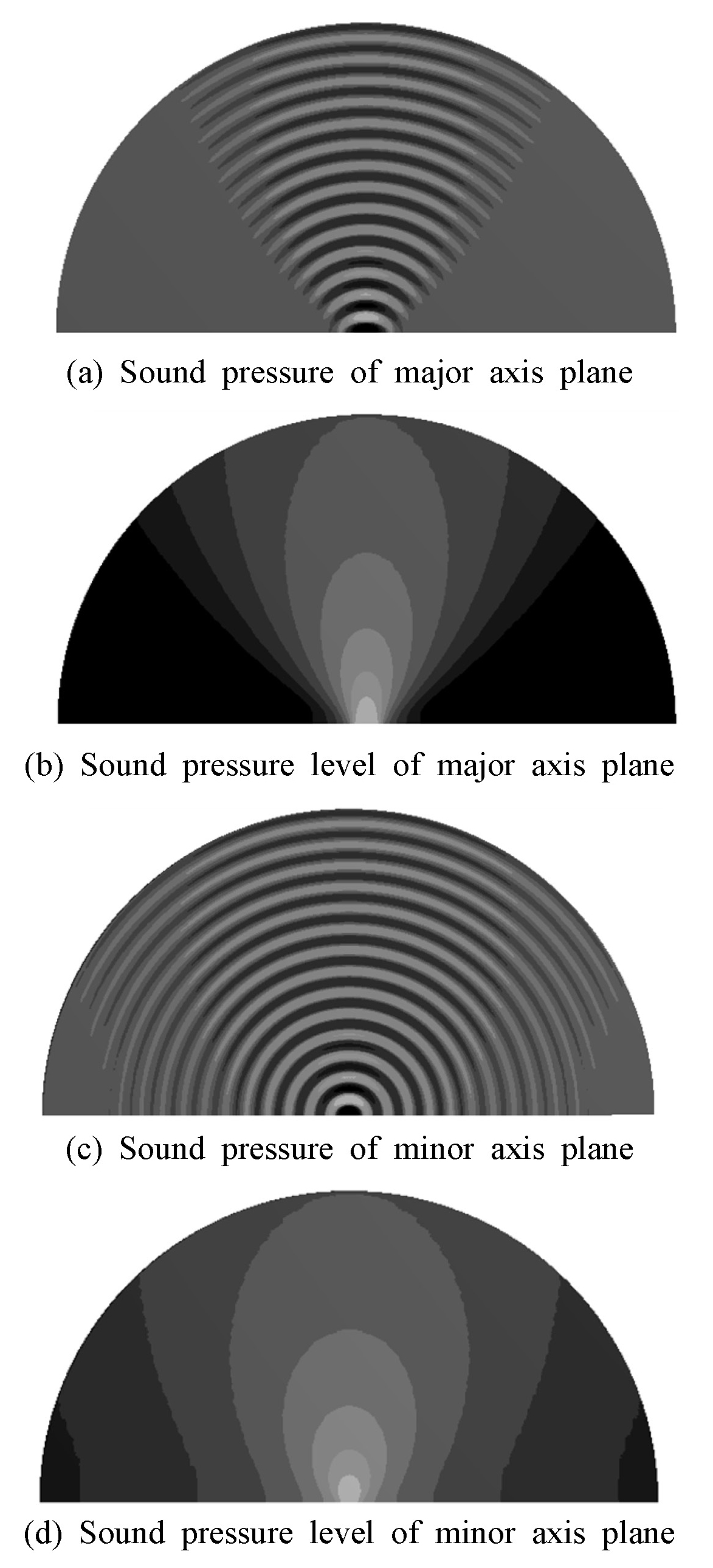
음향 유한요소 해석한 결과를 Figs. 15 ~ 17에 음압과 음압분포의 형태로 제시하였다. Fig. 15는 원판 가진이 균일한 경우에 발생하는 초음파의 반구영역 내 분포이다. Fig. 16은 원판 가진이 축대칭 종 모양 분포인 경우이며, Fig. 17은 원판 가진이 2면 대칭 종 모양 분포인 경우이다. 가진분포가 균일한 경우와 축대칭 종 모양인 경우에 음압분포와 음압레벨분포가 원판 중심축에 대칭이므로, 음향 공간에서 축방향의 어느 단면에서든지 분포도가 같다. 2면 대칭 종 모양 가진의 경우에는 장축 평면과 단축 평면에서 가진분포가 다르므로, 음압분포와 음압레벨 분포가 단면에 따라 다르다.

Fig. 15

Acoustic distribution calculated for uniform plate excitation

Fig. 16

Acoustic distribution calculated for non-uniform plate excitation

Fig. 17

Acoustic distribution calculated for two-sided symmetric non-uniform plate excitation

Figs. 15 ~ 17에 제시된 음압분포도로부터 축방향 거리에 따른 음압을 추출하여 Fig. 18에 그래프로 나타내었다. 거리에 따른 음압은 균일분포 가진의 경우가 가장 크다. 가진 원의 중심 축방향 거리 100 mm에서의 음압과 음압레벨을 Table 2에 가진 분포별로 기재하여 비교하였다. 가진분포가 균일한 경우가 거리별 음압이 크다.

Fig. 18

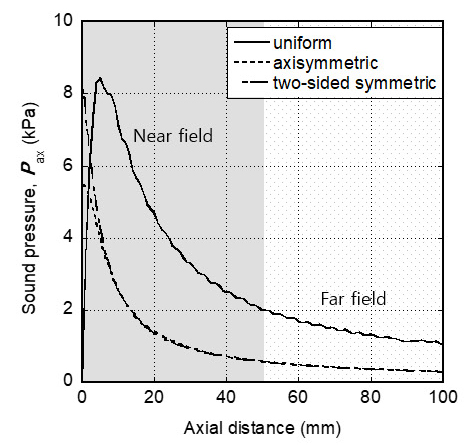
Sound pressure of ultrasound along the axial distance from the plate with uniform and non-uniform vibration distribution

Table 2

Sound pressure and sound pressure level in the axial distance of 100 mm

식 (4)에 정의된 지향성 인자는 가진부의 중심으로부터 일정 거리에서 방향별 음압 데이터로부터 수치 계산된다. 중심축의 음압이 기준이고 원주방향의 데이터들이 기준 음압으로 나누어져 지향성 인자가 얻어진다. Figs. 15 ~ 17에 제시된 음압 분포도에서 반구면 데이터로부터 방향별 음압을 추출하여 Fig. 19에 지향성 인자의 그래프로 표현하였다. 가진부 주변이 배플된 조건에서 균일분포의 가진인 경우에 초음파의 노드면 각도가 약 37.0˚로 나타났으며, 이는 이론적으로 계산된 값인 36.7˚와 유사하다.

Fig. 19

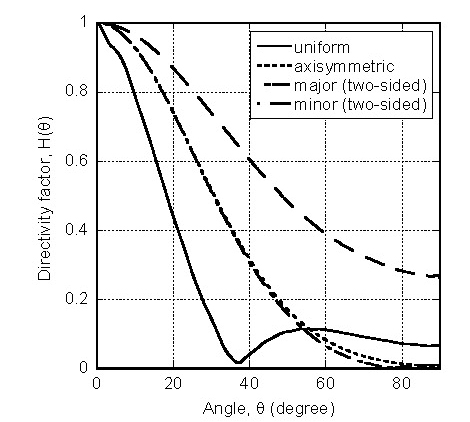
Directivity factor of ultrasound radiating from the plate with uniform and non-uniform vibration distribution

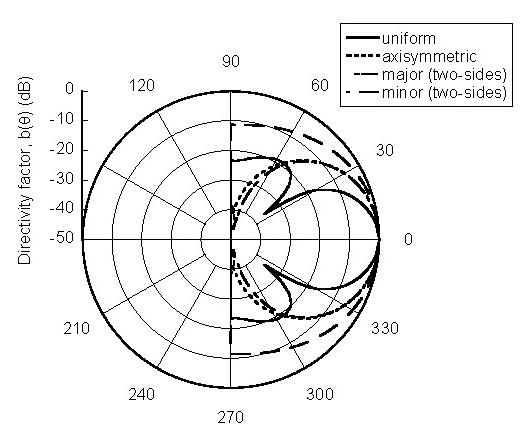
식 (5)에 정의된 상대 음압레벨 b(θ)를 극좌표 형태로 그려낸 것을 빔패턴(beam pattern)이라 하는데, 이를 가진분포에 따라 Fig. 20에 표현하였다. 여기서 빔폭(beam width)을 확인할 수 있다. 빔폭은 원판 중심의 축 방향(θ = 0°) 음압레벨에 비해서 6 dB만큼 작은 값을 갖는 각도를 의미한다. 각도가 작을수록 지향성이 좋은 것이다. 가진분포에 따른 빔폭을 Table 3에 기재하여 비교하였다. 균일분포 가진인 경우에 빔폭이 가장 작게 나타났다.

Fig. 20

Beam pattern calculated for uniform and non-uniform plate excitation

Table 3

Beam width and directivity around 100 mm distance from the vibrating plate

식 (9)를 사용하여 지향성 D를 계산하였다. 원판중심 축 방향에서 음압의 크기가 기준이 된다. 진동분포별로 초음파의 지향성이 계산된 결과를 Table 3에 기재하여 비교하였다. 균일분포 가진인 경우가 지향성이 가장 좋다. 종 모양 진동분포 중 2면 대칭인 경우 단면에 따라 지향성이 다르며, 종 모양의 폭이 큰 장축 단면에서 지향성이 좋다.

균일분포 가진의 경우에 빔폭이 좁다보니 음압분포도와 빔패턴에 노드면과 부엽(sidelobe)이 나타났다. 부엽이 너무 크면 실제 센서의 계측에 부작용이 생길 수 있는데, Fig. 19에서 볼 수 있듯이 부엽 최대값이 주엽(mainlobe)의 10 % 정도로 양호한 수준이었다.

5. 실험

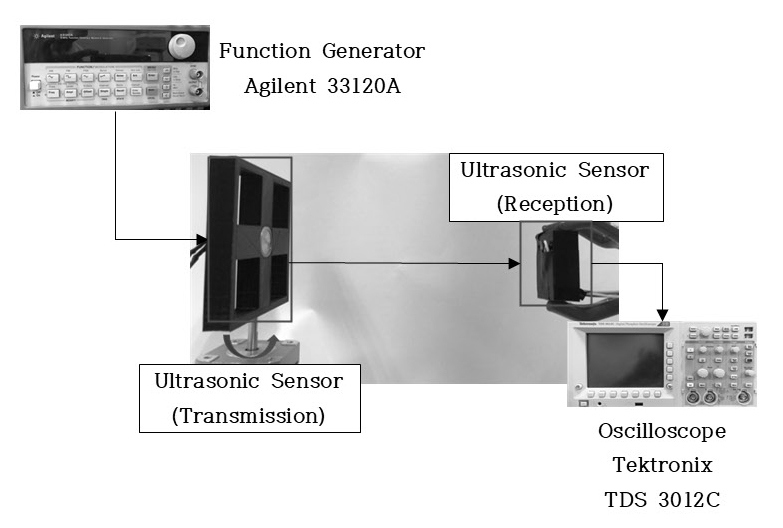
앞절에서 유한요소 해석으로 구한 음향 특성을 검증하기 위해 실험을 하였다. 초음파 센서의 가진에 의해 발생되는 초음파의 음압을 측정하는 실험 장치 구성도를 Fig. 21에 보였다. 사용된 계측기는 신호발생기와 증폭기 및 오실로스코프이다. 초음파 센서를 송신과 수신에 구분하여 사용하였다. 신호 발생기에서 40 kHz 정현파 30 cycle의 신호를 생성하여 송신용 초음파 센서에 입력하여 가진한다. 측정 방법은 2가지로서, 거리별 음압 측정과 방향별 음압 측정이다. 거리별 측정에서는 송신용 초음파 센서와 수신용 초음파 센서의 거리를 변화시켜가며 수신용 초음파 센서에서 음압을 측정하였다. 방향별 측정에서는 거리를 일정하게 하고 송신용 초음파 센서를 스텝 모터로 방향 각도를 변화해가며 수신용 초음파 센서에서 음압을 측정하였다.

Fig. 21

Experimental devices

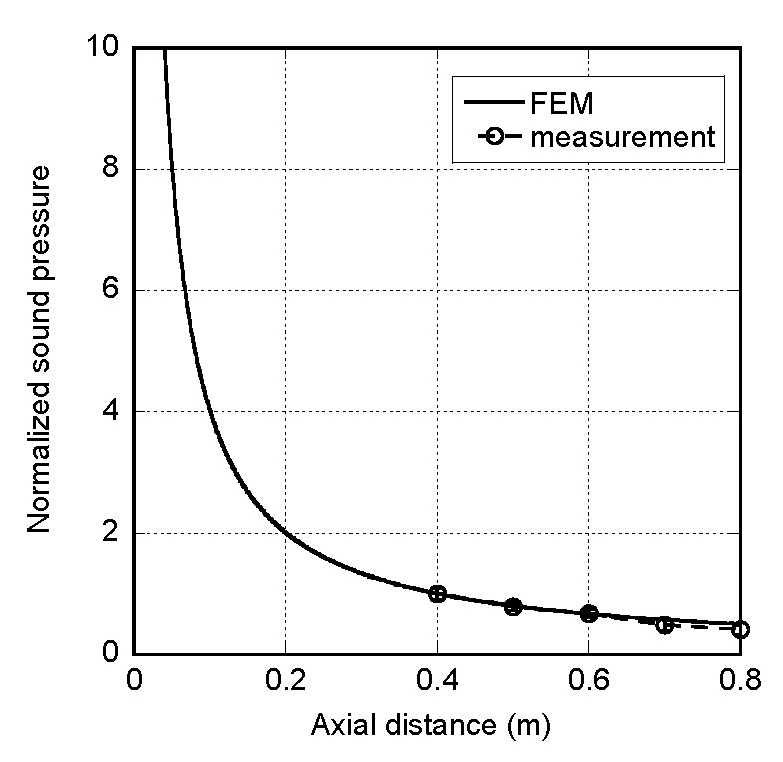
거리별 음압측정 결과를 Fig. 22에서 유한요소 해석 결과와 비교하였다. 유한요소 해석 결과는 종 모양 분포의 가진의 경우이다. 거리별 음압은 유한요소 해석 결과에서 거리에 따라 반비례하는 경향을 보였고, 실험으로 측정된 값은 0.4 m ~ 0.8 m 거리에서 해석결과와 같은 경향을 보였다. 이 거리는 Fig. 18에서 far field로 표시된 구간에 해당한다.

Fig. 22

Comparison of sound pressure according to distance

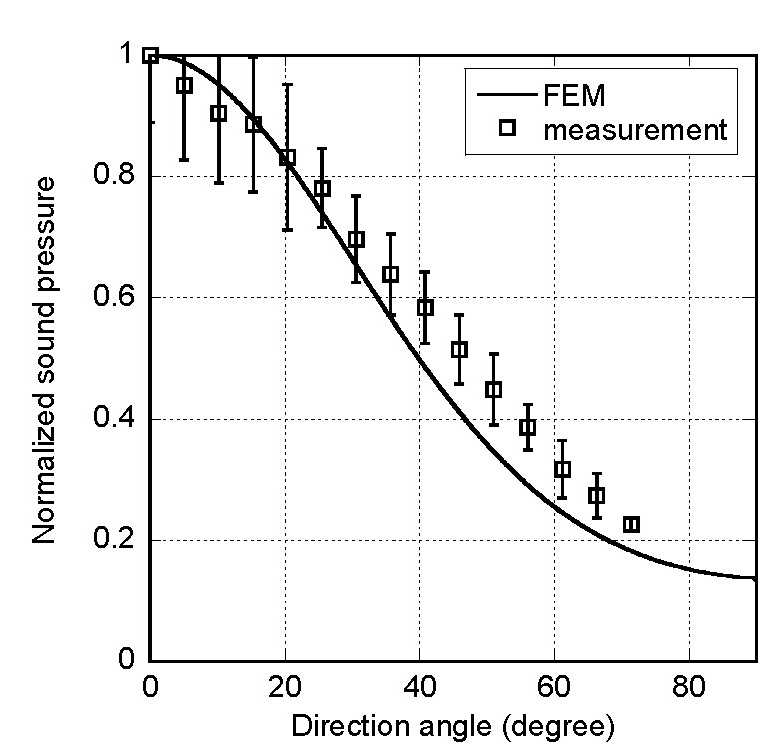
방향별 음압 측정 결과를 Fig. 23에서 유한요소 해석 결과와 비교하였다. 방향별 음압은 유한요소 해석 결과에서 부엽이 나타나지 않는 곡선 형태이다. 실험에서는 0° ~ 71.4° 구간에서 측정 가능하였고, 측정 결과는 해석 결과와 유사한 경향을 보였다. 즉, 거리별 음압과 방향별 음압의 결과가 해석 및 실험에서 유사한 경향을 보였다.

Fig. 23

Comparison of sound pressure according to direction

실제 초음파 센서의 원판 진동분포가 종 모양과 유사함을 확인하였다. 종 모양 분포의 가진인 경우는 부엽을 갖지 않는 빔패턴이 나타났다. 균일분포 가진의 경우에는 부엽이 존재하여 지향성이 좋으므로, 실제 초음파 센서의 지향성을 향상시키려면 초음파 센서 원판의 진동분포를 균일에 가깝게 해야 한다.

6. 결론

거리측정용 초음파 센서의 측정거리 범위 증대를 위해, 센서 원판의 진동분포와 초음파 지향성의 관계를 파악하였다. 센서 원판의 진동분포가 균일한 경우와 종 모양으로 불균일한 경우를 비교하였다. 불균일한 진동분포를 축대칭인 경우와 2면 대칭인 경우로 구분하였다. 진동분포가 균일한 경우에는 이론적 해석과 유한요소 해석으로 초음파 음향 특성을 구하고, 불균일한 경우에는 유한요소 해석으로 음향 분포를 구하여, 거리별 음압 크기와 방향별 음압 분포인 빔 패턴과 지향성을 비교하였다.

실제 초음파 센서의 원판 진동분포는 종 모양 불균일 분포임을 확인하였고, 불균일 분포를 균일 분포에 가깝게 하면 지향성이 향상될 수 있음을 파악하였다. 이 결과를 토대로 센서 구조를 변경하는 설계를 하고자 한다.

Acknowledgments

A part of this paper was presented at the KSNVE 2017 Annual Autumn Conference.

이 연구는 2017년도 산학연협력기술개발사업 (C0531965)의 지원에 의해 수행되었음.

References

• Kim, J, O., (2000), Sensors and Actuators Using Ultrasound, Transactions of the Korean Society for Noise and Vibration Engineering, 10(5), p723-728.
• Alonso, L., Milanės, V., Torre-Ferrero, C., Godoy, J., Oria, J. P., and Pedro, T., (2011), Ultrasonic Sensors in Urban Traffic Driving-Aid Systems, Sensors, 11, p661-673. [https://doi.org/10.3390/s110100661]
• Gross, R. R., (2010), Methods and Device for Ultrasonic Range Sensing, United States Patent US 7,679,996 B2.
• Shim, Y. I., Lee, S. Y., and Byeon, M. H., (2006), Sensor Technology in Automobiles, Korea Institute of Science and Technology Information, p7-14. [https://doi.org/10.1126/science.aam7817]
• Greif, S., Zsebok, S., Schmieder, D., and Siemers, B. M., (2017), Acoustic Mirrors as Sensory Traps for Bats, Science, 357, p1045-1047.
• Yoo, G. S., Lee, T. H., and Chae, M. K., (2017), Ultrasonic Transducer for Vehicle, Korea Patent 10-1,728,225.
• Kinsler, L. E., (1999), Fundamentals of Acoustics, 4th edition, Wiley, New York, p184-193. [https://doi.org/10.1121/1.1903238]
• Dekker, D. L., Piziali, R. L., and Dong, E., (1974), Effect of Boundary Conditions on the Ultrasonic-beam Characteristics of Circular Disks, The Journal of the Acoustical Society of America, 56(1), p87-93.
• Meirovitch, L., (1967), Analytical Methods in Vibrations, Macmillan, New York, p179-189.
• Umchid, S., (2009), Directivity Pattern Measurement of Ultrasound Transducers, International Journal of Applied Biomedical Engineering, 2(1), p39-43. [https://doi.org/10.1088/0957-0233/3/3/001]
• Manthey, W., Kroemer, N., and Mágori, V., (1992), Ultrasonic Transducers and Transducer Arrays for Applications in Air, Measurement Science and Technology, 3(3), p249-261.