혼합 경계를 가진 임의 형상 음향 공동의 고정밀도 고유치 추출 기법 개발
ⓒ The Korean Society for Noise and Vibration Engineering
Abstract
An extended NDIF (non-dimensional dynamic influence function) method is proposed for the eigenvalue analysis of arbitrarily shaped two-dimensional acoustic cavities with a mixed boundary, which consists of the rigid-wall and open boundaries. The original NDIF method was already developed for cavities with the rigid-wall boundary by the author in the years of 2000~2013. The proposed method has the feature of yielding highly accurate eigenvalues compared with other analytical numerical methods. In addition, it successfully eliminates the spurious eigenvalues of acoustic cavities with the mixed boundary. The validity of the proposed method is shown in case studies, by comparing the eigenvalues obtained by the proposed method to those obtained by the exact method or FEM(ANSYS).
Keywords:
Eigenvalue, NDIF Method, Acoustic Cavity, Open Boundary, Rigid-wall Boundary키워드:
고유치, 무차원 동영향 함수법, 음향 공동, 개방 경계, 강체벽 경계1. 서 론
유한요소법 또는 경계요소법은 임의 형상 음향 공동의 고유치를 구하기 위하여 가장 일반적으로 사용되는 기법이다(1,2). 그러나 이들 기법들은 사용되는 기저 함수가 지배 미분방정식을 만족하지 않기 때문에 해의 정밀도에 있어서 한계를 가진다. 이러한 단점을 극복하여 고정밀도 고유치를 추출하기 위한 방법으로 저자는 NDIF법(non-dimensional dynamic influence method)을 처음으로 제안하였다(3). 나중에, 볼록 형상뿐만 아니라 오목 형상의 음향 공동에도 적용이 가능한 분할 영역법 기반 NDIF법을 개발하였다(4). NDIF법은 유한요소법이나 경계요소법과는 달리 기저 함수가 지배 미분방정식을 만족하고, 동시에 적은 노드 개수로 해석 대상물의 경계만을 이산화하기 때문에 수치 계산량이 적어지는 장점을 가진다.
그러나, NDIF법은 유한요소법이나 경계요소법과는 달리 최종 시스템 행렬이 주파수 파라미터에 종속되는 단점을 가진다. 결과적으로 최종 시스템 행렬식은 대수 고유치 문제(algebraic eigenvalue problem)의 형태를 가지지 못하게 되어서, 시스템 행렬로부터 고유치와 고유모드를 추출하는 과정이 매우 번거롭게 된다.
저자는 이러한 문제점을 해결하기 위해, 최근에 기존 NDIF법 이론을 개선하여 임의 볼록 형상 음향 공동의 고유치와 고유모드를 수월하게 추출할 수 있는 개선된 NDIF법인 MNDIF법(Modified NDIF method)을 개발하였다(5). 나중에 상기의 방법을 확장하여, 오목 형상 음향 공동에 대한 MNDIF법을 정립하였다(6).
상기와 같이 임의 형상 음향 공동의 고정밀도 고유치의 효율적인 추출을 위한 다양한 연구가 진행되었으나, 이들 연구는 음향 공동을 둘러싸고 있는 경계를 강체벽 경계(rigid-wall boundary)로만 국한하였다. 이 논문에서는 강체벽 경계를 가진 음향 공동에 제한적으로 적용되었던 NDIF법을 강체벽 경계와 개방 경계(open boundary)로 구성된 혼합 경계를 가진 음향 공동에 확장하는 방안이 연구된다. 최종적으로는, 엄밀해를 가지는 직사각형 음향 공동과 임의 형상 음향 공동에 제안된 방법을 적용하여 이 논문의 타당성이 보여진다.
2. 이론 정식화
2.1 지배방정식과 경계조건
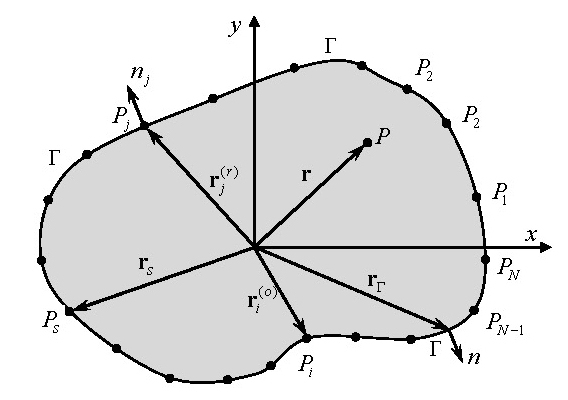
Fig. 1에서 실선으로 표시된 2차원 음향 공동의 고유치 해석을 위한 지배 방정식은 다음과 같이 헤름홀츠 방정식의 형태를 가진다(7).
| (1) |
여기서 r은 음향 공동 내부의 한 점 P에 대한 위치 벡터를 의미하고(Fig. 1 참조), p(r)은 음향 공동 내부의 한 점 P에서의 음압을 나타내며, k는 주파수 파라미터이다.
일반적으로 음향 공동의 경계는 개방 경계와 강체벽 경계로 나뉘어지며, 두 경계에 대한 경계 조건 식은 다음과 같이 각각 주어진다(7).
| (2,3) |
여기서 rΓ는 Fig. 1의 음향 공동의 경계 상의 한 점에 대한 위치 벡터이며, n은 경계에서의 법선 방향을 의미한다.
2.2 혼합경계를 고려한 NDIF법
먼저 해석 대상 음향 공동의 경계는 Fig. 1과 같이 N개의 노드 P1,P2,...,PN 로 이산화된다. 그러면 음향 공동 내부의 한 점 P에서의 음압은 다음과 같이 무차원동영향 함수들의 선형 결합으로 표시된다(3).
| (4) |
여기서 J0는 제1종 0차 베셀 함수를 나타내며, As는 미지 기여도 상수이다. 그리고 rs는 음향 공동 경계에 위치한 노드 Ps에 대한 위치 벡터를 뜻한다. 참고로 식 (4)는 지배방정식 식 (1)을 정확히 만족한다.
다음으로, 음향 공동의 경계를 따라 연속적으로 주어진 경계 조건 식 (2, 3)은 다음과 같이 경계 노드에 대한 식으로 각각 이산화된다.
| (5) |
| (6) |
여기서 는 개방 경계(open boundary)에 놓인 노드 Pi에 대한 위치 벡터를 뜻하며, 와 nj는 강체벽(rigid-wall) 경계에 놓인 노드 Pj에 대한 위치 벡터와 법선 방향을 각각 의미한다. 그리고 No와 Nr은 각각 개방 경계와 강체벽 경계에 놓인 노드 개수를 의미하며, No + Nr = 0이 성립한다.
이제, 음압 식 (4)를 경계조건 식 (5, 6)에 대입하면 다음의 두 식을 각각 얻을 수 있다.
| (7) |
| (8) |
식 (7)과 식 (8)은 다음과 같이 행렬식의 형태로 각각 나타낼 수 있다.
| (9) |
| (10) |
여기서 국부 시스템 행렬 SM(oo), SM(or), SM(ro), SM(rr)의 성분은 다음의 식에 의해 각각 주어진다.
| (11) |
| (12) |
| (13) |
| (14) |
마지막으로, 식 (9)와 식 (10)은 다음과 같이 하나의 행렬식으로 표현될 수 있다.
| (15) |
| (16) |
여기서 전체 시스템 행렬 SM과 기여도 벡터 A는 다음과 같다.
| (17) |
| (18) |
전체 시스템 행렬식 식 (16)이 실용해(non-trivial solution)를 갖기 위해선 시스템 행렬 SM의 판별식이 다음과 같이 0을 만족해야 한다.
| (19) |
여기서 시스템 행렬 SM(k)는 주파수 파라미터 k의 함수이다. 음향 공동의 고유치는 식 (19)를 만족하는 주파수 파라미터에 해당한다. 식 (19)에 의해 구해진 고유치를 식 (16)에 대입하면 고유 벡터가 구해지며, 이 고유벡터의 성분들을 식 (4)에 대입하면 음향 모드 형상을 구할 수 있다.
3. 검증 예제
3.1 혼합 경계를 가진 직사각형 음향 공동
이 논문에서 제안된 방법의 타당성을 검증하기 위해, Fig. 2와 같은 엄밀해를 가진 가로 1.2 m, 세로 0.9 m의 직사각형 2차원 음향 공동이 고려된다. 이 음향 공동의 네 면 중에 우측면은 개방 경계이며 점선으로 표시되어 있으며, 나머지 세 면은 강체벽 경계이며 실선으로 표시되어 있다. Fig. 2는 개방 경계와 강체벽 경계를 각각 3개와 13개의 노드로 이산화하여, 총 16개의 노드를 사용한 경우(N = 16)를 보여준다. 아울러, 직사각형 음향 공동의 네 군데 코너에서의 법선 방향은 Fig. 2에서 화살표로 표시되었다. Fig. 2와 같이, 강체벽 경계끼리 만나는 코너에서의 법선 방향은 코너 각도의 크기에 상관 없이 두 경계의 평균 법선으로 설정하고, 강체벽 경계와 개방 경계가 만나는 코너에서의 법선 방향은 강체벽 경계 법선 방향과 같게 설정하는 것이 가장 정확한 고유치를 제공함이 이 논문에서 확인되었다. 참고로 관련 연구 내용은 지면 관계상 생략한다.
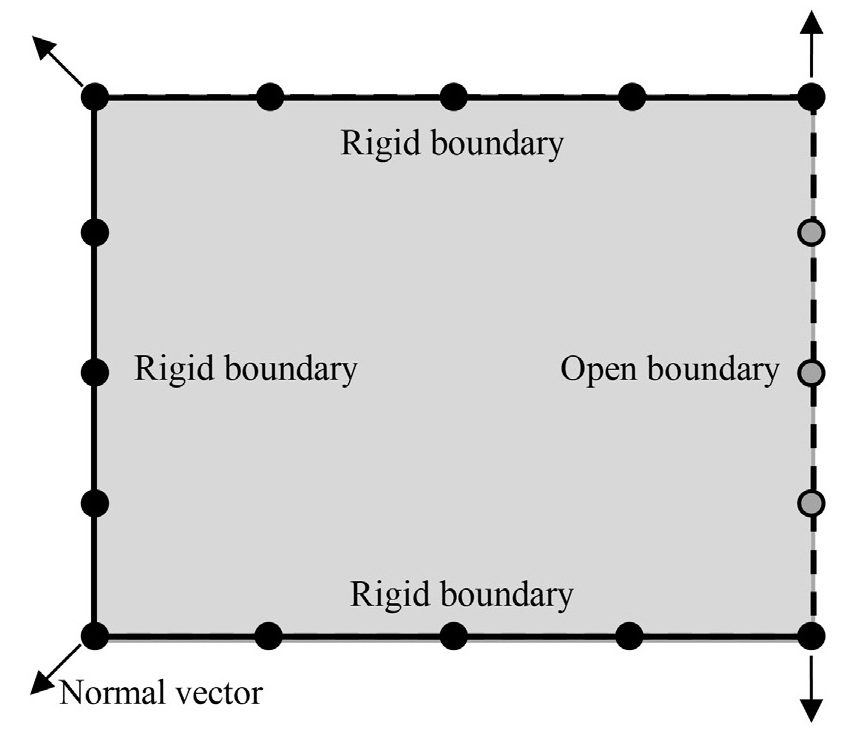
Rectangular cavity discretized with 16 boundary nodes (dotted line: open boundary, solid line: rigid wall boundary)
이 논문에서 제안된 방법을 이용하여 식 (19)의 해에 해당하는 고유치를 추출하기 위하여, Fig. 2와 같이 16개의 노드로 이산화된 경우에 대해 det(SM(k)) 곡선을 그렸으며, 그 결과는 Fig. 3의 실선 곡선에 해당한다. 시스템 행렬 SM의 판별식이 0이 되는 주파수 파라미터에 해당하는 특이치(singular value)는 총 8개(SV1 ~ SV8)가 구해졌으며, SV1 ~ SV8은 Table 1의 N = 16에 해당하는 열에 제시되었다. 마찬가지로, N = 20, N = 24에 대해서도 같은 방식으로 구해진 특이치들도 Table 1에 제시되었다.
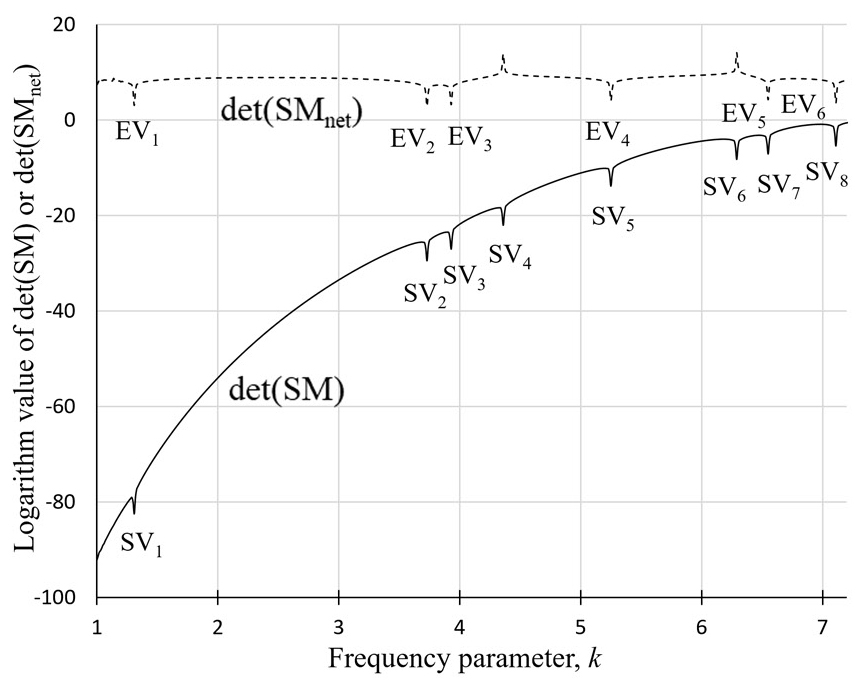
Determinant curves for the rectangular cavity discretized with 16 boundary nodes (solid line: det(SM), dotted line: det(SMnet))

Eigenvalues of the rectangular cavity obtained by the proposed method, the exact solution(8) and FEM (ANSYS)
Table 1에서 N = 16인 경우의 특이치를 엄밀해(exact solution)와 비교해보면, 총 8개의 특이치 중에 6개만이 혼합 경계를 가진 음향 공동의 고유치에 해당하며, 나머지 2개(SV4, SV6)는 허위 고유치(spurious eigenvalue)임을 알 수 있다. 이들 허위 고유치는 전체 경계가 개방된 가상의 개방 경계 음향 공동의 첫 번째와 두 번째 고유치에 각각 해당됨이 확인되었다.
이 논문에서 상기 허위 고유치를 제거하기 위하여, 시스템 행렬 SM 속에는 식 (20)과 같이 가상의 개방 경계 음향 공동에 해당하는 시스템 행렬 SMopen이 포함되어 있다고 가정한다(3).
| (20) |
여기서 SMnet은 허위 고유치가 제거된 시스템 행렬을 의미한다. 식 (20)은 다음의 식을 만족한다.
| (21) |
| (22) |
식 (22)의 det(SMnet)곡선을 그려보면, Fig. 3의 점선 곡선과 같이 허위 고유치를 제외한 실제 고유치만이 구해짐이 확인된다. 이 곡선에서 특이치는 총 6개(EV1 ~ EV8)가 구해지며, 이 값들은 정확히 엄밀해 6개와 일치함을 Fig. 3의 두 곡선을 비교함으로써 확인할 수 있다.
한편, 제안된 방법에서 노드의 개수가 증가하게 되면 첫 번째 고유치가 구해지지 않음을 Table 1에서 확인할 수 있다. 이러한 사실은 고유치가 엄밀해에 이미 수렴되었을 경우 나타나는 현상임을 저자의 이전 연구에서 확인되었다(3). 참고로 사각 형상을 포함하여 임의 형상 음향 공동에 대해, 노드의 개수를 16개 이하로 사용하면, 첫 번째 고유치부터 구해지는 것으로 확인되었다. 또한, 제안된 방법은 1271개 노드를 사용한 FEM에 비해 적은 수의 노드를 사용함에도 엄밀해에 정확히 수렴되는 고유치를 제공하는 것을 확인할 수 있다.
3.2 혼합 경계를 가진 임의 형상 음향 공동
두 번째 검증 예제로 Fig. 4와 같은 형상을 가지는 임의 형상 사각 평판이 고려된다. Fig. 4에서 사각형의 네 면 중에 좌측 면(점선)은 개방 경계이며, 나머지 세 면(실선)은 강체벽 경계이다.
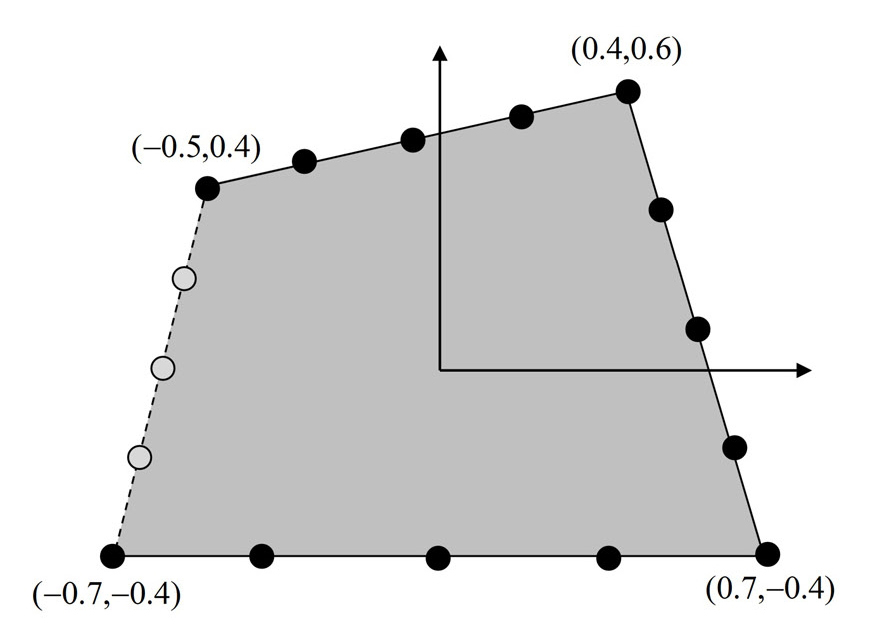
Dimensions of the arbitrarily shaped quadrilateral cavity discretized by 16 nodes (dotted line: open boundary, solid line: rigid wall boundary)
앞의 첫 번째 검증 예제와 마찬가지로, 16개의 노드로 이산화 된 음향 공동(Fig. 4)에 대한 det(SM)곡선과 det(SMnet) 곡선이 그려졌으며, 그 결과는 Fig. 5와 같다. det(SM) 곡선(실선)에서는 총 8개의 특이치가 확인되며, 이들 값들 중에 SV4와 SV7은 허위 고유치임을 det(SMnet) 곡선(점선)에서 확인 할 수 있다. 참고로, 이들 허위 고유치는 개방 경계를 가진 음향 공동의 첫 번째와 두 번째 고유치에 해당함이 확인되었다.
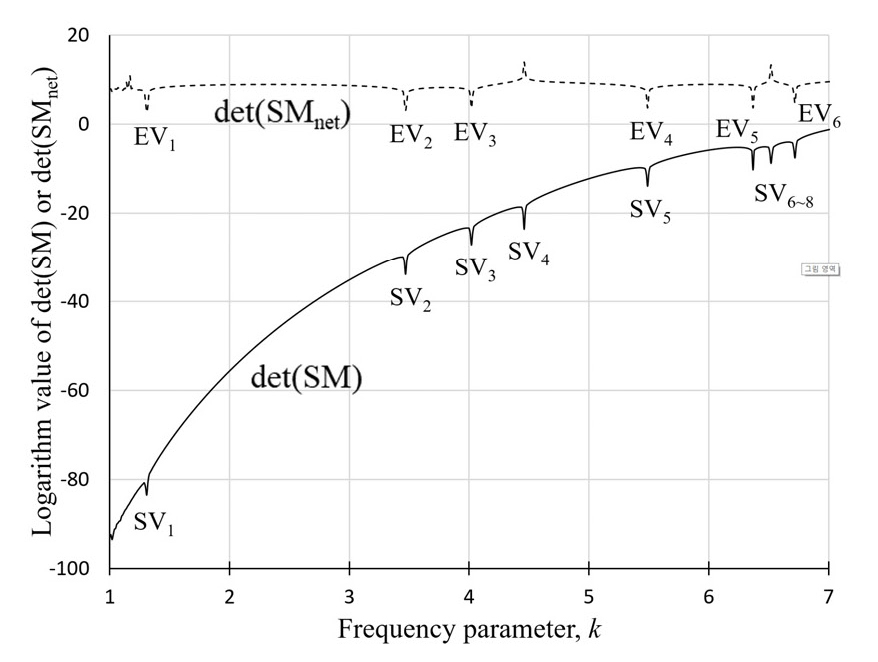
Determinant curves for the arbitrarily shaped, quadrilateral cavity discretized with 16 boundary nodes (solid line: det(SM), dotted line: det(SMnet))
det(SMnet) 곡선에서 구해진 6개의 고유치는 Table 2의 N = 16에 해당하는 열에 제시되었다. 그리고 N = 20와 N = 24에 대해서도 같은 방식으로 고유치가 구해졌으며 그 결과도 Table 2에 제시되었다. 이 예제의 경우는 엄밀해가 존재하지 않기 때문에, 제안된 방법에 의해 구해진 고유치들을 FEM 결과와 비교해보면, 제안된 방법이 타당함을 확인할 수 있다. 한편, 앞의 예제와 마찬가지로 N = 20인 경우에는 첫 번째 고유치가, N = 24인 경우에는 첫 번째와 두 번째 고유치가 추출되지 않음을 확인할 수 있다. 이는 첫 번째 고유치는 N = 16일 때, 두번째 고유치는 N = 20일 때 이미 수렴했기 때문인 것으로 판단된다(3).
4. 결 론
이 논문에서는 개방 경계와 강체벽 경계로 구성된 혼합 경계를 가진 음향 공동에 대한 NDIF법 이론을 정립하였다. 정립된 이론의 정확성과 타당성을 보여주기 위하여, 두 가지 예제 검증이 수행되었다. 현재 혼합 경계를 가진 음향 공동의 모드 형상을 효과적으로 추출하기 위한 연구가 진행 중에 있으며, 향후 논문에서 그 결과를 발표할 예정이다. 추가적으로, 보다 복잡한 형상을 가진 음향 공동에 대한 예제 검증도 향후 연구에서 다루어질 예정이다.
Acknowledgments
이 연구는 한성대학교 교내학술연구비 지원 과제임.
References
- Bathe, K., (1982), Finite Element Procedures in Engineering Analysis, Prentice-Hall, New Jersey.
-
Brebbia, C. A., Telles, J. C. F., and Wrobel, L. C., (1984), Boundary Element Techniques, Springer-Verlag, New York.
[https://doi.org/10.1007/978-3-642-48860-3]

-
Kang, S. W., and Lee, J. M., (2000), Eigenmode Analysis of Arbitrarily Shaped Two-dimensional Cavities by the Method of Point-matching, Journal of the Acoustical Society of America, 107(3), p1153-1160.
[https://doi.org/10.1121/1.428456]

-
Kang, S. W., and Yon, J. I., (2012), Development of a Modified NDIF Method for Extracting Highly Accurate Eigenvalues of Arbitrarily Shaped Acoustic Cavities, Transactions of the Korea Society for Noise and Vibration Engineering, 22(8), p742-747.
[https://doi.org/10.5050/KSNVE.2012.22.8.742]

-
Kang, S. W., and Yon, J. I., (2011), Development of an Improved NDIF Method for Efficiently Extracting Eigenvalues and Eigenmodes of Arbitrarily Shaped Acoustic Cavities, Transactions of the Korea Society for Noise and Vibration Engineering, 21(10), p960-966.
[https://doi.org/10.5050/KSNVE.2011.21.10.960]

-
Kang, S. W., (2013), New Formulation of MNDIF Method for Accurate Eigenvalue Analysis of Concave Acoustic Cavities, Transactions of the Korea Society for Noise and Vibration Engineering, 23(11), p1003-1011.
[https://doi.org/10.5050/KSNVE.2013.23.11.1003]

- Kinsler, L. E., (1980), Fundamentals of Acoustics, Wiley.
- Blevins, R. D., (1979), Formulas for Natural Frequency and Mode Shape, Litton Educational Publishing, New York.

Sang Wook Kang received a B.S., M.S. and Ph.D. degree in Dept. of Mechanical Design Engineering from Seoul National University in 1992, 1994 and 1999, respectively. He is currently working in Hansung University as a professor of the mechanical system engineering. His research interests include the development of NDIF method for free vibration analysis of membrane, acoustic cavities, and plates with general shapes.