난류 경계층 가진에 의한 소나돔 음향창 구조물의 음향 방사 파워
ⓒ The Korean Society for Noise and Vibration Engineering
Abstract
This paper presents analysis results on the acoustic radiated power from the rubber-inserted flat acoustic window of sonar dome, which is excited by pressure fluctuation of turbulent flow. Analysis is based on the well-known RKU theory, Corcos model and modal approach. It is found that increasing the loss factor has less effect on decreasing the radiated sound power despite of significant decrease of vibration level. In addition, increasing the thickness of the rubber layer, under same total thickness, can increase the vibration level in the high frequency range. However, the acoustic radiated power is similar or less than that of the thinner rubber layer.
Keywords:
Turbulent Flow Excitations, Acoustic Radiated Power, Acoustic Window키워드:
난류가진, 음향 방사파워, 음향창1. 서 론
수중에서의 주요 탐지 수단은 소나(SONAR)이며 이러한 소나체계는 배열 센서를 보호하기 위한 소나돔을 포함한다. 소나돔 표면의 난류 변동에 의한 방사소음은 일반적으로 함정의 기계류 및 추진기 소음에 비해 매우 작다. 그러나 일정 운용 속력 이상에서 경계층 유동 변동에 의한 소음방사는 배열 센서의 잡음 수준을 높이며 탐지 성능에 큰 영향을 미친다(1).
따라서 초기 설계 단계에서 난류 경계층 압력 변동에 의한 소나 자체소음 영향 분석은 중요하며 설계인자의 변화에 따른 자체소음 영향 분석이 사전에 수행되어야 한다(1). 난류 경계층 벽면 변동 압력은 유동 소음과 유동의 소나돔 벽면 가진에 의한 구조 기인(structure-induced) 소음으로 구분 할 수 있다(2). 유동 소음은 자유 또는 강체 주변 유동의 변동 압력에 의한 직접 전파 소음으로써 유동 마하수(Mach number)의 6제곱에 비례한다(3). 따라서 함정의 일반적인 운용 속력을 고려하면 마하수는 1보다 매우 작으므로 유동소음의 소나 자체소음 기여도는 무시할 수 있으며 구조 기인 소음이 주된 자체소음원이다.
소나돔 음향창은 일반적으로 구조 강도 조건을 만족시키면서 음향 투과손실이 작은 GRP(glass fiber reinforced plastic) 등의 복합재로 제작된다. 난류 경계층 압력 변동에 의한 소나돔 진동 수준과 자체소음을 감소시키기 위하여 고무 등의 고감쇠 층을 삽입한 샌드위치 구조로 음향창을 제작 할 수 있으며, 이 연구에서는 이와 같은 감쇠 처리된 소나돔 음향창 구조물의 감쇠계수와 감쇠층의 두께변화에 따른 음향 방사파워를 산출함으로써 소나 자체소음에 미치는 영향을 분석하고자 한다. 일반적으로 함정 소나의 운용 주파수는 수십 Hz ~ 수 kHz로써 종류별로 다양하며, 이 연구에서는 50 Hz의 저주파 영역에서부터 4 kHz의 고주파수 영역까지 해석하였다.
2장에서는 다층 음향창의 유효 감쇠계수 계산 및 균질 등가 평판 모델을 기술한다. 3장에서는 난류 경계층 가진에 의한 음향창의 진동 수준과 음향 방사파워 예측 방법을 기술하고, 4장에서 진동 수준과 음향 방사파워 산출 결과를 제시하였으며 5장 결론에서 결과를 요약하였다.
2. 유효 감쇠 계수 추정
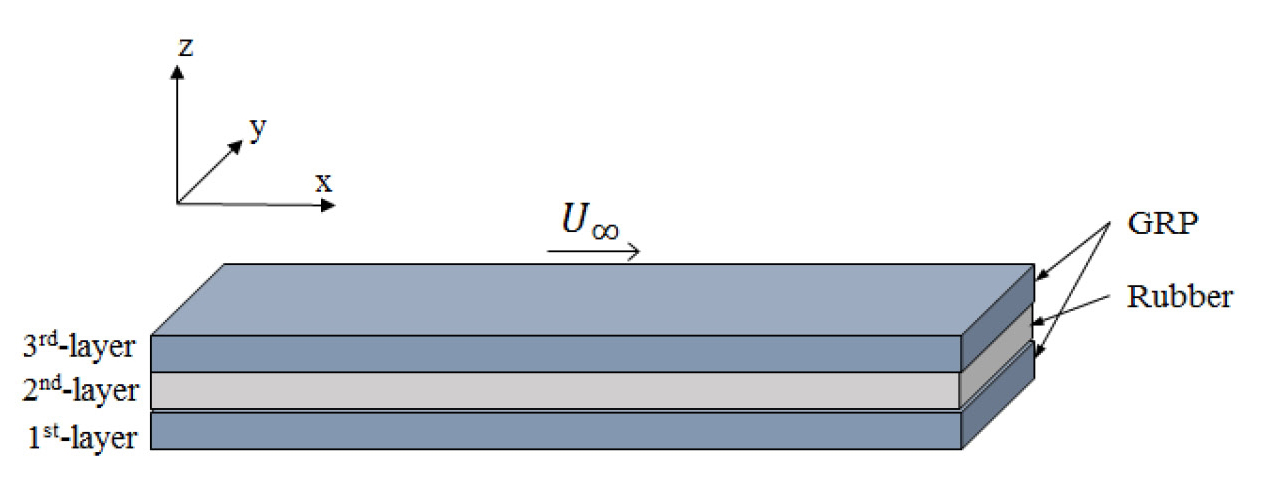
고무층을 삽입하여 감쇠 처리된 음향창 구조는 일반적인 CLD(constrained-layer damping) 기법을 적용한 샌드위치 평판 구조물로 모델링할 수 있으며 Fig. 1과 같다.
CLD 구조의 감쇠 특성 연구에는 Donald Ross, Edward Kerwin, Eric Ungar 등이 크게 기여하였으며 연구결과는 일반적으로 RKU(Ross-Kerwin-Ungar) 방정식으로 잘 알려져 있다. RKU 방정식은 평판의 굽힘파 전파만을 가정하며 각 층에서 모두 동일한 파장의 굽힘파 전파가 발생할 경우에만 적용 가능하다. 즉 고무층이 너무 무르거나 파장이 작으면 각 층에서 독립적인 파동 전파가 발생하기 때문에 적용 불가능하다. 이 연구의 경우에 적용 가능한 주파수 상한은 약 10 kHz()이다(4). RKU 방정식은 식 (1)과 같다(4,5). g는 전단 파라미터(shear parameter), B는 구조물의 복소 유효 굽힘 강성(effective complex bending stiffness), G2는 고무층의 전단 탄성계수(shear modulus), mp은 단위면적당 질량, Ei는 고무층의 감쇠계수(material loss factor), 는 각 층의 탄성계수, Ii는 각 층의 단면의 관성 모멘트(moment of inertia), hi는 각 층의 두께, kb는 굽힘파(bending wave) 파수이다.
| (1) |
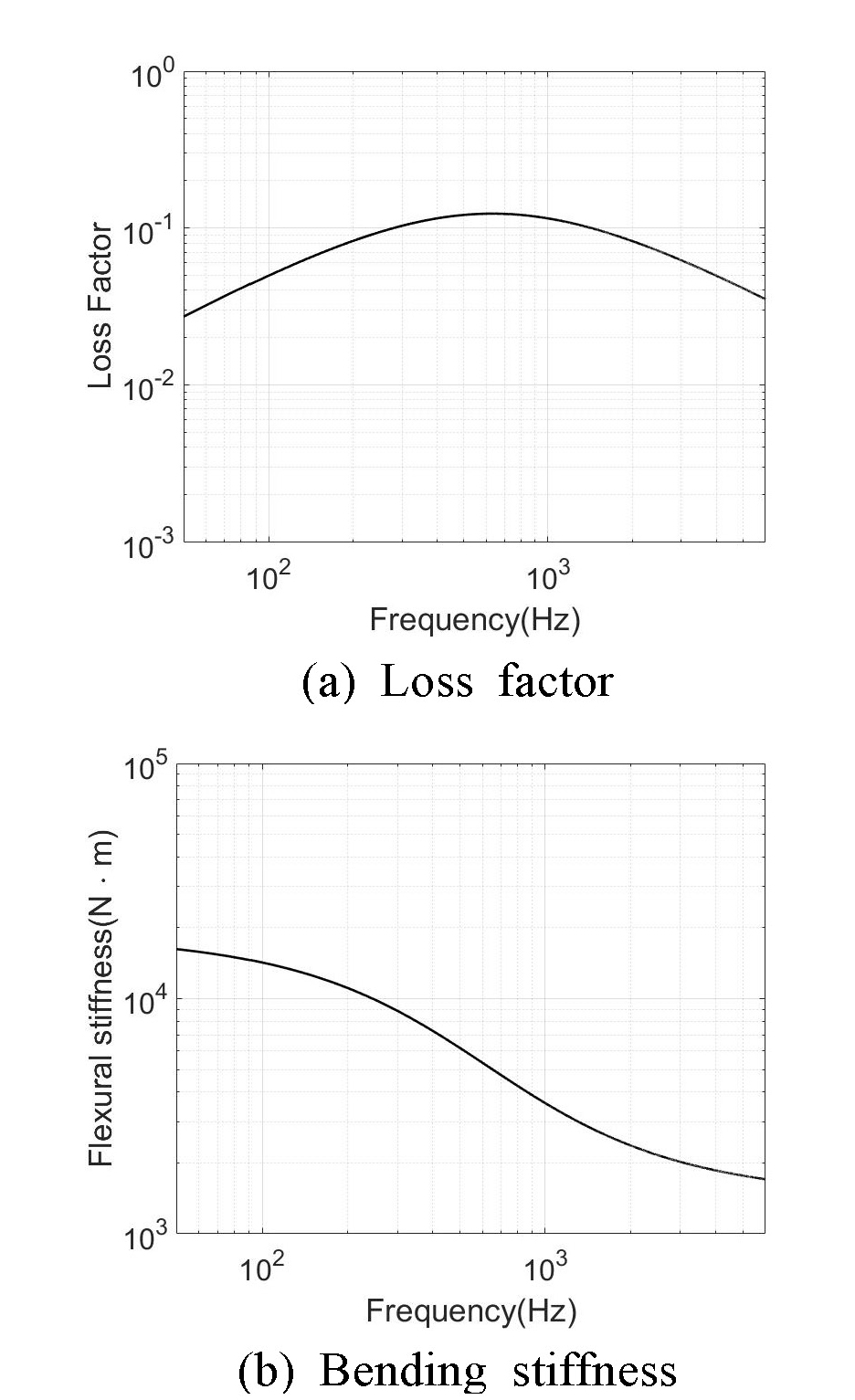
GRP 및 고무층의 물성치는 Table 1과 같다. 유효 감쇠 계수와 굽힘 강성은 Fig. 2와 같다. 유효 감쇠계수는 630 Hz에서 최대값을 갖는다. 유효 굽힘 강성은 주파수 증가에 따라 감소하는 경향을 보이며, 주파수 증가에 따라 전단계수 g가 감소하면서 GRP 층이 서로 독립적인 강성으로 작용하는 것과 같은 효과를 보이면서 각각의 강성을 단순 합한 값에 근접한다.
3. 음향방사파워
음향창을 등가의 질량, 강성, 감쇠 계수를 갖는 단순 지지된 평판으로 가정하면 경계층 변동 압력, ptbl(x,y,ω)에 의한 평판 수직(z-축) 방향 진동 응답은 지배 방정식 (2)와 같다(5). v는 평판의 z-방향 속도이다.
| (2) |
단순 지지된 평판의 고유함수(eigenfunction)는 식 (3)과 같다. km = mπ/a, kn = nπ/b, a, b는 각각 평판의 x-방향, y-방향 길이이다.
| (3) |
식 (2)에서 단위 하중 ptbl = δ(x-x’)δ(y-y’)이 작용하는 경우 주파수 응답 함수는 식 (4), (5)와 같다(5).
| (4) |
| (5) |
Vmn은 (m,n) 모드의 속도의 크기, ωmn은 모드의 공진 주파수이다. 유체하중은 저주파수 영역에서는 부가 질량으로 작용하며 접수된 평판의 부가질량과 접수 평판의 고유진동수는 각각 식 (6), (7)과 같다(6).
| (6) |
| (7) |
ρ0는 매질의 밀도, k0는 수중 음파의 파수이다.
경계층 변동압력 모델은 많은 이론적 실험적 연구들이 이루어져 왔다(7). 이 연구에서는 유동 조건에 대한 입력이 비교적 간단한 Corcos 모델, 식 (8)을 적용하였다. kω = ω/Uc, Φpp(ω)는 점 파워 스펙트럼, Uc는 난류의 대류 속도(convection velocity)이며 이 연구에서는 Uc = 0.7U∞(U∞: 유동 속도)으로 가정하였다.
| (8) |
Liu(8,9)의 연구결과를 이용하면 평판의 진동 속도 파워 스펙트럼은 식 (9)와 같다.
| (9) |
Θmn(ω)는 경계층 압력 변동 가진 항으로써 식 (10), (11)과 같이 나타낼 수 있다(8,9).
| (10) |
식 (11)의 적분은 Liu(8)의 언급처럼 수치적으로 적분할 수도 있지만 Corcos 모델을 적용한 경우 해석적으로 적분 가능하며 계산 시간이 크게 단축된다.
| (11) |
진동 속도 제곱의 평균은 모드형상 함수의 직교성으로 인해 식 (12)와 같다(9). S는 평판의 면적이다.
| (12) |
따라서 단순 지지된 평판의 음향 방사파워는 각 모드의 방사효율 σmn을 이용하여 식 (13)과 같이 나타낼 수 있다.
| (13) |
| (14) |
4. 음향창 응답
고무층의 감쇠계수 및 두께에 따른 평균 진동 속도 및 음향 방사파워를 계산하였다. Φpp(ω)는 유동 조건에 따른 스케일 법칙에 따라 다양한 모델들이 제시되어 왔다(10). 실제적인 음향파워를 계산하기 위해서는 Φpp(ω)에 대한 정확한 산출이 중요하지만 이 연구에서는 고무층의 물성 변화에 대한 음향파워 변화가 주된 관심이므로 논의를 단순화하기 위해 평균 진동 속도 및 음향파워를 Φpp(ω)로 정규화하였다.
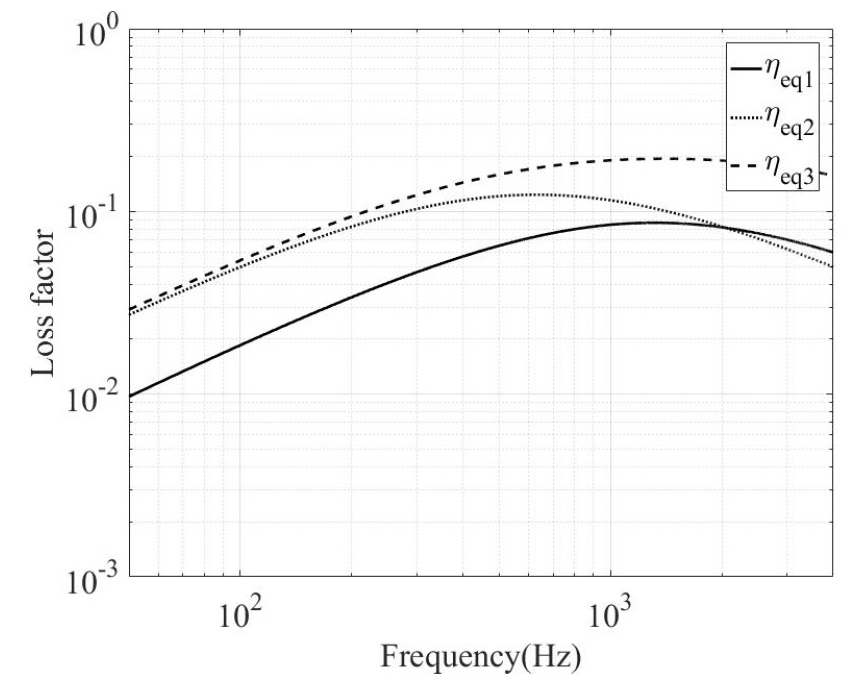
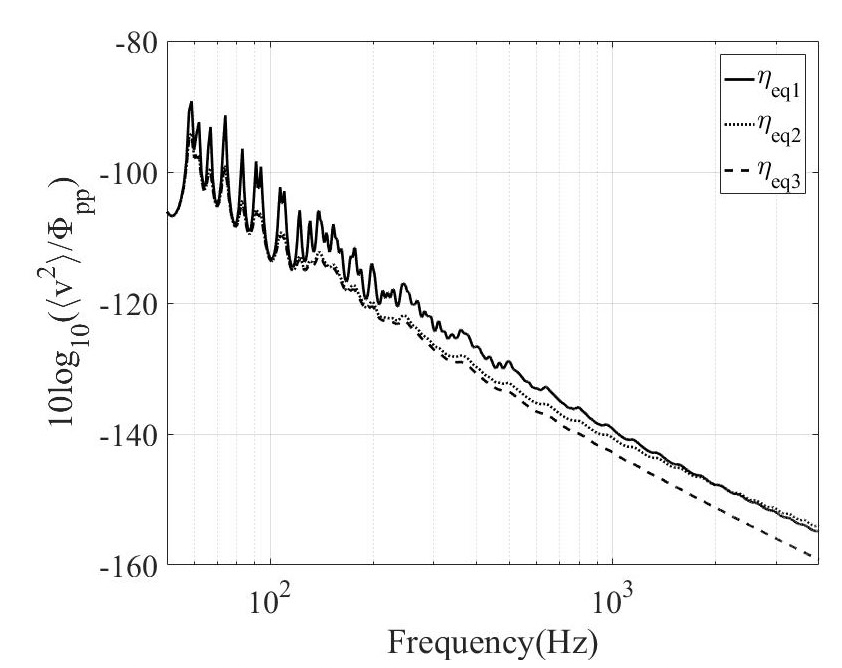
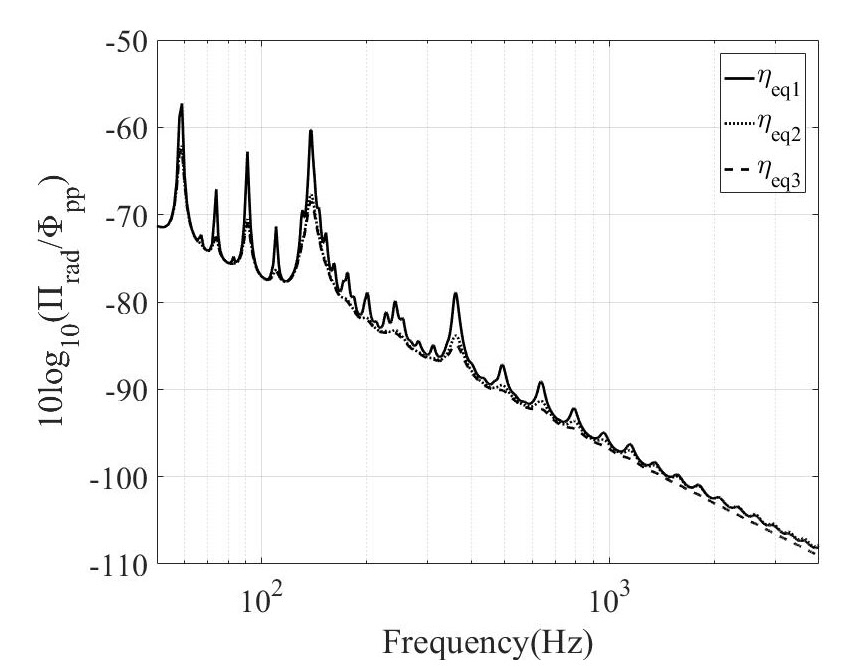
유효 감쇠 계수가 Fig. 3과 같고 다른 모든 물성은 동일하다고 가정할 때 a = 4m, b = 1m, U∞ = 7m/s인 경우 평균 진동속도와 음향 방사파워는 각각 Figs. 4, 5와 같다.
1 Hz 간격으로 계산하였고, x-방향 모드 개수는 150개, y-방향 모드 개수는 40개를 사용하였으며 계산 결과가 수렴함을 확인하였다.
감쇠계수의 증가가 진동속도를 감소시키며 ηeq3인 경우가 ηeq1인 경우보다 200 Hz 이하에서는 약 8 dB 감소하고, 고주파수에서는 약 4 dB 감소한다. ηeq2인 경우 저주파 영역에서는 ηeq1인 경우보다 낮은 진동 수준을 보이지만 주파수 증가에 따라 ηeq2가 ηeq1값에 접근하면서 진동 수준 또한 증가하여 ηeq1의 진동 수준과 비슷한 수준을 보인다.
ηeq3인 경우의 음향 방사파워는 ηeq1인 경우보다 저주파수 영역에서 약 5 dB이상 작으나 고주파수 영역에서는 약 1 dB 작다.
즉 고주파수 영역에서 감쇠계수 증가로 인한 진동 수준의 감소는 크지만 음향 방사파워의 감소는 작다. 이러한 현상은 Yiwei Kou(11)가 설명한 바와 동일한 결과로써 평판에 대한 감쇠 처리는 진동 수준을 효과적으로 감소시킬 수 있으나 음향 방사효율을 증가시킬 수 있어 실질적인 음향 방사파워 감소에는 큰 영향을 주지 못하기 때문이다.
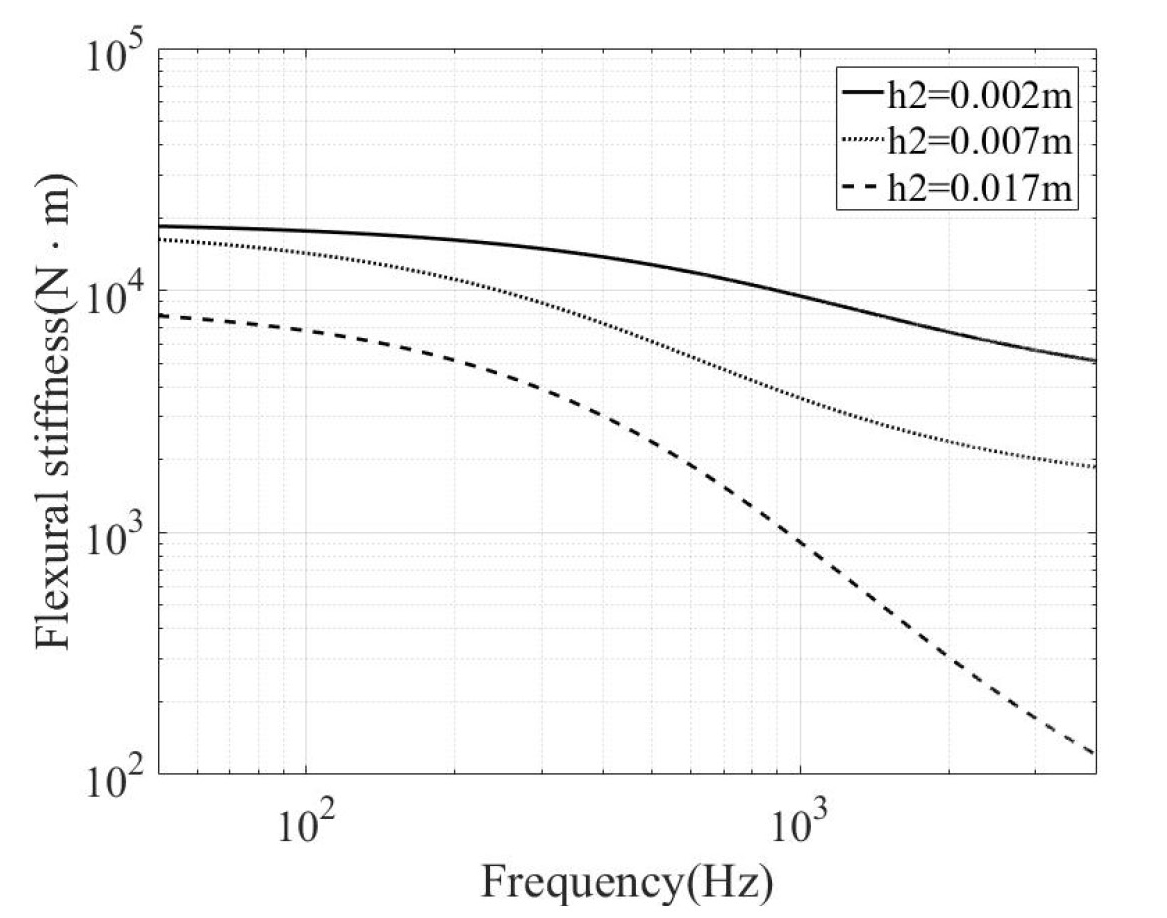
음향창 전체 두께는 일정하게 유지하고 고무층의 두께를 2 mm, 7 mm, 17 mm로 변화시킬 경우 유효 감쇠계수와 유효 굽힘 강성은 주파수의 함수이며 각각 Figs. 3, 6과 같다. 고무층 2 mm인 음향창의 유효 감쇠계수는 Fig. 4의 ηeq1, 7 mm는 ηeq2, 17 mm는 ηeq3와 같다.
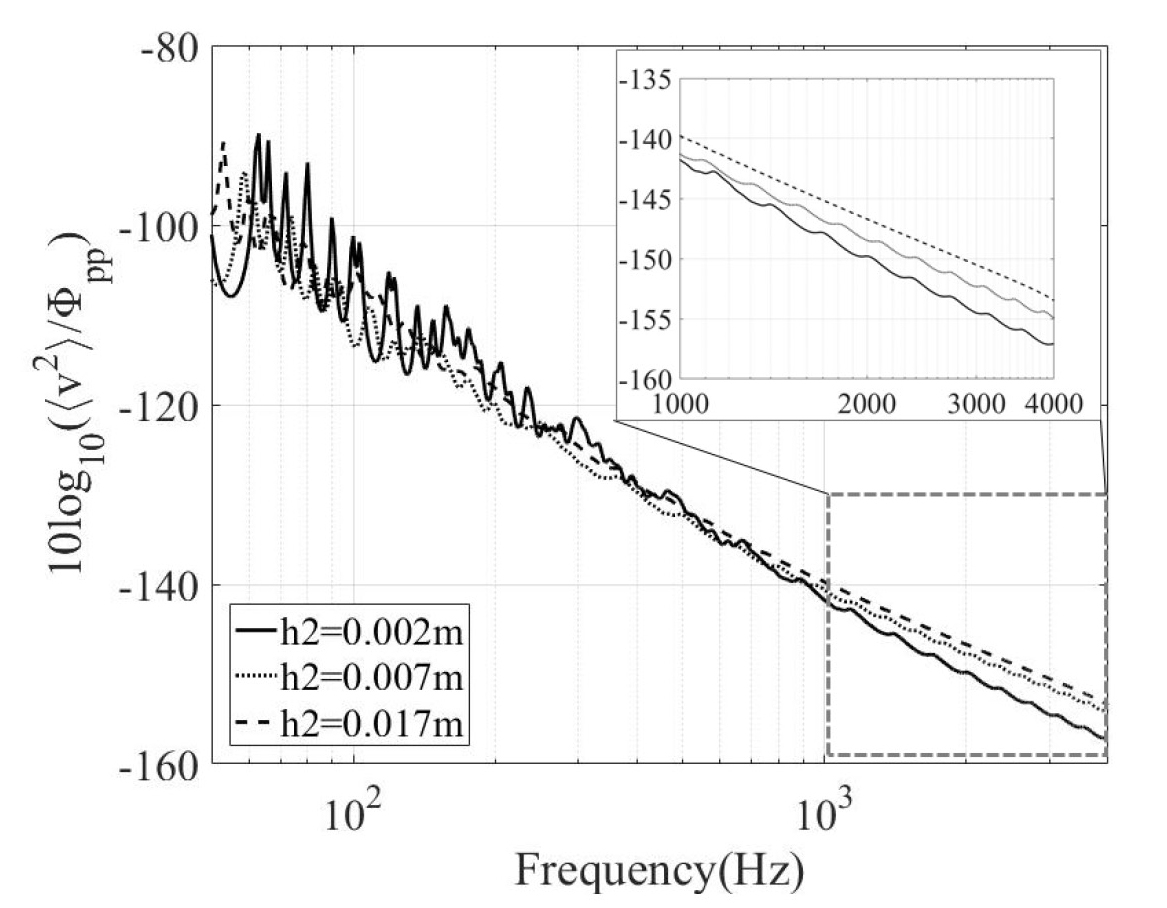
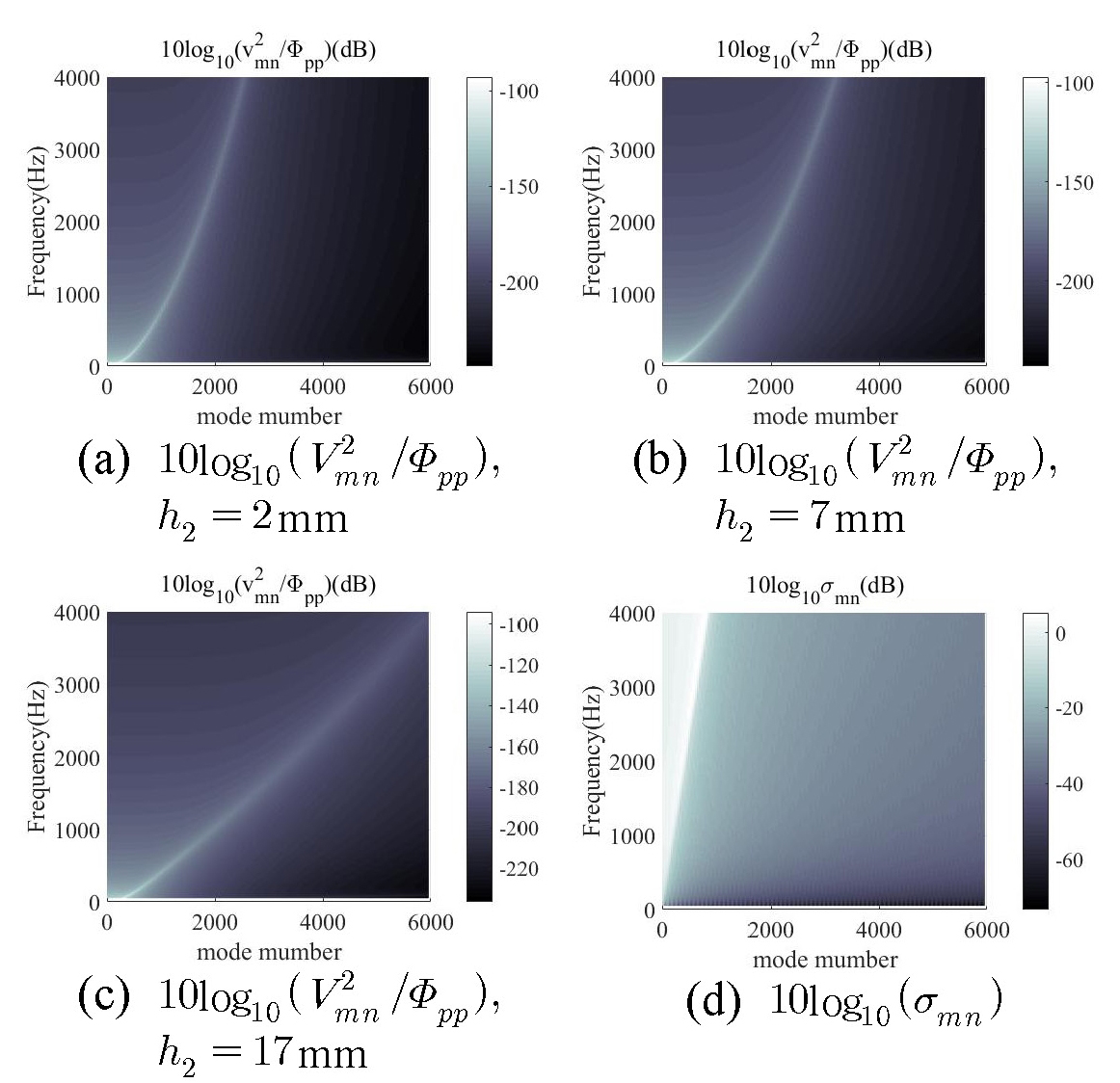
Figs. 7, 8에 고무층 두께(h2) 변화에 따른 평판 음향창의 진동 수준과 음향 방사파워 수준을 각각 나타내었다. 300 Hz 이하의 저주파 영역에서는 고무층 두께 증가에 따라 평균속도 수준이 감소하지만 고주파수 영역으로 갈수록 고무층 두께 증가에 따라 진동 수준이 커지며, 3 kHz에서 2 mm인 경우 보다 17 mm인 경우가 4 dB 더 크다. 이는 고무층의 두께가 증가할수록 고주파 영역에서 유효 굽힘 강성이 크게 감소하고 식 (5), (7)에 따라 모드 속도의 크기가 증가하기 때문이다.
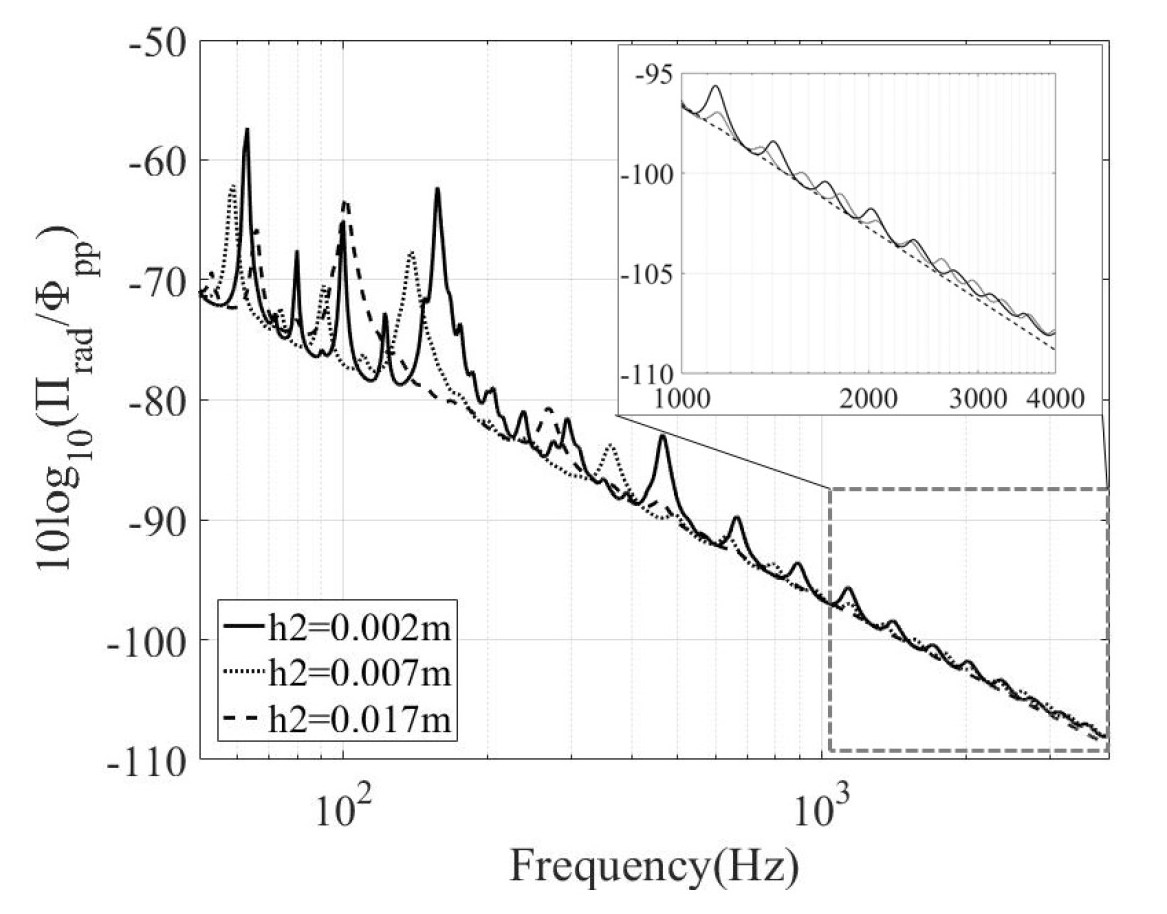
음향 방사파워의 경우 저주파수 영역에서는 고무층 두께 증가에 따라 음향 방사파워가 감소하는 경향을 보인다. 고주파 영역에서도 17 mm 고무층인 경우의 음향 방사파워가 가장 낮은 수준이지만 2 mm인 경우보다 2 kHz 이상에서 1 dB 내외로 감소 크기는 작다.
그리고 고주파 영역에서 고무층 17 mm인 경우가 진동속도 수준이 가장 크지만 음향 방사파워 수준은 가장 낮은 수준임을 알 수 있는데, 유효 강성이 작은 고무층 17 mm인 경우에는 음향 방사효율이 낮은 고차 모드의 영향이 고주파수 영역에서 지배적이기 때문이다. Fig. 9(a) ~ (c)에 각 모드의 진동수준을 모드수와 주파수에 따라 고무층 두께별로 각각 나타내었다. 고무층 두께가 두꺼워질수록 고주파수 영역의 진동수준에 고차 모드의 영향이 크게 기여함을 알 수 있다. 또한 Fig. 9(d)에 나타낸 바와 같이 각 모드의 음향 방사효율이 모드의 차수가 증가할수록 감소함을 알 수 있다.
5. 결 론
RKU 유효 감쇠계수 추정 방식과 Corcos 모델 그리고 모드 합산 방법을 이용하여 경계층 난류 가진에 의한 고무 재질의 감쇠층이 삽입된 소나돔 음향창 구조의 진동 수준과 음향 방사파워를 분석하였다. 계산 결과 다음과 같은 결과를 얻었다. 첫째, 개별 모드의 영향이 지배적인 저주파수 영역에서는 감쇠계수의 증가 또는 고무층의 두께를 증가시키면 진동 수준과 음향 방사 파워 수준을 동시에 비교적 크게 감소시킬 수 있다. 둘째, 음향창의 감쇠 계수를 증가시키면 고주파수 영역에서의 진동 속도는 크게 감소시킬 수 있으나 음향 방사 파워의 감소는 미미하다. 셋째, 음향창 총 두께가 일정한 경우 고무층의 두께를 증가시키면 구조 감쇠가 증가하나 유효 굽힘 강성의 감소로 인해 고주파수에서 진동수준이 증가할 수 있다. 그러나 고차 모드의 낮은 방사효율 때문에 음향 방사파워는 고무층 두께가 작은 경우보다 유사하거나 낮은 수준을 보인다. 따라서 개별 모드의 영향이 작은 고주파수 영역에서는 음향창 감쇠 계수의 증가 또는 고무층 두께의 증가가 자체소음 감소에 미치는 영향은 제한적일 수 있다.
References
-
Shin, K., and Seo, Y., and Kang, M., and Jeon, J., (2013), The Influence of Design Factors of Sonar Acoustic Window on Transfer Function on Self Noise Due to Turbulent Boundary Layer, Transactions of the Korean Society for Noise and Vibration Engineering, 23(1), p56-64.
[https://doi.org/10.5050/KSNVE.2013.23.1.056]

- Vepakomma, B. R., (1987), On the Flow-induced Structural Noise of a Ship’s Sonar Dome, Marine Technology, 24(4), p321-331.
- Patric, L., (1966), A Review of Flow Noise Research Related to the Sonar Self-Noise Problem, Bolt Beranek and Newman, Inc., Mass., USA, p13-15.
-
Cremer, L., and Heckl, M., (1973), Structure-borne Sound, Springer-Verlag, Berlin; Heidelberg, New York.
[https://doi.org/10.1007/978-3-662-10118-6]

- Ver, I. L., and Beranek, L. L., (2006), Noise and Vibration Control Engineering, John Wiley & Sons, Inc., New York.
-
Cheng, Z., Fan, J., Wang, B., and Tang, W., (2012), Radiation Efficiency of Submerged Rectangular Plates, Applied Acoustics, 73(2), p150-157.
[https://doi.org/10.1016/j.apacoust.2011.06.017]

-
Hwang, Y. F., Bonness, W. K., and Hambric, S. A., (2009), Comparison of Semi-empirical Models for Turbulent Boundary Layer Wall Pressure Spectra, Journal of Sound and Vibration, 319(1-2), p199-217.
[https://doi.org/10.1016/j.jsv.2008.06.002]

-
Liu, B., Feng, L., Nilsson, A., and Aversano, M., (2012), Predicted and Measured Plate Velocities Induced by Turbulent Boundary Layers, Journal of Sound and Vibation, 331(24), p5309-5325.
[https://doi.org/10.1016/j.jsv.2012.07.012]

-
Kou, Y., Liu, B., and Chang, D., (2016), Radiation Efficiency of Plates Subjected to Turbulent Boundary Layer Fluctuations, The Journal of Acoustical Society of America, 139(5), p2766-2771.
[https://doi.org/10.1121/1.4949021]

-
Wallace, C. E., (1970), Radiation Resistance of a Rectangular Panel, The Journal of Acoustical Society of America, 51(3B), p946-952.
[https://doi.org/10.1121/1.1912943]

-
Kou, Y., Liu, B., and Tian, J., (2015), Radiation Efficiency of Damped Plates, The Journal of Acoustical Society of America, 137(2), p1032-1035.
[https://doi.org/10.1121/1.4906186]


Seungjin Han received his B.S. and M.S. degree in aerospace engineering from KAIST in 1999 and 2001 respectively. He is currently a senior researcher in Agency for Defense Development. His research interests include naval ship stealth technologies and operation research.

Byung-Kyoo Jung is received B.S., M.S., and Ph.D. degrees from Pusan National University in 2010, 2012 and 2017. He is researcher of Agency for Defence Development. His research interests are in the area of finite/ boundary element analysis of noise and vibration and fluid-structure interactions.

Woo-Jin Jung is received his B.S. and M.S. degrees from Korea Aerospace University in 1985 and 1987 respectively, a Ph.D. degree from Pusan National University. He is currently a principal researcher at the Agency for Defense Development, Korea. His research interests are underwater acoustic stealth technologies.