전달행렬법을 이용하여 지반진동을 받는 전단구조물의 응답해석

1. 서 론

현대 산업의 고도화로 연구, 개발 및 생산, 검사공정 등 다양한 분야에서 정밀장비의 사용이 필수적으로 요구되고 있다. 또한 최근에 반도체 핵심 기술이 소형화, 고용량화, 고집적화 됨에 따라 대다수의 반도체 및 디스플레이 장비에서의 고정밀도 및 신뢰성 확보가 시급한 사항이다^(1~3). 생산 공정에서의 정밀도 허용범위가 마이크로미터에서 나노미터 급으로 정밀해지고 있는 현재, 지반진동은 안정적인 동작과 기능을 저해하는 급격한 문제점으로 나타나고 있다⁽⁴⁾. 지반진동은 지진, 설비, 인근 차량 혹은 사람의 유동 등 많은 복합적인 요소들을 변수로 갖는다. 이를 해석하는 방법은 응답스펙트럼해석법^(5,6)과 시간이력해석법⁽⁷⁾ 등이 있으며 응답스펙트럼해석법은 비교적 계산이 용이하고 간편하지만 시간에 따른 구조물의 응답을 구할 수 없다. 이에 비해 시간이력해석법은 운동방정식을 연속적으로 시간 증분마다 단계적으로 수치적분을 함으로서 시간에 따른 구조물의 응답을 해석할 수 있는 방법이지만 시간이 많이 소요되고 막대한 계산량이 요구되는 단점이 있다. 따라서 간단하게 시간에 따른 구조물의 정상상태의 응답을 구하는 방법이 필요하게 되었다.

이를 위해 전단구조물의 지반응답을 전달행렬법^(8,9)을 사용하여 확장된 전달행렬을 만들었으며 기존의 방법에 비해 비교적 손쉽게 해석하는 방법을 개발하였다. 먼저 지반진동의 입력신호를 작성하기 위해 반도체 장비가 설치 예정인 장소의 지반진동에 대한 가속도 신호를 측정하였다. 이 신호를 필터링을 통해 노이즈를 제거하고 변위신호로 변환하였다. 지반과 각 층의 질점과의 전달함수를 확장된 전달행렬로 해석하는 방법을 새롭게 개발하여 지반진동이 각 층의 변위에 미치는 영향을 검토하였다.

2. 이 론

2.1 전단구조물의 전달행렬법

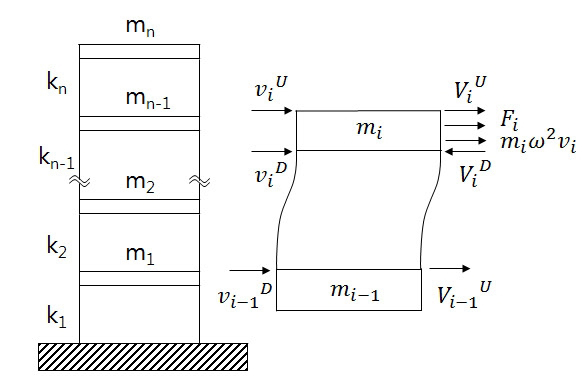
전달행렬법의 전달행렬을 구하기 위하여 Fig. 1과 같이 나타내었다. Fig. 1에서 i번째 요소의 횡 방향 전달행렬은 아래 식과 같다.

$\[ {\left\{\begin{array}{c}v\hfill \\ V\hfill \end{array}\right\}}_i^D=\left[\begin{array}{cc}1\hfill & 1/k_i\hfill \\ 0\hfill & 1\hfill \end{array}\right]{\left\{\begin{array}{c}v\hfill \\ V\hfill \end{array}\right\}}_{i-1}^U \]$

(1)

Fig. 1

Transfer matrix schematic diagram and free-body diagram of mass

여기서 v, V는 각각 횡 변위와 전단력을 나타내는 상태벡터이며 U, D는 요소의 위쪽과 아래쪽을 나타내고 k는 전단구조물 기둥의 횡 방향의 스프링 상수를 의미한다.

i번째 질량 m_i에 대한 위쪽과 아래쪽의 점 전달행렬은 아래와 위 변위가 동일하지만 관성력이 있으므로 다음과 같이 나타낼 수 있다.

$\[ {\left\{\begin{array}{c}v\hfill \\ V\hfill \end{array}\right\}}_i^U=\left[\begin{array}{cc}1\hfill & 0\hfill \\ -m_i{\omega }^2\hfill & 1\hfill \end{array}\right]{\left\{\begin{array}{c}v\hfill \\ V\hfill \end{array}\right\}}_i^D \]$

(2)

여기서 스프링과 질량에 대한 행렬을 동시에 고려하면 다음과 같이 표현된다.

$\[ \begin{array}{c}{\left\{\begin{array}{c}v\hfill \\ V\hfill \end{array}\right\}}_i^U=\left[\begin{array}{cc}1\hfill & 0\hfill \\ -m_i{\omega }^2\hfill & 1\hfill \end{array}\right]\left[\begin{array}{cc}1\hfill & 1/k_i\hfill \\ 0\hfill & 1\hfill \end{array}\right]{\left\{\begin{array}{c}v\hfill \\ V\hfill \end{array}\right\}}_{i-1}^U\hfill \\ =\left[\begin{array}{cc}1\hfill & 1/k_i\hfill \\ -m_i{\omega }^2\hfill & 1-\left(\frac{m_i{\omega }^2}{k_i}\right)\hfill \end{array}\right]{\left\{\begin{array}{c}v\hfill \\ V\hfill \end{array}\right\}}_{i-1}^U\hfill \end{array} \]$

(3)

따라서 i번째 요소의 전달행렬 T_i은 다음과 같이 나타낼 수 있다.

$\[ \left[T_i\right]=\left[\begin{array}{cc}1\hfill & 1/k_i\hfill \\ -m_i{\omega }^2\hfill & 1-\left(\frac{m_i{\omega }^2}{k_i}\right)\hfill \end{array}\right] \]$

(4)

Fig. 1에서 i번째 질량 m_i에 F_i의 주기적인 외부 힘이 작용할 때 관성력을 평형을 고려하면 다음과 같이 나타낼 수 있다⁽⁹⁾.

$\[ {\left\{\begin{array}{c}v\hfill \\ V\hfill \end{array}\right\}}_i^U=\left[\begin{array}{cc}1\hfill & 1/k_i\hfill \\ -m_i{\omega }^2\hfill & 1-\left(\frac{m_i{\omega }^2}{k_i}\right)\hfill \end{array}\right]{\left\{\begin{array}{c}v\hfill \\ V\hfill \end{array}\right\}}_{i-1}^U+{\left\{\begin{array}{c}0\hfill \\ -F\hfill \end{array}\right\}}_{i-1}^U \]$

(5)

외부 힘을 고려하여 단일 항으로 나타내면 다음식과 같이 표현되어진다.

$\[ {\left\{\begin{array}{c}v\hfill \\ V\hfill \\ \cdots \hfill \\ 1\hfill \end{array}\right\}}_i^U=\left[\begin{array}{cccc}1\hfill & 1/k_i\hfill & ⋮\hfill & 0\hfill \\ -m_i{\omega }^2\hfill & 1-\left(\frac{m_i{\omega }^2}{k_i}\right)\hfill & ⋮\hfill & -F_i\hfill \\ \cdots \cdots \cdots \hfill & \cdots \cdots \cdots \hfill & \cdots \cdots \cdots \hfill & \cdots \cdots \cdots \hfill \\ 0\hfill & 0\hfill & ⋮\hfill & 1\hfill \end{array}\right]{\left\{\begin{array}{c}v\hfill \\ V\hfill \\ \cdots \hfill \\ 1\hfill \end{array}\right\}}_{i-1}^U \]$

(6)

따라서 i번째 요소의 확장된 전달행렬 [T_i]은 다음과 같이 나타낼 수 있다.

$\[ \left[\overline{T_i}\right]=\left[\begin{array}{cccc}1\hfill & 1/k_i\hfill & ⋮\hfill & 0\hfill \\ -m_i{\omega }^2\hfill & 1-\left(\frac{m_i{\omega }^2}{k_i}\right)\hfill & ⋮\hfill & -F_i\hfill \\ \cdots \cdots \cdots \hfill & \cdots \cdots \cdots \hfill & \cdots \cdots \cdots \hfill & \cdots \cdots \cdots \hfill \\ 0\hfill & 0\hfill & ⋮\hfill & 1\hfill \end{array}\right] \]$

(7)

이때의 상태벡터는 다음 식과 같다.

$\[ {\left\{\begin{array}{c}v\hfill \\ V\hfill \\ \cdots \hfill \\ 1\hfill \end{array}\right\}}_n^U=\left[\overline{T_n}\right]\left[\overline{T_{n-1}}\right]•••\left[\overline{T_2}\right]\left[\overline{T_1}\right]{\left\{\begin{array}{c}v\hfill \\ V\hfill \\ \cdots \hfill \\ 1\hfill \end{array}\right\}}_0^U \]$

(8)

$\[ =\left[\overline{T_{all}}\right]{\left\{\begin{array}{c}v\hfill \\ V\hfill \\ \cdots \hfill \\ 1\hfill \end{array}\right\}}_0^U=\left[\begin{array}{cccc}{u}_{11}\hfill & u_{12}\hfill & ⋮\hfill & u_{13}\hfill \\ u_{21}\hfill & u_{22}\hfill & ⋮\hfill & u_{23}\hfill \\ \cdots \hfill & \cdots \hfill & \cdots \hfill & \cdots \hfill \\ 0\hfill & 0\hfill & ⋮\hfill & 1\hfill \end{array}\right]{\left\{\begin{array}{c}v\hfill \\ V\hfill \\ \cdots \hfill \\ 1\hfill \end{array}\right\}}_0^U \]$

(9)

전단구조물의 경우 경계조건은 지반이 고정이고 최고층이 자유이므로 상태벡터 {Z_i}는 다음과 같이 나타낼 수 있다.

$\[ \left\{Z_n\right\}={\left\{\begin{array}{c}v\hfill \\ 0\hfill \\ \cdots \hfill \\ 1\hfill \end{array}\right\}}_n, \left\{Z_0\right\}={\left\{\begin{array}{c}0\hfill \\ V\hfill \\ \cdots \hfill \\ 1\hfill \end{array}\right\}}_0 \]$

(10)

자유진동의 경우 하중 F_i = 0이므로 u₁₃ = 0, u₂₃ = 0가 된다. 식 (9)에 식 (10)을 대입하여 고유진동수에 ω대한 n차 방정식을 구하면 전단구조물 고유진동수를 다음과 같이 구할 수 있다.

$\[ f\left(\omega \right)=\mathrm{d}\mathrm{e}\mathrm{t}\left|u_{11}\right| \]$

(11)

이 방정식의 n개의 해를 고유진동수라 한다. 각 차의 고유진동수와 식 (10)의 경계 조건을 식 (11)에 대입하면 각 차에 대한 진동 모드를 구할 수 있다.

강제 진동의 경우 F_i가 존재하므로 전단구조물의 경우 식 (9)은 다음과 같이 나타낼 수 있다.

$\[ {\left\{\begin{array}{c}v\hfill \\ 0\hfill \\ \cdots \hfill \\ 1\hfill \end{array}\right\}}_n^U=\left[\begin{array}{cccc}{u}_{11}\hfill & u_{12}\hfill & ⋮\hfill & u_{13}\hfill \\ u_{21}\hfill & u_{22}\hfill & ⋮\hfill & u_{23}\hfill \\ \cdots \hfill & \cdots \hfill & \cdots \hfill & \cdots \hfill \\ 0\hfill & 0\hfill & ⋮\hfill & 1\hfill \end{array}\right]{\left\{\begin{array}{c}0\hfill \\ V\hfill \\ \cdots \hfill \\ 1\hfill \end{array}\right\}}_0^U \]$

(12)

$\[ 0=u_{22}{V}_0+u_{13} \]$

(13)

$\[ V_0=-\frac{u23}{u22} \]$

(14)

식 (10)에 있는 지반의 상태 벡터를 식 (7)에 대입하면 강제진동이 있을 때 각 지점의 상태벡터를 구할 수 있다. 이를 이용하면 측정 점 i와 가진 점 j의 전달함수 H_i,j(ω)를 해석할 수 있다.

2.2 지반진동 이론

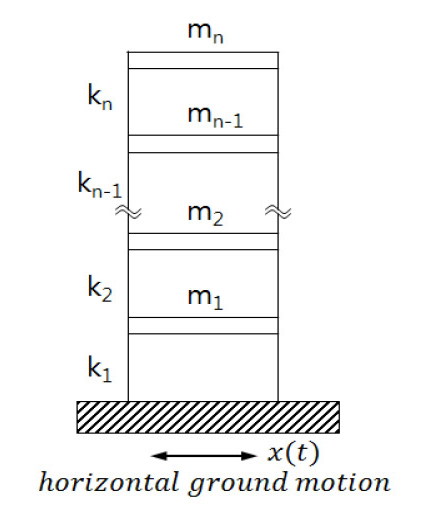
Fig. 2와 같이 지반진동을 받는 비 감쇠계 다자유도계의 운동 방정식은 다음과 같다.

$\[ \left[M\right]\left\{\ddot{x\left(t\right)}\right\}+\left[K\right]\left\{x\left(t\right)\right\}=-{\left\{k_{1}y\left(t\right),0,• •,0\right\}}^T \]$

(15)

Fig. 2

A multi story structure subjected to horizontal ground motion

여기서 [M]은 질량행렬, [K]는 강성행렬, k₁은 지반과 질량 m₁을 연결하는 스프링이고 y(t)는 지반진동의 변위이다.

3. 적용 예

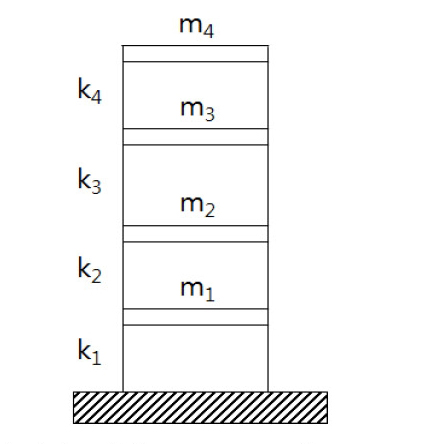
전달행렬법을 이용하고 지반진동을 받는 전단구조물의 응답해석을 검증하기 위하여 Fig. 3과 같이 4층 전단구조물에 대한 고유치 해석을 수행하였다. 수치해석 대상 모델은 제원은 다음과 같다. 질량은 m₁이 4500 kg, m₂와 m₃는 3000 kg, m₄는 500 kg이다. 스프링 탄성상수는 k₁이 3200 kN/m이고 k₂는 2400 kN/m, k₃는 1600 kN/m, k₄는 800 kN/m이다.

Fig. 3

Model of four story shear structure

4. 결과 및 고찰

4.1 고유진동수와 고유모드

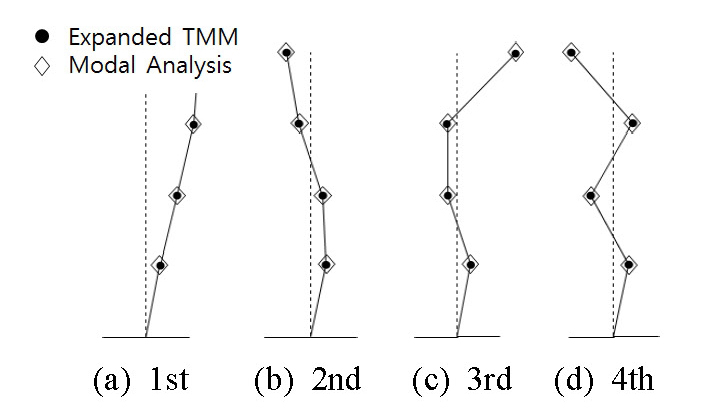
제안된 지반 진동에 확장된 전달행렬법과 모드해석(modal analysis)을 사용하여 Fig. 3에 나타낸 4층 전단구조물의 고유진동수와 고유모드를 구해 각각 Table 1과 Fig. 4에 나타내었다. 4자유도 계이므로 모두 4개의 고유진동수와 고유모드가 구해졌으며 두 방법이 일치하므로 제안된 방법이 타당함을 알 수 있었다.

Table 1

Natural frequencies of four story shear building

Fig. 4

Mode shapes of the four story shear structure

4.2 전달함수

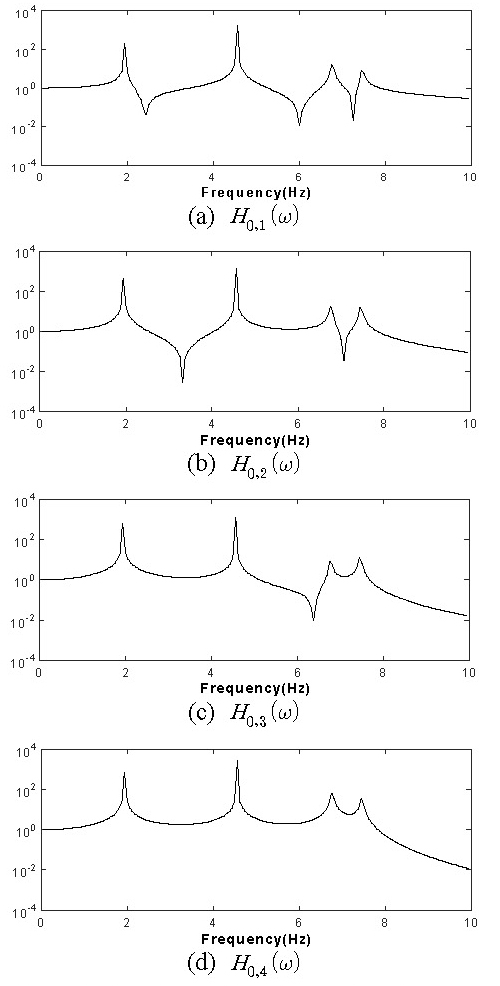
지반 진동에 의한 각 층의 진동을 해석하기 위해서는 지반과 각 층 사이의 전달함수가 필요하게 된다. 지반 변위함수가 y(t)이고 지반과 질량 m₁ 사이의 스프링상수를 k₁으로 하면 지반 진동에 의해 발생되는 힘은 F₀ = k₁y(t)가 된다. 이를 식 (7)과 식 (14)을 이용하여 전달 함수를 구하였으며 Fig. 5에 나타내었다. 지반에 대한 총 4개 층에 대한 전달함수를 나타내었으며 H_i,j(ω)는 가진 점i와 측정 점j의 전달함수를 의미한다.

Fig. 5

Transfer function of the four stories shear structure

4.3 주기함수에 대한 응답 비교

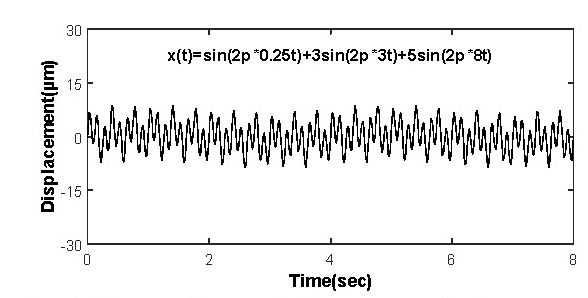
지반에 Fig. 6과 같이 주기함수인 변위 신호를 주고 각 층의 변위응답을 식 (18)을 사용하여 구하였으며 Fig. 7에 나타내었다. 층이 올라갈수록 변위가 많이 발생되었다. 실선은 전달행렬법의 전달함수를 사용하여 예측한 결과이고 점선은 모드 해석(modal analysis)을 사용하여 얻는 결과이다. 두 방법이 잘 일치하였다.

Fig. 6

The displacement time curve for the ground vibration with a period function

Fig. 7

Calculated each floor displacement by the ground vibration with a period function

4.4 지반 가속도의 변위 변환

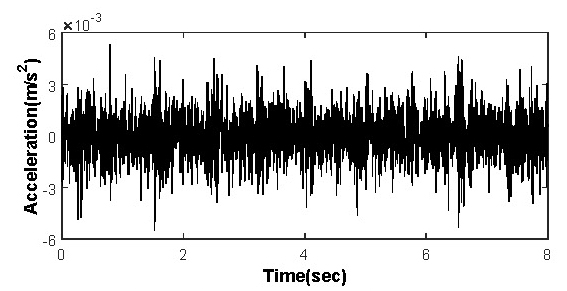
지반진동으로 인한 구조물의 변위응답을 구하기 위해 측정된 지반 가속도를 Fig. 8에 나타내었다.

Fig. 8

Ground acceleration signal from the experiment

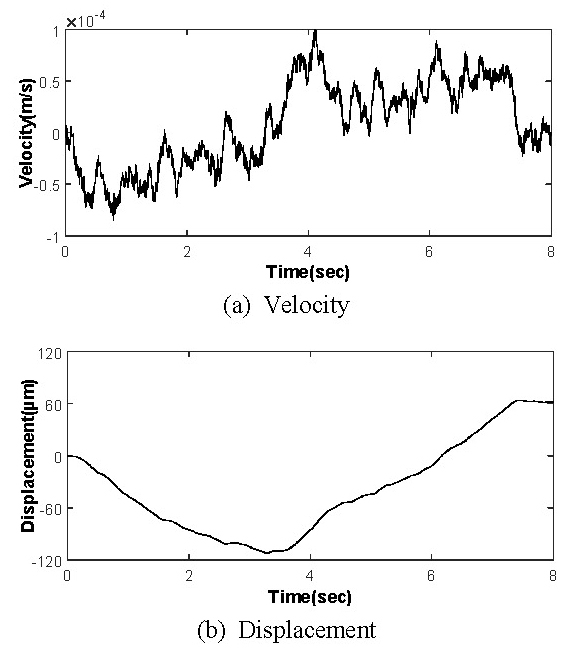
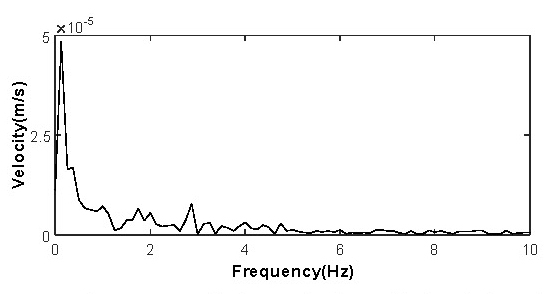
이 지반진동의 가속도를 시간에 따라 적분하여 속도로 Fig. 9(a)에 나타내었으며 이를 다시 적분하여 변위신호로 변환하여 Fig. 9(b)에 나타내었다. 지반진동 특성상 지반의 변위는 어느 기준 위치에서 진동한다고 볼 수 있으므로 시간에 따른 변위신호의 평균 추세선 값이 수평이 되어야 한다. 하지만 Fig. 9(b)의 변위신호는 추세선이 수평과 일치하지 않기 때문에 속도에 대해 푸리에 변환하여 Fig. 10에 나타내었으며 검토한 결과 0.5 Hz 이하 성분이 상당히 높게 나타났다. 이는 가속도계 특성상 저주파는 측정하기 어려워 노이즈를 측정할 가능성이 높기 때문이다.

Fig. 9

Velocity and displacement obtained by integrating acceleration

Fig. 10

The FFT of the velocity obtained by integrating experimental acceleration

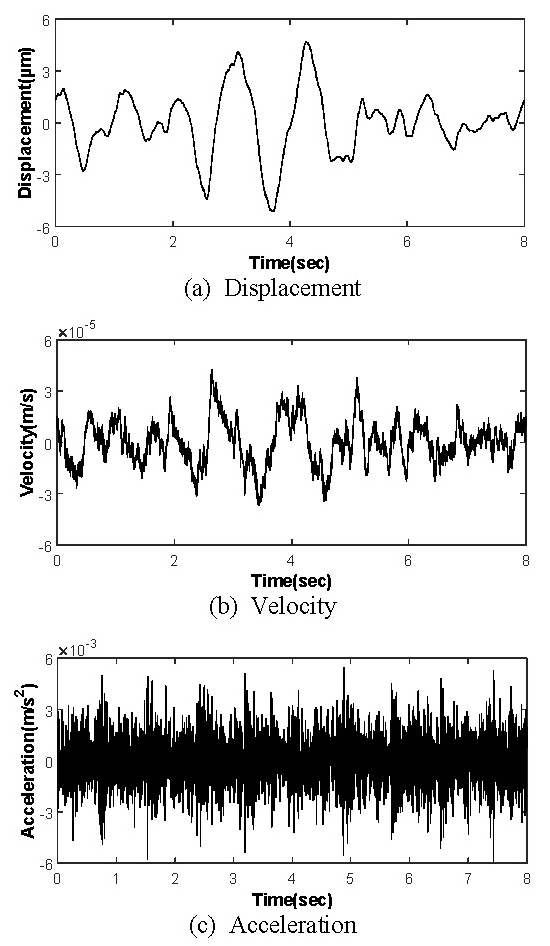
하이패스필터를 사용하여 변위의 추세선이 수평이 되도록 문제되는 0.5 Hz 이하의 저주파 성분을 제거한 다음 역 프리에 변환을 하여 Fig. 11에 나타내었다. Fig. 11에 있는 가속도, 속도, 변위의 추세선을 보면 수평과 잘 일치함을 알 수 있다. 또한 Fig. 8의 실험한 가속도와 필터링한 가속도 신호가 거의 같음을 알 수 있다. 따라서 지반진동의 변위는 Fig. 11(a)를 사용하여 전단구조물의 응답해석을 하였다.

Fig. 11

Displacement, velocity and acceleration with the high-pass filter

4.5 지반 진동에 의한 응답 비교

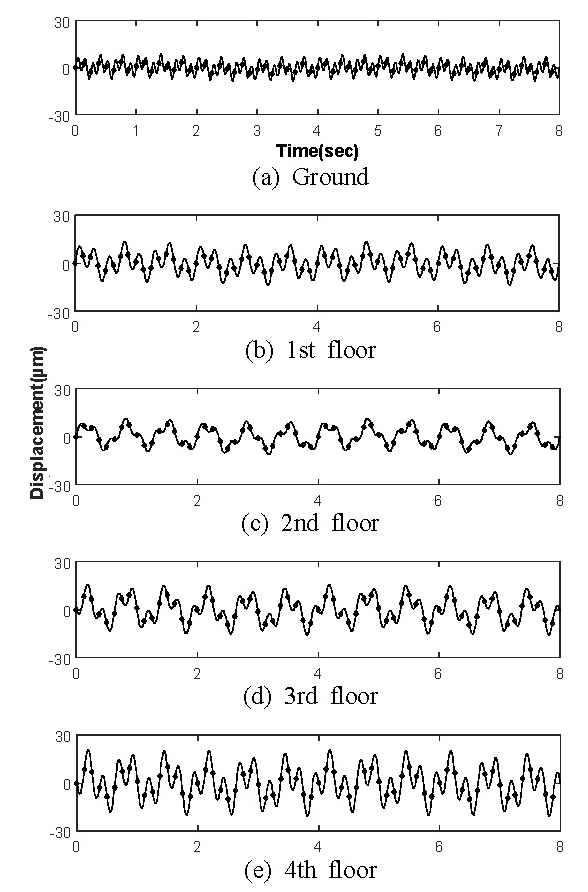
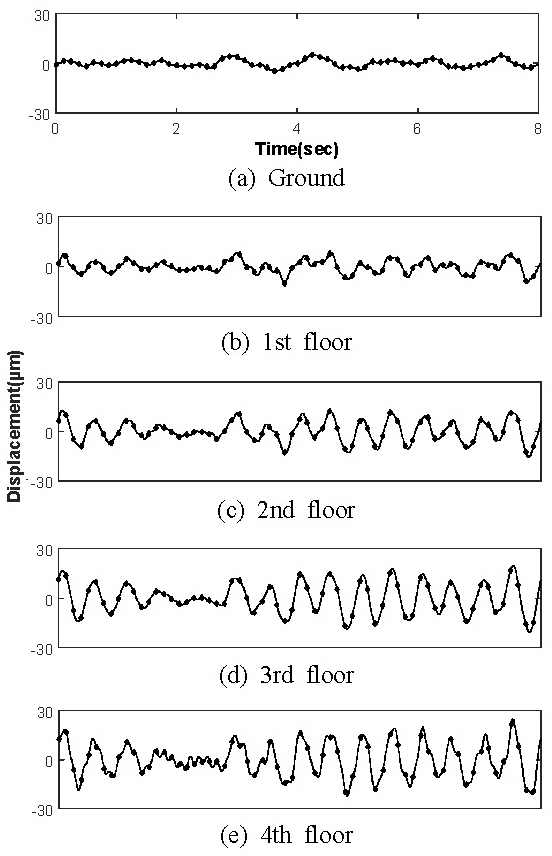
Fig. 11(a)에 있는 지반 변위함수를 입력으로 전단 구조물에 적용한 결과 각 층의 변위응답은 Fig. 12와 같이 나타났다. 실선은 전달행렬법의 전달함수를 사용하여 예측한 결과이고 점선은 모드 해석(modal analysis)을 사용하여 얻는 결과이다. 두 방법이 잘 일치하여 제안한 방법이 타당함을 알 수 있었다.

Fig. 12

Calculated each floor displacement by the ground vibration with experiment

5. 결 론

지반진동이 있을 때 전단구조물의 응답해석을 전달행렬법을 이용하여 해석하였으며 다음과 같은 결론을 얻었다.

(1) 확장된 전달행렬법을 사용하여 전단구조물의 전달함수를 해석하는 방안을 개발하였다.

(2) 지반진동이 있을 때 전달함수와 푸리에 변환과 역 변환을 이용하여 전단 구조물의 응답을 해석하는 방안을 제시하였다.

(3) 측정된 지반 가속도 신호의 노이즈를 제거하여 지반 변위 신호로 변한하는 방법을 제시하였다.

(4) 지반 진동에 의한 전단 구조물의 응답을 제안한 방법과 모드해석으로 해석한 방법으로 비교한 결과 서로 잘 일치하여 제안한 방법의 타당성을 검증하였다.

Acknowledgments

이 연구는 2017학년도 경기대학교 대학원 연구 장학생 장학금 지원에 의해 수행되었음.

References

• Normura, K., Kamiya, T., and Hosono, H., (2011), Ambipolar Oxide Thin-film Transistor, Advanced Materials, 23, p3431-3434. [https://doi.org/10.1002/adma.201101410]
• Park, C., (2017), A Study on Technology Diffusion Trend Considering Technological Performance Enhancement and Economics: Case of Technology Evolution of 32 nm, 22 nm, 14 nm Logic Semiconductors, Journal of the Korea Academia-Industrial Cooperation Society, 18(2), p177-184.
• Lewyn, L. L., Ytterdal, A. C., and Martin, K., (2009), Analog Circuit Design in Nonoscale CMOS Technologies, 97(10), p1687-1714.
• Robert, M. S., (2012), Ultra-precision Engineering in Lithographic Exposure Equipment for the Semiconductor Industry, Philosophical Transactions of the Royal Society, 370, p3950-3972. [https://doi.org/10.1098/rsta.2011.0054]
• Patil, S. S., Ghadge, S. A., Konapure, C. G., and Ghadge, C. A., (2014), Seismic Analysis of High-Rise Building by Response Spectrum Method, International Journal of Computational Engineering Research, 3(3), p272-279.
• Ky, L., Chatpan, C., and Toshiro, H., (2014), Seismic Shear Forces in Shear Walls of a Medium-rise Building Designed By Response Spectrum Analysis, Engineering Journal, 18(4), p73-95. [https://doi.org/10.4186/ej.2014.18.4.73]
• Hosseini, M.,, Hosseini, B., and Safi, Z., (2017), Seismic Design Evaluation of Reinforced Concrete Buildings for Near-source Earthquakes by Using Nonlinear Time History Analyses, Procedia Engineering, 199, p176-181. [https://doi.org/10.1016/j.proeng.2017.09.225]
• Kim, J. H., Kwak, J. H., Lee, J. W., and Lee, J. Y., (2016), Dynamic Analysis of Cracked Timoshenko Beams Using the Transfer Matrix Method, Transactions of the Korean Society for Noise and Vibration Engineering, 26(2), p179-186. [https://doi.org/10.5050/KSNVE.2016.26.2.179]
• Lee, J. W., and Lee, J. Y., (2016), Free Vibration Analysis Using the Transfer-matrix Method on a Tapered Beam, Computers and Structures, 164, p75-82. [https://doi.org/10.1016/j.compstruc.2015.11.007]