반공진을 이용한 대역 차단형 비틀림 진동 절연기의 토크 전달률 해석 및 측정

1. 서 론

자동차 구동계(drivetrain)는 차량의 진동과 소음에 가장 많은 영향을 미치는 요소 중 하나이다. 내연기관(internal combustion engine)에서 발생된 비틀림 진동이 동력전달시스템(powertrain system)에 전달되어 자동차의 NVH(noise, vibration and harshness)문제를 유발시킬 뿐만 아니라 승차감과 내부 부품의 내구성에도 치명적인 영향을 미친다⁽¹⁾.

비틀림 진동을 효과적으로 저감시키기 위해서 저렴하고 신뢰성이 높기 때문에 수동 비틀림 진동 절연기(passive torsional vibration isolators, or damper)가 널리 적용되고 있다⁽²⁾. 수동 비틀림 진동 절연 시스템은 크게 진동절연기(vibration isolators)와 진동 흡진기(vibration absorbers)로 구분된다. 비틀림 진동 절연기의 경우, 일반적으로 토크 컨버터에 설치된 록업 클러치에 삽입하여 코일 스프링을 통해 전달된 비틀림 진동을 감소시키는 역할을 한다.

비틀림 진동 절연을 위해서 또 다른 방법은 동흡진기(dynamic vibration absorbers: DVAs)와 반공진 진동 절연기(dynamic anti-resonance vibration isolators: DAVIs)를 도입하는 것이다. DAVI의 경우, 병진 운동(translation motion)에 대한 연구들은 활발히 진행되었지만 회전 운동(rotational motion)에 대한 연구는 거의 이루어지지 않았다. DAVI는 관성연결(inertial coupling)를 통해 주 진동 시스템에 반공진 주파수를 발생시켜 공진 주파수 이상의 특정 영역에서 진동 절연 효과가 있다⁽³⁾. 이러한 진동 절연기는 기존 질량-스프링-댐퍼의 진동 시스템과 달리 댐핑이 없거나 작음에도 불구하고 진동 절연 효과가 있을 뿐 만 아니라 시스템의 댐핑 증가에 따라 반공진 주파수 영역이후의 토크 전달률이 증가되지 않아서 기존 비틀림 진동 절연기에 대한 고주파수 진동 절연 성능 개선에 적합하다. 반공진을 이용한 진동 절연기는 일반적으로 레버형 반공진 진동 절연기의 작동 원리를 도입한 시스템이다^(3,4). 이 레버형 반공진 진동 절연기는 중간 전달체 역할을 하는 레버(지렛대) 끝단에 부가질량(auxiliary mass)을 달아서 지렛대 원리에 의해서 발생하는 관성력으로 입력과 출력의 사이에 설치된 스프링의 복원력을 효과적으로 상쇄시킬 수 있는 구조이다. 이때, 주 진동 시스템에 반공진 주파수가 발생하여 기존 진동 절연기보다 진동을 더욱 감소시키게 된다. 반공진 주파수는 주로 레버의 길이, 진동 절연기의 질량과 스프링 상수 등에 의존하기 때문에 시스템의 주요 파라미터를 적절하게 설계하면 광대역 진동 절연기를 구현할 수 있는 가능성이 있다⁽⁵⁾. 이러한 진동 절연기를 적용하면 최근에 엔진 사이즈 축소(downsizing), 직결 영역 확대와 같은 연비 개선 시 악화되는 자동차의 진동 및 소음을 보다 효과적으로 절연시킬 수 있다.

이 연구에서는 반공진을 이용한 비틀림 진동 절연기에 대한 적용 가능성과 진동 절연 성능을 이론과 실험을 통해서 검증하였다. 이를 위해서 우선 제안된 진동 절연기의 토크 전달률에 대한 이론식을 유도하고 제안된 진동 절연기와 기존 진동 절연기에 대한 토크 전달률을 MATLAB/Simulink를 이용하여 시뮬레이션을 수행하였다. 그리고 진동 절연기의 성능에 영향을 미치는 주요 설계 변수에 대해 분석한 후, 분석 결과를 바탕으로 진동 절연기를 실제 설계하고 시작품을 제작하였다. 마지막으로 제작한 진동 절연기에 대해 개선된 진동 절연 성능을 입증하기 위해서 기존 진동 절연기에 대한 토크 전달률을 실험 결과를 통해 비교하였다.

2. 대역 차단형 비틀림 진동 절연기

2.1 구조 및 운동 방정식

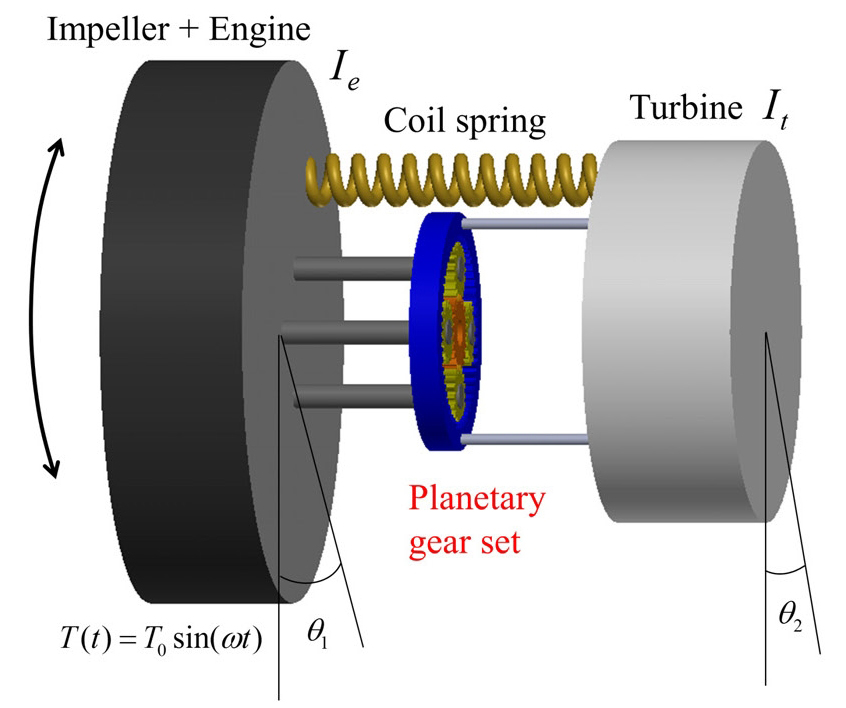
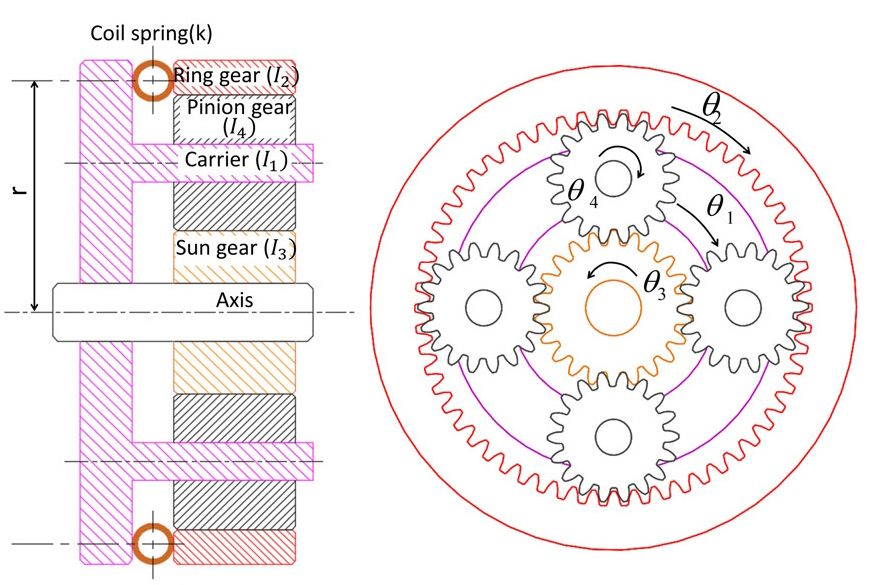
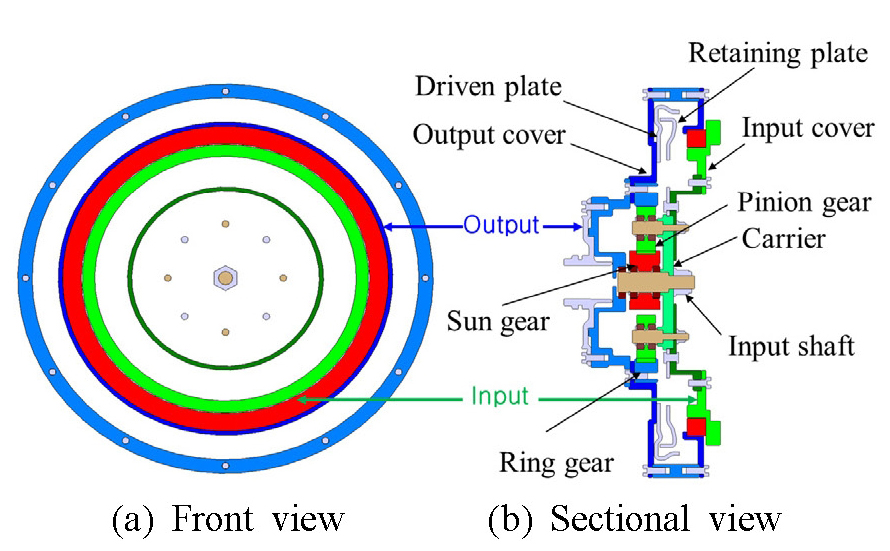
이 연구에서 제안된 진동 절연기의 구조는 Fig. 1과 같다. 기존 클러치 댐퍼용 진동 절연기⁽⁶⁾의 입력 측 엔진과 출력 측 터빈 사이에 반공진을 발생시키는 유성기어열(planetary gear sets, PG)을 연결하였다. 유성기어열은 Fig. 2와 같이 링기어(ring gear), 피니언 기어(pinion gear)와 선기어(sun gear)로 구성된다. 선기어는 충심 축에 위치하고 피니언기어와 링기어는 선기어와 접촉하면서 동심원 형태로 배치되고 있다. 한편, 캐리어(carrier)는 피니언 기어와 연결되어 중심 축을 기준으로 회전운동을 한다.

Fig. 1

Schematic view of a proposed band-stop type torsional vibration isolator

Fig. 2

Configuration of a planetary gear set inside the proposed torsional vibration isolator

운동방정식을 유도하기 위해 다음과 같이 가정한다. 첫째, 유성기어열을 구성하는 모든 기어는 강체이다. 둘째, 코일 스프링은 질량이 없는 1단 선형 비감쇠 스프링이다. 셋째, 엔진의 회전각과 캐리어의 회전각은 같으며 링기어와 터빈의 회전각도 같은 것으로 가정한다. 이러한 가정을 바탕으로 제안된 진동 절연기의 운동방정식은 라그랑지 방정식(Lagrange equation)을 적용하여 다음과 같이 질량-댐퍼-스프링 모델로 간단하게 표현할 수 있다.

$\[ \begin{array}{c}\left[M\right]\ddot{\theta }+\left[C\right]\dot{\theta }+\left[K\right]\theta =0\hfill \\ \left[M\right]=\left[\begin{array}{cc}{I}_e+I_1+I_3{\left(1+\beta \right)}^2+I_4{\left(1-\alpha \right)}^2& I_4\alpha \left(1-\alpha \right)-I_3\beta \left(1+\beta \right)\\ I_4\alpha \left(1-\alpha \right)-I_3\beta \left(1+\beta \right)& I_t+I_2+I_3{\beta }^2+I_4{\alpha }^2\end{array}\right]\hfill \\ \left[C\right]={\left[S\right]}^T\left[\begin{array}{cc}\xi & 0\\ 0& \xi \end{array}\right]\left[S\right],\left[K\right]=\left[\begin{array}{cc}k& -k\\ -k& k\end{array}\right]\hfill \end{array} \]$

(1)

여기서 [M], [C]와 [K]는 각각 시스템의 질량 행렬, 감쇄 행렬과 강성 행렬을 나타낸다. I₁, I₂, I₃, I₄는 각각 캐리어, 링기어, 선기어와 피니언 기어의 관성 모멘트를 나타내고 θ₁, θ₂는 캐리어, 링기어에 대한 회전각이다. I_e와 I_t는 각각 엔진과 터빈에 대한 관성 모멘트이다. α와 β는 기어 비(gear ratio)를 나타내는 다음 식 (2)와 같다.

$\[ \begin{array}{cc}\alpha =\frac{N_2}{N_4},\hfill & \beta =\frac{N_2}{N_3}\hfill \end{array} \]$

(2)

여기서 N₂, N₃, N₄는 각각 링기어, 선기어와 피니언 기어의 잇수를 나타낸다. 시스템의 감쇠 행렬은 모드감쇠비(modal damping ratio)와 모드 행렬 [S]에 의해 정의되고 전체 모드에 대해서 모드 감쇠비 ξ = 0.05로 가정하였다. 또한 시스템의 carrier에 입력 토크 T(t) = T₀e^iωt로 가진할 경우, 입력(carrier)과 출력(ring gear)에 대한 회전각은 θ₁(t) = Θ₁e^iωt, θ₂(t) = Θ₂e^iωt로 가정하면 제안된 진동 절연기에 대한 운동 방정식을 식 (3)과 같이 유도할 수 있다.

$\[ \left(-{\omega }^2\left[I\right]+i\omega \left[C\right]+K\right)\left\{\Theta \right\}=\left\{T\right\} \]$

(3)

이때, 입력과 출력에 대한 회전각의 진폭은 식 (4)와 같이 표현할 수 있다.

$\[ \left\{\Theta \right\}={\left(-{\omega }^2\left[I\right]+i\omega \left[C\right]+K\right)}^{-1}\left\{T\right\} \]$

(4)

여기서 Θ = [Θ₁Θ₂]^T로 하고 A와 T행렬은 다음과 같이 정의한다.

$\[ \begin{array}{c}A=-{\omega }^2\left[M\right]+i\omega \left[C\right]+K=\left[\begin{array}{cc}{a}_{11}\hfill & a_{12}\hfill \\ a_{12}\hfill & a_{22}\hfill \end{array}\right]\hfill \\ T={\left[\begin{array}{cc}{T}_0\hfill & 0\hfill \end{array}\right]}^T\hfill \end{array} \]$

(5)

입력과 출력에 대한 회전각의 진폭은 다음 식 (6)과 같다.

$\[ {\Theta }_1=\frac{a_{22}{T}_0}{a_{11}{a}_{22}-{a_{12}}^2}, {\Theta }_2=-\frac{a_{12}{T}_0}{a_{11}{a}_{22}-{a_{12}}^2} \]$

(6)

이때, 진동 절연기를 통해 전달된 출력 토크는 식 (6)을 이용하여 구할 수 있다.

$\[ T_t=-\left(I_t+I_2\right){\omega }^2{\Theta }_2=\frac{\left(I_t+I_2\right){\omega }^2{a}_{12}{T}_0}{a_{11}{a}_{22}-{a_{12}}^2} \]$

(7)

따라서 식 (7)을 이용하여 입력 토크와 출력 토크에 대한 토크 전달률은 식 (8)과 같이 정의할 수 있다.

$\[ TR=\left|\frac{T_t}{T_o}\right|=\left|\frac{\left(I_t+I_2\right){\omega }^2{a}_{12}}{a_{11}{a}_{22}-{a_{12|}}^2}\right| \]$

(8)

Fig. 3

Torque transmissibility of the proposed torsional vibration isolator and the conventional torsional vibration isolator

2.2 토크 전달률 해석

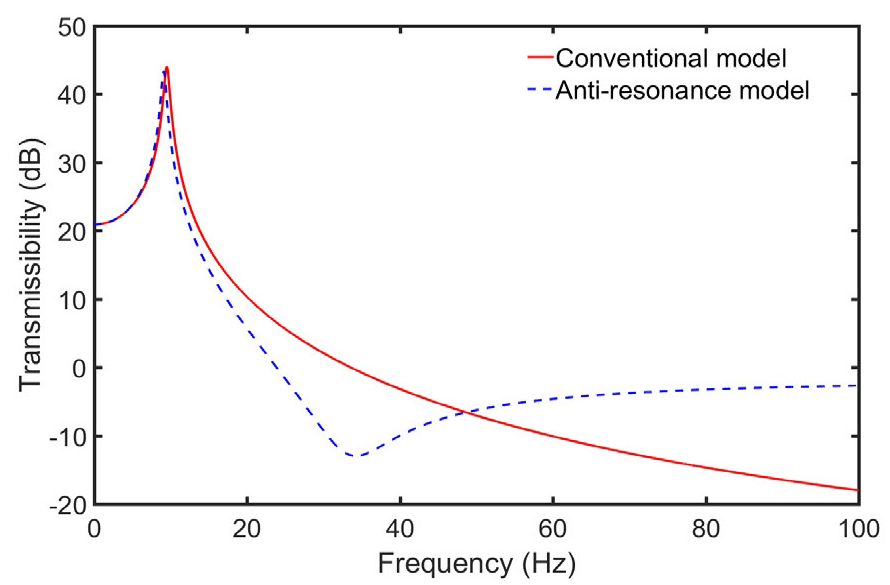
제안된 진동 절연기에 대한 진동 절연 성능을 검증하기 위하여 유도된 식 (8)을 바탕으로 토크 전달률을 시뮬레이션하였다. 시뮬레이션에 사용하는 파라미터들은 Table 1에 정리하였다. 기존 진동 절연기의 성능과 비교하기 위하여 유성기어열이 작동하지 않는 모델(선기어와 피니언기어의 관성이 0)에 대한 시뮬레이션도 수행하였다. 제안된 진동 절연기(anti-resonance model)의 경우, 공진 주파수(극점, poles)가 약 9 Hz, 반공진 주파수(영점, zeros)가 33.4 Hz로 나타났다. 한편, PG가 없는 기존 모델 (conventional model)의 경우, 공진주파수가 9.1 Hz로 확인되었으나 반공진 주파수는 나타나지 않았다.

Table 1

Specifications of the proposed planetary type anti-resonance vibration isolator

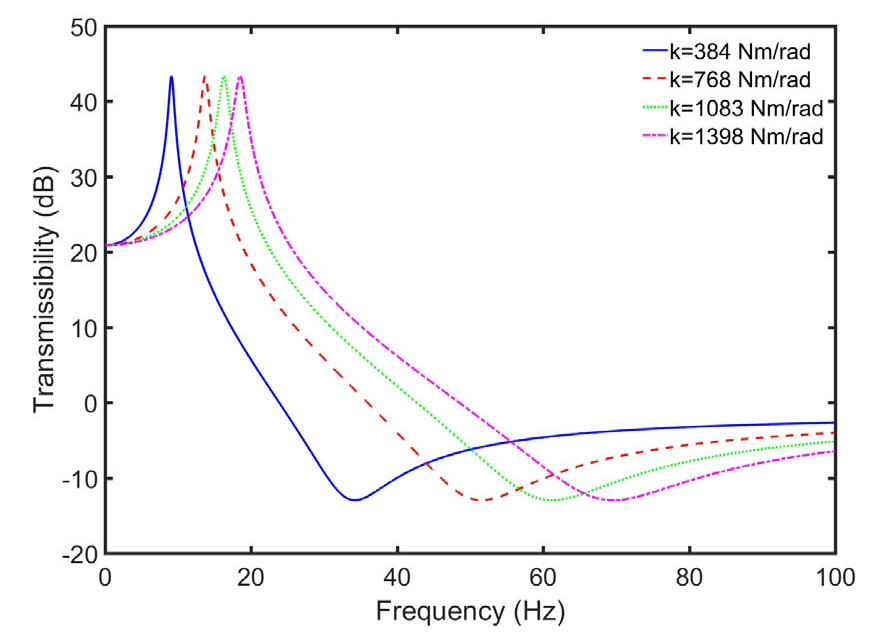
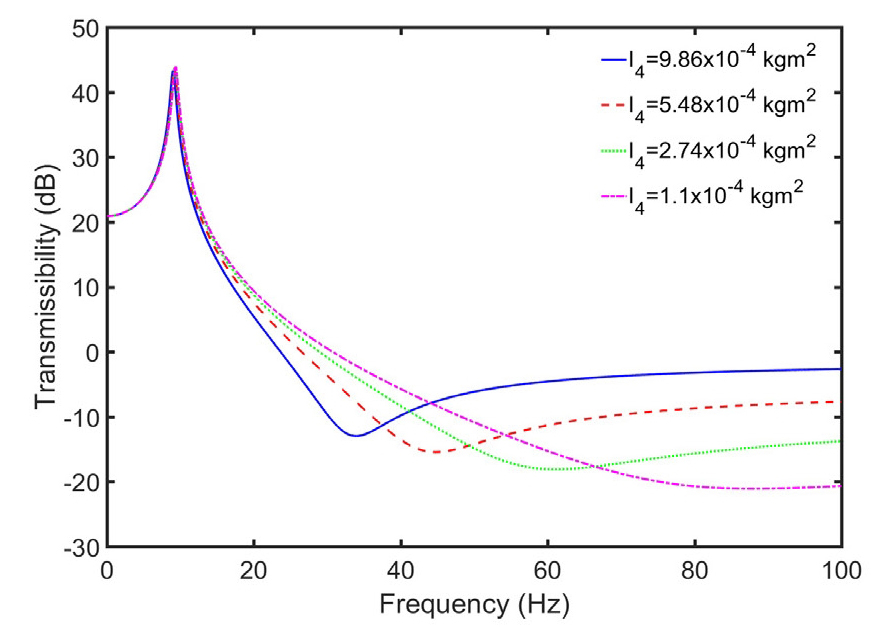
이 연구에서 제안된 진동 절연기의 성능에 영향을 미치는 주요 파라미터들에 대해 분석하였다. 먼저 코일 스프링의 영향을 분석하기 위하여 Fig. 4와 같이 화살표의 방향으로 스프링 강성이 높아질수록 고유진동수가 거의 이동되지 않았으나 반공진 주파수가 크게 고주파 영역으로 옮겨졌다. 스프링 강성 증가로부터 공진주파수 및 반공진 주파수는 같이 증가함을 알 수 있다. 또한 피니언 기어의 관성 모멘트(pinion gear inertia)의 변화에 따른 토크 전달률의 특성도 Fig. 5와 같이 분석하였다. 피니언 기어의 관성 모멘트 감소에 따라 고유진동수는 거의 변화되지 않았으나 반공진 주파수가 고주파 영역으로 이동된 것을 나타냈다. 따라서 피니언 기어의 관성 모멘트가 감소할 수록 반공진 성능이 약해진 것을 알 수 있다. 위의 분석 결과를 통해 제안된 진동 절연기에서 저강성 스프링과 높은 피니언 기어의 관성 모멘트를 설계하는 것이 진동 절연 성능 확보에 유리하다는 것을 알 수 있다.

Fig. 4

Torque transmissibility influenced with different spring stiffness constants

Fig. 5

Torque transmissibility influenced with different pinion gear inertia

3. 토크 전달률 측정

앞서 분석한 결과와 설계 파라미터들을 바탕으로 Fig. 6과 같이 진동 절연기를 설계하였다. 앞서 언급한 대로 입력 측은 캐리어가 되고 출력 측은 링기어인 것을 확인할 수 있다. 입력 토크가 입력 축에 전달될 때 드리븐 플레이트와 리테이닝 플레이트 사이에 설치된 코일 스프링의 작동으로 출력 측에 토크가 전달된다. 이때, 입력 토크에 의해 입력 측에 결합된 캐리어작동으로 인해 유성기어열을 구동시켜 반공진 주파수를 발생시키는 메커니즘을 보여주고 있다. 이러한 구조는 기본적으로 코일 스프링을 통해 진동 절연 효과가 있을뿐더러 추가된 유성기어열로 인해 기존 진동 절연기보다 절연 성능을 더욱 확보할 수 있다. 한편, Fig. 7과 같이 설계한 진동 절연기를 실제 시작품으로 제작하였다. Fig. 7(a)는 제작한 유성기어열의 모습이고 Fig. 7(b)는 조립된 진동 절연기의 완성품이다.

Fig. 6

A designed configuration of the proposed torsional vibration isolator

Fig. 7

A prototype of the proposed torsional vibration isolator

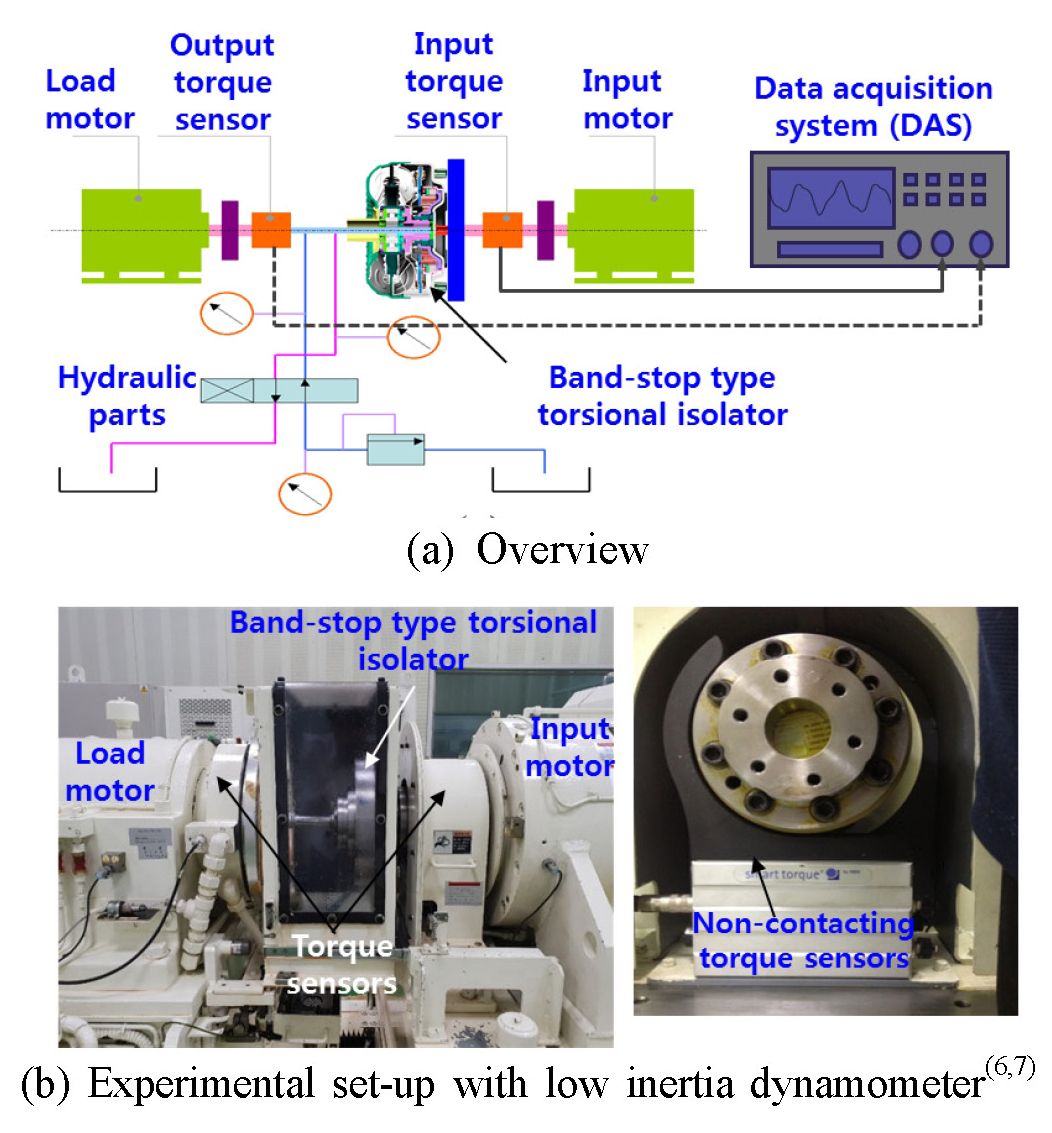
이 연구에서 제안된 진동 절연기에 대한 절연 성능을 토크 전달률을 통해 실험적으로 검증하였다. 실제 자동차 주행 조건과 최대한 구현하기 위해서 입출력 토크를 정밀 모터 제어가 가능한 저 관성 내구 시험기(Meidensha Co. 제작, 최대 입력 토크 3 kNm, 최대 회전수 7000 r/min) 및 최신 토크 측정 방법을 사용하여 측정하였다⁽⁸⁾. 입력 토크와 출력 토크는 각각 입력 토크 센서(model: HBM T12, 3 kNm) 및 출력 토크 센서(model: HBM T10F, 2 kNm)로 계측하였다⁽⁹⁾. 입력 토크 센서는 Fig. 8과 같이 입력 모터와 진동 절연기의 드리븐 플레이트를 연결하는 전달축(transmission shaft)에 설치하였으며 출력 토크 센서는 부하(load)모터와 진동 절연기의 리테이닝 플레이트를 연결하는 전달 축에 설치하였다.

Fig. 8

An experiment apparatus

입출력 토크 신호는 샘플링 주파수(sampling frequency)를 1 kHz로 설정하여 데이터 수집 장비(model: Keyence NR-500)를 사용하여 저장하였다. 신호의 왜곡(aliasing)을 방지하기 위하여 아날로그 저역 통과 필터(analog low-pass filter) 대신 차단 주파수(cut-off frequency)가 200 Hz 설정된 버터워스(Butterworth) 디지털 저역 통과 필터를 사용하여 측정된 토크 신호에 포함된 잡음(noise) 제거하였다. 이 연구에서 토크 전달률은 주파수 응답 함수(frequency response functions, FRFs)를 통해 구하였다. 사인 파형(sinusoidal waveform)의 순간 주파수(instantaneous frequency)가 시간에 따라 선형적으로 증가하도록 주파수 변조(frequency modulation)를 시킨 첩 신호(chirp or sweep signal)를 사용하였다.

여기서 f₀는 시작 주파수(t=0), K는 첩 속도 (chirp rate)이다(K=1.25). 4기통 엔진을 기준으로 엔진 오더(n=2)를 고정하고 저 관성 내구 시험기의 회전 속도를 80초 동안 500 r/min에서 3500 r/min까지 변경하면서 동시에 입력 토크(평균 50 Nm)를 유지하고 입출력 토크를 측정하였다. 측정된 입출력 토크 신호를 MATLAB^Ⓡ에 내장된 Envelope 함수^(7,10,11)를 사용하여 토크 전달률을 추정하였다. 이 방법은 입출력 토크 신호를 주기 신호를 가진 해석적 신호(analytic signal)로 변환한 후 각각 최댓값을 취하는 방식으로 입력과 출력에 대한 토크 진폭을 추출한 후 부드럽게 연결한 포락선(envelope curve)를 이용하여 직접 추정할 수 있다. 해석적 토크 신호는 MATLAB^Ⓡ에 내장된 Hilbert transform^(10,11)를 이용하여 다음과 같이 구할 수 있다.

여기서 Z(t)는 해석적 신호이고 T(t)는 측정된 토크 신호, $$ \widehat{T}\left(t\right)$$는 측정된 토크 신호에 대한 Hilbert transform이다. 이때, 해석적 신호에 대한 진폭은 다음과 같이 정의할 수 있다.

이때, 식 (11)을 이용하여 각각 입출력 토크 진폭을 추출한 후 전체 가진 주파수에 대해서 포락선을 추정할 수 있다. 이 포락선은 앞서 구한 토크 진폭을 바탕으로 스프라인 보정을 적절하게 사용하여 보다 완만하게 추출할 수 있다.

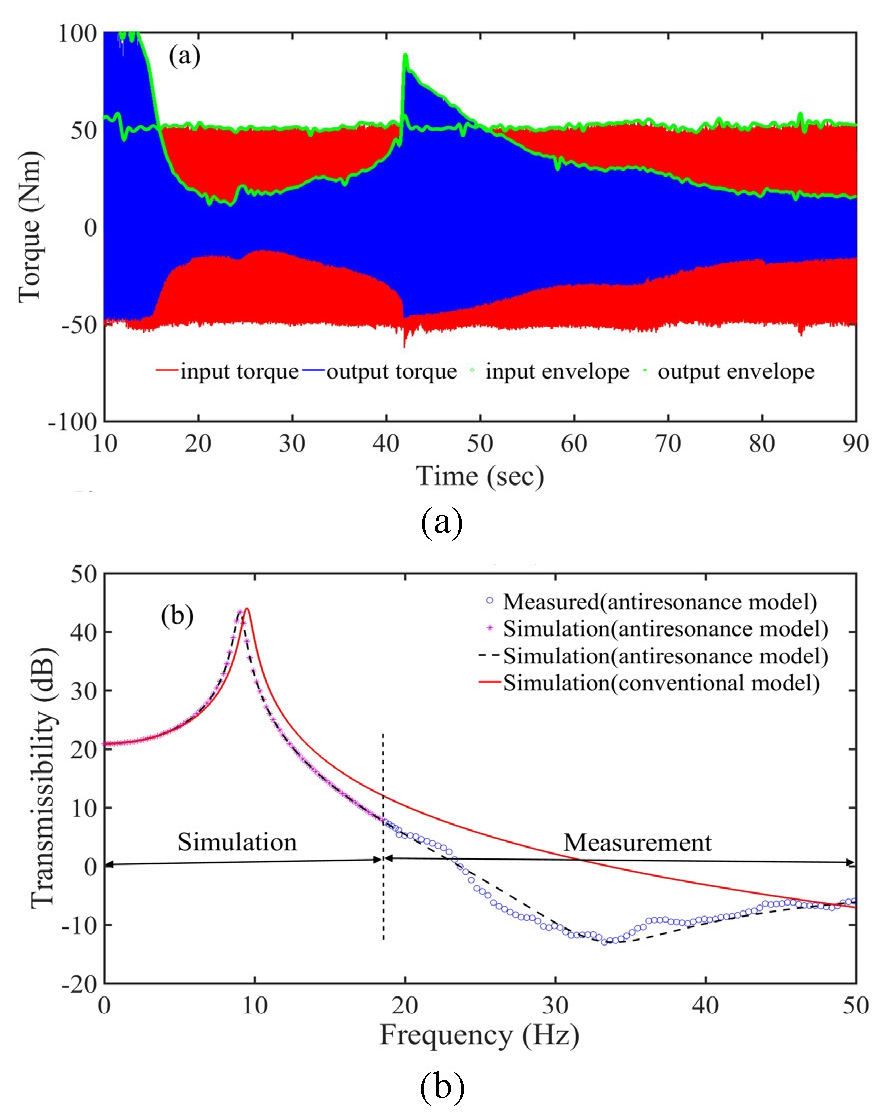
포락선 방법으로 추정된 토크 전달률을 Fig. 9에 표시하였다. X축은 선형적으로 증가시킨 회전 속도로 변환된 주파수를 나타냈다. 반공진 성능을 확연하게 보이기 위해서 주파수 영역을 0에서 50 Hz까지 표시하였다. Fig. 9와 같이, 측정된 토크 전달률은 시뮬레이션 결과와 양호하게 일치하였으며 반공진 주파수는 대략 33.5 Hz에서 나타났다. 이 연구에서 공진에 대한 위험성(진동 절연기와 시험기 파손)을 인식하여 공진 주파수 근처 영역에서 실험을 진행하지 않았기 때문에 측정된 공진 주파수의 결과는 없지만 토크 전달률 그래프의 경향을 살펴볼 때 시뮬레이션 결과로 약 9 Hz인 것을 추정하였다. 한편, 반공진 주파수 33.5 Hz(1005 r/min) 근방에서 기존 비틀림 진동 절연기⁽⁶⁾의 토크 전달률과 비교할 때 최대 -13 dB의 진동 절연 효과가 있는 것을 알 수 있다.

Fig. 9

Measured torque transmissibility using envelope method compared with simulation results of the proposed torsional vibration isolator and conventional torsional isolator

6. 결 론

이 연구에서는 반공진을 이용한 대역 차단형 비틀림 진동 절연기에 대한 진동 절연 특성을 토크 전달률을 통해서 기존 비틀림 진동 절연기와 비교하여 다음과 같은 결론을 도출하였다.

(1) 시뮬레이션과 실험 결과를 통해서 제안된 비틀림 진동 절연기에 대한 적용 가능성이 입증되었으며 반공진에 의한 진동 절연성능도 검증되었다.

(2) 제안된 진동 절연기에 대한 설계 파라미터 변화에 따라 토크 전달률의 변화를 확인하였으며 이를 바탕으로 진동 절연기를 설계하고 실제 제작하였다.

(3) 자동차 클러치 댐퍼에 사용하는 비틀림 진동 절연기에 대한 토크 전달률을 저 관성 시험기를 사용하여 측정한 결과, 기존 비틀림 진동 절연기보다 엔진의 주로 작동 영역에서 우수한 진동 절연 효과가 나타나며 특히, 반공진 주파수 33.5 Hz(1005 r/min) 근방에서 최대 –13 dB 정도로 진동 절연 효과가 향상된 것으로 나타내었다.

(4) 향후 제안된 진동 절연기의 설계 파라미터들을 최적화하여 진동 절연 대역을 확보하고 또한 토크 컨버터에 진동 절연기를 삽입하여 조립 구조물에 대한 진동 절연 성능을 검증할 예정이다.

Acknowledgments

이 논문은 중소기업청 World Class 300 사업 (과제번호: 10050404, 차세대변속기용 융복합 토크컨버터 및 Personal Mobility용 구동장치 개발)으로 지원된 연구결과입니다.

References

• Shaver, F. R., (1987), Manual Transmission Clutch Systems, Chapter 8 Torsional Vibration and Tuning Capacity, SAE International.
• Lee, D. O., and Han, J. H., (2012), A Comparison of Vibration Isolation Characteristics of Various Forms of Passive Vibration Isolator, Transactions of the Korean Society for Noise and Vibration Engineering, 22(9), p817-824. [https://doi.org/10.5050/KSNVE.2012.22.9.817]
• Flannelly, W. G., (1967), Dynamic Anti-resonant Vibration Isolator, U.S. Patent No. 3,322,379.
• Yilmaz, C., and Kikuchi, N., (2006), Analysis and Design of Passive Band-stop Filter-type Vibration Isolators for Low-frequency Applications, Journal of Sound and Vibration, 291(3~5), p1004-1028.
• Liu, C., Jing, X., and Chen, Z., (2016), Band Stop Vibration Suppression Using a Passive X-shape Structured Lever-type Isolation System, Mechanical Systems and Signal Processing, 68, p342-353. [https://doi.org/10.1016/j.ymssp.2015.07.018]
• Jang, J. D., Kim, G. W., and Kim, W. J., (2013), Vibration Transmissibility Analysis and Measurement of Automotive Clutch Spring Dampers, Transactions of the Korean Society for Noise and Vibration Engineering, 23(10), p902-908. [https://doi.org/10.5050/KSNVE.2013.23.10.902]
• Song, S. Y., Shin, S. C., and Kim, G. W., (2016), Torsional Vibration Isolation Performance Evaluation of Centrifugal Pendulum Absorbers for Clutch Dampers, Transactions of the Korean Society for Noise and Vibration Engineering, 26(4), p436-442. [https://doi.org/10.5050/KSNVE.2016.26.4.436]
• http://automotive.meidensha.co.jp/en/dynamometer/index.html
• Schicker, R., and Wegener, G., (2002), Measuring Torque Correctly, Hottinger Baldwin Messtechnik (HBM) GmbH.
• MATLAB/Signal Processing Toolbox V7.6, User’s Guide, (2011), The Mathworks.
• Shin, K., and Hammond, J., (2008), Fundamentals of Signal Processing for Sound and Vibration Engineers, John Wiley & Sons, England, p58-93.