기전연성효과를 고려한 차량용 전기모터의 진동해석

2.1 기전연성해석 과정

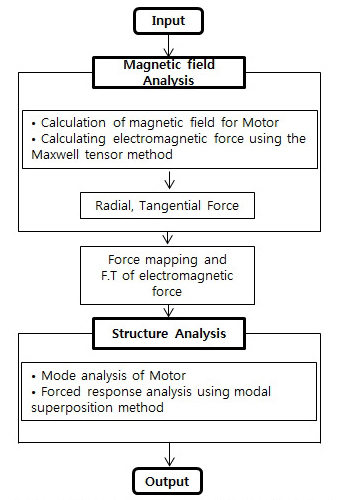
이 연구에서는 전자기적인 효과에 의해 발생된 힘이 구조물에 가해져 진동이 발생하는 현상을 모사하기 위해 기전연성해석을 수행하였다. 이때 진동장이 전자기장의 변화에 영향을 거의 미치지 않는다고 가정하여 one-way coupling으로 해석을 수행하였다. 이는 전자기해석을 먼저 수행하여 고정자에 가해지는 전자기력을 계산한다. 그 후 전자기력을 구조해석 모델의 가진력으로 모델링하여 구조 진동 응답을 해석한다. 이 과정을 Fig. 1에서 보인 기전연성해석의 흐름도에 나타내었다.

Fig. 1

Procedure of the electro-magnetic-structural one-way coupled analysis

전자기력은 맥스웰 응력 텐서법(Maxwell stress tensor method)에 따라 자속밀도(magnetic flux density) 및 투자율(permeability)의 관계로 다음과 같이 맥스웰 응력으로 나타낼 수 있다⁽¹⁰⁾.

여기서, σ는 맥스웰 응력(Maxwell pressure), B는 자속밀도(magnetic flux density), μ₀는 투자율(permeability), 아래첨자 r과 t는 각각 원주방향 및 접선방향을 뜻한다.

효율적인 해석을 위해 고정자에 가해지는 전자기력은 전기모터의 길이 방향으로 일정하다는 가정⁽¹⁰⁾을 통해 2차원해석을 수행하였다. 이 연구에서는 전자기해석 상용프로그램인 JMAG을 이용하여 2차원해석을 수행하였다. 식 (1)을 이용하여 고정자 2차원 단면에 가해지는 응력을 구하고 이를 길이방향 확장을 통해 3차원 고정자 전체에 가해지는 전자기력을 계산하였다.

앞서 전자기해석을 통해 구한 고정자에 가해지는 전자기력을 구조해석용 유한요소모델에 맵핑(mapping)하였다. 이어 유한요소모델에는 적절한 경계 조건을 부여하고 해석소프트웨어인 LMS. Virtual lab을 이용하여 강제진동해석을 수행하였다.

2.2 해석 모델

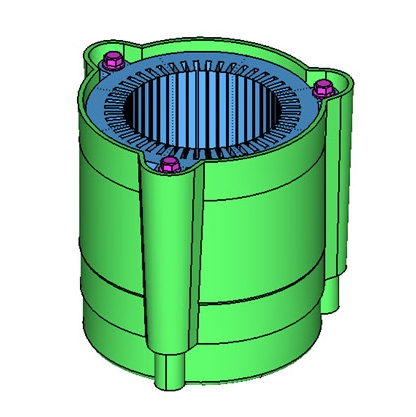
이 논문에서 연구대상 모터는 전기 자동차의 동력원으로 주로 사용되는 매입형 영구자석 동기기이며 극수는 8개, 슬롯 수는 48개이다. 고정자의 경우 하우징과 볼트로 체결되어 있으며 전기모터의 형상은 Fig. 2에 보인 바와 같다.

Fig. 2

Model of the motor under the study: the 8 pole 48 slot permanent magnet synchronous motors

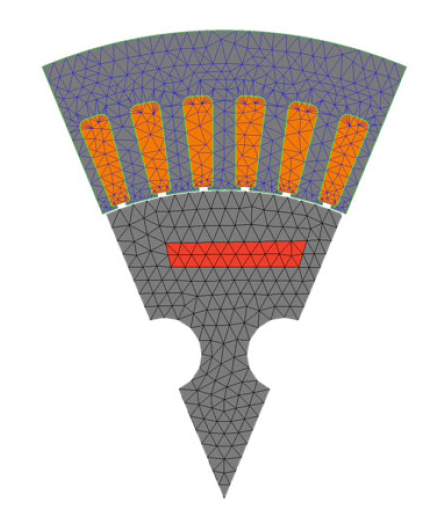
전기모터의 경우 cyclic symmetric의 특징을 가지고 있다. 극수가 8개이므로 극수의 기준으로 모델을 분할하면 Fig. 3과 같은 1/8 분할모델을 이용하여 효율적인 전자기해석이 가능하게 된다.

Fig. 3

1/8 Split finite element model for the electromagnetic field analysis of motors

전기모터의 진동원으로 모델링되는 전자기력을 계산하기 위해 전자기해석을 수행하게 되고 전자기해석에 사용되어지는 유한요소모델은 Fig. 3에 보인바와 같다.

전자기력에 의한 구조진동해석의 대상은 Fig. 2에서 보인 바와 같이 볼트, 고정자, 하우징으로 총 3개의 부품으로 이루어져 있다. 고정자와 볼트는 일반 강철의 재질로 이루어져 있으며 전기모터의 하우징은 알루미늄으로 이루어져 있다. 기전연성해석을 위한 유한요소모델의 물성치는 Table 1에 나타내었으며 볼트는 주요 관심대상이 아니므로 강체로 모델링하였다.

Table 1

Material properties of the motor structure

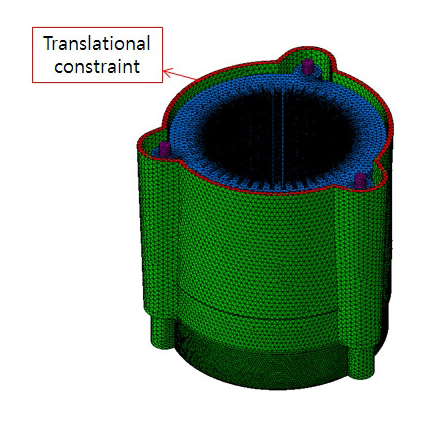
Fig. 4는 구조진동 해석을 위한 모터구조의 유한요소모델을 보이고 있다. 해석모델의 경계조건은 전기모터 하우징 상부 끝단에 병진구속을 적용하였다. 가진력은 앞서 언급한 바와 같이 전자기해석을 통해 얻는 전자기력을 Fig. 4에 보인 구조해석용 유한요소모델에 맵핑하여 모델링하였다.

Fig. 4

Structural finite element model and imposed boundary condition of no translational displacement

해석을 통해 얻은 진동장의 특성을 평가하기 위해 식 (2)에서 보인 하우징 표면에서의 가속도 값의 RMS average값을 사용하였다. 이때 A_n는 하우징 표면에서의 가속도 RMS average값을 뜻하며 A_n은 RMS average값을 취하기 위한 노드에서의 가속도 값이다. Fig. 5에는 가속도 값을 획득한 하우징 표면을 나타내었다.

Fig. 5

Surface of the housing of the motor for calculation of the average acceleration level

N은 하우징 표면 위 절점의 개수를 뜻한다.

3.1 전자기 해석 및 전자기력 특성

Fig. 3에서 보인 전자기 해석 모델에 대하여 JMAG을 이용하여 cyclic symmetric 조건을 부여하여 전자기해석을 수행하게 된다. 회전자가 회전함에 따라 회전자에 매입되어 있는 영구자석이 고정자를 지나가며 자속변화를 만들게 되고 이 자속변화에 의해 전자기력이 발생하게 된다. 현재 8극 48슬롯 모터의 경우 Fig. 3에 보인 바와 같이 cyclic symmetric 조건을 고려하여 하나의 극이 6개의 슬롯을 지날 때의 자속변화를 계산하게 된다. 자속변화의 경우 길이 방향으로 일정하다는 가정⁽¹⁰⁾을 할 수 있고 고정자 전체의 자속변화로 확장하여 전자기력을 계산하게 된다.

Fig. 6은 JMAG을 통한 전자기해석을 수행하여 얻은 분할모델의 자속(magnetic flux)을 보여주고 있다. 계산된 자속밀도는 2.1절에서 설명한 바와 같이 식 (1)을 이용하여 전자기력을 계산하는데 이용된다. Fig. 7은 회전자가 1000 r/min으로 회전할 때 고정자에 유기되는 전자기력을 보이고 있다. 이 계산된 전자기력은 진동해석을 위한 구조모델에 맵핑과정을 거쳐 가진력으로 모델링된다. 이는 전자기해석 모델과 진동해석 모델의 격자가 일치하지 않기 때문이다.

Fig. 6

Magnetic flux density field calculated by 2D magnetic analysis

Fig. 7

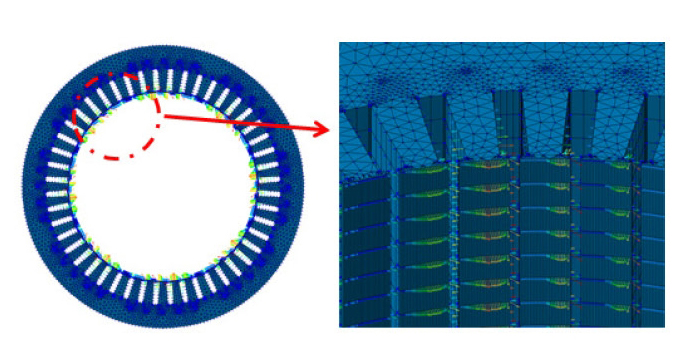
Calculated electromagnetic forces at 1000 r/min by 2D cyclic symmetric model (left) and reconstructed forces on 3D full model (right)

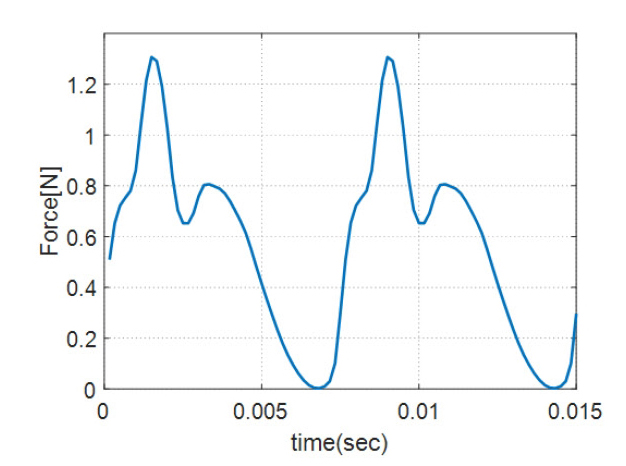
Fig. 8은 Fig. 7에 보인 전자기력 벡터 중 임의의 노드에 가해지는 원주방향의 전자기력의 시간이력을 보이고 있다. 전자기 모델의 한 노드에서의 전자기력을 살펴보면 어떠한 주기를 가지고 있음을 확인할 수 있으며 다음과 같은 전자기력들이 고정자 치 표면에 가해지고 있다.

Fig. 8

Time history of a force at a point of the stator from transient magnetic analysis at 1000 r/min

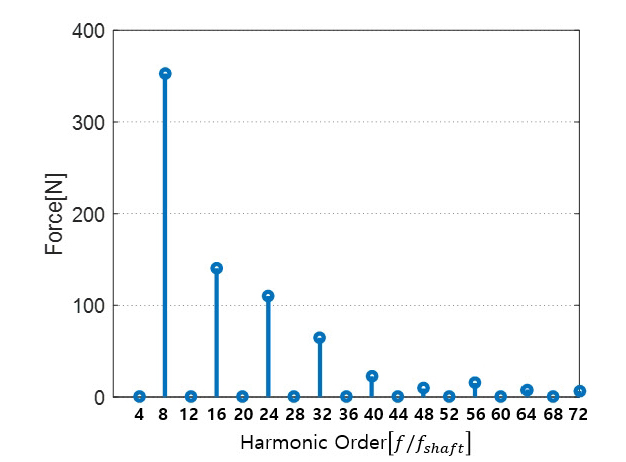
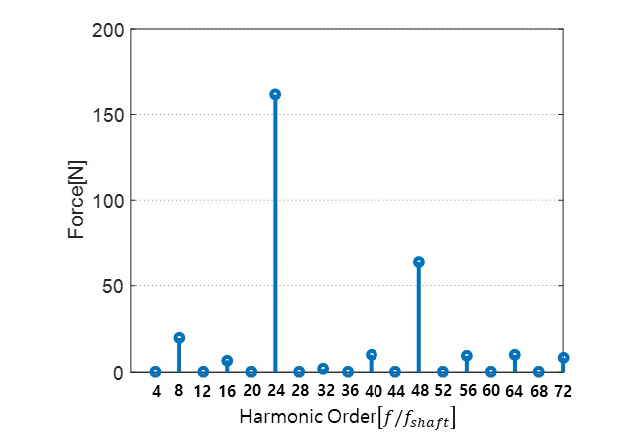
고정자 한 치에 가해지는 원주방향의 전자기력시간이력 합의 푸리에 변환결과는 Fig. 9에 보인바와 같다. 차수 별 특성을 편리하게 확인하기 위하여 주파수를 f/f_shaft와 같이 변환하여 나타내었다. Fig. 9을 살펴보면 8차 성분이 가장 큰 값을 가지고 차수가 높아질수록 크기가 점점 작아지는 것을 확인 할 수 있다. 토크리플의 경우 3상 유도전류에 의해 발생하는 전기적 6차 리플과 극쌍수 곱으로 나타내어지게 된다. 코깅토크의 경우 고정자와 회전자간의 자기저항을 최소화하려는 힘이 원인으로 발생하게 되며 극수와 슬롯 수의 최소공배수로 나타나게 된다. 즉 연구대상인 8극 48슬롯 영구자석 동기기의 경우 24차와 48차 성분에서 각각 토크리플과 코깅토크가 발생하게 된다⁽¹¹⁾. 많은 논문들이 전기모터의 소음이 24차와 48차 성분 즉 토크리플과 코깅토크 성분이 문제가 된다고 언급하고 있다. 하지만 진동 측면에서 살펴보면 Fig. 9와 같은 전자기력이 가해질 경우 24차 및 48차 성분 외에도 다른 차수에서 문제가 발생 할 수 있다. 이를 전자기력 관점에서 확인하기 위해 다음과 같은 관점에서 확인하였다.

Fig. 9

Spectrum of electromagnetic force at 1000 r/min applied to one tooth

구조물에 힘이 가해져 가속도 값을 얻기 위해서는 가진점에서 응답점까지의 전달함수의 관계로 식 (3)과 같이 나타낼 수 있다.

여기서 A는 응답점에서의 가속도 값을 나타내며, H_i(i = 1,2,3… N)은 가진점에서 응답점사이의 전달함수이며 F_i(i = 1,2,3… N)은 가진점에서의 힘을 나타낸다. 이때 하우징이 고강성 설계되어 작동주파수에 대하여 강체로 가정할 수 있다면 하우징 표면의 가속도 응답은 각 치에서 발생하는 힘의 복소 합으로 나타낼 수 있다. 즉 각 치에 작용하는 전자기력에 대한 가속도 전달함수가 일정한 경우 표면 가속도 응답은 식 (4)와 같이 나타난다.

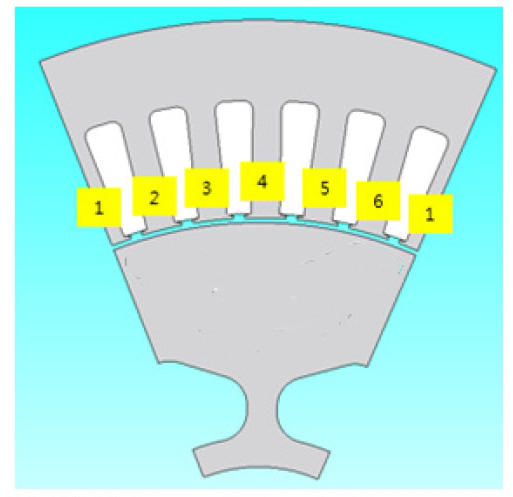
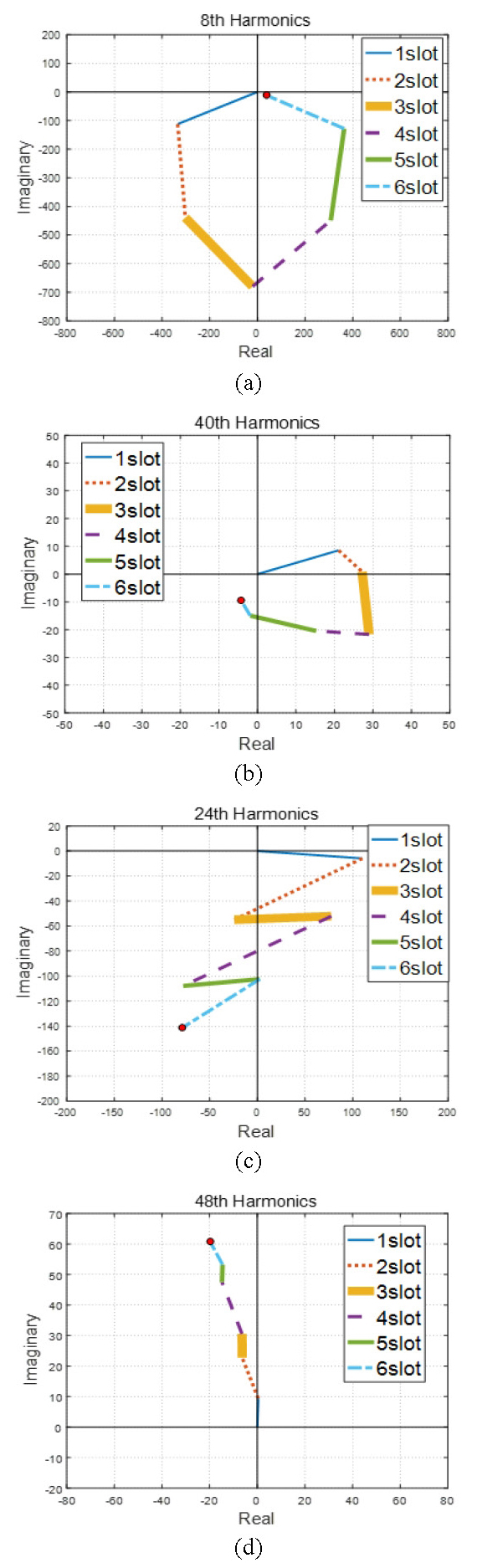
위와 같은 논리를 바탕으로 Fig. 10에 나타나 있는 6개의 치에 걸리는 전자기력의 푸리에 변환한 벡터 합을 Fig. 11과 같은 복소평면에 나타내었다. 이때 Fig. 10은 앞선 절에서 언급한 분할모델에서의 고정자 형상을 나타내고 있다. Fig. 11에 나타나 있는 복소평면을 살펴보면 각 치에 걸리는 힘을 순차적으로 벡터 합을 함으로써 특성을 확인 할 수 있다. Fig. 11의 (a), (b)를 살펴보면 치에 가진되는 전자기력의 벡터 합을 할수록 그 합력의 크기가 작아짐을 확인할 수 있다. 반면 Fig. 11의 (c), (d)를 살펴보면 치에 걸리는 전자기력의 벡터 합을 할수록 그 합력의 크기가 커지고 있음을 확인할 수 있다. 각각의 벡터 합 좌표와 크기를 Table 2에 나타내었다. 결과를 살펴보면 토크리플이 나타나는 24차 성분과 코깅토크가 나타나는 48차 성분은 위상을 고려하여 힘을 더하면 커지고 그 외의 차수는 작아지는 것을 확인 할 수 있다. 이렇듯 구조물이 고강성 설계로 인한 강체 취급이 가능하다는 측면에서 바라본다면 24차와 48차 성분에 의한 가진력이 크게 작용하고 있음을 확인할 수 있다.

Fig. 10

Stator considering electric symmetric

Fig. 11

Electromagnetic force in the complex plane

Table 2

Coordinate and magnitude of vertor sum point

위와 같은 결과를 바탕으로 고정자 전체가 받는 전자기력 시간이력의 합을 푸리에 변환하여 Fig. 12에 나타내었다. Fig. 12에 보인바와 같이 24차 48차 성분이 큰 값을 나타내고 있다. 이렇듯 식 (4)에서 나타내었듯이 구조물이 고강성 설계가 되어 충분히 강체라 가정할 수 있게 된다면 24차와 48차 성분의 큰 가진력에 의해 24차 및 48차 성분만 큰 값을 나타내게 될 것이다. 하지만 실제 전기모터의 측면에서 하우징은 충분한 고강성 설계가 되어있지 않기 때문에 탄성영역에서 진동분석이 필요하다.

Fig. 12

Spectrum of electromagnetic force at 1000 r/min applied to all tooth

3.2 구조해석 결과 및 특성

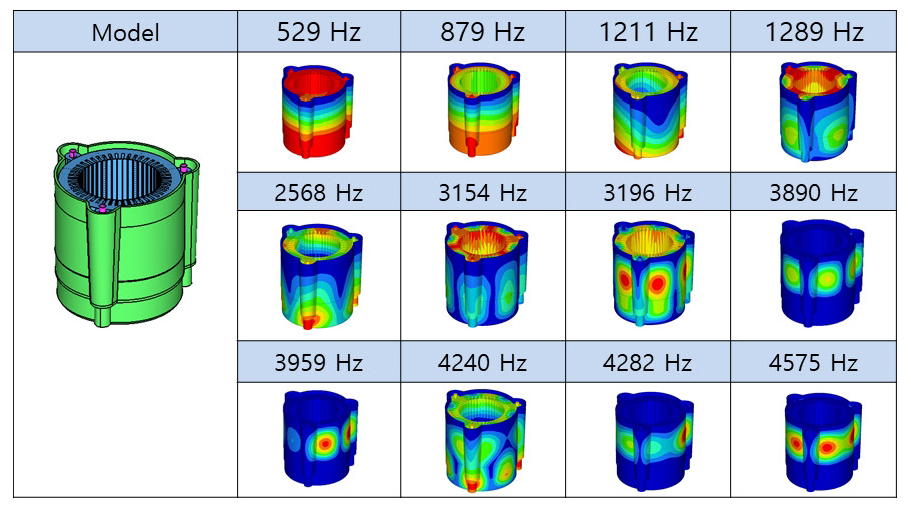
이 절에서는 앞 절에서 계산된 전자기력을 이용하여 기전연성해석을 수행하고 결과에 대해 기술하고자 한다. 먼저 수치해석 모델의 기본적인 신뢰성을 확보하고 동적거동을 파악하기 위해 모드해석을 수행하였으며 Fig. 13에 공진주파수와 모드형상을 나타내었다.

Fig. 13

Mode shapes and their natural frequencies of the motor structure

모드해석 결과를 살펴보면 공진주파수가 529 Hz, 879 Hz, 1211 Hz인 경우는 고정자는 강체로 거동하고 하우징만이 탄성 변형을 보이는 거동을 보이고 있다. 공진주파수가 1289 Hz부터는 하우징과 고정자가 연성되어 탄성모드들이 나타나고 있는 것을 확인할 수 있다. 그리고 공진주파수가 3890 Hz, 4282 Hz, 4575 Hz의 경우 하우징의 로컬 모드들이 나타나고 있음을 확인할 수 있다.

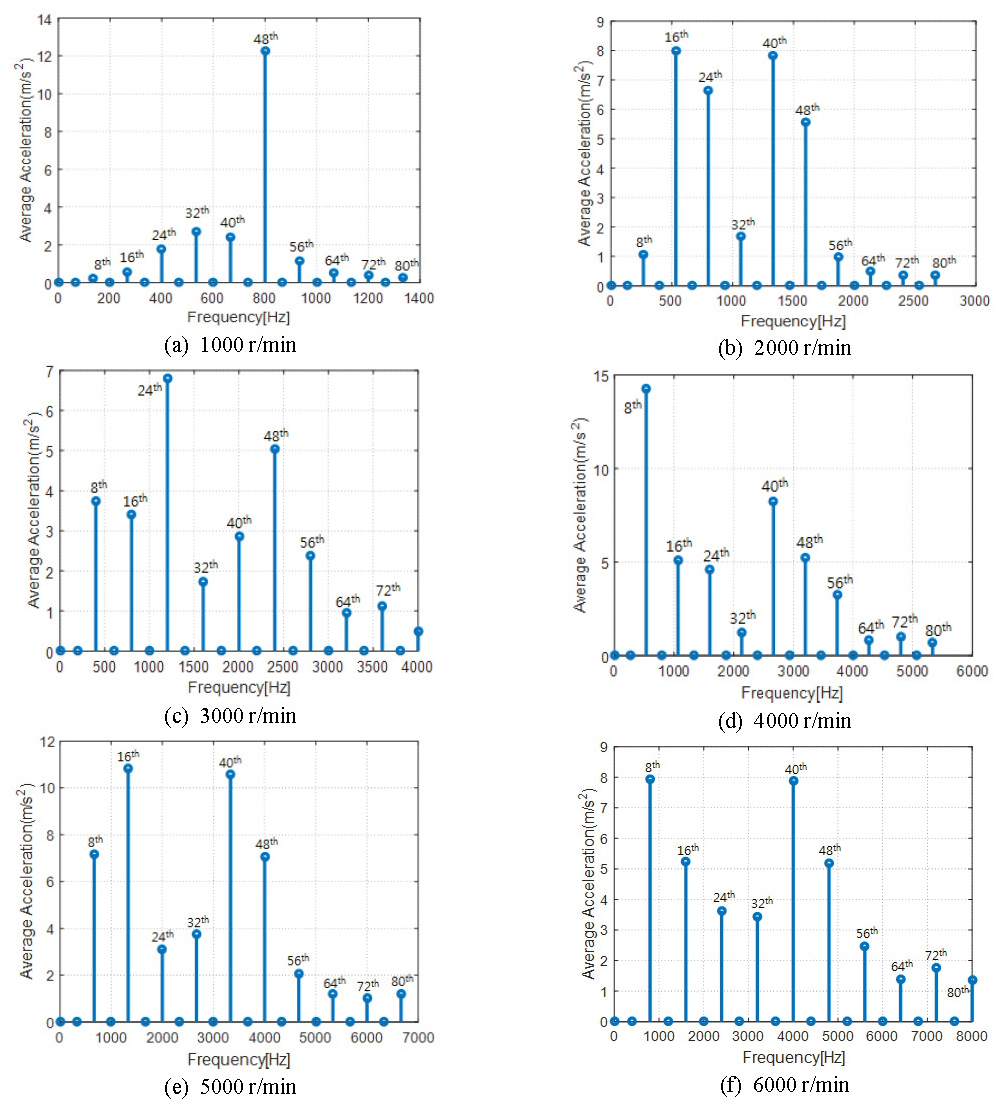
Fig. 14는 회전자 회전수가 1000 r/min부터 6000 r/min까지 1000 r/min 간격으로 Fig. 1에서 보인 절차에 따라 기전연성해석을 수행한 결과이다. 나타낸 결과는 Fig. 5에 보인 하우징 표면상의 가속도를 식 (2)에서 설명한 방법에 따라 제곱 평균한 값이다. Fig. 14에 보인 가속도 스펙트럼은 회전수 별로 다른 주파수 영역에서 나타내었다. 이는 Fig. 9에서 보인 바와 같이 회전자 회전수의 50차 이상에서는 가진력 발생이 약하므로 진동해석 수행 시 주파수 범위를 회전자 회전수의 80차까지 수행하였기 때문이다. 그리고 전자기력은 8의 배수에 해당하는 고조파 성분만이 0이 아닌 값을 가지고 있으므로 가속도 수준도 해당 주파수에서만 0이 아닌 값을 가진다. Fig. 14의 결과를 살펴보면 각 RPM에서의 차수가 공진의 부근에 위치하고 전자기력과 모드간의 상관성이 큰 경우 큰 가속도 수준을 나타내는 것을 알 수 있다. 1000 r/min의 48차 고조파 주파수인 800 Hz에서 큰 값을 나타내고 있다. 이는 두 번째 공진모드인 879 Hz의 공진과 48차 전자기력간의 상관성이 높기 때문이다. 2000 r/min의 경우 첫 번째 공진모드와 두 번째 공진모드와 각 전자기력간의 상관성에 의해서 16차와 48차에서 큰 값을 나타내고 있다. 또한 4번째 공진모드와 전자기력간의 상관성에 의해 40차와 48차에서도 큰 값을 나타내고 있다. 3000 r/min의 경우 24차 고조파 주파수인 1200 Hz에서 큰 값을 나타내고 있다. 이는 세 번째 공진모드인 1211 Hz의 공진주파수 부근이며 공진모드와 전자기력간의 상관성이 높기 때문이다. 4000 r/min의 경우 8차 고조파 주파수인 533 Hz 부근에서 큰 값을 나타내고 있다. 이는 첫 번째 공진모드인 529 Hz의 공진모드와의 상관성이 높기 때문이다. 5000 r/min의 경우 16차와 40차 고조파 주파수인 1333 Hz와 3333 Hz 부근에서 큰 값을 나타내고 있다. 각각 4번째 공진모드 및 7번째 공진모드의 전자기력간의 상관성이 높기 때문이다. 6000 r/min의 경우 8차와 40차 고조파 주파수인 800 Hz와 4000 Hz에서 큰 값을 나타내고 있으며 각각 2번째 공진모드와 8번째, 9번째 하우징 로컬모드가 해당 전자기력과의 상관성이 높기 때문이다.

Fig. 14

Spectrum of acceleration of housing

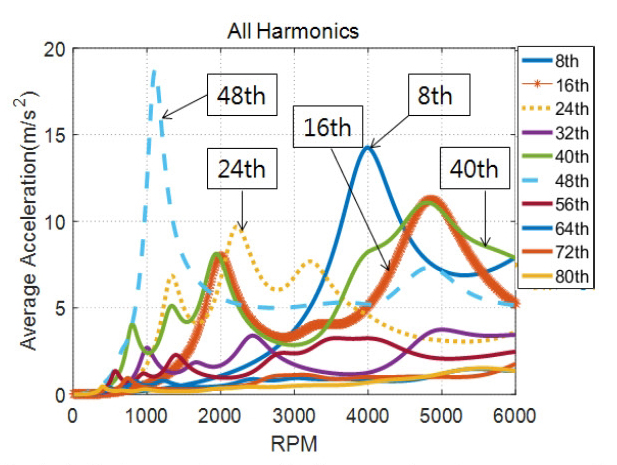
가속도 수준이 회전수 변화에 따라 변하는 하중의 크기와 구조물의 공진 특성에 영향을 받으므로 작동 회전수 영역에서의 진동 특성을 파악하는 것이 필요하다. 이를 위해 전자기력 성분이 존재하여 가속도가 유발되는 8차의 배수에 해당하는 고조파 성분에 대하여 order tracking 분석을 수행하였다. 이 논문에서는 10 r/min 간격으로 기전연성 해석을 수행하여 차수별 가속도 수준을 계산하고 차수별 가속도 수준을 회전수에 따른 변화를 분석하였다.

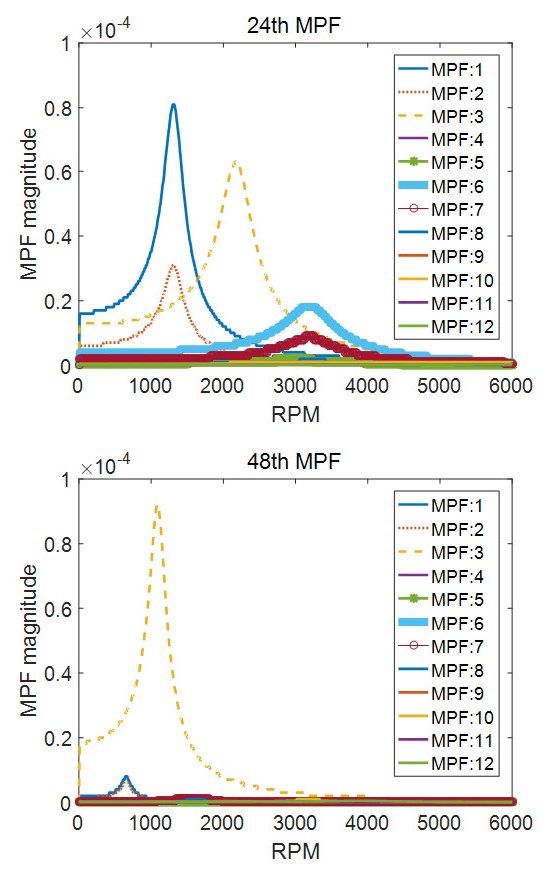
Fig. 15의 결과를 확인해보면 8차, 16차, 24차, 40차 및 48차는 각각 특정 RPM에서 높은 가속도 수준을 나타내고 있는 것을 확인할 수 있다. 반면 32차, 56차, 64차, 72차 및 80차는 다른 차수들에 비해 낮은 가속도 수준을 나타내고 있다. 이 중 24차와 48차의 경우는 각각 토크리플과 코깅토크 성분이 나타나는 차수이다.

Fig. 15

Order tracking of the acceleration averaged on the surface of the housing

Fig. 15에 나타나 있는 8차 성분의 가속도 수준을 살펴보면 4000 r/min에서 공진의 영향에 의해 큰 가속도 수준을 나타내고 있음을 확인할 수 있다. 4000 r/min의 8차 성분의 주파수는 533 Hz로써 모드해석결과에 나타나있는 첫 번째 강체모드에 의한 것임을 알 수 있다. 16차 성분의 경우 5000 r/min 부근에서의 가속도가 큰 값을 가지고 있음을 확인 할 수 있다. 이때 주파수는 약 1290 Hz로 모드해석결과의 4번째 공진모드에 의한 것임을 알 수 있다. 4번째 공진모드는 고정자의 1차 탄성모드로 타원으로 진동하는 모드이다.

24차의 경우 2번째 공진모드에 의한 영향으로 인해 2200 r/min 부근에서 다소 큰 가속도 수준을 나타내고 있다. 40차의 경우도 16차와 비슷한 RPM 대역에서 큰 가속도 수준을 나타내고 있다. 5000 r/min 대역에서의 40차 성분의 경우 3200 Hz의 부근으로 7번째 모드에 의한 것으로 확인 할 수 있다. 48차의 경우는 3번째 모드에 의해 가장 큰 가속도 수준을 나타내고 있다. 이때 주목할 점은 전자기력의 주파수가 각 모드의 공진주파수와 동일할지라도 각 차수별 전자기력의 형태가 해당 모드와는 상관성이 낮으면 공진 모드에 의한 영향은 없다는 점이다.

32차, 56차, 64차, 72차와 80차의 경우도 가속도 수준을 살펴보면 특정 주파수에서 공진 주파수와 일치하는 것을 알 수 있다. 그러나 Fig. 11에 보인 바와 같이 이들 차수에서 전자기력의 크기가 상당히 작은 것을 확인할 수 있다.

전자기력과 전기모터의 공진모드 간의 상관성도 분석함으로써 의미 있는 결과를 얻을 수 있다. 토크리플과 코깅토크의 성분인 24차와 48차의 전자기력에 의한 진동 결과를 대표적으로 살펴보면 24차 성분에서는 나타나는 공진모드들이 48차 성분에서는 나타나지 않는 것을 확인 할 수 있다. 전기모터가 0 r/min ~ 6000 r/min으로 구동할 때의 48차의 주파수 성분은 0 Hz ~ 4800 Hz로 Fig. 13에 나타나 있는 모든 공진모드들을 지나게 된다. 하지만 48차 성분의 기전연성해석 결과에서는 3번째 공진모드에 의한 영향만 받고 있는 것을 확인할 수 있다.

모드 중첩법에 의한 강제진동해석 결과는 모드 기여도(modal participation factor)와 모드벡터의 곱으로 나타내어지게 되는데 모드 기여도를 확인하면 가진력과 모드간의 상관성을 간접적으로 파악할 수 있게 된다.

Fig. 16은 24차 및 48차 전자기력에 의한 모드기여도를 보이고 있다. 48차의 경우 24차 고조파와 달리 특정 한 모드의 모드기여도가 지배적인 것을 확인할 수 있다. 이는 48차 전자기력의 경우 3번째 공진모드 외에는 상관성이 매우 낮으며 영향을 받지 않는다는 것을 확인할 수 있다.

Fig. 16

Magnitude of modal participation factor of the 24th and 48th order

즉, 48차 고조파에 해당하는 고조파의 경우 Fig. 17에 나타나있는 비틀림 모드를 제외한 모드를 가진시키지 못하는 것을 알 수 있다. 48차 고조파 즉 코깅토크에 의한 진동저감을 위해서는 다음과 같은 모드를 억제 할 수 있는 하우징 형상이 유리할 것으로 예상 할 수 있다. 이렇듯 기전연성효과를 고려하여 각 차수별 전자기력에 의해 가진되는 모드를 파악하고 문제가 될 수 있는 차수와 RPM 분석을 통하여 보다 효율적인 전기모터의 하우징 설계를 할 수 있을 것으로 기대된다.

Fig. 17

Modal shape of the 3rd mode