탄소섬유적층 각도에 따른 CFRP 평판의 실내소음 특성
ⓒ The Korean Society for Noise and Vibration Engineering
Abstract
Recently, the researche on the weight lightening of the vehicle body for increasing the fuel efficiency of automobile have been actively carried out. One way to reduce the weight is to change the material applied to the car body. In recent years, CFRP laminated plates, which has lower density and similar strength to conventional metals, has been increasingly applied to the car body. However, since the CFRP laminated plate has different sound and vibration characteristics compared with conventional metal plate, the research on the sound radiation characteristics is required for the successful application. This paper studies the effect of sound and vibration characteristics of CFRP plates according to the fiber lamination angle on interior noise of the enclosure made of CFRP laminated plate. The purpose of this paper is numerically to predict the interior noise of the enclosure caused by the vibration of the CFRP plates with different laminated angles of carbon fiber. The numerical method is validated by theoretical and experimental method.
Keywords:
CFRP, Lamination Angle, Sound and Vibration, Interior Noise, Cavity Mode키워드:
탄소섬유강화플라스틱, 적층 각도, 소음진동, 실내소음, 공동 모드1. 서 론
CFRP(carbon fiber reinforced plastic)는 금속 재료들과 비슷한 강성을 가지면서 낮은 밀도를 갖고 있음으로 최근에 항공, 자동차 그리고 선박 같은 경량화가 필요한 운송수단에 사용이 증가하고 있다. 그리고 CFRP는 이방성 특성과 탄소 섬유 적층 구조에 따라 다른 진동 특징들을 나타냄으로 CFRP 복합재료의 진동 특성에 대한 연구는 계속되고 있다(1,2). 그러나 CFRP의 구조-음향 연성 방사소음 특성에 대한 연구는 부족하다. 실제 산업현장에 적용하기 위해서는 CFRP의 구조-음향 연성 방사소음 특성에 대한 연구가 중요하다. 앞선 연구(3)에서는 자유음장(free field)에서 탄소 섬유 배열에 따른 CFRP 평판의 방사소음이 관찰되었다. 이 연구 결과에 의하면 CFRP 평판의 단 방향 섬유 배열의 변화는 고유진동수, 모드 형상, 진동응답 그리고 평판으로부터 방사되는 방사소음과 같은 진동음향 특성들을 변화시킨다. 구조-음향 연성을 갖는 잔향음장 (reverberant field)에서 실내 소음 예측에 대한 연구는 정확한 이론적 연구는 어려워 수치해석 방법이 많이 사용되어 왔다. 문헌조사에 의하면 Kim과 Brennan(4,5)은 유연한 구조물과 음향학적 완전 강체의 벽으로 둘러싸인 임의의 모양의 실내 공간에 대한 구조-음향 연성 문제를 이론적으로 해석하였다. 이때 사용된 유연한 구조물은 등방성 성질을 갖는 강판이었다. 이 연구 사용된 해석 기법은 모빌리티(mobility) 및 임피던스(impedence) 접근법이었으며, 해석결과로 유연한 구조물의 진동에 의한 실내소음을 정확히 예측하였다. 이 연구에서는 CFRP 평판을 유연한 구조물로 사용되는 임의의 모양의 실내 공간에 대한 구조-음향 연성 문제를 모빌리티 방법으로 해석하였다. 특히 CFRP 판재의 탄소섬유의 적층각도에 따라 구조-음향 연성 구조물의 실내소음이 어떻게 변화하는지를 연구하였다. 해석적 방법을 검증하기 위해서 FEM에 기초한 수치해석과 실험을 시행하였다.
2. 이론적 실내소음 해석
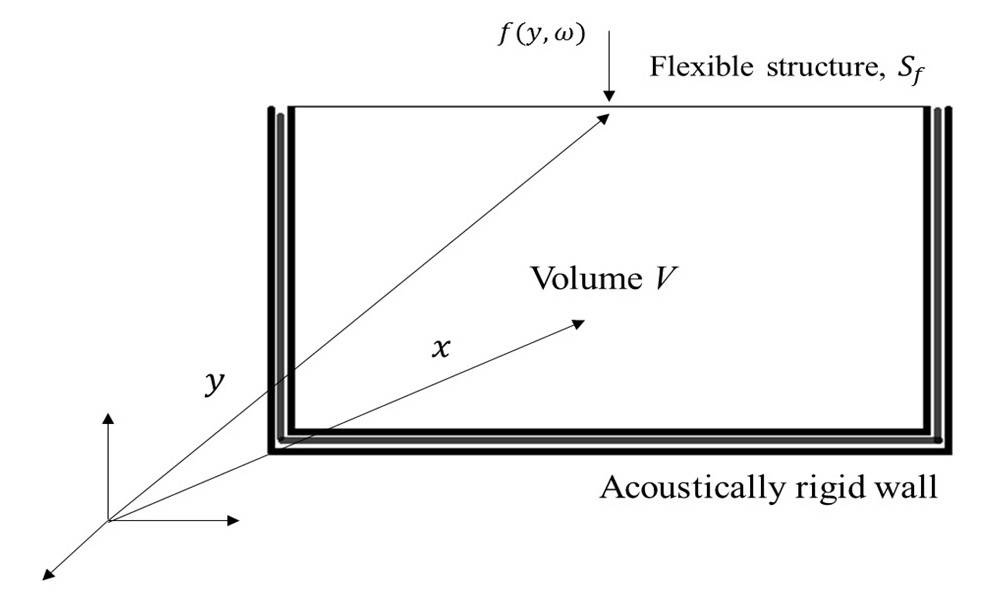
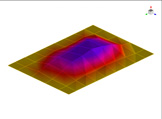
Fig. 1에서 보여주는 바와 같은 잔향특성을 갖는 밀폐된 직육면체 공간에 대한 실내 공명 모드의 주파수는 식 (1)로 표현된다(6).
| (1) |
여기서 c0는 음속, l. m과 n은 상수, Lx, Ly와 Lz는 밀폐된 직육면체 공간의 크기를 나타낸다. 이때 한 면이 유연한 진동체로 구성되는 경우, 공명 모드의 주파수는 진동체의 진동과 공명공간의 소음이 연성되면 유연한 진동체의 인피던스(impedance)가 변화하되 공명 주파수가 이동된다. 이 연구에서는 CFRP판체를 이용한 유연한 진동체를 갖는 공동공간의 임의 점에서 실내소음을 예측하고자 한다. 이론적 방법으로는 임피던스 및 모빌리티(mobility)를 이용한 방법을 적용하여 예측하였다(4).
Fig. 1에서 CFRP 판재에 힘 f 를 가했을 때 직육면체 내부 공간상의 임의 점에서 발생되는 음압은 판재의 진동에 의한 방사소음과 공명모드가 연성되어 나타난다. 이 경우 음향공동 내부의 음압과 진동판의 진동은 각각의 공명모드 및 공진모드의 합으로 표현할 수 있다. 따라서 음향 공동 내부의 x위치에서 음향 음압 p와 y위치에서의 구조 진동 속도 u는 다음과 같이 나타낼 수 있다(4,5).
| (2) |
| (3) |
여기서 N은 공간의 공명 모드 개수이며, M은 진동판의 진동 모드 개수이다. 벡터 Ψ와 a는 비 연성 음향 모드 형상 함수(acoustic mode shape function) ψn (x)와 음향 모드의 복소 진폭 an (ω)의 배열로 구성되어 있다. 마찬가지로 M 길이 벡터 Φ와 b는 비 연성 진동 모드 형상 함수(vibration mode shape function) ϕm(y)와 진동모드의 복소 진폭 bm (ω)의 배열로 구성되어 있다. 진동판의 외부가진에 의한 n차 음향 모드의 복소 진폭은 다음과 같이 나타낼 수 있다(7).
| (4) |
여기서 ρ0와 c0는 각각 공기 중의 밀도와 음속을 나타낸다. 함수 u(y,ω)는 표면 영역 Sf의 유연 구조물 주변의 법선 속도를 나타낸다. 괄호 안의 적분 표현은 u(y,ω)로부터 기여된 n번째 음향가진력(acoustic source) 강도를 나타낸다. 음향 모드 공진 항목 An (ω)는 다음과 같이 나타낸다.
| (5) |
그리고
| (6) |
여기서 Tα는 1차 모드의 시간 상수이고, ωn과 ζn은 각각 n번째 음향 모드의 고유 진동수와 감쇠비이다. 식 (3)를 식 (4)에 대입하면 다음과 같이 나타낼 수 있다.
| (7) |
Cn,m은 진동하는 구조의 표면 Sf에서 비 연성 구조 및 음향 모드 형상 함수 간의 기하학적 연성 관계를 나타내고 다음과 같이 표현된다.
| (8) |
따라서, 모달 음향 음압 벡터는 다음과 같이 표현할 수 있다.
| (9) |
qs = C b는 구조의 진동으로 인한 음향가진력의 강도 벡터이며, 이는 유연 구조물에 음향가진력의 벡트로 작용한다. M 길이 b는 복소 진동 모드 진폭 벡터이고 (N×M) 행렬의 C는 구조 음향 모드 형상 연성 행렬이다. 는 비 연성 음향 모드 임피던스 행렬로 정의되는 (N×N) 행렬이다. 비 연성 모달 임피던스 행렬은 비 연성 모드의 직교성 때문에 대각행렬이다. 행렬 A는 (N×N) 대각 행렬이며, 각 (n, n) 대각 항은 An으로 구성된다. Fig. 1의 유연 구조물이 얇은 등방성 평판이라고 가정하면, m번째 모드의 복소 진동 속도 진폭은 다음과 같이 표현할 수 있다.
| (10) |
ρs는 평판의 밀도, h는 평판의 두께, Sf는 평판의 면적이고, f(y,ω)와 p(y,ω)는 각각 평판의 표면에서 힘 분포 함수와 cavity 음압 분포를 나타낸다. 괄호 안의 두 개의 적분 방정식은 각각 f(y,ω)와 p(y,ω)로 인한 일반화된 m번째 진동 모달 힘을 나타낸다. 외력의 방향과 음압의 방향이 반대이기 때문에 괄호 안의 두 번째 적분 항 앞에 작은 기호가 있다. 구조 모드 공진 항 Bm(ω)는 다음과 같이 표현할 수 있다.
| (11) |
ωm과 ζm은 각각 m번째 모드의 고유 진동수와 감쇠비이다. 식 (2)를 식 (10)에 대입하고 일반화된 모달 힘 를 도입하면
| (12) |
이다. 따라서, 모달 진동 진폭 벡터 b는 다음과 같이 표현할 수 있다.
| (13) |
g는 외력 분포 f(y,ω)에 의한 일반화 된 모달 힘 벡터이고, gα = CTa는 음향 시스템에 작용하는 모달 힘 벡터, 즉 음향 음압 변동에 의한 반력이다. Ys = B/(ρshSf)는 비연성 구조 시스템의 모달 좌표에서 구조 가진과 구조 응답 사이의 관계를 결정하는 비연성 구조 모달 이동 행렬로 정의 된 (M×M) 대각행렬이다. 비연성 음향 임피던스 행렬 Zɑ에서와 같이, Ys는 대각행렬이다. 행렬 B는 각 (m,m) 대각항이 Bm으로 구성된 (M×M) 크기의 대각 행렬이고, CT는 C의 전치 행렬이며 M 길이의 벡터 g는 외부 힘 분포 f(y,ω)에 의한 일반화된 모달 힘 벡터이다. 식과 식을 결합하면, 음향 및 구조 모달 진폭 벡터 a와 b는 모달 가진 벡터 q와 g로 표현할 수 있다.
| (14) |
| (15) |
3. FEM 이용한 수치적 해석과 실험
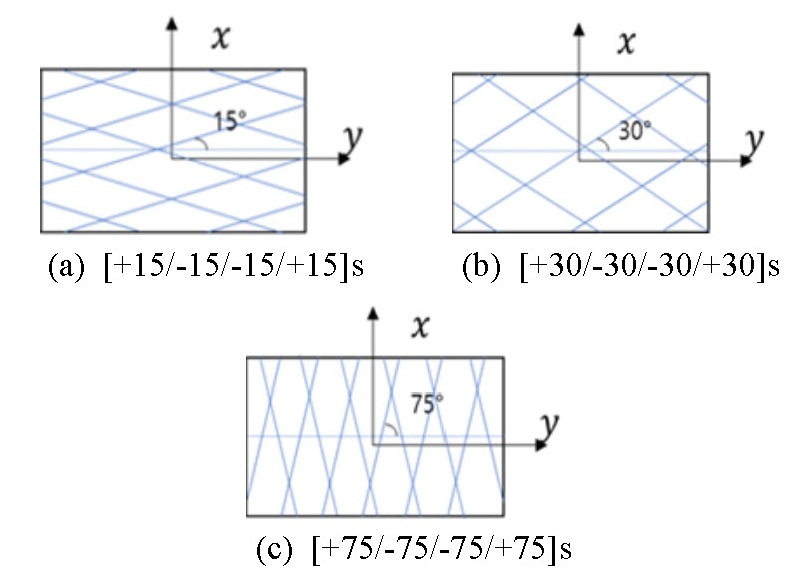
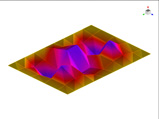
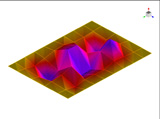
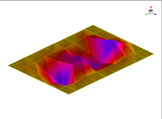
이 연구에서는 Fig. 2에서 보여주는 바와 같이 섬유배열 각도가 각각 ±15°, ±30° 그리고 ±75°로 적층된 총 3개의 CFRP 판재로 구성된 유연한 진동체를 Fig. 1에서 보여주는 공동 공간의 한 면을 구성할 때, 공동 공간의 실내 소음을 예측하는 연구를 수행하였다. 먼저 FEM에 기초한 수치 해석을 실행하고 수치해석 결과를 검증하기 위하여 3개의 경우에 대한 CFRP 판재를 제작하여 실험을 시행하였다.
3.1 수치적 해석
수치해석용 상용프로그램은 Siemens사의 Virtual Lab을 이용하였다. 적층 각도가 각각 ±15°, ±30° 그리고 ±75°인 3개의 CFRP 판재의 수치적모달 해석을 수행하였다. CFRP 판재는 shell type과 4개의 노드로 구성된 2D elements로 mesh를 형성하였다. 평판의 경계조건은 각 모서리의 25 mm를 clamped 조건으로 고려하였다. 해석에 사용된 판재의 재료 특성은 Table 1과 같다. 실험에 사용된 CFRP 판재의 규격은 700 × 500 mm이며 두께는 1.6 mm이다.
Siemens사의 Virtual Lab을 이용하여 임팩트 가진에 의한 3개의 CFRP 평판들의 실내 방사 소음 해석을 수행하였다. 적층각에 따른 기계적 물성치는 Table 1과 같다. 평판의 mesh는 위의 모달 해석에서 사용한 mesh를 사용하였고 음향 공동은 3D hexa mesh로 형성하였다. 경계조건은 모달 해석과 동일하다. 임팩트 가진에 의한 CFRP 평판들의 실내 소음을 측정하기 위해서 진동해석이 필요하다. 가진 힘에 의해 방사되는 음향 음압은 진동 데이터를 기반으로 계산되기 때문이다. 따라서 진동 해석은 진동 데이터를 얻기 위하여 평판의 임의의 한 점에 1 N 크기의 힘을 입력하여 수행하였다. 진동 해석을 통해 얻은 진동 데이터를 기반으로 구조적 평판과 음향 공동을 연성하여 임팩트 힘에 의한 음향 응답을 얻었다. 음향 응답의 측정은 평판의 중심으로부터 수직으로 200 mm 떨어진 지점에서 측정하였다.
3.2 실험
이론적, 수치적 해석 방법의 타당성을 검증하기 위해서 실험을 수행하였다. 모달 분석 실험은 Fig. 3에 보이는 바와 같이 수행하였다.
평판의 임의의 한 점을 가진 하기 위하여 Impulse Force Hammer(PCB, 086E80)를 사용하였고, 평판의 32개의 지점에서 임팩트 가진에 의해 발생하는 평판의 진동 응답을 측정하기 위해 Laser displacement sensor (MICRO-EPSILON, ILD1420-10(001))를 사용하였다. 전반적인 모달 분석 실험은 지멘스사의 LMS Test Lab을 이용하여 수행하였다.
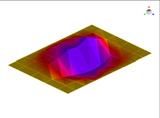
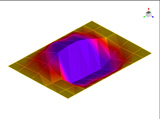
실내 소음을 측정하기 위해 Fig. 4에서 보여주는 바와 같이 아크릴로 만들어진 직육면체 음향 공동을 제작하였다. 아크릴로 만들어진 다섯 개의 강체 벽은 잔향음장을 갖고 있다. 직육면체 공동의 크기는 0.7 m × 0.5 m × 1.175 m이고 아크릴의 두께는 25 mm이다. 실내 소음을 측정하기 위한 마이크로폰(B&K 4189)은 평판의 중심으로부터 200 mm 떨어진 공동의 내부 지점에 설치하였다. 평판들은 아크릴 공동의 상단 부분에 고정시켰다. 경계 조건을 위해 평판의 각 모서리의 25 mm를 나사 구멍이 있는 스틸 바로 평판과 아크릴 공동을 고정시켰다.
이 실험에서는 Impulse Force Hammer (PCB, 086E80)를 이용하여 평판의 중심부를 임팩트 가진하여 발생하는 실내소음을 측정하였다. 실험은 지멘스사의 LMS Test Lab을 사용하여 수행하였다.
4. 결과 분석
4.1 모달 해석 결과 분석
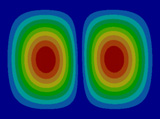
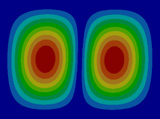
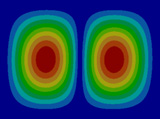
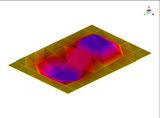
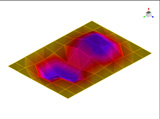
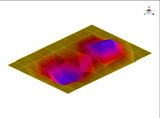
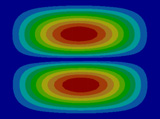
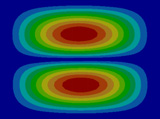
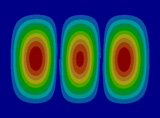
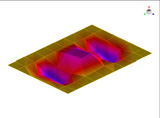
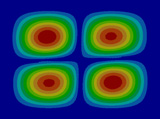
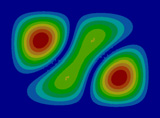
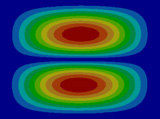
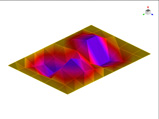
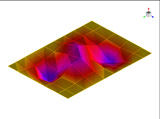
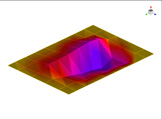
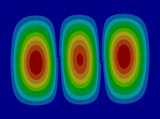
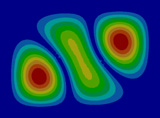
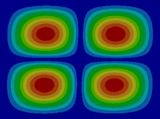
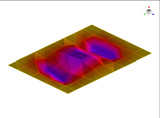
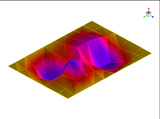
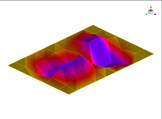
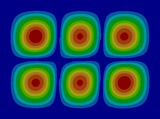
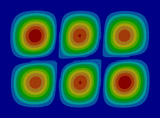
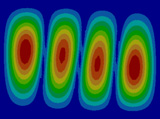
FEM에 의한 수치석 모달해석과 실험을 통한 실험적 모달 분석의 결과는 Table 2에 나타나 있다. 이론적 모달 해석은 CFRP 평판의 경우 고유진동 해석은 참고문헌 (3)에 있으며, 이 논문에서는 실내소음 예측이 주 목적임으로 논의를 생략하며, 수치적 모달해석과 실험적 모달 해석에 대해서 결과를 논 한다. Table 2는 해석 방법과 실험에 의해 도출된 적층 각도에 따른 세 개의 평판들의 가장 낮은 6개의 고유진동수와 모드 형상을 보여준다. 각 모드의 고유진동수는 적층 각도에 따라 다르게 나타났다. 첫 번째 모드의 고유진동수는 적층 각도가 큰 [±75°]에서 가장 높게 나타났고 적층 각도가 작은 [±15°]와 [±30°]에서는 낮게 나타났다. 모든 적층 각도에서 첫 번째 모드와 두 번째 모드에서 각각 (1,1) 모드 형상과 (2,1) 모드 형상이 나타났다. 하지만 [±15°]와 [±30°]에서 (1,2) 모드 형상이 세 번째 모드에서 나타났지만 [±75°]의 네 번째 모드에서 (1,2) 모드 형상이 나타났다. 마찬가지로 [±75°]에서 (3,1) 모드 형상이 세 번째 모드에서 나타났지만 [±15°]와 [±30°]에서는 다섯번 째 모드에서 나타났다. 그러므로 적층 각도에 따라 고유진동수와 모드 형상에서 차이가 나타난다고 볼 수 있다. CFRP 평판의 적층 각도를 조절함으로써 특정 주파수에서 고유진동수와 모드 형상 같은 진동 특성을 제어할 수 있다. 이러한 진동 특성 변화는 실내 소음에도 영향을 미칠 것이다. 수치적 해석의 결과의 주파수 옆 괄호 안 수치는 실험과의 고유 진동수에 대한 오차를 나타내며 대부분의 오차가 5% 이내이다.
4.2 공동 공간의 공명 모드(Cavity mode)
온전 밀폐된 직육면체 공동의 음향 공동 모드는 이론적으로 식 (1)에 의해 144.68 Hz에서 발생한다. 하지만 실험에 사용된 유연한 진동체를 갖는 공동공간의 경우 유연한 진동의 임피던스가 강체 벽이 아님으로 음향 공명모드의 공명주파수는 이동되어 150 Hz 이상에서 발생한다. 주파수 이동은 적층 각도가 작을수록 크게 발생하였고, 적층 각도가 클수록 작게 발생하였다. 그러므로 CFRP 평판의 적층 각도를 조절하면 음향 공동 모드의 주파수 역시 제어할 수 있다. 이러한 공명 주파수 이동 특성을 잘 활용하면 외부 가진력에 의한 음향 공동 모드에서 발생하는 음향 공명 현상을 피할 수 있다.
4.3 실내 소음 분석 결과
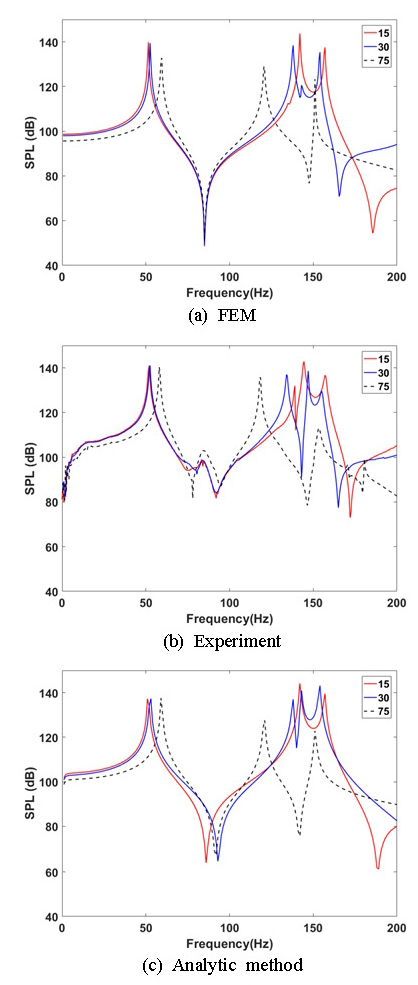
적층 각도에 따른 CFRP 평판의 실내 소음의 해석적, 실험적 그리고 이론적 결과들은 Fig. 5에 나타나 있다. Fig. 5는 적층 각도에 따른 세 개의 평판의 실내 소음을 비교하였다. 이 그래프들은 평판의 중심으로부터 200 mm 떨어진 내부 지점에서 측정한 소음 음압 레벨이다.
Fig. 5(a)는 FEM 결과이며, Fig. 5(b)는 실험적 결과이다. 해석적 결과는 Fig. 5(c)에서 보여준다. 이 결과에 의하면 이론적 및 수치적 결과들은 실험적 결과와 다른 부분이 87 Hz 부근에서 나타나는데 이것은 CFRP 판재의 대칭모드(symmetric mode)이기 때문이다. Fig. 5에서 실내 음압이 증가하는 곳은 CFRP 판재의 비대칭(non-symmetric) 공진 모드인 (1,1) 및 (3,1) 모드에서 발생하였고, 또한 공동 공간의 공명모드에서 발생하였다. 평판의 중심부를 가진하여 평판의 중심으로부터 수직으로 떨어진 지점에서 음압 레벨을 측정하였기 때문에 대칭모드에서는 피크가 나타나지 않아야 한다. 하지만 실험에서는 위의 조건들을 완벽하게 만족시키기 어렵기 때문에 대칭모드의 영향인 87 Hz에서 낮은 음압레벨의 피크가 나타난다. 50 Hz 부근에서 나타난 첫 번째 피크에서의 음압 레벨 차이는 크게 두드러지게 나타나지는 않았다. 두 번째 피크인 (3,1) 모드 형상에서는 피크의 주파수 차이가 크게 나타났다. 위의 모달 분석에서 (3,1) 모드 형상이 [±15°]에서는 다섯 번째 모드에서, [±30°]에서는 네 번째 모드에서, 그리고 [±75°]에서는 세 번째 모드에서 발생했기 때문이다. 그리고 적층 각도가 클수록 음압 레벨이 낮게 나타났다. 공명 모드인 세 번째 피크에서도 (3,1) 모드 형상과 비슷한 경향이 나타났다. 적층 각도가 클수록 상대적으로 낮은 주파수에서 나타나고 낮은 음압레벨을 나타내었다. 전반적으로 적층 각도가 커짐에 따라 낮은 음압레벨을 나타내었다. 특히 실내 공명모드에 해당하는 모드에서 실내 음압을 적층각에 대해서 나타내면 Table 3과 같다. 각도가 ±75°인 경우 8 dB 정도 낮다. 적층각을 잘 조정하면 공명에 의한 음압을 조정할 수가 있음을 발견할 수 있다.
5. 결 론
이 연구는 탄소 섬유 적층 각도에 따른 CFRP 평판의 실내소음을 해석적, 이론적 그리고 실험적인 방법들을 통해서 예측 및 측정하였다. 적층된 CFRP 판재가 이방성을 갖고 있기 때문에 적층 각도에 따른 물성치 차이로 인해 고유진동수와 모드 형상의 차이가 나타났다. 이러한 차이들은 직육면체 공동에서의 실내 소음 차이를 발생시켰다. 고유진동수와 모드 형상 차이에 의해 음향 음압의 피크가 다른 주파수에서 발생하였다. 전반적인 실내 소음 레벨 값은 적층 각도가 클수록 낮게 측정되었다. 따라서 적층 각도를 변화함으로써 특정 주파수에서 외부가진에 의한 공명 현상을 피할 수 있다.
기 호 설 명
| c0 : | : 음속 |
| Lx : | : 직육면체 공동의 x축 방향 길이 |
| Ly : | : 직육면체 공동의 y축 방향 길이 |
| Lz : | : 직육면체 공동의 z축 방향 길이 |
| ψn(x) : | : 비 연성 음향 모드 형상 함수 |
| Ψ : | : ψn(x)의 벡터 |
| an (ω) : | : 음향 음압 모드의 복소 진폭 |
| a : | : an (ω)의 벡터 |
| ϕm (y) : | : 비 연성 진동 모드 형상 함수 |
| Φ : | : ϕm (y)의 벡터 |
| bm (ω) : | : 진동 속력 모드의 복소 진폭 |
| b : | : bm (ω)의 벡터 |
| V : | : 실내공간의 부피 |
| Sf : | : 구조물의 표면적 |
| ρ0 : | : 공기 밀도 |
| An (ω) : | : 음향 모드 공진 항 |
| Tα : | : 1차 모드의 시간 상수 |
| ωn : | : n번째 음향 모드의 고유진동수 |
| ζn : | : n번째 음향 모드의 감쇠비 |
| Cn,m : | : 비 연성 구조 및 음향 모드 형상 함수 간의 기하학적 연성 관계 |
| qs : | : 구조의 진동으로 인한 모달 소스 강도 벡터 |
| Zα : | : 비 연성 음향 모드 임피던스 행렬 |
| A : | : An으로 구성된 (n,n) 대각 행렬 |
| ρs : | : 평판의 밀도 |
| f(y,ω) : | : 평판의 표면에서 힘 분포 함수 |
| p(y,ω) : | : Cavity 음압 분포 |
| Bm (ω) : | : 구조 모드 공진 항 |
| ωm : | : m번째 구조 모드의 고유진동수 |
| ζm : | : m번째 구조 모드의 감쇠비 |
| g : | : 외력 분포 f(y,ω)에 의한 일반화 된 모달 힘 벡터 |
| ga : | : 음향 시스템에 작용하는 모달 힘 벡터 |
| Ys : | : 비 연성 구조 모달 이동 행렬 |
| B : | : Bm으로 구성된 (m,m)대각 행렬 |
Acknowledgments
# A part of this paper was presented at the KSNVE 2018 Annual Spring Conference
이 논문은 2016년도 정부(교육과학기술부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구입니다(No. 2016R1A2B2006669).
References
- Han, E. K., Oh, J. E., and Bang, T. K., (1989), A Study on the Dynamic Characteristics of CFRP Plate by Modal Analysis Method, Transactions of the KSAE, 11(1), p44-50.
-
Kim, C. J., (2016), Dynamic Analysis of Carbon-fiber-reinforced Plastic for Different Multi-layered Fabric Structure, Transactions of the Korean Society for Noise and Vibration Engineering, 26(4), p375-382.
[https://doi.org/10.5050/KSNVE.2016.26.4.375]

-
Lee, S. K., Kim, M. W., Park, C. J., Choi, M. J., Kim, G. H., Cho, J. M., and Choi, C. H., (2016), Effect of Fiber Orientation on Acoustic and Vibration Response of a Carbon Fiber/epoxy Composite Plate: Natural Vibration Mode and Sound Radiation, International Journal of Mechanical Sciences, 117, p162-173.
[https://doi.org/10.1016/j.ijmecsci.2016.08.023]

-
Kim, S. M., and Brennan, M. J., (1999), A Compact Matrix Formulation Using the Impedance and Mobility Approach for the Analysis of Structural-acoustic Systems, Journal of Sound and Vibration, 223(1), p97-113.
[https://doi.org/10.1006/jsvi.1998.2096]

-
Kim, S. M., and Brennan, M. J., (1999), Active Control of Harmonic Sound Transmission into an Acoustic Enclosure Using Both Structural and Acoustic Actuators, Journal of the Acoustical Society of America, 107(5), p2523-2534.
[https://doi.org/10.1121/1.428640]

-
Pretlove, J., (1965), Free Vibrations of a Rectangular Panel Backed by a Closed Rectangular Cavity, Journal of Sound and Vibration, 2, p197-209.
[https://doi.org/10.1016/0022-460X(65)90108-2]

-
Dowell, E. H., Gorman, G. F. Ⅲ, and Smith, D. A., (1977), Acoustoelasticity: General Theory, Acoustic Modes and Forced Response to Sinusoidal Excitation, Including Comparisons with Experiment, Journal of Sound and Vibration, 52(4), p519-542.
[https://doi.org/10.1016/0022-460X(77)90368-6]


Sang-Kwon Lee studied mechanical engineering at the Pusan National University, Pusan, Korea for B.S. In 1998 he received a Ph.D. degree in signal processing at the ISVR (Institute of Sound and Vibration Research) of the University of Southampton in U.K. He has continued the sound and vibration research in the department of mechanical engineering Inha University since 1999.