해수윤활 선미관 베어링에서 발생되는 비선형 Stick-slip 마찰진동 발생 조건 및 주요인자 분석
© The Korean Society for Noise and Vibration Engineering
Abstract
Seawater-lubricated bearings applied to stern tubes are widely used to support ship propeller shafts. Generally, the material of these seawater-lubricated bearings is rubber or polymer. Because the lubricating fluid for this kind of bearing is sea water, its coefficient of friction is somewhat higher than that of an oil-lubricated bearing. In particular, in the case of a low-speed regime where the slope of the speed-friction coefficient curve is negative, the shaft system becomes unstable because of the friction force, and self-excited vibration can be generated. This phenomenon is called nonlinear friction-induced vibration by stick-slip motion. In this paper, a simplified model of the propeller shaft and bearing system with two degrees of freedom is suggested to define the mechanism of the stick-slip motion; the stability of the shaft-bearing system according to the change in vertical force, damping coefficient, and friction coefficient on the bearing surface was investigated with the virtual shaft model. In addition, an actual improvement case for the stick-slip non-linear vibration problem occurring in the propulsion shaft of a typical naval vessel is introduced by applying the result from the investigation of the virtual shaft model described in this research.
Keywords:
Stick-slip, Non-linear Friction Induced Vibration키워드:
스틱슬립, 비선형 마찰진동1. 서 론
스프링에 연결된 물체를 컨베이어 벨트 위에 놓아둔 상태에서 컨베이어를 동작시킬 경우 최초 컨베이어가 움직이기 시작한 지 얼마 되지 않아 스프링의 변위가 작을 때는 물체와 컨베이어 경계에서의 마찰력이 스프링에 의한 탄성 복원력보다 크므로 물체는 컨베이어 벨트의 운동방향으로 컨베이어 벨트위에 고정된 상태로 움직인다. 하지만 스프링의 변위가 점점 커져서 스프링에 의한 탄성복원력이 마찰력보다 커지게 되면 물체는 더 이상 컨베이어 벨트위에 고정되어 컨베이어와 같이 움직이지 않고 컨베이어 벨트 운동방향과 반대인 스프링의 복원력 방향으로 미끄러진다. 이러한 운동은 물체가 스프링 복원력이 마찰력보다 작은 지점으로 돌아간 후 반복적으로 발생하며 이러한 반복운동을 스틱-슬립(stick-slip)에 의한 비선형 마찰진동이라고 한다. 스틱-슬립에 의한 비선형 마찰진동은 물체와 컨베이어 벨트 사이의 경계면의 마찰계수가 충분히 작아 마찰력을 무시할 정도가 될 경우 발생하지 않는다.
베어링 면에서의 축의 회전 운동의 경우도 컨베이어 벨트의 물체와 같이 윤활막이 충분하게 형성되지 않는 저속 구간에서 마찰력이 충분히 크게 되면 스틱-슬립에 의한 마찰진동이 발생될 수 있다. 이후 회전속도가 증가하여 축-베어링 간 윤활막을 충분히 유지시켜 줄 수 있는 상태가 되면 이러한 마찰진동은 소멸된다.
선박용 추진축과 같이 저속운전을 피할 수 없는 경우 저속구간에서 스틱-슬립 운동에 의한 비선형 마찰진동을 피하기 어려우므로 마찰진동 발생 시 이를 최소화 할 수 있도록 추진축계를 설계해야하지만 실제 선박의 추진축계 설계 시 이에 대한 고려가 이루어지지 않고 있는 실정이다.
Simpson(1)은 축과 베어링을 컨베이어 위에서 스틱-슬립 운동을 하는 물체와 동일한 운동을 한다고 가정하고 회전속도에 따른 마찰력의 변화가 음의 관계를 가지는 경계윤활영역 및 혼합 윤활영역에서 스틱-슬립에 의한 마찰진동 및 추진축계의 안정도문제를 다루었다. Bhushan(2)은 실험실에서 시편시험을 통해 해수윤활베어링에서 발생하는 스틱-슬립 현상을 분석하였으며 베어링에 작용하는 수직력, 축의 회전수, 베어링의 표면상태 및 재질을 변경해 가면서 스틱-슬립에 의한 비선형 마찰진동을 평가하였다. 실험결과로부터 스틱-슬립 마찰진동에 의해 소음이 발생되는 조건을 여러 인자에 대해 정리하여 제안하였다. Peng(3)은 고무 재질의 해수윤활베어링에 대해 수압 및 온도 변화에 따른 동마찰계수를 평가하고, 스틱-슬립 마찰진동이 발생하는 구간을 실험적으로 제안하였다. Herbst(4)는 자동차 클러치에서 발생되는 채터링(chattering) 소음의 발생원인이 특정속도에서 클러치판에 작용하는 수직력 변화에 따른 스틱-슬립 마찰진동임을 파악하였다. 이러한 스틱-슬립 현상에 의한 마찰진동이 크게 발생할 경우 베어링의 마모 또한 크게 발생될 수 있으므로 마모와 연관한 마찰진동의 연구도 활발히 이루어지고 있다(5~7).
이와 같이 오일베어링에 비해 상대적으로 마찰계수가 큰 고무 또는 폴리머 계열의 해수윤활베어링의 경우 저속구간에서 스틱-슬립에 의한 비선형 진동에 대한 축계 시스템의 안정도 평가가 필요하다. 또한 이러한 스틱-슬립에 의한 비선형 마찰진동이 크게 발생할 경우 마찰진동을 저감하기 위한 시스템 파라미터 선정이 필요하다. 하지만 앞서 언급한바와 같이 대부분의 선박용 추진축계의 설계 시 이러한 현상에 대해서는 설계적으로 검증하지 않으며, 이러한 마찰진동이 발생한 경우에 대해서도 정확한 원인규명 및 개선대책을 수립하지 못하고 있다.
따라서 이 연구에서는 축-베어링 간 스틱-슬립현상에 의한 비선형 마찰진동을 회전-병진 2자유도 모델을 이용하여 설명하고 가상축계에 대해 마찰진동을 최소화하기 위한 주요 인자를 식별하고자 한다. 또한 실제 스틱-슬립 비선형 마찰진동이 발생한 축에 대해 가상 축계 예제를 통해 식별된 주요인자의 변경으로부터 축계 마찰진동이 감소할 수 있음을 보여줌으로써 스틱-슬립에 의한 마찰진동 발생 메카니즘을 검증하고자 한다.
2. 스틱-슬립 마찰진동 메카니즘
2.1 해수윤활베어링의 수학적 모델
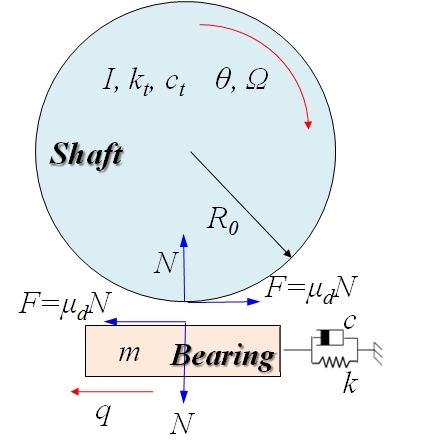
일반적으로 베어링과 축간의 비선형 진동은 베어링과 축의 상대운동만을 고려한 단순 모델을 가지고 설명되고 있다(1). 이 연구에서도 Fig. 1과 같이 해수윤활베어링과 추진축을 2자유도 모델로 가정하여 축과 베어링에 대한 운동방정식을 식 (1)과 같이 정의하였다.
| (1) |
여기서 I는 축의 질량관성모멘트, θ는 베어링의 각변위, ct는 축의 회전방향 댐핑, kt는 축의 회전방향 강성, m은 베어링의 질량, c는 베어링의 댐핑계수, k는 베어링의 강성, F는 마찰력, R0은 축반경, μd는 축-베어링간 등가 마찰계수, N은 베어링에 작용하는 수직력이다.
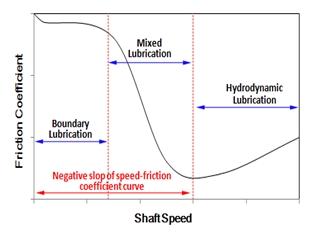
일반적으로 축의 속도에 따른 베어링-축간 마찰계수의 변화는 Fig. 2와 같다.
Fig. 2에서 마찰계수-회전속도 곡선의 기울기가 음수를 가지는 경계 또는 혼합 윤활 영역에서 등가 마찰계수(μd)는 식 (2)와 같이 축과 베어링의 상대속도의 항으로 표현된다(1).
| (2) |
여기서 μ0는 베어링-축간의 동마찰계수, μ1는 베어링-축간의 정마찰계수, a는 상수, 은 축-베어링 간 상대속도이다.
따라서 식 (1) 우항의 마찰력을 마찰에 의한 감쇠계수(cʹ)와 축-베어링 간 상대속도의 항으로 표현할 수 있으며() 좌항의 감쇠항과 동일한 형태로 표현할 수 있다. 여기서 식 (1) 우항의 축계 마찰력항의 감쇠계수(cʹ)가 좌항의 진동 시스템 감쇠계수(c)보다 클 경우 전체 등가 진동 시스템의 감쇠계수를 음수로 만들 수 있으며 이 때 축계 진동은 시간에 따라 발산하게 되어 불안정한 상태가 되며 고유진동수에서의 자려진동을 유발할 수 있다. 따라서 이 절에서는 스틱-슬립 마찰진동 발생 시 축계 시스템의 응답을 파악하고 시스템이 안정된 상태가 되기 위한 조건을 검토하고자 한다.
진동이 사라지고 안정화된 이후 축 및 베어링의 응답을 θ* 및 q*라 두면 이는 식 (3) ~ (4)와 같다.
| (3) |
| (4) |
여기서 Ω는 축 회전수이다.
및 를 식 (5)와 같이 정적변위를 제거한 순수한 진동 변위로 정의하고 이를 이용하여 식 (1)의 운동방정식을 다시 정리하면 운동방정식은 식 (6) ~ (7)과 같이 나타낼 수 있다.
| (5) |
| (6) |
| (7) |
여기서 Fʹ은 진동력이 제거된 안정상태에서의 마찰력이다.
식 (6) ~ (7)에서 마찰계수-회전속도 곡선의 기울기가 음수일 때 우항의 진동 마찰력 항은 식 (2)의 마찰계수 식을 이용하여 식 (8)과 같이 나타낼 수 있다.
| (8) |
식 (8)에서 Taylor 급수전개를 이용하여 를 선형화하면 식 (9) ~ (11)과 같이 나타낼 수 있다.
| (9) |
| (10) |
| (11) |
여기서 정적인 힘은 무시하여 식 (9)를 재정리하면 외력항은 식 (12)와 같이 단순하게 정리할 수 있다.
| (12) |
따라서 식 (12)를 식 (6) ~ (7)의 미분방정식에 대입하여 재정리하면 식 (13) ~ (15)와 같다.
| (13) |
| (14) |
| (15) |
식 (13) ~ (14)의 해를 “”, “”라 두면 식 (13) ~ (14)는 식 (16)과 같이 나타낼 수 있다.
| (16) |
여기서 고유해를 구하기 위한 특성방정식은 식 (17) ~ (21)과 같다.
| (17) |
| (18) |
| (19) |
| (20) |
| (21) |
일반적으로 식 (13) ~ (14) 미분방정식의 일반해는 축 및 베어링의 변위로 식 (22)와 같이 나타낼 수 있다.
| (22) |
여기서 D1, D2, D3, D4는 상수, ai ± bi는 i차 고유진동수, 는 i차 고유벡터이다.
식 (22)에서 축 및 베어링의 변위 고유치의 실수부(a1, a2)가 양의 값을 가질 경우 해당 고유치를 가지는 고유진동수에서 시스템 변수인 축 및 베어링 진동 변위인 및 는 발산하게 되므로 추진 축계는 스틱-슬립 마찰진동에 의한 자려진동을 하게 되어 시스템은 매우 불안정한 상태가 된다.
따라서 시스템이 자려진동을 하지 않는 안정된 상태가 되기 위해서는 모든 해의 실수부가 음수가 되어야 하며 이를 위해서는 특성방정식의 모든 계수인 C1, C2, C3가 식 (23) ~ (25)와 같이 양의 값을 가져야만 한다(1).
| (23) |
| (24) |
| (25) |
이와 같이 해수윤활베어링의 수학적 모델링을 통해 스틱-슬립 마찰진동에 대한 안정도 평가를 수행할 수 있으나 베어링에서의 댐핑계수 및 마찰계수를 파악하기 힘드므로 정확하게 시스템의 안정성 평가 및 스틱-슬립 마찰진동에 의한 자려진동 가능성을 예측하기 어렵다. 따라서 이 연구에서는 스틱-슬립에 대한 설계 평가보다는 스틱-슬립 현상이 발생했을 때 이를 개선하기 위한 제어인자를 도출하는 것에 초점을 두고 가상축계 예제를 통해 스틱-슬립 마찰진동에 영향을 미치는 주요인자와 이를 제어하기 위한 방법을 분석하고자 한다.
2.2 가상축계의 수직하중 및 댐핑 변화에 따른 안정도 변화
해수윤활베어링의 수직방향 반력, 댐핑계수 및 축-베어링 간 마찰계수에 따른 축계의 안정도 변화를 분석하기 위해 Table 1과 같이 가상 축계를 선정하였다.
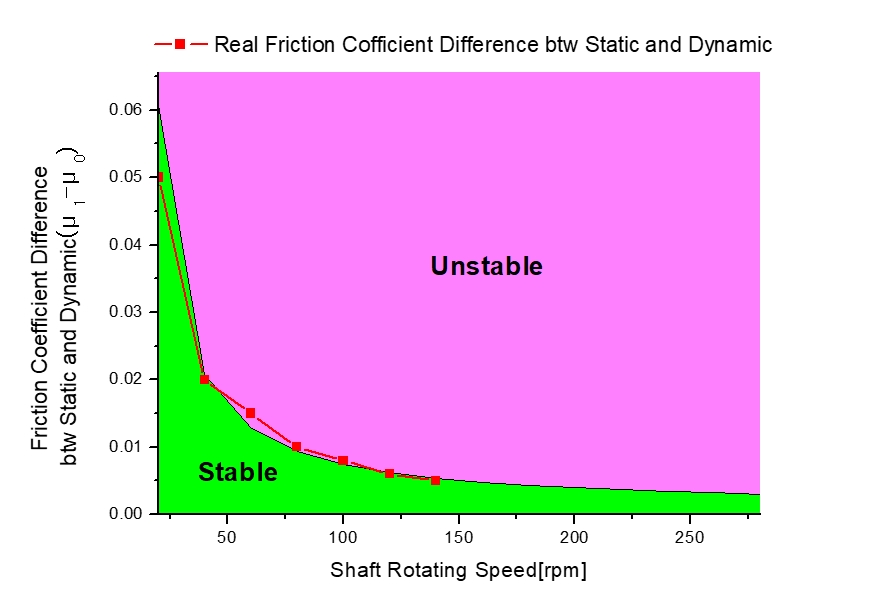
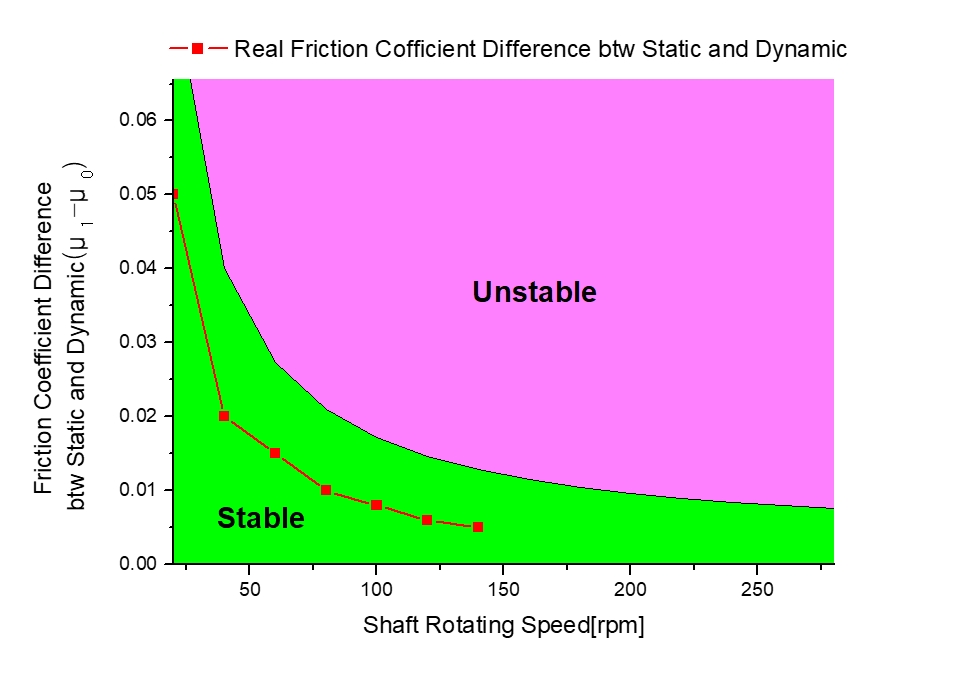
이 절의 가상축계에서 베어링의 정마찰계수와 동마찰계수의 차이(μ1—μ0)는 Zhimin et al.의 시험결과를 참고하여(6)회전수가 증가하면서 감소하다가 140 r/min 이상에서 증가하는 것으로 가정하였다. 이 조건에서 시스템의 안정도를 식 (23) ~ (25)를 가지고 평가해 보면 Fig. 3과 같다. Fig. 3에서 축계 시스템은 60 r/min ~ 100 r/min 구간에서 불안정영역에 있으며 이로 인해 스틱-슬립 마찰에 의한 자려진동이 크게 발생할 수 있음을 알 수 있다. 여기서 140 r/min을 초과하는 구간의 경우 마찰계수-회전수 곡선의 기울기가 (+)가 되어 스틱-슬립 운동은 발생하지 않으며 시스템은 항상 안정한 상태가 되므로 이 구간에서의 마찰계수는 별도로 도시하지 않았다.
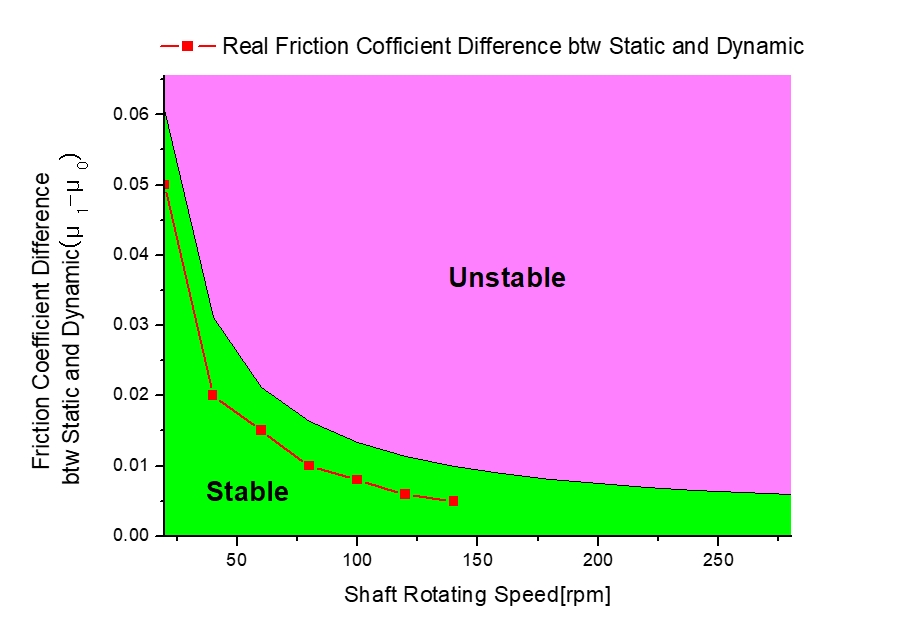
베어링에 작용하는 수직력은 축과 프로펠러의 하중 및 편심추력과 같은 유체력에 의해 발생되며 축정렬 및 베어링의 배치 조건에 따라 달라진다. 따라서 Table 1과 같은 가상 축계 모델에 대해 베어링에 작용하는 수직력이 축정렬 및 베어링 배치 최적화 등으로 인해 “100+200(r/min/20) [N]”에서 “100+100(r/min/20) [N]”으로 작아졌다고 가정하면 Fig. 4와 같이 시스템이 안정해지는 영역은 Fig. 3에 비해 더 넓어진다. Fig. 3에서 축 회전수가 60 r/min ~ 100 r/min일 경우 베어링의 하중은 “700 N ~ 1100 N” 이며 이때 축계는 불안정한 상태가 되어 스틱-슬립 마찰에 의한 자려진동이 발생하지만 이 하중이 “400 N ~ 600 N”으로 감소할 경우 축계는 Fig. 4와 같이 안정-불안전 경계선이 우측 상단으로 이동함에 따라 축계 상태는 모두 안정한 상태가 되어 스틱-슬립 마찰에 의한 자려진동은 발생하지 않을 것으로 예측되었다.
Table 1과 같은 가상 축계 모델에 대해 Fig. 5와 같이 베어링의 댐핑이 커질 경우(0.1 → 0.15) 시스템이 안정해지는 영역은 Fig. 3에 비해 더 넓어지게 된다.
Fig. 5에서 축 및 베어링의 댐핑계수가 50 % 증가했을 경우(0.1 → 0.15) Fig. 3의 불안정영역(60 r/min ~ 100 r/min)은 안정-불안전 경계선이 우측 상단으로 이동함에 따라 모두 안정 영역에 있음을 알 수 있다. 따라서 베어링의 댐핑계수가 커지면 스틱-슬립 마찰에 의한 자려진동은 소멸할 수 있음을 알 수 있었다.
Fig. 6에서 축-베어링간 마찰계수 감소로 인해 정마찰계수와 동마찰계수의 차이가 줄어들 경우 안정-불안정 경계선의 변화는 없지만 마찰계수 저감에 따라 축계는 모든 운전조건에서 스틱-슬립 마찰진동에 대해 안정 영역에 있음을 알 수 있다.
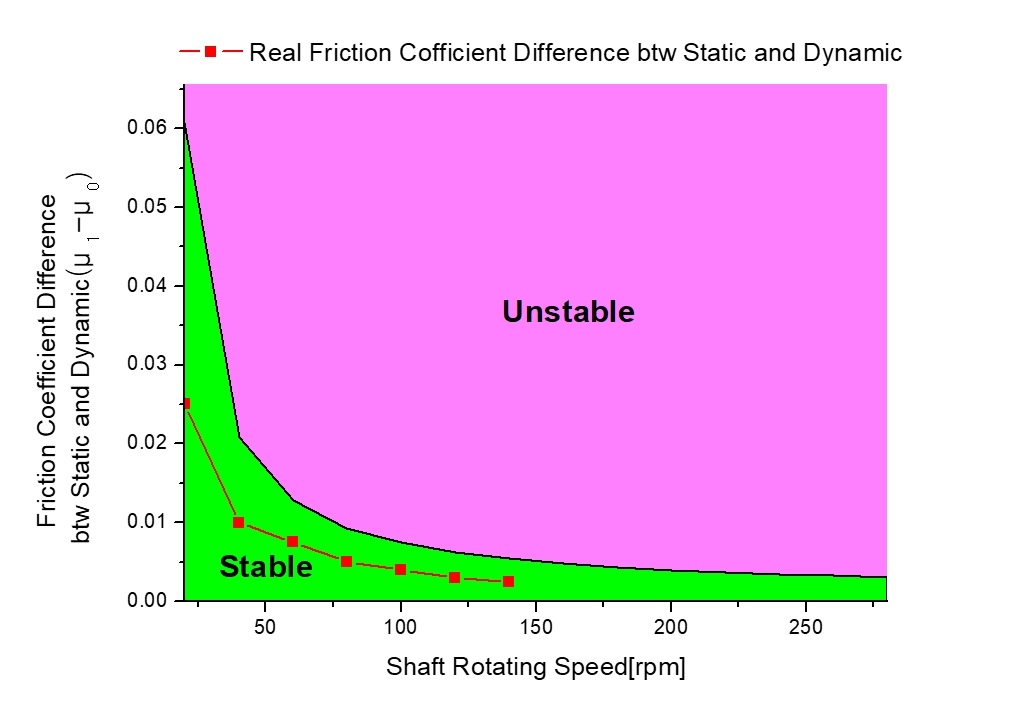
Boundary of the system safety with respect to the stick-slip nonlinear friction vibration when the friction coefficient on the bearing is reduced
따라서 축-베어링 시스템이 불안전 영역에 있어 스틱-슬립에 의한 마찰진동이 발생한 경우 마찰계수 감소로부터 스틱-슬립 진동 문제를 해결할 수 있음을 예측할 수 있었다.
3. 실선에서 발생한 추진축계 스틱-슬립 비선형 마찰진동 및 개선
이 장에서는 실제 추진축계에서 발생한 스틱-슬립 마찰에 의한 자려진동 현상을 기술하고 이에 대한 개선 결과를 2장의 가상축계 시스템의 현상과 연계하여 기술하고자 한다.
3.1 실선에서 발생한 추진축계 스틱-슬립 마찰진동
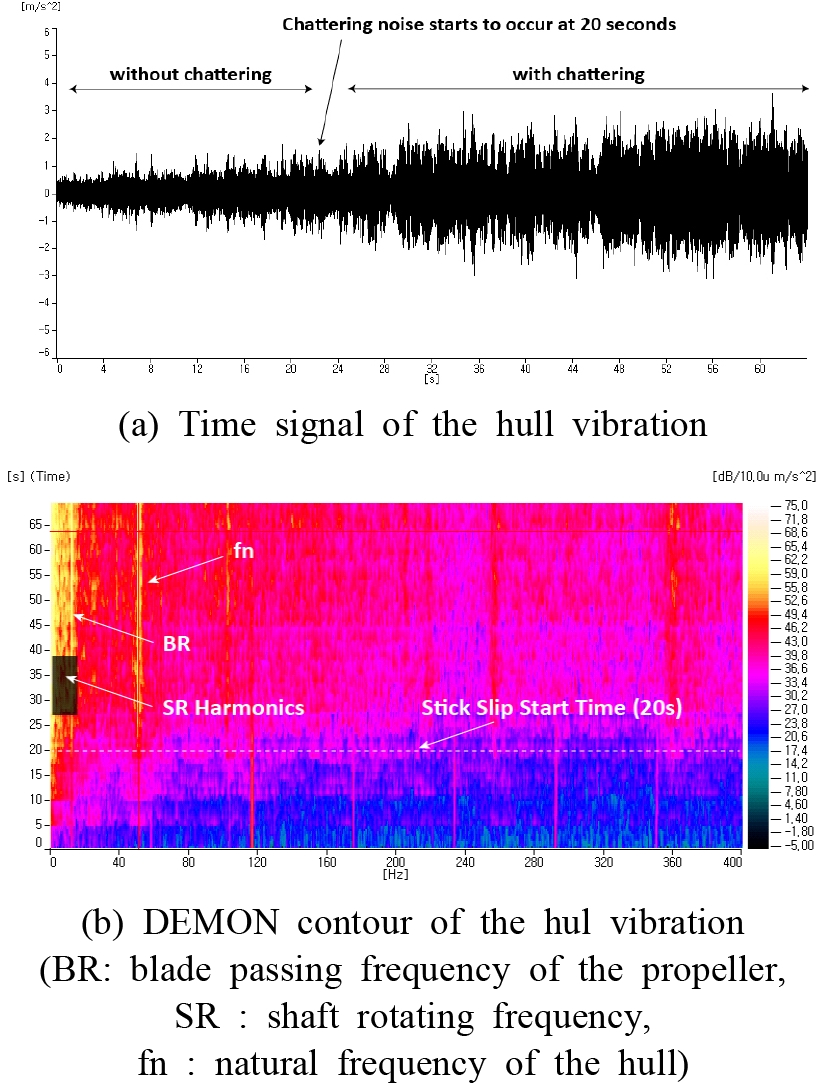
이 연구에서 기술하고자 하는 추진축은 함정용 추진축으로 축을 지지하는 스턴튜브베어링은 폴리머계열의 해수윤활베어링을 사용하고 있다. 이 함정의 시운전중 특정 회전수(“N-20” ~ “N” r/min)에서 스틱-슬립에 의한 비선형 마찰진동으로 예측되는 현상이 관측되었다. Fig. 7(a)와 같이 “N-20” r/min에서 조용하던 추진축계에서 시간에 따라 불규칙적으로 변하는 채터링(chattering) 소음을 유발시키는 진동이 증가함을 알 수 있었다. 일반적으로 마찰에 의한 채터링 소음은 광대역 고주파 마찰진동이 회전주파수 또는 특정 주파수에 동조되어 불규칙적으로 발생하게 된다. 2장에서 기술한 바와 같이 스틱-슬립에 의한 비선형 마찰진동은 마찰이 일어나는 동안 베어링의 고유진동수에서 가진되는 자려진동의 형태이며 이때 마찰에 의해 발생된 고주파 광대역 진동 신호는 자려진동이 발생하는 베어링의 고유진동수에 동조되어 나타나게 된다.
따라서 스틱-슬립에 의한 비선형 마찰진동은 베어링 또는 베어링 하우징을 포함한 구조물에서 구조진동을 계측하고 고주파 광대역 마찰 진동 신호에 대해 DEMON(detection of envelope modulation on noise) 분석을 수행할 경우 DEMON 스펙트럼 상에 회전주파수나 프로펠러 블레이드 통과주파수 외에 베어링 또는 베어링 주변구조물의 고유진동수의 피크 성분이 감지되어야 한다.
이러한 이론적 배경을 바탕으로 이 연구에서 기술하는 추진축계의 소음이 스틱-슬립 비선형 마찰진동에 의한 현상인지를 확인하기 위해 해수윤활베어링 하우징 주변 선체에 가속도계를 설치하고 Fig. 7(a)의 가속도 신호를 가지고 6.4 kHz +/– 3.2 kHz 주파수 통과필터를 적용하여 DEMON 분석을 수행하였다.
그 결과 Fig. 7(b)와 같이 채터링 소음이 발생하는 시점인 20초 후부터 추진축의 회전주파수(SR) 조화성분 및 프로펠러의 블레이드 통과 주파수(BR)뿐만 아니라 베어링 및 베어링 주변구조물의 고유주파수로 추정되는 주파수(fn)에서 피크가 명확하게 드러남을 알 수 있었다. 앞서 언급한 바와 같이 DEMON 스펙트럼에서의 회전주파수(SR) 조화성분 및 프로펠러 블레이드 통과주파수(BR) 성분의 출현은 일반적인 마찰진동 특성이지만 베어링 및 주변 선체의 고유진동수 성분(fn)의 출현은 스틱-슬립 현상에 의한 비선형 마찰진동의 전형적인 특성이므로 이 연구에서 다루는 추진축계의 채터링 소음의 발생원인은 스틱-슬립에 의한 마찰진동임을 확인할 수 있었다.
3.2 스틱-슬립 마찰진동의 개선
2장에서 가상추진축계의 스틱-슬립에 대한 안정도 분석결과를 바탕으로 스틱-슬립에 의한 마찰진동을 개선하기 위한 방법을 아래와 같이 정리하였다.
- (1) 베어링의 재질변경 또는 축-베어링 간 틈새치수변경을 통한 댐핑계수 증가 및 마찰계수 감소
- (2) 베어링의 배치 또는 축정렬을 통한 베어링에 작용하는 수직력 감소
(1)항의 경우 베어링의 재질변경을 위해서는 베어링을 교체해야만 하고 베어링의 축-베어링 간 치수조정을 위해서는 베어링 내경가공을 다시 해야하기 때문에 현 상태에서 적용하기가 매우 어렵다. 따라서 (1)항보다는 (2)항에 대한 검토를 수행하였다.
(2)항의 검토로부터 최초 시운전 시 축과 엔진을 연결하는 커플링의 상태가 불량하였으므로 커플링의 교체를 수행하고 축정렬을 재수행한 결과 Figs. 8 ~ 9와 같이 스틱-슬립에 의한 비선형 마찰진동이 사라짐을 확인할 수 있었다.
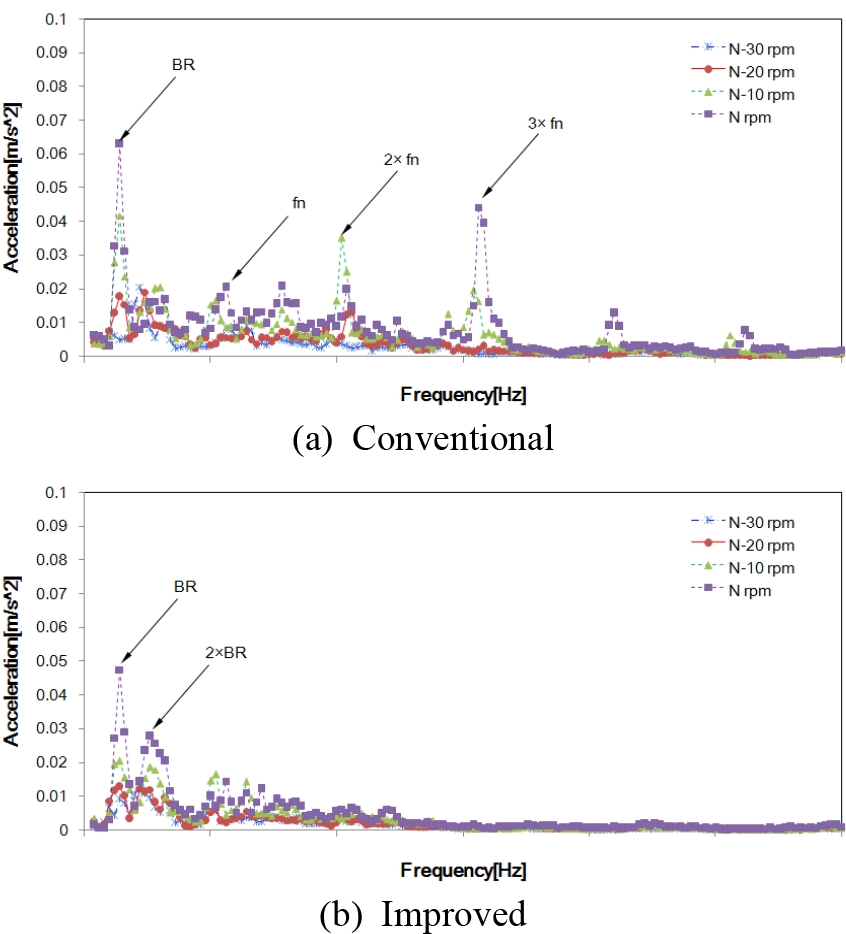
FFT spectra for the hull vibration adjacent to the stern tube bearing (BR: blade passing frequency of the propeller, SR: shaft rotating frequency, fn: natural frequency of the hull)
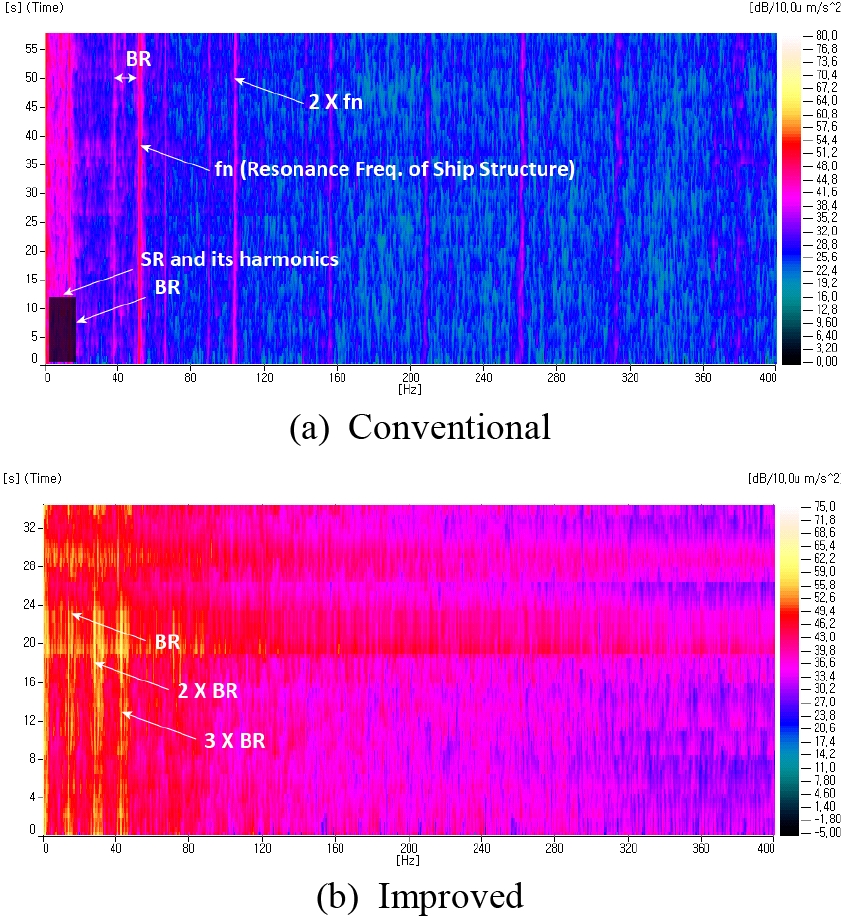
DEMON contour for the hull vibration adjacent to the stern tube bearing (BR: blade passing frequency of the propeller, SR: shaft rotating frequency, fn: natural frequency of the hull)
프로펠러축의 베어링과 커플링의 힘에 대한 자중방향 변위 모델을 Fig. 10과 같이 가정하면, 추진축 정렬상태, 커플링의 강성 및 댐핑 변화에 따라 전후부 선미부 베어링에 작용하는 수직력이 달라질 수 있으며, 이로 인해 스틱-슬립이 일어나는 조건의 변화가 발생할 수 있다. 따라서 채터링 소음과 같은 이상소음 발생 조건이 2장의 사례와 유사하게 스틱-슬립 비선형 마찰진동에 의해 발생한다고 가정하면 커플링 강성, 댐핑을 포함한 축정렬 개선을 통해 이러한 문제를 개선할 수 있다.
4. 결 론
선박에 적용되는 해수윤활베어링은 저속운전 시 회전속도에 대한 마찰계수의 변화가 음의 관계를 가지는 구간인 경계윤활 및 혼합 윤활구간에서 스틱-슬립 운동에 의한 비선형 마찰진동이 발생할 수 있으며 이 경우 이상소음 및 베어링 마모 등의 문제를 야기할 수 있다.
이 연구에서는 축-베어링 모델을 축회전과 베어링 병진운동으로 구성되는 2자유도 단순계로 가정하여 스틱-슬립에 의한 비선형 마찰진동 및 이에 대한 시스템의 안정도를 분석하였다. 이러한 메카니즘을 바탕으로 가상축계에 대해 안정도 분석을 통하여 스틱-슬립 마찰진동에 의해 시스템이 불안정한 상태가 되었을 때의 개선 방향을 다음과 같이 수립할 수 있었다.
- (1) 베어링 표면 가공, 재질변경 등을 통한 축-베어링 간 마찰계수 감소
- (2) 베어링의 재질변경을 통한 베어링의 감쇠계수 증가
- (3) 축정렬 및 베어링 최적 배치를 통한 베어링 표면에 가해지는 수직력의 최소화
가상축계 예제를 통해 도출된 개선방법 중 축정렬 방법을 실제 스틱-슬립에 의한 마찰진동이 발생한 축에 대해 적용한 결과 특정회전수에서 발생하던 이상 채터링 소음이 모두 사라짐을 확인할 수 있었다.
Acknowledgments
A part of this paper was presented and selected as one of best papers at the KSNVE 2018 Annual Spring Conference
이 연구는 국방기술품질원 자체연구로 실시된 것으로 군사보안상 문제가 없음을 확인함.
References
- Simpson, T. A., and Ibrahim, R. A., (1996), Nonlinear Friction-induced Vibration in Water-lubricated Bearing, Journal of Vibration and Control, 2(1), p87-113.
-
Bhushan, B., (1980), Stick-slip Induced Noise Generation in Water-lubricant Compliant Rubber, Journal of Lubricant Technology, 102(2), p201-210.
[https://doi.org/10.1115/1.3251470]

-
Peng, E., Liu, Z., Zhou, X., Tian, Y., and Zhao, M., (2012), Study on Nonlinear Friction-induced Vibration in Water-lubricated Rubber Stern Tube Bearings, The Open Mechanical Engineering Journal, 6, p140-147.
[https://doi.org/10.2174/1874155X01206010140]

- Albers, A., and Herbst, D., (1998), Chatter-causes and Solutions, Proceedings of the 6th LuK Symposium, p23-45.
-
Hirani, H., and Verma, M., (2009), Tribological Study of Elastomeric Bearings for Marine Propeller Shaft System, Tribology International, 42(2), p378-390.
[https://doi.org/10.1016/j.triboint.2008.07.014]

-
Zhimin, Y., Xincong, Z., Hongling, Q., Wanying, N., Hao, W., Kai, L., and Yumin, T., (2015), Study on Tribological and Vibration Performance of a New UHMWPE/Graphite/NBR Water Lubricated Bearing Material, Wear, 332-333, p872-878.
[https://doi.org/10.1016/j.wear.2014.12.054]

-
Wang, H., Liu, Z., Zou, L., and Yang, J., (2017), Influence of Both Friction and Wear on the Vibration of Marine Water Lubricated Rubber Bearing, Wear, 376-377, p920-930.
[https://doi.org/10.1016/j.wear.2017.02.006]


HyungSuk Han received a B.S. in Production and Mechanical Engineering from Pusan National University in 1996. He then went on to receive his M.S. and Ph.D. degrees in Mechanical Engineering from Pusan National University in 1998 and 2007, respectively. Dr. Han is currently a Senior Researcher at Defense Agency for Technology and Quality, Busan, Korea.

KyoungHyun Lee received a B.S. and M.S. in Naval Architecture and Ocean Engineering from Seoul National University in 2008 and 2011 respectively. Mr. Lee is currently a Researcher at Defense Agency for Technology and Quality, Busan, Korea.

SungHo Park received a B.S. in Mechanical Engineering from Hanyang University in 2011 and MS in Mechanical Engineering from KAIST in 2013 respectively. Mr. Park is currently a Researcher at Defense Agency for Technology and Quality, Busan, Korea.

SooHong Jeon received a B.S. in Mechanical Engineering from Pusan National University in 2007. He then went on to receive his M.S. and Ph.D. degrees in Mechanical Engineering from Pusan National University in 2009 and 2014, respectively. Dr. Jeon is currently a Senior Researcher at Defense Agency for Technology and Quality, Busan, Korea.