표면 근전도를 이용한 손동작 인식
© The Korean Society for Noise and Vibration Engineering
Abstract
In the present study, the performance of hand gesture recognition using surface electromyogram (EMG) was evaluated experimentally. To obtain the surface EMG data of a human, a wearable armband-type commercial measurement device including an eight-channel EMG sensor array was used. The mean absolute value was extracted from the measured EMG data for use as the feature value to be applied to the pattern recognition algorithm. A k-nearest neighbors (kNN) machine-learning algorithm was applied to recognize the hand gesture patterns. The accuracy of the classification was confirmed according to the k value and the type of distance function applied to the algorithm. To evaluate the performance of the applied classification algorithm, EMG signals of five subjects were measured, and their gesture classification was performed. It was demonstrated that the surface EMG can be successfully used for hand gesture recognition with the classification algorithm.
Keywords:
Surface Electromyogram, Hand Gesture Classification, Pattern Recognition, Machine Learning, k-nearest Neighbor키워드:
표면 근전도, 손동작 분류, 패턴 인식, 기계 학습법, k-근접 이웃1. 서 론
사람과 기계(또는 로봇)의 인터페이스(human-machine(or robot) interface, HMI or HRI) 방식은 버튼을 누르거나, 화면을 터치하거나, 조이스틱을 조종하는 등 손을 이용한 방식이 가장 많이 활용되고 있다. 그러나 최근 가상 현실, 증강 현실, 원격 제어 등의 기술이 발달함에 따라 보다 직관적인 인터페이스 기술에 대한 요구가 증가하고 있으며, 이에 따라 동작 인식을 이용한 인터페이스에 대한 연구가 활발하게 이루어지고 있다. 사람의 동작을 인식하는 방법에는 가속도 센서를 이용한 동작 인식 기술, 카메라를 이용한 비전 정보 기반의 동작 인식 기술, 마커를 이용한 동작 인식 기술, 착용형 장치를 이용한 동작 인식 기술 등이 있다. 가속도 센서를 이용한 동작 인식 기술의 대표적인 예는 닌텐도 사의 Wii로 리모컨 속에 가속도 센서를 내장하여 사용자의 동작을 인식하고 이를 게임에 표현할 수 있도록 하였다(1). 그러나 가속도 신호가 노이즈에 민감하고, 3축 가속도 정보만으로 동작을 인식하는 것은 한계가 있다. Microsoft사의 KINECT는 깊이 정보를 추출할 수 있는 카메라를 이용하여 사용자의 동작을 인식하고 게임 인터페이스에 활용할 수 있도록 한 것으로 카메라를 이용한 동작 인식 기술의 대표적인 예이다(2). 카메라를 이용하는 방법은 카메라가 있는 장소에서만 활용이 가능하고, 카메라 각도 안에서만 동작 인식이 이루어지는 단점이 있다. 마커를 이용한 동작 인식 기술은 신체 부위에 마커를 부착하고 카메라를 이용하여 이를 추적하는 방법이다(3). 마커를 이용한 기술은 제한된 공간에서만 적용될 수 있는 단점이 있고, 사용자가 마커를 부착해야 하고, 마커의 수가 많아지면 구분이 어려워지는 한계가 있다. 착용형 장치를 이용한 기술은 대부분 관성측정장치(inertia measurement unit, IMU)를 이용한 것으로 3축 가속도 센서, 3축 자이로 센서, 3축 지자기 센서가 포함되어 있다. Xsens MVN과 Virtunix Omni는 IMU를 이용한 대표적인 착용형 센서이다(4,5). 이러한 착용형 센서는 많은 수의 IMU를 활용하므로, 측정하는 데이터 양이 많고, 특수 제작된 수트나 로봇을 착용해야 하는 단점이 있다.
최근에는 사용자의 신체에서 발생하는 생체 신호 중 근전도 신호를 이용하여 동작을 인식하고자 하는 연구가 다양하게 진행되고 있다. 근전도는 골격근의 운동에 대하여 발생하는 근육의 활동전위에 대한 기록으로 의학적으로는 신경 및 근질환의 보조진단에 사용되고 있다. 최근 이러한 근전도를 동작 인식 등 공학적으로 활용하고자 하는 연구가 다양하게 진행되고 있다. Francesco 등은 손가락의 동작과 근전도 신호의 관계를 분석하였고(6), Englehart 등은 wavelet 분석을 이용하여 근전도 신호로부터 연속적인 동작을 인식하는 연구를 수행하였다(7). Chu 등은 근전도 신호로부터 선형 및 비선형 특징을 추출하여 동작 인식을 수행하였다(8). Hong 등은 발목 관절의 근전도 신호와 보행 운동의 관계를 확인하고 재활 로봇에 활용하고자 하는 연구를 수행하였다(9). Geng 등은 표면 근전도 신호의 이미지를 이용하여 동작을 인식하고자는 새로운 방법을 제시하였다(10). Kim 등은 근전도 신호를 이용한 손동작 인식 기법을 이용하여 한국 수화를 인식하고자 하는 연구를 수행하였다(11). 그러나, 실시간 동작 인식을 통한 사람과 기계의 인터페이스로 활용하기에는 측정 장치의 단순화 등 부족한 부분이 많이 있다.
따라서, 이 연구에서는 사용자의 손동작에 따른 근전도 신호를 측정하고, 측정된 신호에 대한 패턴 인식을 통하여 실시간으로 손동작을 분류하는 시스템에 대한 성능 평가를 수행한다. 사용자의 피부에서 근전도 신호를 측정할 수 있는 장치를 이용하여 6가지 손동작에 따른 근전도 신호를 측정하고, 측정된 신호에 대하여 특징을 추출한다. 추출된 특징들을 기계 학습법의 하나인 k-근접 이웃 알고리듬을 통하여 학습을 수행하고 분류 정확도를 확인한다. k-근접 이웃 알고리듬에서 k 값과 적용하는 거리 함수에 따른 분류 정확도를 확인한다. 5명의 피실험자의 근전도 신호를 측정하여 제안된 분류 알고리듬의 성능을 평가한다.
2. 근전도 측정
이 연구에서는 사용자의 표면 근전도 측정을 위해 Fig. 1에 나타낸 바와 같이 팔에 착용하여 사용하는 암밴드 형태의 상용 장치를 사용하였다(12). 사용된 근전도 측정 장치는 8채널의 근전도 센서가 장착되어 있으며, 측정된 데이터는 블루투스 무선 통신을 통해 실시간으로 컴퓨터로 전송되어 저장된다. 사용된 장치에는 3축 가속도, 3축 각속도, 3축 지자기 정보를 측정하는 관성 센서가 포함되어 있으나, 이 연구에서는 근전도 신호만을 사용하여 손동작을 인식하도록 하였다. 근전도 신호의 샘플링 주파수는 200 Hz로 설정되어 있으며, 측정된 신호는 전원에 의한 노이즈를 제거하기 위해 60 Hz 노치 필터를 통과한 후에 저장된다. Fig. 2에 나타난 바와 같이 근전도 측정 장치를 왼팔 팔꿈치 아래쪽에 착용하였다. 근전도 측정 장치가 착용된 부위는 손목을 굽히는 근육인 요측수근굴근(flexor carpi radialis), 척측수근굴근(flexor carpi ulnaris), 장장근(palmaris longus)과 손목을 펴는 근육인 장요측수근신근(extensor carpi radialis longus), 단요측수근신근(extensor carpi radialis brevis), 척측수근신근(extensor carpi ulnaris) 등이 위치한 곳이다.
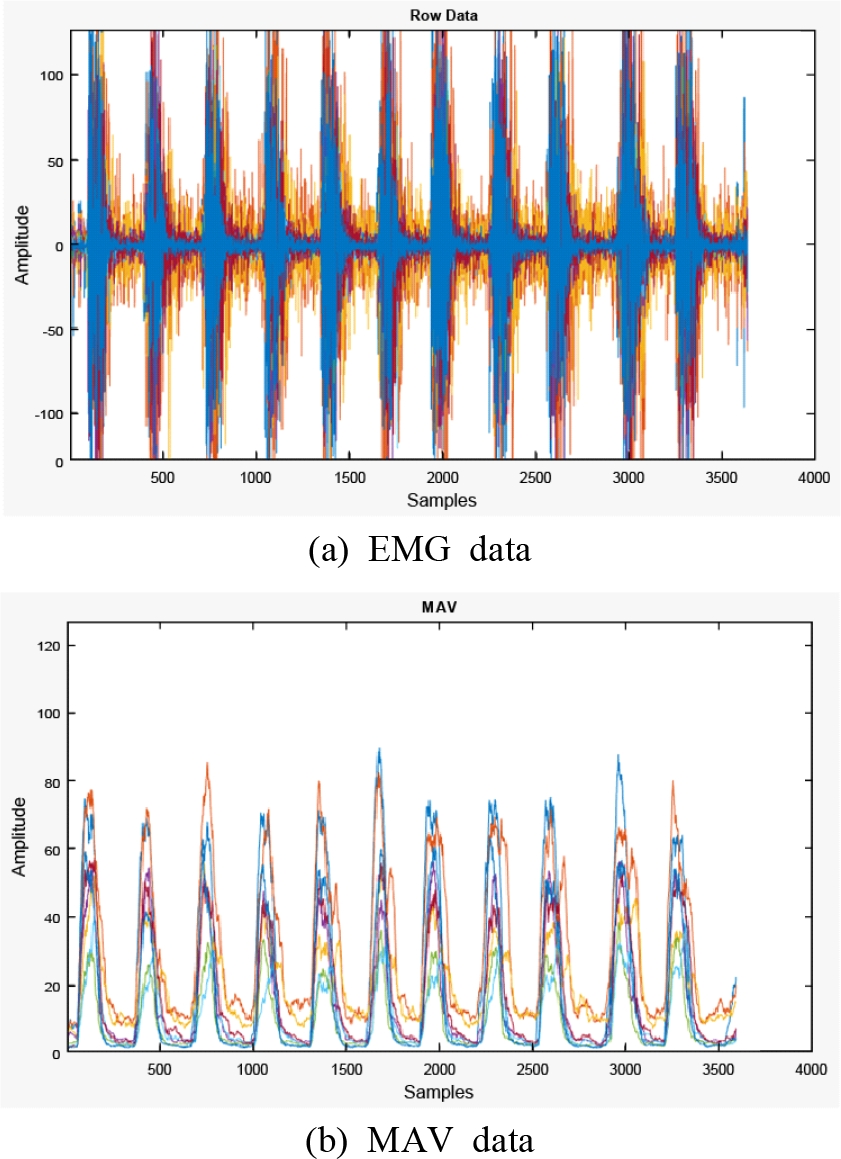
이 연구에서는 근전도를 측정하고 저장하기 위하여 MATLAB을 이용하였으며, 근전도 측정 장치 MYO와 MATLAB의 인터페이스를 위하여 오픈 소스 코드를 다운받고 수정하여 사용하였다(13). 실제 근전도 신호는 mV 단위로 측정이 되어 전기적 잡음 등에 민감하므로 증폭하여 사용하여야 한다. MYO는 근전도 신호의 미가공 원 데이터를 제공하지 않고 “activation”이라는 단위로 표현되는 -128에서 128 사이의 정수값을 제공하는데, 이는 측정된 신호를 증폭한 결과이다. MYO를 이용하여 실시간으로 측정된 근전도 신호를 Fig. 3(a)에 나타내었다. 이 연구에서는 Fig. 3(b)와 같이 사용자의 손동작에 따라 측정된 값의 평균절대값(mean, absolute value, MAV)을 특징값으로 실시간 출력하도록 하였다. 평균절대값은 다음과 같은 식으로 표현된다.
| (1) |
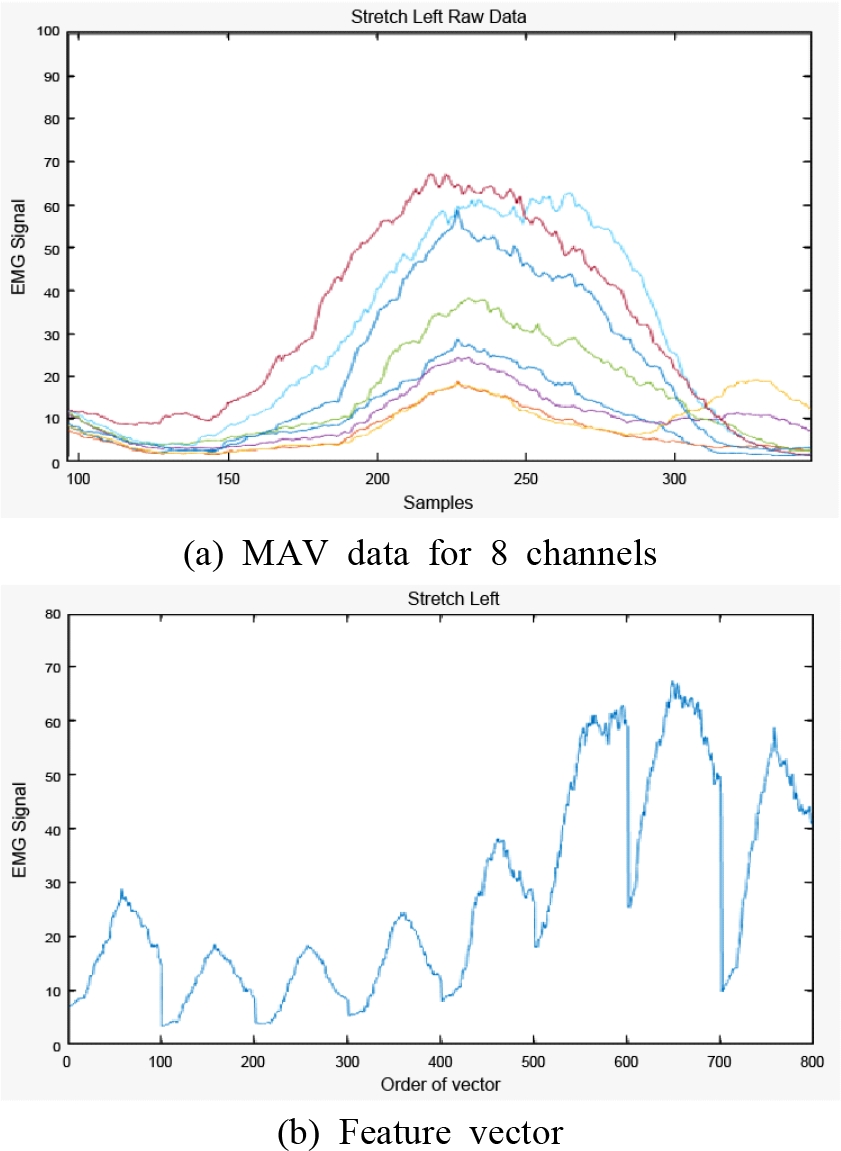
여기서 x(i)는 측정된 데이터이고, L은 윈도우의 크기로, 샘플링 주파수가 200 Hz이고, 0.5초 동안 윈도잉(windowing)하므로 L=100으로 계산하였다. 의도하지 않은 손의 움직임 또는 미세한 움직임에도 근전도가 측정되므로, 25를 임계값으로 정하여 측정된 값의 평균절대값이 25가 넘는 경우에 0.5초 동안 데이터를 저장하도록 하였다. Fig. 4(a)에 손바닥을 펴서 왼쪽으로 펴는 동작에 대하여 측정한 8채널 근전도 데이터의 평균절대값을 나타내었다. 각 동작에 대하여 다른 크기의 근전도 신호가 각 채널에서 측정되는 것을 확인할 수 있다. 이러한 데이터는 100 × 8 크기의 행렬로 저장된다. Fig. 4(a)의 근전도 신호를 채널 1번부터 채널 8번까지의 순서로 연결하여 하나의 특성 벡터로 정의하였으며, 이를 Fig. 4(b)에 나타내었다. 이러한 과정을 통하여 각 동작에 대하여 800 × 1 크기의 벡터 형태로 데이터가 저장된다.
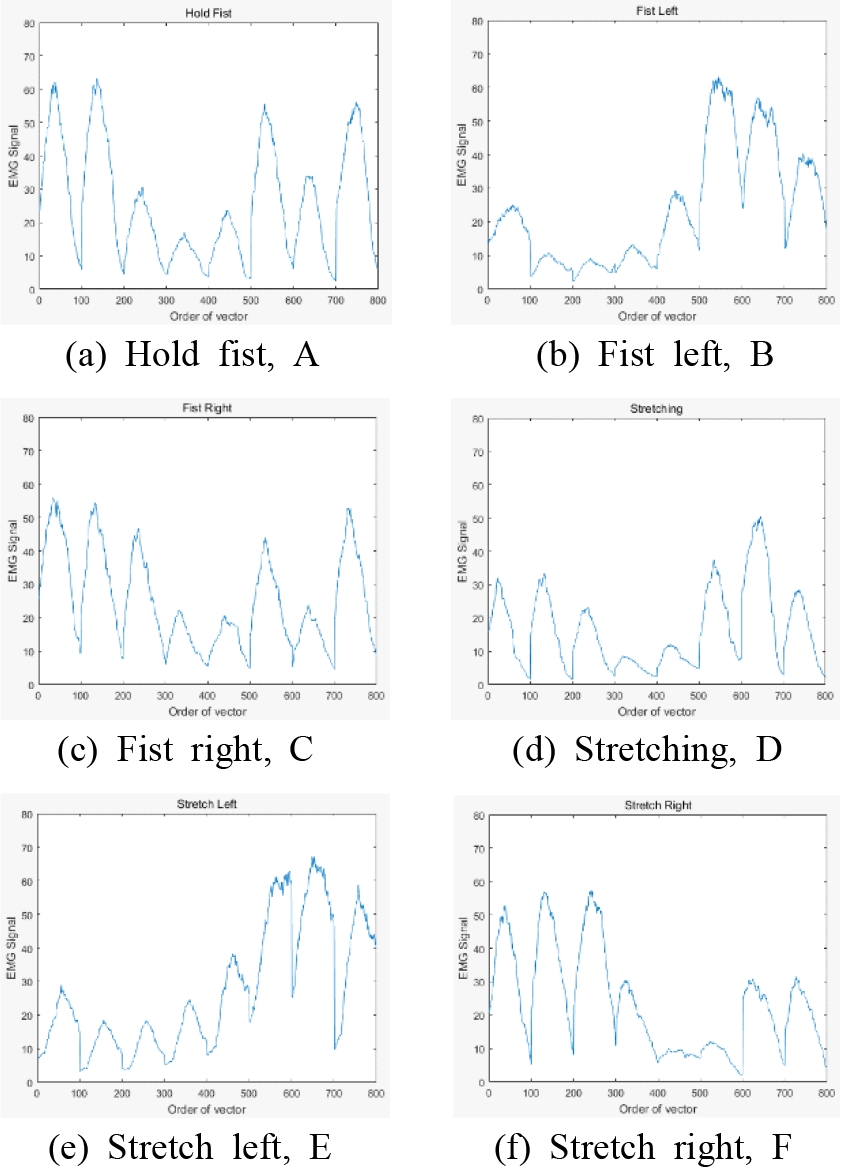
이 연구에서 인식한 6가지 손동작을 Fig. 5에 나타내었다. 주먹을 쥐는 동작, 주먹쥔 상태에서 왼쪽과 오른쪽으로 굽히는 동작, 손바닥을 펴는 동작, 손바닥을 편 상태에서 왼쪽과 오른쪽으로 굽히는 동작 등 6가지 동작이다. Fig. 5의 각 동작에 대해서 측정된 근전도 신호를 이용하여 추출한 6개의 특성 벡터는 Fig. 6에 나타내었다. 동작에 따라 사용하는 근육이 다르므로, 각 동작에 따라 8개의 근전도 센서에서 측정되는 신호가 각각 다르게 된다. 따라서 동작에 따라 명확하게 다른 특성 벡터가 획득된 것을 확인할 수 있으며, 이 특성 벡터를 이용하여 손동작을 인식하고, 분류 알고리듬을 통하여 어떤 동작이 수행되었는지 판별하게 된다.
3. 동작 인식 실험
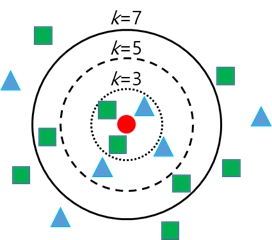
이 연구에서 근전도 신호의 패턴 분류를 위해 k-근접 이웃(k-nearest neighbor, k-NN) 분류 알고리듬을 이용하였다. k-근접 이웃 분류알고리듬의 기본 개념을 Fig. 7에 나타내었다. 가운데 원형 데이터가 자신의 클래스(class)를 확인하기 위해서 주위의 다른 데이터들의 클래스를 이용하는데, 주변에 가장 많이 존재하는 데이터의 클래스로 자신의 클래스를 결정하게 된다. 이 때 주변에서 몇 개의 데이터를 검토하는가에 따라 결과가 달라지게 되는데, Fig. 7에서는 3개의 데이터를 고려할 경우 원형 데이터는 자신의 클래스를 사각형으로 결정하게 되고, 5개의 데이터를 고려할 경우 자신의 클래스를 삼각형으로 결정하게 된다. k의 값에 따라 분류 클래스가 달라지거나 정확도가 변하게 되고, 과다적합(overfitting) 또는 과소적합(underfitting)이 발생할 수 있으므로, k에 따른 분류 정확도를 확인하여야 한다. 또한, 적용하는 거리 함수에 따라 분류 정확도가 달라지게 되는데, 이 연구에서는 유클리디언(eulidean), 코사인(cosine), 체비쇼프(chebyshev)의 세 가지 거리 함수를 고려하였고, 거리 함수에 따른 분류 정확도를 확인하였다. 세 가지 거리 함수는 다음과 같은 식으로 표현된다.
| (2) |
| (3) |
| (4) |
실험에는 5명의 실험자가 참가하였고, 실험자들의 정보를 Table 1에 나타내었다. 실험자들은 각자 동일한 위치에 근전도 측정 장치를 착용하고, 동일한 동작을 64회씩 반복하면서 근전도를 측정하고, 각 동작에 대하여 64개씩, 6개의 동작에 대하여 전체 384개의 근전도 데이터를 확보하였다. 이 연구에서는 MATLAB의 classification learner app을 이용하여 학습을 수행하였다(14). 실험자 A의 전체 384개의 측정 데이터를 이용하고, k값을 1, 3, 5, 7, 9로 변경하면서, 세 가지 거리 함수에 대한 분류 정확도를 Table 2에 나타내었다. k값이 5이고 체비쇼프 거리 함수를 사용한 경우를 제외하고는 모두 100 %의 분류 정확도를 갖는 것을 확인하였다.
실험자 A의 근전도 신호를 이용한 학습 결과를 바탕으로 손동작에 대한 분류 성능을 평가하였다. 동일한 동작에 대해 실험자 A의 근전도 신호를 다시 측정하여 각 동작에 대하여 64개씩, 6개의 동작에 대하여 전체 384개의 데이터를 추가로 확보하였다. 실험자 A의 동작 인식 결과를 Table 3에 나타내었다. k값이 1이고, 유클리디언 거리 함수를 사용할 경우 최대 95.8 %의 분류 정확도를 갖는 것을 확인할 수 있으며, 동일한 거리 함수의 경우 k값이 커짐에 따라 분류 정확도가 감소하였다. 동일한 k값에 대해서는 유클리디언 거리 함수를 사용할 경우 분류 정확도가 가장 높은 것을 확인할 수 있다. 학습 결과에 비해서는 분류 정확도가 다소 감소하지만, 유클리디언 거리 함수를 사용할 경우 90 % 이상의 분류 정확도를 갖는 것을 확인할 수 있다.
학습 데이터와 평가 데이터의 실험자가 다른 경우에 대한 동작 인식 평가를 수행하였다. 실험자 A의 근전도 신호를 이용한 학습을 바탕으로 실험자 B, C, D의 근전도 신호를 이용한 평가 결과를 Table 4에 나타내었다. 학습 데이터와 평가 데이터의 실험자가 다른 경우 최대 69.5 %, 최소 24.7 %의 분류 정확도를 가지며, 학습 데이터와 평가 데이터의 실험자가 동일한 Table 3의 결과와 비교해서 분류 정확도가 급격히 감소되는 것을 확인할 수 있다. 학습 데이터 수를 증가시킬 경우 분류 평가 결과가 향상되는지 확인하기 위하여, 실험자 A, C, D, E의 근전도 신호를 학습 데이터로 사용하고, 실험자 B의 근전도 신호를 평가 데이터로 이용한 경우의 분류 정확도를 Table 5에 나타내었다. 실험자 A, C, D, E의 근전도 신호를 이용한 학습 과정에서는 최대 99.1 %, 최소 97.3 %의 분류 정확도를 가지는 것을 확인하였다. 그러나, Table 5에 나타난 바와 같이 평가에서는 최대 67.7 %의 분류 정확도를 가지는 것을 확인하였다. 실험자 A의 근전도 신호만 학습 데이터로 사용하고, 실험자 B의 근전도 신호를 평가 데이터로 사용한 Table 4의 결과에서 최대 69.5 %의 분류 정확도를 갖는 것과 비교하여 분류 정확도는 크게 변하지 않았으며, 학습 데이터와 평가 데이터의 실험자가 다를 경우, 학습 데이터를 증가시키는 것만으로는 분류 정확도의 향상이 얻어지지 않는 것을 확인할 수 있다. 평가자의 데이터가 일부라도 학습 데이터에 포함되어 있는 경우에 대하여 분류 정확도가 향상되는지 확인하기 위하여 다른 평가를 수행하였다. 실험자 A, C, D, E의 근전도 데이터 1536개(384 × 4)와 실험자 B의 근전도 데이터 중 절반인 192개를 학습데이터로 사용하고, 실험자 B의 나머지 절반 데이터를 평가로 사용한 경우의 결과를 Table 6에 나타내었다. 유클리디언 또는 코사인 거리 함수를 사용한 경우 95 % 이상의 높은 분류 정확도를 갖는 것을 확인할 수 있다. Table 6의 결과로부터 학습 데이터를 일부 제공한 경우에는 테스트에서 분류 정확도가 높은 것을 확인할 수 있다.
4. 결 론
이 연구에서는 사용자의 표면 근전도 신호를 측정하고, 기계 학습법 기반의 패턴 인식 알고리듬을 적용하여, 손동작을 분류하는 방법에 대한 실험적 연구를 수행하였다. 착용 가능한 암밴드 형태의 8채널 근전도 신호 측정 장치를 이용하여 사용자의 손동작에 따른 근전도 신호를 측정하였다. 측정된 근전도 신호로부터 절대평균값을 특징으로 추출하여 패턴 인식을 수행하였다. 근전도 신호에 따른 손동작 분류를 위해서 기계 학습법의 하나인 k-근접 이웃 알고리듬을 적용하였으며, k값과, 거리 함수에 따른 분류 정확도를 확인하였다. 동일한 실험자의 근전도 신호를 이용하여 학습하고, 평가한 경우에는 최대 95.8 %의 높은 분류 정확도를 가지나, 학습과 평가 데이터의 실험자가 다른 경우에는 최대 69.5 %로 분류 정확도가 감소하는 것을 확인하였다.
이 연구의 한계점 중 하나는 상용 측정 장치를 활용하여 측정 샘플링 주파수를 변경할 수 없고, 다소 많은 8개의 근전도 센서를 이용한 것으로 파악된다. 다음 단계 연구에서는 근전도 센서의 수를 줄이고, 암밴드 형태의 측정 장치를 직접 개발할 예정이다. 또한, 사용자가 측정 장치를 착용하는 위치가 다른 경우, 특성 벡터 형태가 달라지게 되므로, 분류 정확도가 낮아질 것으로 예상된다. 센서 위치에 대해 강건한 알고리듬에 대한 검토가 필요하다. 동일한 사람의 동일한 동작에 대해서도 다른 크기의 근전도 신호가 측정될 수 있으므로, 이를 보완하기 위하여 표준화 과정을 적용을 검토할 예정이다.
이 연구를 통해 근전도 신호만을 이용하여 다양한 손동작을 인식할 수 있음을 확인하였으며, 다음 단계에서는 실제 슬레이브 로봇의 동작 제어를 통해 제안된 시스템의 우수성을 확인할 예정이다. 인공 신경망 등 다른 알고리듬을 적용한 연구도 수행될 것이며 이러한 연구는 게임 인터페이스, 로봇 의수 등에도 효과적으로 활용될 수 있을 것으로 기대된다.
Acknowledgments
A part of this paper was presented at the KSNVE 2018 Annual Spring Conference
이 논문은 2017년도 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(NRF-2017R1C1B2012207).
References
- http://www.nintendo.co.kr/Wii/wii/thebody.php
- http://support.xbox.com/ko-KR/browse/xbox-360/accessories/Kinect
- Guerra-filho, G. B., (2005), Optical Motion Capture: Theory and Implementation, Journal of Theoretical and Applied Informatics (RITA), 12(2), p61-89.
- http://www.xsens.com
- http://www.virtuix.com
-
Francesco, V. G. T., Ramos, A., Fahmy, A., Acharya, S., Etienne-cummings, R., and Thakor, N. V., (2009), Decoding of Individuated Finger Movements Using Surface Electromyography, IEEE Transactions on Biomedical Engineering, 56(5), p1427-1434.
[https://doi.org/10.1109/TBME.2008.2005485]

-
Englehart, K., Hudgin, B., and Parker, P. A., (2001), A Wavelet-based Continuous Classification Scheme for Multifunction Myoelectric Control, IEEE Transactions on Biomedical Engineering, 48(3), p302-311.
[https://doi.org/10.1109/10.914793]

-
Chu, J.-U., Moon, I., and Mun, M.-S., (2006), A Real-time EMG Pattern Recognition System Based on Linear-nonlinear Feature Projection for a Multifunction Myoelectric Hand, IEEE Transactions on Biomedical Engineering, 53(11), p2232-2239.
[https://doi.org/10.1109/TBME.2006.883695]

-
Hong, J. H., Chun, H. Y., Jeon, J. H., Jung, S. I., Kim, J. O., and Park, K. H., (2011), Experimental Study on Walking Motion by Ankle Electromyograms, Transactions of the Korean Society for Noise and Vibration Engineering, 21(10), p934-939.
[https://doi.org/10.5050/KSNVE.2011.21.10.934]

-
Geng, W., Du, Y., Jin, W., Wei, W., Hu, Y., and Li, J., (2016), Gesture Recognition by Instantaneous Surface EMG Images, Scientific Reports, 6, p36571.
[https://doi.org/10.1038/srep36571]

-
Kim, J. S., Jang, W., and Bien, Z., (1996), A Dynamic Gesture Recognition System for the Korean Sign Language, IEEE Transactions on Systems, Man and Cybernetics-Part B: Cybernetics, 26(2), p354-359.
[https://doi.org/10.1109/3477.485888]

- http://www.myo.com
- http://github.com/Lif3line/Myo-MATLAB-Interface-EMG-GYRO-ACCEL/find/master
- http://kr.mathworks.com/products/statistics/classification-learner.html

Jung Woo Sohn received his Ph.D. degree in the Department of Mechanical Engineering from Inha University in 2008. He is now working as an assistant professor in the Department of Mechanical Design Engineering of Kumoh National Institute of Technology. He has interest on the design and control of smart structures and systems.