입력 성형기와 가속도 피드백을 이용한 단진자 진동 제어
© The Korean Society for Noise and Vibration Engineering
Abstract
In this study, we developed a method to suppress the residual vibration from a pendulum when the trolley moves to a certain position. In general, an input shaping technique is applied to reduce the vibration of the pendulum after the trolley moves. The zero vibration input shaping technique can be used to effectively suppress the residual vibration of the pendulum after operation. However, because the input shaping technique is an open-loop control, it is difficult to suppress the vibration caused by disturbances. To solve this problem, a control method consisting of the input shaping technique and acceleration feedback control was developed to suppress the residual vibration under disturbance conditions. A testbed was designed to validate the proposed method. Dynamic models of testbed were derived, and a numerical simulation was performed. The stability of the acceleration feedback controller was mathematically proven. It was proved both theoretically and experimentally that the proposed method can suppress the residual vibration of the pendulum effectively.
Keywords:
Pendulum Swing, Input Shaping, Acceleration Feedback, Vibration Experiment키워드:
단진자 스윙, 입력 성형기, 가속도 피드백, 진동 실험1. 서 론
부둣가나 산업 현장에서 크레인을 이용하여 짐 또는 컨테이너를 옮길 때 진동이 발생할 수 있다. 물건이 계속 흔들릴 경우 안정적인 화물 운송이 어려울 뿐만 아니라 심할 경우 다른 구조물과 충돌하는 사고가 발생할 수 있다. 화물 운송 시 발생하는 진동을 최대한 줄이기 위해 매우 천천히 물건을 이동시키는 방법을 쓰곤 하는데, 이럴 경우 작업 시간이 길어져서 작업 효율이 떨어지는 문제가 있다. 이러한 문제를 해결하기 위해 크레인을 통해 짐을 빠르게 이동시키면서, 동시에 이동시 발생하는 진동의 억제 연구가 오래전부터 수행되어왔다.
Smith(1,2)는 zero vibration input shaper(ZVIS)에 대한 개념에 대해 최초로 소개하였다. Singer and Seering(3)은 ZVIS의 강건성의 향상을 위해 zero vibration derivative(ZVD)와 zero vibration derivative derivative(ZVDD) input shaper를 개발하였다. Input shaper 기법을 바탕으로 실제 구현에 관한 연구들이 진행되었다. Hyde and Seering(4)은 기존의 ZVD나 ZVDD기법을 기반으로 구조물의 다중 모드 진동 저감을 위한 입력 성형 방법을 개발하였다. Murphy and Watanabe(5)는 기존에 개발된 입력 성형 기법을 기반으로 실제 디지털 성형 필터(digital shaping filter)를 구현하여 입력 성형 기법의 성능을 검증한 바 있다. Tzes and Yurkovich(6)는 유연 구조물의 진동을 억제하기 위해 frequency domain identification scheme을 적용한 능동 입력 성형 기법을 개발하였다. Kwak et al.(7)은 회전 유연보 작동시 발생하는 진동을 억제하기 위해 bang-bang 제어기와 입력 성형기를 결합한 제어 방법을 제안하였다.
기존의 입력 성형 방법 중 ZVDD나 zero vibration and triple derivative(ZVDDD) 기법은 ZV나 ZVD에 비해 둔감도(insensitivity)가 개선되었으나, 작동 시간이 길어진다는 문제점이 있다. 이를 개선하기 위해 ZVD와 동일한 작동 시간을 가지며, 더 나은 둔감도를 가지는 extra-insensitive(EI) 입력 성형기(8,9)가 개발되었다. 이외에도 입력 성형 방법의 성능 개선을 위해 specified-insensitivity(SI) 입력 성형 방법(10)과 modified input shaping(MIS) 기법(11) 등이 개발되었다.
다중 모드를 가지는 유연 구조물의 운행 중 발생하는 다중 모드 진동을 억제하기 위한 연구(5,6)들이 수행되었는데, 부드러운 입력(smooth command)을 적용하여 고차 모드가 가진되지 않도록 하는 입력 성형 방법을 개발하였다(12,13).
입력 성형 방법에 대한 많은 연구가 진행됨에 따라 다양한 기법들이 개발되었고, 각각의 기법들에 대해 효율과 둔감도를 기반으로 하는 성능 분석 방법이 제시되었다(14).
입력 성형 기법은 기본적으로 개루프(open-loop) 제어 방식인데, 외란이 작용하는 환경하에서는 성능이 저하되는 문제가 있다. 이러한 문제를 해결하기 위해 입력 성형 기법과 피드백 제어기를 결합한 방식이 제안되었다(15). Zuo et al.(16)은 개루프 제어 기반의 입력 성형 방법의 한계점을 극복하기 위해 linear quadratic regulation(LQR) 방법을 결합한 형태의 제어 방법을 제안하였다. Kapila et al.(17)은 full-state feed-back 제어 방법과 입력 성형 기법을 결합하여 유연 구조물의 진동 문제를 해결하였다. 이외에 크레인에 바람과 같은 외란이 가해져서 발생하는 진동을 억제하는 연구도 수행되었다(18).
현재까지 구조물 작동 후 발생하는 잔여 진동을 억제하기 위해 입력 성형 방법을 포함하여 다양한 제어 기법이 개발되었다. 하지만, 이러한 방법들의 경우 실제 구현하기에는 복잡하다는 문제가 있다. 이에 따라 이 연구에서는 복잡도가 높지 않고, 강건성이 검증된 ZVIS 방법과 가속도 피드백 제어 방법을 결합한 제어 알고리듬을 제안하였다. 이를 위해 이 연구에서는 단진자가 설치된 대차를 구동할 수 있는 실험장치를 제작하고 타당한 동적 모델을 구축하였다. 그리고 제안한 제어 알고리듬의 효용성을 확인하기 위하여 동적 모델을 활용한 수치 계산을 수행하였고, 제안한 방법의 실제 시스템에서의 성능을 확인하기 위해 진동 제어 실험을 수행하였다. 실험을 통해 외란이 가해지는 경우에도 제안한 알고리듬을 통해 효과적으로 진동을 억제할 수 있음을 확인하였다.
2. 실험 장치 구성
이 연구에서는 단진자가 달려 있고, 좌우로 이동 가능한 대차로 구성된 실험장치를 Fig. 1과 같이 제작하였다.
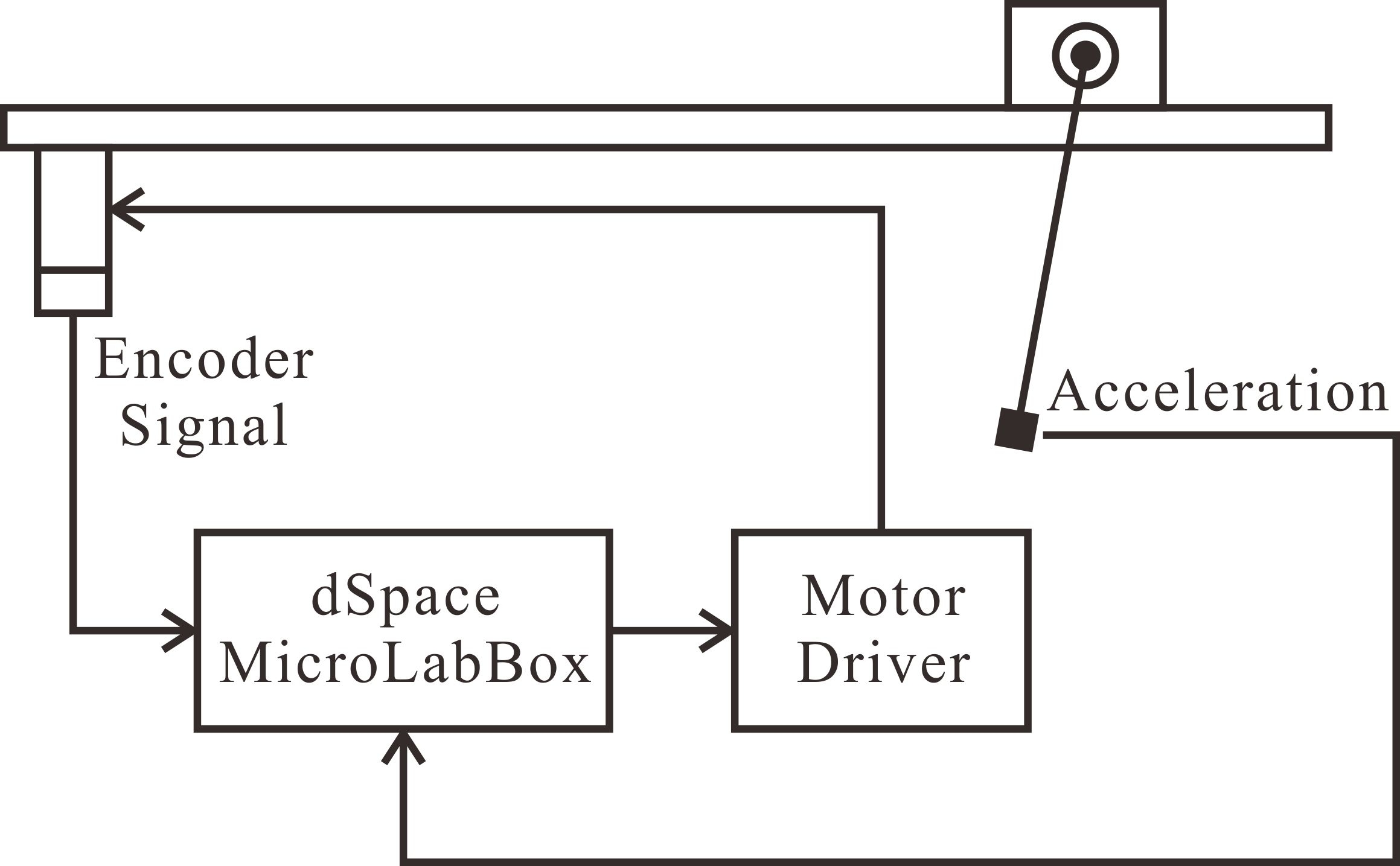
실험을 위해 구성한 장비들의 구성도는 Fig. 2에 나타내었다. 대차를 구동하기 위해 엔코더가 부착된 DC 모터(D&J WITH, IG-32PGM+Encoder 02TYPE, 1/5 Gear ratio)를 사용하였다. 그리고 모터를 회전시켜서 대차를 좌우로 이동시키기 위해 DC 모터를 레일 끝에 부착한 다음 모터 축에 풀리를 연결하였다. 그리고 벨트를 대차에 부착하여 DC 모터로 좌우로 움직일 수 있는 시스템을 구성하였다. 벨트와 풀리의 피치는 3 mm이다. 대차를 좌우로 이동시키기 위해 W rail (Igus, Drylin, W-10-40-1000)를 사용하였다. DC 모터 구동을 위해 모터 드라이버(sabertooth, dual 12A motor driver)를 사용하였다. 대차를 변위 제어하기 위해서 DC 모터에 부착된 엔코더 값을 피드백 받아서 제어를 수행하였다. 모터의 변위 제어를 위해서 PID 제어기를 적용하였다. 대차에는 단진자 각도를 측정하기 위해 엔코더(autonics, E30S-1000-3-2MJ)를 설치하였다. 또한 단진자의 각가속도를 계측하기 위해 가속도센서(PCB, 393B31)를 단진자 끝에 매달았다. 또한 플레이트를 부착하여 바람의 영향을 받을 수 있도록 하였다.
대차를 구동시키기 위해서 이 연구에서는 Simulink 소프트웨어를 이용하여 프로그램을 구현하였다. 대차를 이동시키기 위해 변위 명령을 입력하면, 대차를 구동하는 모터에 부착된 엔코더의 신호와 비교한다. 비교하여 계산된 에러 값을 이용하여 PD 제어를 통해서 모터 위치 제어를 위한 제어 신호를 생성하도록 하였다. 그리고 단진자의 각도와 각가속도를 계측하기 위해 엔코더 신호 및 가속도계 신호를 추가로 입력받았다.
3. 이론 모델 유도
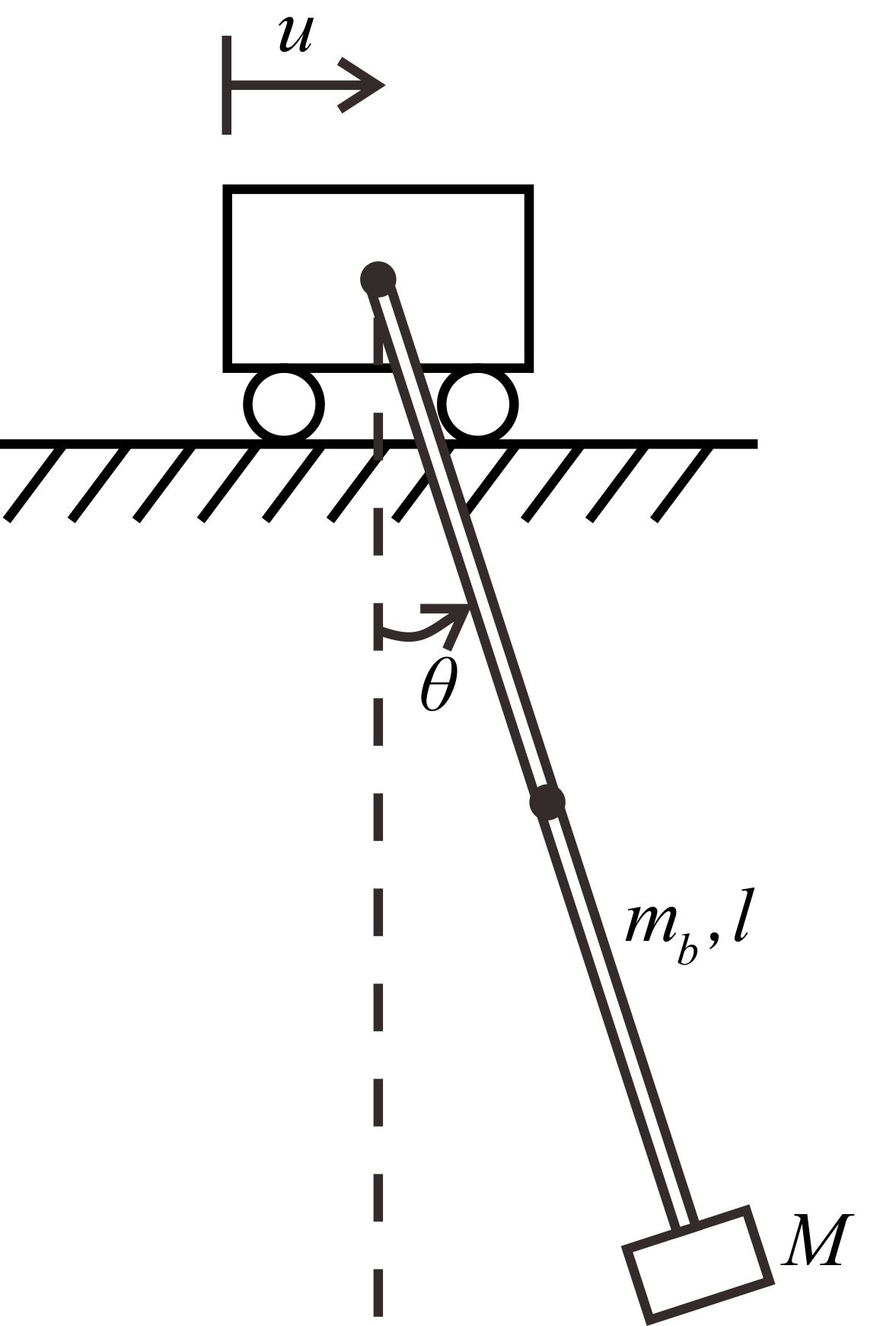
이 연구에서는 앞 절에서 설명한 실험장치를 기준으로 구조물의 동적 모델링을 수행하였다. Fig. 3은 대차와 단진자를 대상으로 한 구성도를 나타낸다.
여기서 l는 대차의 중심에서 단진자 끝의 질량 중심까지의 거리를 나타내며, mb는 봉의 무게를 나타낸다. 그리고, θ는 단진자의 각도를 나타내며, u는 대차의 변위를 나타낸다. M은 단진자 끝의 무게를 나타낸다.
운동 에너지와 위치 에너지는 각각 다음과 같다.
| (1) |
| (2) |
θ가 1보다 충분히 작다고 가정했을 때, 라그랑주 방정식을 통해 운동방정식을 다음과 같이 유도할 수 있다.
| (3) |
| (4a) |
| (4b) |
식 (3)의 양변을 Mt로 나누면 다음과 같다.
| (5) |
여기서, g = Ut/Mt이며, ζ와 ωn는 각각 단진자의 감쇠비와 고유진동수를 나타낸다.
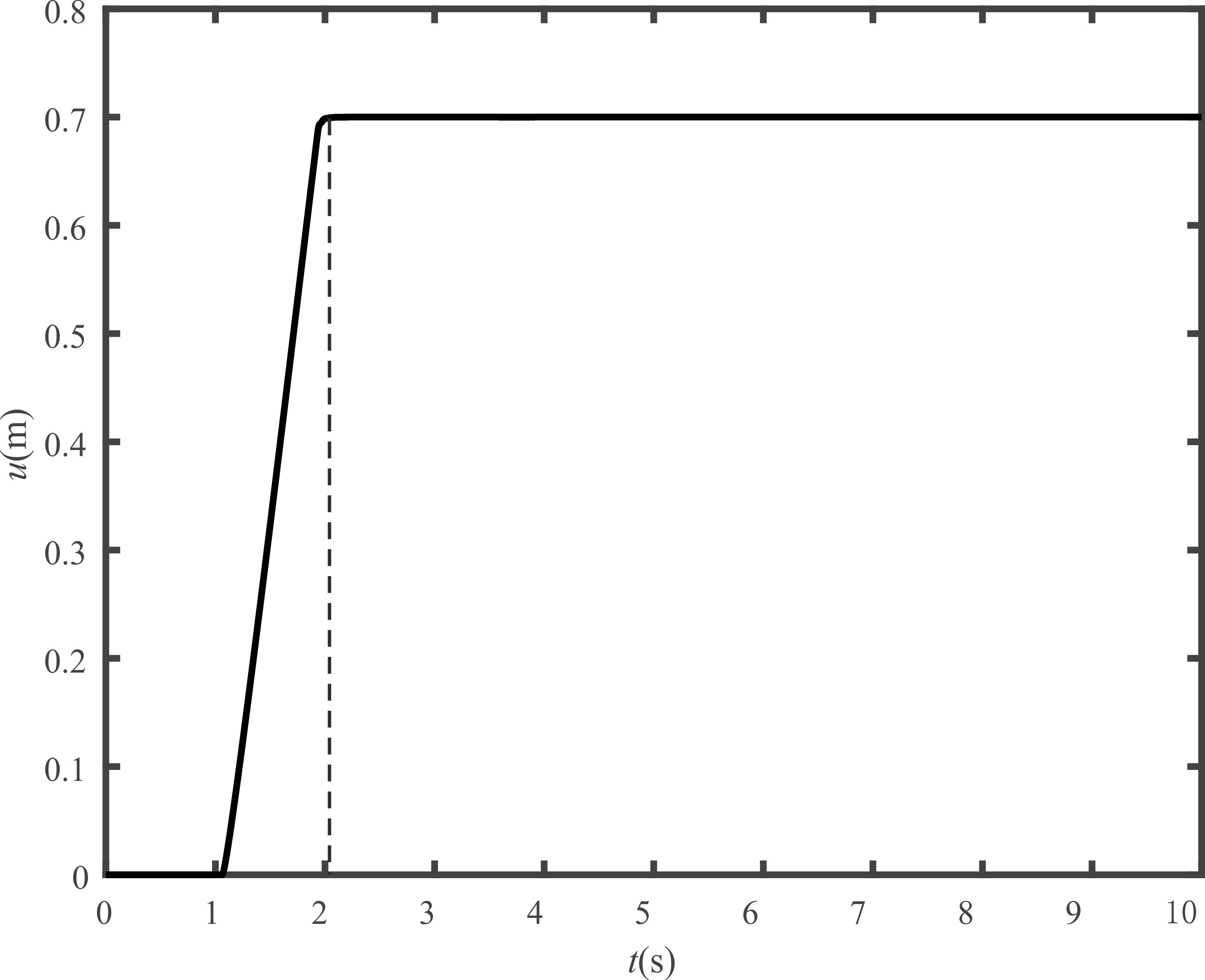
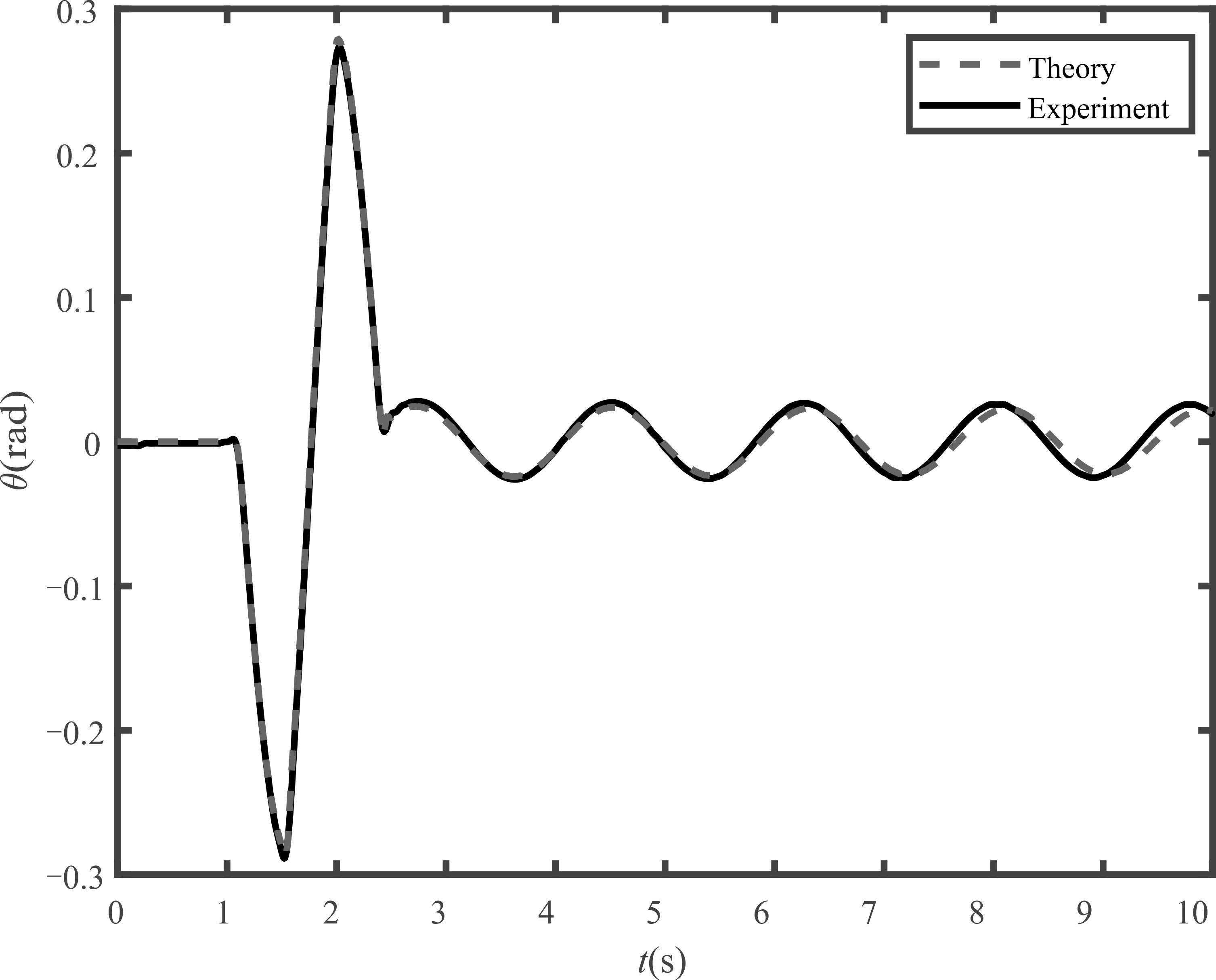
이 연구에서 유도한 동적 모델링의 타당성 검증을 위해 수치 계산과 실험을 수행하였다. 대차가 Fig. 4와 같이 움직였을 경우에 단진자의 각도를 동적 모델을 이용하여 계산하였으며, 실험을 통해 실제 각도를 계측하고 서로 비교하였다. 대차가 목표 지점에 도달한 시간은 2.1초이다.
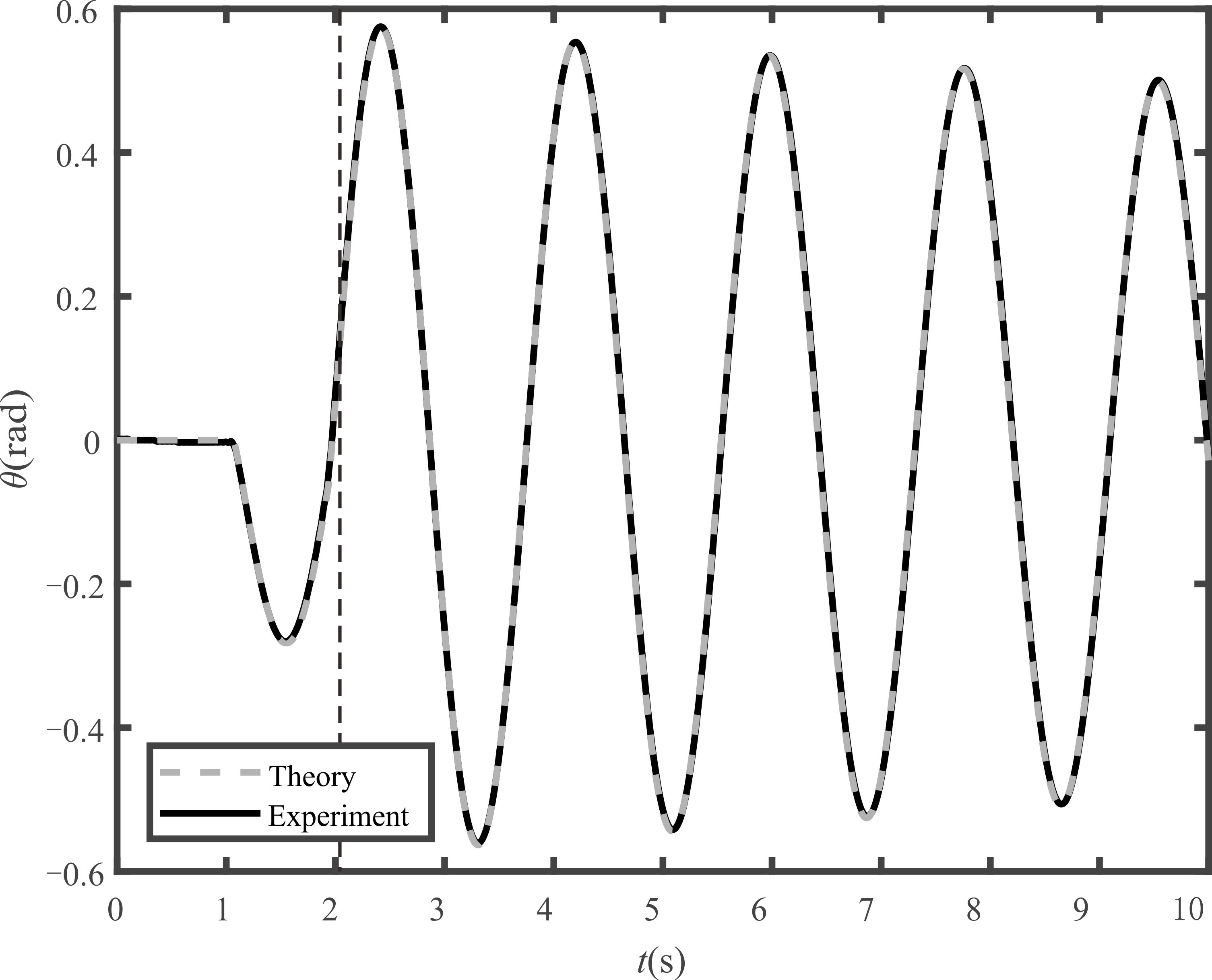
이론 결과와 실험결과에서의 단진자의 각도를 서로 비교하여 Fig. 5에 나타내었으며, 유도한 동적 모델링의 타당성을 입증하였다. 수치 계산을 위해 Table 1의 매개변수들을 사용하였다. 감쇠비는 실험을 통해 측정된 값이다.
4. Zero Vibration Input Shaper
이 연구에서는 대차가 이동한 후 발생하는 잔여 진동을 줄이기 위해 zero vibration input shaper(ZVIS)를 고려하였으며, 다음과 같이 쓸 수 있다.
| (6) |
| (7) |
여기서, δ(t)는 dirac delta 함수이며, , 이다.
위에서 구한 ZVIS 함수와 대차를 이동시키기 위한 기존의 입력 신호를 convolution integral해서 나온 입력 성형된 신호를 적용할 경우 단진자의 잔여진동을 억제할 수 있다.
5. 잔여 진동 제어를 위한 제어기 설계
입력 성형 방법만을 적용할 경우 구조물에 바람이나 구조 진동 등에 의한 외란이 가해질 때 발생하는 잔여 진동에는 취약하다. 이에 따라 이 연구에서는 외란이 가해지는 상황에서 발생하는 단진자의 잔여 진동을 줄이기 위해 가속도 피드백 제어기 acceleration-input position-output(AIPO)를 다음과 같이 제안하였다.
| (8) |
여기서, ξc 는 제어기의 감쇠비이며, gc는 제어 이득 값을 나타낸다. AIPO 제어기는 단진자의 가속도 응답을 피드백 받아 잔여 진동을 억제하도록 만드는 대차의 변위를 생성한다.
제어기를 나타내는 식 (8)을 실제로 구현하기 위해 다음과 같이 전달 함수로 나타낼 수 있다.
| (9) |
식 (9)는 가속도를 피드백 받아서 구조물의 진동을 제어하기 위해 개발된 negative acceleration feedback (NAF) 제어기(19)와 동일한 형태를 가진다.
이 연구에서 제안한 제어기의 안정성 평가를 수행하였다. 대차-단진자 장치의 동적 모델 식 (5)를 라플라스 변환하여 다시 나타내면 다음과 같다.
| (10) |
| (11) |
Routh-Hurwitz criteria를 적용하여 구해진 제어기의 안정 조건은 다음과 같다.
| (12) |
6. 실 험
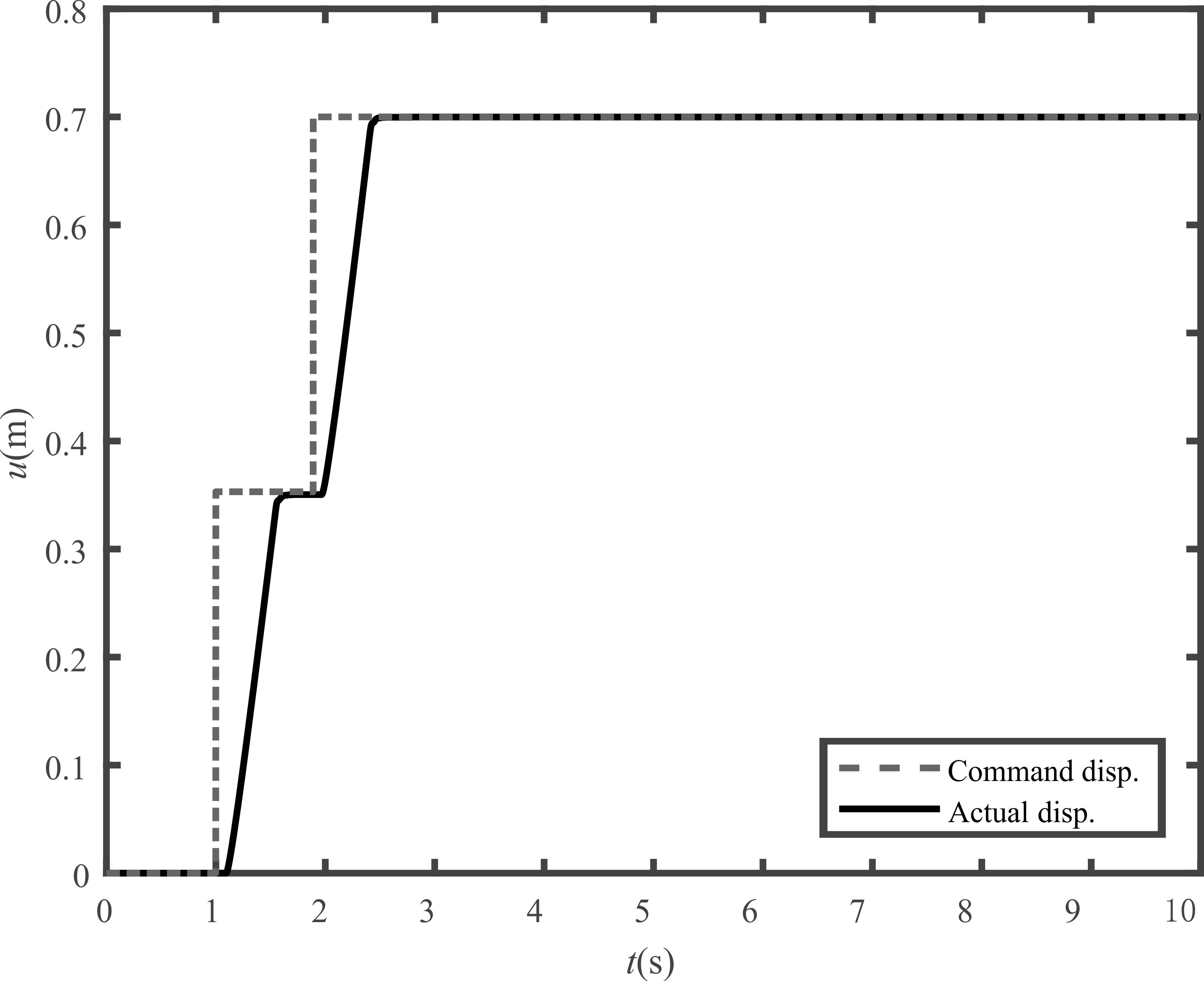
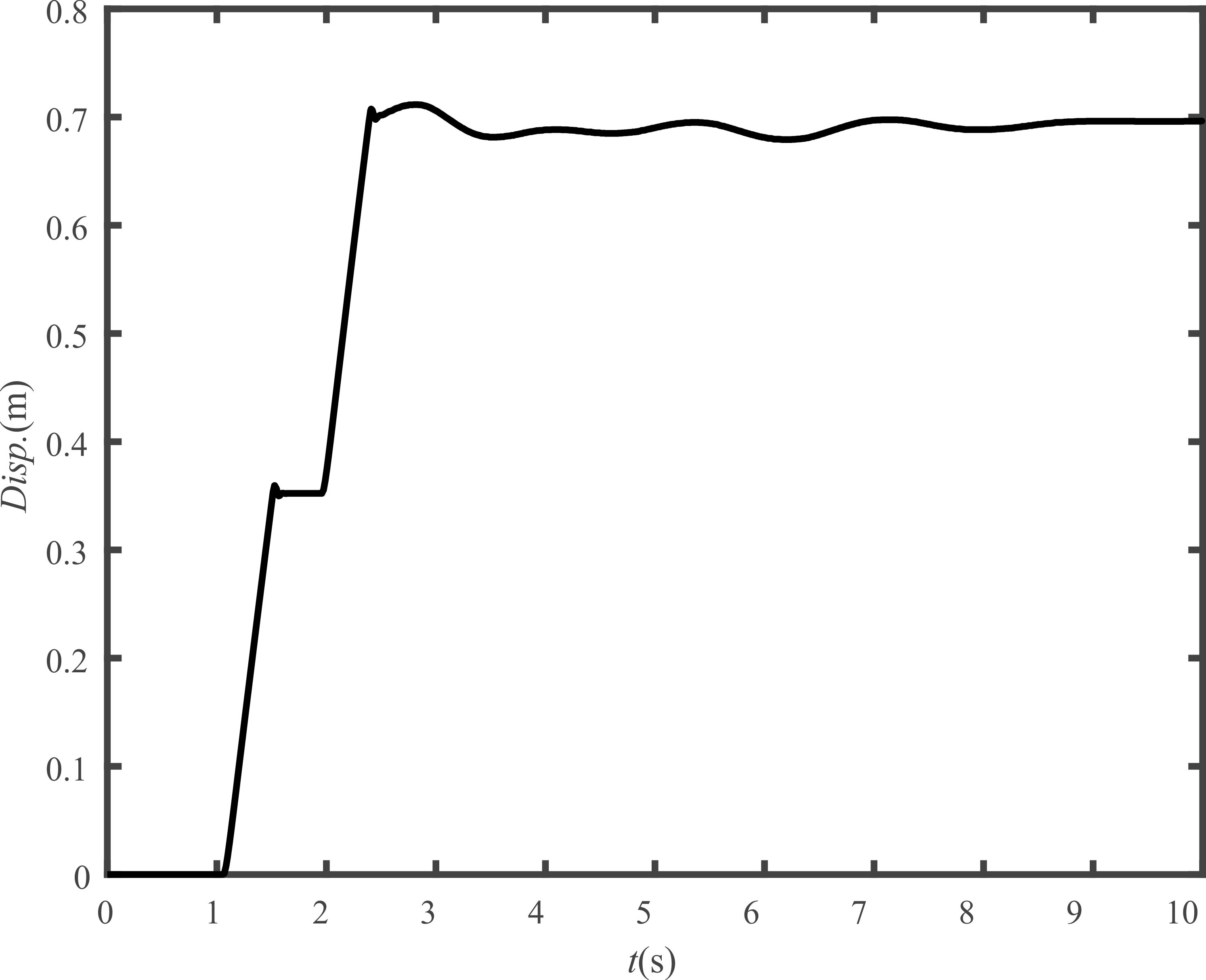
이 연구에서는 제안한 진동 제어 알고리듬의 효용성을 확인하기 위해 실험장치를 이용하여 실험을 수행하였다. ZVIS를 통해 구해진 입력 성형된 신호는 Fig. 6의 점선과 같은데, 이러한 명령을 모터에 줄 경우 모터 성능의 한계로 인해 그래프의 실선처럼 이동하게 된다.
Fig. 4와 같이 단순 램프 입력을 통해 대차를 0.7 m 지점까지 최대 속도로 이동시킬 경우 Fig. 5처럼 단진자의 잔여 진동이 매우 크게 발생한다. 하지만, ZVIS 기법을 적용할 경우 Fig. 7처럼 잔여 진동이 현저하게 감소하는 것을 확인할 수 있다.
ZVIS 방법을 적용하면 대차 이동 시 발생하는 단진자의 잔여 진동을 매우 효과적으로 억제할 수 있다. 하지만, 입력 성형 방법의 경우 개루프 제어 방법이다 보니 외란이 시스템에 가해질 경우에 발생하는 진동을 억제하는 것이 불가능하다. 이 연구에서는 이러한 외란 조건하에서 진자 운동하는 구조물의 진동을 억제하기 위해 가속도를 피드백 받는 제어기 AIPO를 적용하여 실험을 통해 그 효과를 입증하였다.
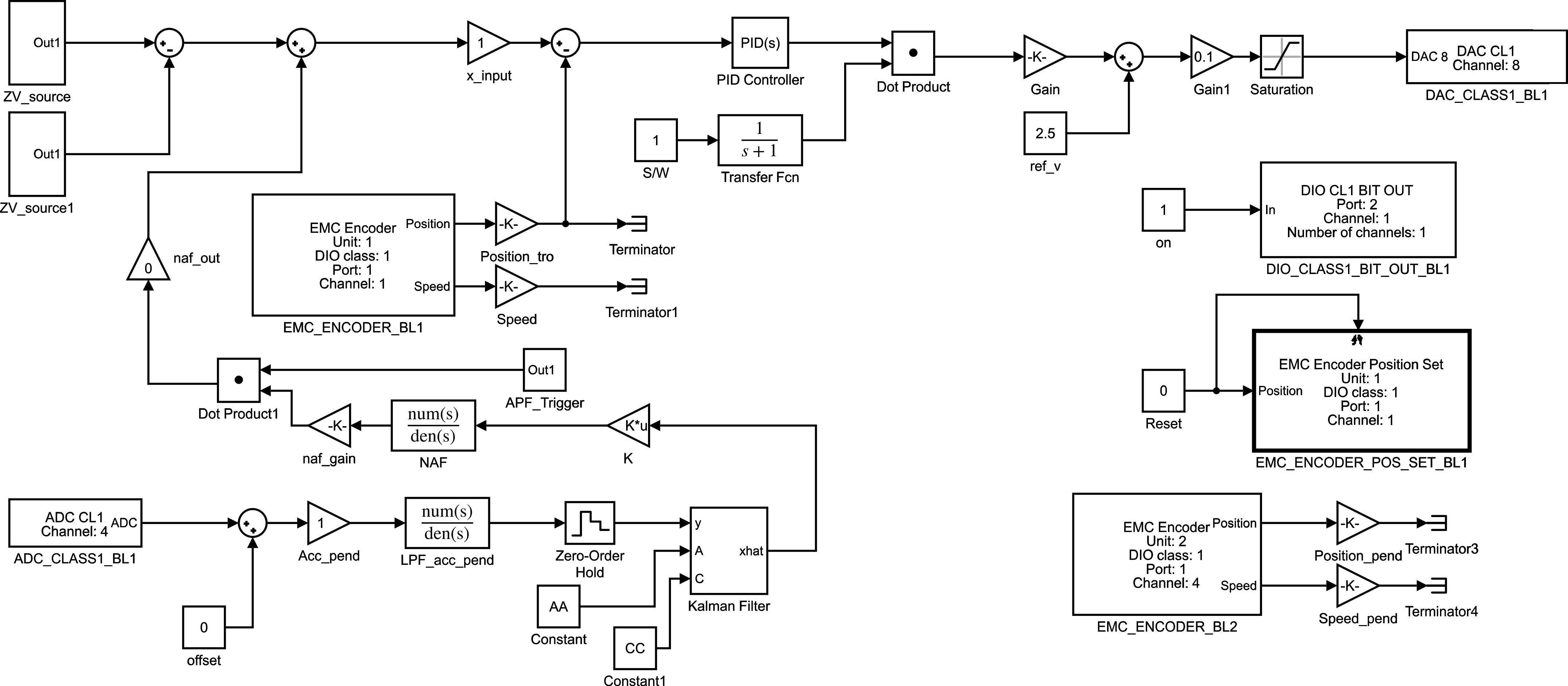
가속도 피드백 제어기를 추가한 제어기를 구현하기 위해 Simulink 소프트웨어로 Fig. 9와 같은 블록 다이어그램을 제작하였다. 가속도 피드백 제어기를 단진자의 각도 값이 나오는 부분 다음에 추가하였다. 가속도 피드백 제어기에 의해 생성된 제어 신호 변위는 대차의 변위 입력단에 더하도록 하였다. 즉 ZVIS에 의해 생성된 신호에 제어 신호가 더해지게 된다. 그리고 가속도 피드백 제어기의 신호는 대차의 이동이 완료된 다음에 적용되도록 하였다. AIPO 제어기는 전달 함수 형태로 구현하였다. 제어기에서의 감쇠비 ζc는 0.3, 제어 이득 gc는 1000으로 각각 설정하였다. 감쇠비를 0.3으로 설정한 이유는 제어기가 정확하게 튜닝되지 않더라도 제어력을 유지할 수 있도록 하기 위함이다. 그리고 제어 이득은 최적의 제어 성능이 나오는 값을 휴리스틱 방법을 통해 산출하였다.
블로워 홴으로 단진자에 바람을 가하여 시스템에 불안정성을 주었다. 외란 조건하에서 단진자 진동 제어를 위한 대차의 변위는 Fig. 10과 같다. 목표 지점까지 이동 후 잔여 진동을 억제하기 위해 추가적으로 이동한 것을 확인할 수 있다.
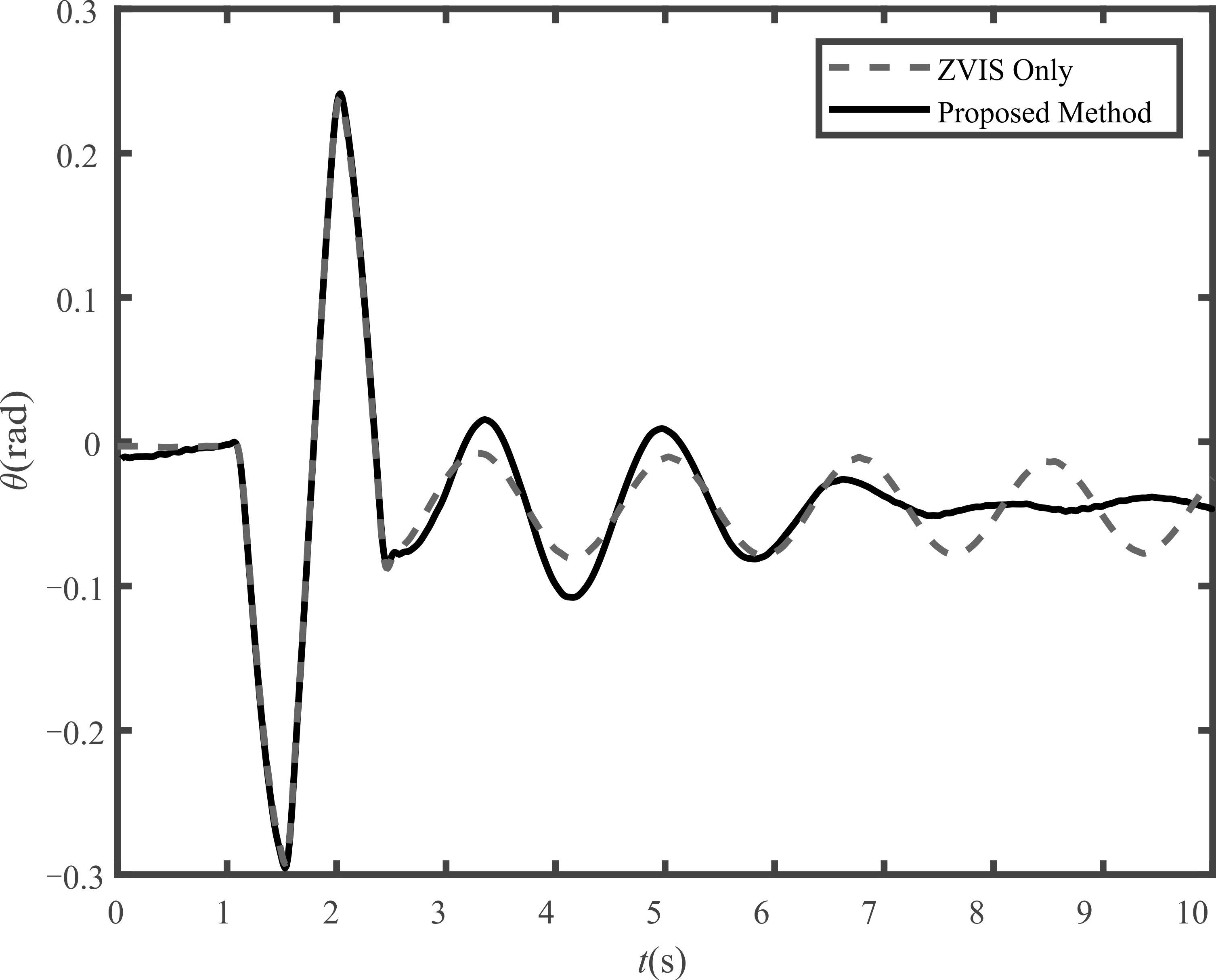
이 연구에서 개발한 제어기를 적용한 경우 단진자의 시간에 따른 각도는 Fig. 8과 같다. 피드백 제어를 할 경우 약 두 주기 안에 진동이 억제되는 것을 확인할 수 있다. ZVIS만 적용하였을 경우 잔여 진동이 크게 발생함을 확인할 수 있다. 하지만, ZVIS와 가속도 피드백 제어기를 함께 적용하면 잔여 진동이 매우 효과적으로 억제된다.
7. 결 론
이 연구에서는 외란 조건하에서 대차가 이동할 때 발생하는 단진자의 진동을 억제하기 위한 제어 방법을 개발하였다. 이를 위해 DC 모터로 구동되는 풀리 벨트 메커니즘을 통해 대차를 운행하고, 단진자의 각도를 엔코더를 통해 계측할 수 있는 실험장치를 제작하였다. 제작된 실험장치를 대상으로 이론 모델을 유도하였으며, 수치 계산과 실험결과를 통해 유도한 이론 모델이 타당함을 입증하였다. 그리고 대차가 이동한 후 발생하는 단진자의 잔여 진동을 억제하기 위해 가속도 피드백 제어기를 개발하였으며, 제안한 제어기에 대한 안정성 평가를 수행하였다.
ZVIS와 가속도 피드백 제어기를 결합한 단진자의 진동 억제 방법을 실제로 구현하고, 실험을 수행하였다. 이 연구에서는 단진자에 바람을 가하여 시스템의 불안정성을 야기시켰다. ZVIS만을 이용할 경우 대차가 특정 지점까지 이동한 후 잔여 진동이 매우 크게 나타남을 확인하였다. 하지만, ZVIS와 가속도 피드백 제어기를 함께 적용할 경우 잔여 진동이 매우 빠르게 억제되는 것을 확인할 수 있었다. 실험결과를 통해 이 연구에서 제안한 피드백 제어기가 외란 조건에서도 진동을 억제할 수 있음을 확인하였다.
Acknowledgments
A part of this paper was presented and selected as one of best papers at the KSNVE 2018 Annual Spring Conference
References
-
Smith, O. J. M., (1957), Posicast Control of Damped Oscillatory Systems, Proceedings of the IRE, 45(9), p1249-1255.
[https://doi.org/10.1109/JRPROC.1957.278530]

- Smith, O. J. M., (1958), Feedback Control Systems, McGraw-Hill, New York, U.S.A.
-
Singer, N. C., and Seering, W. P., (1990), Preshaping Command Inputs to Reduce System Vibration, Journal of Dynamic Systems, Measurement, and Control, 112(1), p76-82.
[https://doi.org/10.1115/1.2894142]

-
Hyde, J. M., and Seering, W. P., (1991), Using Input Command Pre-shaping to Suppress Multiple Mode Vibration, Proceedings of the 1991 IEEE International Conference on Robotics and Automation, Sacramento, California, p2604-2609.
[https://doi.org/10.1109/ROBOT.1991.132020]

-
Murphy, B. R., and Watanabe, I., (1992), Digital Shaping Filters for Reducing Machine Vibration, IEEE Transaction on Robotics and Automation, 8(2), p285-289.
[https://doi.org/10.1109/70.134281]

-
Tzes, A., and Yurkovich, S., (1993), An Adaptive Input Shaping Control Scheme for Vibration Suppression in Slewing Flexible Structures, IEEE Transactions on Control Systems Technology, 1(2), p114-121.
[https://doi.org/10.1109/87.238404]

-
Kwak, M. K., Yang, D. H., and Lee, J. H., (2012), Maneuvering and Active Vibration Control of Slewing Flexible Beam Using Input Shaper, Transactions of the Korean Society for Noise and Vibration Engineering, 22(6), p542-549.
[https://doi.org/10.5050/KSNVE.2012.22.6.542]

-
Singhose, W., Seering, W., and Singer, N., (1994), Residual Vibration Reduction Using Vector Diagrams to Generate Shaped Inputs, Journal of Mechanical Design, 116(2), p654-659.
[https://doi.org/10.1115/1.2919428]

-
Singhose, W., Derezinski, S., and Singer, N., (1996), Extra-insensitive Input Shapers for Controlling Flexible Spacecraft, Journal of Guidance, Control, and Dynamics, 19(2), p385-391.
[https://doi.org/10.2514/3.21630]

- Singhose, W., Seering, W., and Singer, N., (1996), Input Shaping for Vibration Reduction with Specified Insensitivity to Modeling Errors, Proceedings of the 1996 Japan-USA Symposium on Flexible Automation, Boston, MA, p307-313.
-
Shan, J., Liu, H. T., and Sun, D., (2007), Modified Input Shaping for a Rotating Single-link Flexible Manipulator, Journal of Sound and Vibration, 285, p187-207.
[https://doi.org/10.1016/j.jsv.2004.08.035]

-
Singhose, W., Eloundou, R., and Lawrence, J., (2010), Command Generation for Flexible Systems by Input Shaping and Command Smoothing, Journal of Guidance, Control, and Dynamics, 33(6), p1697-1707.
[https://doi.org/10.2514/1.50270]

-
Xie, X., Huang, J., and Liang, Z., (2013), Vibration Reduction for Flexible Systems by Command Smoothing, Mechanical Systems and Signal Processing, 39, p461-470.
[https://doi.org/10.1016/j.ymssp.2013.02.021]

-
Vaughan, J., Yano, A., and Singhose, W., (2008), Comparison of Robust Input Shapers, Journal of Sound and Vibration, 315, p797-815.
[https://doi.org/10.1016/j.jsv.2008.02.032]

-
Huey, J. R., Sorensen, K. L., and Singhose, W. E., (2008), Useful Applications of Closed-loop Signal Shaping Controllers, Control Engineering Practice, 16(7), p836-846.
[https://doi.org/10.1016/j.conengprac.2007.09.004]

-
Zuo, K., Drapeau, V., and Wang, D., (1995), Closed Loop Shaped-input Strategies for Flexible Robots, The International Journal of Robotics Research, 14(5), p510-529.
[https://doi.org/10.1177/027836499501400507]

-
Kapila, V., Tzes, A., and Yan, Q., (2000), Closed-loop Input Shaping for Flexible Structures Using Time-delay Control, Journal of Dynamic Systems, Measurement, and Control, 122(3), p454-460.
[https://doi.org/10.1115/1.1286269]

-
Tang, R., and Huang, J., (2016), Control of Bridge Cranes with Distributed-mass Payloads Under Windy Conditions, Mechanical Systems and Signal Processing, 72, p409-419.
[https://doi.org/10.1016/j.ymssp.2015.11.002]

-
Yang, D. H., Shin, S. H., Lee, H. W., Kim, S. K., and Kwak, M. K., (2017), Active Vibration Control of Structure by Active Mass Damper and Multi-modal Negative Acceleration Feedback Control Algorithm, Journal of Sound and Vibration, 293, p18-30.
[https://doi.org/10.1016/j.jsv.2016.12.036]


Ji-Hwan Shin received B.S., M.S. and degree in Mechanical Engineering from Dongguk University in 2014 and 2016. He is currently a Ph.D. degree candidate at the Department of Mechanical Engineering of Dongguk University in Seoul, Korea. His research interests are in the area of active vibration control of smart structure.

Dong-Han Lee received B.S., M.S. and Ph.D. degree in Department of Mechanical, Robotics and Energy Engineering of Dongguk University in 2013 and 2016. He is currently a Ph.D. degree candidate at the Department of Mechanical Engineering of Dongguk University in Seoul, Korea. His research interests are in the area of active control of smart structure.

Moon K. Kwak received B.S. and M.S. degree in Naval Architecture from Seoul National University in 1981 and 1983. He then received his Ph.D. degree from the Dept. of Engineering Science and Mechanics of Virginia Tech in 1989. He is currently a professor at the Department of Mechanical, Robotics and Energy Engineering of Dongguk University in Seoul, Korea. His research interests are dynamics and control of flexible multibody system, and active vibration control of smart structure.