스마트 타이어 적용을 위한 센서모듈 전원공급용 전자기 에너지 하베스터 설계
© The Korean Society for Noise and Vibration Engineering
Abstract
A smart tire monitoring system uses information such as tire temperature, pressure, acceleration, force, and tire-road friction coefficient in real time to monitor the driving safety of cars. A vibration energy harvester for a smart tire monitoring system converts the tire dynamic strain energy into electrical energy that is used as the power source of the wireless sensor module. The self-powered wireless sensor module consists of an electromagnetic energy harvester, a power conversion circuit, an acceleration sensor, and a radio communication circuit. The aim of this work was to achieve high energy conversion efficiency, lightweight design, and long durability of the harvester that is located at the inner surface of a tire and hence, experiences extremely high pressure and acceleration. The designed energy harvester is cylindrical with a length and weight of 28 mm and 9.4 g, respectively. It was tested using tire driving test equipment. An average output power of approximately 5.9 mW was obtained at a driving speed of 60 km/h.
Keywords:
Smart Tire, Vibration, Electromagnet, Energy Harvester키워드:
스마트 타이어, 진동, 전자기, 에너지 하베스터1. 서 론
스마트 타이어 모니터링 시스템용 진동에너지 변환 기술은 스마트 타이어 시스템을 위한 각종 센서 및 무선통신 모듈의 전원 공급을 위하여 타이어 내부에서 발생하는 진동 및 동역학 에너지로부터 압전이나 전자기와 같은 에너지 변환방식을 통해 전기 에너지를 만들어 내는 기술을 말한다. 스마트 타이어 시스템은 정밀한 타이어 센서를 통해 타이어의 정보(온도, 압력, 가속도, 힘, 노면 마찰계수)를 실시간으로 계측하여 지능형 샤시 제어 시스템의 성능 향상을 통해 차량의 안전성을 개선하고 사고를 저감하는 시스템이다(1).
스마트 타이어 구현을 위해서는 타이어 거동의 물리량을 실시간으로 측정해야 하며 동시에 무선으로 데이터를 전송할 수 있어야 한다. 무선 계측이 가능한 센서의 구동 방식은 전원이 필요 없는 passive 방식과 전원을 필요로 하는 active 방식으로 나눌 수 있으며 SAW (surface acoustic wave)(2,3)와 같은 passive 방식의 경우 신호에 잡음이 많이 포함되어 있어 정확한 측정값을 얻을 수 없는 한계가 있다. Active 방식의 센서는 기존 상용 센서 및 무선 시스템의 활용이 가능하고 보다 정확한 데이터 수신이 가능하다는 장점이 있지만 전원 공급을 해주어야 하는 문제가 있다. 타이어 내에서 공기압과 온도를 측정하는 TPMS(tire pressure monitoring system)의 경우 데이터 전송 주기가 약 1분에 한 번 정도를 요구하고 있기 때문에 전력 사용량이 적어 배터리로 충분하다고 할 수 있지만 스마트 타이어용 센서 시스템은 많은 데이터를 측정하고 자주 전송하기 때문에 배터리를 사용하기에는 부적합하다. 가속도 신호 측정 및 무선으로 신호를 송신하는데 필요한 전력은 최소 5 mW정도 필요하게 되는데 타이어의 불 평형 진동을 방지하기 위하여 에너지 하베스터의 질량은 10 g 이하로 제작되어야 한다. 따라서 타이어 내부의 진동, 변형, 충격 등의 동적 에너지를 전기 에너지로 변환, 저장하여 센서 시스템에 전원을 공급하는 자가발전 시스템 개발이 연구되어 왔다(4~7). 진동을 이용한 에너지 하베스팅의 방법으로는 크게 두 가지로 나뉘는데 한 가지는 압전 물질을 이용하는 것(8~10)과, 다른 한 가지는 자석과 코일을 이용한 전자기형(11~14)의 에너지 하베스터가 있다. 압전 물질은 깨지기 쉽기 때문에 타이어가 고속으로 회전할 때 발생하는 가속도가 100 g이상에서 내구성 확보에 어려움이 있다. 그러므로 이 연구에서는 전자기형 에너지 하베스터에 관하여 연구하였다.
스마트 타이어 구현을 위한 모듈의 전원 공급을 위하여 타이어 내부에 장착하여 전자기형 에너지하베스터 설계에 대하여 연구하고자 하였다. 이에 이 연구에서는 전자기 에너지 하베스터 구성에 대하여 알아보고 상세 설계 및 해석에 따른 예상 전압을 예측하였다. 또한 제작된 전자기 에너지 하베스터를 타이어 내부에 장착하여 타이어가 회전할 때 발생하는 전압을 무선으로 측정하고, 해석결과와 실험결과를 비교하였다.
2. 에너지 하베스터 구성
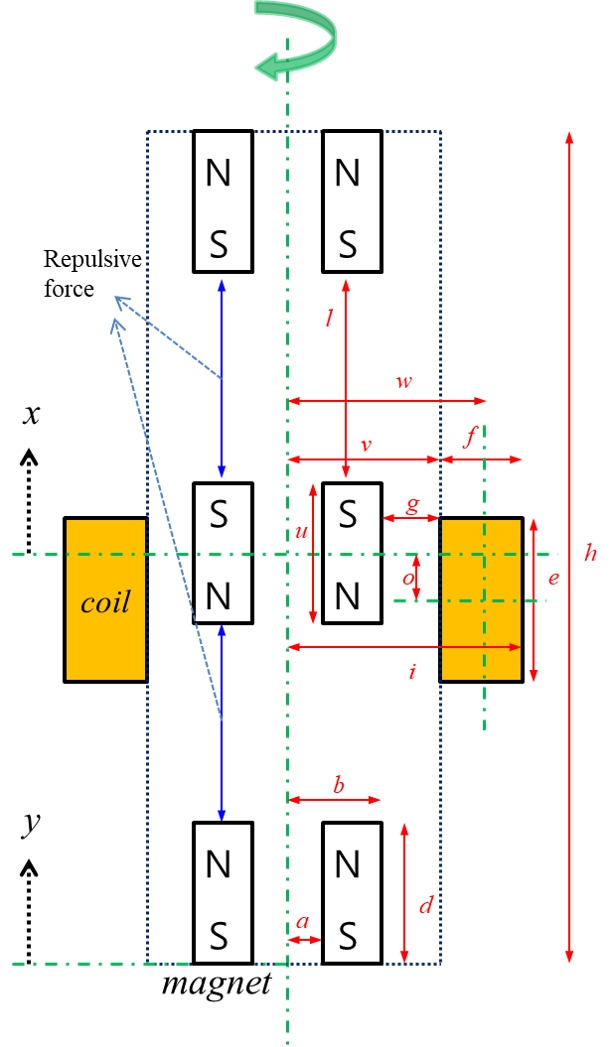
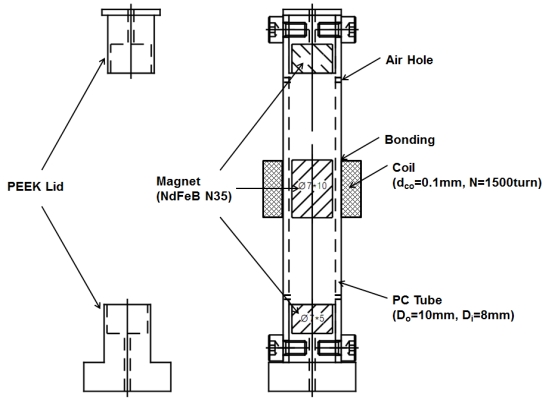
Fig. 1은 전자기형 에너지 하베스터의 단면도로 주요 부품을 나타내었다(15). 하우징은 전체 부품을 감싸는 역할을 하고, 코일은 하우징 외부 중간에 감겨 운동에너지가 전기 에너지로 변환하는 역할을 한다. 가운데 자석은 코일과 상대 상하 운동을 통하여 유도전류를 발생시킨다. 상하 양쪽 끝의 고정된 자석은 스프링 역할을 하여 가운데 자석이 공중에 떠서 유지되며 외부에서 가진될 경우 가운데 자석이 움직이게 한다. 하우징이 외부 가진에 의해 반복적으로 움직이게 되면 중간의 자석이 원통형의 하우징의 내부를 따라 움직이게 된다. 자석과 코일의 상대적인 움직임에 따라 자속의 변화는 전압을 발생시킨다. 가운데 자석의 동작을 안내하고 코일과 자석 사이의 간극을 유지하기 위해서는 하우징 내부에 가이드 핀이 필요하고 테프론 코팅 등을 하여 최소한의 마찰력으로 운동할 수 있도록 하였다. 왜냐하면 가운데 자석이 수직 방향으로 운동할 때 하우징 벽면에 자석이 과도하게 접촉하게 되면 마찰로 인한 움직임의 손실이 발생하기 때문이다. 에너지 하베스터의 구조를 단순화하기 위하여 가이드 핀 장치는 자석의 축 방향으로 구멍을 뚫고 그 축으로 핀이 결합되어 하우징과 일직선이 되도록 하였다. 이 메커니즘은 기계적 베어링보다 기름의 보충이 필요하지 않아 유지보수가 원활하고 비용 절감이 가능하다. Fig. 1의 고려되어야 할 설계변수는 기호설명과 Table 1에 설명과 함께 나타내었다. 각각의 변수는 서로 간섭되지 않도록 주의하여야 하고, 너무 크게 되면 질량 증가에 불리하고, 타이어 이너라이너에 부착 시 휠에 간섭이 되지 않도록 전체 높이도 크게 설계되어서는 안 되는 제한 조건이 있다.
전자기형 에너지 하베스터의 운동 방정식은 다음과 같다.
Fig. 1의 전기 연성 역학 방정식은 다음과 같다.
| (1) |
여기서 m은 질량, cm는 기계적감쇠, k는 스프링 계수이다. kt는 기계-전기 변환계수이다. i(t)는 시간에 따른 전류의 값이다. 하우징의 변위와 영구자석 변위의 상대변위는 z(t) = x(t) – y(t)이다. x(t)는 시간에 따른 하우징 내부에서 중간 자석의 변위이고, y(t)는 에너지 하베스터 하우징의 변위이다. 하우징에 가해지는 힘을 F(t) = – mÿ(t)라고 하면 다음과 같이 정리할 수 있다.
| (2) |
또한 중간 자석 코일의 상대 변위를 이용하여 역학 연성 전기회로 방정식을 표현하면 다음과 같다.
| (3) |
Lcoil은 코일의 인덕턴스, Rcoil은 코일의 저항, Rload은 외부에서 연결하는 외부저항이다. 식 (2)와 (3)은 기계-전기 변환계수 kt에 의해 서로 결합되어 있는 것을 알 수 있다. 시스템의 고유진동수를 ωn, 기계적 감쇠율을 ζm, 라고 할 때, cm와 k는 다음과 같이 나타낼 수 있다(14).
| (4) |
| (5) |
이때, ωn = 2πf 이며 일반적으로 이동자석에 연결된 스프링 계수는 질량에 따라 가변적인 값을 갖지만 스프링 상수 Fig. 1과 같이 이동자석의 아래위에 자석의 척력으로 스프링 역할을 하게 되면 거리에 따른 척력에 따라 스프링 계수가 달라진다. 또한 출력 파워를 최대화하는 최적부하저항 Rload.opt는 식 (6)과 같이 계산된다.
| (6) |
부하저항으로 출력되는 전압의 실효전압 Vrms는 식 (7)과 같으며, 출력되는 평균전력 Pavg는 식 (8)과 같다.
| (7) |
| (8) |
부하저항으로 또한 식 (2), (3) 및 Table 1과 같은 설계 변수는 상대적으로 쉽게 계산되지만 기계-전기 변환계수에 대해서는 보다 상세한 분석이 요구된다. Fig. 1과 같은 형태의 에너지 하베스터의 경우 모두 코일의 회전축과 자석의 상대 운동 방향이 일치하므로 코일의 면적은 변하지 않는 반면 코일과 교차하는 자속 밀도가 시간에 따라 변하므로 와 같은 식으로 변환계수를 계산해야 한다. n은 코일의 전체 턴 수, B는 자속, Z는 자속과 코일의 상대 운동 변위, A는 자속과 교차하는 코일의 면적이다. 기계-전기 변환계수를 구하기 위해서는 코일 면적 전체에 대한 적분이 필요하지만, 계산의 효율성을 위해 코일 면적을 수직으로 분할하고 각 셀 별로 계산된 변환계수를 평균하여 최종 변환계수를 구한다. 해석결과는 4장에서 다루도록 하겠다.
3. 에너지 하베스터 설계
자석 스프링 타입 전자기형 에너지 수확장치의 레이아웃은 Fig. 2과 같다. 원통 모양의 하우징이 타이어 내면에 부착되고 타이어 회전 시 발생하는 진동 충격에 의해 하우징이 가진되면 하우징 내부에서 이동 자석이 상하로 진동한다. 이동 자석과 하우징 사이에는 미끄러짐을 위한 약간의 간극이 필요하며 마찰계수를 줄이기 위해 별도의 윤활 방식을 추가할 수 있다. 하우징 양끝 단의 고정 자석은 이동 자석과 서로 같은 극을 마주보게 위치하며, 고정 자석과 이동 자석 간에 발생되는 척력이 진동 시스템의 복원력으로 작용하였다. 하우징 외부에는 코일이 감겨 있어서 이동 자석이 상하로 진동할 때 전자기 유도 법칙에 의해 기전력이 발생한다. Table 1과 같이 에너지 수확장치의 중량 제한조건(10 g 이하)을 만족하면서 고정 자석의 크기 및 이동 자석과 고정 자석 간의 거리를 조정하는 방식으로 설계 안을 도출하였다. 자석 스프링 타입의 전자기형 에너지 수확장치 시제를 설계하였다. Fig. 2와 같이 하우징은 PC 튜브로 제작되며 이동 및 고정 자석은 네오디뮴(NdFeB) 계열을 선정하였다. 고정 자석을 지지하기 위한 홀더는 peek 재질로 제작되며 이동 자석의 원활한 움직임을 위해 고정 자석 근방에 공기 구멍을 확보하였다. 코일은 선경 0.1 mm 와이어를 사용하였다. Type1과 type2의 차이는 이동 자석의 높이를 변경함으로써 자속의 변경으로 인한 위치별 척력(스프링계수), 기계전기변환계수 변경과, 질량변경으로 인한 이동자자석의 변위차이 및 이동속도의 차이로 인한 발생 전력의 차이를 확인하였다.
4. 에너지 하베스터 성능 해석
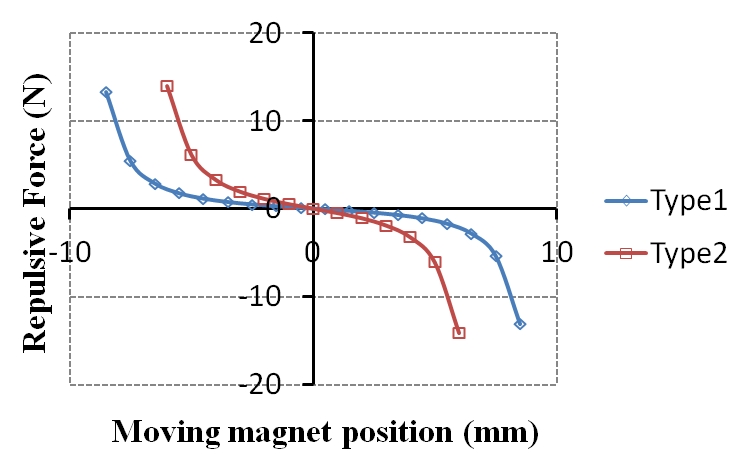
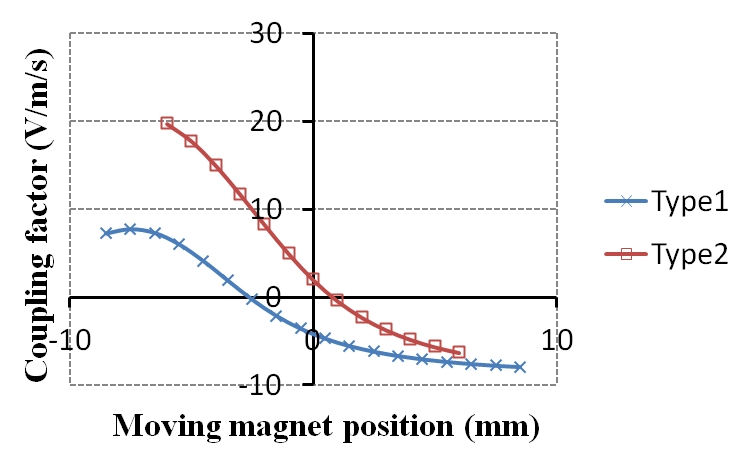
전자기형 에너지 수확장치 설계 안에 대한 출력 성능을 예측하기 위해서 전자기 유한요소해석을 통해 이동자석의 위치에 따른 기계-전기 변환계수와 자석 간의 척력 변화를 계산하였다. 이동 자석의 경우 설계된 치수와 밀도의 계산에 의한 질량이며, 그에 의한 값을 Table 1에 표시하였다. 스프링계수는 실제 스프링을 사용하지 않고 자석의 척력을 이용하기 때문에 숫자 하나로 표현하기 어려운 점이 있다. Fig. 4와 같이 위치별 자석의 척력 값을 이용하여 시스템해석을 할 때 위치별로 스프링계수(k)값을 반영하였다. 감쇠는 기계적 감쇠와 전기적 감쇠로 나뉘는데 기계적 감쇠는 감쇠기를 설치한 것이 아니기에 보통 사용하는 기계계 대수 감쇠율(0.015)과 이동자 자석의 위치에 따라 다른 전기계에 의한 감쇠가 계산되어 반영하였다. Fig. 3과 같이 이동 자석의 위치를 이동하며 코일에 걸리는 반경 방향의 자속 밀도로부터 기계-전기 변환계수의 변화를 계산하고, 고정 자석에 의해 받는 힘을 측정하여 복원력의 변화를 계산하였다.
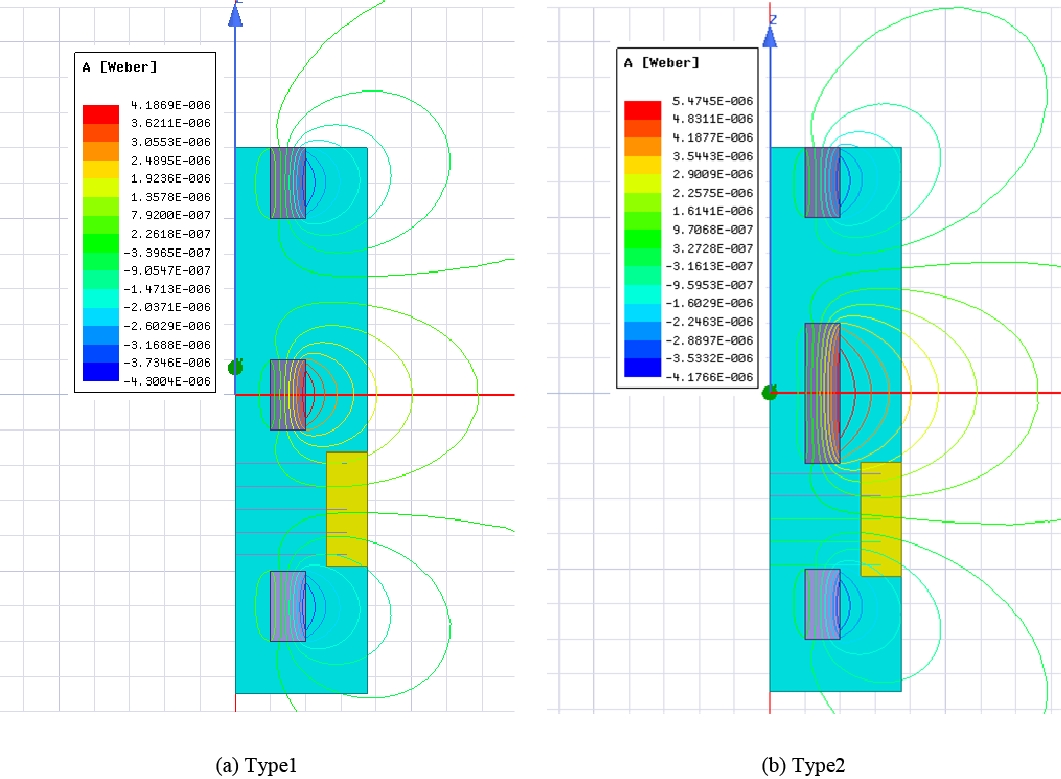
Mechanical-electrical conversion factor and repulsive force calculation of using finite element analysis
Fig. 4는 이동 자석의 위치에 따른 척력의 변화를 계산한 그래프이다. 이동 자석이 정 중앙에 위치했을 경우에는 양쪽 고정 자석으로부터 받는 힘이 평형을 이루지만 한쪽으로 이동하게 되면 반대쪽으로 밀어내는 힘이 점점 커지며 고정 자석과 가까워질수록 힘의 크기는 급격히 커지게 된다. 이와 같은 척력의 비선형적인 특성은 저속 주행 시 작은 크기의 가진에 의해서도 이동 자석이 일정 구간 내에서 쉽게 움직일 수 있도록 하고, 고속 주행 시 큰 가진에 의해서 이동 자석의 변위가 커지더라도 양끝 단으로 갈수록 급격히 커지는 척력에 의해서 일정 범위를 벗어나지 않도록 해주는 효과가 있다.
Fig. 5는 이동 자석의 위치에 따른 기계-전기 변환계수의 변화를 계산한 그래프이다. 이동 자석의 양쪽 끝 단에서 반경방향의 자속 밀도가 가장 크게 발생하므로 이동 자석의 양쪽 끝 단이 코일의 중앙부에 위치하는 경우 변환계수의 크기도 가장 크게 나타난다. 이동 자석이 하우징의 끝 단으로 갈수록 코일과의 거리는 멀어지므로 변환계수의 크기가 점점 줄어들며, 이동 자석이 하우징의 정 중앙에 위치했을 경우에는 나가고 들어오는 반경방향의 자속 밀도가 코일 내부에서 서로 상쇄되므로 변환계수의 크기가 0이 된다.
입력 가속도에 따른 전자기형 에너지 수확장치의 출력 성능을 예측하기 위해서 MATLAB/simulink를 이용하여 시뮬레이션을 수행하였다. 다양한 형태의 입력 가속도와 지배 방정식을 적용할 수 있고, 자석 간의 척력이나 기계-전기 변환계수와 같은 비선형 데이터를 lookup-table 형태로 입력할 수 있으며 동적 전자기 유한요소해석에 비해 빠른 속도로 시간에 따른 출력 성능을 확인할 수 있다.
입력 가속도에 따른 전자기형 에너지 수확장치의 출력 성능을 예측하기 위해서 MATLAB/simulink를 이용하여 시뮬레이션을 수행하였다. 다양한 형태의 입력 가속도와 지배 방정식을 적용할 수 있고, 자석 간의 척력이나 기계-전기 변환계수와 같은 비선형 데이터를 lookup-table 형태로 입력할 수 있으며 동적 전자기 유한요소 해석에 비해 빠른 속도로 시간에 따른 출력 성능을 확인할 수 있다.
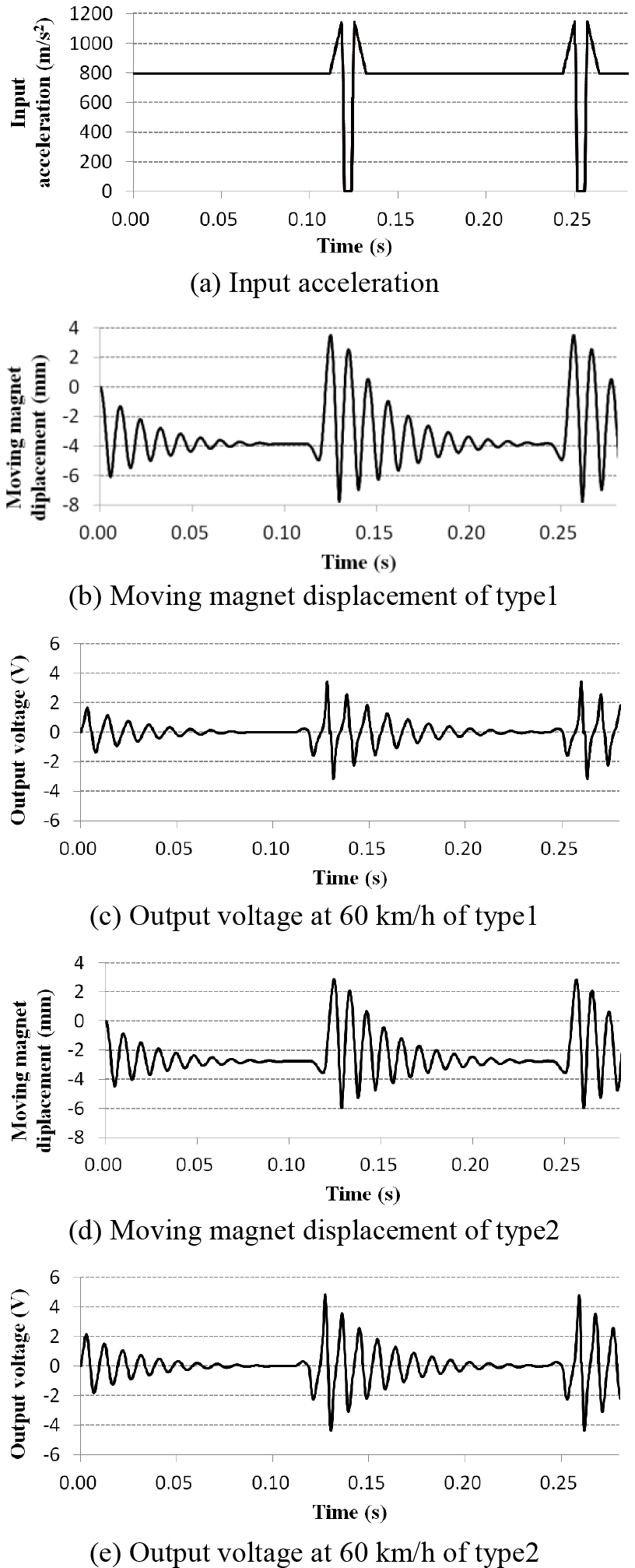
Fig. 6과 Fig. 7은 식 (2)와 (3)를 바탕으로 MATLAB/ simulink 모델에 타이어 반경 방향의 진동을 입력하여 시뮬레이션한 결과를 나타낸다. 먼저 타이어 내부에 타이어반경방향으로 가속도계를 설치하여 가속도신호를 측정하였고, 실제 가속도 신호를 그대로 과도응답해석에 적용할 경우 해석 시간이 과도하게 발생하고, 비연속성으로 인한 에러가 발생하여 타이어반경방향의 가속도 신호를 단순화하여 표시하였다. Fig. 6(a)는 차량이 60 km/h로 이동할 때 타이어에서 발생하는 가속도의 크기를 나타내었다. 식 (2)의 F(t)의 값을 나타낸다. Fig. 6(b)는 타이어 내부의 에너지 하베스터가 노면에 닿았을 때 중간 자석의 변위를 나타내었다. Fig. 6(c)는 Fig. 6(b)에서 이동자석의 변위가 발생했을 때 발생하는 전압의 크기를 나타내었다. 자석의 변위를 살펴보면, 타이어가 회전할 때 원심력과 척력이 평형을 이루는 위치에 이동 자석이 머무르다가 타이어가 노면과 접지하는 시점에 변위가 크게 발생하며 타이어가 노면과 분리되면 다시 평형점으로 돌아가면서 진동하는 형태를 보인다. 출력 전압은 큰 변위가 발생하는 시점에서 큰 출력을 보이며 감쇠에 의해 서서히 감소하면서 진동하는 형태를 보인다.
5. 성능 실험
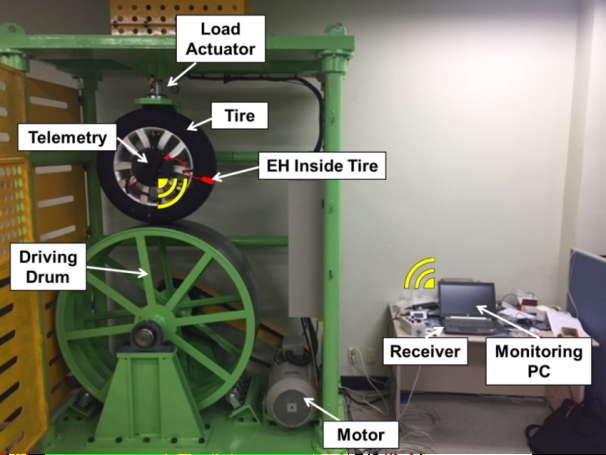
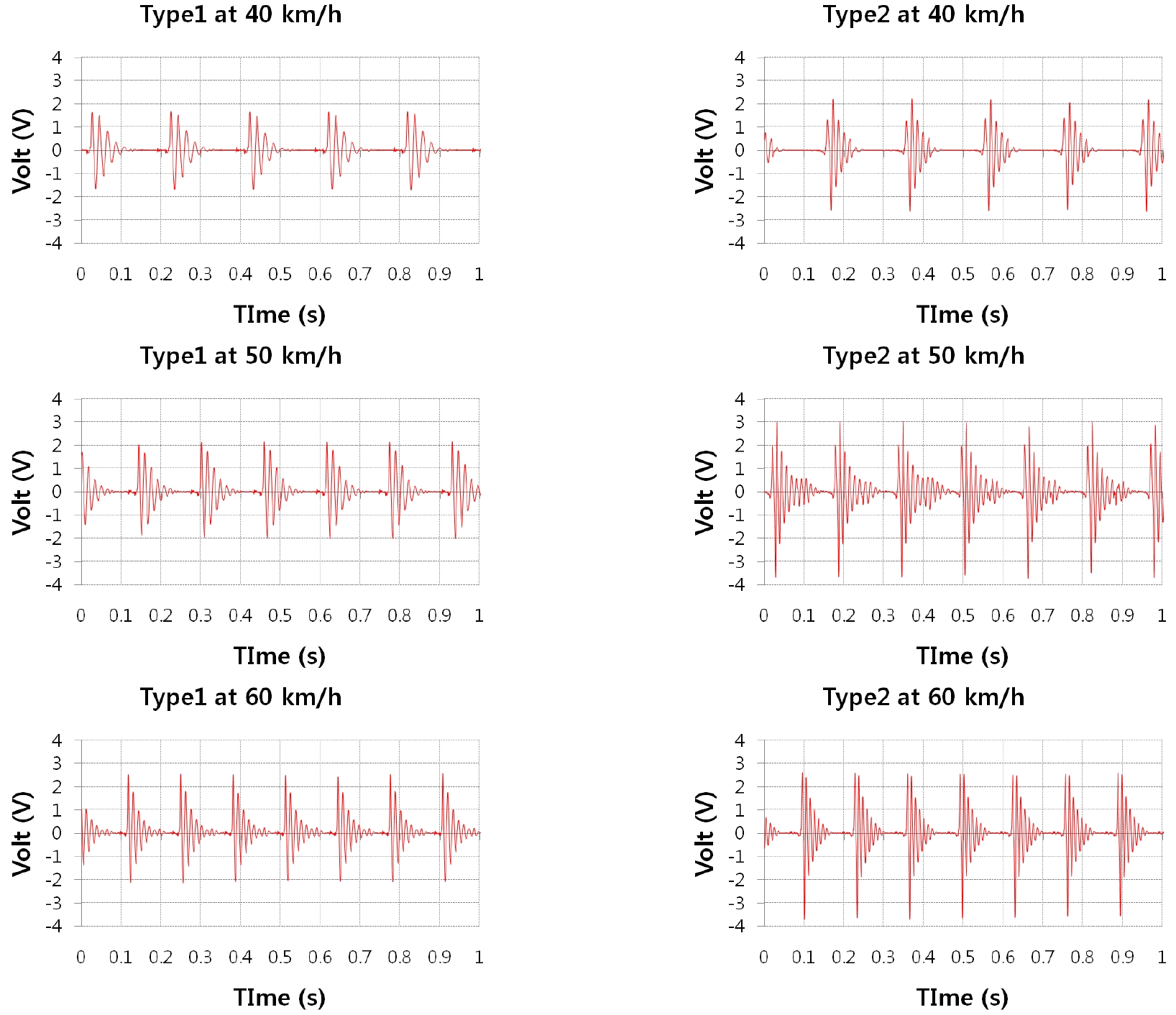
Table 1과 같이 정한 설계값을 바탕으로 Fig. 7과 같이 제작하였다. 전체 질량은 9.4 g으로 제작되었다. Fig. 8과 같이 접착제를 이용하여 타이어 반경방향으로 부착하였다. Fig. 9는 타이어 내부에 제작된 에너지 하베스터를 부착하고 자동차가 도로 위를 주행할 때의 상황을 모사할 수 있는 시험장치이다. 실제 자동차의 하중이 타이어에 가해지고 아래쪽의 드림이 모터에 의해 회전하게 되면 타이어가 수직하중을 받으며 회전하게 되는 원리로 제작되었다. 타이어를 장착한 자동차가 전방으로 주행한다고 가정할 때 약 100 km/h로 회전 가능하지만 안전을 위하여 60 km/h까지만 시험을 진행하였다. 에너지 하베스터를 타이어 내면에 부착하고 전선을 휠 바깥쪽에 고정한 텔레메트리(코아칩스사, 실시간 고전압 무선 측정장치)에 연결하였다. 텔레메트리는 유선으로 신호를 받고 무선으로 신호를 모니터링 컴퓨터에 보내주는 배터리로 작동하는 장치이다. 20 km/h ~ 60 km/h 속도별로 에너지 하베스터에서 발생하는 전압을 무선 송수신 장치에서 수신하여 컴퓨터로 전송하여 실시간으로 측정하였다. 최대 전력을 계산하기 위하여 100 Ω의 외부저항을 병렬로 연결하였다. 속도별 최적저항을 연결할 경우 발생전력을 증가하는 효과는 있지만, 실제 스마트타이어의 센서모듈에 적용하기 위해서는 가변적인 저항을 적용할 수 없기에 한 종류의 저항만 연결하여 실험하였다. 속도별로 에너지 하베스터에서 발생하는 전압을 측정하였으며, Fig. 10은 type1, type2 실험결과 중 40 km/h ~ 60 km/h로 주행 시 에너지 하베스터에서 발생하는 전압을 그래프로 나타내었다. 속도가 증가할수록 에너지 하베스터가 전압을 발생시키는 주기는 점점 짧아지고 발생하는 전압은 증가한다. 노면에 한 번 진동 시 에너지 하베스터의 중간 자석이 자유진동하는 횟수도 함께 증가하여 발생하는 전압 및 평균전력(Pavg)도 증가하는 현상을 볼 수 있다. Type2의 60 km/h의 그래프를 보면 225/60R17사이즈의 타이어의 경우 직경이 702 mm의 타이어가 한 바퀴 회전하는데 걸리는 시간은 0.132초이며 1초당 7.56회 반복되는 그래프가 나타났다. 에너지 하베스터가 노면에 닿는 순간 발생하는피크 전압은 -3.5 V에서 2.5 V까지 나타났으며 에너지 하베스터가 노면에 한 번 닿고 타이어가 한 바퀴 회전하는 동안 7회 정도 자체진동이 발생하는 것을 알 수 있다.
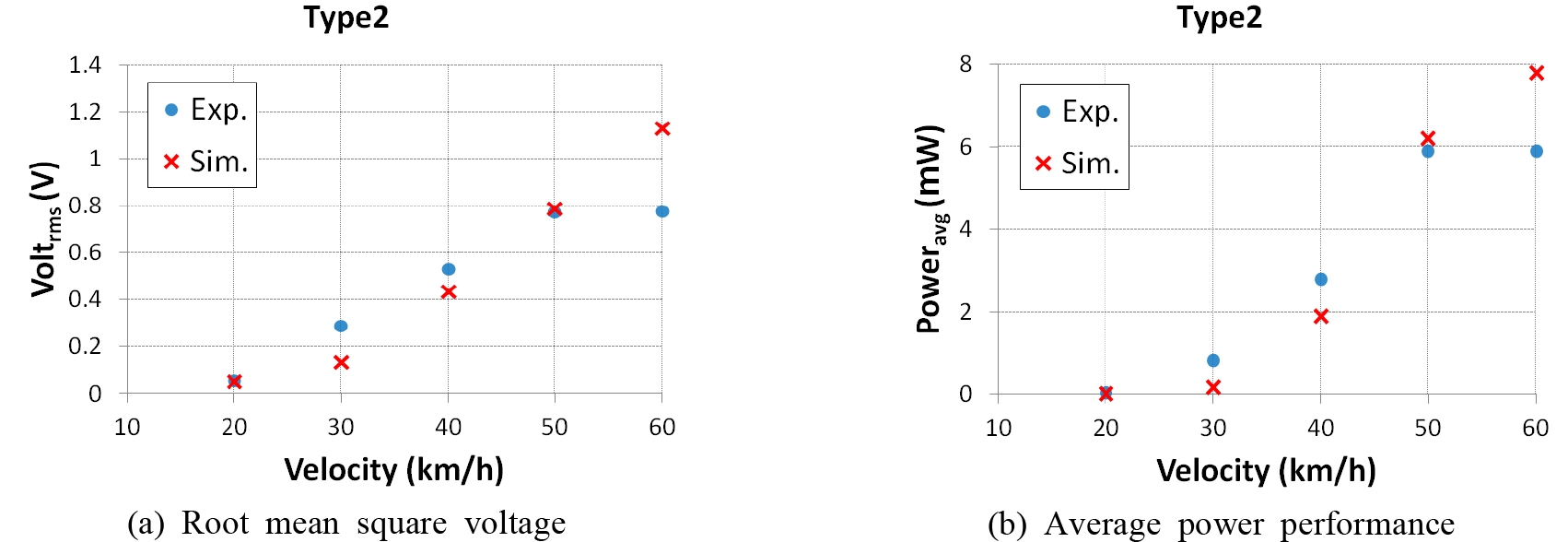
Fig. 11, Fig. 12는 식 (2), 식 (3)의 해석결과로 나타낸 Fig. 6과 Fig. 10의 실험결과를 비교하여 그래프로 나타내었다. 속도가 증가할수록 입력되는 가속도가 커지기 때문에 에너지 하베스터에서 발생하는 Voltrms와 Poweravg은 유사하게 증가하는 추세를 보인다. Type2의 에너지 하베스터가 60 km/h에서의 실험결과 중 최대값인 Vrms은 0.9 V이고, Poweravg는 약 5.9 mW이다. 60 km/h에서 해석값과 실험값의 차이가 보이는데 실험값의 경우 실제 제작된 에너지 하베스터의 중간자석과 고정자석의 척력의 비선형으로 인해서 중간자석이 끝까지 이동하지 못하는 현상이 있는 것으로 보인다. 이를 해결하기 위해서 고정자석의 척력을 줄이거나 중간자석의 이동 거리를 더 확보하면 해석과 실험이 유사한 결과를 얻을 것이라 기대된다. 또한 출력 전압이 1 V 내외로서 직류 전기로 정류할 경우 전력 손실로 인하여 출력 전압이 예상되지만, 실시간 측정은 최대 ± 3 V ~ 4 V 정도 나오게 된다. 센서모듈이나 배터리에 사용하기 위해서는 직류 변환을 위한 정류과정을 거치게 되는데 그 과정에서 부스트 컨버터 등의 회로를 이용하여 전압을 올려주는 작업을 거쳐서 전력손실을 최소화할 수 있을 것으로 예상된다.
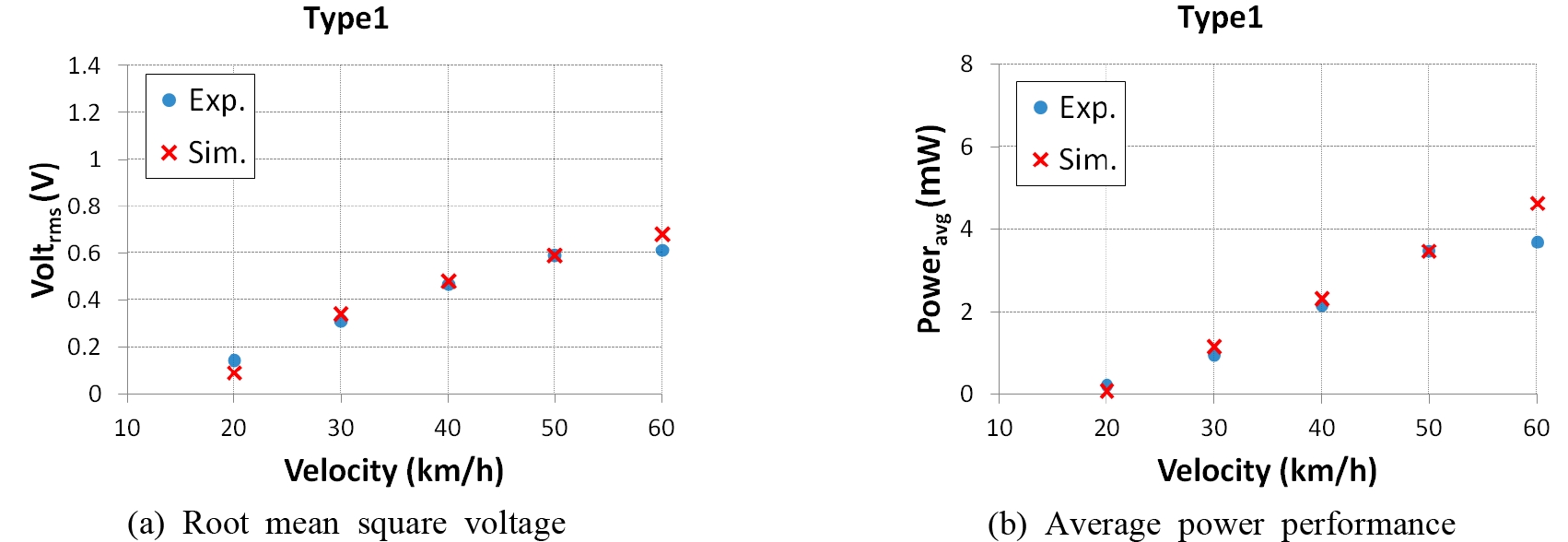
Comparison of energy performance harvester (a) root mean square voltage (b) average power performance analysis results and experiment results of type1 by traveling speed
6. 결 론
이 연구에서는 스마트타이어 적용을 위한 센서모듈 전원공급용 전자기 에너지 하베스터 설계를 하고 해석 및 제작하여 실험을 통하여 성능을 확인하였다. 타이어가 회전할 때 타이어의 반경방향의 가속도 변화를 입력 가속도를 갖는 에너지 하베스터를 설계하였고, 유한요소 해석을 통하여 자석과 자석의 척력관계 및 자석과 코일의 기계-전기 변환계수를 유추하였다. 타이어 내부 인너라이너에 에너지 하베스터를 부착하고 무선통신 모듈을 통하여 에너지 하베스터의 성능을 확인하였다. 따라서, 이 연구를 통하여 스마트 타이어의 센서 모듈이 정상적으로 작동할 수 있는 전원공급이 가능할 것으로 판단된다.
기호설명
| a : | Inner radius of magnet (zero for disk) |
| b : | Outer radius of magnet |
| cm : | Mechanical damping constant |
| d : | Height of fixed magnet |
| e : | Height of coil |
| f : | Width of coil |
| g : | Gap of magnet and coil |
| h : | Height of housing |
| i : | Radius of outermost |
| j : | Diameter of coil |
| k : | Spring coefficient |
| l : | Gap of moving magnet and fixed magnet |
| m : | Moving magnet weight |
| n : | Number of coil |
| o : | Offset of coil |
| p : | Resistance per unit length |
| q : | Inductance of coil |
| r : | Total coil resistance |
| s : | Cooper fill factor of coil |
| u : | Height of moving magnet |
| v : | Radius of housing |
| w : | Radius of center line of winding coil |
Acknowledgments
A part of this paper was presented at the KSNVE 2018 Annual Autumn Conference
References
- Lee, H., and Taheri, S., (2017), Intelligent Tires: A Review of Tire Characterization Literature, IEEE Intelligent Transportation Systems Council, p114-135.
-
Reindl, L., Pohl, A., Scholl, G., and Weigel, R., (2001), SAW-based Radio Sensor Systems, IEEE Sensors J., 1(1), p69-78.
[https://doi.org/10.1109/JSEN.2001.923589]

-
Pohl, A., Steindl, R., and Reindl, L., (1999), The ‘Intelligent Tire’ Utilizing Passive SAW Sensors Measurement of Tire Friction, IEEE Trans. Instrum. Meas., 48(6), p1041-1046.
[https://doi.org/10.1109/19.816111]

-
Sadeqi, S., Arzanpour, S., and Hajikolaei, K. H., (2015), Broadening the Frequency Bandwidth of a Tire-embedded Piezoelectric-based Energy Harvesting System Using Coupled Linear Resonating Structure, IEEE/ASME Transactions on Mechatronics, 20(5), p2085-2094.
[https://doi.org/10.1109/TMECH.2014.2362685]

-
Lee, J., and Choi, B., (2014), Development of a Piezoelectric Energy Harvesting System for Implementing Wireless Sensors on the Tires, Energy Conversion and Management, 78, p32-38.
[https://doi.org/10.1016/j.enconman.2013.09.054]

-
Singh, K. B., Bedekar, V., Taheri, S., and Priya, S., (2012), Piezoelectric Vibration Energy Harvesting System with an Adaptive Frequency Tuning Mechanism for Intelligent Tires, Mechatronics, 22(7), p970-988.
[https://doi.org/10.1016/j.mechatronics.2012.06.006]

- Park, H., (2017), Vibratory Electromagnetic Induction Energy Harvester on Wheel Surface of Mobile Sources, International Journal of Precision Engineering and Manufacturing - Green Technology, 4(1), p59-66.
-
Butt, Z., Pasha, R., Qayyum, F., Anjum, Z., Ahmad, N., and Elahi, H., (2016), Generation of Electrical Energy Using Lead Zirconate Titanate (PZT-5A) Piezoelectric Material: Analytical, Numerical and Experimental Verifications, Journal of Mechanical Science and Technology, 31(9), p3553-3558.
[https://doi.org/10.1007/s12206-016-0715-3]

-
Cook-Chennault, K., Thambi, N., and Sastry, A., (2008), Powering MEMS Portable Devices: A review of Non-regenerative and Regenerative Power Supply Systems with Special Emphasis on Piezoelectric Energy Harvesting Systems, Smart Materials and Structures, 17(4), p043001.
[https://doi.org/10.1088/0964-1726/17/4/043001]

-
Vasic, D., Chen, Y., and Costa, F., (2014), Self-powered Piezoelectric Energy Harvester for Bicycle, Journal of Mechanical Science and Technology, 28(7), p2501-2510.
[https://doi.org/10.1007/s12206-014-0407-9]

-
Dahari, Z., Chye, W., Sidek, O., and Miskam, M., (2011), A Comparative Study of Electromagnetic Generator via Finite Element Analysis, Paper Presented at the 2011 International Conference on Electrical Engineering and Informatics, Bandung, Indonesia.
[https://doi.org/10.1109/ICEEI.2011.6021747]

-
Spreemann, D., Hoffmann, D., Folkmer, B., and Manoli, Y., (2008), Numerical Optimization Approach for Resonant Electromagnetic Vibration Transducer Designed for Random Vibration, Journal of Micromechanics and Microengineering, 18(10), p104001.
[https://doi.org/10.1088/0960-1317/18/10/104001]

- Spreemann, D., Folkmer, B., and Manoli, Y., (2009), Optimization and Comparison of Back Iron Based Coupling Architectures for Electromagnetic Vibration Transducers Using Evolution Strategy, Proceedings of the Power MEMS, p372-375.
-
Kim, S., Kim, Y., Seo, J., and Lee, H., (2017), Design Optimization of Electromagnetic Vibration Energy Harvesters Considering Aspect Ratio, Transactions of the Korean Society for Noise and Vibration Engineering, 27(3), p360-371.
[https://doi.org/10.5050/KSNVE.2017.27.3.360]

-
Mann, B. P., and Sims, N. D., (2009), Energy Harvesting from the Nonlinear Oscillations of Magnetic Levitation, Journal of Sound and Vibration, 319, p515-530.
[https://doi.org/10.1016/j.jsv.2008.06.011]


Jongho Seo received his B.S. in mechanical engineering from Chungbuk National University in 2008. He is a currently taking a M.S.~Ph.D. joint course in Department of Mechanical Engineering, Hanyang University. His current research interest is electromagnetic and piezoelectric vibration energy harvesting.

Young-Cheol Kim is a principal researcher at Korea Institute of Machinery and Materials (KIMM). He received his B.S. and M.S. in mechanical engineering from Pusan National University in 1990 and 1993, respectively, and Ph.D. in mechanical engineering from Korea Advanced Institute of Science and Technology (KAIST) in 2008. His current research interests include rotordynamics, tribology, and energy harvesting.