기초 질량부가 포함된 마운트 모듈 지지 시스템의 응답 특성 분석
© The Korean Society for Noise and Vibration Engineering
Abstract
The characteristics of response of a supported system with a mount module are subject to the selection of mechanical sub-components such as mass, spring, damper, and basement mass-block. The role of a basement mass-block, normally installed beneath the target system, is to control the dynamics of the supported system. The dynamic effect of the mount module varies according to the combination of sub-components. If the basement mass-block is tightly connected with the target system, it will solely lower the critical frequency of the modified system, and the resultant system may display rigid body motion during operational frequency range. However, the contribution of the basement mass-block becomes difficult to predict accurately in cases where it is located between mechanical sub-components such as the spring or damper. In a recent study, we proposed a simplified mount module for use in mounting a heavy emergency electric power plant over the reaction force at the plant side. The investigation of the dynamic contribution of the base mass-block beyond that of the original mount module, required to verify the proposed simplified mount module is still appropriately fit for purpose, remained outstanding. In this paper, the contribution of the basement mass-block is assessed by comparison of the response index for different basement mass-block weights.
Keywords:
Basement Mass-block, Response Index, Response Analysis, Emergency Electric Generator, Mount Module키워드:
기초 질량, 응답 인덱스, 응답 분석, 비상 발전기, 마운트 모듈1. 서 론
중량이 큰 대상체를 지지하는 마운트 모듈에서 자주 사용되는 기초 질량부는 마운트 모듈에서 사용되는 요소부품들인 스프링, 댐퍼 등과 함께 자주 사용되는 요소이다. 마운트 모듈은 작동 방식에 따라 수동(passive), 반 능동(semi-active) 및 능동(active)으로 구분할 수 있다(1~5). 특히 수동형 마운트 모듈은 타 방식 대비 가격이 저렴하고 수리가 쉬운 장점 등에 따라 발전기 등의 산업용으로 많이 활용되고 있다. 기초 질량부는 통상 지지되어야 하는 대상 시스템에 직접 단단히 연결시킴으로써 대상체의 전체 질량을 증가시켜 대상체의 1차 공진점을 최소화시키는 역할을 수행할 수 있다. 이와 같은 경우에는 기초 질량부가 동적으로 시스템에 영향을 주지 않는 경우이기 때문에 마운트 모듈이나 대상체에 동적으로 영향을 주는 가능성이 없기 때문에 대상체 아래에 고정된 강체의 중량을 고려하여 시스템 전체의 모달 파라미터를 예측함으로써 기초 질량의 최솟값을 얻어낼 수 있다. 하지만 만약 기초질량이 지지되어야 하는 대상체와 직접적으로 단단히 고정되지 않는 상황에서는 기초 질량과 연결되어 있는 마운트 요소 부품들 간의 상호 작용에 의해 대상 시스템의 응답 특성을 변경시키는 역할을 하게 된다. 따라서 마운트 모듈의 구조에서 중간 부분에 기초 질량을 가진 복잡한 경우에 대해 동적 거동을 파악하기 위해서는 기초 질량부의 민감도 해석 등을 통해 지지되는 시스템과의 관계를 식별하는 것이 바람직하다.
기존 연구에서 비상발전기에 사용되는 기존 복잡한 구조의 마운트 모듈을 보다 간단한 형태로 변경하기 위해 기초 질량부를 제거한 신규 모델을 제안하였다. 해당 연구에서는 기초 질량 값을 업체에서 보유하고 있는 시공 규격 안에 따라 6900 kg으로 고정한 다음 해석을 진행하였다. 시뮬레이션 결과에 따라 신규 마운트 모듈의 최적 상태를 도출하기는 하였으나 해당 조건은 기초 질량부를 고정한 상태에서 얻어진 결과이며 만약 기존 마운트 구조에서 기초 질량부의 동적 민감도가 큰 경우 신규 마운트 모듈이 기존 마운트 대비 우수한 응답 특성을 보였다는 기존 연구결과가 달라질 가능성도 존재한다.
이 연구에서는 기초 질량부를 가지는 복잡한 구조의 마운트와 신규 마운트의 응답 특성을 기초 질량부의 값을 변경시켜가면서 비교 평가하였다. 응답 특성의 변화는 응답 인덱스를 활용하여 나타내었으며 해당 인덱스가 유효한 이유는 신규 마운트 구조에서 기초 질량부가 없기 때문에 민감도 해석을 수행하는데 있어서 기준값으로 적당하기 때문이다. 2가지 마운트 모듈에 대한 조건을 이론적으로 해석하기 위해 발전기를 포함한 전체 시스템을 선형 등가 모델로 구성하였다. 이론 모델에 대한 응답 시뮬레이션 결과를 통해 다양한 기초 질량부 조건을 가진 기존 마운트 구조와 신규 마운트 구조를 비교 평가하였다.
2. 구조물의 이론적 가진 응답
2.1 대상 구조물 및 이론적 마운트 모델
마운트 모듈을 통해 지지하고자 하는 대상 구조물은 비상용 발전기로서 기존 연구에서 활용되었던 대상체와 동일하다(6,7). 용량은 750 kW 급이며 자체 무게는 6070 kg이고 부산 소재의 ㈜대흥기전 업체에서 생산한 제품이다. 이 발전기는 정전 등의 특수한 상황에서 전기에너지를 계속적으로 공급해야 하는 건물의 지하에 통상 설치되며 전기에너지를 생산하기 위해 디젤엔진(두산인프라코어/한국)을 활용하여 1800 rev/min 회전속도로 작동된다. 따라서 관심 영역의 주파수 대역은 회전 주파수의 4차 하모닉 성분인 120 Hz 정도까지의 저주파 영역으로 한정하였다. Fig. 1은 대상 750 kW급 비상발전기 시스템을 보여준다.
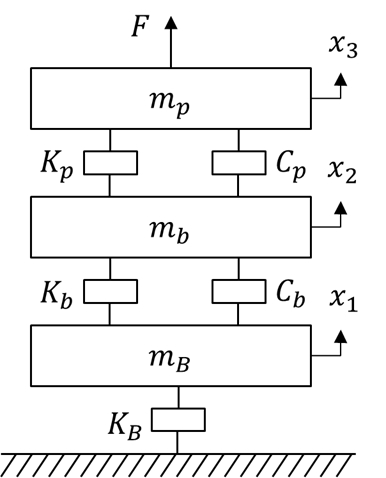
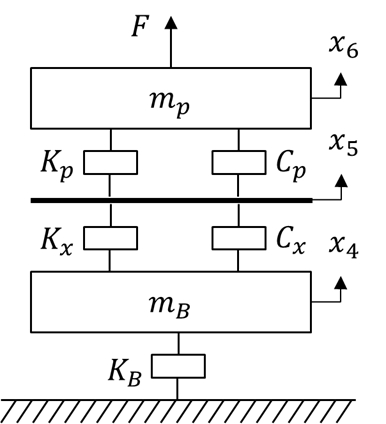
해당 발전기 시스템은 운전 중 상당한 진동이 발생되기 때문에 마운트 모듈을 부착하여 발전기 자체의 반력으로 나타나는 진동 혹은 바닥으로 전달되는 진동을 동시에 방지하는 것이 필요하다. 기존 마운트 모듈은 스프링, 댐퍼 및 기초 질량부로 이루어져 있으며 특히 기초 질량부의 경우 초기 시공하는 과정에서 상대적으로 까다로운 시공 노력이 필요하다. 또한 바닥면과 이격시키기 위한 감쇠 패널이 시간이 지남에 따라 기존 감쇠 역할을 수행하지 못하는 경우 변경하는 과정에서 기초 질량부는 큰 부담이 될 수밖에 없다. 이를 극복하기 위해 기존 연구에서 기초 질량부를 배제시킨 간단한 구조의 마운트 모듈을 제안하였으며 해당 마운트 모듈의 기계적 특성에 대한 시뮬레이션 결과를 획득하였다(7). 기존 마운트 모듈과 신규 마운트 모듈의 간략화된 모델을 Fig. 2와 Fig. 3에(4) 도시하였으며 해당 모델에 대한 물성치는 Table 1에 정리하였다. 해당 물성치 중 대상 발전기와 직접 연결되는 부분의 기계 특성은 전용 시험기인 MTS 835 모델 장비를 활용하여 계측된 값을 사용하였으며, 나머지 기계요소들의 값들은 실제 계측된 응답 값과 이론적인 응답 값을 비교하여 주요 주파수 대역 내에서 보정된 값을 사용하였다(3). 신규 마운트 모듈은 스프링 요소와 감쇠 패널 부분이 상하 직렬로 연결되어 있으나 물리적으로 각각의 기계요소가 등가강성과 등가감쇠를 각각 보유하고 있기 때문에 양쪽 사이에 질량이 존재하지 않는 직렬연결 형태로 모델링을 하였다.
여기서, 등가중량 변수인 Mp, Mp, Mp는 각각 비상 발전기, 기초 질량, 빌딩 중량을 나타낸다. Kp, Kb, KB, Kx는 각각 상부 스프링, 기존 마운트 감쇠 패널, 빌딩 바닥부, 제안된 마운트 감쇠 패널의 각각의 등가 스프링 상수이다. Cp, Cb, Cx는 각각 상부 스프링, 기존 마운트 감쇠 패널, 제안된 마운트 감쇠 패널의 각각의 등가 감쇠계수이다.
기존 연구에서 선정된 등가모델의 상수 값들과 Table 2에서 정리된 이 연구에서의 상수 값의 차이는 제안된 마운트 모듈의 감쇠 패널에 대한 등가 강성(Kx)과 감쇠 계수(Cx)이다. 기존 연구에서는 해당 값이 응답 인덱스에 미치는 영향을 분석하였으나 결론적으로 상부 반력 응답에는 어떤 값을 선정하더라도 큰 차이가 없다는 결론을 얻었기 때문에 기존 마운트 모듈의 감쇠 패널에 적용된 값을 그대로 사용하였다.
2.2 이론적 가진 응답
기존 비상발전기용 마운트 모듈을 간략하게 나타낸 시스템 모델(Fig. 2 참고)에 대한 운동방정식은 아래와 같다.
| (1a) |
| (1b) |
| (1c) |
발전기에서 발생된 하중(F)에 대한 마운트 상단(X3)의 응답은 식 (2)로 정리가 된다.
| (2) |
신규 마운트 구조에 대해서도 운동방정식은 식 (3a)~ (3c)로 나타낼 수 있으며, 마운트 상단(X6)에서의 응답은 식 (4)로 표현된다. 여기서, x5에 해당하는 질량은 다른 질량들 대비 상대적으로 작아 식 (3c)의 계산 과정에서 생략하였다.
| (3a) |
| (3b) |
| (3c) |
| (4) |
기존 마운트를 설치한 조건 대비 제안 마운트의 응답 특성을 상대적으로 판단하기 위해 기존 연구에서 응답 인덱스(response index)를 제안하였으며 식 (2)와 식 (4)를 통해 식 (5)로 표현이 된다(6). 응답 인덱스는 기존 마운트 대비 신규 마운트의 응답의 크기 비를 나타내는 값으로 관심 있는 주파수 대역에서 응답을 크기를 비교함으로써 신규 마운트의 응답 특성을 효율적으로 평가하는 값이다. 해당 인덱스 값을 활용하여 모든 주파수 대역에서 1보다 작은 값을 가지는 경우에 한정하여 신규 마운트의 진동저감 특성이 우수함을 보일 수 있다.
| (5) |
3. 기초 질량부의 민감도 분석
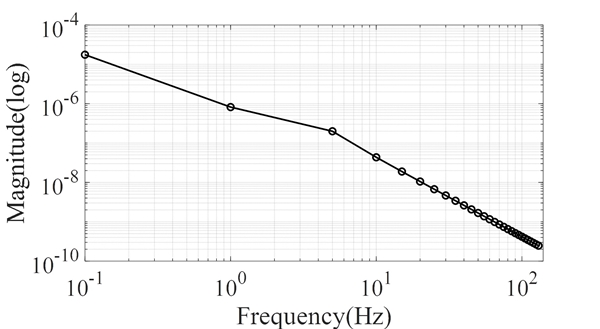
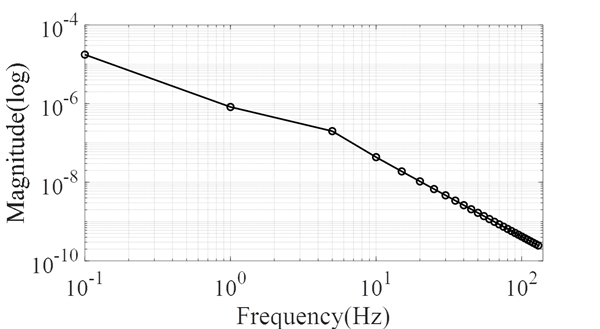
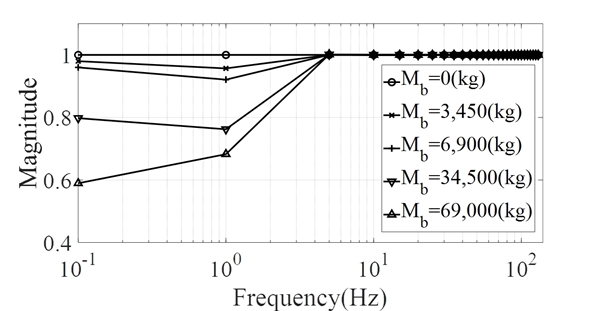
기초 질량부의 민감도 해석은 식 (5)로 나타낸 응답 인덱스를 활용하였다. 신규 마운트 모듈에서는 기초 질량부가 존재하지 않을 것이기 때문에 기초 질량부가 변화함에 따라 응답 인덱스가 변화하는 것은 기존 마운트 모듈 부분에서만 영향을 줄 것이다. 업체에서 내부 규정으로 사용되는 기초 질량부가 750 kW 발전기에 대해 6900 kg이므로 해당 값을 기준으로 5개의 조건에 대해 시뮬레이션을 진행하였다. 기존 마운트 모듈에 해당하는 식 (2)의 주파수응답함수, 식 (4)의 제안 마운트의 주파수응답함수는 각각 Fig. 3과 Fig. 4에 각각 나타내었으며 5개의 응답함수 중 6900 kg 조건에 대해서만 대표로 도시를 하였다. 다른 질량을 갖는 주파수응답함수들은 유사한 그래프 형태를 보여 도시를 생략하였다. 도시된 모든 주파수응답함수들은 모두 주파수가 높아짐에 따라 응답이 급격하게 줄어들고 있음을 확인할 수 있다. 2가지 주파수 응답함수를 활용하여 식 (5)의 응답 인덱스 값을 얻을 수 있으며 해당 시뮬레이션 결과를 Fig. 6에 보여준다.
주파수응답함수 값들은 서로 유사한 경향을 보임에 따라 서로 다른 점을 확인하기 어려우나 Fig. 6의 응답 인덱스 값을 통해서 기초 중량의 변화에 따라 5 Hz 이하의 저주파에서 응답 특성이 차이가 나타남을 확인할 수 있다. 기본적으로 기초 중량이 존재하지 않는 경우에는 Fig. 2와 Fig. 3의 모델이 동일한 값을 가질 수밖에 없다. 하지만 기초 중량이 증가함에 따라 저주파에서의 응답이 기존 마운트 대비 신규 마운트의 경우에 낮은 값을 가짐을 알 수 있다.
이러한 결과가 나타난 원인을 판단하기 위해 주파수의 변화에 따라 주파수응답함수에 영향을 주는 인자를 확인해 볼 필요가 있다. 관심 주파수가 증가(최대 120 Hz)함에 따라 식 (2)와 식 (4)의 주파수응답함수는 강성보다는 질량 부분이 주요한 응답 값을 보일 수밖에 없다. 따라서 주파수응답함수 값들은 아래와 같이 근사적으로 나타낼 수 있다.
| (6) |
| (7) |
따라서 이와 같은 관계에서는 응답 인덱스 값이 모두 “1”의 값을 가지는 것을 알 수 있다. 하지만 주파수 값이 작아지는 경우에는 질량 성분의 기여도가 급격하게 줄어들기 때문에 강성의 영향이 증가할 수밖에 없다. 물론 주파수응답함수에는 강성이나 질량 이외에도 감쇠 항이 존재하지만 상대적으로 해당 항은 값이 상대적으로 작기 때문에 고려 대상에서 제외하였다. 관심 주파수가 낮은 경우에는 강성의 영향이 상대적으로 매우 부각되며 강성 중 Kb의 값이 상대적으로 매우 크기 때문에 Kx의 값이 유사하다고 할 때 아래와 같이 근사식이 도출된다.
| (8) |
| (9) |
따라서 관심 주파수가 DC 성분으로 수렴하는 과정에서 Kb와 Kx의 값이 동일하다고 하면 다시 응답 인덱스 값이 “1”로 수렴할 것이다. Fig. 6에서 감소하던 응답 인덱스가 다시 증가하는 것은 이러한 저주파 특성이 반영되었다고 판단된다.
중요한 변화는 약 1 Hz 근방의 성분인데 기초 중량이 증가할수록 갑자기 응답 인덱스 값이 크게 감소함을 알 수 있다. 해당 조건에서는 질량의 영향이 줄어들고 강성이 영향이 증가하는 천이 과정으로 2개의 주파수 값을 근사적으로 표현하기 어렵다. 이 경우 기초 중량은 응답 크기를 줄이는데 기여하기 때문에 저주파 대역에서 기초 중량은 중요한 역할을 수행한다고 볼 수 있다. 특히, 해당 주파수 대역은 내구 측면에서 변위 값이 상대적으로 큰 영역이기 때문에 대상 발전기의 피로 손상도를 증가시키는 원인이 된다. 하지만 대상 발전기의 경우 작동 환경이 30 Hz(= 1800 rev/min)으로 고정되어 있기 때문에 가진 조건이 해당 주파수를 만족하는 조건은 엔진이 기동하여 회전수를 높이는 과정에서 잠깐 지나가는 구간이므로 큰 영향이 없을 가능성이 크다.
시뮬레이션 결과는 기존 연구(7)에서 기초 질량을 제거한 간단한 마운트지지 구조가 대상 시스템의 신규 마운트 조건으로 적당하는 결론과 상이한 점이다. 하지만 서로 다른 조건은 관심 주파수 대역의 차이에서 나오는 것이다. 이 연구 결과는 기초 중량이 스프링이나 댐퍼의 중가에 존재하는 마운트 구조에서 저주파 영역에서의 기여도를 확인하였다는 점에서 의미가 있다. 더불어 최소 주파수 대역을 30 (Hz)으로 설정하여 최적의 마운트 조건을 찾은 기존의 연구(7) 결과에 대해서는 유사한 결과를 제공하는 것으로 기존 최적 마운트 조건은 유효하다.
다른 관점에서는 마운트의 역할이 바닥면으로 전달되는 진동을 방지하는데 중요한 역할을 수행하기 때문에 하부 진동이 전달되는 측면에서는 하부 전달력을 증가시킴으로써 부정적인 영향을 줄 가능성이 크다(8). 관심 주파수 영역이 아닌 상황에서 저주파 대역의 전달율 개선을 위해 기초 질량부를 증가시키는 것은 시공 측면에서도 비용이나 설치비용이 상당한 부담을 준다. 따라서 실제 마운트 시공 시 기초 질량부의 증가 여부는 바닥면 진동전달 측면까지를 고려하여 신중하게 결정되어야 한다.
4. 결 론
이 연구에서는 기초 중량이 지지된 시스템 자체에 어떤 응답 기여를 하는지를 판단하기 위해 선형화된 전체 시스템에 대해 주파수응답함수를 획득한 후 서로 다른 기초 중량 조건에 대해 시뮬레이션을 수행하였다. 해당 시뮬레이션 결과 대상 시스템인 750 kW급 비상발전기 시스템에서는 큰 영향이 없음을 확인하였다. 하지만 만약 지지 시스템의 작동 영역에 5 Hz 이하의 저주파 영역을 포함하는 경우에는 응답 값을 줄여주는 역할이 있음을 확인하였다. 따라서 마운트 구조가 기계요소 부품인 스프링이나 댐퍼 중간에 기초 중량이 존재하는 경우에 저주파의 진동을 줄이는데 효과적이라고 판단된다.
Acknowledgments
A part of this paper was presented at the KSNVE 2018 Annual Autumn Conference
이 연구는 한국연구재단에서 주관하는 이공학개인기초연구지원사업(2017R1D1A1B3034520)의 성과물로 관계 분들에게 감사드립니다.
References
-
Moshrefi-Torbati, M., Forrester, J. A., Forrester, A. I. J., Keane, A. J., Brennan, M. J., and Elliott, S. J., (2012), Novel Active and Passive Anti-vibration Mountings, Journal of Sound and Vibration, 331(7), p1532-1541.
[https://doi.org/10.1016/j.jsv.2011.12.005]

-
Yang, B., Hu, Y., Fang, H., and Song, C., (2017), Research on Arrangement Scheme of Magnetic Suspension Isolator for Multi-degree Freedom Vibration Isolation System, Journal of Industrial Information Integration, 6, p47-55.
[https://doi.org/10.1016/j.jii.2017.04.003]

-
Wu, Z., Jing, X., Sun, B., and Li, F., (2016), A 6DOF Passive Vibration Isolator Using X-shape Supporting Structures, Journal of Sound and Vibration, 380, p90-111.
[https://doi.org/10.1016/j.jsv.2016.06.004]

-
Yang, J., Xiong, Y. P., and Xing, J. T., (2016), Vibration Power Flow and Force Transmission Behavior of a Nonlinear Isolator Mounted on a Nonlinear Base, International Journal of Mechanical Sciences, 115~116, p238-252.
[https://doi.org/10.1016/j.ijmecsci.2016.06.023]

-
Siami, A., Karimi, H. R., Cigada, A., Zappa, E., and Sabbioni, E., (2018), Parameter Optimization of an Inerter-based Isolator for Passive Vibration Control of Michelangelo’s Rondanini Pieta, Mechanical Systems and Signal Processing, 98, p667-683.
[https://doi.org/10.1016/j.ymssp.2017.05.030]

-
Kim, C. J., Seo, J. K., and Hwang, J. B., (2017), Simplified Structure Design of Supporting Mount Module at Emergency Electric Generator, Transactions of the Korean Society for Noise and Vibration Engineering, 27(7), p863-869.
[https://doi.org/10.5050/ksnve.2017.27.7.863]

-
Kim, C. J., (2018), Design Criterion of Damper Component of Passive-type Mount Module without Using Base Mass-block, Energies, 11(6), p1548.
[https://doi.org/10.3390/en11061548]

- Rao, S. S., (2011), Mechanical Vibration, 5th Edition, Pearson, Singpore.

Chan-Jung Kim received Ph. D. degree from Seoul National University in 2011. He was senior researcher at Korea Automotive Technology Institute over 12 years (2003-2015). Since 2015, he has been joined as the faculty of Pukyong National university, where he is assistant professor of Mechanical Design Engineering. His research interests are in the area of the vibration fatigue, noise and vibration issue of mechanical systems.