전달행렬법을 이용한 유성기어형 반공진 진동 절연기 특성 연구

1. 서 론

기계 및 전기 시스템 내의 각 요소 사이에서 진동 전달을 저감하기 위하여 수동형 진동 절연기(passive vibration isolator) 또는 동흡진기(dynamic absorber) 등이 전통적으로 사용되어 왔다^(1,2). 이러한 방법들과 함께 시스템 내에 관성 연성을 이용한 반공진 특성을 도입하여 진동 전달을 저감하는 반공진 진동 절연기 (dynamic anti-resonance vibration isolator: DAVI) 에대한 연구도 진행되어 왔다^(3~9). 전통적으로 DAVI는 주로 병진운동(translational motion) 시스템을 대상으로 검토 및 연구되어 왔으나^(3~7)최근에는 회전운동(rotational motion) 시스템을 대상으로 유성기어형 반공진 절연기(planetary gear type dynamic anti-resonance vibration isolator: PG-DAVI)가 소개되었다^(8,9). 회전운동 시스템을 대상으로 하는 PG-DAVI는 유성기어를 이용하여 시스템 내의 관성요소들을 연성시키는 방법의 절연기이다^(8,9).

공학에서는 복잡한 대형 시스템을 여러 하위 시스템으로 나누고 각 하위 시스템의 특성을 이용하여 전체 시스템의 특성을 정의하는 방법이 많이 사용되고 있다⁽⁷⁾. 이들 중 하나가 각 하위 시스템의 전달행렬을 정의하고 이를 이용하여 전체 시스템에 대한 전달행렬을 유도하여 시스템 특성을 파악하는 전달행렬법이다⁽¹⁰⁾. 단수입력-단수출력(single-input/single-output: SISO) 시스템의 경우 각 하위 시스템의 전달행렬을 시스템의 입력단과 출력단 사이의 관계를 네 개의 주파수 함수를 이용하여 정의하는 기계적 4단 정수법으로 유도하는 경우가 많다⁽¹¹⁾. 이러한 접근 방법은 전체 시스템의 전달행렬을 단순히 시스템을 구성하고 있는 하위 시스템의 전달행렬을 곱하여 구할 수 있다는 장점이 있다^(12~14).

L-DAVI 시스템에 대한 전달행렬을 유도했던 이전 연구의 후속 연구로 이 연구에서는 PG-DAVI 시스템에 대한 전달행렬을 유도한다. 이렇게 정의된 PG-DAVI 시스템 전달행렬의 타당성을 검증하기 위하여 이 시스템이 포함된 간단한 진동계의 응답 특성을 유도된 행렬을 적용한 전달행렬법으로 계산한 다음 그 결과를 전통적으로 사용해오던 행렬과 주파수전달함수를 이용한 결과와 비교한다. 다음으로 3자유도 회전진동계의 각변위 전달률을 개선하기 위하여 PG-DAVI 시스템을 적용하는 방법을 검토한다. 위에서 유도된 전달행렬을 이용하여 주어진 목표주파수 영역의 응답특성을 개선하기 위한 PG-DAVI 시스템의 최적 구성을 검토하고, 도출된 PG-DAVI 시스템을 적용했을 때 나타나는 응답특성 개선 효과를 전달행렬법을 이용하여 검토한다. 마지막으로 동일한 목표주파수에 대해 선정된 종래의 동흡진기를 적용한 경우와 비교하여 PG-DAVI의 효율성을 검증한다.

2. 유성기어형 반공진 절연기(PG-DAVI)

반공진 진동 절연기는 연성된 관성을 이용, 반공진 효과를 도입함으로써 진동 전달을 감소시키는 시스템이다^(3~9). 병진운동 진동계의 경우에는 레버 메커니즘, 회전운동 진동계의 경우에는 유성기어를 이용하여 관성요소를 연성시킨다^(8,9). 이러한 진동 절연기는 기존의 질량, 스프링 및 감쇠요소로 구성된 일반 절연기나 동흡진기와 달리 감쇠가 작음에도 불구하고 충분한 절연 효과를 나타내는 동시에 시스템의 반공진 주파수 이상 영역에서의 진동 전달률이 우수하므로 고주파수 절연 성능 개선에 적합하다. 따라서 시스템의 주요 변수를 적절하게 선정하면 광대역 진동 절연기를 구현하는 것이 가능하다⁽⁹⁾.

2.1 PG-DAVI의 개념

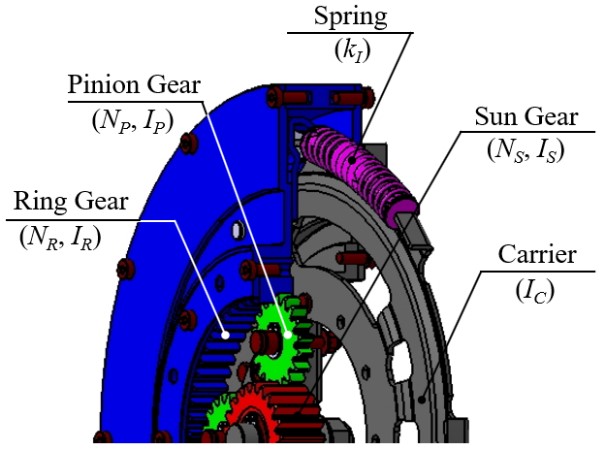
유성기어형 반공진 진동 절연기(PG-DAVI)는 제어 관성과 입·출력 측 사이의 관성 연성을 이용하여 특정한 주파수 영역 내에 반공진 효과를 유도하는 진동 절연기이다. PG-DAVI 시스템의 개략적인 설명도가 Fig. 1에 주어져 있다⁽⁹⁾. 그림에서 알 수 있는 바와 같이, PG-DAVI 시스템은 시스템의 중심축을 기준으로 회전하는 링기어, 태양기어와 캐리어에 고정된 자체 중심축을 기준으로 자전하는 동시에 시스템 중심축을 기준으로 공전하는 피니언 및 스프링으로 구성되어 있다. 시스템 내부에는 피니언, 태양기어로 구성된 절연기와 스프링이 병렬로 연결되어있다.입력 측 캐리어에 가해진 토크는 스프링과 피니언을 통해 출력 측 링기어로 전달된다. 이 과정에서 태양기어는 피니언의 도움을 받아 입력 및 출력 측에 관성 연성을 발생시킨다. 이 연구에서는 시스템 내에서 관성 연성을 유도하는 피니언의 관성모멘트는 무시할 수 있다고 가정하였다. 실제 상황에서는 피니언의 관성모멘트는 다른 기어에 비해 아주 작은 경우가 대부분이다.

Fig. 1

Schematic model of the PG-DAVI system

3. PG–DAVI의 전달행렬

3.1 PG-DAVI 전달행렬의 유도

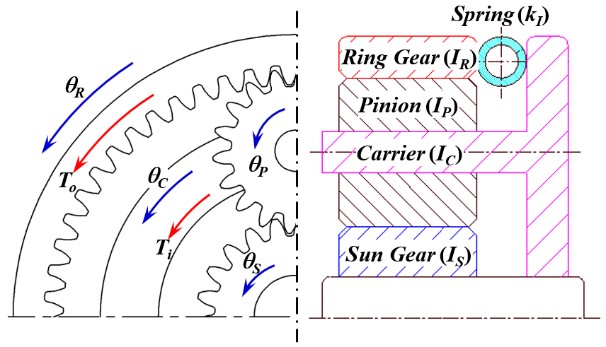
PG-DAVI 시스템의 작동원리가 Fig. 2에 설명되어 있다. 앞장에서 설명한 바와 같이 링기어, 태양기어, 캐리어는 전체 시스템의 중심축을 기준으로 회전하며 피니언은 캐리어에 고정된 자체 중심축을 기준으로 자전하는 동시에 캐리어와 함께 시스템 중심축을 기준으로 공전한다⁽⁹⁾.

Fig. 2

Dynamic model of the PG isolator

이전 연구⁽⁷⁾에서 레버형 반공진 절연기 운동방정식을 유도하기 위해 사용되었던 방법을 참고하여 주어진 조건 하에서 캐리어에 고정된 피니언 축에 가해진 입력 토크(T_i) 및 회전속도(Ω_i)와 출력 측 링기어에 전달되는 출력 토크(T_o) 및 회전속도(Ω_o) 사이의 관계를 분석하면 다음과 같이 유성기어 쌍에 대한 전달행렬을 유도할 수 있다. 앞에서 언급한 바와 같이, 이 과정에서 피니언의 관성모멘트는 무시할 수 있다고 가정하였다.

$\[ {\Gamma }_I=\left[\begin{array}{cc}{\left({\alpha }_{11}\right)}_I& {\left({\alpha }_{12}\right)}_I\\ {\left({\alpha }_{21}\right)}_I& {\left({\alpha }_{22}\right)}_I \end{array}\right] \]$

(3a)

$\[ {\left({\alpha }_{11}\right)}_I={\left.\frac{T_i}{T_o}\right|}_{{\Omega }_o=0}=\frac{\beta +1}{\beta } \]$

(3b)

$\[ {\left({\alpha }_{12}\right)}_I={\left.\frac{T_i}{{\Omega }_o}\right|}_{T_o=0}=0 \]$

(3c)

$\[ {\left({\alpha }_{21}\right)}_I={\left.\frac{{\Omega }_i}{T_o}\right|}_{{\Omega }_o=0}=\frac{1}{i\omega \beta \left(\beta +1\right)I_S} \]$

(3d)

$\[ {\left({\alpha }_{22}\right)}_I={\left.\frac{{\Omega }_i}{{\Omega }_o}\right|}_{T_o=0}=\frac{\beta }{\beta +1} \]$

(3e)

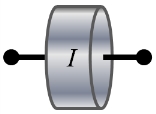
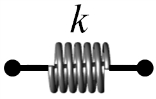
또한 Fig. 2에서 알 수 있는 바와 같이, 전체 PG-DAVI 시스템은 절연기와 관성체, 스프링 및 감쇠기 등이 연결되어 있으므로 이들 요소에 대한 전달행렬도 정의되어야 한다. 이전의 연구결과에 따르면 상기요소들의 전달행렬은Table 1과 같이 정의된다⁽¹⁰⁾.

Table 1

Transfer matrices for the basic vibration elements

위에서 정의된 절연기, 스프링, 관성요소 및 감쇠요소의 전달행렬들을 이용하여 전체 PG-DAVI 시스템의 전달행렬(Γ_DAVI)을 유도할 수 있다. Fig. 2에서 유추할 수 있는 바와 같이, 전체 시스템은 기어절연기와 직렬로 연결된 캐리어 및 링기어의 관성요소로 모델링할 수 있으며 기어 절연기는 기어쌍과 병렬 연결된 스프링, 감쇠기로 모델링될 수 있다. 따라서 기어 절연기의 전달행렬은 각 요소들의 전달행렬들을 이용하여 다음 식과 같이 구할 수 있다⁽¹⁰⁾.

$\[ {\Gamma }_{GI}=\left[\begin{array}{cc}{\left({\alpha }_{11}\right)}_{GI}& {\left({\alpha }_{12}\right)}_{GI}\\ {\left({\alpha }_{21}\right)}_{GI}& {\left({\alpha }_{22}\right)}_{GI} \end{array}\right] \]$

(4a)

$\[ \begin{array}{c}{\left({\alpha }_{11}\right)}_{GI}=P/Q,{\left({\alpha }_{12}\right)}_{GI}=\left(PR-Q^2\right)/Q,\\ {\left({\alpha }_{21}\right)}_{GI}=1/Q,{\left({\alpha }_{22}\right)}_{GI}=R/Q\end{array} \]$

(4b)

$\[ P=\sum _{i=1}^3\frac{{\left({\alpha }_{11}\right)}_i}{{\left({\alpha }_{21}\right)}_i},Q=\sum _{i=1}^3\frac{1}{{\left({\alpha }_{21}\right)}_i},R=\sum _{i=1}^3\frac{{\left({\alpha }_{22}\right)}_i}{{\left({\alpha }_{21}\right)}_i} \]$

(4c)

이 식에서 (α_mn)_GI은 기어 절연기에 대한 전달행렬의 각 요소이며 (α_mn)_i는 각각 기어쌍 (i= 1), 스프링 (i= 2) 및 감쇠요소 (i= 3)에 대한 전달행렬의 각 요소이다. 식 (4)와 Table 1에 주어진 이들 행렬을 이용하여 기어 절연기의 전달행렬을 다음 식 (5)과 같이 구할 수 있다.

$\[ {\left({\alpha }_{11}\right)}_{GI}=\frac{\left\{k_I-{\left(\beta +1\right)}^2{I}_S{\omega }^2\right\}-i\omega c_I}{\left\{k_I-\beta \left(\beta +1\right)I_S{\omega }^2\right\}-i\omega c_I} \]$

(5a)

$\[ {\left({\alpha }_{12}\right)}_{GI}=\frac{-{\omega }^2{cI}_S+i\omega k_I}{\left\{k_I-\beta \left(\beta +1\right)I_S{\omega }^2\right\}-i\omega c_I} \]$

(5b)

$\[ {\left({\alpha }_{21}\right)}_{GI}=\frac{i\omega }{\left\{k_I-\beta \left(\beta +1\right)I_S{\omega }^2\right\}-i\omega c_I} \]$

(5c)

$\[ {\left({\alpha }_{22}\right)}_{GI}=\frac{\left\{k_I-{\beta }^2{I}_S{\omega }^2\right\}-i\omega c_I}{\left\{k_I-\beta \left(\beta +1\right)I_S{\omega }^2\right\}-i\omega c_I} \]$

(5d)

이 식에서 k_I는 DAVI 내의 코일 스프링의 강성이고 c_I는 도입된 감쇠요소의 감쇠계수이다.

앞에서 설명한 바와 같이 전체 PG-DAVI 시스템은 기어절연기와 직렬 연결된 캐리어 및 링기어의 관성요소로 이상화될 수 있으므로 전체 시스템의 전달행렬(Γ_DAVI)은 다음 식과 같이 두 관성요소와 기어절연기 행렬을 곱하여 구할 수 있다.

$\[ {\Gamma }_{DAVI}={\Gamma }_C {\Gamma }_{GI} {\Gamma }_R=\left[\begin{array}{cc}{\left({\alpha }_{11}\right)}_{DAVI}& {\left({\alpha }_{12}\right)}_{DAVI}\\ {\left({\alpha }_{21}\right)}_{DAVI}& {\left({\alpha }_{22}\right)}_{DAVI}\end{array}\right] \]$

(6a)

$\[ \begin{array}{cc}{\Gamma }_C=\left[\begin{array}{cc}1& i\omega I_C\\ 0& 1\end{array} \right],& {\Gamma }_R=\left[\begin{array}{cc}1& i\omega I_R\\ 0& 1\end{array}\right]\end{array} \]$

(6b)

위에서 얻어진 행렬을 이용하여 전체 PG-DAVI 시스템의 입력 및 출력 측 토크와 각속도 사이의 관계가 다음 식으로 주어진다.

$\[ \left\{\begin{array}{c}{T}_i\\ {\Omega }_i\end{array}\right\}=\left[\begin{array}{cc}{\left({\alpha }_{11}\right)}_{DAVI}& {\left({\alpha }_{12}\right)}_{DAVI}\\ {\left({\alpha }_{21}\right)}_{DAVI}& {\left({\alpha }_{22}\right)}_{DAVI}\end{array}\right]\left\{\begin{array}{c}{T}_o\\ {\Omega }_o\end{array}\right\} \]$

(7)

따라서, 위의 식으로부터 PG-DAVI 시스템의 입력토크와 출력 각속도 사이의 관계는 다음 식으로 주어진다.

$\[ {\Omega }_o={\left.\frac{T_i}{{\left({\alpha }_{12}\right)}_{DAVI}}\right|}_{T_o=0} \]$

(8a)

$\[ \left(i\omega \right)\frac{{\Omega }_o}{T_i}={\left.\frac{i\omega }{{\left({\alpha }_{12}\right)}_{DAVI}}\right|}_{T_o=0} \]$

(8b)

3.2 전달행렬의 검증

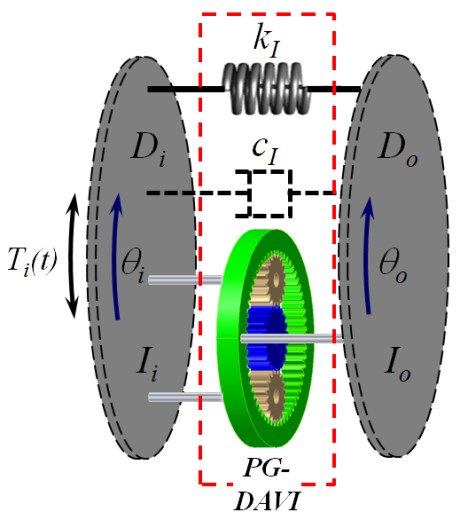
위에서 유도된 전달행렬을 이용한 전달행렬법으로 간단한 검증 시스템의 응답 특성을 구한 다음 그 결과를 관성, 강성 및 감쇠행렬을 이용하여 전통적인 주파수전달함수를 이용한 결과와 비교함으로써 PG-DAVI 시스템의 전달행렬의 정확도를 확인한다. 이 과정에서 사용된 검증시스템의 개략도가 Fig. 3에 설명되어 있다. 그림에서 보는 바와 같이 이 시스템은 PG-DAVI 시스템에 연결된 두 개의 디스크로 구성되어있다. 두 디스크 D_i및 D_o는 각각 캐리어와 링기어에 직접, 강체로 연결되어 있다. 또한 이 시스템의 기계적인 제원은 Table 2에 설명되어 있다. 이 시스템에서 D_i및 D_o의 관성모멘트를 무시할 수 있다고 가정하면 그 결과는 PG-DAVI 시스템만의 응답특성이라고 할 수 있다. 그림과 Table에 주어진 시스템의 각 엑셀러런스(angular accelerance: α_o/ T_i)를 아래에 설명한 두 방법을 이용하여 계산한 다음 그 결과를 비교하였다.

Fig. 3

Mechanical model of the validation system

Table 2

Specifications of the validation system

식 (8)에 주어진 운동방정식은 관성, 강성 및 감쇠행렬을 이용하여 다음 식 (9)와 같이 행렬식의 형태로 재구성할 수 있다.

$\[ \left[I\right]\left\{\ddot{\Theta }\right\}+\left[C\right]\left\{\dot{\Theta }\right\}+\left[K\right]\left\{\Theta \right\}=\left\{T\right\} \]$

(9a)

$\[ \left[I\right]=\left[\begin{array}{cc}{I}_i+I_C+I_S{\left(1+\beta \right)}^2& -I_S \beta \left(1+\beta \right)\\ -I_S \beta \left(1+\beta \right)& I_R+I_S {\beta }^2+I_o\end{array}\right] \]$

(9b)

$\[ \left[C\right]=\left[\begin{array}{cc}{c}_I& -c_I\\ -c_I& c_I\end{array}\right] \]$

(9c)

$\[ \left[K\right]=\left[\begin{array}{cc}{k}_I& -k_I\\ -k_I& k_I\end{array}\right] \]$

(9d)

따라서, 검증시스템의 D_i에 조화함수 형태의 토크가 가해지는 경우에 D_o에서 발생하는 각변위 응답은 식 (9)의 행렬들을 이용하여 다음 식과 같이 계산할 수 있다.

$\[ \left\{\Theta \right\}={\left(-{\omega }^2\left[I\right]+i\omega \left[C\right]+\left[K\right]\right)}^{-1}\left\{T\right\} \]$

(10)

이 식에서 {Θ} = {Θ_iΘ_o}^T는 입·출력 측의 응답 벡터이고 ω는 입력 토크와 출력 변위의 각진동수이며 {T} = {T_i0}^T는 입력토크벡터이다.

Fig. 3에서 알 수 있는 바와 같이, 검증 시스템은 두 개의 디스크와 PG-DAVI 시스템이 직렬로 연결되어 있다. 이러한 시스템의 전체 전달행렬은 각 요소의 전달행렬을 순서대로 곱해서 구할 수 있다⁽¹⁰⁾. 결과적으로 검증시스템의 입·출력단 사이의 관계는 식 (11a)로 주어지며, 전체 전달행렬 Γ₁₄는 다음 식과 같이 각 구성요소의 행렬을 순서대로 곱한 행렬로 정의된다.

$\[ \left\{\begin{array}{c}{T}_i\\ {\Omega }_i\end{array}\right\}={\Gamma }_{14}\left\{\begin{array}{c}{T}_o\\ {\Omega }_o\end{array}\right\}={\Gamma }_{12}{\Gamma }_{23}{\Gamma }_{34}\left\{\begin{array}{c}{T}_o\\ {\Omega }_o\end{array}\right\} \]$

(11a)

$\[ {\Gamma }_{12}=\left[\begin{array}{cc}1& i\omega \left(I_I+I_C\right)\\ 0& 1\end{array}\right] \]$

(11b)

$\[ {\Gamma }_{23}={\Gamma }_{DAVI}=\left[\begin{array}{cc}{\left({\alpha }_{11}\right)}_{DAVI}& {\left({\alpha }_{12}\right)}_{DAVI}\\ {\left({\alpha }_{21}\right)}_{DAVI}& {\left({\alpha }_{22}\right)}_{DAVI}\end{array}\right] \]$

(11c)

$\[ {\Gamma }_{34}=\left[\begin{array}{cc} 1 & i\omega \left(I_R+I_O\right)\\ 0& 1\end{array}\right] \]$

(11d)

이 식에서 Γ_(i)(i+1)는 i번째 요소의 전달행렬이다.

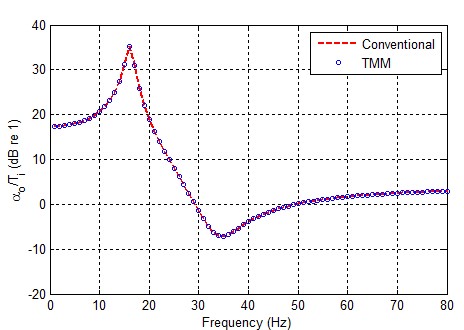
위의 전달행렬을 이용하여 계산된 샘플 시스템의 조화응답을 다음 그림에 전통적인 방법을 이용하여 계산된 결과와 비교하였다(Fig. 4).

Fig. 4

αo/Ti of the validation system

그림에서 알 수 있는 바와 같이 전달행렬법을 이용하여 계산된 α_o/T_i는 주어진 주파수 영역 내에서 전통적인 방법을 이용한 결과와 정확하게 일치하고 있다. 이 결과를 바탕으로 전체 PG-DAVI 시스템에 대하여 정의된 전달행렬은 이와 같은 절연기를 포함한 회전진동계의 진동 전달 특성을 충분히 정확하게 해석할 수 있다고 할 수 있다.

4. 제안된 전달행렬의 적용

이 장에서는 유성기어형 반공진 절연기를 적용하여 회전진동계의 각변위 전달률을 저감하는 방법에 대해 검토한다. 앞 장에서 유도된 절연기의 전달행렬을 적용한 전달행렬법을 이용하여 시스템의 응답특성을 계산한다. 절연기 적용의 효과는 전달행렬법을 이용하여 계산된 원래 시스템과 절연기 적용 시스템의 전달특성을 비교하여 파악한다. 또한, 동일한 방법을 통하여 주어진 목표주파수 범위에서 가장 효과적인 절연기 제원을 검토한다.

4.1 대상 시스템

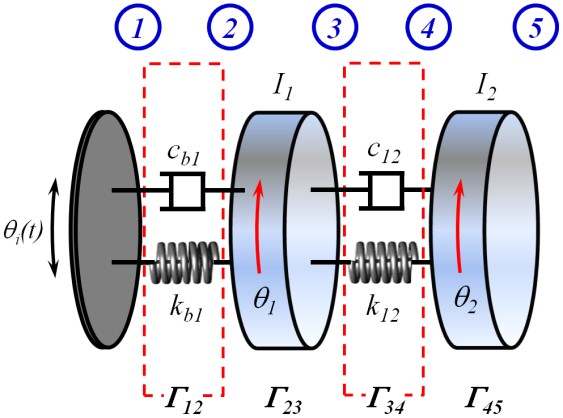
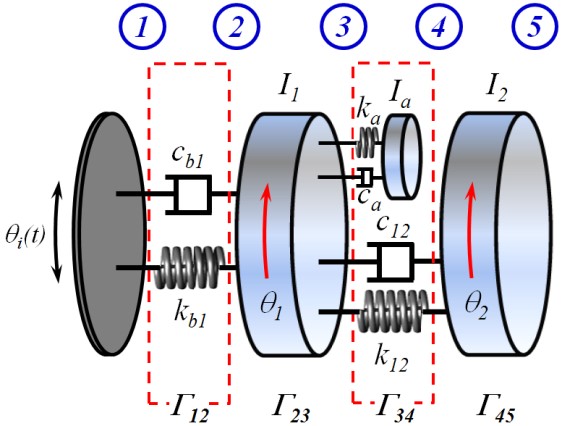
이 연구에 사용된 3자유도 회전 진동계의 구성이 Fig. 5에 설명되어 있다. 그림에서 보는 바와 같이 대상 시스템은 관성모멘트가 무시할 수 있는 기저에 연결된 2자유도 회전 진동 시스템이며 시스템의 제원은 Table 3에 설명되어 있다. 그림에서 유추할 수 있는 바와 같이 대상시스템은 관성모멘트를 무시할 수 있는 기저부와 두 개의 관성요소 및 이들을 연결하는 두 개의 스프링 + 감쇠기 결합요소로 이루어진 2자유도, 비고정 회전 진동계이다.

Fig. 5

Mechanical model of the target system for the PG-DAVI system

Table 3

Specifications of the validation system

또한 이 진동계를 전달행렬로 나타내면 Fig. 5와 같이 각 부분에 대한 전달행렬 4개로 표현할 수 있으며 전체 전달행렬은 다음 식과 같이 각 행렬을 순서에 따라 곱한 것으로 나타난다.

$\[ {\Gamma }_{15}={\Gamma }_{12}{\Gamma }_{23}{\Gamma }_{34}{\Gamma }_{45} \]$

(12a)

$\[ {\Gamma }_{\left(2i\right)\left(2i+1\right)}={\Gamma }_{I_i}=\left[\begin{array}{cc}1& i\omega I_i\\ 0& 1\end{array}\right]i=\mathrm{1,2} \]$

(12b)

$\[ {\Gamma }_{12}=\left[\begin{array}{cc}1& 0\\ \frac{i\omega }{k_{bI}+i\omega c_{bI}}& 1\end{array}\right] \]$

(12c)

$\[ {\Gamma }_{34}=\left[\begin{array}{cc}1& 0\\ \frac{i\omega }{k_{12}+i\omega c_{12}}& 1\end{array}\right] \]$

(12d)

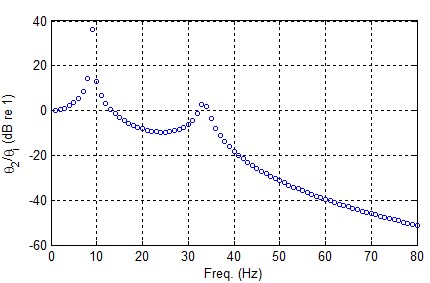
다음으로 대상 시스템의 각변위 전달률 Θ₂/Θ_i은 다음 식 (13)을 이용하여 구할 수 있다.

$\[ \left\{\begin{array}{c}{T}_i\\ {\Omega }_i\end{array}\right\}={\Gamma }_{12}{\Gamma }_{23}{\Gamma }_{34}{\Gamma }_{45}\left\{\begin{array}{c}{T}_2\\ {\Omega }_2\end{array}\right\} \]$

(13)

위 식을 이용하여 계산된 각변위 전달률 Θ₂/Θ_i이 Fig. 6에 설명되어 있다. 그림에서 알 수 있는 바와 같이 전달률은 9 Hz 및 34 Hz 부근에 두 개의 peak을 가지고 있다.

Fig. 6

Θ2/Θi of the target system obtained by TMM

4.2 PG-DAVI 전달행렬의 적용

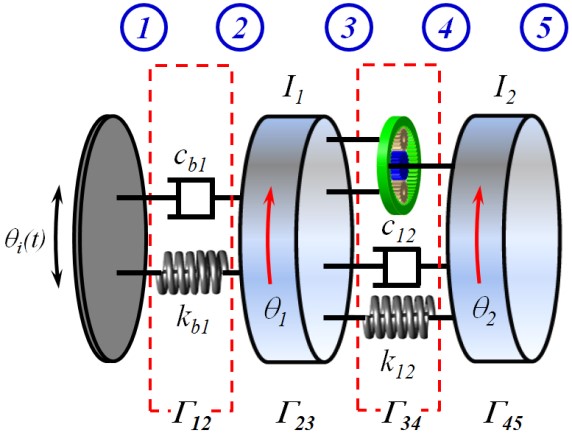
이 절에서는 Fig. 6에 주어진 대상 시스템의 변위 전달률을 저감하기 위한 최적 PG-DAVI의 제원을 검토하고 이를 적용했을 경우 나타나는 변위전달률 저감효과를 파악한다. 대상 시스템에 PG-DAVI를 적용한 예가 Fig. 7에 설명되어 있다.

Fig. 7

Configuration of the target system modified with PG-DAVI system

절연기의 제원은 대상 시스템의 두 번째 고유진동수 부근의 전달률을 저감할 수 있도록 최적화한다. 이 연구에서는 간이적으로 계산된 대상 시스템의 고유진동 특성을 고려하여 PG-DAVI 시스템의 위치를 I₁와 I₂사이로 선정하였다. 또한 기존 시스템에 사용되었던 스프링(k₁₂)와 감쇠기(c₁₂)는 그대로 적용한다.

(1) PG-DAVI의 최적 제원

앞에서 언급한 바와 같이 이 연구에서는 PG-DAVI 시스템을 통하여 34 Hz 부근의 전달률을 감소시키고자 한다. 따라서, PG-DAVI 시스템의 반공진 진동수(ω_AR)를 이 주파수와 일치하도록 설정한다. 식 (6)에 주어진 PG-DAVI 시스템의 전달행렬을 고려하면 ω_AR은 다음 식으로 계산될 수 있다.

$\[ {\omega }_{AR}=\sqrt{\frac{k_{12}}{\beta \left(1+\beta \right)I_S}} \]$

(14)

따라서, 주어진 목표주파수에 반공진 현상을 유도하기 위해서는 위 식에 따라 β와 I_S를 적절하게 설정하여야 한다. k₁₂를 원래 시스템과 동일하게 적용하였으므로 ω_AR≅ 34 × 2π (rad/s)이 될 수 있도록 β와 I_S를 각각 2.6364 및 0.0042 kgm²으로 선정하였다. 또한, 간이적으로 계산된 대상 시스템의 고유진동 특성을 고려하여 PG-DAVI 시스템의 위치를 I₁와 I₂사이로 선정하였다.

전체 전달행렬은 식 (12a)에 주어진 방법을 동일하게 이용하여 구할 수 있으나 PG-DAVI 시스템이 추가된 Γ₃₄는 다음 식 (13)에 설명된 Γ₃₄^'로 대치되어야 한다.

$\[ {{\Gamma }_{34}}^{\text{'}}={\left[\begin{array}{cc}{\left({\alpha }_{11}\right)}_{DAVI}& {\left({\alpha }_{12}\right)}_{DAVI}\\ {\left({\alpha }_{21}\right)}_{DAVI}& {\left({\alpha }_{22}\right)}_{DAVI}\end{array}\right]}_{34} \]$

(15)

위 식의 주어진 전달행렬의 각 요소는 식 (6)을 이용하여 계산할 수 있다.

(2) PG–DAVI의 효과

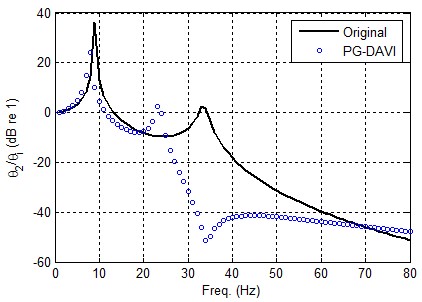
PG-DAVI 시스템을 적용하여 개선된 대상 시스템의 변위전달률 Θ₂/Θ_i을 위의 전달행렬을 이용하여 계산한 다음 원래 시스템의 Θ₂/Θ_i와 비교한 결과가 Fig. 8에 설명되어 있다. 그림에서 보는 바와 같이, PG-DAVI를 적용함에 따라 도입된 반공진 효과로 인해 두 번째 peak 주변의 Θ₂/Θ_i가 크게 저감되는 반면 23 Hz 부근에 새로운 peak이 나타남을 알 수 있다.

Fig. 8

Θ2/Θis of original and modified systems

(3) 전통적 동흡진기와 성능 비교

이 절에서는 PG-DAVI 시스템 적용 시 나타나는 각변위전달률 저감 효과를 전통적인 동흡진기의 저감 효과와 비교함으로써 해당 시스템의 효율성을 확인한다. 전통적인 동흡진기를 적용한 대상 시스템의 개략도가 Fig. 9에 설명되어 있다.

Fig. 9

Configuration of the target system modified with classical dynamic absorber

그림에서 보는 바와 같이 이 시스템은 PG-DAVI 시스템과 동일한 위치에 관성요소 I_a, 강성요소 k_a및 감쇠요소 c_a로 구성된 동흡진기를 구비하고 있다. $$ {\omega }_A=\sqrt{k_a/I_a}\cong 34\times 2\pi $$(rad/s)를 만족할 수 있도록 I_a및 k_a를 선정하였으며 c_a는 비례감쇠를 이용하여 선정하였다. 이와 같이 I₁과 I₂연결부위가 변경됨에 따라 해당 부분의 전달행렬은 다음과 같이 수정되어야 한다⁽¹⁰⁾.

$\[ \left\{\begin{array}{c}{T}_3\\ {\Omega }_3\end{array}\right\}={{\Gamma }_{34}}^{˝}\left\{\begin{array}{c}{T}_4\\ {\Omega }_4\end{array}\right\}=\left[\begin{array}{cc}1& Z_a\\ 0& 1\end{array}\right]\left[\begin{array}{cc}1& 0\\ \frac{i\omega }{k_{12}+i\omega c_{12}}& 1\end{array}\right]\left\{\begin{array}{c}{T}_4\\ {\Omega }_4\end{array}\right\} \]$

(16)

이 식에서 Z_a는 동흡진기의 구동점 임피던스로 다음 식과 같이 주어진다.

$\[ Z_a=\frac{i\omega I_a}{1+i\omega I_a\left(\frac{i\omega }{k_a+i\omega c_a}\right)} \]$

(17)

동흡진기를 적용한 시스템의 변위전달률은 식 (12)의 Γ₃₄를 식 (16)에 주어진 Γ₃₄^"로 대치함으로써 구할 수 있다.

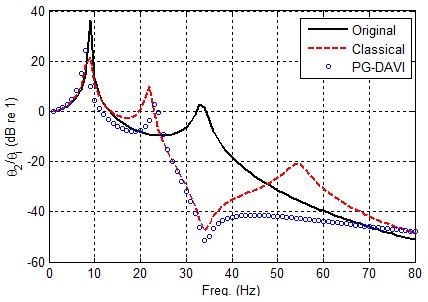
이렇게 계산된 결과를 위에서 얻어진 원래 시스템 및 PG-DAVI 시스템 적용 시의 결과와 Fig. 10에 비교하였다.

Fig. 10

Θ2/Θi of original and modified systems

그림에서 알 수 있는 바와 같이 동흡진기를 적용하는 경우 목표주파수에는 PG-DAVI 시스템과 유사한 변위전달률 저감효과를 얻을 수 있으나 23 Hz 인근의 peak 외에 54 Hz 인근에도 추가로 peak이 발생하여 Θ₂/Θ_i가 오히려 증가함을 알 수 있다. 이 결과를 Table 4에 정리하여 나타냈다.

Table 4

Comparison of Θ2/Θi for 3 systems

따라서, 목표주파수 이상의 주파수 영역에서 각변위전달률의 증가를 초래하지 않는 PG-DAVI 시스템이 전통적인 동흡진기에 비해 우월한 절연성능을 갖는다고 할 수 있다.

5. 결 론

L-DAVI에 대한 전달행렬을 유도했던 이전 연구를 응용하여 PG-DAVI 시스템에 대한 전달행렬을 유도하였다. 이 행렬을 적용한 전달행렬법으로 계산한 단순한 검증시스템의 각 엑셀러런스를 주파수 응답 특성을 이용한 전통적인 방법의 결과와 비교하여 유도된 행렬의 정확도를 검증하였다.

이 전달행렬을 적용한 전달행렬법으로 3자유도 회전진동 시스템의 각변위 전달률을 저감하는 방안을 검토하였다. 초기 시스템의 전달률을 기준으로 설정된 목표주파수에 대한 최적의 PG-DAVI 시스템을 전달행렬을 이용하여 검토하였다. 이렇게 정의된 PG-DAVI 시스템을 대상 시스템에 적용했을 경우 얻어지는 전달률과 초기 시스템의 전달률을 비교하여 PG-DAVI 시스템이 충분한 전달률 저감 효과를 제공함을 확인하였다. 또한, PG-DAVI 시스템이 포함된 회전진동계의 응답특성을 유도된 행렬을 적용한 전달행렬법으로 정확히 계산할 수 있음을 알 수 있었다. 마지막으로 목표주파수를 기준으로 설계된 전통적인 동흡진기를 적용했을 경우의 전달률을 전달행렬법으로 계산한 다음 그 결과를 PG-DAVI 시스템을 적용한 결과와 비교, 검토하여 PG-DAVI 시스템이 우월한 효율성을 나타냄도 확인하였다.

향후 연구에서는 이 연구에서 유도된 행렬을 이용하여 PG-DAVI 시스템을 자동차 구동계와 같은 실제적인 진동계에 적용하는 방안에 대하여 검토하고자 한다.

Acknowledgments

이 논문은 2018년도 정부(교육부)의 재원으로 한국연구재단의 지원을 받아 수행된 기초연구사업임(No. 2010-0020089).

References

• Lee, D. O., and Han, J. H., (2007), A Comparison of Vibration Isolation Characteristics of Various Forms of Passive Vibration Isolator, Transactions of the Korean Society for Noise and Vibration Engineering, 22(9), p817-824. [https://doi.org/10.5050/ksnve.2012.22.9.817]
• Kwag, D. G., Bae, J. S., Hwang, J. H., and Kim, H. S., (2011), An Experimental Study on the Vibration Absorber for Vibration Attenuation of Cantilever Beam Structure, Transactions of the Korean Society for Noise and Vibration Engineering, 21(11), p991-996. [https://doi.org/10.5050/ksnve.2011.21.11.991]
• Flannelly, W. G., (1967), Dynamic Anti-resonant Vibration Isolator, Patent No. 3,322,379.
• Yilmazr, C., and Kikuchi, N., (2006), Analysis and Design of Passive Band-stop Filter-type Vibration Isolators for Low-frequency Applications, Journal of Sound and Vibration, 291(3), p1004-1028.
• Li, K., and Gohnert, M., (2010), Lever Mechanism for Vibration Isolation, Applied Technologies & Innovations, 1(1), p21-28. [https://doi.org/10.15208/ati.2010.3]
• Yun, J. H., Kim, G. W., and Lee, H., (2016), Study on Performances of the Lever Type Anti-resonance Vibration Isolator, Transactions of the Korean Society for Noise and Vibration Engineering, 26(2), p187-194. [https://doi.org/10.5050/ksnve.2016.26.2.187]
• Yun, J. H., and Lee, H., (2018), Study on Performances of the Lever Type Anti-resonance Vibration Isolator Using Transfer Matrix Method, Transactions of the Korean Society for Noise and Vibration Engineering, 28(5), p574-581. [https://doi.org/10.5050/ksnve.2018.28.5.574]
• Ngoc, M. V., Yun, J. H., and Kim, G. W., (2018), Vibration Transmissibility Analysis and Measurement of Band-stop Type Torsional Vibration Isolator Using Anti-resonance, Transactions of the Korean Society for Noise and Vibration Engineering, 28(5), p582-588.
• Kim, G. W., Yun, J. H., Lee, H., and Shin, S. C., (2017), Torsional Vibration Isolation for Automotive Clutch Dampers Using Anti-resonance, Proceedings of Torsional Vibration Symposium, p24.
• Snowdon, J. C., (1971), Mechanical Four-pole Parameter and Their Application, Journal of Sound and Vibration, 15(3), p307-323. [https://doi.org/10.1016/0022-460x(71)90427-5]
• Ha, J. Y., and Kim, K. J., (1994), Analysis of Mimo Mechanical Systems Using the Vectorial Four Pole Parameter Method, Ph.D. Thesis, Korean Advanced Institute of Technology, Daejeon, Korea. [https://doi.org/10.1006/jsvi.1995.0082]
• Ha, J. Y., and Kim, K. J., (1995), Analysis of Mimo Mechanical Systems Using the Vectorial Four Pole Parameter Method, Journal of Sound and Vibration, 180(2), p333-350. [https://doi.org/10.1006/jsvi.1995.0082]
• Attar, M. A., (2012), Transfer Matrix Method for Free Vibration Analysis and Crack Identification of Stepped Beams with Multiple Edge Cracks and Different Boundary Conditions, International Journal of Mechanical Sciences, 57(1), p19-33. [https://doi.org/10.1016/j.ijmecsci.2012.01.010]
• Lee, J. W., and Lee, J. Y., (2016), Development of a Transfer Matrix Method to Obtain Exact Solutions for the Dynamic Characteristics of a Twisted Uniform Beam, International Journal of Mechanical Sciences, 105, p215-226. [https://doi.org/10.1016/j.ijmecsci.2015.11.015]