굽힘 파동 전달 특성을 이용한 빔 형상 구조물의 결빙 감지 기법

1. 서 론

항공기의 성능 요구조건 중 가장 중요한 한 가지는 가혹한 기상조건 하에서도 안전하게 비행할 수 있는 능력이다. 수분 함유량이 높은 대기 중을 비행하는 항공기는 공기에 함유되어 있는 물 입자가 과냉각인 상태에서 빙점 이하의 온도인 항공기 기체의 표면에 부딪히면 결빙이 생성될 수 있다⁽¹⁾. 항공기 기체의 표면에 결빙이 생성되면 항공기의 안전한 비행을 크게 위협하게 된다. 특히 날개에 생성된 결빙은 항력을 증가시키고 양력을 감소시켜서 항공기의 조종성능과 안정성을 크게 저하시킨다⁽²⁾. 따라서 항공기는 결빙이 발생할 가능성이 적은 경로를 선택하여 비행하는 것이 바람직하나 만약 불가피하게 항공기에 결빙이 발생하였을 때는 이를 신속히 감지하고 해당 구역을 회피하거나 제빙장치를 작동하여 생성된 얼음을 신속히 제거하여야 한다. 또한 생성되었던 결빙이 완전히 제거되었음도 알 수 있어야 한다.

항공기 기체의 표면에 결빙이 생성되었음을 감지하는 방법으로는 여러 가지가 개발되어 사용되고 있다. 그 중 대표적인 것들을 살펴보면 진동자 방식, 융해열 방식, 광학/입자 빔 차단 방식, 회전 실린더/토크 측정 방식 등이 있다⁽³⁾. 진동자 방식은 대기 중에 노출된 진동자를 전기/자기적으로 계속 가진하고 있는 상태에서 진동자의 표면에 얼음이 생성되면 진동자의 고유진동수가 변화하고 정해진 진동 크기를 유지하기 위해 필요한 전력의 변화를 감지하여 얼음의 생성을 감지하는 방식이다. 진동자 방식은 현재 대부분의 항공기에 가장 많이 사용되고 있는 방식이다. 융해열 방식은 대기 중에 노출된 탐침의 표면에 가는 전선을 감고 이 전선에 전력 펄스를 주기적으로 인가하고 있는 상태에서 전선의 표면에 얼음이 생성되면 전선이 전력에 의해 가열될 때 얼음의 융해열 때문에 전선의 온도가 상승하는 패턴이 달라지는 것을 감지하여 얼음의 생성을 감지하는 방식이다. 융해열 방식은 주로 군용 항공기에 많이 사용되는 방식이다. 광학/입자 빔 차단 방식은 전자 빔 또는 적외선 빔을 발신부에서 방사하고 일정 거리에 떨어져 있는 수신부에서 이를 감지하고 있다가 빔의 전송 경로에 얼음이 생성되면 전자 빔 또는 적외선 빔이 차단되어 얼음의 생성을 감지하는 방식이다. 광학/입자 빔 차단 방식은 헬리콥터에 많이 사용되는 방식이다. 회전 실린더/토크 측정 방식은 실린더를 공기 흐름 경로에 설치하여 일정한 속도로 회전시키고 실린더의 한쪽 면에 근접하게 칼날을 설치한다. 실린더의 표면에 얼음이 생성되면 이 얼음이 회전하면서 칼날에 걸리게 되고 실린더를 회전시키는데 필요한 토크가 증가하여 얼음의 생성을 감지하는 방식이다. 회전 실린더/토크 측정 방식은 소형 항공기에 많이 사용되는 방식이다.

위에서 언급한 결빙 감지 방법들은 감지 장치들이 설치되어 있는 국부적인 위치에서의 결빙을 감지하여 항공기 전체의 결빙을 추정하는 방식이다. 특정한 위치에서의 결빙으로 항공기 전체의 결빙을 추정하는 것은 오류가 있을 수 있고 이를 보완하기 위해서는 감지 장치를 여러 위치에 많이 설치해야 한다.

이 연구에서는 빔 형상 구조물에서의 굽힘 파동 전달 특성을 이용하여 결빙을 감지하는 방법을 제안하였다. 빔 전달함수 방법은 구조 진동의 이론적 해를 기반으로 하므로 더 적은(둘 또는 셋) 진동 측정이 요구된다⁽⁴⁾. 피로하중이 가해진 중합체 콘크리트의 강성과 손실계수를 측정하는데 빔 형상의 시편에 두 개의 가속도센서를 이용한 전달함수 방법이 사용된 사례가 있다⁽⁵⁾. 여기서는 항공기의 날개를 빔으로 모사하고 빔의 길이방향으로 전달되는 굽힘 파동 전달 특성이 빔 위에 얼음이 생성되었을 때 변화하는 점을 이용한 것으로 전체 빔의 길이방향으로 단 두 개 위치에서의 진동 측정만으로 얼음의 생성을 감지할 수 있다. 따라서 이 방법은 날개 전체에서의 결빙을 직접 감지할 수 있으며 진동 측정용 센서를 날개 내부에 설치할 수 있어 센서가 가혹한 항공기 외부 환경에 노출되지 않는다는 장점이 있다.

2. 빔 결빙 감지 실험

2.1 실험장치 구성

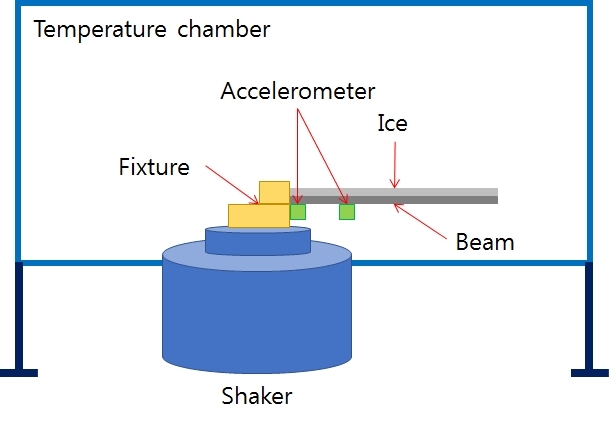
항공기의 날개를 모사하기 위한 빔 실험 시편은 AL6061-T6로 제작하였으며 길이는 40 cm, 폭은 5 cm, 두께는 4 mm로 하였다. 빔을 가진하기 위하여 진동시험기의 아마추어 헤드 위에 알루미늄 지그를 설치하고 그 위에 빔 시편을 고정하였다. 빔의 고정 형상은 clamped-free 조건을 만족하도록 설치하였다. 빔의 진동을 측정하기 위하여 빔 위에 두 개의 가속도센서를 빔의 고정단, 그리고 고정단으로부터 8 cm 떨어진 위치에 설치하였다. 빔을 포함한 진동실험장치를 온도시험챔버의 내부에 설치하고 빔 위에 물을 채워 놓은 상태에서 온도시험챔버의 내부 온도를 영하로 냉각하여 얼음이 생성되도록 하였다. 이 연구에서 사용한 빔 결빙 실험장치의 구성을 Fig. 1과 Fig. 2에 보여주고 있다.

Fig. 1

Experimental setup schematic for detection of icing on a beam

Fig. 2

Experimental setup picture for detection of icing on a beam

3. 실험결과 및 검토

빔에 얼음이 생성되었을 때의 동특성 변화를 측정하기 위한 실험은 다음과 같이 수행하였다. 온도시험챔버의 공기온도를 조절하여 빔과 얼음의 온도가 실험 목표온도에 도달하게 하였다. 빔 위의 고정단에 설치된 가속도센서를 제어 목표점으로 설정하고 진동시험기를 제어하여 주파수 범위(10 Hz ~ 1000 Hz), 진동 크기는 전체 주파수 범위에서 0.001 g²/Hz가 되도록 랜덤 진동을 인가하였다. 비행 진동의 가장 일반적인 가진원은 항공기를 둘러싼 공기 흐름에서의 난류와 관련되며 공기역학적 유동으로부터 발생한 진동은 주로 광대역 랜덤 진동이다⁽⁸⁾. 항공기 진동의 주요한 원인은 항공기 주위의 공기역학적 유동이며 변동하는 압력(난류)은 항공기 구조의 표면을 가진한다. 제트 항공기에서의 진동환경은 사실상 광대역 랜덤 진동이다⁽⁹⁾.

빔의 탄성계수의 추정 초기값은 68.9 GPa, 밀도는 2698.8 kg/m³의 값을 사용하였으며 얼음의 탄성계수의 추정 초기값은 8.826 GPa, 밀도는 918.5 kg/m³의 값을 사용하였다.

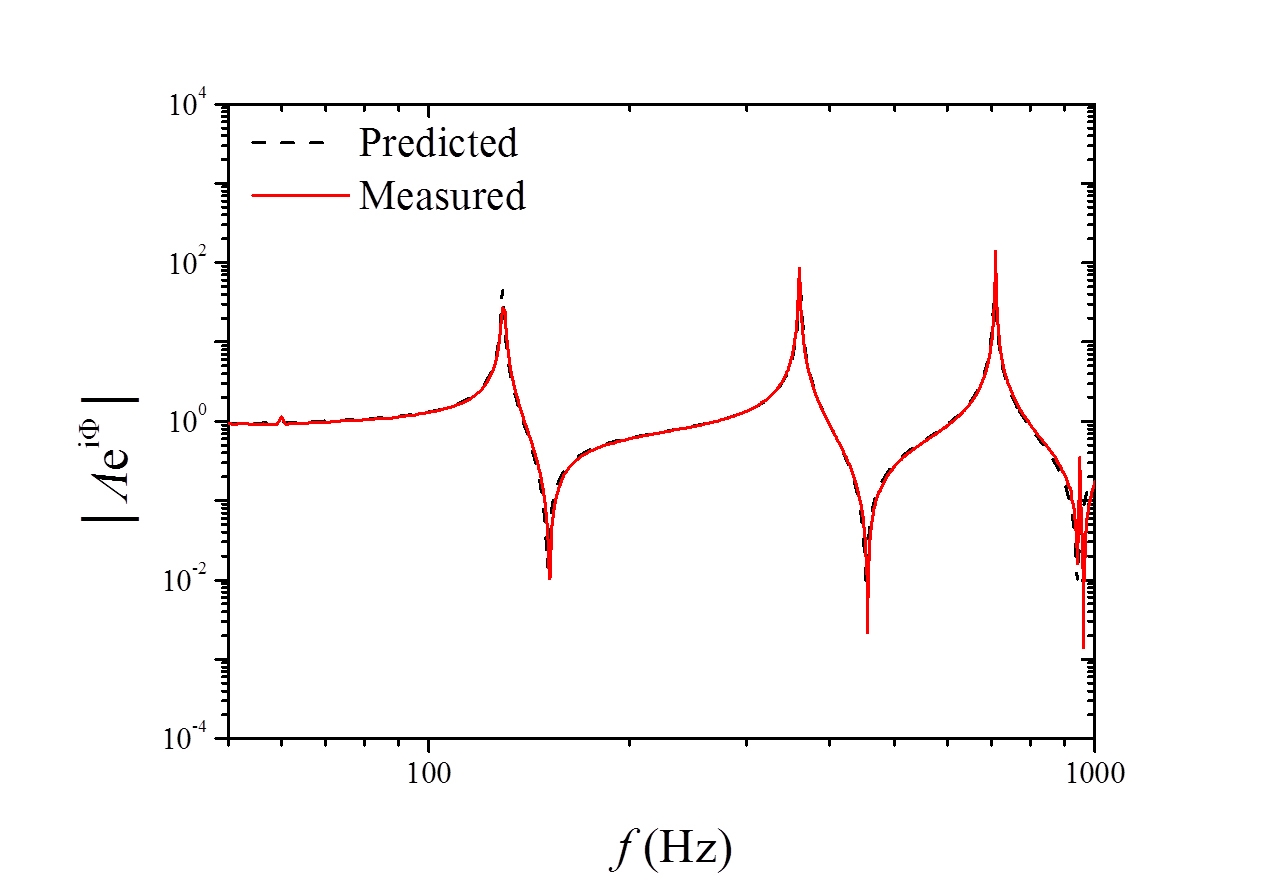
먼저 빔만 있는 상태에서 가진하여 측정된 전달함수와 이론적으로 추정된 전달함수를 주파수 영역에서 서로 비교하였다. Fig. 3은 $$ \frac{\hat{w}\left(x_1\right)}{\hat{w}\left(x_0\right)}$$의 관계에서 측정된 전달함수와 이론적으로 추정된 전달함수를 같이 나타내고 있는데 측정된 전달함수가 전체 주파수 범위에서 이론적으로 추정된 전달함수와 거의 일치하는 것을 확인할 수 있다.

Fig. 3

Comparison between estimated transfer function and measured transfer function

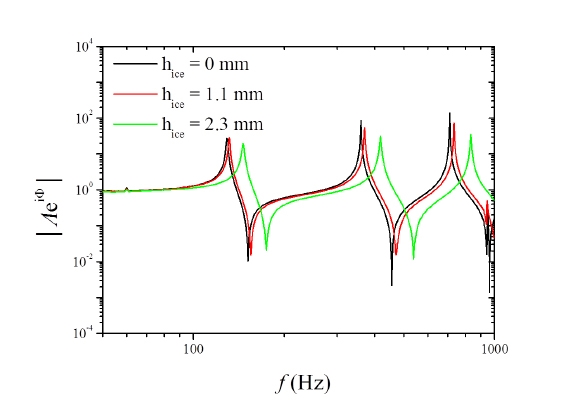
다음으로 빔만 있을 때와 빔 위에 얼음이 생성되었을 때 빔의 동특성 변화를 비교하기 위하여 얼음의 두께를 두 가지의 경우로 하여 실험을 실시하였다. Fig. 4는 빔만 있을 때와 빔 위에 얼음의 두께가 두 가지의 경우로 생성되었을 때 $$ \frac{\hat{w}\left(x_1\right)}{\hat{w}\left(x_0\right)}$$의 관계에서 측정된 전달함수를 나타낸다.

Fig. 4

Transfer function depending on thickness of ice

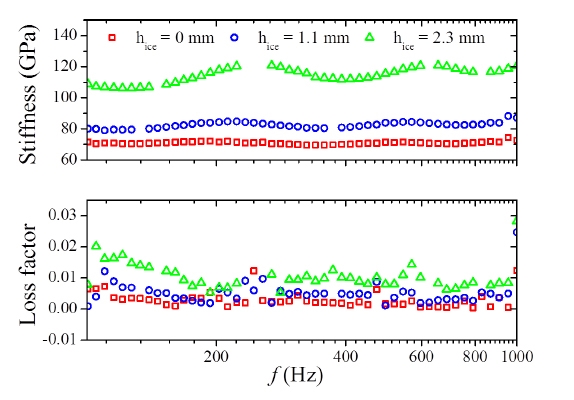
Fig. 5는 $$ \frac{\hat{w}\left(x_1\right)}{\hat{w}\left(x_0\right)}$$의 관계에서 측정된 전달함수로부터 구한 얼음의 두께에 따른 빔의 탄성계수 및 손실계수를 나타낸다.

Fig. 5

Young’s modulus of elasticity and loss factor depending on thickness of ice

Fig. 5에서 보면 빔만 있을 때와 비교하여 빔 위에 얼음이 생성된 경우 전 주파수 범위에서 탄성계수와 손실계수가 증가된 것을 알 수 있다. 또한 얼음이 얇은 경우와 비교하여 얼음이 두꺼운 경우 전 주파수 범위에서 탄성계수와 손실계수가 더 증가된 것을 알 수 있다.

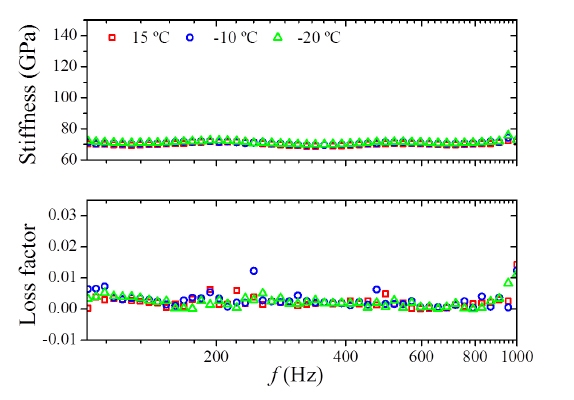
다음으로 빔 자체의 동특성이 온도의 변화에 얼마나 민감한지 확인하기 위하여 빔만 있을 때 온도를 다르게 하여 실험을 실시하였다. Fig. 6은 빔만 있을 때 온도의 변화에 따른 빔의 탄성계수 및 손실계수를 나타낸다.

Fig. 6

Young’s modulus of elasticity and loss factor of the beam depending on temperature

Fig. 6에서 보면 온도가 감소할수록 빔의 탄성계수가 약간 증가하나 얼음이 생성되었을 때의 증가량보다는 훨씬 작으므로 빔 자체의 온도에 따른 탄성계수와 손실계수의 변화는 얼음의 생성을 감지하는데 영향을 주지 않음을 알 수 있다.

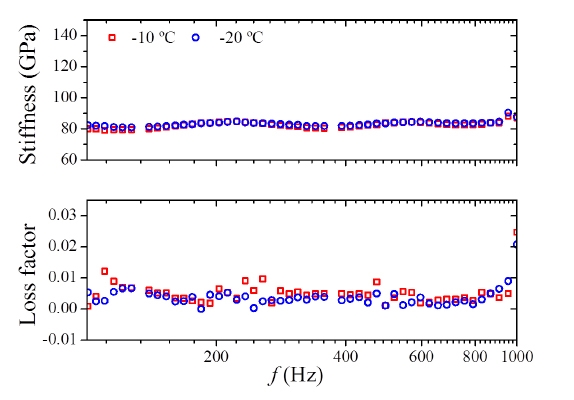
다음으로 빔과 얼음이 합성되었을 때의 동특성이 온도의 변화에 얼마나 영향을 받는지 확인하기 위하여 빔에 얼음이 생성되었을 때 온도를 다르게 하여 실험을 실시하였다. Fig. 7은 빔에 얼음이 생성되었을 때 온도의 변화에 따른 빔과 얼음의 합성된 탄성계수 및 손실계수를 나타낸다.

Fig. 7

Young’s modulus of elasticity and loss factor of the combined beam and ice depending on temperature

Fig. 7에서 보면 온도가 감소하면 빔과 얼음의 합성된 탄성계수와 손실계수가 약간 증가하나 얼음의 생성에 따른 증가량보다는 훨씬 작으므로 온도의 변화는 얼음의 생성을 감지하는 데 영향을 주지 않음을 알 수 있다.

Table 1에 지금까지 언급한 다양한 실험조건의 변화에 따른 탄성계수와 손실계수의 변화를 정리하여 나타내었다.

Table 1

Young’s modulus of elasticity and loss factor for various conditions

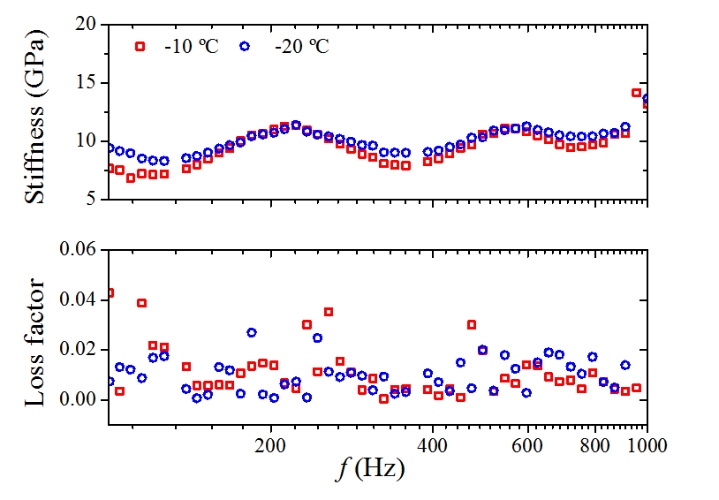
추가로 얼음만의 탄성계수와 손실계수를 Fig. 8에 나타내었으며 기존 논문⁽¹⁰⁾에 제시된 값과 비교한 결과를 Table 2에 나타내었다. 얼음의 탄성계수가 가진 주파수의 증가에 따라 증가하는 경향이 서로 일치함을 알 수 있다. 기존 논문에는 얼음의 손실계수에 대한 정보는 없었다.

Fig. 8

Young’s modulus of elasticity and loss factor of ice depending on temperature

Table 2

Young’s modulus of elasticity and loss factor of ice at -10 ℃

이 연구결과를 항공기에 적용하기 위해서는 먼저 날개의 길이방향으로 서로 다른 두 위치에 가속도 센서를 설치하고 날개에 얼음이 없는 상태에서 항공기의 운항 시 날개에 진동이 가해질 때 탄성계수와 손실계수를 계산하여 이를 기준값으로 삼는다. 그 후 항공기의 운항 중 계속적으로 진동을 측정하여 탄성계수와 손실계수를 계산하여 감시하다가 이 값들이 기준값보다 커지게 되면 날개에 얼음이 생성된 것으로 간주하고 조치를 취할 수 있다. 얼음의 두께에 따른 탄성계수와 손실계수의 변화량은 항공기 날개의 형상과 재질에 따라 달라질 것이므로 각 항공기에 대한 얼음 생성의 정도에 대한 추정값은 각 항공기별로 실험을 통하여 얻어야 한다.

4. 결 론

이 연구에서는 항공기 날개에 얼음이 생성되었을 때 이를 감지하기 위하여 빔의 굽힘 파동 전달 특성을 이용하는 방법을 제안하였다. 항공기 날개를 모사한 빔 위에 얼음이 생성되었을 때 빔의 탄성계수와 손실계수가 넓은 주파수 범위에서 크게 변화함을 알 수 있었다. 또한 이 동특성들의 변화량은 온도의 변화에는 민감하지 않아 실제 운용환경에서 사용하는데도 적합할 것으로 예상된다.

이 연구에서 사용한 방법은 항공기 날개에 얼음이 생성되었음을 감지하는데 단 두 개의 가속도센서만을 이용하므로 기존의 다른 결빙 감지방법들에 비해 사용이 매우 간편하고 운용/유지비용을 크게 감소시킬 수 있을 것으로 판단된다. 향후 실제 항공기 날개를 이용하여 이 연구에서 사용한 방법을 적용하고 검증하는 연구가 필요하다.

References

• Heinrich, A., (1993), Aircraft Icing Handbook, Department of Transportation Federal Aviation Administration, Atlantic City, New Jersey, USA, p12-26.
• Caliskan, F., and Hajiyev, C., (2013), A Review of In-flight Detection and Identification of Aircraft Icing and Reconfigurable Control, Progress in Aerospace Sciences, 60, p12-34. [https://doi.org/10.1016/j.paerosci.2012.11.001]
• Jackson, D. G., and Goldberg, J. I., (2007), Ice Detection Systems: A Historical Perspective, SAE Technical Paper 2007-01-3325. [https://doi.org/10.4271/2007-01-3325]
• Park, J., (2008), Identification of Damage in Beam Structures Using Flexural Wave Propagation Characteristics, Journal of Sound and Vibration, 318(4-5), p821-829. [https://doi.org/10.1016/j.jsv.2008.05.008]
• Ahn, S., Jeon, E. B., Koh, H. I., Kim, H. S., and Park, J., (2016), Identification of Stiffness Distribution of Fatigue Loaded Polymer Concrete Through Vibration Measurements, Composite Structures, 136, p11-15. [https://doi.org/10.1016/j.compstruct.2015.09.026]
• Park, J., (2005), Transfer Function Methods to Measure Dynamic Mechanical Properties of Complex Structures, Journal of Sound and Vibration, 288(1-2), p57-79. [https://doi.org/10.1016/j.jsv.2004.12.019]
• Inman, D. J., (2014), Engineering Vibration, 4th Ed., Pearson, Harlow Essex, England, p495.
• Ministry of Defense, (2006), DEF STAN 00-35 Part 5, Issue 4, Chapter 7-01, p124-125.
• Department of Defense, (2014), MIL-STD-810G w/change1, Method 514.7, p514.7A-9-514.7F-4.
• Sinha, N. K., Timco, G. W., and Frederking, R. M. W., (1987), Recent Advances in Ice Mechanics in Canada, Applied Mechanics Review, 40(9), p1214-1231. [https://doi.org/10.1115/1.3149553]