[ Article ]

Transactions of the Korean Society for Noise and Vibration Engineering - Vol. 29, No. 2, pp.255-261

ISSN: 1598-2785 (Print) 2287-5476 (Online)

Print publication date 20 Apr 2019

Received 24 Jan 2019 Revised 12 Apr 2019 Accepted 17 Apr 2019

DOI: https://doi.org/10.5050/KSNVE.2019.29.2.255

급수 함수를 이용한 임의 형상 평판의 고정밀도 고유치 해석의 응용

강상욱^†

Application of Highly Accurate Eigenvalue Analysis of Arbitrarily Shaped Plates Using Series Functions

Sang-Wook Kang^†

Correspondence to: ^† Member, Hansung University E-mail: swkang@hansung.ac.kr ‡ Recommended by Editor Woo Ju Jeon

Abstract

An extended method for free vibration analysis using series functions is proposed to obtain the accurate eigenvalues of arbitrarily shaped plates with both clamped and simply supported edges. The proposed method can minimize the amount of numerical calculation because it has the advantage of not needing to divide the plate of interest unlike FEM. As the result, it offers very accurate eigenvalues despite employing smaller amount of numerical computation than FEM. Two case studies show that the proposed method is valid and accurate when the eigenvalues by the proposed method are compared to those by FEM (ANSYS) or another analytical method.

Keywords:

NDIF Method, Eigenvalue Analysis, Arbitrarily Shaped Plate, Series Function, Free Vibration

키워드:

무차원 동영향 함수법, 고유치 해석, 임의 형상 평판, 급수 함수, 자유진동

1. 서 론

유한요소법⁽¹⁾과 경계요소법⁽²⁾은 임의 형상 평판의 고유치와 고유모드를 추출하기 위해 가장 일반적으로 사용되는 수치 해석 기법이다. 이들 수치해석 기법은 평판의 내부 또는 경계를 분할하기 위해 많은 노드가 필요하고, 노드들 사이에 지배방정식을 만족하지 않는 보간 함수를 사용하기 때문에, 해의 정밀도가 다소 떨어지는 문제점이 발생한다. 상기와 같은 문제점을 극복하기 위해, 이 논문의 저자는 임의 형상 고정단 평판의 고정밀도 고유치 해석을 위한 방법으로, NDIF법(non-dimensional dynamic influence function method)을 처음 개발하였다⁽³⁾. 이후 저자는 NDIF법을 혼합 경계조건을 가진 평판⁽⁴⁾, 직선 경계 또는 곡선 경계를 가진 자유단 평판⁽⁵^~⁸⁾으로 확장하였다. 추가적으로 저자는 분할 영역법을 이용한 단순지지 평판⁽⁹^,¹⁰⁾과 멤브레인⁽¹¹⁾의 자유진동 해석에도 NDIF법을 응용하였다. 근래에 와서는 NDIF법의 효율성을 높이기 위한 연구의 일환으로, NDIF의 대수 고유치 문제로의 정식화 방법에 대한 다양한 연구⁽¹²^~¹⁵⁾를 수행하였다.

NDIF법의 가장 큰 특징은 경계요소법과 마찬가지로 해석 대상 물체의 경계만을 이산화하나, 노드와 노드 사이에는 어떠한 보간함수도 사용하지 않는 것이다. 이러한 특징으로 인해 NDIF법은 유한요소법 및 경계요소법에 비해 보다 정밀한 해를 제공할 뿐 아니라 적은 수치 계산량을 필요로 하는 장점을 가지고 있다.

그러나 NDIF법에서 노드의 개수를 증가시킬 경우, 노드와 노드 사이가 너무 근접하게 되어서, 각각의 노드에 대해 독립적으로 정의되는 기저 함수(base function)들 간의 독립성이 떨어지게 된다. 결과적으로는 시스템 행렬이 특이 특성(singular characteristics)을 가지게 되어서 수렴된 해를 제공 못하는 문제점이 NDIF법에서는 발생하게 된다.

저자는 이러한 문제점을 극복하기 위해, 평면파(plane wave) 형태의 급수 함수(series function)를 이용한 고정밀도 고유치 추출 기법을 개발하여 고정단 임의 형상 평판⁽¹⁶⁾, 멤브레인⁽¹⁷⁾, 음향 공동⁽¹⁸⁾에 적용하였다. 이 논문에서는 저자의 이전 연구⁽¹⁶^~¹⁸⁾를 확장하여 단순지지 경계와 고정단 경계로 구성된 혼합 경계를 가진 임의 형상 평판을 적은 수치 계산량으로도 자유진동 해석이 가능한 효율적인 이론을 정립하고자 한다.

한편, 저자의 이전 연구⁽¹⁶^~¹⁸⁾와는 달리, 가정된 해에 포함된 미지수의 개수와 경계조건 식의 개수가 달라서, 시스템 행렬이 정사각 행렬로 추출되지 않는 문제점이 혼합 경계조건을 가진 평판을 다루는 이 연구에서 발생한다. 이 논문에서는 이러한 문제점을 해결하기 위한 새로운 방안이 제안된다.

2. 이론 정식화

2.1 지배방정식과 경계조건

임의 형상 평판의 자유진동 지배방정식은 다음과 같이 주어진다⁽¹⁹⁾.

∇ 4 W - Λ 4 W = 0

(1)

Λ = ρ ω 2 ∕ D E 1 ∕ 4

(2)

여기서 W는 평판의 진동 변위, Λ는 주파수 파라미터, ρ는 평판의 면밀도, ω는 각주파수(angular frequency), D_E는 판강성(flexural rigidity of plate)을 나타낸다.

고정단 경계조건 식은 다음과 같이 주어진다⁽¹⁹⁾.

W Γ = 0, ∂ W Γ / ∂ n = 0

(3,4)

여기서 Γ는 평판의 경계를 의미하며, n은 경계에서의 법선 방향을 의미한다.

그리고 단순지지 경계조건 식은 다음과 같이 주어진다⁽¹²⁾.

W Γ = 0, ∂ 2 W Γ ∂ n 2 + ν R ∂ W Γ ∂ n = 0

(5,6)

여기서 R, n, ν는 각각 경계 곡률 반경, 경계 법선 방향, 푸아송비(Poisson’s ratio)를 나타낸다. 만약 직선 경계들로만 구성된 다각형 평판으로만 가정한다면, 식 (5)에 의해 자동으로 만족하므로, 식 (6)은 고려될 필요가 없다⁽¹⁹⁾. 결과적으로 고차 미분항이 포함된 경계조건 항을 계산할 필요가 없게 되어서 수치 계산량을 줄이는 효과가 발생하나(해의 수렴성도 좋아짐), 앞에서 언급한 바와 같이 시스템 행렬이 비정사각 행렬이 되는 문제점이 발생한다.

2.2 자유진동해 가정

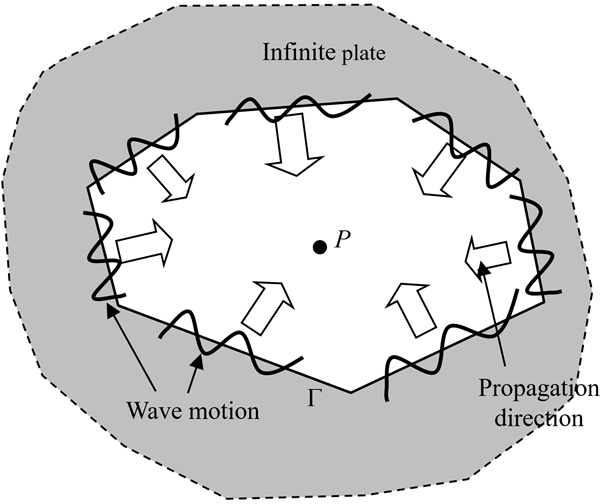
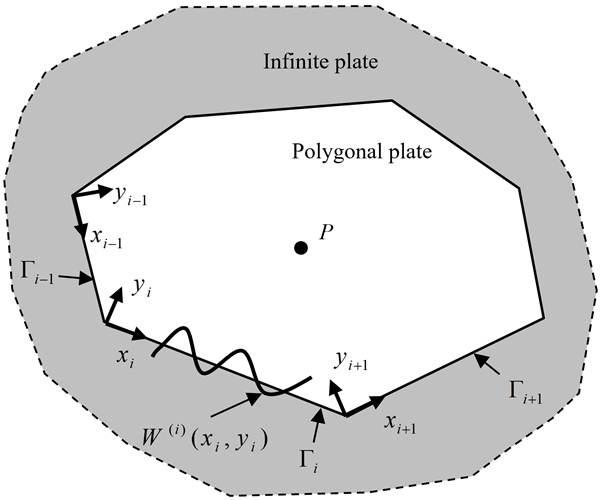
Fig. 1 또는 Fig. 2와 같이 무한 평판 위에 Ne개의 모서리를 가진 해석 대상 다각형 평판이 놓여 있다고 가정한다. 그리고 해석 대상 평판의 모서리들 Γ₁, Γ₂, … Γ_N_e에서 식 (7)과 같은 시리즈 함수들의 중첩으로 표현되는 파동이 발생하여 평판의 내부로 전파되어간다고 가정한다⁽¹⁶^,¹⁹⁾. 참고로 파동의 진동 방향은 (평판의 진동 방향과 동일하게) 지면에 수직 방향이다.

Fig. 1

Polygonal plate located on an infinite plate

Fig. 2

Local coordinates (xi,yi) and wave motion W(i) at boundary Γi

W i x i, y i = ∑ m = 1 N h [A m (i) s i n m π x i L i e x p (j ω 2 - (m π L i) 2 y i) + B m i s i n m π x i L i e x p (ω 2 + m π L i 2 y i)], i = 1,2, ⋯, N e

(7)

여기서 $A m i$ 과 $B m i$ 은 파동의 진폭과 관련된 미지 계수, x_i와 y_i는 i번째 모서리 Γ_i에 정의된 지역 좌표계 좌표를 의미한다. 그리고 L_i는 모서리 Γ_i의 길이, ω는 각주파수, j는 순허수, Nh는 파동을 표현하기 위해 사용된 시리즈 함수의 개수를 의미한다. 참고로 식 (7)은 지배방정식 식 (1)을 만족한다.

한편, 무한 평판 위에 놓인 다각형 평판의 내부 점 P에서의 진동 변위는 모서리에서 발생한 파동들이 점 P에 도달했을 때의 변위들의 중첩으로 가정한다. 그러면 점 P에서의 진동 변위는 식 (8)과 같이 표현될 것이다.

W t o t a l x, y = ∑ i = 1 N e W i x i, y i

(8)

여기서 x와 y는 광역 좌표계(global coordinates)에 대한 평판 내부 또는 경계 상의 점 P의 좌표를 나타낸다. 이 논문에서는 식 (8)을 해석 대상 다각형 평판의 자유진동해로 가정한다. 가정된 자유진동해 식 (8) 또한 지배방정식 식 (1)을 만족한다. 왜냐하면 식 (8)은 지배방정식을 만족하는 식 (7)의 선형결합이기 때문이다.

2.3 경계 변위와 경계 기울기 가정

먼저 해석 대상 평판의 Ne개의 모서리 중에 Nc개는 고정단 경계조건을 가지며 Ns개는 단순지지 경계조건을 가지는 것으로 가정한다. 그리고 잠정적으로 고정단 경계(모서리)에서의 변위와 기울기는 식 (9)와 식 (10)과 같이 시리즈 함수의 중첩으로 각각 가정한다.

W t o t a l (x, y) | y r = 0 = ∑ n = 1 N h C n (r) s i n n π x r L r, r = 1,2, ⋯, N c

(9)

∂ ∂ y r W t o t a l x, y | y r = 0 = ∑ n = 1 N h D n (r) s i n n π x r L r, r = 1,2, ⋯, N c

(10)

여기서 ∂/∂y_r는 r번째 모서리의 법선 방향으로의 편미분을 의미한다. 마찬가지로, 단순지지 경계(모서리)에서의 변위도 식 (11)과 같이 시리즈 함수의 중첩으로 가정한다.

W t o t a l (x, y) | y r = 0 = ∑ n = 1 N h C n (r) s i n n π x r L r, r = N c + 1, N c + 2, ⋯, N e

(11)

식 (9) ~ 식 (11)에서 사인 함수 대신 코사인 함수를 사용해도 무방하나, 나중에 변위와 기울기 0 조건을 만족시키 위해 필요한 시리즈 함수의 개수가 사인 함수가 코사인 함수 보다 적게 필요한 것으로 이 연구에서 밝혀졌기 때문이다.

2.4 경계조건 적용 및 시스템 행렬 추출

앞에서 가정한 다각형 평판의 자유진동해 식 (8)은 지배방정식을 만족한다. 그래서 식 (8)이 자유진동해가 되기 위해서는 잠정적으로 가정된 경계조건 식 (9) ~ 식 (11)을 만족하기만 하면 된다. 이를 위해 식 (9) ~ 식 (11)에 식 (8)을 대입하면 다음과 같은 식을 각각 얻을 수 있다. 참고로 아래 식에서 r번째 모서리의 지역 좌표는 y_r= 0에 해당한다.

∑ i = 1 N e W i x i, y i | y r = 0 = ∑ n = 1 N h C n (r) s i n n π x r L r, r = 1,2, ⋯, N c

(12)

∑ i = 1 N e ∂ ∂ y r W i x i, y i | y r = 0 = ∑ n = 1 N h D n (r) s i n n π x r L r, r = 1,2, ⋯, N c

(13)

∑ i = 1 N e W i x i, y i | y r = 0 = ∑ n = 1 N h C n (r) s i n n π x r L r, r = N c + 1, N c + 2, ⋯, N e

(14)

먼저 식 (7)을 식 (12)에 대입한 후에, 사인 시리즈 함수들의 직교성을 이용하기 위하여 양변에 sin qπx_r/L_r을 곱한 후 0에서 L_r까지 적분하면 다음과 같은 식이 얻어진다.

∑ i = 1 N e ∑ m = 1 N h ∫ 0 L r [A m (i) s i n m π x i L i e x p (j ω 2 - (m π L i) 2 y i) + B m (i) s i n m π x i L i e x p (ω 2 + (m π L i) 2 y i)] s i n q π x r L r d x r = ∑ n = 1 N h ∫ 0 L r C n (r) s i n n π x r L r s i n q π x r L r d x, r = 1,2, ⋯, N c; q = 1,2, ⋯, N h

(15)

사인시리즈 함수들 간의 직교성을 식 (15)의 우변 항에서 고려하면 식 (15)의 우변은 다음과 같이 간단히 된다.

∑ n = 1 N h ∫ 0 L r C n (r) s i n n π x r L r s i n q π x r L r d x = L r 2 C q (r)

(16)

식 (16)의 결과를 식 (15)에 대입한 후 정리하면 다음과 같이 된다.

∑ i = 1 N e ∑ m = 1 N h 2 L r ∫ 0 L r [A m i s i n m π x i L i exp ⁡ j ω 2 - m π L i 2 y i + B m i s i n m π x i L i e x p ⁡ (ω 2 + m π L i 2 y i)] s i n q π x r L r d x r = C q r, r = 1,2, ⋯, N c; q = 1,2, ⋯, N h

(17)

식 (17)을 간단한 형식으로 표현하면 다음과 같이 된다.

∑ i = 1 N e ∑ m = 1 N h A m i G M q, m i, r + B m i H M q, m i, r = C q r, r = 1,2, ⋯, N c; q = 1,2, ⋯, N h

(18)

여기서 $G M q, m i, r$ 와 $H M q, m i, r$ 은 다음과 같다.

G M (q, m) (i, r) = 2 L r ∫ 0 L r s i n m π x i L i × e x p (j ω 2 - (m π L i) 2 y i) s i n q π x r L r d x r

(19)

H M (q, m) (i, r) = 2 L r ∫ 0 L r s i n m π x i L i × e x p (ω 2 + (m π L i) 2 y i) s i n q π x r L r d x r

(20)

마지막으로 식 (18)을 행렬식의 형태로 표현하면 다음과 같이 된다.

G M c ⋅ A + H M c ⋅ B = C c

(21)

여기서 아래 첨자 c는 고정단(clmaped) 경계를 의미하며, 행렬 GM_c과 HM_c, 미지 계수 벡터, A, B, C_c는 다음과 같다.

G M c = G M (1,1) G M (1,2) ⋯ G M (1, N e) G M (2,1) G M (2,2) ⋯ G M (2, N e) ⋮ ⋮ ⋱ ⋮ G M (N c, 1) G M (N c, 2) ⋯ G M (N c, N e)

(22)

H M c = H M (1,1) H M (1,2) ⋯ H M (1, N e) H M (2,1) H M (2,2) ⋯ H M (2, N e) ⋮ ⋮ ⋱ ⋮ H M (N c, 1) H M (N c, 2) ⋯ H M (N c, N e)

(23)

A = {A (1), A (2), ⋯, A (N e)} T

(24)

B = {B (1), B (2), ⋯, B (N e)} T

(25)

C c = {C (1), C (2), ⋯, C (N e)} T

(26)

참고로, 식 (22), 식 (23)에서 알 수 있듯이 행렬 GM과 HM의 크기는 둘다 (Nh·Nc) × (Nh·Ne)이다.

다음으로, 식 (13)에 대해서도 식 (15) ~ 식 (26)의 과정을 반복하면 다음과 같은 행렬식이 얻어진다.

J M c ⋅ A + K M c ⋅ B = D c

(27)

여기서 행렬 JM_c과 KM_c의 크기는 둘다 (Nh·Nc) × (Nh·Ne)이며 성분은 다음과 같다.

J M (q, m) (i, r) = 2 L r ∂ ∂ y r ∫ 0 L r s i n m π x i L i × e x p (j ω 2 - (m π L i) 2 y i) s i n q π x r L r d x r

(28)

K M (q, m) (i, r) = 2 L r ∂ ∂ y r ∫ 0 L r s i n m π x i L i × e x p (j ω 2 + (m π L i) 2 y i) s i n q π x r L r d x r

(29)

마지막으로, 식 (14)에 대해서도 식 (15) ~ 식 (26)의 과정을 반복하면 다음과 같은 행렬식이 얻어진다.

G M s ⋅ A + H M s ⋅ B = C s

(30)

여기서 아래 첨자 s는 단순지지(simply-supported) 경계를 의미하며, 행렬 GM_s과 HM_s의 크기는 둘다 (Nh·Nc) × (Nh·Ne)이며 성분은 식 (19), 식 (20)에 의해 각각 주어진다.

위에서 얻은 세 개의 행렬식 식 (21), 식 (27), 식 (30)을 하나의 시스템 행렬식으로 통합하면 다음과 같이 된다.

G M c H M c J M c K M c G M s H M s A B = C c D c C s

(31)

식 (31)을 살펴보면, 미지 벡터 A와 B에 포함된 미지수의 개수는 Nh·2Ne개인데, 이들 미지수가 포함된 식들의 개수는 Nh·(2Nc + Ns)개로, 식의 개수가 부족하다. 그래서 추가적으로 Ns개 식이 필요하다. 저자의 이전 연구⁽¹⁷⁾에서 단순지지 평판(또는 멤브레인)의 경우 식 (7)에서 우변의 첫 번째 항만 자유진동해로 사용되기 때문에 미지 벡터 B가 시스템 행렬식에 나타나지 않는다는 사실을 고려하면, 식 (30)으로부터 다음과 같은 추가 조건식이 구해진다.

H M s ⋅ B = 0

(32)

이제 식 (32)를 식 (31)에 포함시키면 다음과 같이 된다.

G M c H M c J M c K M c G M s H M s 0 H M s A B = C c D c C s 0

(33)

식 (33)으로부터 주파수 파라미터 Λ의 함수인 최종 시스템 행렬 VM(Λ)은 다음과 같이 정의된다.

V M Λ = G M c H M c J M c K M c G M s H M s 0 H M s

(34)

참고로 시스템 행렬 VM(Λ)은 정사각 행렬이며, 크기는 (Nh·2Ne) × (Nh·2Ne)이다. 한편, 해석 대상 평판의 고정단 경계에서는 변위와 기울기가 동시에 0이고 단순지지 경계에서는 변위가 0이므로, 이들 조건을 만족하기 위해서는 미지 계수 벡터 C_c, D_c, C_s는 모두 0 벡터가 된다. 이러한 사실로부터 식 (33)은 다음과 같이 된다.

V M Λ = A B 0000

(35)

마지막으로, 평판의 고유치는 시스템 행렬 VM(Λ)의 판별식(determinant)이 0이 되게 하는 주파수 파라미터 값으로부터 구해질 수 있다.

3. 정립된 정식 검증

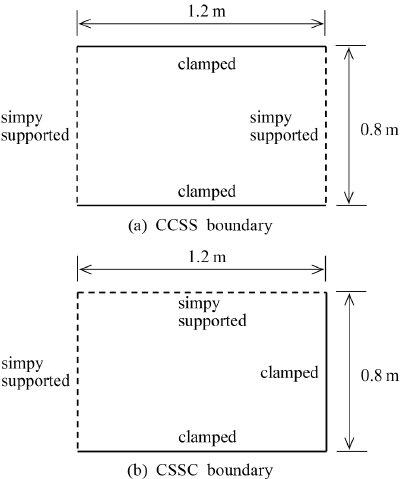
앞의 2장에서 정립된 정식을 증명하기 위하여, Fig. 3과 같이 다양한 경계조건을 가진 직사각형 평판이 검증 예제로 고려된다. 먼저 Fig. 3(a)의 CCSS 경계를 가진 평판에 대한 고유치가 이 논문에서 제안된 방법에 의해 구해졌다. 그 결과는 Table 1에 요약되었다.

Fig. 3

Rectangular plate with various boundary conditions

Table 1

Eigenvalues of the rectangular plate with CCSS boundary by the proposed method, FEM (ANSYS) and Leissa(20) method

Table 1에서 제안된 방법과 FEM(ANSYS)에 의해 구해진 고유치 값들을 비교해보면, 제안된 방법은 급수 함수를 4개만을 사용(Nh = 4)해도 1677개의 노드를 사용한 FEM에 수렴하는 결과를 제공함을 확인할 수 있다. 그리고 Nh = 3인 경우에는 6번째 고유치가 구해지지 않음을 확인할 수 있는데, 이는 6번째 고유모드 형상을 3개의 급수 함수의 중첩으로 나타낼 수가 없기 때문인 것으로 추정된다. 추가적으로, 제안된 방법은 Leissa⁽²⁰⁾ 방법보다 FEM 결과에 더 근접한 고유치들을 제공함을 확인할 수 있다. 참고로 이 평판에 대한 고유 모드 형상들도 제안된 방법에 의해 성공적으로 추출되었으며, 지면 관계상 제시를 생략한다.

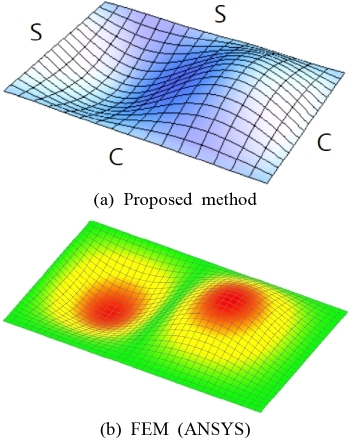
다음으로, Fig. 3(b)의 CSSC 경계를 가진 평판에 대한 고유치가 제안된 방법에 의해 구해졌으며, 그 결과는 Table 2에 요약되었다. Table 2에서 Nh = 3인 경우 2번째와 4번째 고유치가 아직 수렴이 되지 않았음을 확인할 수 있다. 급수 함수의 개수를 하나씩 증가시켜 보면, Nh = 4인 경우에 고유치들은 이미 수렴되었음을 확인할 수 있으며, 이들 수렴된 값은 FEM 결과와 정확히 일치함도 확인할 수 있다. Fig. 4는 제안된 방법에 의해 구해진 CSSC 경계를 가진 평판의 두 번째 모드를 보여 주며, 이 모드 형상이 ANSYS에 의해 구한 모드 형상과 잘 일치함을 확인할 수 있다.

Table 2

Eigenvalues of the rectangular plate with CSSC boundary by the proposed method and FEM (ANSYS)

Fig. 4

The second mode shapes of the CSSC plate obtained by the proposed method and FEM (ANSYS)

4. 결 론

이 논문에서는 혼합 경계(단순지지 및 고정단 경계)를 가진 임의 형상 평판에 대한 ‘평면파 형태의 급수 함수를 이용한 고정밀도 고유치 해석 기법’을 성공적으로 제안하였다. 또한 두 가지 예제 검증을 통해 제안된 기법의 정확성과 수렴성을 확인하였다. 향후 추가 연구에서는 보다 다양한 형상의 평판에 대해 제안된 기법의 타당성 검증이 이루어질 예정이다.

Acknowledgments

이 연구는 한성대학교 교내학술연구비 지원 과제임.

References

Bathe, K, (1982), Finite Element Procedures in Engineering Analysis, Prentice-hall, New Jersey.
Brebbia, C. A., Telles, J. C. F., and Wrobel, L. C., (1984), Boundary Element Techniques, Springer-verlag, New York.
Kang, S. W., and Lee, J. M., (2001), Free Vibration Analysis of Arbitrarily Shaped Plates with Clamped Edges Using Wave-type Functions, Journal of Sound and Vibration, 242(1), p9-26. [https://doi.org/10.1006/jsvi.2000.3347]
Kang, S. W., (2002), Free Vibration Analysis of Arbitrarily Shaped Plates with a Mixed Boundary Condition Using Non-dimensional Dynamic Influence Functions, Journal of Sound and Vibration, 256(3), p533-549. [https://doi.org/10.1006/jsvi.2002.5009]
Kang, S. W., Kim, I. S., and Lee, J. M., (2003), Free Vibration Analysis of Arbitrarily Shaped Plates with Free Edges Using Non-dynamic Influence Functions, Transactions of the Korean Society for Noise and Vibration Engineering, 13(10), p821-827.
Kang, S. W., (2007), Free Vibration Analysis of Arbitrarily Shaped Polygonal Plates with Free Edges by Considering the Phenomenon of Stress Concentration at Corners, Transactions of the Korean Society for Noise and Vibration Engineering, 17(3), p220-225.
Kang, S. W., Kim, I. S., and Lee, J. M., (2008), Free Vibration Analysis of Arbitrarily Shaped Plates with Smoothly Varying Free Edges Using NDIF Method, Journal of Vibration and Acoustics, 130(4), p041010.1-041010.8. [https://doi.org/10.1115/1.2730531]
Kang, S. W., and Atluri, S. N., (2008), Development of Meshless Method for Free Vibration Analysis of Arbitrarily Shaped Free Plates Using Local Polar Coordinates, Transactions of the Korean Society for Noise and Vibration Engineering, 18(6), p674-680.
Kang, S. W., and Yoon, J. I., (2011), Development of NDIF Method for Highly Accurate Free Vibration Analysis of Arbitrarily Shaped Plates with Simply Supported Boundary Condition, Transactions of the Korean Society for Noise and Vibration Engineering, 21(2), p186-193. [https://doi.org/10.5050/ksnve.2011.21.2.186]
Kang, S. W., and Yoon, J. I., (2012), Development of the NDIF Method Using a Sub-domain Method Approach for Extracting Highly Accurate Natural Frequencies of Arbitrarily Shaped Plates, Transactions of the Korean Society for Noise and Vibration Engineering, 22(9), p830-836.
Kang, S. W., Atluri, S., and Kim, S. H., (2012), Application of Nondimensional Dynamic Influence Function Method for Free Vibration Analysis of Arbitrarily Shaped Membranes, Journal of Vibration and Acoustics, 134(4), p041008.1-041008.8. [https://doi.org/10.1115/1.4006414]
Kang, S. W., and Yon, J. I., (2013), New Formulation of MNDIF Method for Extracting Accurate Natural Frequencies of Plates, Transactions of the Korean Society for Noise and Vibration Engineering, 23(8), p725-733. [https://doi.org/10.5050/ksnve.2013.23.8.725]
Kang, S. W., and Atluri, S., (2015), Improved Non-dimensional Dynamic Influence Function Method Based on Two-domain Method for Vibration Analysis of Membranes, Advances in Mechanical Engineering, 7(2), p1-8. [https://doi.org/10.1177/1687814015571012]
Kang, S. W., and Atluri, S., (2016), Improved NDIF Method for Vibration Analysis of Arbitrarily Shaped Plates with Clamped Edges, Advances in Mechanical Engineering, 8(3), p1-8.
Kang, S. W., (2017), New Formulation of NDIF Method for Highly Accurate Eigenvalue Analysis of Arbitrarily Shaped Plated, Transactions of the Korean Society for Noise and Vibration Engineering, 27(5), p622-628. [https://doi.org/10.5050/ksnve.2017.27.5.622]
Kang, S. W., (2007), Free Vibration Analysis of Clamped Plates with Arbitrary Shapes Using Series Functions, Transactions of the Korean Society for Noise and Vibration Engineering, 13(10), p531-538.
Kang, S. W., and Yon, J. I., (2009), Eigenvalue Analysis of Arbitrarily Shaped, Concave Membranes with a Deep Groove Using a Sub-domain Methods, Transactions of the Korean Society for Noise and Vibration Engineering, 19(10), p1069-1074.
Kang, S. W., (2018), Eigenvalue Analysis of Arbitrarily Shaped, Acoustic Cavities using Two-domain Method, Transactions of the Korean Society for Noise and Vibration Engineering, 28(4), p410-416. [https://doi.org/10.5050/ksnve.2018.28.4.410]
Meirovitch, L., (1967), Analytic Methods in Vibrations, Macmillan Publishing, New York, p179-182.
Blevins, R. D., (1979), Formulas for Natural Frequency and Mode Shape, Litton Education Publishing, New York, p239-245.

Sang-Wook Kang received a B.S., M.S. and Ph.D. degree in Dept. of Mechanical Design Engineering from Seoul National University in 1992, 1994 and 1999, respectively. He is currently working in Hansung University as a professor of the mechanical system engineering. His research interests include the development of NDIF method for free vibration analysis of membrane, acoustic cavities, and plates with general shapes.

	Proposed method			FEM (1677 nodes)	Leissa⁽²⁰⁾
	Nh = 3	Nh = 4	Nh = 5	FEM (1677 nodes)	Leissa⁽²⁰⁾
1	6.25	6.25	6.25	6.25	6.26
2	7.40	7.40	7.40	7.40	7.41
3	9.24	9.24	9.24	9.24	9.25
4	10.1	10.1	10.1	10.1	10.1
5	10.9	10.9	10.9	10.9	10.9
6	None	11.5	11.5	11.5	11.5

	Proposed method				FEM (1677 nodes)
	Nh = 3	Nh = 4	Nh = 5	Nh = 6	FEM (1677 nodes)
1	5.58	5.58	5.58	5.58	5.58
2	7.28	7.29	7.29	7.29	7.29
3	9.21	9.21	9.21	9.21	9.21
4	9.46	9.47	9.47	9.47	9.47
5	10.3	10.3	10.3	10.3	10.3