철도 브레이크 스퀼 소음 해석 연구

1. 서 론

철도 품질의 고급화 및 승객들의 높아진 요구로 인해 열차가 승강장에 정차할 때 발생하는 브레이크 스퀼 소음의 이슈가 크게 대두되고 있다. 브레이크 스퀼 소음은 보통 80dB ~ 112dB이⁽¹⁾ 발생하는데 이는 많은 사람들에게 불쾌감을 주기 때문에 조속히 해결해야 할 필요가 있다.

브레이크 스퀼 소음에 관한 연구는 수학적 모델을 통한 이론적 접근법, 제동 다이나모미터를 이용한 스퀼 소음 시험법, 유한요소 모델을 이용한 해석법 등 많은 연구가 진행되어 왔다. Kang은⁽²⁾ 유한요소방법을 통해 인플레인 모드와 댐핑 심에 스퀼 성향을 연구하였다. Lee et al.은⁽³⁾ 기여도 분석법과 복소수 고유치 해석을 통해서 저주파 스퀼 소음을 예측하였다. Choi et al.⁽⁴⁾은 압력을 변화시키면서 주파수 응답 시험과 복소수 고유치 해석을 통하여 아웃 오브 플레인 모드를 연구하였다. Nam et al.은⁽⁵⁾ 유한요소 모델을 이용하여 복소수 고유치 해석을 통해 발생한 불안정 실수부와 음의 기울기에 의해서 발생하는 불안정 실수부를 연구하였다. Goo는⁽⁶⁾ 철도 브레이크를 복소수 고유치 해석을 하였고 탄성계수와 마찰계수를 변환시키면서 불안정 진동 모드에 미치는 영향에 분석하였다. Cha et al.은⁽⁷⁾ 틸팅 차량용 휠 제동장치를 유한요소 모델을 만들어 소음 발생 영역대의 복소수 고유치 해석을 하였고 실험과 비교하였다. Liu et al.은⁽⁸⁾ 자동차 브레이크의 압력, 속도, 강성의 조건을 바꾸면서 복소수 고유치 해석을 하고 분석하였다.

철도 브레이크의 경우 복소수 고유치 해석 시 불안정 모드가 0Hz ~ 16000Hz 사이에 광범위하고 과도하게 많이 나타난다.⁽⁹⁾ 철도 브레이크 시스템은 휠과 슈에 의한 조합, 휠과 레일에 의한 조합, 디스크와 패드에 의한 조합으로 다양한 메커니즘에 의해 스퀼 소음이 발생한다. 이중 가장 기본적으로 스퀼을 발현시키는 패드와 제동디스크의 조합에 대해서 연구하였다. 또한 마찰 소음 해석에서 모드연성 불안정성을 발현시키는 주요 인자인 접촉강성을 해석을 통해 유추하고 Rayleigh 댐핑을 적용하여 철도 브레이크에 대한 스퀼 소음해석을 수행하였다. 추가적으로 Rayleigh 댐핑을 파라미터로 선정하여 Rayleigh 댐핑에 대한 스퀼 영향도를 분석하였다.

2. 본 론

2.1 FEM 해석 모델

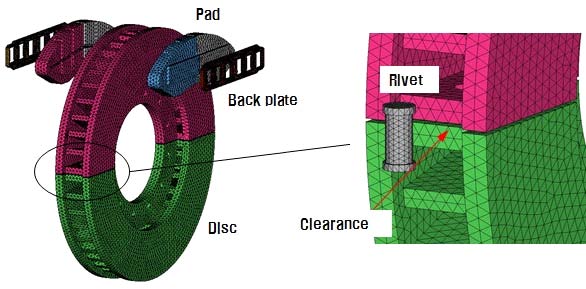
Fig. 1에서 보듯이, 이 해석 모델은 디스크, 패드, 백 플레이트, 리벳으로 구성되어 있으며, 2개의 디스크 반쪽 모형이 리벳을 통해서 연결되어 있다. 또한 현 차 조건과 동일하게 디스크 사이에 2.5mm의 공차(clearance)를 두었다. 메쉬타입은 tetra mesh이고 노드는 33310개, 요소는 109345개이다. 복소수 고유치 해석은 상용 해석 프로그램인 ABAQUS를 이용하였다.

Fig. 1

FEM model of rail brake

2.2 모달 테스트(Modal Test)

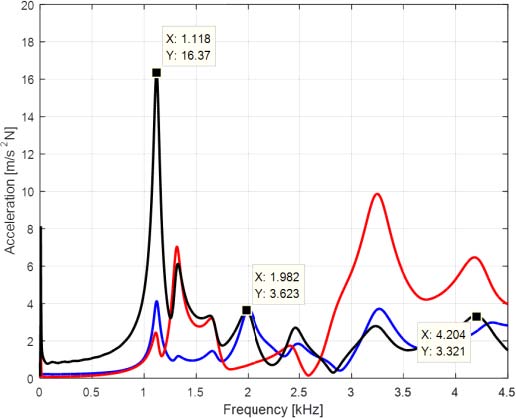
철도 디스크 브레이크 해석을 하기 전에 단품 모델에 대한 모달 테스트를 수행하였다. 철도 패드의 고유진동수를 측정하기 위해서 철도 패드 단품을 Fig. 2와 같이 설치한 후에 3축 가속도계를 부착하고 분석 소프트웨어(B&K)를 이용하여 Fig. 3과 같은 주파수 응답함수(frequency response function)를 구하였다.

Fig. 2

Pad for modal test

Fig. 3

Frequency response function of pad

고유진동수 측정결과 1147.3Hz에서 1차 굽힘 모드, 2073Hz에서 2차 굽힘 모드, 4243.8Hz에서 3차 굽힘 모드가 발생하였다.

이 연구에서 스퀼 해석의 신뢰성을 높이기 위해 모달 테스트에서 얻은 고유진동수와 자유경계상태에서 모달 해석결과를 비교하였다. 두 결과의 오차는 5% 이내로 나타났다. 탄성계수는 일반적인 물성치 범위를 초과하지 않는 범위에서 보정하였고, 밀도는 3D 모델로 구현화한 모델의 질량과 직접 계측한 질량을 비교하여 산출하였다. 실험결과를 기반으로 해석에서 적용된 철도패드의 기계적인 물성은 다음과 같다. 마찰재의 밀도는 2516kg/m³, 탄성계수는 5.2GPa, 푸아송비는 0.3이다.

Table 1

Correlation of frequency response function of pad

다만 이 연구에서는 철도 브레이크 디스크의 모달 시험은 해석으로 대체하였고, 차후 연구에서 진행할 예정이다.

2.3 복소수 고유치 해석 조건

이 연구는 스퀼 소음을 분석하는 방법 중 복소수 고유치 해석을 이용하였다. 복소수 고유치 해석절차는 다음과 같다.

(1)제동 실린더 압력에 의한 제동디스크와 패드의 접촉 해석

(2)제동 디스크의 회전을 고려한 디스크와 패드 마찰 해석

(3)디스크와 패드의 마찰과 감쇠를 무시한 고유 모드해석

(4)디스크와 패드 마찰을 고려한 복소수 고유치 해석

복소수 고유치 문제는 다음과 같이 표현된다.

$\[ \left({\lambda }^2\left[M\right]+\lambda \left(\left[C_1\right]+\left[C_2\right]\right)+\left[K\right]\right)\left\{u\right\}=0 \]$

(1)

여기서 [M]는 대칭인 질량행렬, [C₁]는 마찰 감쇠효과에 의한 행렬, [C₂]는 Rayleigh 감쇠 행렬, [K]는 강성행렬을 나타낸다. 또한 λ는 고유값을 나타내고, u는 고유값에 상응하는 고유벡터를 나타낸다. 위의 운동방정식을 질량 정규화 및 선형화시켜 풀면 복소수 형태의 고유값 λ를 얻을 수 있다. λ의 실수부가 양수이면, 시스템이 불안정함을 나타내고, 음수이면 안정함을 나타낸다⁽¹⁰⁾.

복소수 고유치 해석을 수행하기 위해 물성치 적용, 접촉조건 결정, 압력 부여, 경계조건 등을 결정하였다. 이 해석에 패드에 가해는 압력은 4.9 bar로 백 플레이트와 패드에 수직으로 가해주었다. 디스크의 마운팅 볼트 부분은 모든 방향의 변위를 구속하였고, 리벳과 패드와 백 플레이트 사이의 접촉은 타이(tie) 조건으로 구속하였다.

일반적인 정적 구조해석의 결과는 상대적으로 접촉강성 값에 넓은 범위에서 의존적이지 않다. 그러나 복소수 고유치 해석의 경우 접촉강성에 따라 모드연성에 의한 불안정성이 매우 민감하게 나타난다. 따라서 정적 구조해석을 통해 추정된 접촉강성을 반영하였다. 접촉강성은 다음과 같이 표현할 수 있다.

$\[ k_c=\frac{P_c}{u} \]$

(2)

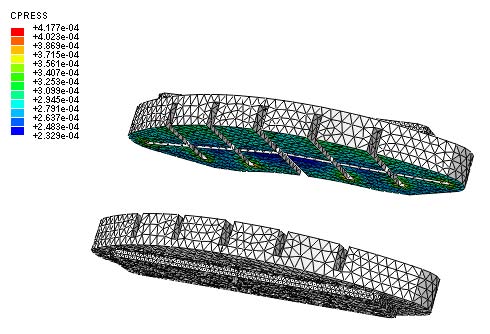
여기서 P_c는 접촉 압력, k_c는 접촉강성, u는 변위를 나타낸다. 패드의 접촉압력을 구하기 위해 강제 변위를 제어하여 정적 구조해석을 수행하였다. 결과로 나타난 최대 접촉압력을 이용하여 실제 패드의 최대 접촉강성을 추정하고, 복소수 고유치 해석에 적용하였다. 정적 해석을 통해 나타난 접촉압력 및 접촉압력의 분포는 Fig. 4에서 보여준다.

Fig. 4

Contact pressure on contact surface

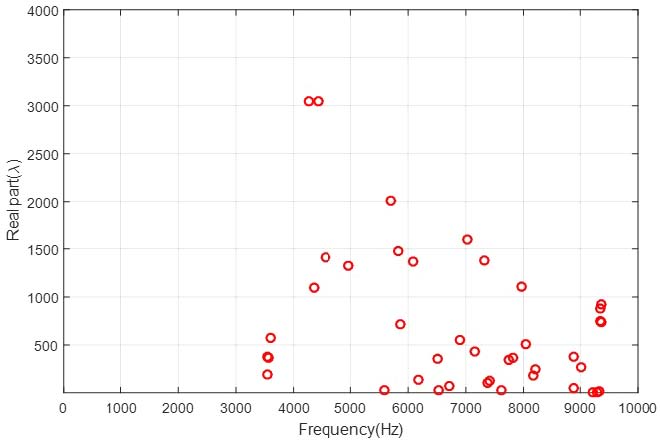
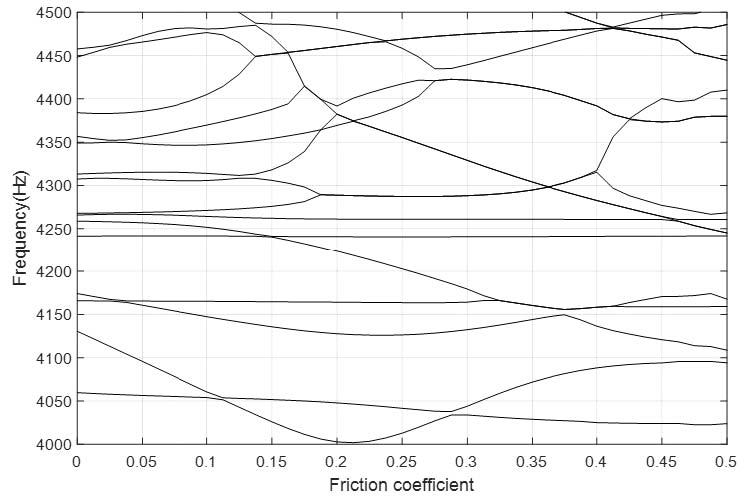
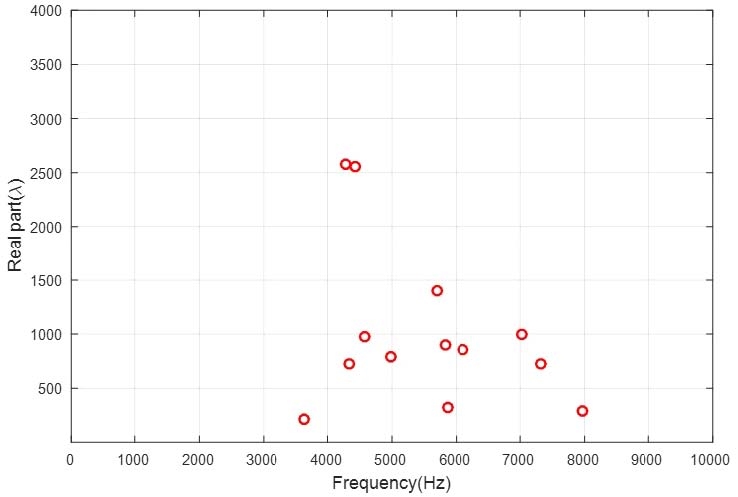
또한 마찰 댐핑을 적용하여 속도항에 의존적인 댐핑항을 고려하였다. 위와 같은 해석조건을 기반으로 복소수 고유치 해석을 하였다. Fig. 5는 주파수에 대한 양의 실수부(real part)를 나타낸다. 양의 실수부는 불안정한 모드를 말하며 스퀼 소음이 발생할 수 있는 것을 의미한다. 불안정한 모드가 3000Hz ~ 10000Hz 사이에 광범위하게 발생했으며 주로 패드 모드에서 불안정 실수부가 많이 발현되었다. Fig. 6은 Fig. 5의 불안정 모드들의 모드연성 특성을 나타낸 그림이다. Fig. 5의 4000Hz ~ 4500Hz에서 특정 모드들이 모드 결합(mode-merging)됨을 보여주고 있다.

Fig. 5

Instability modes of rail brake

Fig. 6

Frequency variation with respect to friction coefficient

2.4 레일리 댐핑(Rayleigh Damping) 적용

자동차 브레이크 스퀼 대비 패드에 의한 스퀼모드가 많이 발생하였다. 패드의 의한 스퀼 영향도를 분석하기 위해서 패드와 디스크에 Rayleigh 댐핑을 적용하여 해석을 수행하고 Rayleigh 댐핑에 의한 파라미터 스터디를 하였다.

Rayleigh 댐핑은 다음과 같이 표현할 수 있다.

$\[ \left[C\right]=\alpha \left[M\right]+\beta \left[K\right] \]$

(3)

이 때 α[M]은 질량에 비례하는 댐핑, β[M]는 강성에 비례하는 댐핑이다. Rayleigh 댐핑을 시스템에 적용시키기 위해 α, β 값을 다음과 같은 식으로부터 얻을 수 있다⁽¹¹⁾.

$\[ \xi =\frac{\alpha }{2\omega }+\frac{\beta \omega }{2} \]$

(4)

이 때 ξ는 댐핑 계수이고 ω는 고유주파수이다. ξ, ω 값은 모달 테스트를 이용하여 구할 수 있다. 이 연구는 Mohammad et al.⁽¹²⁾이 위의 계산식을 이용하여 구한 α, β 값을 ABAQUS에 적용하여 복소수 고유치 해석을 하였다. 디스크의 α=3.911, β=2.524×10^-7이고 패드의 α=731.98, β=5.870×10^-7이다.

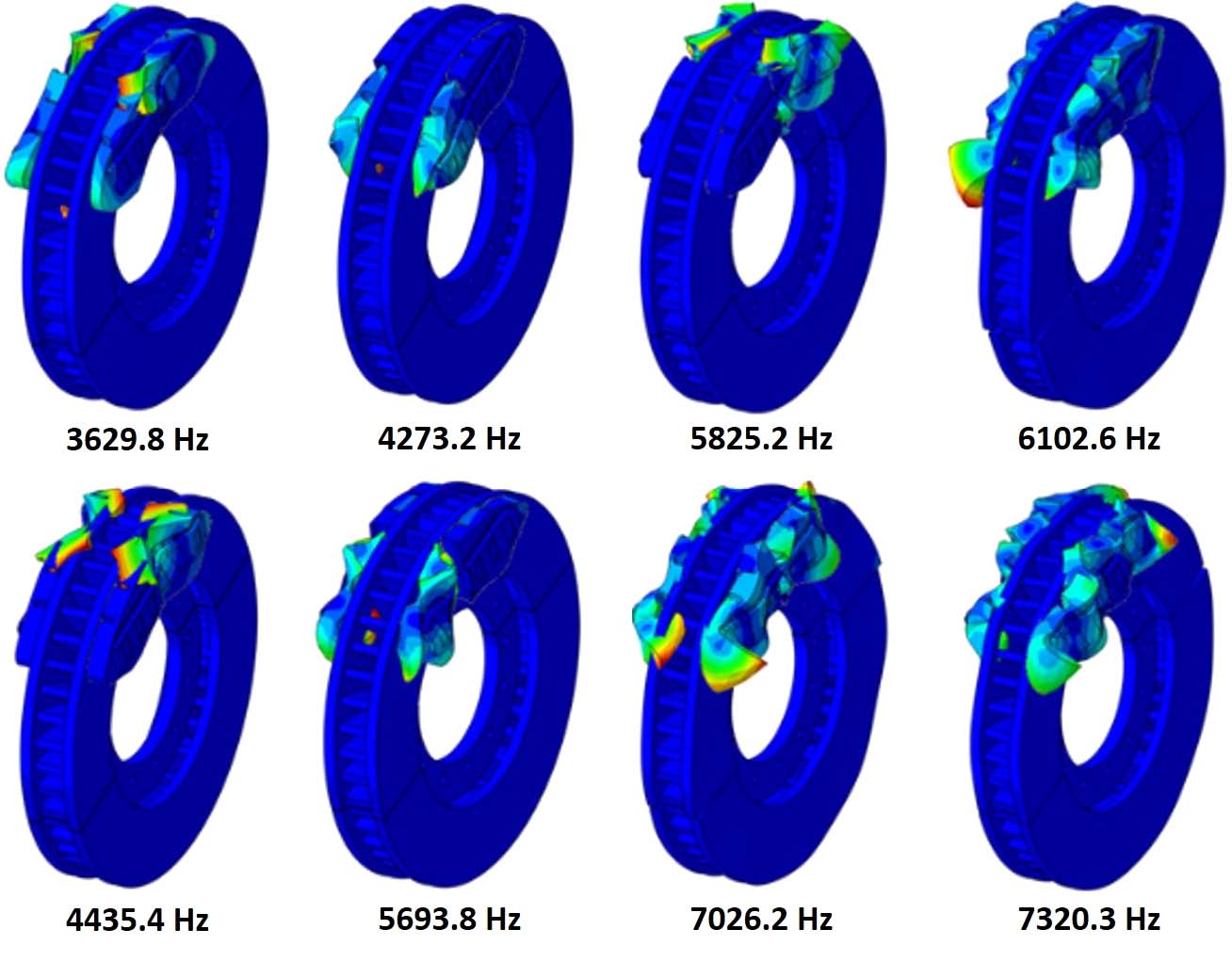
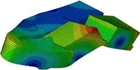
Fig. 7은 Rayleigh 댐핑을 적용하여 해석한 결과이다. 댐핑을 적용하였을 때 전체적으로 실수부의 크기가 작아지고 여러 불안정 모드들이 없어진 것을 볼 수 있다. 하지만 여전히 스퀼 소음이 3000Hz ~ 8000Hz 사이에서 발생할 것으로 예측할 수 있다. Fig. 8은 주요 불안정 모드 형상을 나타낸 그림이다. 불안정 모드가 발생한 주파수에서 모드 형상을 확인한 결과 철도 패드 모드가 철도 브레이크 스퀼 발생에 중요한 진동모드임을 알 수 있다.

Fig. 7

Instability modes with Rayleigh damping

Fig. 8

Instability mode shape

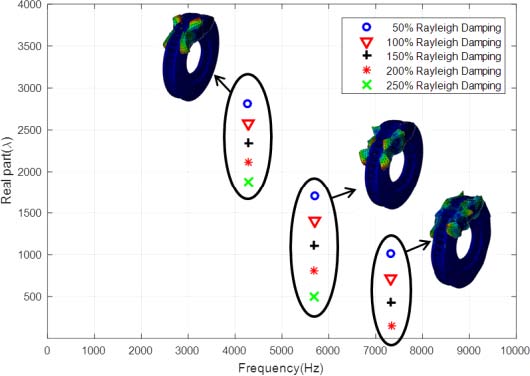
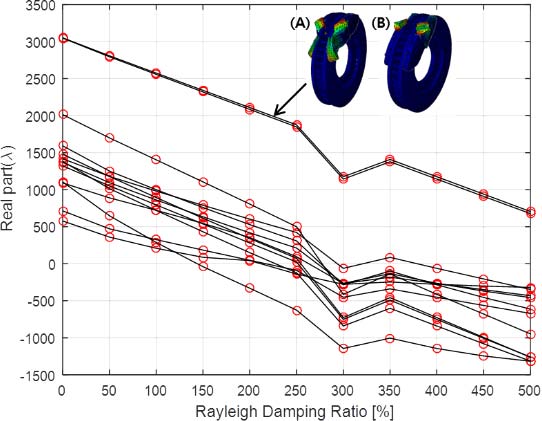
Fig. 9는 위의 Rayleigh 댐핑 α, β 값을 100%로 정의하고 0%, 50%, 100%, 150%, 200%, 250%에서 해석을 수행한 결과를 보여준다. 대표적으로 4273.2Hz, 5693.9Hz, 7320.3Hz 근방의 불안정 실수부는 댐핑이 커질수록 선형적으로 불안정 실수부의 크기가 감소한다. 특히, 7320.3Hz의 불안정 실수부는 Rayleigh 댐핑이 250%가 되면, 양의 실수를 발현시키지 않고 안정화되는 것을 보여준다. Fig. 10은 0Hz ~ 4000Hz 사이에 발생되는 모든 불안정 모드에 대한 댐핑효과를 나타낸 그림이다. 불안정 모드들은 Rayleigh 댐핑이 커질수록 불안정한 실수부의 크기가 감소하는 경향이 있다. 또한 A,B를 제외한 대부분의 모드들은 300%가 되었을 때 더 이상 양의 실수부를 발현시키지 않으며, 안정적인 모드로 변화되었다. 반면에 A,B모드는 Rayleigh 댐핑이 500%가 되어도 여전히 큰 양의 실수부를 발현시키는 불안정 모드임을 보여준다.

Fig. 9

Parameter study with respect to Rayleigh damping

Fig. 10

Real part variation with respect to Rayleigh damping

3. 결 론

이 연구에서는 철도 브레이크 모델을 이용하여 모달 테스트를 수행하였으며 모달 해석과 비교하여 오차를 5% 이내의 오차에서 신뢰성을 확보하였다. 패드와 디스크에 Rayleigh 댐핑을 적용하여 Rayleigh 댐핑 효과가 불안정성에 기인하는 영향도를 보여주고, Rayleigh 댐핑에 대한 파라미터 스터디를 수행하였다. 그 결과 다음과 같다.

• (1) Rayleigh 댐핑 적용 시 전체적으로 실수부의 크기가 줄어들었다.
• (2) Rayleigh 댐핑을 적용하면 8000Hz ~ 10000Hz 대역의 불안정 실수부는 감소되지만 3000Hz ~ 8000Hz 대역의 양의 실수부는 지속적으로 발현된다.
• (3) 철도 브레이크 스퀼 소음은 브레이크 패드 모드가 불안정성에 큰 기여를 한다.
• (4) Rayleigh 댐핑이 철도 브레이크 스퀼에 중요한 인자이다.

철도 해석에 대한 검증을 위해 현차 시험은 준비중에 있으며, 추후 해석결과와 비교검증하여 연구될 예정이다.

Acknowledgments

연구는 2018년 국토교통과학기술진흥원에서 주관하는 국책과제 도시철도 제동 마찰 재개발 및 표준화 연구의 일부분이며, 이 연구를 통하여 소음 우수 제품을 개발하고 도시철도 분야의 소음해석 관련 신기술을 확보하는 것이 목표이다.

References

• Kim, H. S., Yoo, Y. H., Yoon, C. J., Kim, S. Y., and Lee, J. H., (2007), Study on the Braking Noise Reduction of KTX, KORAIL, Report KORI-Technology-​Yong-06-06.
• Kang, J., (2012), Finite Element Modelling for the Investigation of In-plane Modes and Damping Shims in Disc Brake Squeal, Journal of Sound and Vibration, 331(9), p2190-2202. [https://doi.org/10.1016/j.jsv.2011.12.033]
• Lee, J. G., Lim, H. S., Kim, H. Y., and Baek, J. W., (2009), The Prediction of Brake Corner Module Squeal Noise Using Participation Factor Analysis, Transactions of the Korean Society of Mechanical Engineers A, 33(10), p1074-1080. [https://doi.org/10.3795/ksme-a.2009.33.10.1074]
• Choi, H., Kang, J., and Gil, H., (2014), Numerical and Experimental Analysis for Disc Brake Squeal Induced by Caliper Mode, Transactions of the Korean Society of Mechanical Engineers A, 38(12), p1351-1358. [https://doi.org/10.3795/ksme-a.2014.38.12.1351]
• Nam, J., and Kang, J., (2014), Investigation of Friction Noise with Respect to Friction Curve by Using FEM and Its Validation, Transactions of the Korean Society for Noise and Vibration Engineering, 24(1), p28-34. [https://doi.org/10.5050/ksnve.2014.24.1.028]
• Goo, B. C., (2013), Analysis of Unstable Vibration Modes Due to KTX Brake Disc/Pad interaction, Journal of the Korean Society for Railway, 16(4), p253-261. [https://doi.org/10.7782/jksr.2013.16.4.253]
• Cha, J.-K., and Park, Y.-I., (2010), Analysis on the Squeal Noise of Wheel Brake System for Tilting Train, Transactions of the Korean Society for Noise and Vibration Engineering, 20(1), p98-105. [https://doi.org/10.5050/ksnve.2010.20.1.098]
• Liu, P., Zheng, H., Cai, C., Wang, Y. Y., Lu, C., Ang, K. H., and Liu, G. R., (2007), Analysis of Disc Brake Squeal Using the Complex Eigenvalue Method, Applied Acoustics, 68(6), p603-615. [https://doi.org/10.1016/j.apacoust.2006.03.012]
• Goo, B. C., and Oh, S. H., (2012), Analysis of the Brake Squeal Noise of KTX Train, Proceedings of the Korean Society for Railway Annual Spring Conference, p358-362.
• ABAQUS Analysis User’s Manual, Ver. 6.14.
• Chowdhury, I., and Dasgupta, S. P., (2003), Computation of Rayleigh Damping Coefficients for Large System, The Electronic Journal of Geotechnical Engineering, 8, p1-11.
• Mohammad, E., Richard, T., and Oluremi, O., (2013), Effect of Damping in Complex Eigenvalue Analysis of Brake Noise to Control Over-prediction of Instabilities: An Experimental Study, SAE Technical Paper 2013-01-2034. [https://doi.org/10.4271/2013-01-2034]