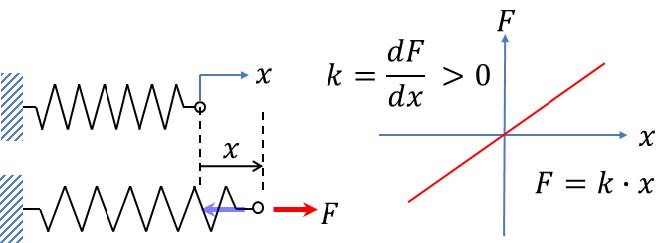진동 절연을 위한 KDamper 모델링

1. 서 론

지진 및 풍하중을 받는 건물 및 교량, 풍하중을 받는 풍력발전기, 조파하중을 받는 선박이나 해양구조물, 각종 회전기계 등에서 발생하는 진동을 절연하기 위한 방법이 많이 연구^{(1 ~ 3)}되어 왔다.

그 중에서 TMD(tuned mass damper) 방법⁽²⁾은 구조물에 질량과 스프링으로 이루어진 진동시스템을 추가하여 간단하게 진동을 절연할 수 있는 방법으로, 현재까지도 널리 이용되는 진동 절연 방법 중 하나이다. 실제로 대만에 있는 101층 빌딩에서도 진동 절연 방법으로 TMD를 이용하고 있다. 그러나 TMD는 효과적인 진동절연을 달성하기 위하여 큰 부가질량으로 이루어진 진동시스템을 적용해야 하는 단점을 가지고 있다.

이러한 단점을 보완하기 위해 고안된 KDamper는 기존 TMD 시스템에 음강성(negative stiffness) 요소⁽³⁾를 추가로 배치하여 진동 절연 및 감쇠를 효과적으로 달성하는 새로운 “강성+감쇠=K+Damper”라는 개념을 제시하고 있다.

KDamper는 지진 및 외부 가진에 의한 산업기계류, 발전설비 등의 진동절연 및 감쇠, 건물과 교량 등의 내진설계 등에 적용되어 기존 방법의 한계점을 보완하고 진동 절연 및 감쇠에 큰 효과를 달성할 수 있을 것으로 기대된다.

이 논문에서 기존의 TMD^(1,2)와 KDamper의 운동방정식을 유도하고 TMD와 KDamper의 진동절연 효과를 비교 고찰하여 KDamper의 진동절연 및 감쇠 효과의 우수성을 확인하였다.

2. 진동 감쇠 모델의 운동방정식

2.1 음강성의 정의 및 활용

양강성(positive stiffness)을 갖는 일반적인 스프링은 Fig. 1과 같이 외력이 작용하면 외력과 동일한 방향으로 변위가 발생하고, 변위에 의한 스프링의 내력은 변위를 복원하려는 방향으로 작용하며, 해당 변위에서 내력과 외력은 평형을 이룬다. Fig. 1의 외력과 변위의 관계 그래프에서 기울기가 강성(stiffness)을 나타내며, 기울기는 양(positive)의 값을 갖는다.

Fig. 1

Relationship between the external force and the displacement of positive stiffness

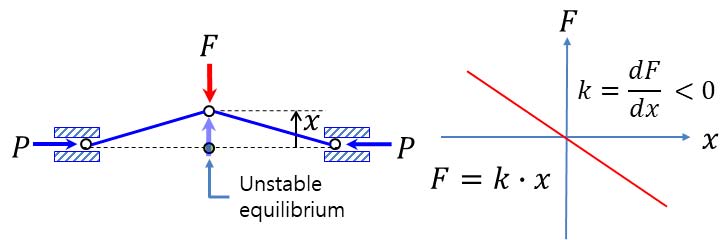
Fig. 2는 음강성을 구현한 형상이다. 두 개의 바(bar)가 힌지로 연결되어 있고, 바(bar) 끝단에 압축방향으로 힘이 작용하고 있다. 외력(F)이 작용하지 않는 평형상태는 바(bar)가 일직선으로 놓인 상태이다. 변위가 발생하면 변위에 따른 내력은 변위를 확대시키려는 방향으로 작용하며, 해당 변위에서 내력과 평형을 이루기 위한 외력은 변위의 방향과 반대로 작용한다. 이러한 외력과 변위의 관계를 그래프에서 기울기, 즉 강성(stiffness)은 음(negative)의 값을 갖는다.

Fig. 2

Relationship between the external force and the displacement of negative stiffness

음강성을 이용한 기존 진동절연방법으로 QZS(quasi zero stiffness)은 진동시스템에 양강성 스프링과 평행하게 음강성을 배치하여 전체 시스템의 고유진동수를 거의 0(zero)에 가깝게 만듦으로써 시스템의 전달률을 낮추어 진동절연을 구현하는 방법으로, 전체 시스템의 정적강성이 낮아지므로 외부의 추가적인 하중변화에 대한 시스템의 정적안정성이 취약하다는 단점이 있다.

2.2 TMD 시스템

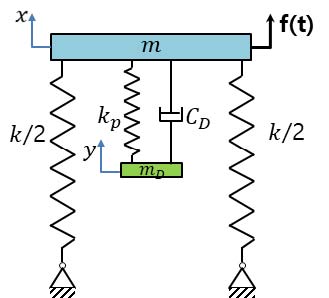
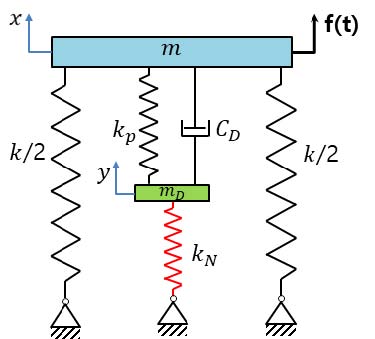
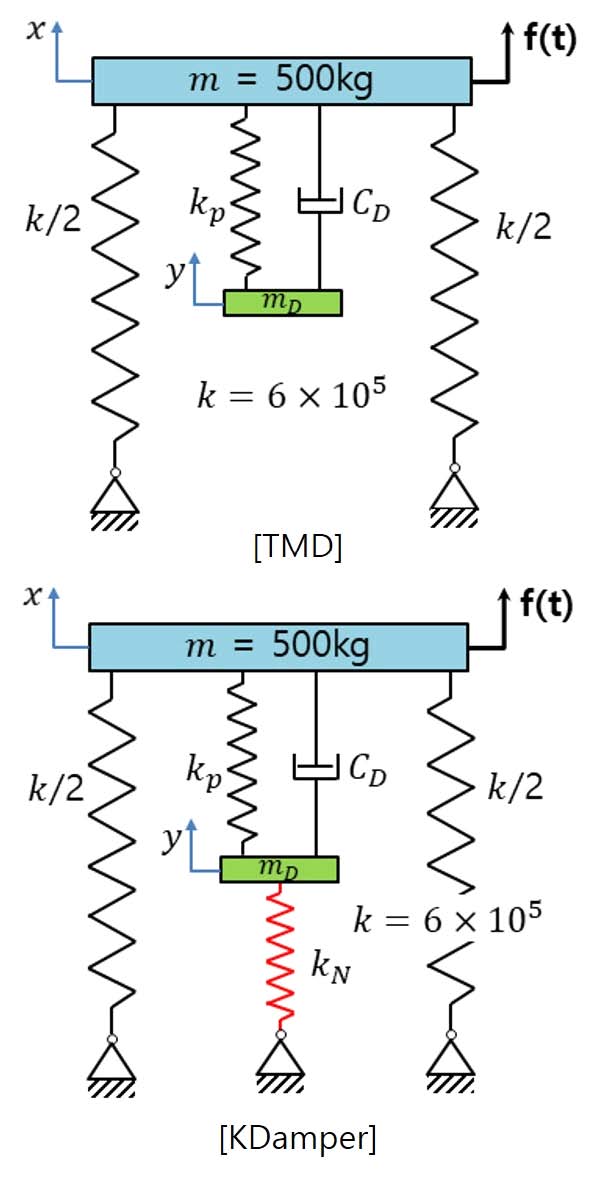
TMD(tuned mass damper)의 진동절연 방법은 Fig. 3과 같이 기존 절연시스템의 절연 대상인 주질량(m)에, 부가질량(m_D), 스프링(k_p), 댐퍼(C_D)로 구성된 진동시스템을 추가하여 외력(f(t))에 의한 운동에너지를, 추가된 부가질량(m_D)의 운동에너지로 전환하여 주질량(m)의 진동을 절연하는 방법이다. 힘의 관점에서 살펴보면 주질량(m)에 가해지는 외력과 부가질량(m_D) 운동에 의해 주질량(m)에 전달되는 힘이 평형을 이루어 주질량(m)의 진동을 절연하게 된다.

Fig. 3

TMD(tuned mass damper) system

Fig. 3의 TMD 시스템의 운동방정식은 식 (1), 식 (2)와 같이 유도된다.

$\[ m\ddot{x}+c_D\left(\dot{x}-\dot{y}\right)+kx+k_P\left(x-y\right)=f \]$

(1)

$\[ m_D\ddot{y}-c_D\left(\dot{x}-\dot{y}\right)-k_P\left(x-y\right)=0 \]$

(2)

여기에서 외력을 조화가진(harmonic excitation)으로 가정하면 외력 f(t)는 식 (3)으로 표현되며, X_ST는 외력에 의한 시스템의 정적 처짐을 의미한다. 시스템의 조화응답을 식 (4), 식 (5)로 표현할 수 있으며, $$ \tilde{X}, \tilde{Y}$$는 일반적으로 복소수(complex)이다.

$\[ f\left(t\right)=k{X}_{ST}\mathrm{e}\mathrm{x}\mathrm{p}\left(j\omega t\right) \]$

(3)

$\[ x\left(t\right)=\stackrel{\sim }{X}\mathrm{e}\mathrm{x}\mathrm{p}\left(jwt\right),y\left(t\right)=\stackrel{\sim }{Y}\mathrm{e}\mathrm{x}\mathrm{p}\left(jwt\right) \]$

(4,5)

식 (1), 식 (2)에 식 (3), 식 (4), 식 (5)의 관계를 적용하여 정리하면 식 (6), 식 (7)을 얻으며, 식 (7)을 식 (6)에 대입하면 식 (8)을 얻는다.

$\[ -{\omega }^{2}m\stackrel{\sim }{X}+j\omega c_D\left(\stackrel{\sim }{X}-\stackrel{\sim }{Y}\right)+k\stackrel{\sim }{X}+k_P\left(\stackrel{\sim }{X}-\stackrel{\sim }{Y}\right)={kX}_{ST} \]$

(6)

$\[ -{\omega }^2{m}_D\stackrel{\sim }{Y}-j\omega c_D\left(\stackrel{\sim }{X}-\stackrel{\sim }{Y}\right)-k_P\left(\stackrel{\sim }{X}-\stackrel{\sim }{Y}\right)=0 \]$

(7)

$\[ -{\omega }^{2}m\stackrel{\sim }{X}+k\stackrel{\sim }{X}-{\omega }^2{m}_D\stackrel{\sim }{Y}=k{X}_{ST} \]$

(8)

식 (8)에서 TMD 시스템에 가해진 외력(kX_ST)은 주질량의 관성력($$ {\omega }^{2}m\tilde{X}$$), 변위에 의한 스프링력($$ k\tilde{X}$$), 부가질량의 관성력($$ {\omega }^2{m}_D\tilde{X}$$)과 평형을 이루며, 부가질량의 관성력을 통해 주질량의 변위 감소, 즉 절연의 효과를 얻을 수 있다.

TMD시스템의 외력에 의한 정적 처짐(X_ST)과 진동하중에 의한 변위 $$ \tilde{X}, \tilde{Y}$$의 비, 즉 전달함수(transfer function)는 식 (6), 식 (7)을 이용하여 정리하면 식 (9)와 같이 얻을 수 있다.

$\[ \begin{array}{l}{\stackrel{\sim }{T}}_{XMT}=\frac{\stackrel{\sim }{X}}{X_{ST}}=\\ \frac{\left(-{\omega }^2{m}_D+j\omega c_D+k_P\right)k}{\left(-{\omega }^{2}m+j\omega c_D+k+k_P\right)\left(-{\omega }^2{m}_D+j\omega c_D+k_P\right)-{\left(j\omega c_D+k_P\right)}^2}\\ {\stackrel{\sim }{T}}_{YMT}=\frac{\stackrel{\sim }{Y}}{X_{ST}}=\\ \frac{\left(j\omega c_D+k_P\right)k}{\left(-{\omega }^{2}m+j\omega c_D+k+k_P\right)\left(-{\omega }^2{m}_D+j\omega c_D+k_P\right)-{\left(j\omega c_D+k_P\right)}^2}\end{array} \]$

(9)

무차원화된 변수를 이용하여 전달함수를 구하기 위하여 식 (10)과 같이 무차원 변수⁽⁴⁾를 정의하였다. 식 (10)을 적용하면 식 (9)는 식 (11)과 같이 표현된다.

$\[ \begin{array}{l}q=\omega /{\omega }_0,\rho ={\omega }_D/{\omega }_0,\\ {\omega }_0=\sqrt{k/m},{\omega }_D=\sqrt{k_P/m_D},\\ {\xi }_D=C_D/2\sqrt{k_P{m}_D},\mu =m_D/m\end{array} \]$

(10)

$\[ \begin{array}{l}{\stackrel{\sim }{T}}_{XMT}=\\ \frac{\stackrel{\sim }{X}}{X_{ST}}=\frac{\left({\rho }^2-q^2\right)+j2{\xi }_D\rho q}{\left\{\left[q{}^4-q^2\left(1+{\rho }^2+\mu {\rho }^2\right)+{\rho }^2\right]+j2{\xi }_D\rho q\left[1-q^2\left(1+\mu \right)\right]\right\}}\\ {\stackrel{\sim }{T}}_{YMT}=\frac{\stackrel{\sim }{Y}}{X_{ST}}=\\ \frac{{\rho }^2+j2{\xi }_D\rho q}{\left\{\left[q{}^4-q^2\left(1+{\rho }^2+\mu {\rho }^2\right)+{\rho }^2\right]+j2{\xi }_D\rho q\left[1-q^2\left(1+\mu \right)\right]\right\}}\end{array} \]$

(11)

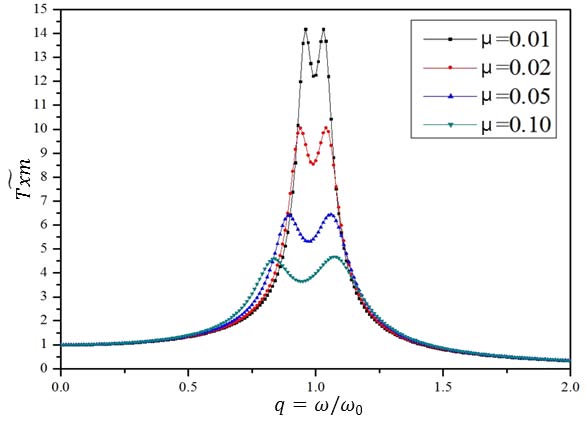
Fig. 4는 식 (11)에서 정의된 $$ {\tilde{T}}_{XMT}$$를 무차원 가진주파수 q의 함수로 나타낸 그래프이다. TMD 시스템의 최대 전달율은 부가질량비(μ)의 값이 클수록 전달률($$ {\tilde{T}}_{XMT}$$)의 값이 작아진다. 즉, TMD 시스템에서 진동절연 향상을 위해서는 부가질량(m_D)의 크기를 증가시켜야 한다. Fig. 4에서 전달함수 $$ {\tilde{T}}_{XMT}$$는 전체 그래프의 통일성을 위해 $$ {\tilde{T}}_{XM}$$으로 나타내었다.

Fig. 4

TXM vs. q for 4 different μ’s

2.3 KDamper 시스템

KDamper 시스템은 Fig. 5와 같이 Fig. 3의 TMD 시스템에 음강성 요소(k_N)를 추가 배치한 형태이다. 전체 시스템 강성(k_eq)값은 음강성(k_N)과 기존 강성 값(k_p, k)의 함수로, 음강성과 기존 스프링의 직렬, 병렬 관계에 의해 식 (12)와 같이 정리된다.

Fig. 5

Configuration of a KDamper system

$\[ k+\frac{k_P{k}_N}{k_P+k_N}=k_{eq} \]$

(12)

Fig. 5에서 m, m_D에 대하여 각각 뉴턴의 운동법칙을 적용하여 유도된 운동방정식은 아래와 같다.

$\[ m\ddot{x}+c_D\left(\dot{x}-\dot{y}\right)+kx+k_P\left(x-y\right)=f \]$

(13)

$\[ m_D\ddot{y}-c_D\left(\dot{x}-\dot{y}\right)-k_P\left(x-y\right)+k_{N}y=0 \]$

(14)

식 (13), 식 (14)에 식 (3) ~ (5)를 적용하면 식 (15), 식 (16)이 유도되며, 식 (16)을 식 (15)에 대입하여 정리하면 식 (17)을 얻을 수 있다.

$\[ -{\omega }^{2}m\stackrel{\sim }{X}+j\omega c_D\left(\stackrel{\sim }{X}-\stackrel{\sim }{Y}\right)+k\stackrel{\sim }{X}+k_P\left(\stackrel{\sim }{X}-\stackrel{\sim }{Y}\right)=k_{eq}{X}_{ST} \]$

(15)

$\[ -{\omega }^2{m}_D\stackrel{\sim }{Y}-j\omega c_D\left(\stackrel{\sim }{X}-\stackrel{\sim }{Y}\right)-k_P\left(\stackrel{\sim }{X}-\stackrel{\sim }{Y}\right)+k_N\stackrel{\sim }{Y}=0 \]$

(16)

$\[ -{\omega }^{2}m\stackrel{\sim }{X}+k\stackrel{\sim }{X}-{\omega }^2{m}_D\stackrel{\sim }{Y}+k_N\stackrel{\sim }{Y}=k_{eq}{X}_{ST} \]$

(17)

2.4 KDamper 시스템의 특성

KDamper의 운동방정식 식 (17)을 TMD의 운동방정식 식 (8)과 비교하여 살펴보면, 식 (17)에는 음강성에 의한 스프링력($$ k_N\tilde{Y}$$)이 추가되어 있다. 여기서 k_N은 음의 값을 가지므로 음강성에 의한 스프링력($$ k_N\tilde{Y}$$)과 부가질량에 의한 관성력($$ {-\omega }^2{m}_D\tilde{Y}$$)은 동일한 위상을 갖는다. TMD 시스템의 경우 절연효과 향상을 위하여 부가질량(m_D)의 크기 증가를 통한 부가질량의 관성력 증가가 필요하지만 KDamper의 경우 부가질량(m_D)의 크기를 증가시키지 않고 음강성의 스프링력을 통해 TMD 시스템의 부가질량 관성력 증가와 같은 절연효과를 달성할 수 있다.

KDamper의 외력에 의한 정적처짐(X_ST)과 진동변위 $$ \tilde{X}, \tilde{Y}$$의 비, 즉 전달함수(transfer function)는 식 (18), 식 (19)과 같으며 전달함수 식에서 k_D는 식 (20)으로 정의된다.

$\[ \stackrel{\sim }{T}{}_{XMK}=\frac{\stackrel{\sim }{X}}{X_{ST}}=\frac{\left(-{\omega }^2{m}_D+j\omega c_D+k_D\right)k_{eq}}{\left(-{\omega }^{2}m+j\omega c_D+k+k_P\right)\left(-{\omega }^2{m}_D+j\omega c_D+k_D\right)-{\left(j\omega c_D+k_P\right)}^2} \]$

(18)

$\[ {\stackrel{\sim }{T}}_{YMK}=\frac{\stackrel{\sim }{Y}}{\stackrel{\sim }{X}}{\stackrel{\sim }{T}}_{XK}=\frac{\left(j\omega c_D+k_P\right)k_{eq}}{\left(-{\omega }^{2}m+j\omega c_D+k+k_P\right)\left(-{\omega }^2{m}_D+j\omega c_D+k_D\right)-{\left(j\omega c_D+k_P\right)}^2} \]$

(19)

$\[ k_D=k_P+k_N \]$

(20)

식 (21)과 같이 무차원 변수(κ)를 정의하면, k_N이 음수이므로 κ는 항상 양의 값을 갖으며 κ값의 증가는 음강성(k_N)의 증가를 의미한다.

$\[ \kappa =-k_N/k_D=-k_N/\left(k_P+k_N\right) \]$

(21)

식 (10)에 정의된 변수들과 식 (21)의 κ로 식 (18), 식 (19)을 정리하면 식 (22), 식 (23)과 같다.

$\[ {\stackrel{\sim }{T}}_{XMK}=\frac{\stackrel{\sim }{X}}{X_{ST}}=\frac{\left({\rho }^2-q^2\right)+j2{\xi }_D\rho q}{\left\{\left[q^4-q^2\left(1+{\rho }^2+{\left(1+\kappa \right)}^2\mu {\rho }^2\right)+{\rho }^2\right]+j2{\xi }_D\rho q\left[\left(1+{\kappa }^2\mu {\rho }^2\right)-q^2\left(1+\mu \right)\right]\right\}} \]$

(22)

$\[ {\stackrel{\sim }{T}}_{YMK}=\frac{\stackrel{\sim }{Y}}{X_{ST}}=\frac{\left(1+\kappa \right){\rho }^2+j2{\xi }_D\rho q}{\left\{\left[q^4-q^2\left(1+{\rho }^2+{\left(1+\kappa \right)}^2\mu {\rho }^2\right)+{\rho }^2\right]+j2{\xi }_D\rho q\left[\left(1+{\kappa }^2\mu {\rho }^2\right)-q^2\left(1+\mu \right)\right]\right\}} \]$

(23)

Figs. 6 ~ 14 그래프에서 TMD($$ {\tilde{T}}_{XMT}$$)와 KDamper 시스템($$ {\tilde{T}}_{XMT}$$)의 전달 함수 크기 비교를 위해서, 통합적으로($$ {\tilde{T}}_{XM}$$)으로 나타내었다.

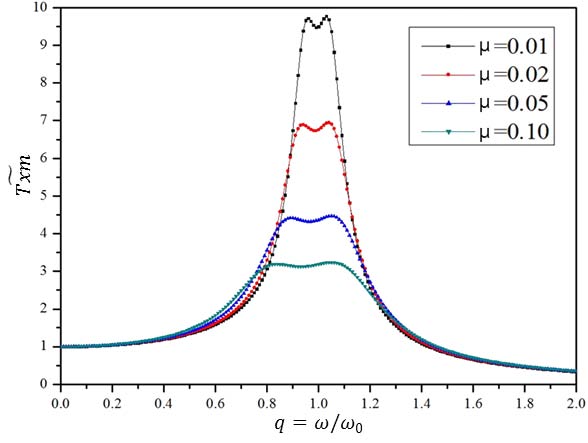
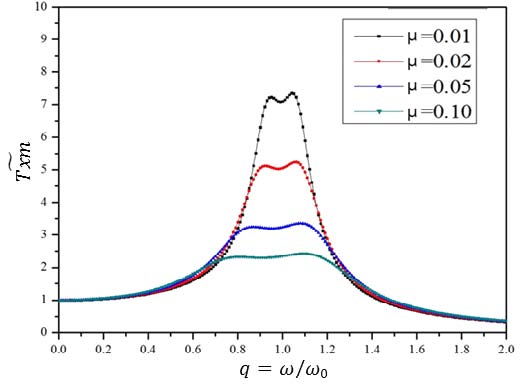
Figs. 6 ~ 7은 부가질량비(μ)와 음강성비(κ)에 따른 KDamper 시스템의 전달함수($$ {\tilde{T}}_{XMT}$$)를 나타낸다. TMD 시스템과 마찬가지로 부가질량비(μ)가 증가할수록 절달률이 감소, 즉 절연효과가 향상되며, 동일한 부가질량비(μ)를 갖는 경우 음강성비(κ)가 클수록 절연효과가 향상됨을 알 수 있다.

Fig. 6

Transfer function TXM vs. q for different mass ratios (κ = 0.5)

Fig. 7

Transfer function TXM vs. q for different mass ratios (κ = 1.0)

KDamper는 TMD에 음강성을 추가함으로써, 진동절연효과 향상을 위해 부가질량을 증가시켜야 하는 TMD의 단점을 극복하고 음강성의 크기를 증가시킴으로써 진동절연을 효과적으로 달성할 수 있다.

3. TMD와 KDamper 진동절연효과 비교

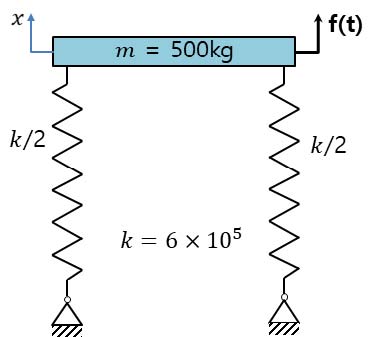
TMD 시스템과 KDamper 시스템의 진동절연효과를 비교하기 위하여 Fig. 8과 같이 주질량(m=500kg)과 스프링(k=6×10⁶N/m)으로 구성된 진동절연대상을 고려하였다.

가진력에 따른 주질량의 절연효과를 비교하기 위해 TMD와 KDamper를 Fig. 9와 같이 구성했다.

Fig. 8

Mass-spring system to be isolated from external vibration force

Fig. 9

TMD and KDamper system to isolate mass (m)

TMD 시스템의 부가질량(m_D)의 증가에 따른 진동절연효과를 살펴보기 위하여 Table 1과 같이 부가질량을 부여하였으며, 주질량과 부가질량 사이의 스프링(k_P)과 댐퍼(C_D)의 값은 부가질량에 따라 TMD 시스템의 전달함수 값이 최소화되는 최적값⁽⁴⁾을 사용하였다.

Table 1

Material properties of TMD system

KDamper 시스템의 경우 음강성 증가에 따른 진동절연효과를 살펴보기 위하여 부가질량을 5kg로 고정하고 음강성을 Table 2와 같이 부여하였다. 주질량과 부가질량 사이의 스프링(k_P)과 댐퍼(C_D)의 값은 전달함수의 최대값이 최대한 작아지는 값을 찾아 적용하였다.

Table 2

Material properties of KDamper system

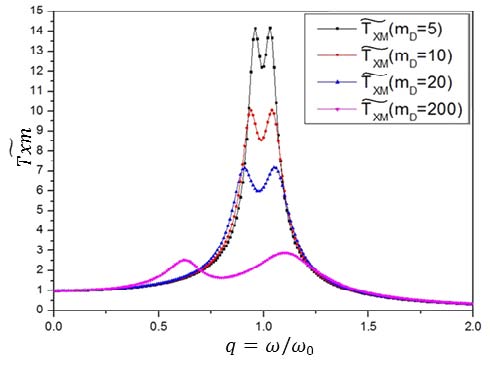
Fig. 10은 TMD 시스템을 적용한 경우 주질량(m)의 가진주파수에 따른 전달률을 나타내고 있다. 부가질량(m_D) 증가에 따라 주질량의 전달률이 감소하나 부가질량이 200kg(주질량의 40%)으로 증가시켜도 전달률 1이상 되는 영역이 존재하여 TMD 시스템을 통한 모든 주파수 영역에서 진동절연 달성에 어려움이 존재한다.

Fig. 10

Transfer function TXM vs. q for 4 different values of mD (TMD)

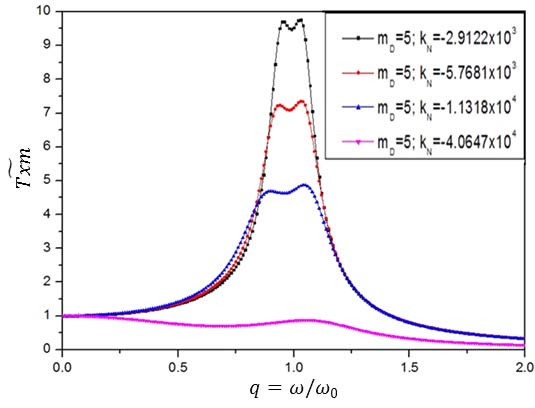
Fig. 11은 KDamper 시스템을 적용한 경우 주질량(m)의 가진주파수에 따른 전달률을 나타내고 있다. 부가질량(m_D)이 동일할 때 (즉, 부가질량의 증가 없이) 음강성(k_N)이 증가함에 따라 진동절연효과가 향상됨을 알 수 있다. 특히 음강성이 가장 큰 경우(k_N=‒40647 N/m) 모든 주파수 영역에서 전달률이 1이하가 되며, KDamper 시스템을 이용할 경우 음강성의 크기를 증가시켜 모든 주파수 영역에서 절연효과를 달성할 수 있음을 알 수 있다.

Fig. 11

Transfer function TXM vs. q for 4 different values of kN (KDamper)

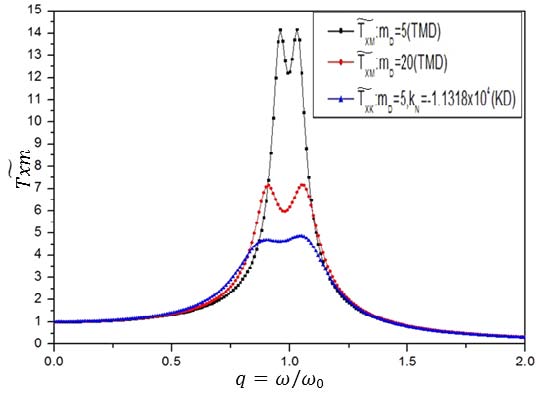
Fig.12는 TMD와 KDamper의 진동절연효과를 비교하기 위하여 부가질량(m_D) 5kg, 20kg인 경우의 TMD 전달률과 부가질량(m_D) 5kg, 음강성 k_N=‒11318N/m을 적용한 KDamper 전달률을 나타낸 것이다. 부가질량의 크기를 4배로 증가시킨 TMD보다 음강성을 이용한 KDamper의 진동절연이 더 효과적임을 알 수 있다.

Fig. 12

Comparison of transmissiblities of TMD and KDamper systems (I)

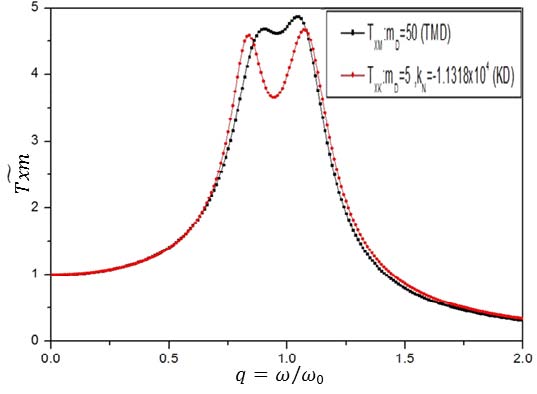
Fig. 13은 KDamper의 부가질량(m_D) 5kg, 음강성(k_N) ‒11318N/m인 경우의 진동절연효과와 TMD 시스템의 부가질량(m_D)이 50kg일 때의 진동절연효과를 비교하였다. 이를 통해 TMD 시스템이 KDdamper 시스템과 동일한 진동절연효과를 갖기 위해 부가질량을 10배 가까이 증가시켜야 함을 보여준다. 이러한 부가질량의 증가 때문에 기계분야에서의 TMD 적용이 제한적임을 알 수 있다.

Fig. 13

Comparison of transmissiblities of TMD and KDamper systems (II)

4. 결 론

이 논문에서 TMD(tuned mass damper)와 KDamper 시스템의 운동방정식을 유도하고 각 시스템의 진동절연효과에 대하여 비교 고찰하여 다음과 같은 결론을 얻었다.

• (1)TMD 시스템의 진동절연효과를 향상시키기 위해서는 부가질량을 크게 증가시켜야 하며, 부가질량을 주질량의 40%까지 증가시켜도 모든 주파수 영역에서 진동절연효과 달성이 어려움을 확인하였다.
• (2)KDamper 시스템은 TMD의 단점인 부가질량의 증가 없이 음강성의 크기를 증가시켜 효과적으로 진동절연을 달성할 수 있음을 확인하였다.
• (3)KDamper 시스템은 음강성의 크기를 증가시켜 모든 주파수 영역에서 진동절연효과를 달성이 가능함을 확인할 수 있었다.

Acknowledgments

이 논문은 2018년도 교육부의 재원으로 한국연구재단의 지원을 받아 수행된 기초연구사업임(No. 2017R1D1A1B03031601).

References

• Carrella, A., Brennan, M. J., and Waters, T. P., (2007), Static Analysis of a Passive Vibration Isolator with Quasi-zero-stiffness Characteristic, Journal of Sound and Vibration, 301(3-5), p678-689. [https://doi.org/10.1016/j.jsv.2006.10.011]
• Bae, S. R., Jung, W. J., Ham, I. B., Han, H. H., and Son, S. W., (2017), Structureborne Noise Reduction of Floating Raft System Using Tuned Mass Dampers, Transactions of the Korean Society for Noise and Vibration Engineering, 27(10), p784-789. [https://doi.org/10.5050/ksnve.2017.27.6.784]
• Antoniadis, I., Chronopoulos, D., Spitas, V., and Koulocheris, D., (2015), Hyper-damping Properties of a Stiff and Stable Linear Oscillator with a Negative Stiffness Element, Journal of Sound and Vibration, 346(13), p37-52. [https://doi.org/10.1016/j.jsv.2015.02.028]
• Den Hartog, J. P., (1956), Mechanical Vibrations, 4th edition, Chap. 3, McGraw-Hill, New York.
• Brzeski, P., Kapitaniak, T., and Perlikowski, P., (2015), Novel Type of Tuned Mass Damper with Inerter which Enables Changes of Inertance, Journal of Sound and Vibration, 349(4), p56-66. [https://doi.org/10.1016/j.jsv.2015.03.035]
• Carrella, A., Brennan, M. J., Waters, T. P., and Lopes Jr., V., (2012), Force and Displacement Transmissibility of Nonlinear Isolator with High-static-low-dynamic-stiffness, International Journal of Mechanical Sciences, 55(1), p22-29. [https://doi.org/10.1016/j.ijmecsci.2011.11.012]