[ Article ]

Transactions of the Korean Society for Noise and Vibration Engineering - Vol. 29, No. 3, pp.414-421

ISSN: 1598-2785 (Print) 2287-5476 (Online)

Print publication date 20 Jun 2019

Received 09 Apr 2019 Revised 30 Apr 2019 Accepted 02 May 2019

DOI: https://doi.org/10.5050/KSNVE.2019.29.3.414

탄성경계조건을 가지는 회전하는 보의 자유진동 해석

이정우^* ; 유충준^* ; 이정윤^†

Free Vibration Analysis for a Rotating Beam with an Elastic Boundary Condition

Jung Woo Lee^* ; Chung Jun You^* ; Jung Youn Lee^†

*Member, School of Mechanical System Engineering, Kyonggi University

Correspondence to: ^†Fellow Member, School of Mechanical System Engineering, Kyonggi University E-mail : jylee@kyonggi.ac.kr ‡ Recommended by Editor Won Ju Jeon

Abstract

This paper presents a transfer matrix method to accurately determine the natural frequencies and mode shapes of the free vibration characteristics of a rotating Bernoulli–Euler beam with an elastic boundary condition (EBC) at its root. The proposed method can accurately determine the desired number of natural frequencies for such problems using a single element. The EBC is modeled for translational and rotational springs, and its effects are expressed in an independent transfer matrix. Structures with an EBC are altered according to the structures with other various conditions by appropriately controlling the stiffness values of the springs. The roots of the differential equation are solved for a bending vibration by applying the Frobenius method. In addition, the variation in mode shape depending on the change in the stiffness of springs is investigated in detail.

Keywords:

Transfer Matrix Method, Elastic Boundary Condition, Rotating Beam, Frobenius Method

키워드:

전달행렬법, 탄성경계조건, 회전보, 프로베니우스법

1. 서 론

회전하는 구조물의 자유진동 특성은 다양한 방법으로 많은 연구자들에 의해 연구되어 왔다^{(1 ~ 3)}. 그리고 이들 구조물의 진동특성은 헬리콥터 로터블레이드, 터빈 블레이드 등 공학적 설계에 폭넓게 사용되었다. 기존의 연구들은 대부분 완전 고정 조건으로 경계조건을 가정하여 진동해석을 수행하였다^(4,5). Hodges et al.은 유한요소법과 멱급수를 사용하여 회전하는 구조물의 고유진동수를 평가하였고⁽⁶⁾, Stafford et al.은 전달행렬법을 사용하여 고유치 문제를 풀었다⁽⁷⁾. 많은 연구자들은 고정 조건하에 보다 정확한 결과들을 산출하기 위해 멱급수 중 Frobenius 법을 사용하였다^(8,9).

그러나, 이들 연구들은 탄성경계조건을 고려하지 않았고^{(1 ~ 9)}, 탄성경계조건하에서의 모드형상의 변화 또한 고려하지 않았다⁽¹⁰⁾.

회전하는 구조물에서 완벽한 고정 조건을 부여하는 것은 어렵기 때문에 실제 구조물들은 강성에 의해 지지되었다고 볼 수 있다. 따라서, 지지부의 강성을 탄성경계조건을 사용하여 회전하는 구조물의 경계조건을 부여한다면 보다 정확한 고유진동수를 분석하는 것이 가능하다.

탄성경계조건은 지지부에서 회전스프링와 병진스프링으로 모델링할 수 있고, 이들 스프링의 값을 변화시킴으로써 핀-자유, 고정-자유, 자유-자유 경계조건을 표현할 수 있다.

이 연구는 Lee et al.에 의해 연구된 기존의 연구를 토대로 수행되었고⁽⁹⁾, 탄성경계조건하에서 모드형상을 예측할 수 있는 방법을 상세하게 제시하였다.

이 연구의 목적은 회전하는 오일러-베르누이 보의 자유진동특성을 탄성경계조건을 고려하여 분석할 수 있는 방법론을 제안하는 것이다. 회전속도와 허브반경의 영향이 고려되었고, 경계조건의 변화에 따라 변화하는 고유진동수와 모드형상의 변화가 예측되었다.

2. 이 론

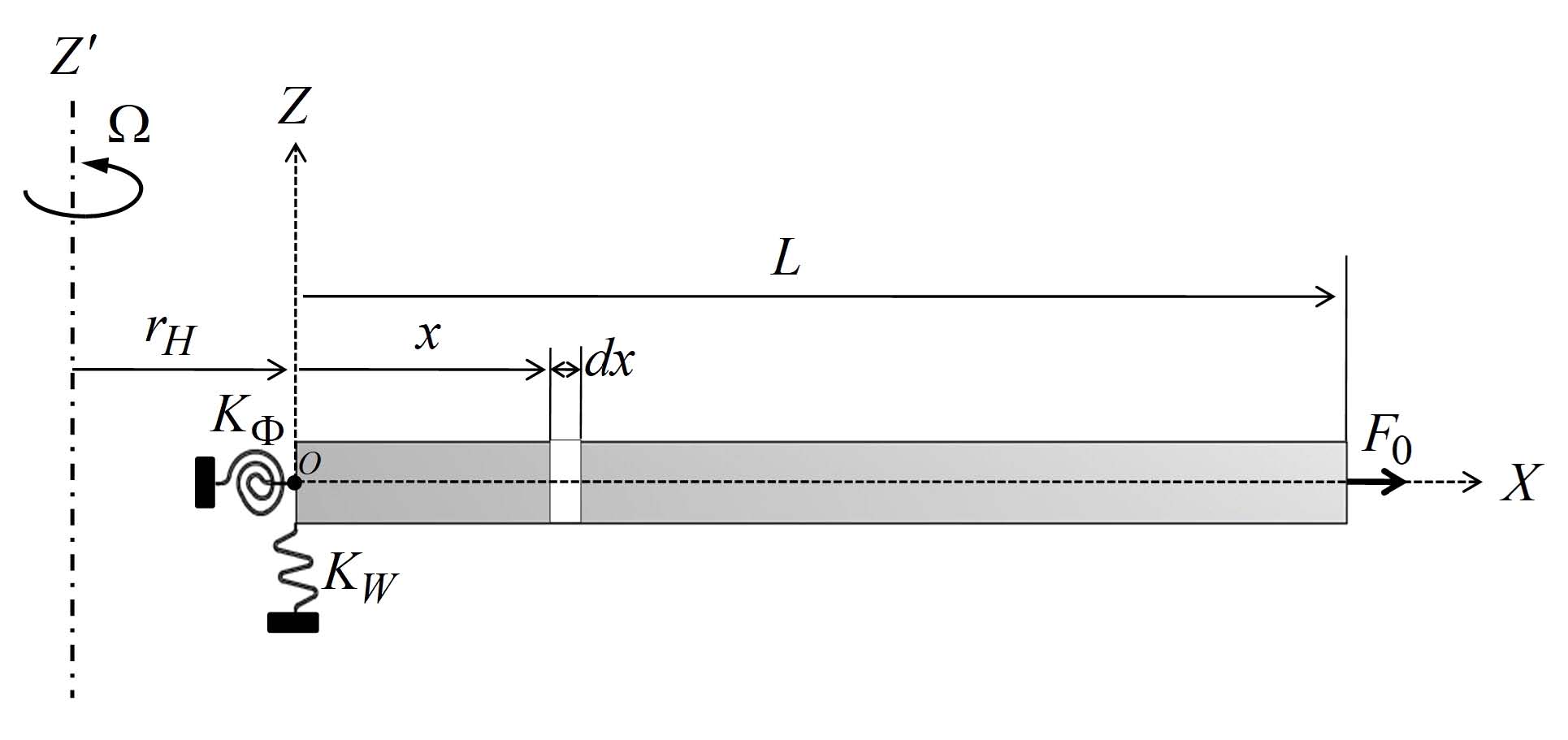
이 연구는 오일러-베르누이 보를 고려하였고, Fig. 1에서와 같이 고정부를 회전스프링(K_Φ)과 병진스프링(K_W)으로 모델링하였다. Z′는 회전 중심축이고, rH는 허브반경, Ω는 회전속도이다. dx는 미소요소까지의 거리이고, F₀는 상수 축력으로 값을 0으로 가정함으로써 무시할 수 있다. L은 보요소의 전체 길이이다.

Fig. 1

Notation and coordinate systems used for a rotating beam with EBC

2.1 전달행렬

회전하는 보에 대한 전달행렬은 다음과 유추될 수 있다⁽⁹⁾.

균일한 단면을 가지는 보의 회전력에 의해 발생되는 원심력은 다음과 같다.

F x = ∫ x L m Ω 2 r H + x d x + F 0

(1)

회전하는 보의 미분방정식, 전단력, 굽힘 모멘트는 다음과 같이 표현된다.

E I w'''' - F x ω'' + m w ¨ = 0

(2)

V = E I w''' - F (x) w'

(3)

M = - E I w ″

(4)

각진동수를 가지고 조화진동을 하는 것으로 가정한다면,

w x, t = W x c o s ω t

(5)

식 (2) ~ 식 (4)에 식 (1)과 식 (5)를 대입하여 풀면 다음과 같은 무차원 4차 미분방정식을 얻을 수 있다.

W'''' - Ω 2 ¯ 0.5 x 2 ¯ + r H ¯ x ¯ + C 1 W ″ + Ω 2 ¯ x ¯ + r H ¯ W' + ω 2 ¯ W = 0

(6)

여기서,

Ω 2 ¯ = m Ω 2 L 4 E I, r H ¯ = r H L, x ¯ = x L, ω 2 ¯ = - m ω 2 L 4 E I

C 1 = - Ω 2 ¯ 0.5 + r H ¯ - F 0 L 2 E I

미분방정식 (6)의 해는 멱급수의 하나인 Frobenius법을 사용하여 얻을 수 있고, 다음과 같이 해를 가정할 수 있다.

W x ¯, k = ∑ i = 0 ∞ a i + 1 ζ k + i

(7)

식 (7)을 식 (6)에 대입함으로써 다음과 같이 결정방정식(식 (8))과, 순환관계식(식 (9)), Frobenius계수(식 (10) ~식 (14))들을 결정할 수 있다.

k k - 1 k - 2 k - 3 a 1 = 0

(8)

a i + 5 = - C 1 k + i + 3 k + i + 4 a i + 3 - r H ¯ Ω 2 ¯ k + i + 1 k + i + 2 k + i + 3 k + i + 4 a i + 2 - Ω 2 ¯ k + i + 0.5 Ω 2 ¯ k + i - 1 k + i + ω 2 ¯ k + i + 1 k + i + 2 k + i + 3 k + i + 4 a i + 1

(9)

a 1 = 1

(10)

a 2 = 0

(11)

a 3 = - C 1 k + 1 k + 2 a 1

(12)

a 4 = - r H ¯ Ω 2 ¯ k k + 1 k + 2 k + 3 a 1

(13)

a 5 = C 12 - 0.5 Ω 2 ¯ k k + 1 - ω 2 ¯ k + 1 k + 2 k + 3 k + 4 a 1

(14)

결국 균일한 단면을 가지는 회전하는 보의 굽힘 변위는 다음과 같이 유추된다.

W x ¯ = A 1 f x ¯, 0 + A 2 f x ¯, 1 + A 3 f x ¯, 2 + A 3 f x ¯, 3

(15)

여기서, 함수 f(x, k)는 다음과 같다.

f x ¯, k = ∑ i = 0 ∞ a i + 1 ζ k + i

(16)

식 (15)를 미분함으로써 곡선의 기울기(Φ)를 결정할 수 있고,

Φ = 1 L A 1 f' x ¯, 0 + A 2 f' x ¯, 1 + A 3 f' x ¯, 2 + A 3 f' x ¯, 4

(17)

식 (3)과 식 (4)에 식 (5)와 식 (7)을 대입하면 전단력과 굽힘 모멘트는 다음과 같이 표현될 수 있다.

M = N 1 ∑ j = 1 4 f ″ (x ¯, j - 1) A j

(18)

V = N 2 ∑ j = 1 4 f' ″ x ¯, j - 1 - Ω 2 ¯ 0.5 x 2 ¯ + r H ¯ x ¯ + C 1 f' x ¯, j - 1 A j

(19)

여기서, N₁=-EI/L², N₂=EI/L³

식 (15), 식 (17), 식 (18) 그리고 식 (19)에 x=0을 대입하고 행렬 형태로 표현하면 다음과 같이 된다.

W Φ M V x = 0 = C 11 C 12 C 13 C 14 C 21 C 22 C 23 C 24 C 31 C 32 C 33 C 34 C 41 C 42 C 43 C 44 A 1 A 2 A 3 A 4

(20)

여기서,

C 1 j = ∑ j = 1 4 f 0, j - 1, C 2 j = 1 L ∑ j = 1 4 f' 0, j - 1, C 3 j = N 1 ∑ j = 1 4 f ″ 0, j - 1, C 4 j = N 1 ∑ j = 1 4 f' ″ 0, j - 1 - C 1 f' 0, j - 1 .

식 (20)을 단순화하면,

Z x = 0 = C i j A j

(21)

식 (21)으로부터 상수 {A_j}는 다음과 같이 결정할 수 있다.

A j = C i j - 1 Z x = 0

(22)

동일한 방법에서 x=1을 식 (15), 식 (17), 식 (18) 그리고 식 (19)에 대입하여 다음의 행렬을 얻을 수 있다.

W Φ M V x = 1 = H 11 H 12 H 13 H 14 H 21 H 22 H 23 H 24 H 31 H 32 H 33 H 34 H 41 H 42 H 43 H 44 A 1 A 2 A 3 A 4

(23)

여기서,

H 1 j = ∑ j = 1 4 f 1, j - 1, H 2 j = 1 L ∑ j = 1 4 f' 1, j - 1, H 3 j = N 1 ∑ j = 1 4 f ″ 1, j - 1, H 4 j = N 2 ∑ j = 1 4 f' ″ 1, j - 1 - Ω 2 ¯ 0.5 + r H ¯ + C 1 f' 1, j - 1 .

(23-1)

식 (23)를 단순화하고,

Z x = 0 = H i j A j

(24)

식 (24)에 식 (22)를 대입하여 다음과 같은 전달행렬표현을 얻을 수 있다.

Z x = 1 = T i j Z x = 0

(25)

여기서 [T_ij]=[H_ij][C_ij]^-1

2.2 탄성경계조건

Fig. 1과 같이 회전하는 보의 root에서의 탄성경계조건은 회전스프링과 병진스프링으로 모델링되었고, 전단력과 굽힘 변형에 의해 발생된 변위들로 표현할 수 있다.

이들 스프링들을 행렬로 표현한다면 다음과 같이 된다.

W Φ M V x = 1 = 100 η 1 01 η 2 0 00100001 W Φ M V x = 0

(26)

여기서, η₁=-1/K_W, η₂=-1/K_Φ이고

K_W(=K_WL³/EI)와 K_Φ(=K_ΦL/EI)은 무차원 스프링 상수 값이다⁽¹⁰⁾.

식 (26)은 다음과 같이 단순화할 수 있다.

Z x = 1 = K i j Z x = 0

(27)

탄성경계조건을 가지는 회전하는 보의 전달행렬표현은 식 (27)을 식 (25)에 대입함으로써 다음과 같이 된다.

Z x = 1 = T i j * Z x = 0

(28)

여기서, $T i j * = T i j K i j$

2.3 진동수 방정식

식 (28)로부터 고정-자유 조건이 고려되었고, 이 끝 조건은 스프링의 상수 값들을 변화시켜 탄성경계조건을 포함하는 자유-자유, 핀-자유 조건을 만족한다. 따라서, 고정-자유 조건에 대한 표현은 다음과 같다.

T 34 * T 44 * T 43 * T 44 * M V 0 = 0

(29)

진동수방정식은 식 (29)로부터 다음과 같이 표현된다.

T 34 * T 44 * T 43 * T 44 * = 0

(30)

식 (30)으로부터 회전하는 보의 고유진동수를 결정할 수 있고, 모드형상은 전단력을 1로 가정함으로 다음의 방법에서 얻을 수 있다.

결국 x=0에서의 상태량은 다음과 같이 된다.

Z x = 0 = 00 M 0 1 T

(31)

그러나, 모드 현상을 얻기 위해 탄성 경계조건을 고려하기 위해서는 주의를 기울여야 한다. x=0에서의 상태량 {Z}_x=0는 식 (31) 대신에 다음의 방정식을 사용하여야 한다.

Z x = 0 = K i j 00 M 0 1 T

(32)

식 (32)를 사용하여 회전스프링과 병진스프링의 값을 변경함으로써 탄성경계조건이 고려된 모드형상을 결정할 수 있다.

Case 1: 고정-자유 조건

η 1 = η 2 = 0

(33)

Case 2: 핀-자유 조건

η 1 = 0 과 n 2 = ∞

(34)

3. 결과 및 고찰

회전스프링 및 병진스프링의 값을 변경함으로써 기존의 경계조건을 만족한다는 것을 보여주기 위해, 현재의 방법으로부터 얻어진 결과들이 기존의 연구에서 토론된 결과들과 비교되었다. 비교 결과들은 Table 1에 제시되었고, 무차원 허브반경이 r_H = 0와 r_H = 1이 고려되었을 때 계산된 결과들을 비교하였다. 비교 결과들은 우수한 일치를 보였고, 제안된 방법론을 검증하였다. 무차원 회전속도는 0부터 10까지 고려하였다. 고유진동수를 계산하기 위하여 사용된 멱급수에서의 항의 수는 60개이다. 이 비교를 바탕으로, 핀-자유 조건을 가지는 회전하는 보의 무차원 고유진동수를 계산하였고 Table 2에 제시하였다.

Table 1

Comparison results on the first four non-dimensional natural frequencies of rotating beams with the fixed free end condition when rH=0 and 1

Table 2

The first four non-dimensional natural frequencies of rotating beams with the pinned-free end condition

고정-자유조건을 표현하기 위한 무차원 스프링 상수 값 (K_Φ와 K_W)은 각각 지수함수 exp(25)와 exp(‒25)를 사용되었다. exp(25)가 사용되었을 때 고정이 되고, exp(‒25)를 사용하였을 때 자유 조건이 된다. 따라서, 고정 끝 조건은 K_W=K_Φ=exp(25)이고, 자유 끝 조건은 K_W=K_Φ=exp(‒25)이며, 핀 조건은 K_W=exp(25)과 K_Φ=exp(‒25)을 사용하면 된다.

Table 1과 Table 2의 결과들은 스프링의 값들을 변경함으로써 제안된 방법이 고정-자유, 핀-자유조건과 같은 경계조건을 표현할 수 있다는 것을 보여준다.

이 결과들을 토대로, 변화하는 스프링 값에 관한 무차원 고유진동수에서의 변화를 분석하였고, Fig. 2에 결과들이 제시되었다. 자유-자유 끝 조건으로부터 고정-자유 끝 조건으로 스프링 값을 제어함으로써 변경되었고, 허브반경은 r_H=0,0.5와 r_H=1을 고려하였다. 또한, 회전속도는 Ω=10을 고려하였다.

Fig. 2

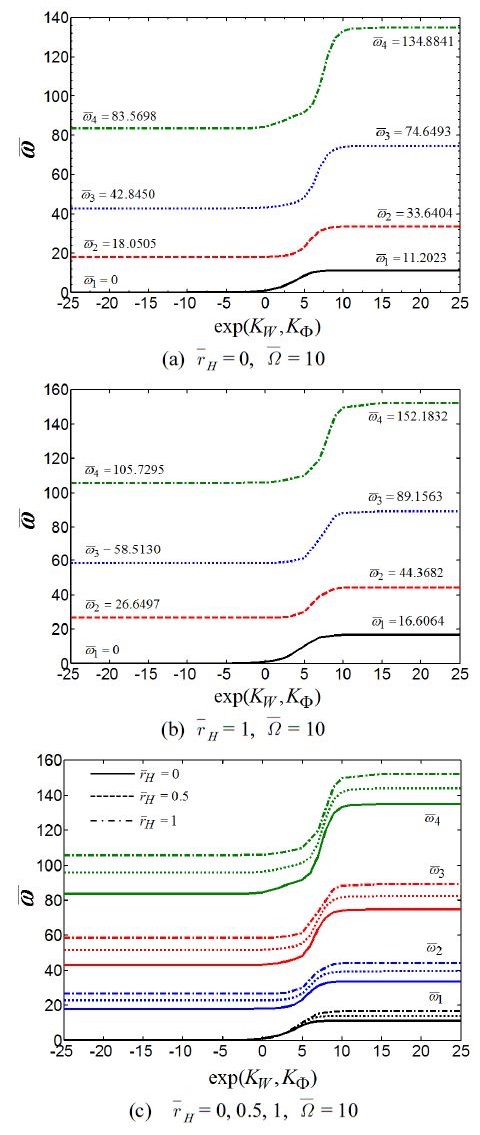
The changes in the first four non-dimensional natural frequencies from the free-free condition to the fixed-free condition

계산의 편의를 위해 무차원 스프링 상수 값(K_Φ와 K_W)은 동시에 동일한 간격에서 증가시켰고, exp(0)과 exp(10) 사이에서 무차원 고유진동수들은 가장 크게 변화하였다. 다른 값에서는 작은 변화만을 보였다. 강체모드에 대해 고유진동수가 0이 된다는 것은 잘 알려진 사실이다. 그러므로, 1차 모드는 0부터 시작되었다. Fig. 2(c)에서 보여지는 것과 같이 자유-자유 조건부터 고정-자유조건으로 변화될 때 1차 고유진동수는 허브반경에 관계없이 스프링 상수 값이 exp(3)이 될 때 까지 거의 동일한 값을 가졌다. 2차, 3차, 4차 고유진동수들은 유사한 경향을 가지고 스프링 값의 증가에 상응하는 고유진동수에서의 증가를 보였다.

결과적으로, 지지부의 강성의 변화에 따라 고유진동수는 크게 변화된다는 것을 알 수 있다.

마지막으로, 이 연구의 목적 중에 하나인 지지부에서의 강성의 변화에 따른 모드형상의 변화를 검토하였다. 1차 ~ 4차 모드형상이 검토되었고, 허브 반경 r_H= 0일 때 회전속도는 Ω=0과 Ω=10을 고려하였다. 모드 형상은 자유-자유 조건부터 자유-고정 조건으로 스프링 상수 값을 제어함으로써 계산되었고, 스프링 상수 값들은 exp(‒10)부터 exp(25)까지 임의간격에서 증가되었다.

증가하는 경향은 유사하나 각 고유진동수마다 요구되는 스프링 상수 값의 범위가 exp(0)과 exp(10) 사이에서 다소 차이를 보였기 때문에 모드형상을 검토하기 위해 사용된 스프링 상수 값들은 각 모드마다 다소 차이가 난다.

스프링 상수 값의 변화에 상응하는 모드형상의 변화는 Fig. 3에 제시되었고, exp(‒10)일 때가 자유-자유 끝 조건이며 exp(25)일 때가 고정-자유 끝 조건에 대한 모드형상이다.

Fig. 3

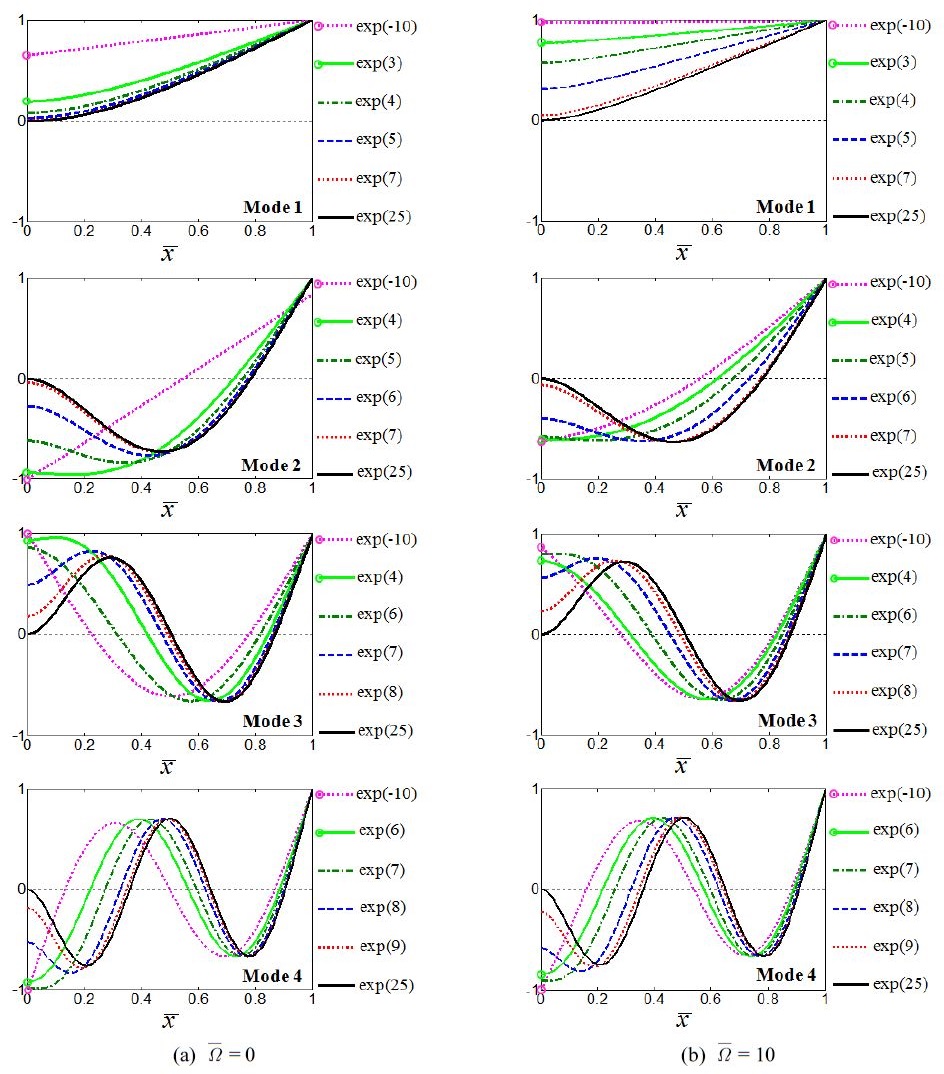
The variation of the first four mode shapes with respect to the change of the spring constant values

예상했던 대로, 스프링 상수 값들이 증가할 때 탄성 스프링에 의해 지지된 root부에서의 변위가 0에 가까워진다는 것을 확인하였다. 잘 알려진 것과 같이 자유-자유 조건일 때 강체 모드형상을 제외하고, 1차 ~ 3차 모드형상은 스프링 상수 값의 증가에 의해 고정-자유 조건으로 변화하면서 2차 ~ 4차 모드형상으로 변화된다는 것을 Fig. 3에서 확인할 수 있다.

게다가, 모든 모드형상에서 회전속도의 영향을 보이나, 가장 분명하게 영향을 보이는 1차와 2차 모드를 비교했을 때 동일한 스프링 상수 값을 사용하더라도 지지부에서 0으로의 수렴에 명확한 차이를 보였다. 또한, 0으로 수렴해가는 과정을 지지부의 강성 값을 변화시킴으로써 분명하게 보여주었다.

따라서, 현재 제안한 방법은 완벽한 고정조건을 부여하기 어려운 회전하는 구조물의 설계에 유용하게 사용될 수 있을 것으로 기대된다.

4. 결 론

이 연구는 지지부의 강성이 변화할 때 회전하는 구조물의 고유진동수와 모드형상을 명확하게 평가할 수 있는 전달행렬법을 제안하였다. 게다가, 한 개의 요소를 사용하여 고유진동수와 모드형상을 결정할 수 있는 방법론을 제안하였고, 제안된 방법론은 기존의 연구 결과와의 비교를 통하여 우수성을 확인하였다.

또한, 지지부에서의 스프링 상수 값들을 제어함으로써 탄성경계조건을 포함하여 자유-자유 조건, 고장-자유 조건 등의 경계조건이 자유롭게 변화될 수 있음을 확인하였다.

Acknowledgments

이 연구는 2018년도 한국연구재단 이공학개인기초연구과제의 지원을 받아 수행되었음(Grant No. NRF-2018R1D1A1B07047019).

References

Lee, H. L., and Yoo, H. H., (2009), Vibration Analysis of a Rotating Cantilever Beam Having Tapered Cross Section, Transactions of the Korean Society for Noise and Vibration Engineering, 19(4), p363-369.
Bazoune, A., Kulief, Y. A., Stephen, N. G., and Mohiuddin, M. A., (2001), Dynamic Response of Spinning Tapered Timoshenko Beams Using Modal Reduction, Finite Elements in Analysis and Design, 37(3), p199-219. [https://doi.org/10.1016/s0168-874x(00)00030-5]
Gunda, J. B., and Ganguli, R., (2008), New Rational Interpolation Functions for Finite Element Analysis of Rotating Beams, International Journal of Mechanical Sciences, 50(3), p578-588.
Lee, J. W., Kwak, J. H., and Lee, J. Y., (2016), Exact Solution for Bending Vibration of Rotating Cantilever Beam with Tapered Width Using Transfer Matrix Method, Transactions of the Korean Society for Noise and Vibration Engineering, 26(1), p75-81. [https://doi.org/10.5050/ksnve.2016.26.1.075]
Lee, J. W., and Lee, J. Y., (2018), An Exact Transfer Matrix Expression for Bending Vibration Analysis of a Rotating Tapered Beam, Applied Mathematical Modelling, 53, p167-188. [https://doi.org/10.1016/j.apm.2017.08.022]
Hodges, D. H., and Rutkowski, M. J., (1981), Free-Vibration Analysis of Rotating Beams by a Variable-Order Finite Element Method, AIAA Journal, 19(11), p1459-1466. [https://doi.org/10.2514/3.60082]
Giurgiutiu, V., and Stafford, R. O., (1977), Semi-Analytic Methods for Frequencies and Mode Shapes of Rotor Blades, Vertica, 1, p291-306.
Banerjee, J. R., (2000), Free Vibration of Centrifugally Stiffened Uniform and Tapered Beams Using the Dynamic Stiffness Method, Journal of Sound and Vibration, 233(5), p857-875. [https://doi.org/10.1006/jsvi.1999.2855]
Lee, J. W., and Lee, J. Y., (2017), In-plane Bending Vibration Analysis of a Rotating Beam with Multiple Edge Cracks by Using the Transfer Matrix Method, Meccanica, 52(4-5), p1143-1157. [https://doi.org/10.1007/s11012-016-0449-4]
Lee, S. Y., Lin, S. M., and Hsu, J.J., (2008), In-plane Vibration of a Rotating Curved Beam with an Elastically Restrained Root, Journal of Sound and Vibration, 315(4-5), p1086-1102.

Jung Woo Lee received B.S., M.S., and Ph.D. degrees from Kyonggi University in 2002, 2004, and 2017, respectively. He is currently an assistant professor at the Department of Mechanical System Engineering of Kyonggi University. His research interests are in structural vibration, composite structures, continuum mechanics, and the transfer matrix method.

Chung Jun You completed his Doctoral Degree in Mechanical Engineering from TU Berlin in 1999 and Aerospace Engineering. He is currently a Professor at the Department of Mechanical Engineering of University of Kyonggi.

Jung Youn Lee is Professor of Dept. of Mechanical System Engineering at Kyonggi University, where he has been since 1996. He received a B.S., an M.S. and his Ph.D. from Hanyang University in 1979, 1989 and 1992 respectively. His research interests are in System Identification, Structural Modification, Inverse Problem, Modal Analysis and Sensitivity Analysis of Vibration.

Table 1

Comparison results on the first four non-dimensional natural frequencies of rotating beams with the fixed free end condition when rH=0 and 1

Ω	Non-dimensional natural frequency
	ω₁		ω₂		ω₃		ω₄
	Present	Exact	Present	Exact	Present	Exact	Present	Exact
(a) r_H=0
0	3.5160	3.5160	22.0345	22.0345	61.6972	61.6972	120.9019	-
1	3.6816	3.6816	22.1810	22.1810	61.8418	61.8418	121.0509	-
2	4.1373	4.1373	22.6149	22.6149	62.2732	62.2732	121.4967	-
3	4.7973	4.7973	23.3203	23.3203	62.9850	62.9850	122.2355	-
4	5.5850	5.5850	24.2733	24.2733	63.9668	63.9668	123.2615	-
5	6.4495	6.4495	25.4461	25.4461	65.2050	65.2050	124.5664	-
6	7.3604	7.3604	26.8091	26.8091	66.6839	66.6839	126.1405	-
7	8.2996	8.2996	28.3341	28.3341	68.3860	68.3860	127.9722	-
8	9.2568	9.2568	29.9954	29.9954	70.2930	70.2930	130.0490	-
9	10.2257	10.2257	31.7705	31.7705	72.3867	72.3867	132.3576	-
10	11.2023	11.2023	33.6404	33.6404	74.6493	74.6493	134.8841	-
(b) r_H=1
0	3.5160	3.5160	22.0345	22.0345	61.6972	61.6972	120.9019	-
1	3.8888	3.8888	22.3750	22.3750	62.0431	62.0431	121.2632	-
2	4.8337	4.8337	23.3660	23.3660	63.0675	63.0675	122.3395	-
3	6.0817	6.0817	24.9277	24.9277	64.7338	64.7338	124.1090	-
4	7.4750	7.4750	26.9573	26.9573	66.9868	66.9868	126.5373	-
5	8.9404	8.9404	29.3528	29.3528	69.7607	69.7607	129.5803	-
6	10.4439	10.4439	32.0272	32.0272	72.9863	72.9863	133.1875	-
7	11.9691	11.9691	34.9116	34.9116	76.5964	76.5964	137.3049	-
8	13.5074	13.5074	37.9538	37.9538	80.5295	80.5295	141.8780	-
9	15.0541	15.0541	41.1154	41.1154	84.7315	84.7315	146.8540	-
10	16.6064	16.6064	44.3682	44.3682	89.1563	89.1563	152.1832	-

Table 2

The first four non-dimensional natural frequencies of rotating beams with the pinned-free end condition

Ω	Non-dimensional natural frequency
	r_H=0				r_H=1
	ω₁	ω₂	ω₃	ω₄	ω₁	ω₂	ω₃	ω₄
0	0.0000	15.4182	49.9649	104.2477	0.0000	15.4182	49.9649	104.2477
1	1.0000	15.6242	50.1437	104.4202	1.5806	15.9161	50.4068	104.6765
2	2.0000	16.2261	50.6760	104.9358	3.1586	17.3179	51.7069	105.9511
3	3.0000	17.1807	51.5498	105.7890	4.7333	19.4142	53.7937	108.0370
4	4.0000	18.4313	52.7463	106.9708	6.3056	21.9897	56.5662	110.8810
5	5.0000	19.9197	54.2419	108.4691	7.8765	24.8804	59.9120	114.4162
6	6.0000	21.5944	56.0099	110.2695	9.4467	27.9770	63.7221	118.5685
7	7.0000	23.4133	58.0223	112.3555	11.0166	31.2103	67.9002	123.2611
8	8.0000	25.3436	60.2513	114.7094	12.5865	34.5373	72.3664	128.4200
9	9.0000	27.3601	62.6705	117.3126	14.1563	37.9304	77.0570	133.9761
10	10.0000	29.4439	65.2554	120.1464	15.7263	41.3720	81.9224	139.8677