스프링 요소를 이용한 멀티와이어쏘 장비의 베어링 배치 설계에 관한 연구

1. 서 론

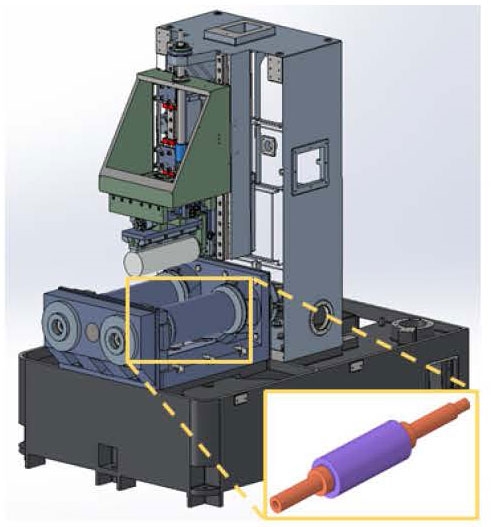
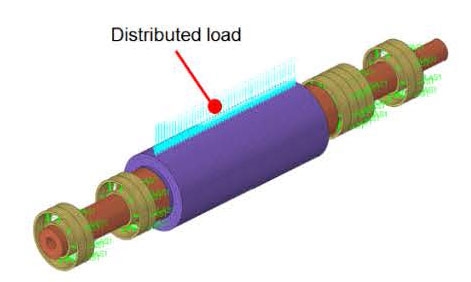
멀티와이어쏘(multi-wire saw, MWS)는 사파이어와 같은 단단한 물질을 절삭하는 장비이다. MWS 장비는 원통형의 잉곳(ingot) 형태로 구성된 절삭 대상 재료를 공업용 다이아몬드가 코팅된 여러 줄의 강선이 고속으로 이송시켜 절삭을 수행한다. 따라서, 절삭 대상 재료를 일정한 두께로 동시에 여러 개의 시편으로 절단할 수 있다. 여러 개의 강선이 일정한 간격으로 설치되어있는 회전축이 구동 모터에 의해 회전하고 작동 모듈이 잉곳을 하향시켜 강선과 잉곳의 직접적인 마찰로 인하여 여러 개의 절단된 가공물이 생산된다. 사파이어의 경우 가공과정에서 강선이 절삭물에 약 15kN ~ 20kN의 하중을 주게 된다. 이 하중에 따른 처짐이 강선과 절삭물에 발생하게 되며, 절삭 방향이 정확하게 수직이 되지 않으면서 절삭면이 곡면을 가지게 된다. 따라서, 절삭된 가공물의 단면을 평면화시키기 위하여 MWS 장비를 통한 절삭 작업 후 평면화 후처리를 한다. 가공물 단면의 곡면 화는 후처리 작업 시간과 재료 손실에 많은 영향을 미치므로 절삭 과정에서 최대한 평면에 가까운 가공물을 생산하는 것이 유리하다.

멀티와이어쏘 장비를 대상으로 많은 연구가 선행되었다. 사파이어 웨이퍼의 두께 변화가 강선의 초기 처짐에 미치는 영향에 관한 연구⁽¹⁾, 절삭물의 표면 거칠기 손상에 관한 연구⁽²⁾, 작은 구동 모터를 사용하기 위한 메인 롤러의 질량이나 관성 모멘트에 대한 단면 최적 설계에 관한 연구⁽³⁾, 강선의 침입량이 절삭 능력에 미치는 영향에 관한 연구⁽⁴⁾가 있었다.

멀티와이어쏘 장비를 대상으로 최대한 평면에 가까운 가공물을 만들기 위한 주축의 강성을 확보하는 연구가 필요하다. 위의 절삭 장비와 연관하여 주축의 강성 확보를 위해 베어링 배치 설계에 관한 여러 연구가 진행되었다. 주축의 초고속 회전으로 인한 프레임의 열 변위를 고려한 베어링 배치 연구⁽⁵⁾, 수직으로만 지지하는 볼 베어링의 간격 선정에 관한 연구⁽⁶⁾, 베어링 배열 방식이 스핀들의 동특성에 미치는 영향에 관한 연구⁽⁷⁾가 있었다.

멀티와이어쏘 장비에서 회전축 결합 모델의 강성 설계를 위해 고려해야 할 베어링 모델링은 매우 중요하다. 이것은 베어링의 접촉부가 볼이나 롤러로 구성되어 점접촉이나 선접촉으로 이루어지게 되어 두 금속재료의 면접촉보다 약 1/10의 접촉 강성⁽⁸⁾을 가지기 때문이다. 이전 연구에서는 베어링을 모델링하는데 있어서 베어링 볼을 모델링하지 않고 내경과 외경이 직접 접촉하는 모델을 사용하거나, 베어링 볼을 반경방향으로만 지지하는 모델링⁽⁹⁾을 수행했거나 혹은 베어링 자리에 6자유도 스프링 부시(bush) 모델⁽¹⁰⁾을 적용하여 해석을 진행하였기 때문에 강성 설계를 위한 모델로서는 한계가 있었다.

이 연구에서는 Fig. 1에서 나타낸 멀티와이어쏘 장비를 대상으로 회전축의 강성 증가를 위한 베어링 배치 설계 연구를 진행한다. 베어링 배치 설계는 질량에 대한 변화가 없기 때문에 고유진동수를 증가시켰을 때 주축의 정강성, 동강성을 모두 향상시킬 수 있다는 장점이 있다. 이는 회전축의 처짐을 감소시켜 절삭물의 재료 손실과 절삭 시간을 절감하는 효과가 있다. 회전축의 베어링 배치 설계를 위하여 베어링을 등가 강성 스프링 요소로 모델링을 실시한다. 그 후, 베어링을 다른 경계 조건으로 구성한 회전축 결합 모델들을 선형 정적 해석과 고유진동수 해석을 통해 평가한다. 이 결과를 토대로 베어링 배치 설계를 위한 초기 모델을 도출한다. 초기 모델을 연구 대상으로 베어링 배치를 실시하고, 등가 강성 스프링 요소의 축 방향 위치와 지지하는 각을 고려하는 베어링 배치 타입을 설계 변수로 설정하여 동강성이 최대인 모델을 확인하고 초기 모델과 비교하여 검증한다.

Fig. 1

Spindle assembly of a multi-wire saw machine

이 논문은 다음과 같이 구성된다. 2절에서는 베어링을 등가 강성 스프링 요소로 모델링하는 과정을 제시하며, 스프링 유한 요소를 사용한 회전축 결합 모델을 선형 정적 해석과 고유진동수 해석 결과를 토대로 모델을 검증한다. 3절에서는 선정된 모델을 대상으로 회전축 강성 증가를 위해 베어링 배치 설계를 수행하고, 고유진동수 해석을 통해 그 효과를 확인한다. 마지막으로, 4절에서는 결론을 제시한다.

2. 회전축 결합 모델의 구성

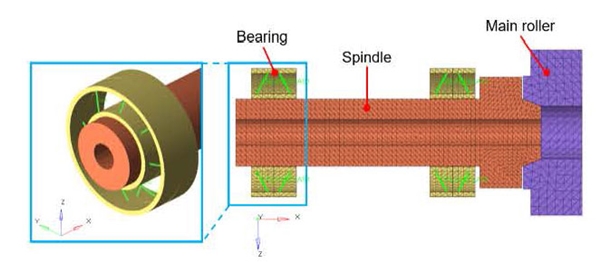
회전축의 강성을 증가시키기 위하여 물리적인 베어링 배치 연구가 필요하기 때문에 베어링과 회전축이 결합된 회전축 결합 모델을 연구 대상으로 모델링을 실시하였다. 베어링 모델은 베어링의 외경, 내경은 솔리드 요소로 베어링의 볼은 스프링 요소로 구성한 이전 연구⁽⁹⁾를 따라 구성하였다. 또한, 반경 방향, 축 방향의 하중을 고려하여 Fig. 2와 같이 베어링이 갖는 기하학적 방향성인 베어링의 외경과 내경 간 지지하는 각을 스프링 요소를 통해 구현하였다. 회전축과 메인 롤러의 접촉면은 본딩 접촉(bonding contact), 주축과 베어링의 접촉면은 x축 회전 방향을 제외한 5자유도에 대하여 구속 조건으로 모델을 구성하였다. 마지막으로, 베어링 강성을 등가 모델로 구성하기 위해 베어링 1개당 외경과 내경을 연결되는 스프링 요소의 개수, 스프링 요소의 개수에 따른 강성 배분을 수행하였다.

Fig. 2

FE model of spindle assembly

2.1 스프링 요소를 이용한 베어링 모델링

베어링을 등가 강성 스프링 요소로 구성하기 위하여 스프링 요소의 개수를 변화시키며 회전축 결합 모델 후보들을 구성하였다.

베어링을 몇 개의 스프링 요소로 구성되는 등가 강성 스프링 모델로 대치하는 과정에서 고려해야 할 것이 스프링 요소 정렬 오차이다. 스프링 요소 정렬 오차는 해석모델에서 주축부와 프레임부가 유한 요소로 모델링 구성되는 경우에 발생한다. 등가 강성 모델에 필요한 스프링 요소의 주축부 부착위치와 프레임부 부착 위치가 각각의 유한 요소 모델의 노드에 위치하기 때문에 발생하는 오차이다. 즉, 유한 요소 구성 과정에서 요소 간 접합 시 사용자가 노드의 위치를 정확하게 정할 수 없어 스프링 요소 사이의 대칭이 정확하게 맞지 않기 때문에 발생한다. 스프링 요소 정렬 오차는 정강성 해석에서는 크게 영향을 주지 않으나 동강성의 경우에는 오차의 영향이 발생하게 된다. 즉, 정렬 오차가 존재하는 경우 주축의 공진주파수의 값에 오차가 발생할 수 있다.

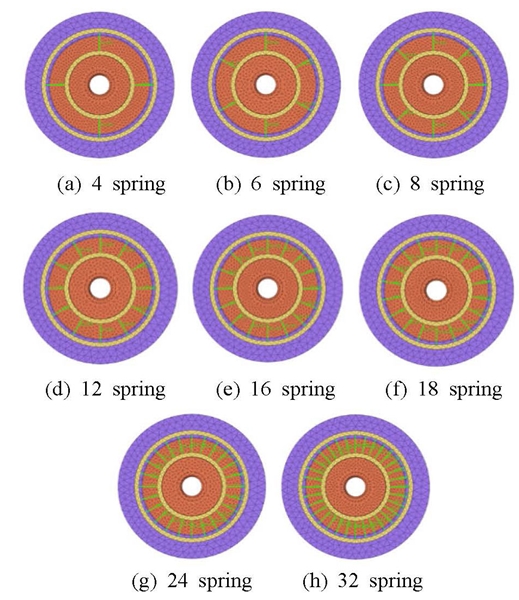
스프링 요소의 개수에 따른 강성 배분은 에너지 보존 법칙을 이용하여 베어링 강성을 계산한 이전 연구(9)를 따라 수행하였다. 스프링 요소는 개수에 따라 전체 베어링 강성이 일정하여야 한다. 따라서, 스프링 개수에 따른 모델에 대해 다른 스프링 강성을 사용하였다. Fig. 3에서 스프링 요소가 4개, 6개, 8개, 12개, 16개, 24개, 32개로 이루어진 모델을 제시하였다.

Fig. 3

Spindle assembly model considering the number of bearings

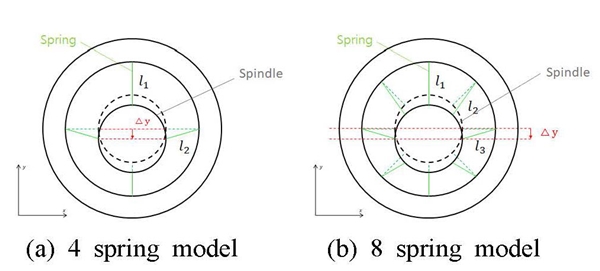
Fig. 4는 스프링 요소와 회전축이 결합된 경우에 y축 방향의 처짐 ∆y가 발생한 모델을 표시하고 있다. 식 (1)에서 4개의 스프링으로 이루어진 베어링 등가 강성 모델의 경우 사용된 스프링의 강성을 K₄로 설정하고, 8개의 스프링으로 이루어진 베어링모델의 스프링 강성을 K₈로 설정하였다. 두 등가 강성 베어링 모델들에서 같은 처짐 ∆y가 발생한다고 하면, 두 모델에서 저장되는 탄성에너지는 동일해야 한다. 식 (1)에서 4-스프링 모델에서 저장되는 탄성에너지 S₁과 식 (2)에서 8-스프링 모델에서 저장되는 탄성에너지 S₂는 같아야 한다. 즉, 이 경우 두 등가 강성 모델의 탄성에너지의 총합은 일정하므로 S₁=S₂이다. 이에 따라, 모델 간 스프링 강성 관계식 (3)이 도출된다. 같은 방법으로 4-스프링 모델의 스프링 강성을 기준으로 여러 스프링 요소의 수를 가지는 등가강성모델의 스프링 강성을 정의하였다.

$\[ S_1=K_4{\left(△y\right)}^2+K_4{\left(△y\cos \left(\frac{\pi }{2}\right)\right)}^2 \]$

(1)

Fig. 4

Deformation of the spring elements in spindle system

$\[ \begin{array}{l}{S}_2=K_8{\left(△y\right)}^2+2K_8{\left(△y\cos \left(\frac{\pi }{4}\right)\right)}^2 \\ +K_8{\left(△y\cos \left(\frac{\pi }{2}\right)\right)}^2\end{array} \]$

(2)

$\[ K_4=2K_8 \]$

(3)

2.2 선형 정적 해석

스프링 요소의 개수에 대한 회전축 결합 모델들의 등가 강성 여부를 확인하기 위해 해석 프로그램(nastran, MSC)을 이용하여 선형 정적 해석을 진행하였다. Fig. 5에서 나타낸 정강성 해석의 경계 조건은 베어링 외경을 6자유도 구속하고 롤러에 약 17kN의 하중을 부여하였다. 그 결과, 최대로 처짐이 일어나는 점은 모두 동일 하였고, Table 1에서 각 모델들의 처짐량을 나타내었다. 4-스프링 모델은 선형 정적 해석에서 최대 처짐량이 다른 모델보다 약 9 % ~ 15 %의 차이를 보이고 있으며, 이는 스프링 유한 요소를 구성할 때 발생하는 스프링 요소 정렬 오차 때문인 것으로 예상된다. 따라서, 4개의 스프링 요소로는 스프링 요소 정렬오차를 제거할 수 없다고 판단하였다.

Fig. 5

Boundary condition of linear static analysis (FE model of spindle assembly)

Table 1

Result of linear static analysis according to the number of spring elements

2.3 고유진동수 해석

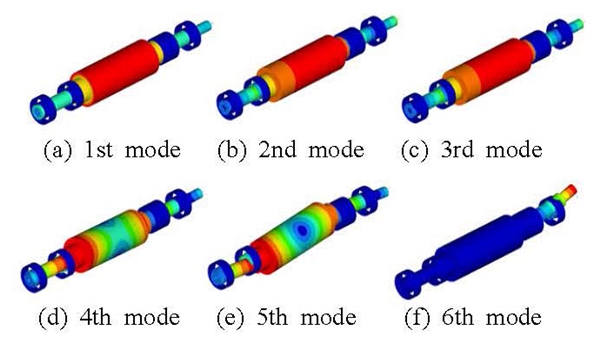
회전축 모델의 동강성 특성을 확인하기 위하여 고유진동수 해석을 진행하였다. Fig. 6은 첫 번째 ~ 여섯번째 모드에 대하여 회전축 결합 모델의 모드 형상이다. 첫 번째 모드는 축이 회전하는 모드, 두 번째 ~ 세번째 모드는 1차 굽힘 모드, 네 번째 ~ 다섯 번째 모드는 2차 굽힘 모드 그리고 여섯 번째 모드는 롤러와 결합되어 있는 오른쪽 스핀들의 굽힘 모드를 나타낸다. Table 2는 각 결합 모델들의 모드별 고유진동수를 나타내었다.

Fig. 6

Mode shape (spindle assembly model)

회전축 결합 모델들의 고유진동수 해석 결과에 따라 초기 모델을 선정하였다. 먼저, 6스프링, 18스프링 모델은 두 번째 ~ 세 번째 모드가 1차 굽힘 모드, 네 번째 ~ 다섯 번째 모드가 2차 굽힘 모드이다. 서로 같은 모드지만 다른 주파수 영역을 가진다. 이는 6스프링, 18스프링 요소가 4분면에 대하여 대칭으로 구성되지 않았기 때문에 상, 하, 좌, 우로 거동하는 굽힘 모드에 대하여 같은 조건으로 해석하지 못하는 모델이라고 예상된다. 1차 굽힘 모드, 2차 굽힘 모드에 대해서 약 460 Hz, 990 Hz로 수렴하는 값과 5 % 미만의 차이를 가지며, 모델 구성과 해석 과정에서 가장 경제적인 8스프링 모델을 초기 모델로 선정하였다.

Table 2

Natural frequency result according to the number of spring elements

3. 베어링 배치 설계

배치할 베어링의 수는 하중 조건에서의 설정 수명, 각 접촉 볼 베어링의 특성을 고려하였다. 주축이 받는 하중 약 17kN에서 기대 수명 100000시간을 만족하기 위해 각 접촉 볼 베어링(150 t × 85 t × 28 t) 8.53개 이상을 배치해야 된다. 베어링 제조사에서 제공하는 볼 베어링 기대 수명 메뉴얼⁽¹¹⁾을 참고하여 이론적으로 계산하였다. 또한, 각 접촉 볼 베어링을 홀수로 사용할 경우 편심 거동이 일어날 수 있다는 단점이 있기 때문에 쌍으로 사용한다. 따라서, 베어링은 총 10개(5쌍)를 배치하기로 하였다. 베어링의 배치 영역을 선정하기 위하여 회전축 모델을 프리-프리 경계 조건에서 고유진동수 해석을 진행하였다.

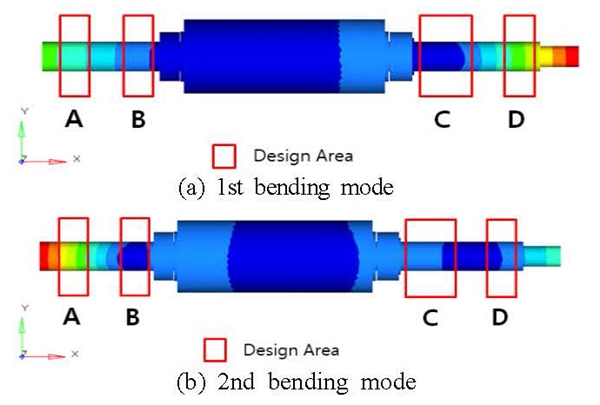
Fig. 7에서는 다른 부품과의 간섭으로 인해 배치를 할 수 없는 영역을 제외한 최소 변위 점을 설계 영역으로 나타낸 것이다. 설계 영역에 5쌍의 베어링을 배치해야 되기 때문에 A, B, D 영역은 각각 1쌍을 배치하고 C 영역은 2쌍을 배치하였다.

Fig. 7

Mode shape of spindle assembly model before bearing arrangement

3.1 베어링 배치 타입 선정

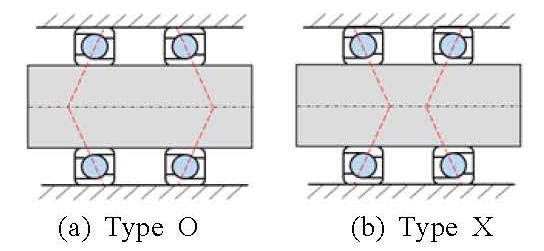
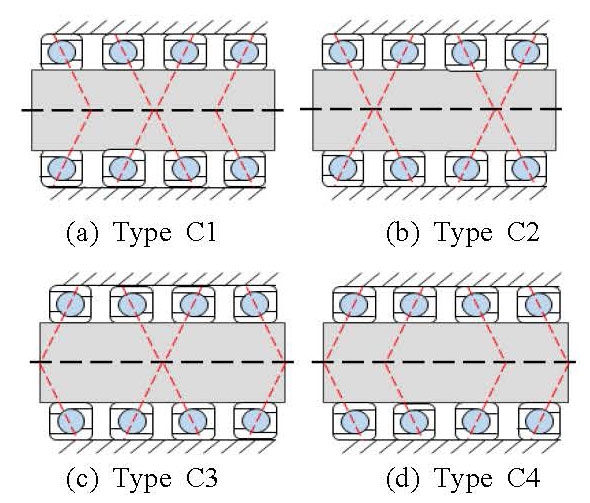
회전축 모델의 최대 동강성 확보를 위한 베어링배치 타입 선정을 실시하였다. 베어링의 배치 타입은 A, B, D영역에는 1쌍 배치이므로 Fig. 8에서 나타낸 베어링 외경의 지지점이 서로 가까운 타입 O, 서로 먼 타입 X 선정을 실시한다. C영역은 2쌍이므로 Fig. 9에서 나타낸 베어링의 지지점을 점선으로 표시한 타입 1 ~ 4를 배치하였다. 베어링 2쌍을 좌측의 한 쌍과 우측의 한 쌍으로 구분했을 때 좌측 한 쌍의 베어링에서 외경을 지지하는 점보다 내경을 지지하는 점이 축방향을 기준으로 우측에 있고, 우측의 한 쌍의 베어링에서 외경을 지지하는 점보다 내경을 지지하는 점이 축방향을 기준으로 좌측에 있으면 타입 C1, 좌, 우측의 한 쌍의 베어링이 각각 타입 X로 배치되었을 때 타입 C2, 좌, 우측의 한 쌍의 베어링이 각각 타입 O로 배치되었을 때 타입 C3, 좌측 한 쌍의 베어링에서 외경을 지지하는 점보다 내경을 지지하는 점이 축방향을 기준으로 좌측에 있고, 우측의 한 쌍의 베어링에서 외경을 지지하는 점보다 내경을 지지하는 점이 축방향을 기준으로 우측에 있으면 타입 C4 배치이다.

Fig. 8

Arrangement method of 1 pair bearings (type O, X)

Fig. 9

Arrangement method of 2 pair bearings (type C1 ~ C4)

Table 3에서는 A, B, D영역에서의 배치를 변수로 설정하고 C 영역의 타입을 고정시켜 총 8개의 비교 모델의 고유진동수를 나타내었다. A, B, D영역 모두 타입 O로 선정했을 때 최대 고유진동수 결과를 도출하는 것을 확인할 수 있다. 다음으로, Table 4에서는 2쌍을 기준으로 베어링을 배치하는 C영역을 변수로 두고 타입 C1 ~ C4인 4개의 모델에 따른 고유진동수를 나타내었다. 타입 C4 모델에서 최대 고유진동수를 확인하였다. 초기 모델(model 1, Table 3)과 비교한 결과, 배치 타입 선정으로 고유진동수가 1차 굽힘 모드에서 약 4.5 %, 2차 굽힘 모드에서 약 3.9 % 증가하는 C1 모델을 도출하였다.

Table 3

Comparison of arrangement type and natural frequency in A, B, D design area

Table 4

Comparison of arrangement type and natural frequency in C design area

3.2 베어링의 축 방향 위치 변경

베어링의 위치 변경을 진행하였다. 베어링 배치 타입 선정 이후에 B, C영역에서 여유 공간을 확인하였고 모드 형상을 통해 베어링 배치 이후에 롤러에서 상대적으로 변위가 많이 일어나는 것을 확인하였다.

변위가 많이 발생하는 영역을 지지해야 회전축 결합 모델의 동강성이 증가하므로 설계 영역 내에서 롤러와 가장 가깝게 베어링 위치 변경을 실시하였다. B영역의 베어링을 +x축 방향으로 12 mm, C영역의 베어링을 –x축 방향으로 6 mm 위치 변경하였다. Table 5에서 초기 모델과 비교하여 고유진동수가 1차 굽힘 모드에서 약 8.8 %, 2차 굽힘 모드에서 약 9.9 %가 증가한 것을 확인하였다.

Table 5

Natural frequency of models after change of bearing location

4. 결 론

이 연구에서는 멀티와이어쏘 장비를 대상으로 생산 과정에서 소요 시간과 재료 손실을 감소시키기 위하여 주축의 정적, 동적 강성 향상을 위한 연구를 진행하였다.

설계 변수는 베어링 배치로 선정하였고, 베어링을스프링 요소로 모델링하는 과정을 수행하였다. 실제로 회전축을 지지하는 각 접촉 볼 베어링은 회전축과 프레임을 지지하는 각, 베어링을 모델링한 스프링 요소의 수, 스프링 요소의 수에 따른 강성 배분을 고려하여 회전축 결합 모델을 구축하였다. 유효한 모델을 선정하기 위해 정강성 해석 및 고유진동수 해석을 진행하였다. 그 결과, 4개 ~ 6개의 스프링요소로 구성된 모델이 유효하지 않다는 판단을 내리고 유효한 모델 중 모델링과 해석 과정에서 가장 경제적인 8 스프링 모델을 초기 모델로 선정하여 연구를 수행하였다.

베어링 배치 설계는 배치할 베어링의 수, 베어링 배치 타입 선정 그리고 베어링 위치 변경 순으로 진행하였다. 회전축에 사용하는 베어링의 수명과 특성을 고려하여 총 10개(5쌍)를 배치하기로 했고, 1쌍 배치 영역에는 타입 O, X를, 2쌍 배치 영역에는 타입 C1 ~ C4을 선정하였다. 그 후, 위치 변경을 한 결과 초기 모델 대비 고유진동수가 1차 굽힘 모드에 대하여 약 8.8 %, 2차 굽힘 모드에 대하여 약 9.9 %가 증가하였다.

Acknowledgments

This works was supported by the Technology Innovation Programs(10063367, 10052882), funded by the Ministry of Trade, industry & Energy(MI, Korea).

References

• Kim, D. Y., Kim, S. J., and Jeong, H. D., (2015), Effect of Initial Deflection of Diamond Wire on Thickness Variation of Sapphire Wafer in Multi-wire Saw, International Journal of Precision Engineering and Manufacturing-Green Technology, 2(2), p117-121. [https://doi.org/10.1007/s40684-015-0015-x]
• Teomete, E., (2011), Roughness Damage Evolution due to Wire Saw Process, International Journal of Precision Engineering and Manufacturing, 12(6), p941-947. [https://doi.org/10.1007/s12541-011-0126-4]
• Lee, J. Y., Lee, S. E., Yim, H. J., and Jeong, J. I., (2017), Topology Optimization of Main Rollers for Multi-wire Saw Systems, Journal of the Korean Society for Precision Engineering, 34(10), p677-681. [https://doi.org/10.7736/kspe.2017.34.10.677]
• Lee, S. J., Kim, H. J., Kim, D. Y., and Park, C. J., (2016), Investigation on Diamond Wire Break-in and Its Effects on Cutting Performance in Multi-wire Sawing, International Journal of Advanced Manufacturing Technology, 87(1), p1-8. [https://doi.org/10.1007/s00170-015-7984-3]
• Park, S. S., and Chung, W. J., (2011), A Study on Select Position of High Speed Spindle Considering the Thermo Behavior, Journal of the Korean Society of Manufacturing Technology Engineers, 20(6), p767-772.
• Lim, J. S., Chung, W. J., and Lee, C. M., (2009), Selection of Bearing Position for Improving Static and Dynamic Stiffness of 40,000rpm High-speed Spindle, Journal of the Korean Society of Manufacturing Process Engineers, 8(1), p10-17.
• Hong, S. W., Choi, C. S., and Lee, C. H., (2013), Effects of Bearing Arrangement on the Dynamin Characteristics of High-speed Spindle, Journal of the Korean Society for Precision Engineering, 30(8), p854-863. [https://doi.org/10.7736/kspe.2013.30.8.854]
• Kim, H. Y., Jeong, J. K., Won, J. J., and Jeong, J. I., (2012), A Computational Modeling Reflecting Static and Dynamic Characteristics of LM Bearings for Machine Tools, Journal of the Korean Society for Precision Engineering, 29(10), p1062-1069. [https://doi.org/10.7736/kspe.2012.29.10.1062]
• Kim, H. M., Seo, J. W., and Park, H. W., (2012), Computational Modeling of the Bearing Coupling Section of Machine Tool, Journal of the Korean Society for Precision Engineering, 29(10), p1050-1055. [https://doi.org/10.7736/kspe.2012.29.10.1050]
• Cha, J. K., Choi, J. H., Kim, J. H., Hwang, T. G., and Kim, S. J., (2009), Structural Strength Analysis of Eccentric Bearing Bush for Assembly in the Low Temperature, Proceeding of the KSME Annual Autumn Conference, p730-735.
• NSK Rolling Bearings Catalog, No. E1102m, pA24-27, B46~49, B62.