가변형 Magneto-rheological Elastomer 동흡진기의 설계
© The Korean Society for Noise and Vibration Engineering
Abstract
Magnetic-rheological elastomer is a smart material that can change its shear modulus. This study suggested magneto-rheological elastomer (MRE)-based dynamic vibration absorber (DVA). The MRE-based DVA can change its stiffness instantly by controlling the magnetic field. To control the magnetic field, a magnetic flux generator was designed using electromagnetic finite element method analysis and the response surface method. Moreover, the shear modulus of MREs was evaluated by being applied to DVA, and the mass of the MRE-based DVA was calculated. Finally, a variable dynamic vibration absorber was manufactured to reduce the vibration according to changes in the magnetic field. The variable performance of the MRE-based DVA was conducted using current control.
Keywords:
Magneto-rheological Elastomer, Dynamic Vibration Absorber키워드:
자기유변고무, 동흡진기1. 서 론
가전 제품 및 자동차 등 소비자의 생활에 밀접한 영향을 미치는 제품들은 경량화와 더불어 진동 및 소음 개선에 대한 요구는 꾸준히 증대되어 왔다. 특히 진동 및 소음의 저감을 위해서는 가진원 자체에 대한 대책을 수립하거나 가진원으로부터의 진동 전달을 방지하는 방안이 널리 사용되고 있다. 이와 같은 진동 제어 기술은 구조물의 파손과 공해를 방지할 뿐만 아니라 신뢰성과 내구성을 향상시키는 장점을 지니고 있다.
가진원으로부터의 진동 전달을 방지하려는 목적으로 가장 대표적인 방법이 방진고무이다. 방진고무는 생산성과 적용성 그리고 저비용이라는 여러 장점을 가지고 있으므로 가전 제품 및 자동차 분야에 널리 사용되고 있다. 방진고무는 형상자유도가 높아 형상, 치수를 조절하면 상하, 좌우, 전후의 3방향 강성을 일정 한계 내에서 자유롭게 설정 가능하다는 특징이 있으며, 금속과 쉽고 견고하게 접착되어 소형 및 경량화가 가능하고 지지방법도 간단하다는 장점을 지니고 있다. 또한, 금속 스프링의 경우에는 고주파 진동에 대해 스프링 자체에서 생기는 탄성진동이 문제가 되며 진동수에 따라서 방진성을 잃을 뿐만 아니라 진동의 증폭 작용까지도 초래하는 경우가 있지만 방진고무는 이러한 단점을 가지고 있지 않다.
하지만 방진고무는 수동적인 방진대책으로써 특정 주파수 대역의 진동을 주로 흡수하는 한계가 있어 보다 넓은 주파수대의 진동을 저감시킬 필요성이 대두되고 있다(1). 이를 위해 최근 기존 상용 방진고무의 제어를 위해 자기반응성입자(magnetic reactive particle)를 이용한 가변형 물성을 가지는 지능형 소재인 자기유변고무(magneto-rheological elastomer, MRE)에 대한 연구가 국내외에서 진행되고 있다(2 ~ 4).
자기유변고무는 자기장의 인가에 따라 전단계수가 변화하는 고무로 가변형 진동 저감 대책으로 각광받고 있다(5 ~ 7). 이를 기존의 진동 저감 대책인 동흡진기에 적용한다면 기존의 동흡진기의 단점인 일정한 주파수대역에서의 진동 저감뿐만 아니라 가변하는 입력 주파수에 따라 진동을 저감할 수 있는 가변형 동흡진기를 개발할 수 있을 것이라 기대된다.
따라서 이 연구에서는 기존의 동흡진기에 자기유변고무를 적용하여 가변형 동흡진기를 설계하려 한다. 이를 위해 자기장인가장치를 동흡진기의 질량부로 적용하였고, 자기장 성능과 동흡진기의 성능을 만족하기 위해 반응표면법을 이용하여 형상최적화를 수행하였다.
2. 자기유변고무 적용 동흡진기의 개념 설계
동흡진기는 질량부와 강성부로 구성된다. 질량부와 강성부의 설계를 통해 진동 저감 주파수를 결정하게 된다. 또한, 자기유변고무는 자기장의 세기에 따라서 물성이 변화하므로 자기장 인가 장치가 반드시 필요하다. 따라서 이 연구에서는 기존의 동흡진기에 자기유변고무를 적용하기 위해서 자기장 인가 장치를 동흡진기의 질량부로 하였다.
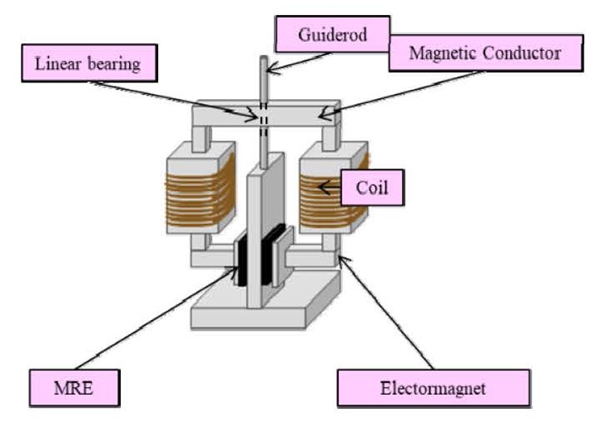
동흡진기의 질량부는 Fig. 1과 같이 구성된다. 먼저 자기장이 흐를 수 있도록 폐회로와 솔레노이드 코일 그리고 자기유변고무의 접합부로 구성된다(Fig. 1).
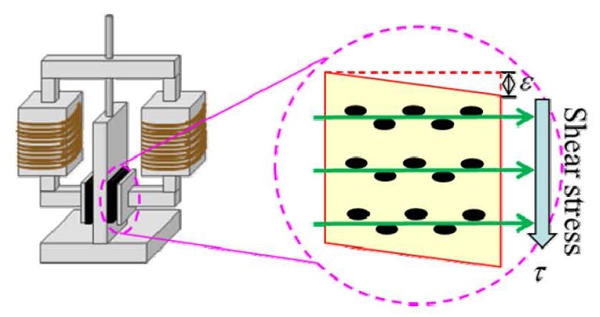
자기유변고무는 자기장 인가에 따라 전단계수가 변화하는 고무로 가변형 동흡진기에 적용 시 전단계수를 가변 할 수 있어야 한다. 따라서 자기유변고무는 Fig. 2와 같이 전단변형을 일으킬 수 있도록 동흡진기의 질량부에 적용된다.
3. 동흡진기의 진동 저감 주파수 선정
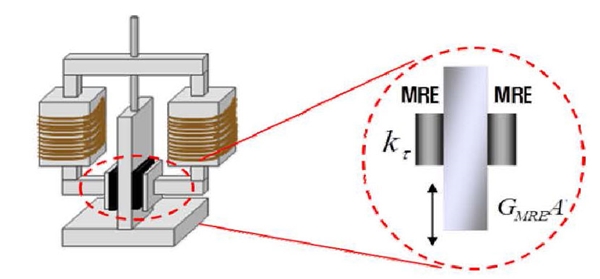
동흡진기는 질량부와 강성부로 구성된다. 가변형자기유변고무 적용 동흡진기의 강성부는 자기유변고무의 전단 변형을 이용한다. 또한 자기유변고무는 폐회로로 구성된 자기장인가장치를 필요로 하기 때문에 Fig. 3과 같이 두 개의 자기유변고무를 붙여 동흡진기의 강성부로 하였다.
자기유변고무의 강성을 측정하기 위하여 자기유변고무의 자기장 인가에 따른 강성을 측정하였다.
윤지현(4)은 자기유변고무의 측정 시스템을 구축하여 전단계수를 측정하였다. 전단계수는 FFT analyzer를 이용하여 다음의 수식을 이용하여 도출하였다.
| (1) |
여기서, G는 전단계수, f는 시스템의 2차 고유진동수, m은 측정 시스템에서 oscillator의 질량, h는 시편의 두께, A는 시편의 면적을 말한다. 또한 전단방향의 강성은 다음과 같이 정의하였다.
| (2) |
자기유변고무의 강성 측정 방법으로는 측정 시스템에서 2차 고유진동수를 측정하고 식 (2)를 이용하여 자기유변고무의 강성을 구하였다. 이때 2차 고유진동수는 측정 시스템에서 자기유변고무에 의해 변화하는 주파수이다. 실험에 사용된 자기유변고무는 natural rubber(NR)을 기본 매트릭스로 하고 첨가제는 Table 1와 같다. 또한 자기유변고무의 자기반응입자 체적비는 30 %로 선정하고 CIP 체인 사슬이 형성되도록 이방성(anisotropic)으로 배향시켜 인가자기장에 따른 기계적 물성 변화가 가장 크게 하였다(Fig. 4).
4. 반응표면법을 이용한 동흡진기 질량부의형상 최적화
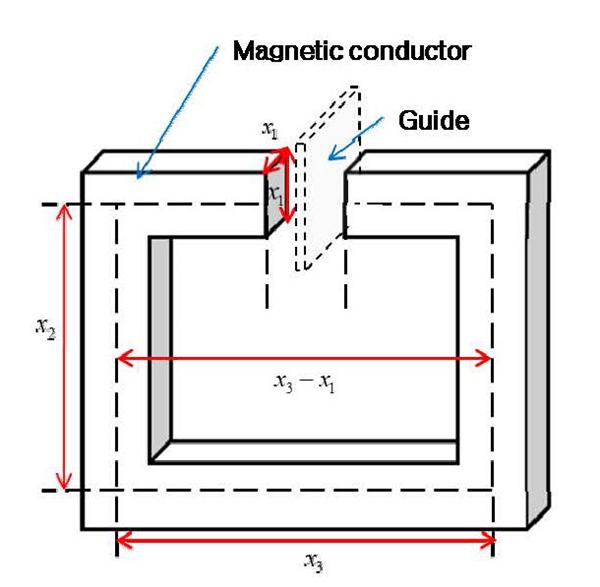
동흡진기의 질량부는 자기장이 흐르는 컨덕터와 솔레노이드로 구성된다(Fig. 1). 일정한 질량에서 자기장의 세기가 클수록 가변형 동흡진기의 가변 성능 최대가 된다. 따라서 동흡진기의 질량은 윤지현이 실험한 자기장인가장치의 질량과 동일한 질량으로 선정하였다. 또한 전류를 인가하여 자기장을 유도할 솔레노이드는 코일의 턴 수는 700회로 솔레노이드 한 개의 질량은 800g이다. 다음으로 자기장인가장치 중 자기장 컨덕터의 형상을 최적화하기 위해 인자를 Fig. 5와 같이 3개로 결정하였다. 인자의 수준을 결정하기 위해 다음과 같은 가정을 하였다. 자기장의 세기는 단면적의 크기에 가장 민감하므로 x1의 값은 제작 가능한 시편의 길이인 1.8cm 이상 2.0cm 이하로 결정하였다.
또한 x3의 크기가 작을수록 자기장이 강하기 때문에 솔레노이드의 부피를 고려하여 x3과 x1의 차가 5cm가 되도록 하였다. 자기유변고무가 삽입되는 부분은 guide 부분과 시편의 두께를 고려하여 0.8cm가 되도록 고정하였고 재질은 철을 사용하였다. 따라서 부피를 계산하면 다음과 같다.
| (3) |
앞서 가정을 정리하면 다음과 같다.
| (4) |
식 (3)에 식 (4)를 대입하면 3인자 3수준은 다음과 같다.
| (5) |
이를 활용한 반응표면법의 해석 순서와 상용소프트웨어인 Maxwell을 이용하여 자기장 해석을 진행한 결과는 Table 1와 같다.
여기서 해석 진행 시 코일에 입력한 전류는 4A이다. 자기장 측정위치는 자기유변고무가 부착될 위치이다.
해석결과를 이용하여 2차 다중 회귀식을 도출하였다. 회귀 모델의 결과로 상관계수는 0.87로 회귀 모델의 신뢰성이 높은 것을 알 수 있다.
최종적인 회귀 식은 다음과 같다.
| (6) |
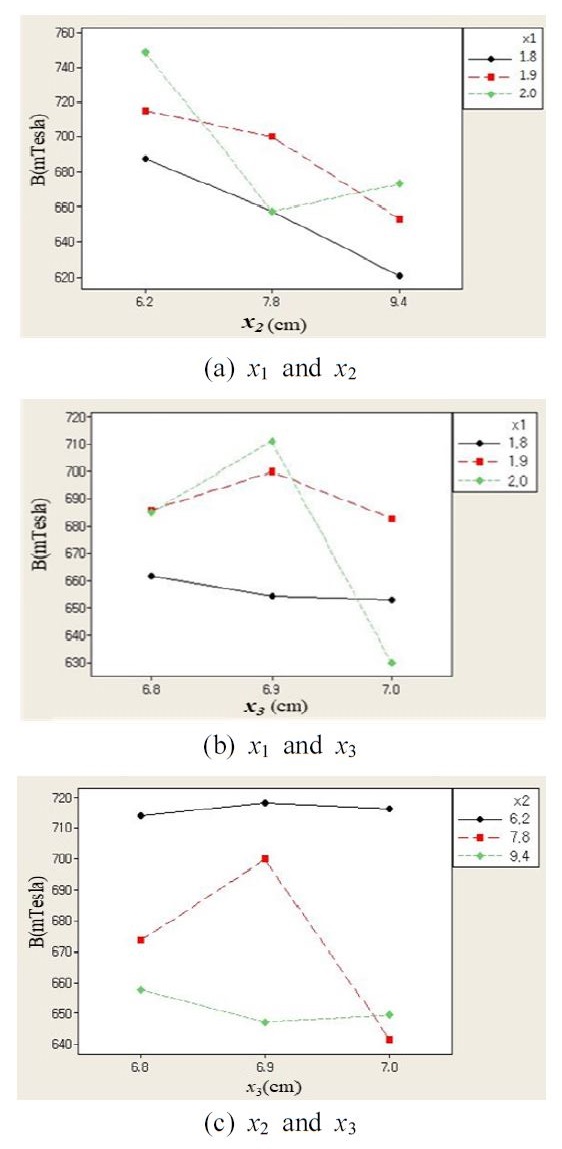
다음으로 자기장에 대한 각 인자들의 교호 작용을 확인하였다(Fig. 6).
교호 작용 해석 결과로 세 가지 경우 모두 선이 교차하는 부분이 존재하여 인자간 교호 작용이 존재함을 알 수 있다. 각각의 경우를 분석해보면 x1이 커지고 x2가 작아질수록 자기장 값이 커지는 경향을 보이며, x1이 커지고 x2가 중간 값을 가질 때 자기장 값이 커지는 경향을 보인다. 마지막으로 x2가 작아지고 x3가 커질수록 자기장 값이 커지는 경향을 보인다. 따라서 x1이 커지고 x2가 작으며 x3가 크면 자기장 값이 커짐을 알 수 있다.
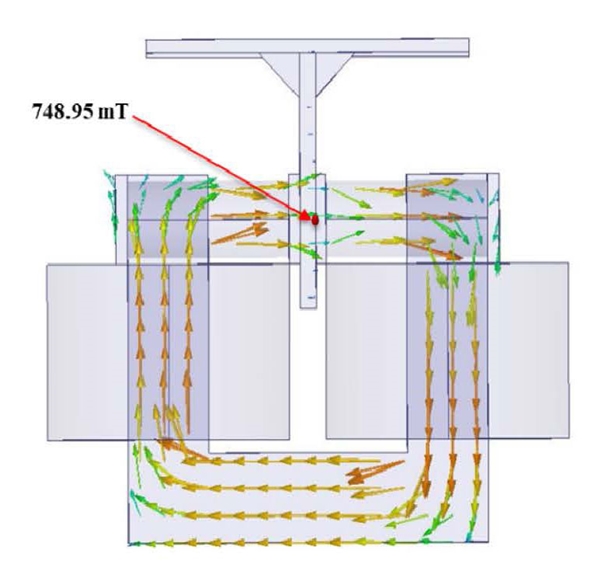
따라서 자기장을 최대로 인가할 수 있는 형상과자기장 해석 결과는 Fig. 7과 같다.
5. 가변형 동흡진기의 진동 저감 주파수 측정
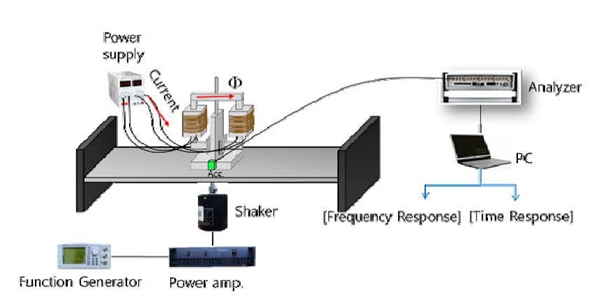
가변형 동흡진기의 자기장 인가에 따른 가변 진동 저감 주파수 특성을 파악하기 위한 실험 장치도는 Fig. 8에 나타내었다.
진동 저감 주파수를 가변 시키기 위하여 솔레노이드에 전류를 1A ~ 4A까지 1A 간격을 두고 인가하였다.
이를 통해 자기장을 인가하여 자기유변고무의 전단 강성을 변화 시켰다. 가변형 동흡진기는 양단 고정보의 중앙에 설치하였다. 또한, 주파수 응답 함수를 이용하여 진동 저감 주파수를 측정하므로 양단 고정보의 아래에 shaker를 설치하였고 전주파수 특성을 규명하기 위해 white noise로 가진 하였다. 측정은 가속도계를 동흡진기의 근접 위치에 설치하여 진동 저감 특성을 규명하였다. 측정은 PAK mobile MKII를 사용하였다. 가변하는 주파수 특성을 보여주기 위해 전류를 0A에서 4A까지 1A의 간격으로 인가하여 각각의 진동 저감 주파수를 확인하였다.
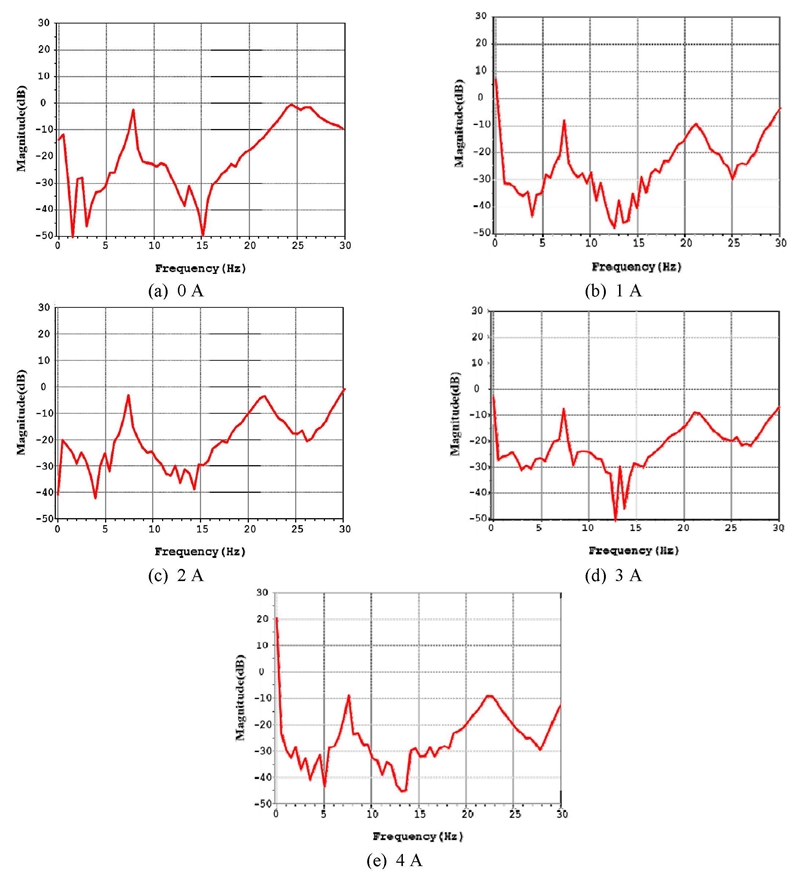
가변형 동흡진기의 진동 저감 성능은 Fig. 9와 같다. 진동을 저감하고자 하는 진동 저감 대상체의 주파수는 넓은 대역에서 높은 진동 특성을 가지는 약 24 Hz ~ 27 Hz를 대상으로 하였다. 가변형 동흡진기는 0A에서 25 Hz에서 진동 저감을 수행하며 약 22 Hz ~ 28 Hz까지의 진동 저감을 수행하는 것을 알 수 있다(Fig.(a)). 또한, 1A 전류 인가 시 주요 저감 주파수는 약 26.5 Hz로 가변하며, 최종적으로 4A를 인가하였을 때 28 Hz까지 가변하는 것을 알 수 있다.
위 실험을 통해 가변형 동흡진기는 강성을 가변하게 함으로써 진동 저감 주파수를 가변하는 것을 알 수 있다. 자기유변고무의 강성 변화율이 더 크게 변화 할 수 있다면 가변형 동흡진기의 진동 저감 주파수 대역도 더욱 넓어질 것으로 예상된다.
또한 동흡진기의 진동 저감 주파수는 질량과 강성으로 조절할 수 있다. 동흡진기의 질량이 작아지면 가변 성능은 커지게 된다. 따라서 동흡진기의 질량 부는 최소로 설계하여 동흡진기의 진동 저감 주파수 가변 성능을 최대로 할 필요가 있다.
6. 결 론
이 연구에서는 자기유변고무를 동흡진기에 적용하였다. 이를 통해 진동 저감 주파수가 가변 가능한 동흡진기를 설계하였다. 가변형 동흡진기 설계를 위해 진동 저감 주파수 대역을 선정하였고, 이를 위해 자기유변고무 적용을 위한 설계와 자기인가장치의 반응표면법을 이용한 형상 최적설계를 수행하였다. 최종적으로 가변형 동흡진기를 제작하여 자기장 변화에 따른 진동저감 주파수 성능을 확인하였다. 가변형 동흡진기의 가변 성능은 12 % 가변하는 것을 보였다. 가변 성능은 자기유변고무의 개선 또는 진동 저감 주파수 대역을 조금 더 높은 주파수 대역으로 변경 시 더욱 높은 가변 성능을 보일 것으로 예상된다.
References
-
Carlson, J. D., and Jolly, M. R., (2000), MR Fluid, Form an Elastomer Devices, Mechatronics, 10, p555-569.
[https://doi.org/10.1016/s0957-4158(99)00064-1]

- Deng, H. X., and Gong, X. L., (2007), Application of Magnetorheological Elastomer to Vibration Absorber, Nonlinear Science and Numerical Simulation, 13, p1938-1947.
- Yoon, J.-H., Jeong, J.-E., Yang, I.-H., Lee, J.-Y., and Oh, J.-E., (2009), Experimental Identification on Shear Modulus of Magneto-rheological Elastomer Based on Silicon Matrix due to Induced Current, Proceedings of the KSNVE Annual Autumn Conference, p623-624.
- Oh, J.-E., Yoon, J.-H., Yoon, K.-S., Chung, K.-H., Cho, H.-C., and Lee, S.-H., (2008), Measurement of Mechanical Properties of Magneto-rheological Elastomer due to Current and Volume Ratio of Carbonyl Iron Powder, Proceedings of the KSME fall annual meeting, p791-794.
-
Zhang, X. Z., Li, W. H., and Gong, X. L., (2008), An Effective Permeability Model to Predict Field-dependent Modulus of Magnetorheological Elastomers, Communications in Nonlinear Science and Numerical Simulation, 13, p1910-1916.
[https://doi.org/10.1016/j.cnsns.2007.03.029]

- Woodson, H. H., and Melcher, J. R., (1968), Electromechanical Dynamics, John Wiley & Sons, Part2, p418-478.
-
Davis, L. C., (1998), Model of Magnetorheological Elastomers, Journal of Applied Physics, 85(6), p3348-3351.
[https://doi.org/10.1063/1.369682]


Jae-Eung Oh received his B.S. form Hanyang University(1975), M.S. from Yokohama National University(1980) and Ph.D. degree in Environment Engineering from the graduate school from the Tokyo Institude of Technology(1983) with his thesis in the area of Noise & Vibration and Signal Processing. Since 1985, he has been a Member of Korean Society for Noise and Vibration Engineering.