프로펠러 BPF 유발 선체 가진력 저감을 위한 복수개 풍선의 설계
© The Korean Society for Noise and Vibration Engineering
Abstract
The marine propellers installed at the rear of ships experience the cavitation phenomenon, producing vibratory hull-excitations at several orders of blade passing frequency. The current investigation establishes a practical design method of multi air-balloons to suppress the propeller cavitation-induced excitation at multiple frequencies. The theoretical formulation begins with the existing modal series solution of a multiple scattering problem. We propose an approximated solution in a low-frequency system that is useful in the analysis and design stages. The parametric variation of the separation distance between the balloons reveals a rational proof that their mutual interaction can be ignored unless they are too close together. Therefore, it is emphasized that each balloon can be designed individually without reflection of the coupling characteristics among them.
Keywords:
Propeller, Cavitation, Air-balloon, Destructive Interference키워드:
프로펠러, 캐비테이션, 공기풍선, 상쇄간섭1. 서 론
물속에서 동작하는 프로펠러는 캐비테이션 현상을 수반하며, 선박의 주요한 진동-소음 문제를 야기한다. 캐비테이션이 유발하는 선체 가진력을 저감하기 위해, 음향 반사의 원리를 응용한 단수노즐 공기분사 방법이 제안된 바가 있다(1). 부연하면, 캐비테이션에 기인한 압력파가 수중에서 전파하는 가운데 공기층을 만나게 되면, 일부는 투과하고 나머지는 주변으로 반사한다. 특히, 상쇄간섭 주파수(frequency of destructive interference)라 지칭하는 특정 주파수 대역에서의 반사파는 입사파에 대비하여 위상이 역전된다. 따라서, 입사파와 반사파의 중첩으로 구성된 전체 압력장에서는 두 파(입사파, 반사파) 성분이 서로 상쇄되어 가진력이 ‘영(0)’이 되는 현상, 즉 상쇄간섭(destructive interference)이 발생하게 되어, 공기층 외부의 가진 압력을 크게 저감할 수 있었다.
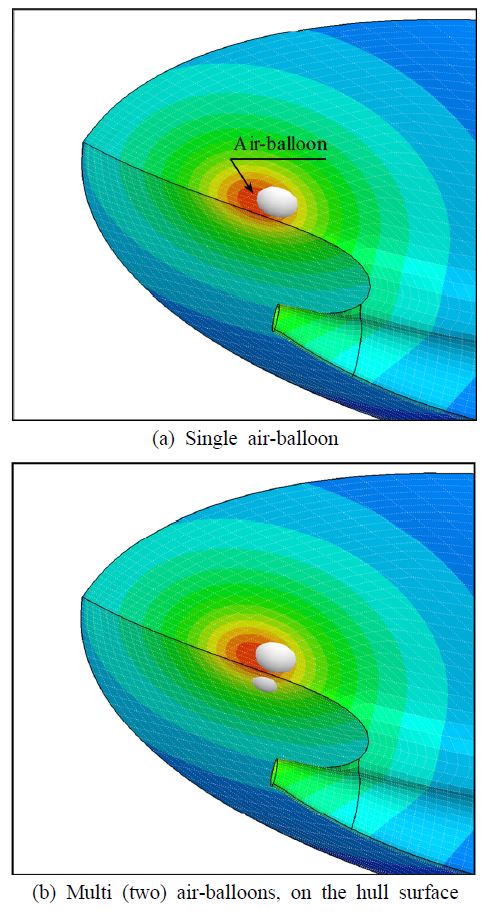
이후, 물(또는 해수)과 고무재질 사이의 임피던스가 서로 유사함에 착안하여 Fig. 1(a)와 같은 고무풍선 방법이 제안되었다(2). 공기를 고무풍선의 형태로 감싸게 되면, 임피던스 유사성에 의해 고무막은 공기를 가두어두는 보자기 역할을 할 뿐이지 상쇄간섭 현상에는 어떠한 영향도 미치지 않게 된다. 따라서, 기존의 공기 분사 방법을 에너지 소모 없는 풍선과 같은 단순한 방법으로 대체할 수 있었다.
전술한 바에 따라, 상쇄간섭은 특정주파수, 즉 상쇄간섭 주파수에서만 발생한다. 바꾸어 말하면, 단수(single) 풍선은 특정 하나의 가진 주파수 성분만 저감 가능하다는 것이다. 프로펠러가 선박의 후미, 즉, 불균일 반류장에서 동작하므로 날개 통과 주파수(blade passing frequency, BPF) 및 고조파(harmonics) 가진 성분이 발생한다(3). 따라서, 여러 가지 주파수에 대응하기 위해 Fig. 1(b)와 같이 풍선 다수가 필요함을 강조할 수 있으며, 그에 대한 설계를 이 연구를 통해 제안하고자 한다. 풍선이 서로 근접할 경우, 상호 간의 산란/반사가 발생하게 되어 다중산란(multiple scattering) 이론 도입이 필요하다(4). 일반적인 N개 풍선에 대해서는 그 해가 매우 복잡한 형태를 띠게 되어, 우선 두 개 풍선에 대한 해석을 통해 문제에 접근할 필요가 있다. 그러나, 이 마저도 급수해로 표현되어 설계현장에 쉽게 적용되지 못하는 한계가 있다. 여기서는 풍선이 BPF 성분과 같이 비교적 저주파 영역에서 사용되는 것에 착안하였으며, 해당 영역에서의 근사화를 통해 비교적 간단한 대수식 형태의 해를 유도할 수 있음을 제안한다. 아울러, 풍선이 서로 일정 거리 이상 이격되어 있다면 다중산란 효과를 무시하여 각 풍선의 독립적 설계가 가능함을 증명하는데, 상세 내용은 다음절부터 다루기로 한다.
2. 문제의 정식화 및 이론해
프로펠러 회전수 성분에 대응하는 파장의 크기가 풍선에 비해 매우 크다고 볼 수 있을 정도로, 이 연구의 관심 주파수는 저주파 대역에 속한다. 따라서, 풍선을 가진하는 압력파 즉, 입사파를 평면파로 간주할 수 있다. 또한, 저주파 영역에서의 반사/산란 현상은 풍선의 상세 형상 보다는 등가 부피에 주된 영향을 받으므로, 수학적 편의를 위해 그 기하를 구형으로 가정할 수 있다.
공기를 가두는 역할을 하는 풍선의 고무층은 그 두께가 매우 얇을 뿐만이 아니라, 기 언급한 해수와의 임피던스 유사성으로 인해 무시 가능하다. 그러므로, 이후 기포와 풍선이라는 단어를 혼용해서 사용하기로 한다.
추가적인 가정으로, 풍선이 부착되는 선체 벽면도 무시하였다. 벽면의 존재는 기포의 공진주파수를 10 % ~ 17 % 가량 저주파 대역으로 이동시키는 것으로 알려져 있으나(5), 실제 적용시 공기충전과 같은 튜닝(tuning)을 통해 주파수 이동을 보상할 수 있으므로 선체 벽의 영향을 고려하지 않기로 한다.
이상의 가정을 바탕으로, Fig. 2에 나타낸 바와 같이, 반경이 각각 a1, a2이며 (단, a1 > a2) 중심간 거리가 d인 두 개 구형 풍선 A, B를 고려할 수 있다. 두 좌표계 O1(x1-y1-z1)과 O2(x2-y2-z1)은 z1-축을 따라 동축 배치를 따르는 한편, 공간 내 한 점은 극좌표를 이용하여 (r1, θ1, Φ1) 또는 (r2, θ2, Φ1)로 표현 가능한다.
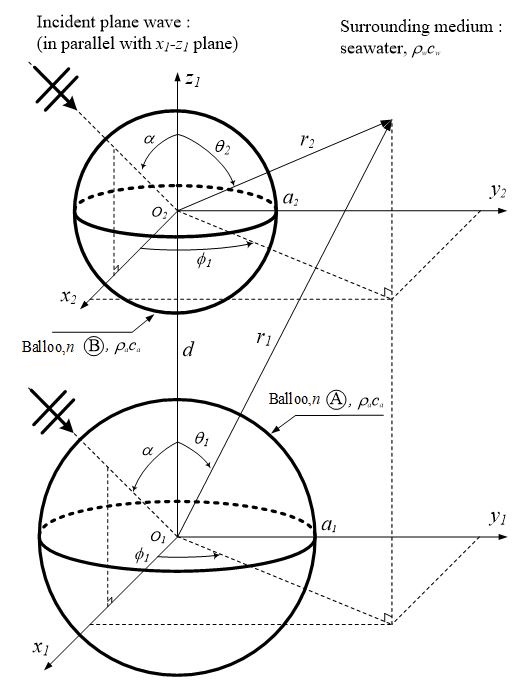
Geometrical description for the acoustic scattering of two spherical balloons. Note that the balloons are in a coaxial arrangement with z1-axis
매질의 특성은 밀도 ρ와 음속 c의 곱인 임피던스 Z =ρc 로 정의되며, k(= ω/c)는 파수(wavenumber), ω(=2πf)는 각 주파수(angular frequency, (rad/s))를 의미한다. 하첨자 w, a는 각각 물, 공기를 지칭한다.
입사파가 풍선을 가진할 때, 외부 산란파 pscat과 내부파가 발생하는데, 풍선에 의한 상쇄간섭 현상을 설명하기 위해서는 입사파와 산란파가 중첩되어 만드는 전체 압력장 ptotal(=pinc+pscat)을 기술해야 한다. 먼저, 평면파로 가정한 입사파 pinc의 일반화를 위해 전파 방향이 x1-z1(또는 x2-z1) 평면에 나란하되 z1-축과 a 만큼의 각도를 가진다고 하자. 강도 p0인 입사파에 대해, 구형조화(spherical harmonics) 함수를 이용한 모달(modal) 표현은(6),
| (1) |
이다. q는 파의 차수, hq(=jq+inq)는 q차 제1종 구형 한켈함수(q-th order spherical Hankel function of the first kind), jq는 구형 베셀(Bessel) 함수, nq는 구형 노이만(Neumann) 함수, 그리고 Pqp( |p|≤q, q≥0)는 르장드르 연관 함수(associated Legendre function)이다. 위 식에서 시간인자 exp(-iωt)는 생략되었으며, 계수 apq는 아래와 같다.
| (2) |
식 (1)은 좌표계 O1을 원점으로 하는 좌표계(r1, θ1, Φ1)에 대하서만 유효한 표현이며, 다른 좌표계(r2, θ2, Φ1)로 표현할 경우 좌표계를 의미하는 첨자 1을 2로, 그리고 위상인자 exp(ikd·cosα)를 곱해야 한다. 산란파 pscat 역시 두 좌표계에 대한 표현이 가능한데, 이때에는 덧셈정리(scalar addition theorem)(7)를 이용해야 한다. Gaunaurd et al.(8)이 얻은 결과는 O1-좌표계를 기준으로 아래와 같이 나타난다.
| (3) |
계수 bpq,1(혹은 bpq,2)는 풍선 B(혹은 A)가 존재할 때 풍선 A(혹은 B)에 의한 산란진폭(scattering amplitude)을 의미한다. 풍선 표면의 압력과, 표면에 수직한 속도 성분이 연속이라는 경계조건을 이용하면, 두 계수에 대한 선형 연립방정식을 유도할 수 있다.
| (4) |
여기서,
| (5) |
기호 ′는 괄호 속 인자에 대한 미분을, g(=ρa/ρw))와 h (=ca/cw)는 각각 상대밀도, 음속을 나타낸다. Cq(an)는 기포 상호 간 작용이 없는 상태, 즉 독립기포에 의한 산란진폭을 의미하는데, Anderson(9)이 유도한 결과와 같다. 따라서, 식 (4)에서 두 번째 항들은 풍선간 다중산란 효과를 설명한다.
이동계수 Q(pqpm)는 덧셈정리 도입에 따른 결과로서
| (6) |
와 같으며 σ는 |q-m|에서 q+m까지 2씩 증가한다. bσ(=bσ(qpmp))는 원래 두 Wigner 3-j 계수(Clebsch-Gordan 계수라고도 칭함)의 곱으로 정의되나(7), 계승(factorial)을 포함하여 많은 계산량을 요한다. 그러나, 현재 경우와 같이 풍선이 z1-축을 따라 나란한 경우, 비교적 간단한 다음의 점화식을 이용할 수 있다(10).
| (7) |
여기서,
| (8) |
이며, 두 개의 초기조건은 다음과 같다.
| (9) |
| (10) |
이제 식 (4)의 연립방정식 풀이를 각 주파수별로 반복하여 엄밀해 pscat을 구할 수 있다. 그러나, 무한 급수형태의 해 특성상 실제적인 계산을 위해서는 여러 모드를 충분히 합한 후에 수렴성을 판단해야 한다. 그 최고 차수를 Q라 하면, 식 (4)에서 고려할 항은 q=0에서 Q까지 이며, 식 (4)는 행렬크기 2(Q+1)2 × 2(Q+1)2의 표준화된 선형 연립방정식으로 구성된다. 이는 잘 알려진 LU 분해등의 기법으로 풀 수 있으나, 적정한 Q의 수준은 주파수에 따라 증가하며 당연히 연산량도 그에 따라 크게 증가한다. 한편, 이 연구에서 설정된 풍선의 동축배치에 대해, Gaunaurd et al.(8)은 이동계수 Q(pqpm)의 대칭성, 즉 Q(pqpm) = Q(-pq-pm)을 이용할 수 있음을 제안하였으며, 이 경우 행렬크기는 2(Q-|p|+1) × 2(Q-|p|+1)로 줄어들어 연산의 부담을 크게 완화할 수 있다.
3. 저주파 영역에서의 근사화
식 (3)의 엄밀해는 전 주파수 대역에서 유효하나, 산란파의 물리적 거동에 대해서는 직관을 주지 않는다. 앞에서 설명한 관심 저주파 대역에서는, q=0인 0차 모드, 즉 반경방향으로만 숨쉬는 공의 형태인 단극(monopole) 모드가 전체응답을 지배한다. 단 하나의 모드만 고려하면, 급수연산이 사라지게 되어 식 (11)과 같은 단순화가 가능하다. 우선 산락진폭은,
| (11) |
가 된다.
무차원 파수 kian, kid (i = w, a, n = 1, 2) 역시 해당 저주파수에서 ‘1’ 보다 매우 작다고 볼 수 있다. 이에 따라, 입사각과 관련된 위상인자는 exp(ikd·cosα) ≅ 1이 되고, 구형 조화함수들은 아래의 근사표현을 가진다(6).
| (12) |
위 식을 식 (5)에 대입하면, 미분이 사라진 형태의 결과를 얻을 수 있다.
| (13) |
여기서
| (14) |
는 자유공간 내 반경 an인 구형 풍선의 공진주파수를 의미하며, Minnaert(11)가 유도한 공진주파수 결과와 일치한다. 마지막으로, 0차 르장드르 연관 함수가 P00(x) ≅ 1 임을 이용하면, pscat에 대한 저주파 영역 근사화를 완성할 수 있다.
| (15) |
참고로, 0차 모드만을 고려한 근사화이므로 그 결과도 반경만의 함수로 표현됨에 주목할 필요가 있다.
식 (15)에서 괄호내의 항을 관찰하면 풍선간 이격거리 d가 증가함에 따라 상호작용 효과가 감소함을 알 수 있고, 충분히 큰 d에 대해서 식 (15)는 더욱 간소해진다.
| (16) |
즉, 상호 작용이 없는 두 풍선 산란 응답이 독립적으로 나타나며, 이를 일반화한 N개 풍선에 대해서는 다음과 같이 나타날 것을 예상할 수 있다.
| (17) |
식 (16)이 시사하는 또 다른 바는, 충분히 이격된 풍선에 대해서는 상호작용에 대한 고려없이 각 풍선에 대한 독립적 설계가 가능하다는 것인데, 풍선 설계에 대해서는 근사화의 적절함을 검증한 후에 계속하기로 한다.
이를 위해, 식 (3), (15), (16)의 세가지 모형 (편의상 각각 ‘엄밀모형(exact)’, ‘단극모드모형(monopole)’, ’비상호작용모형(no interaction)’으로 칭함)을 고려하자. 풍선의 반경 비율 a1/a2를 2로, 해수와 공기의 임피던스를 각각 1.5 × 106 Rayls, 340 Rayls로 설정하였으며, 이 경우 각 풍선의 공진주파수는 무차원 파수 kwa1을 기준으로 각각 0.0125, 0.0250의 값을 가진다. 엄밀모형의 산출을 위해 첫 10개 모드를 포함하여(Q = 9) 수렴성을 확인하였고, 두 풍선 중심(r1 = r2 = d/2)에서 응답을 관찰하였다.
Fig. 3의 첫 행은 이격거리 변화에 따른 pscat의 진폭을 비교하고 있다. 단극모드모형의 경우 이격에 상관없이 kwa1«1인 저주파 영역에서 엄밀 모형과 잘 일치하고 있다. 한편, 공진점 진폭에 있어서는 큰 차이를 보이고 있다. 이는 식 (12)의 구형조화함수 근사화로 인해 계의 감쇠 특성을 무시함에 따라, 단극모드모형이 비감쇠에 가까운 특성을 지니게 되기 때문이다. 그러나 이후에 설명하듯이, 풍선 설계는 공진 및 상쇄 간섭 ‘주파수’ 자체에만 관심이 있지 해당 진폭과는 상관없기 때문에 진폭 불일치는 큰 문제가 되지 않는다.
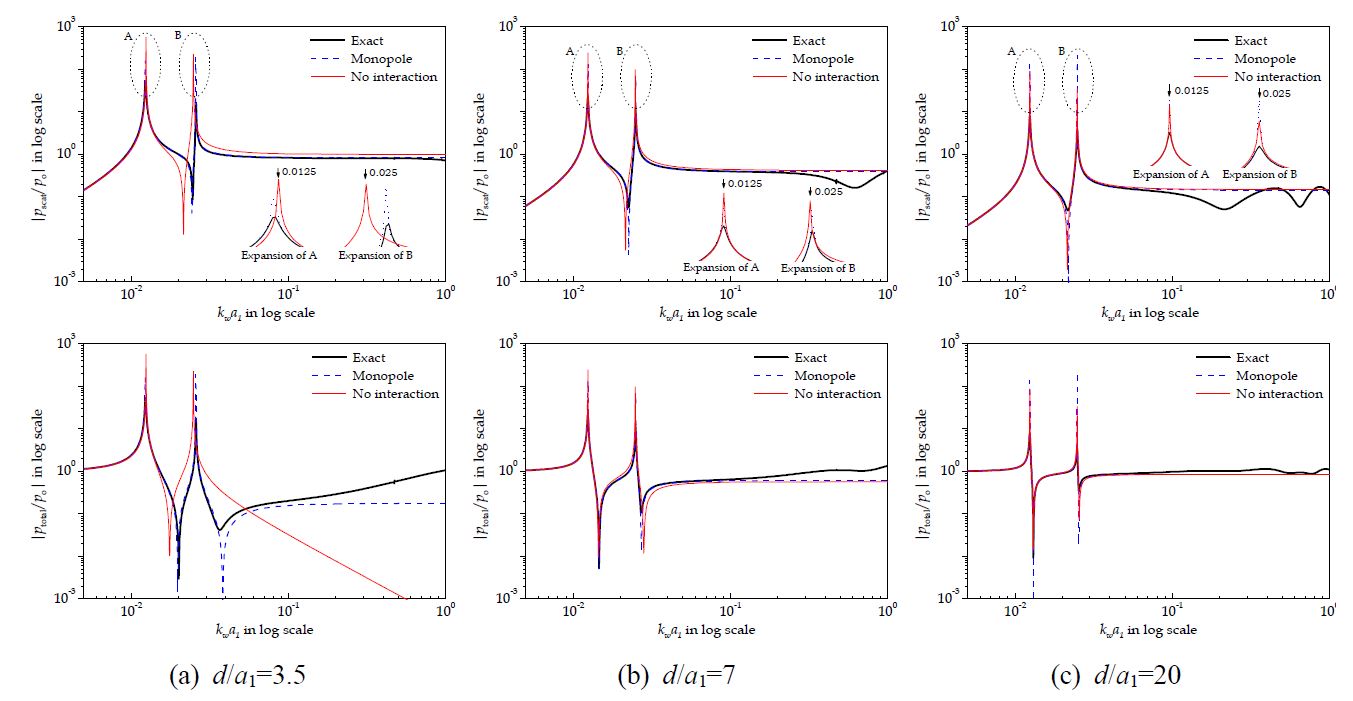
Evaluation of the scattered pressure pscat (upper row) and total pressure ptotal (lower row) by varying the separation distance; all responses were calculated at the halfway between the balloons, i.e. r1=r2=d/2
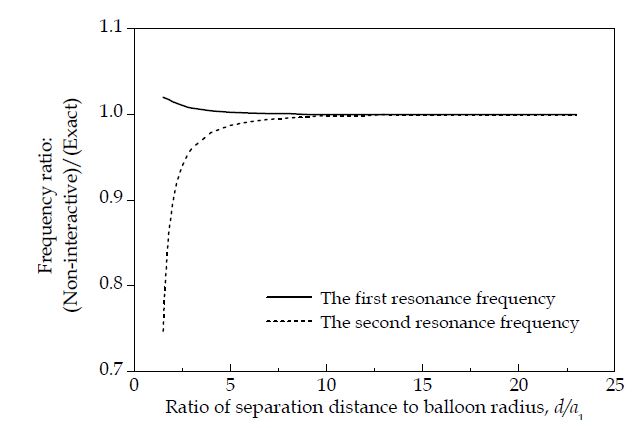
비상호작용모형은 단극모드모형에서 파생되었으므로 공진점 진폭 불일치 현상은 그대로 유지된다. 예상한 바와 같이, 이격거리가 증가할수록 좋은 근사화 결과를 얻을 수 있음을 볼 수 있다. 그러나, 풍선이 서로 가까워질수록, 첫 번째 공진주파수는 다른 두 모형에 대비하여 과대 예측되며, 두 번째 공진주파수는 반대로 과소 예측되고 있다. Fig. 4에는 이격에 따른 공진주파수의 변화를 더 자세하게 나타내었으며, 서로 근접함에 따라 공진주파수 이동현상이 더욱 심화됨을 확인할 수 있다. 이에 대한 물리적 근거는 다음과 같은 기여도 분석을 통해 설명할 수 있다.
Parametric variation of the separation distance and its effect on the change of resonance frequencies
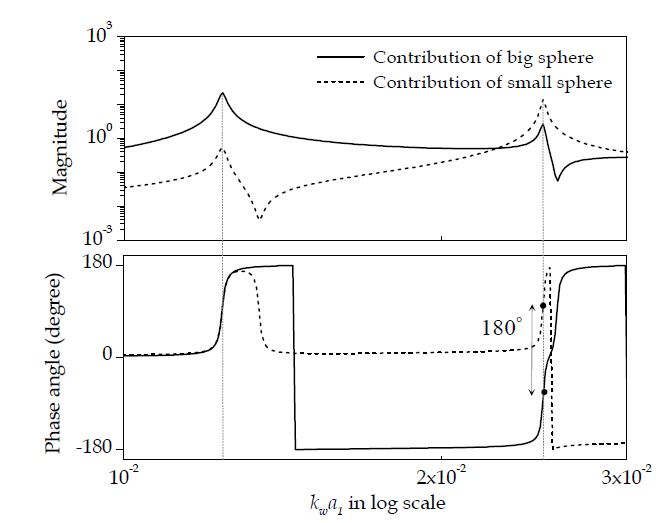
Fig. 5는 pscat에 대한 각 풍선의 기여도를 엄밀해 모형을 통해 조사한 결과이다. 큰 풍선의 기여가 주요한 1차 공진주파수 근방에서는, 위상 차이가 없음을 볼 수 있는데 두 풍선이 서로 같은 위상으로 운동하고(숨쉬고) 있음을 암시한다. 바꾸어 말하면, 두 풍선은 동시에 팽창-수축을 반복하며 주변의 유체(해수)를 가속-감속한다. 이와 같은 동시적 운동은 큰 풍선 주변에 양의 부가질량(positive added mass) 효과를 야기하며, 결국 주변의 다른(작은) 풍선이 없는 독립적인 경우보다 공진주파수가 감소하는 결과로 이어진다.
반대로, 작은 풍선의 기여가 큰 2차 공진주파수 영역에서는 반대 개념의 설명이 가능하다. 즉, 두 풍선은 서로 반대 위상으로 운동하고, 이는 작은 풍선주변의 관성을 경감시키는 음의 부가질량(negative added mass) 효과를 가져다 준다. 따라서, 큰 풍선의 영향을 받는 작은 풍선은 그렇지 않을 때보다 높은 공진주파수를 가지게 된다.
Fig. 4가 나타내는 바와 같이 이격거리가 증가함에 따라, 풍선간 상호작용에 의한 부가질량 효과가 사라지고, 공진주파수도 점차적으로 독립적인 경우로 수렴한다. 정량적으로, 무차원화된 이격거리 d/a1이 5 이상이면 비상호작용모형은 공진주파수를 2 % 이내 수준의 오차로 예측함을 알 수 있다. 이는, 풍선이 서로 너무 가깝이 있지 않는 한, 실제적인 응용 측면에서 상호작용 효과를 무시할 수 있다는 주장의 중요 근거가 된다.
4. 복수개 풍선의 설계
비상호작용모형(식 (16))을 이용하여 전체압력 ptotal에 대한 식을 쓰면,
| (18) |
와 같으며, 그 결과를 Fig. 3의 하단에 도시하였다. Fig. 6에도 개략적인 특성을 보였는데, 피크(peak)-언더피크(under peak)의 조합 두 쌍이 나타나고 있다. 이미 수식 ptotal = pinc + pscat을 통해서도 말하고 있지만, 전체적으로 ptotal은 입사파와 각 개별 풍선 응답의 선형조합으로 이루어진다. kw < kres,1인 주파수 영역에서는 첫 째항의 분자인 (kres,1/kw)2-1이 두번째 항의 그것보다는 작기 때문에, 해당 영역에서 전체응답은 큰 풍선 혹은 1차 모드가 지배하고 있다. 1차 고유주파수 kres,1을 지난 후에는 식 (18)의 첫 번째 항은 양에서 음수로의 부호 변화가 발생하지만, 여전히 전체적인 응답은 1차 모드가 지배하고 있다.
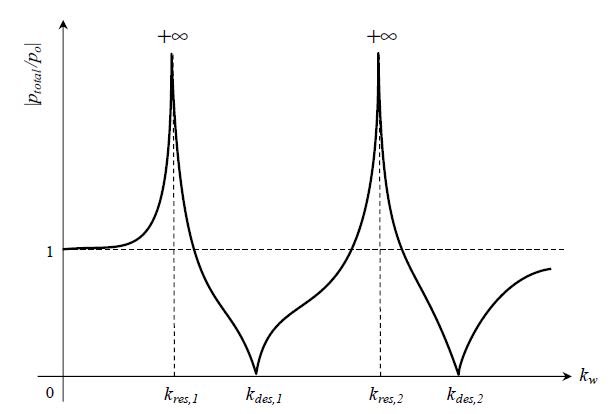
Schematic sketch of the total pressure ptotal with two balloons. As ptotal is normalized by the incident pressure p0, |ptotal/p0| < 1 means a pressure reduction with the balloons, while |ptotal/p0| > 1 an amplification
부호 변화는 큰 풍선에 의한 위상역전반사가 시작됨과, 또한 나머지 두 항과의 상쇄가 시작됨을 알리는 것이다. 이것이 바로 풍선에 의한 가진압력 저감효과를 설명하는 상쇄간섭 현상이다. Fig. 6의 첫 언더피크로 나타나듯이, 첫 항이 나머지 두 항과 완벽하게 상쇄되어 간섭효과가 최대화되는 주파수 kdes,1이 존재한다. 식(18)이 ‘0’이 되는 조건을 이용하여 그 주파수를 찾을 수 있지만, 매우 복잡한 표현을 가진다. 그러나 풍선 반지름의 비율(a1/a2)이 2 이상이라면, 작은 풍선의 기여를 무시하여 다음과 같이 간단하게 쓸 수 있다.
| (19) |
주파수가 더욱 증가함에 따라, 작은 풍선에 의한 두 번째 모드가 전체 응답을 지배하기 시작한다. 앞에 설명한 동일한 이유로 또 다른 한 쌍의 피크-언더피크 조합이 발생하며, 두 번째 최대 상쇄간섭 주파수는 다음과 같다.
| (20) |
따라서, 풍선 하나당 피크-언더피크, 즉 공진-상쇄간섭 한 쌍의 조합을 만든다고 볼 수 있으며, N개 풍선으로 확장하여 n(=1, 2, ···, N)번째 풍선에 의한 상쇄간섭 주파수는 다음과 같이 일반화할 수 있다.
| (21) |
단수 풍선 설계의 경우, 주어진 가진 주파수 ftarget과 상쇄간섭 주파수 fdes를 서로 일치시켜 상쇄간섭의 효과를 최대한으로 이용하고자 하였다(2). 또한, 다른 설계변수들 가운데 풍선의 크기가 fdes를 튜닝(tuning)하기 위한 주요 설계변수로 취급되었다. 고무재질 본연의 유연성으로 인해, 공기 충전/방출을 통해 풍선의 크기를 쉽게 변화시킬 수 있다는 점도 풍선크기를 주요 설계변수로 고려하는 또 다른 이유가 되었다.
앞 절에서 분석된 바와 같이, 풍선간 이격거리가 상호작용을 무시할 수 있을 정도로 충분하다면, 복수개 풍선의 경우에도 동일한 설계기법이 적용될 수 있다. 즉, 주어진 N개의 가진 주파수 ftarget,n (n = 1, ···, N)를 저감하기 위한 N개의 풍선은 각각 식 (21)의 fdes,n을 만족하여야 하며, 또한 각 풍선의 반경 an이 주요 설계변수로 취급된다는 것이다.
마지막으로, 공진주파수 영역에서의 가진압력 증폭에 대해서도 언급할 필요가 있다. 풍선은 익히 알려진 동흡진기 장치와 유사한 특징을 갖는다. 그러므로, 풍선 튜닝이 잘못되었거나 가진주파수가 fres,n ~ fdes,n 보다 넓은 광대역 특성을 지닐 경우, 풍선은 가진의 증폭을 초래하여 상부 구조물의 진동을 되리어 악화시킨다. 그러나, 캐비테이션이 유발하는 가진은 저주파 대역 날개통과주파수(BPF) 성분과 그 이상의 고주파 대역 광대역 소음 성분으로 크게 양분된다(12). 서론에서 기술한 바와 같이 현재 연구에서는 전자에 관심을 두고 있으며, 이는 주파수 영역에서 매우 이산적(discrete)으로 발생한다. 풍선이 가진주파수에 잘 튜닝되었다고 가정하면, 증폭될 가진 성분이 없으므로 제기된 문제로부터 자유로워질 수 있다. 물론, 풍선은 특정 대역 성분을 과도하게 증가시킬 우려가 있기 때문에, 고주파수 영역 소음 저감용으로 사용하기에는 부적합하다.
5. 결 론
프로펠러 캐비테이션이 유발하는 여러 가진주파수에 대응하기 위한 복수개 풍선 설계 기법을 이 연구를 통해 제안하고자 하였다. 풍선간 상호작용을 다루기 위한 기존의 다중산란이론이 소개되었으며, 산란현상에 대한 이해 및 설계 측면에서의 유용한 관계식을 도출하기 위해 엄밀해에 대한 저주파 영역 근사화 기법을 제안하였다. 이후, 풍선간 이격거리에 대한 매개변수분석을 통해 상호작용을 무시할 수 있는 조건을 제안할 수 있었다. 즉, 무차원화된 이격거리 d/a1이 5 이상이면 다중산란 효과를 무시하여 각 풍선의 독립적 설계가 가능하다는 것이다. 상기의 조건을 만족하는 한, 비교적 간단한 형태의 수식만으로도 복수개 풍선 설계가 가능하기 때문에, 제안된 방법은 실제 현장에서도 쉽게 적용될 것으로 기대된다.
물론, 이 연구에서 도출된 결과는 몇 가지 중요가정에 기초한 것이며, 이를 고려한 해석 예를 들어 풍선의 형상, 벽면의 고려 등이 보완될 필요가 있다. 또한, 풍선의 긍정적인 효과인 가진력 저감에 대해서만 논의하였으나, 마찰 저항 증가 등 부정적 영향에 대한 논의는 미미하였다. 이에 대한 서술은 향후의 연구 주제로 남겨두기로 한다.
Acknowledgments
이 논문은 2019년 ~ 2020년도 창원대학교 자율연구과제 연구비 지원으로 수행된 연구결과임.
References
-
Lee, J. H., Lee, K. J. and Park, H. G., 2018, Exploiting Air-bubble Reflection for Reducing Propeller Caviation Induced Hull Excitation, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 27, No. 6, pp. 730~739.
[https://doi.org/10.5050/KSNVE.2017.27.6.730]

-
Lee, J. H. and Lee, K. J., 2018, Balloon for Reducing Propeller Caviation Induced Hull Excitation, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 28, No.1, pp. 39~49.
[https://doi.org/10.5050/KSNVE.2018.28.1.039]

- Carlton, J., 2007, Marine Propellers and Propulsion(2nd edition), Butterworth-Heinemann, Oxford, UK.
-
Brunning, J. and Lo, Y., 1971, Multiple Scattering of EM Waves by Spheres, Parts I and II, IEEE Transactions on Antennas and Propagation, Vol. 19, No. 3, pp. 378~400.
[https://doi.org/10.1109/TAP.1971.1139944]

-
Strasberg, M., 1953, The Pulsation Frequency of Nonspherical Gas Bubbles in Liquids, Journal of the Acoustical Society of America, Vol. 25, No. 3, pp. 536~537.
[https://doi.org/10.1121/1.1907076]

- Morse, P. M. and Ingard, K. U., 1987, Theoretical Acoustics, Mcgraw-Hill Book Company, New York, USA
-
Felderhof, U. and Jones, R. B., 1987, Addition Theorems for Spherical Wave Solutions of the Vector Helmholtz Vquation, Journal of Mathematical Physics Vol. 28, No. 4, pp. 836~839.
[https://doi.org/10.1063/1.527572]

-
Gaunaurd, G. C., Huang, H. and Strifors, H. C., 1995, Acoustic Scattering by a Pair of Spheres, Journal of the Acoustical Society of America, Vol. 98, No. 1, pp. 495~507.
[https://doi.org/10.1121/1.414447]

-
Anderson, V. C., 1950, Sound Scattering from a Fluid Sphere, Journal of the Acoustical Society of America, Vol. 22, pp. 426~431.
[https://doi.org/10.1121/1.1906621]

-
Xu, Y. I., 1997, Fast Evaluation of Gaunt Coefficients: Recursive Approach, Journal of Computational and Applied Mathematics, Vol. 85, No. 1, pp. 53~65.
[https://doi.org/10.1016/S0377-0427(97)00128-3]

-
Minnaert, M., 1933, On Musical Air-bubbles and Sounds of Running Water, Philosophical Magazine, Vol. 16, No. 104, pp. 235~248.
[https://doi.org/10.1080/14786443309462277]

-
Pereira, F. A., Felice, F. D. and Salvatore, F., 2016, Propeller Cavitation in Non-uniform Flow and Correlation with the Near Pressure Field, Journal of Marine Science and Engineering, Vol. 4, No. 4, p. 70.
[https://doi.org/10.3390/jmse4040070]


Jeung-Hoon Lee received B.S. degree in Mechanical Engineering from Hanyang Univ. in 2001, M.S. and Ph.D. degrees from KAIST in 2002 and 2007, respectively. After industrial experiences in SSMB of Samsung Heavy Industries Co. Ltd. for 9 years, he in 2016 joined the department of mechanical engineering of Changwon National Univ. as associate professor. His research interest includes several fields such as air-spring, acoustic cavitation and etc.