기저선 변동 제거를 위한 정수 계수 고역 통과 디지털 필터의 개선

2.1 정수계수 고역 통과 필터

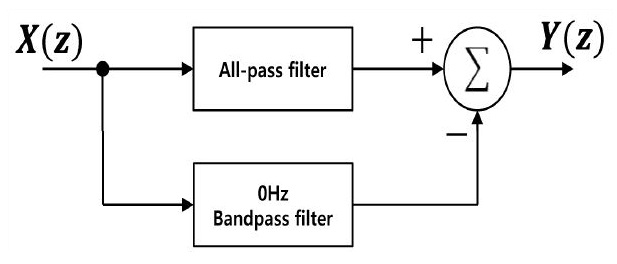
고역 통과 필터는 Fig. 1에서 보인 바와 같이 선형위상 전역 통과 필터에서 동일 위상의 0 Hz 중심주파수를 가지는 대역 통과 필터를 빼서 설계할 수 있다⁽³⁾.

Fig. 1

High pass filter design method suggested by Lynn

대역 통과 필터가 선형위상을 갖게 하기 위해 z평면의 단위 원 위에 영점을 균일한 간격으로 분포시키고, 통과시키고자 하는 주파수 위치에 극점을 배치하여 영점을 상쇄시킴으로써 극점에 해당하는 주파수만 통과시키도록 하였으며. 이때 필터의 전달함수는 z-평면에서 식 (1)과 같이 쓸 수 있다.

이때 m은 단위 원에 분포되는 영점의 수이며, p와 t는 각각 단위 원 상의 영점 개수와 극점 개수와 관계되는 필터의 차수로 필터 차수의 증대는 필터 이득과 측엽의 감쇠를 증가시킨다. θ는 단위원에서 극점의 위치를 의미한다.

필터의 계수가 정수가 되도록 하기 위해서는 θ의 위치가 0°, ±60°, ±90°, 120°, ±180°로 제한된다. 고역 통과 필터 설계를 위해서는 밴드패스 필터의 중심주파수가 0 Hz가 되어야 하므로 θ를 0°로 제한하고 단위원 상의 극점수와 영점수를 일치시키기 위하여 p와 2t를 k로 통일 하는 경우 식은 (2)와 같이 간소화된다.

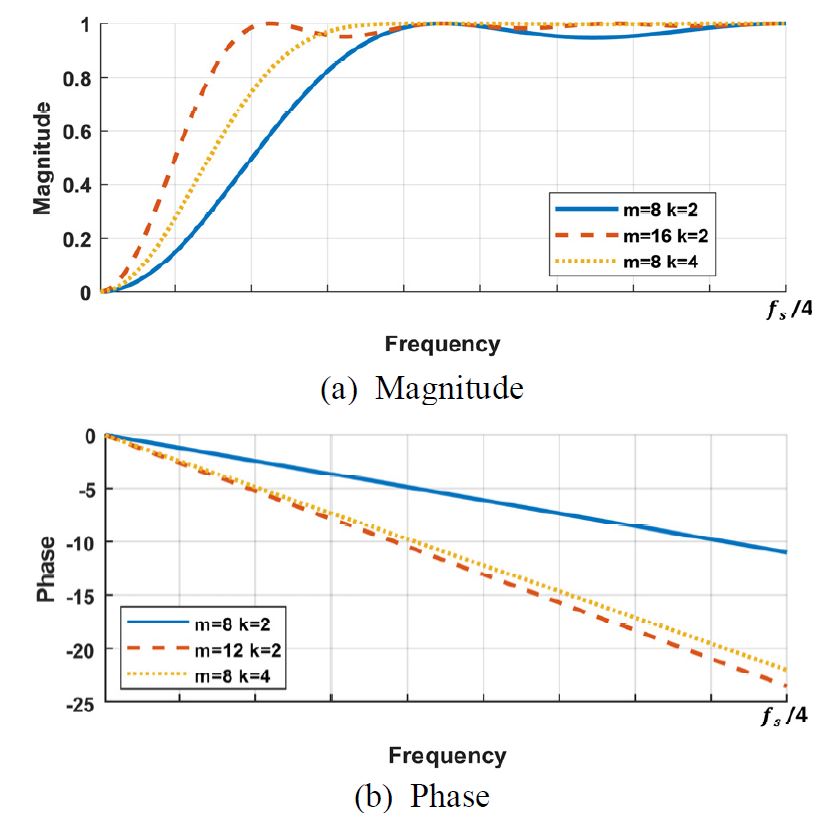
여기서 m은 영점 수이고 k는 필터 차수이다. z-평면의 전달함수를 주파수 식으로 표현하여 나타내는 경우 전달함수, 진폭 및 위상은 각각 식 (3), (4) 및 (5)와 같다. 필터의 진폭은 영점 수와 필터 차수에 의해 Fig. 2(a)와 같이 나타나며 Fig. 2(b)와 같이 모든 영점 수와 필터 차수에서 완전한 선형 위상을 가진다.

Fig. 2

Variation of the response of 0 Hz bandpass filter with m and k

설계된 0 Hz 대역 통과 필터와 같은 필터 이득과 위상을 가지는 전역 통과 필터를 식 (6)과 같이 나타낸다.

Fig. 1의 구조와 같이 전역 통과에 0 Hz 대역 통과 필터를 선형적으로 빼 설계한 고역 통과 필터의 전달함수는 식 (7)로 나타낼 수 있다.

설계된 고역 통과 필터의 진폭과 위상 특성은 식 (8)과 식 (9)와 같다.

필터의 진폭은 영점 수와 필터 차수에 의해 Fig. 3과 같이 나타나며 식 (9)와 같이 모든 영점 수와 필터 차수에서 완전한 선형 위상을 가진다.

Fig. 3

Variation of the response of high pass filter with m and k

설계된 고역 통과 필터는 0 Hz 대역 통과 필터와 동일한 차단주파수를 가지며 영점 수와 차수에 의해 차단 대역이 좁아지며 필터가 첨예해지는 것을 Fig. 2와 Fig. 3으로부터 확인 할 수 있다.

3.1 추가시간지연을 통한 필터 설계 이론

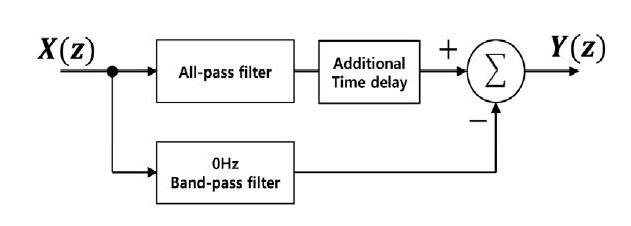
이 연구에서는 Fig. 4와 같이 전역 통과 필터에 추가로 시간지연효과를 주어 대역 저지 필터의 저지 대역을 좁히는 방법에 대해 제시한다. 전역 통과 필터에 추가시간지연 τ를 삽입할 때의 전달함수는 식 (10)과 같다.

Fig. 4

High pass filter design method with additional time delay

Fig. 4의 설계 구조와 같이 식 (3)으로 나타나는 0 Hz 대역 통과 필터를 식 (10)으로 나타나는 전역 통과 필터에 뺌으로써 나오는 고역 통과 필터는 식 (11)과 같다.

추가시간지연이 부과된 고역 통과 필터의 진폭과 위상은 식 (12)와 식 (13)과 같이 나타낼 수 있다.

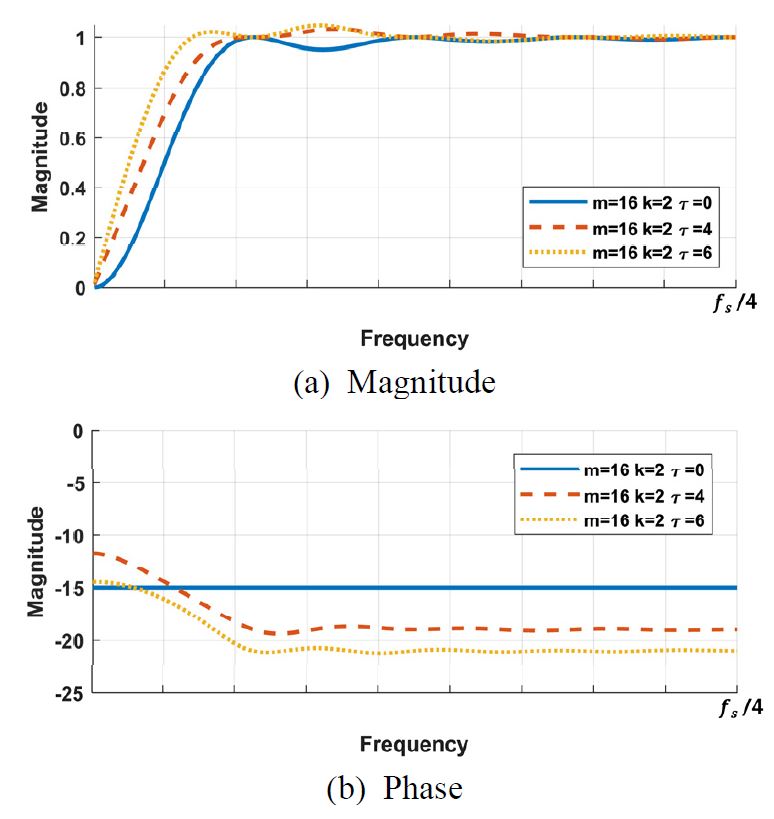
설계된 고역 통과 필터의 진폭은 부과된 추가시간 지연 τ에 따라 Fig. 5(a)와 같이 나타난다. 시간지연이 추가로 전역 통과 필터에 부과됨에 따라 설계된 고역 통과 필터의 차단 대역이 좁아지며 필터가 첨예해지는 것과 리플이 증대되는 것을 확인할 수 있다. 시간지연에 의한 필터의 비선형성을 확인하기 위해 필터의 위상 변동을 식 (14)와 같이 정규화해 위상 변동을 천이되는 sample 수로 Fig. 5(b)에 나타내었다.

Fig. 5

Variation of the response of high pass filter with the additional time delay (τ)

Fig. 6

Representation of the magnitude characteristics of high pass filters

추가시간지연이 부과되는 경우 차단주파수 중심인 0 Hz로부터 위상변동이 발생하며, 이후 통과 대역 부근에서 점차 줄어들어 작은 변동 폭을 가지는 것을 확인할 수 있다.

3.2 m, k, τ 파라미터에 대한 진폭 특성

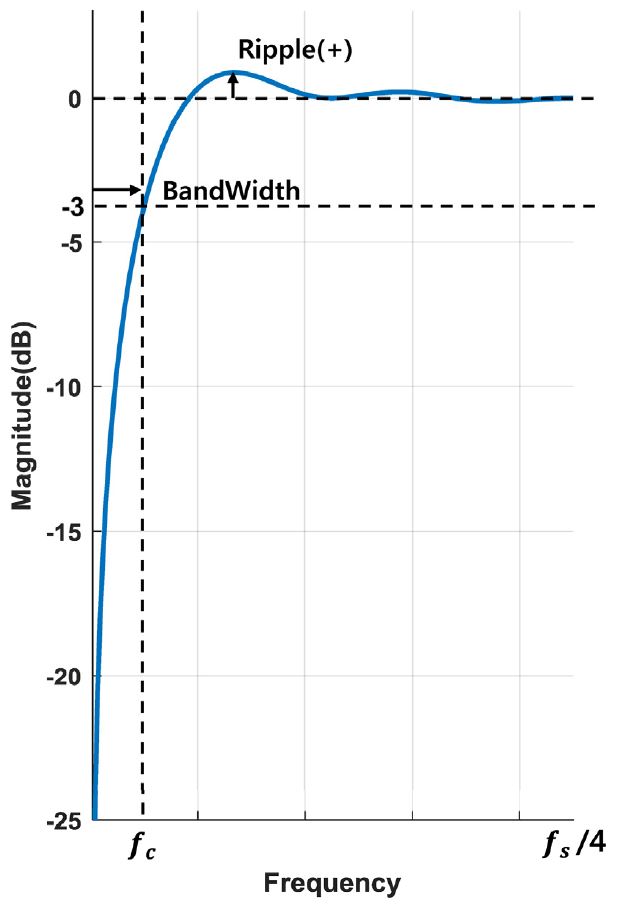
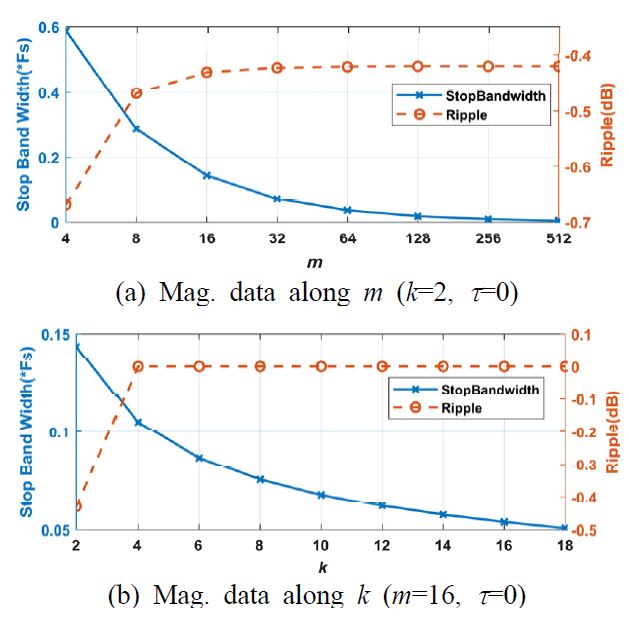
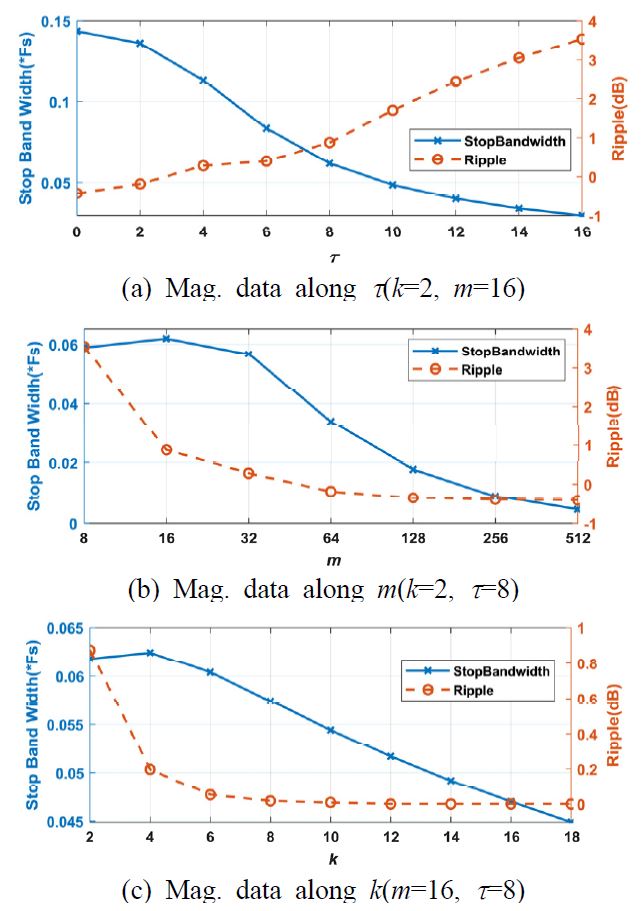
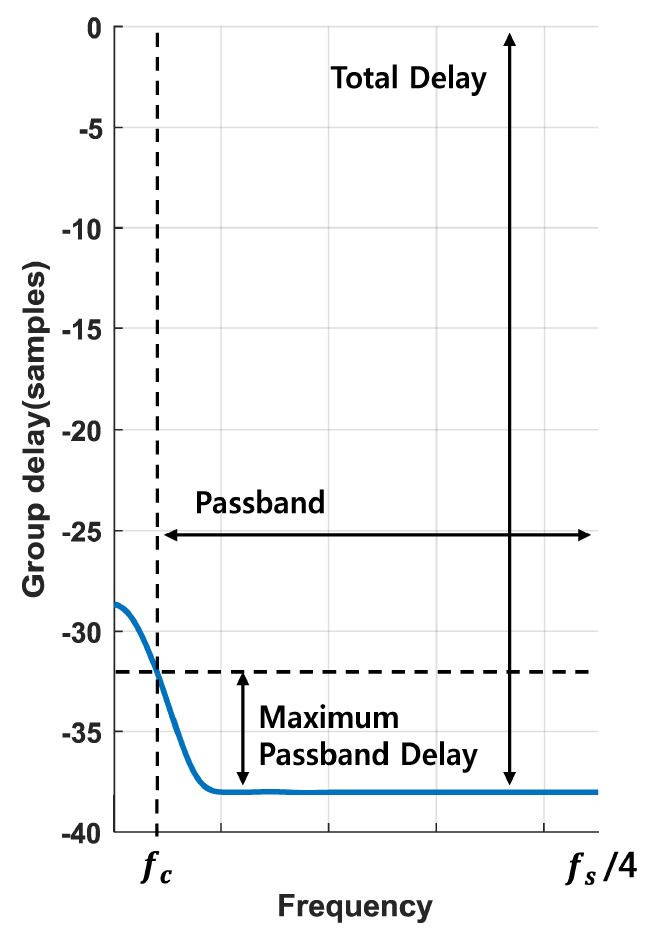
영점 분포 m, 필터 차수 k, 추가시간지연 τ에 대한 고역 통과 필터의 진폭 특성을 저지 대역 폭과 리플의 크기로 나누어 수치해석적으로 제시하였다. 정의되는 저지 대역의 폭과 리플은 Fig. 7과 같이 나타낸다. 저지 대역의 폭은 중심 주파수로부터 –3 dB 감쇠가 일어나는 차단주파수까지의 폭으로 한다. 통상적으로 리플은 출렁거림 현상이 일어나는 전체 폭을 기준으로 얘기하나, m, k, τ에 따라서 리플을 상승시키거나 아래로 하강시키는 영향을 달리 보이므로 정확한 현상 표현을 위해 0 dB를 기준으로 양과 음의 값으로 제시한다. 영점 수, 필터 차수, 시간지연의 독립적인 영향을 관측하기 위하여 3가지 파라미터를 하나의 독립변수와 두 개의 통제변수로 지정을 하고 저지대역 폭과 리플의 최대 변동 폭을 종속변수로 하여 각각의 영향을 나타내었다. 각 파라미터가 통제변수로 지정되는 경우에 양상이 잘 나타날 수 있는 최소 변수값을 기준으로 각각 m=16, k=2, τ=8에 고정하였다. 시간지연이 없을 때(τ=0)의 m, k의 영향에 대해서 Fig. 7에 나타내었으며, 시간 지연이 있을 때의 m, k, τ의 영향에 대해서 Fig. 8에 나타내었다.

Fig. 7

Effects of m and k on the bandwidth and ripple of the high pass filter with no time delay

Fig. 8

Effects of τ, m and k on the bandwidth and ripple of the high pass filter with time delay

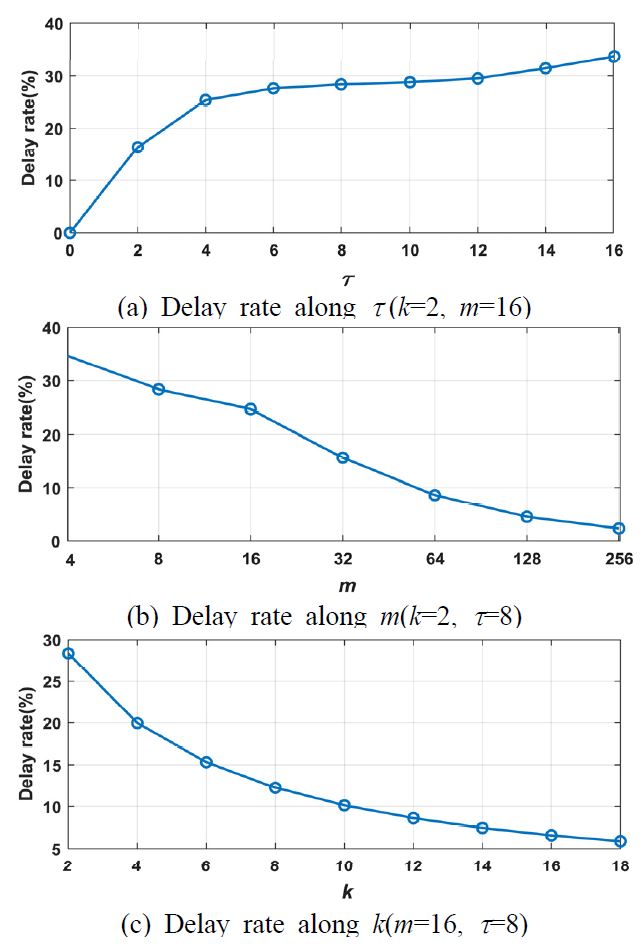
시간지연이 없는 경우 m과 k가 상승할 때 저지 대역폭은 좁아지면서 대역 저지 필터를 첨예하게 만드는 것을 Fig. 7에서 확인할 수 있다. 또한 Fig. 7(a)에서 영점 수 m이 작을 때 0 dB 아래로 하강하는 리플이 발생하나 이후 m이 증가하면 할수록 리플이 –0.42 dB 부근으로 수렴하는 것을 확인 가능하고 Fig. 7(b)에서 차수 k가 증가하는 경우에 리플이 0 dB로 수렴하는 것을 확인할 수 있다. 이러한 경향은 m, k가 증가할 때 설계에 이용되는 0 Hz 대역 저지 필터의 부엽이 감소함으로써 나타난다. 시간지연이 있는 경우에 대한 m, k, τ 파라미터의 영향은 Fig. 8과 같다. Fig. 8(a)에서 시간지연 τ가 커짐에 따라 저지 대역이 좁아지며 리플이 양의 방향으로 증가하는 것을 확인할 수 있다. 시간지연이 있을 때도 시간지연이 없는 경우와 마찬가지로 m과 k가 상승할 때 저지 대역의 폭은 좁아지면서 대역 저지 필터를 첨예하게 만든다. 시간지연 τ에 의해 양의 방향으로 상승한 리플은 m, k가 커지면서 줄어들게 된다. 시간지연이 없을 때까지와 마찬가지로 m에 의해 0 dB보다 약간 낮은 –0.42 dB 근방에 수렴하는 것을 Fig. 8(b)에서 확인 가능하며, k에 의해 0 dB로 수렴하는 것을 Fig. 8(c)에서 확인 할 수 있다. 이는 m, k가 커짐에 따라 필터 이득이 커져 시간지연 τ에 의한 리플 증가의 영향이 줄어들기 때문이다. 따라서, 시간 지연이 있는 경우와 없는 경우 모두 m, k가 커짐에 따라 리플의 절대 크기가 줄어드는 방향으로 수렴하는 것을 확인 능하다.

3.3 m, k, τ 파라미터에 대한 위상 특성

식 (9), 식 (13)과 Fig. 5(b)를 확인할 때, 시간지연이 없는 경우 위상은 완벽한 선형을 이루게 되고 시간지연이 생기는 경우 선형위상에 비선형 위상변동이 추가되는 것을 확인할 수 있다. 비선형성을 확인하기 위해 군지연으로 나타내는 경우 시간지연량을 샘플 수로 정규화가능하다. Fig. 9와 같이 시간지연에 의해 발생하는 군지연위상의 변동은 대역 저지 필터의 중심 주파수에서 최대가 되고 이후 통과 대역 부근으로 갈수록 줄어들게 된다. 통과 대역 내에서의 최대 왜곡을 확인하기 위해 전체 군지연과 차단주파수에서의 군지연의 비율로 군지연 변동률을 식 (15)와 같이 제시하였다. 제시된 군지연 변동률은 시간지연의 효과로 인해 총 지연되는 샘플 개수의 비를 의미한다. 통과 대역 내 최대 군지연 변동률에 대한 m, k, τ 파라미터의 영향을 Fig. 11에 수치해석적으로 제시하였다. 수치해석적으로 영향을 제시하는 과정에서의 독립변수, 통제변수 및 종속변수는 3.2절에서 진폭특성을 나타내는 경우와 동일하게 하였다.

Fig. 9

Representation of the group delay characteristics

Fig. 10

Effects of τ, m and k on the distortion rate of the high pass filter with time delay

Fig. 11

Panel impact detecting system

Fig. 10으로부터 영점 수, 필터 차수, 추가시간지연이 위상 변동에 미치는 영향을 확인 가능하다. 추가시간지연 τ가 커짐에 따라, 통과 대역 내의 최대 군지연 변동률이 증가하는 것을 Fig. 10(a)에서 확인 가능하다. m, k가 상승함에 따라 전체 시간지연량이 증가해 위상지연에 따른 군지연 변동이 차지하는 비중이 줄어들어 최대 군지연 변동률이 감소하는 것을 Fig. 10(b)에서 확인할 수 있다. 만약 영점 수와 필터 차수를 적절히 증가시키는 경우 군지연 변동률을 효과적으로 감소시켜 통과 대역 위상을 거의 선형에 근접하게 가지도록 하는 필터의 설계가 가능하다. 또한, 필터의 특성상 추가시간지연에 의해 발생한 위상 왜곡은 통과 대역으로 가면서 빠르게 감소하여 이후 주파수 영역에서 근사 선형을 이루게 되므로 목표로 하는 신호를 최소한의 왜곡으로 필터링하는 것이 가능하다.

4.1 신호 특성

제안된 필터가 기존 선형 위상 정수계수 필터에 대해 메모리, 곱 연산수, 필터 지연량에서 어떤 차이를 가지는지 보이기 위해 충격감지 알고리듬의 기저선 변동 제거에 적용하여 비교하였다.

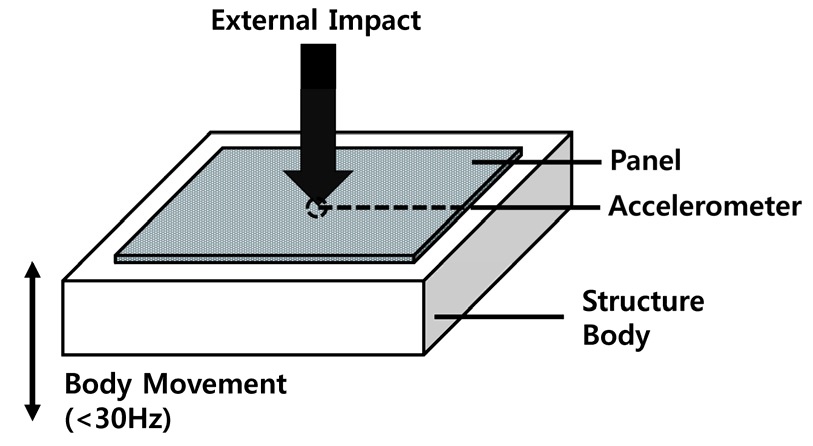
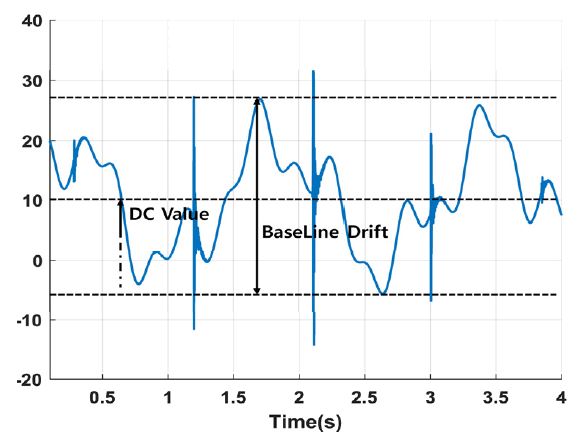
구조물에 대하여 패널에 가해지는 충격의 크기를 비교하는 경우를 Fig. 11에 나타내었다. 시스템은 구조물과 구조물 상부에 위치한 패널로 구성되어 있으며 패널에 부착된 가속도 센서가 외부에서 들어오는 충격의 크기를 실시간으로 계측한다. 30 Hz 아래의 주파수를 가지는 본체의 움직임에 의해 기저선 변동이 존재하는 경우 신호는 Fig. 12와 같이 충격 신호의 크기를 구분하는 데 영향을 준다. 충격에 의한 패널의 응답을 정확하게 받아드리는 시스템을 설계하기 위해서는 고역 통과 필터를 통한 저주파 잡음 제거를 필요로 한다.

Fig. 12

Low-frequency noise of the impact signal

4.2 고역 통과 필터 설계

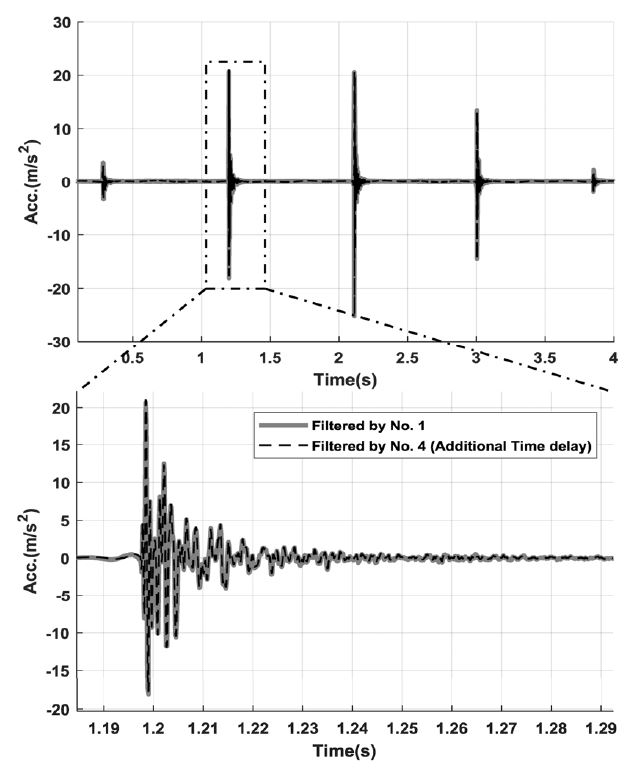
패널에 가해지는 충격의 크기를 정확하게 계측하기 위해서 저주파 잡음 대역을 제거하며 통과 대역 리플의 크기를 제한한 필터 요구 조건을 Table 1에 나타내었다. Table 1에 제시된 설계 요구 조건을 만족하는 6개 필터 설계안의 차단주파수, 리플, 메모리, 곱 연산 수, 필터 탭 수, 지연 시간을 Table 2에 나타내었다. 영점 수는 연산 효율성을 위해 2의 제곱수로 하고 필터 차수는 설계 조건에 의해 2의 배수로 제한하였다. 메모리는 요구되는 필터를 설계할 때 변수 공간 수로 나타내었으며, 영점 수에 의해 결정되는 소요 신호 길이와 필터 차수에 의한 필터 계수의 합이다. 곱 연산수는 필터 차수에 의해 증가하는 필터 계수의 수이고 필터 탭 수는 필터의 최대 군지연 샘플 수와 동일한 크기를 가진다. 추가시간지연이 없는 설계군은 1번, 2번, 3번이며 추가시간지연 τ를 도입함으로써 4번, 5번, 6번의 3가지 설계 후보군을 추가로 제시할 수 있다.

Table 1

High pass filter design requirements

Table 2

Filter design candidates

4.2 기저선 변동 제거 결과

Fig. 12에 제시되어있는 입력파형에 대하여 필터링을 수행하였다. Table 2에 제시된 설계 후보군은 각각 기존 설계법과 제안하는 설계법으로 설계되었으며, 각각 최소 영점 수, 최소 필터 차수, 최소 시간 지연량에서 Table 1의 설계 요구 조건을 만족한다. 각 설계 변수의 곱 연산, 필터 탭 수, 메모리 등의 연산성능 비교는 Table 2에 제시하였으며, 필터링의 결과로 기저선이 제거된 입력파형은 Fig. 13에서 확인 가능하다. 공통적으로 시간지연 τ가 추가될 경우 더 낮은 차수 또는 영점 수에서 요구되는 차단 주파수를 만족 시킬 수 있다. 시간 지연이 추가된 4번 필터는 설계 후보군 중 최소 곱 연산 수 및 최소 지연시간을 가지며 5번 필터의 경우 소요 메모리를 최소로 가져, 각각 추가시간지연이 없는 기존 설계에 대비하여 약 38 % 낮은 delay time과 약 30 % 낮은 메모리에서 설계요구 조건을 만족하였다. 군지연 변동률에 의한 파형 왜곡을 고려하여 군지연 변동률을 30 %로 제한하였으므로 시간지연이 추가되더라도 전체 탭 수의 절반 이상을 초과하는 시간지연 변동률은 없다. 추가시간 지연에 의한 파형 왜곡을 확인하기 위해 군지연 변동률이 없는 완전 선형 필터인 1번 필터와 군지연 변동률이 가장 큰 4번 필터에 대한 필터링 결과를 비교하였다. Fig. 13와 같이 4번 필터 설계안으로 필터링 된 충격 신호의 각 피크 점들을 확인한 결과 완전 선형 필터인 1번 필터의 필터링 결과와 모든 peak에 대해 근접하였다. 0 Hz 주파수에서 최대로 발생한 군 지연 변동은 통과 대역에서 급격하게 감소하므로, 목표로 하는 신호가 차단 주파수에서 떨어져 있을 경우 완전 선형 필터와 동일하게 사용 가능하며, 근접한 경우에도 허용수준 이하로 경감시키는 경우에 근접 선형 필터로의 활용이 가능하다.

Fig. 13

The impact signal filtered by HPF