순환정상성을 이용한 캐비테이션 초생 속도 분석기법 연구

1. 서 론

최근 함정 스텔스 성능 향상을 위한 수중방사소음(URN, underwater radiated noise) 관련 연구가 활발히 진행 중이다. 특히, 고속항해 시에 지배적으로 나타나는 캐비테이션 소음은 음향탐지체계에 의한 피탐 확률을 크게 증가시킬 뿐만 아니라 자함 추진기와 관련된 음향징표를 적에게 제공할 수 있기 때문에 캐비테이션이 발생하기 시작하는 캐비테이션 초생 속도(CIS, cavitation inception speed)를 정확하게 추정하기 위한 연구들이 수행되었다^(1,2).

일반적으로 캐비테이션 초생 속도 분석을 위해 데몬 신호처리 기법(DEMON, detection of envelope modulation on noise)과 속도에 따른 음압준위분석(SPL, sound pressure level)을 주로 활용한다⁽³⁾. 하지만, 데몬 신호처리 기법은 특정 대역의 진폭변조 성분만을 확인할 수 있다는 한계점이 있고, 음압준위 분석은 외부 및 순간소음의 영향을 받을 경우 정확한 분석이 어렵다는 단점이 있다.

따라서 기존 캐비테이션 초생 속도 분석 방법의 한계점을 해결하기 위하여 필터 뱅크(filter bank)를 적용한 후 자기상관기를 이용한 데몬 신호처리를 수행하는 방법⁽⁴⁾이 연구되었다. 이 방법은 함정 수중방사소음과 상관관계가 없는 외부 및 순간소음을 억제하여 진폭변조 성분의 식별율을 향상시키는 장점이 있지만, 미리 정해진 각각의 필터 뱅크의 포락선을 구한 후 평균을 취하기 때문에 기존 데몬 신호처리 기법과 같이 특정 대역의 진폭변조에 대한 정보만을 얻게 된다. 이와 유사하게 속도에 따른 연속 웨이브렛 변환(CWT, continuous wavelet transform)을 수행한 후 캐비테이션 현상으로 인해 연속적인 임펄스 열(impulse train)이 발생하는 시점 및 주파수 대역을 선정하여 데몬 신호처리를 수행하는 연구를 수행한 바 있다⁽⁵⁾. 이 분석방법은 특정 주파수 대역의 진폭 변화뿐만 아니라 시간에 따라 변하는 캐비테이션 소음의 주파수 특성을 고려할 수 있기 때문에 보다 정확한 캐비테이션 초생 속도 추정이 가능하다. 하지만 연속 웨이브렛 분석 결과에서 변화가 뚜렷하게 나타나지 않을 경우, 이 분석방법 또한 데몬 신호처리를 위한 대역 선정에 어려움을 가진다. 마지막으로 함정 내 변조 성분 식별을 위하여 순환정상성을 이용한 연구⁽⁶⁾한 바 있었다. 이 연구는 캐비테이션 초생 속도 추정을 위한 연구는 아니었지만, 기존 데몬 신호처리와 달리 수신된 신호 전체의 주기성을 한 번에 확인할 수 있으므로 데몬 신호처리보다 변조 성분에 대한 판단 및 식별의 용이성을 향상시켰다. 따라서 이 논문에서는 데몬 신호처리 과정을 보완한 방법을 대신하여 측정된 수중방사소음에 포함된 순환정상성(cyclostationary)을 검출함으로 함정의 캐비테이션 초생 속도를 추정하는 분석기법을 제안하였다.

이 논문은 2장에서 순환정상성 검출 방법에 대하여 간단히 설명한 후 3장에서 순환정상성을 이용한 캐비테이션 초생 속도 추정기법을 제안한다. 4장에서 해상실험을 통하여 제안 분석기법의 우수성을 검증하였고 그 후 마지막으로 결론을 기술하였다.

2. 순환정상성 분석 방법

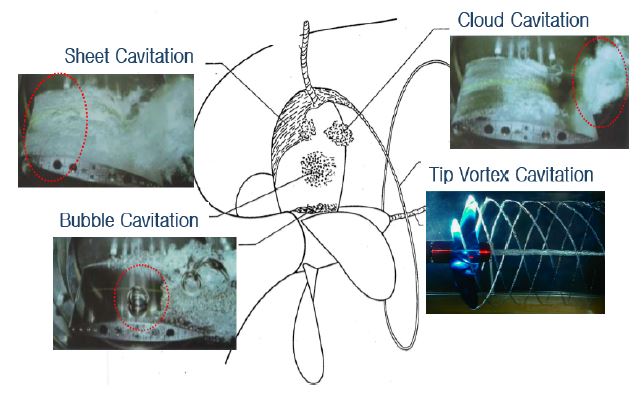
일반적으로 함정 캐비테이션 소음은 압력 변화로 인하여 발생된 공동(cavity)이 파열하면서 발생하는 강한 폭발성 소음이 기계류 장비의 회전운동으로 인해 발생된 토널성 소음을 변조시키게 된다. 이때 공동의 발생 위치 및 크기에 따라 발생되는 광대역 소음의 주파수 특성이 달라진다. 해군함정의 경우, 대체로 추진기의 날개 끝 보텍스 캐비테이션(tip vortex cavitation)이 가장 먼저 발생하는데, 날개 끝에서 생성된 공동은 일반적으로 크기가 작아 높은 주파수 대역에서 광대역 소음이 약하게 확인된다. 반면 고속에서 주로 발생하는 기포형 캐비테이션(bubble cavitation)의 경우 날개 끝 보텍스 캐비테이션에 비해 공동이 크기 때문에 비교적 낮은 주파수 대역에서 강하게 나타나게 된다⁽⁷⁾. 즉, 캐비테이션의 발생 위치에 따라 광대역 소음 특성이 달라질 뿐만 아니라 진폭변조 성분이 발생하는 주파수 대역 또한 변하게 된다. 따라서 특정 대역의 포락선만을 이용하는 데몬 신호처리 기법은 변조 성분의 주파수 대역 특성을 한 번에 확인하기 어렵다. 따라서 이 논문에서는 수신된 소음의 주기뿐만 아니라 공동으로 인해 발생된 광대역 소음의 에너지 분포를 동시에 확인할 수 있는 순환정상성 검출 방법을 이용하여 캐비테이션 초생 속도를 추정하였다.

먼저 순환정상성을 이용하여 수신된 소음의 주기적인 특성을 추정하기 위하여 스펙트럴 상관 밀도 함수(spectral correlation density function)을 이용하였다. 스펙트럴 상관 밀도 함수는 다음과 같이 정의된다⁽⁸⁾.

여기서 α는 순환 주파수(cyclic frequency)를, τ는 지연(lag)을 나타낸다. 그리고 $$ R_x^{\alpha }\left(\tau \right)$$는 순환자기상관함수(cyclic autocorrelation function)를 의미하며 다음과 같이 나타낼 수 있다⁽⁹⁾.

여기서 ∆t는 측정 샘플 간 시간 차이를 나타낸다. 즉, 수신된 신호 x(t)가 특정 주기를 가지는 신호라면 x(t)의 자기상관함수 R_x(t,τ) 또한 x(t)와 동일한 주기를 가지게 된다. 따라서 해당 순환 주파수에서 R_x(t,τ)의 푸리에 계수에 해당되는 순환자기상관함수를 구한 후 푸리에 변환 후 정규화를 수행하면 위너-킨친 정리(Wiener-Khinchine theory)에 의해서 해당 순환 주파수에 대한 에너지 분포를 주파수 영역에서 구할 수 있게 된다⁽⁶⁾. 그 결과 연속적인 순환 주파수에 대하여 스펙트럴 상관 밀도 함수를 구함으로 수신된 수중방사소음에 포함된 변조 주파수뿐만 아니라 반송파 주파수 대역까지 추정할 수 있다⁽¹⁰⁾.

3. 순환정상성을 이용한 캐비테이션 초생 속도 분석 결과

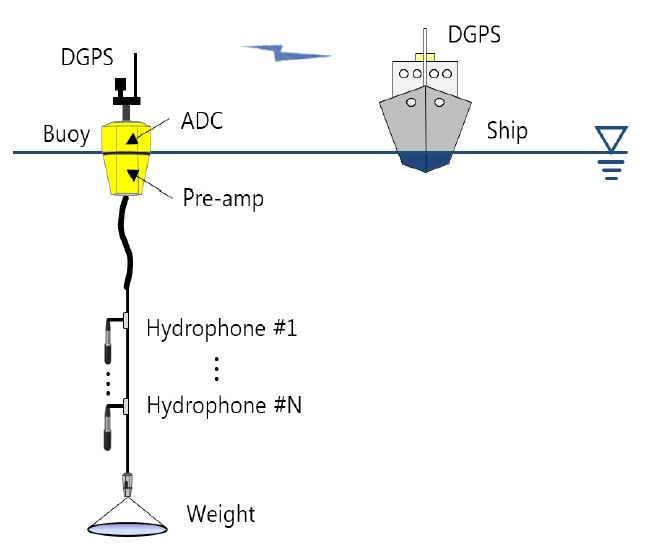
먼저 함정의 수중방사소음을 측정을 위한 시험 구성은 Fig. 2와 같으며, 측정에 사용된 부이(buoy)는 Fig. 3에서 확인할 수 있다. 이때 캐비테이션 초생 시에 발생하는 미세한 변화를 감지하기 위해 수신감도가 높은 하이드로폰(B&K 8106)을 사용하였고, 고주파수 대역의 변화를 확인하기 위하여 표본 추출 비율(sampling rate)이 높은 아날로그―디지털 변환기(ADS 1672)를 이용하였다. 그리고 높은 이득(gain) 조절을 위해 전치증폭기를 자체 제작하였다. 제작된 전치증폭기는 0 dB에서 40 dB까지 5단계로 조절이 가능하며, 전체 고조파 왜곡(THD, total harmonic distortion)이 약 –95 dB의 성능을 가진다. 마지막으로 측정된 데이터는 DGPS(differential global positioning system)에서 계산된 거리와 함께 저장된다. 시험 항목은 LP(lever position) 단계별로 증속하며 측정하였다.

Fig. 1

The classification of propeller cavitations depending on a cavity occurrence location

Fig. 2

Test environment of underwater rrdiated noise measurement

Fig. 3

Underwater radiated noise measurement buoy

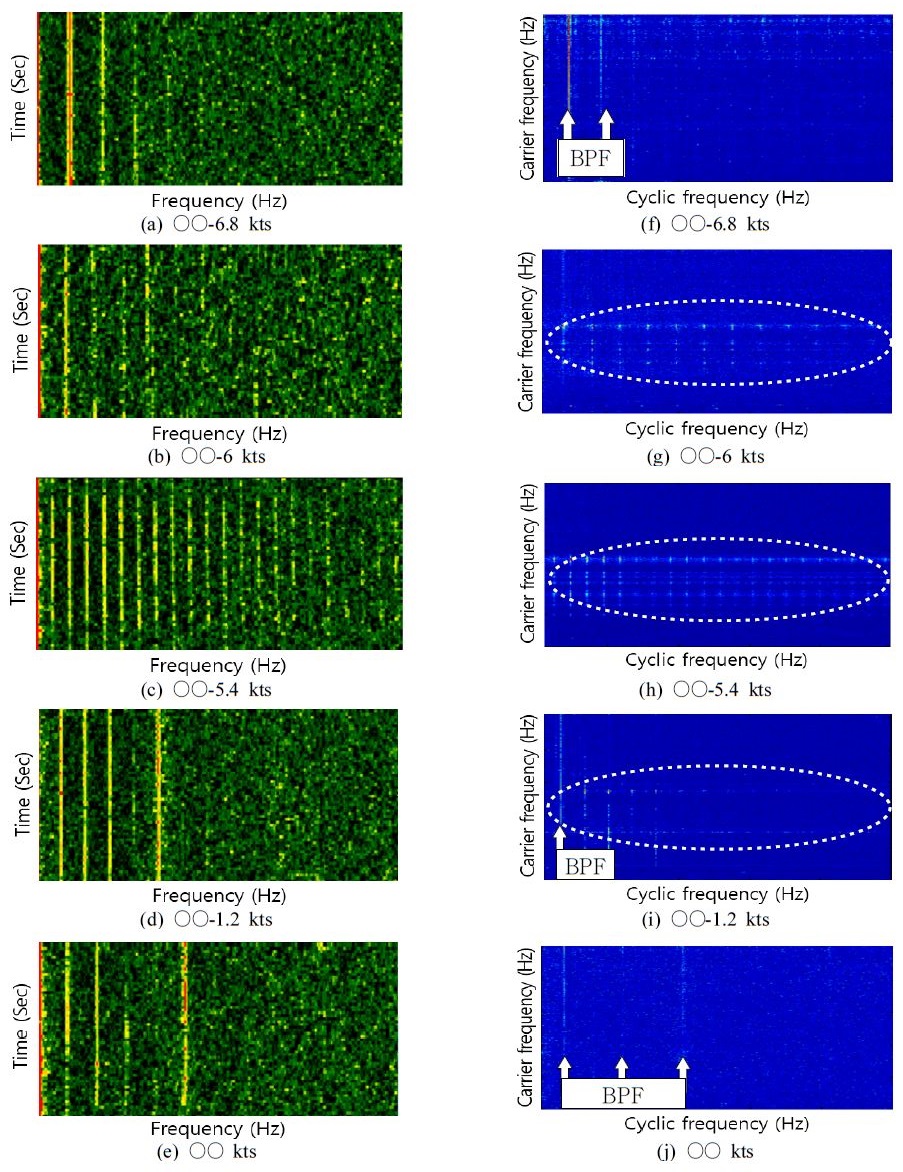
Fig. 4는 위 측정환경 하에서 실제 함정에 대하여 측정된 수중방사소음을 데몬 신호처리 및 순환정상성 분석결과이다. 이 논문에서는 시험항목 중에서 이전 측정에서 관측된 캐비테이션 초생 속도(○○노트) 이하 5개 속력구간에 대한 결과만을 수록하였으며 그래프의 가로축 및 세로축의 정보는 함정의 음향징표를 제공할 수 있기 때문에 제외하였다.

Fig. 4

DEMON and cyclo-stationarity analysis results according to the ship speed

데몬 신호처리 결과(Fig. 4(a)∼(e))에서는 날개 통과 주파수(BPF, blade passage frequency)의 배수(harmonic)에 해당하는 주파수 성분이 모든 속력구간에서 나타난다. 따라서 위 경우 데몬 신호처리 결과만을 이용하여 캐비테이션 초생 속도 산출하는 것은 매우 어려운 문제이다.

반면, 순환정상성 분석 결과(Fig. 4(f)∼(j))에서는 데몬 신호처리 결과와 유사하게 날개 통과 주파수 성분이 측정된 모든 속력구간에서 확인되나, 반송파 주파수(carrier frequency) 영역에서 보면 속력에 따라 날개 통과 주파수 성분이 존재하는 주파수 대역이 변경되는 것을 확인할 수 있다. 구체적으로 Fig. 4 (f)에서는 흰색 화살표로 표시된 날개 통과 주파수 성분이 모든 반송파 주파수에서 강하게 확인되는 것과 반대로 Fig. 4(g)∼(i)에서는 흰색 점선으로 표시한 부분과 같이 특정 반송파 주파수에서만 날개 통과 주파수와 동일한 주기의 배수로 발생함을 확인할 수 있다. 그 후, Fig. 4(i)의 그래프에서는 Fig. 4(g)∼(h)에서와 같이 특정 반송파 주파수에서 발생하는 성분뿐만 아니라 Fig. 4(f)에 확인된 성분과 같이 모든 반송파 주파수에서 확인되는 성분도 약하게 발생한다. 마지막으로 Fig. 4(j)에서는 다시 Fig. 4(f)와 동일한 추세의 그래프가 나타난다. 이때 공동에 의해서 발생한 소음은 매우 넓은 주파수 대역에서 발생함으로 Fig. 4(g) ∼ (i) 그래프에서 흰색 점선으로 표시된 성분은 캐비테이션이 아닌 감속기어 또는 축과 관련된 진폭변조 성분으로 판단되며, Fig. 4(f)에서 확인되는 성분은 가변 피치 프로펠러(CPP, controllable pitch propeller) 활용에 따른 현상으로 사료된다⁽¹¹⁾. 따라서 날개 통과 주파수 성분이 공동소음으로 인해 진폭변조가 발생하는 캐비테이션 초생 속도는 ○○-1.2 노트로 내외로 추정된다. 이때 낮은 피치율(pitch ratio)로 인한 저속에서의 캐비테이션 현상 및 발생속도 또한 함정 방사소음 관리에 있어 매우 중요한 요소이나, 아직 공식적인 기준이 미비하여 이 논문에서는 다루지 않았다.

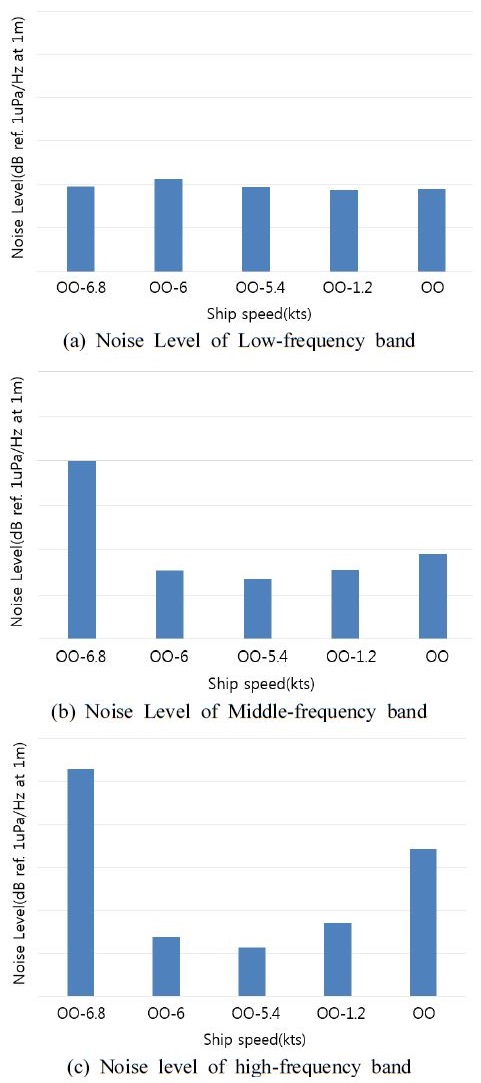
Fig. 5는 증속 시에 주파수 대역별 소음준위의 변화를 나타낸 그래프이며, 여기서 그래프의 한 눈금은 5 dB를 나타낸다. 먼저, Fig. 5(a)는 증속시 저주파수 대역의 소음준위 변화를 나타낸다. 그래프에서 확인할 수 있듯이 속력이 증가함에도 저주파수 대역 소음준위는 거의 일정한 것을 확인할 수 있다. 이는 저주파수 대역에서는 캐비테이션 초생 속도로 인한 소음변화보다 함정 기계류 소음성분이 크게 발생함으로 전체 소음준위에서는 큰 변화가 없는 것으로 추정된다. 이와 반대로 고주파수 대역 소음준위 변화를 나타낸 Fig. 5(c) 그래프에서는 앞서 순환정상성 분석에서 추정한 캐비테이션 초생 속도(○○-1.2 노트) 주변에서 소음준위가 급격하게 증가되는 것을 확인할 수 있다. 일반적으로 캐비테이션 발생 시에는 고주파수 대역의 소음준위가 급격하게 증가된다는 것을 고려했을 때 ○○-1.2 노트에서 캐비테이션이 발생했다는 추정을 뒷받침하는 근거로 볼 수 있다. 추가적으로 저속에서 소음준위가 높게 확인되는 지점(○○-6.8 노트) 또한 순환정상성 분석과 동일함을 확인할 수 있다. 그리고 고주파수와 저주파수 사이 대역에서는 Fig. 5(b)의 그래프와 같이 캐비테이션으로 인한 소음준위가 변화가 고주파수 대역보다는 보다 더 완만하게 이루어지는 것을 확인할 수 있었다.

Fig. 5

Noise level according to frequency bands

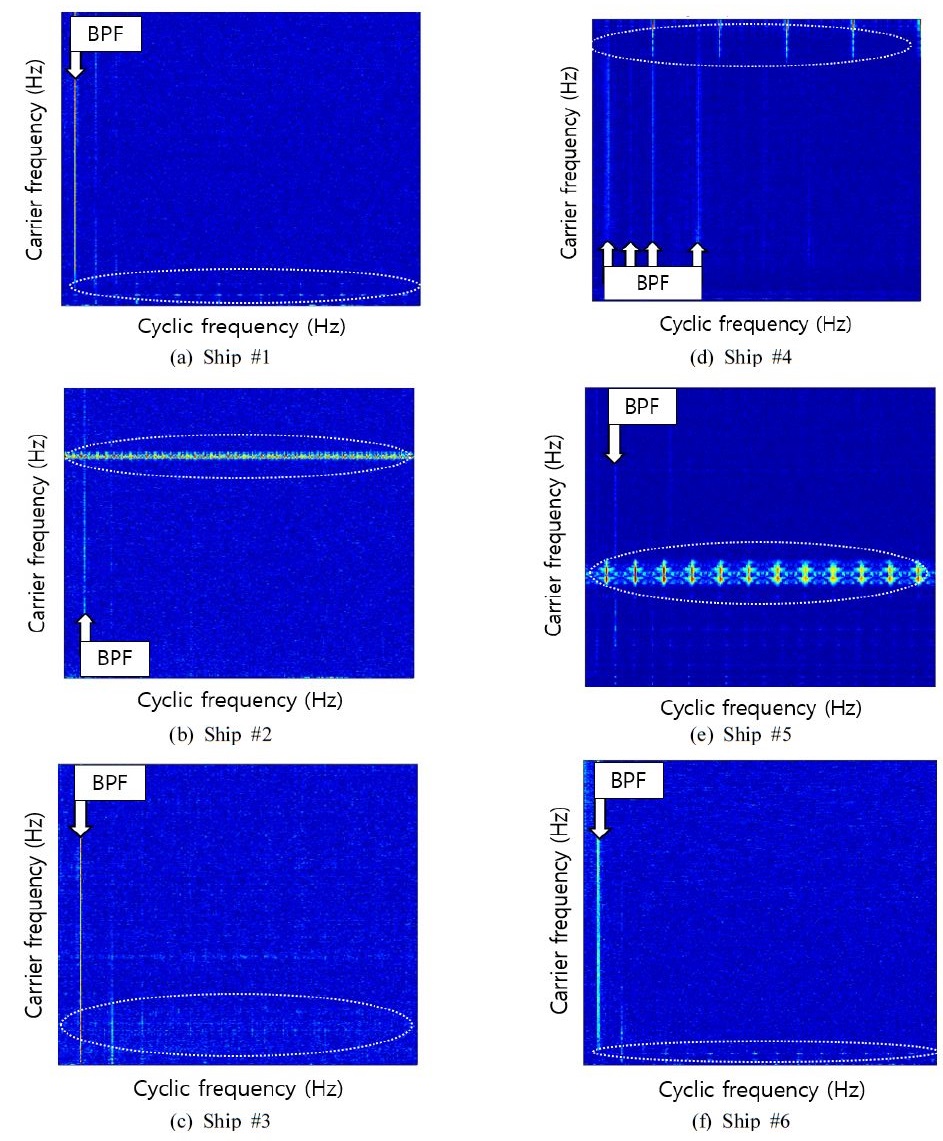
마지막으로 Fig. 6은 위와 동일한 방법으로 측정된 21척의 함정 중에서 추진기 변조성분 이외의 별도의 변조성분이 발생하는 6척의 순환정상성 분석 결과를 나타내고 있다. 이때 개별 그래프의 속력 구간은 그래프마다 조금씩 다르지만 캐비테이션 초생 속도 주변의 속력 구간으로 선정하였다.

Fig. 6

Cyclo-stationarity analysis results of various ships

그 결과, Fig. 6(a)∼(f) 그래프에서 추진기 캐비테이션에 의해 발생된 날개 통과 주파수 성분은 모든 반송파 주파수에서 강하게 확인되는 반면 추진기 변조성분 이외의 별도의 변조성분들은 특정 반송파 주파수에서만 확인된다. 즉 실제 해상실험들에서도 순환정상성 분석을 통하여 추진기 캐비테이션의 의한 변조성분과 그 외의 변조성분을 구별할 수 있게 되었고 이를 통하여 보다 정확한 추진기 캐비테이션 초생 속도 추정이 가능해졌다.

위 실험내용들을 요약하면 캐비테이션 초생 속도 분석에 순환정상성을 이용하게 되면 반송파 주파수 특성을 확인할 수 있으므로 다른 장비의 변조성분으로 인하여 캐비테이션 초생 속도를 오검출할 가능성이 줄어들 뿐만 아니라 추진기 캐비테이션으로 발생한 날개 통과 주파수 특성에 대한 이해를 높일 수 있을 것으로 판단된다.

4. 결 론

이 논문은 함정 캐비테이션 초생 속도 분석을 위하여 순환정상성을 이용하는 방법을 제시한 후에 실제 해상실험을 통해 제안 방법의 유효성을 검증하는 과정을 거쳤다. 또한 추가적으로 다수의 함정에 대하여 추가 분석을 수행하여 제안된 순환정상성 분석의 유용함으로 증명하였다. 이 연구를 바탕으로 향후 가변 피치 프로펠러 사용시 발생하는 저속 캐비테이션 감소대책에 대한 연구를 수행할 예정이다.

References

• Song, I. H., Ahn, J. W., Kim, K. S. and Moon, I. S., 2000, Characteristics of Cavitation Noise on High-Speed Propellers, Journal of the Society of Naval Architects of Korea, Vol. 37, No. 2, pp. 22~29.
• Ahn, B. K., Lee, C. S., Yu, Y. W. and Moon, I. S., 2007, Prediction of the Propeller Face Cavity Inception and Experimental Verification, Journal of the Society of Naval Architects of Korea, Vol. 44, No. 5, pp. 467~473. [https://doi.org/10.3744/SNAK.2007.44.5.467]
• Lee, P. H., Ahn, B. G., Lee, C. S. and Lee, J. H., 2011, An Experimental Study on Noise Characteristics of Propeller Cavitation Inception, Journal of the Society of Naval Architects of Korea, Vol. 48, No. 1, pp. 1~7. [https://doi.org/10.3744/SNAK.2011.48.1.1]
• Lim, J. S., Hong, W. Y. and Pyeon, Y. G., 2014, Hidden Period Estimation in the Broad Band Propeller Noise Using Auto-correlation and Filter-bank Structure, Journal of Korea Information and Communications Society, Vol. 39B, No. 8, pp. 538~543. [https://doi.org/10.7840/kics.2014.39B.8.538]
• Lee, H. C., Kim, T. H., Sohn, K. and Lee, P. H., 2017, Cavitation Noise Detection Method Using Continuous Wavelet Transform and DEMON Signal Processing, Journal of the KIMST, Vol. 20, No. 4, pp. 505~513.
• Lee, H. C., 2017, Study on Classification of Modulated Noise Sources in a Naval Vessel Using Cyclo-stationarity, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 27, No. 6, pp. 790~797. [https://doi.org/10.5050/KSNVE.2017.27.6.790]
• Lecoffre, Y., 1997, Cavitation Bubble Trackers, A. A. Bakema Publishers.
• Antoni, J., 2009, Cyclostationarity by Examples, Mech. Syst. Signal Process, Vol. 23, pp. 987~1036. [https://doi.org/10.1016/j.ymssp.2008.10.010]
• Kim, S. Y., Lee, H. C., Choi, J. Y. and Oh, J. S., 2017, Study on the Analysis of Cavitation Inception Speed Using Hull Vibration, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 27, No. 5, pp. 602~607. [https://doi.org/10.5050/KSNVE.2017.27.5.602]
• Napolitano, A., 2012, Generalizations of Cyclo-stationary Signal Processing: Spectral Analysis and Applications, Wiley & Sons. [https://doi.org/10.1002/9781118437926]
• Bertetta, D., Brizzolara, S., Gaggero, S., Viviani, M. and Savio, L., 2012, CPP Propeller Cavitation and Noise Optimization at Different Pitches with Panel Code and Validation by Cavitation Tunnel Measurements, Ocean Engineering, Vol. 53, No. 15, pp. 177~195. [https://doi.org/10.1016/j.oceaneng.2012.06.026]