달팽이관 필터뱅크 및 ZCPA 청각모델에 기반한 두 귀의 시간차 추정기법
‡ Recommended by Editor Jun Hong Park
© The Korean Society for Noise and Vibration Engineering
Abstract
This study presents a method for estimating interaural time difference (ITD) by modeling the human auditory system. The proposed model simulated the response of the human inner ear by signal processing. The response of the cochlea consists of the mechanical vibration of the basilar membrane and the neural transduction of the inner hair cells. The traveling waves on the basilar membrane were represented by a cascade of digital filter sections that function as a series of bandpass filters. We mimicked the neural firing pattern from the inner hair cells by the zero-crossings with peak amplitudes (ZCPA) auditory model in which frequency information of the signal is obtained by zero-crossing intervals. Zero-crossings have been used to find noise-robust speech features. The ITD between two channels was estimated by obtaining the ZCPA pattern of each channel and then calculating an interaural cross-correlogram by center frequencies between the two patterns. We examined the feasibility of the proposed method by simulation, in which binaural speech signals were mixed with normally distributed noise. As a result, the proposed method was able to provide an accurate estimate of ITDs and was robust to Gaussian noise.
Keywords:
Interaural Time Difference, Cochlear Filter Bank, ZCPA Auditory Model, Human Auditory System키워드:
두 귀의 시간차, 달팽이관 필터뱅크, ZCPA 청각모델, 인간의 청각계1. 서 론
오늘날 인간-기계 상호작용 관련 분야 중에서 가장 빠르게 발전하고 있는 기술 중 하나가 음성인식이다. 최근 음성인식 기술은 인공지능과 결합하여 다양한 분야에서 활용되고 있으며 산업적으로 고부가가치의 기술로 성장하고 있다. 그러나 잡음 환경으로 인한 인식성능 저하는 사용자로 하여금 불편을 느끼게 하고 음성인식기능의 사용을 꺼리게 하는 원인이 되고 있다. 따라서 잡음 환경에서 화자의 위치 파악을 통한 전처리 과정은 잡음 환경에 강인한 음성인식을 위해 필수적이다(1).
화자, 즉 음원의 위치를 추정하는 방법으로 머리전달함수(head related transfer function, HRTF) 데이터베이스를 이용한 방법(2), 다수의 마이크로폰 배열을 이용한 빔형성(beamforming) 방법(3,4), 음향 인텐시티(sound intensity) 추정을 통한 음향 인텐시티 방법(5) 그리고 다수의 마이크로폰 배열을 이용한 음향 홀로그래피(acoustic holography) 방법(6) 등이 제안되고 있다. 머리전달함수 방법은 소수의 마이크로폰 만을 사용하여 음원의 위치를 추정할 수 있는 장점이 있지만, 마이크로폰 장착부에 대한 머리전달함수를 모든 머리 형상에 대해 직접 측정해야 하는 번거로움과 이를 저장하기 위해 많은 저장공간을 필요로 하는 단점이 있다. 빔형성 방법은 다수 음원의 위치를 추정할 수 있다는 장점이 있지만, 마이크로폰의 수에 따라 추정 가능한 음원의 수가 결정되므로 다수의 마이크로폰이 필요한 단점이 있다. 음향 인텐시티 방법은 탐침으로 측정된 음압 및 입자속도로 벡터량인 음향 인텐시티를 추정하여 음원의 위치를 추정하는 방식으로, 저주파 음원 추정의 경우 빔형성 방법에 비해 측정 장치의 크기가 작다는 장점이 있으나 고주파 음원 추정의 경우 센서의 간격에 의해 측정 가능한 고주파의 한계가 제한되는 단점이 있다. 마지막으로 음향 홀로그래피 방법은 임의의 음원으로부터 방사되는 음장을 재현함으로써 음원의 위치를 파악하는 방식으로서 1회의 측정으로 음장을 분석할 수 있는 장점이 있으나 마이크로폰 배열을 사용해야 하기 때문에 다수의 마이크로폰이 필요하고 데이터 처리가 길며 대용량의 저장공간을 필요로 하는 단점이 있다. 이와 같은 음원의 위치 추정 방법들은 고용량의 데이터베이스가 필요하거나 다수의 마이크로폰 및 많은 연산량이 요구되기 때문에 음성인식기술이 적용되는 소형 단말기에 적용하기에는 제약이 많다.
따라서 최소의 마이크로폰으로 음원의 위치를 추정하기 위해서 인간의 청각계(human auditory system)를 고려해 보았다. 인간의 청각계는 현재 개발되어 있는 어떠한 음향 감지 시스템 보다 더 좋은 성능을 보이고 있다. 또한 인간의 청각 기관은 초소형으로 넓은 영역의 신호를 고감도로 감지할 수 있는 최적화된 구조를 가지고 있다. 그러므로 이 연구에서는 잡음 환경에서 최소의 입력 채널로 화자의 위치를 추적하기 위해, 인간의 청각계를 모사한 청각모델(auditory model)을 사용하여 두 채널 간의 두 귀의 시간차(interaural time difference, ITD)를 추정하는 기법을 제안하고자 한다.
2. 인간의 청각계 및 청각모델
2.1 인간의 청각계
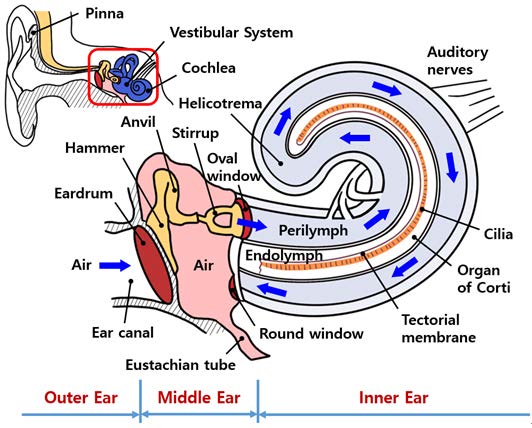
인간의 청각계는 Fig. 1과 같이 외이(outer ear), 중이(middle ear) 그리고 내이(inner ear)로 분류된다.
외이는 우리의 눈으로 볼 수 있는 청각계의 최 외각에 있으며, 귓바퀴(pinna), 외이도(ear canal), 고막(eardrum)을 포함한다. 귓바퀴는 소리를 모아 외이도로 안내할 뿐만 아니라, 그 모양은 소리에서 방향 정보를 추출하는 데 도움이 된다. 외이도는 약 2.5 cm 길이의 관이며, 1/4 파장의 공명기 역할을 한다. 그래서 인간 청력의 최대 감도 영역이 이 파장에 해당 하는 3400 Hz 주변에서 형성된다. 외이도를 통과한 소리는 고막을 통해 음향 에너지에서 진동 에너지로 변환되어 중이로 전달된다.
중이는 고막과 달팽이관(cochlea) 사이에 있으며, 귓속뼈(auditory ossicle), 즉 망치뼈(hammer), 모루뼈(anvil), 등자뼈(stirrup)로 이루어져 있고, 아래쪽으로 이관(Eustachian tube)이 인두(pharynx)로 연결되어 외기와 통한다. 귓속뼈의 주요기능은 외이의 고막과 내이의 난원창(oval window) 사이에서 임피던스 정합을 하는 것이다. 고막 이전의 매질은 기체인 공기 이지만 난원창 이후의 매질은 액체인 림프액(lymph)이기 때문에 두 매질 간의 밀도 차가 커서 결과적으로 큰 임피던스 차가 발생한다. 그럼에도 불구하고 귓속뼈의 지렛대 작용으로 고막에서 난원창으로 전달되는 힘은 약 1.3배 커진다(7). 그리고 고막의 면적은 55 mm2, 난원창의 면적은 3.2 mm2로 약 17배의 면적 차이가 난다. 따라서 고막에서 난원창으로 전달되는 압력은 약 22배가 된다. 결과적으로 고막과 난원창 사이에 임피던스 정합이 이루어지게 되는데, 특히 음성 대역인 300 Hz ~ 3000 Hz에서 에너지 전달이 극대화된다.
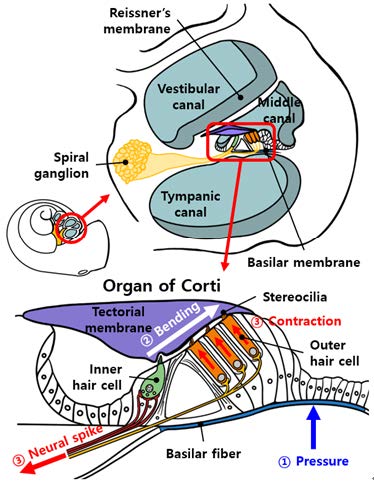
내이는 청각계에서 가장 복잡한 기관으로 청각 기관인 달팽이관과 평형 감각 기관인 전정계(vestibular system)로 구성되어 있다. 달팽이관의 해부학적 구조는 Fig. 2와 같다.
달팽이관은 나선형으로 2.75바퀴 꼬여져 있으며, 그 외곽은 뼈로 둘러싸여 있다. 달팽이관 내부에는 세 개의 관이 있는데, 각각 전정계(vestibular canal or scala vestibuli, SV), 중앙계(middle canal or scala media, SM), 고실계(tympanic canal or scala tympani, ST) 이다. 전정계와 고실계는 달팽이관의 맨 꼭대기에 있는 나선구멍(helicotrema)으로 연결되어 있으며 내부에 외림프액(perilymph)으로 차있다. 그리고 중앙계는 내림프액(endolymph)으로 차있다. 전정계와 중앙계는 전정막(Reissner’s membrane)으로 구분되어 있으며, 중앙계와 고실계는 기저막(basilar membrane)으로 구분되어 있다. 기저막은 대략 20 000개 ~ 30 000개의 기저섬유(basilar fiber)로 이루어져 있으며 달팽이관 꼭대기로 갈수록 길이가 길어지고 굵기는 감소한다. 참고로, 기저막의 폭은 난원창 근처에서 가장 좁고(0.08 mm ~ 0.16 mm) 달팽이관 꼭대기에서 가장 넓어지며(0.42 mm ~ 0.65 mm), 강성은 기저섬유의 굵기가 얇아져서 100배 이상 감소한다. 따라서 기저막은 난원창 근처에서 고주파에 공진하고, 달팽이관 꼭대기에서 저주파에 공진한다. 중앙계에는 코르티 기관(organ of Corti)이 있는데, 기저막의 진동을 능동적으로 증폭시키는 외유모세포(outer hair cell, OHC)와 증폭된 기저막 진동에 반응하여 청각 신호를 발생시키는 내유모세포(inner hair cell, IHC)로 구성된다. 내유모세포는 달팽이관의 길이방향으로 한 줄로 배열되어 있으며 개수는 약 3500개이다. 외유모세포는 3줄 ~ 4줄로 배열되어 있으며 개수는 약 12 000개이다. 각 유모세포는 상단에 부동섬모(stereocilia)가 있으며, 하단으로 신경 섬유와 연결되어 있다. 그리고 부동섬모 위에 덮개막(tectorial membrane)이 있다.
달팽이관의 난원창에 전달된 압력 변화가 청각 신호로 변환되어 청신경(auditory nerve)으로 전달 되는 과정은 다음과 같다. 난원창의 진동으로 압력 구배가 형성되면, 압력파가 진행파(traveling wave)의 형태로 전정계를 거쳐 고실계로 전파된다. 이때, 특정 공진 대역의 기저막이 Fig. 2와 같이 압력에 의해 위로 들리면 부동섬모들이 덮개막에 의해 꺾이면서 유모세포들을 작동시킨다. 외유모세포는 전기운동적 변환(electro-mobility transduction, EMT) 과정을 통해 수축하여 기저막을 들어올림으로써 그 진폭을 증폭시킨다. 그리고 내유모세포는 증폭된 기저막의 기계적 진폭을 전기적 신호로 변환하여 청신경으로 발화한다. 반면에, 기저막이 아래로 내려가면 부동섬모가 구부러지지 않아 신경 발화가 일어나지 않는다. 따라서, 청각 신호는 반파 정류된 신경 가시(neural spike) 형태로 기저막의 각 공진 부위별로 발화된다. 이것은 마치 실시간의 단시간 푸리에 변환(short-time Fourier transform, STFT)과 같다. 각 대역별 청각 신호 열은 그후 나선 신경절(spiral ganglion)을 통해 뇌줄기(brainstem)를 거쳐 청각 피질(auditory cortex)로 전달된다. 또한 고실계를 통과한 잔여 압력파는 원창(round window)을 수동 방사기(passive radiator)처럼 가진 시켜서 달팽이관의 외부인 중이에서 그 에너지가 소멸된다.
2.2 인간의 청각모델
인간의 청각 기관은 초소형, 고효율, 고감도의 최적화된 구조를 지닌 감각기관으로, 이를 모사하여 구현할 경우 새로운 개념의 인공청각기구, 각종 음향센서 그리고 음성인식 등에 활용할 수 있다. 따라서 이를 모사하기 위한 다양한 청각모델(auditory model)이 개발되어 왔다.
Flanagan은(8) Békésy에 의해 측정된 생리학적 데이터를 바탕으로 청각 메커니즘에 대한 수학적 계산 모델을 제안하였다. 그의 청각모델 대상은 중이(middle)와 기저막(basilar membrane)이었다. 그는 중이와 기저막이 수동적이고 선형적으로 진동한다고 가정하여 전달함수로 모델링하였고, 기저막의 공진 특성을 Constant-Q 필터뱅크(filter bank)로 근사화 하였다. Lyon과 Mead는(9) 아날로그 전자 달팽이관 모델을 개발하였는데, 관측된 매체의 특성을 기반으로 달팽이관의 유체-동적 파형 매체(fluid-dynamic wave medium)를 직렬의 필터로 모델링하였다. 또한 외유모세포의 작용은 자동 이득 제어(automatic gain control, AGC)로, 내유모세포의 기능은 반파 정류기(half-wave rectifier)로 각각 모델링 하였다. 이 모델의 출력은 각 대역별 청신경의 시간에 따른 발화 확률로서, 달팽이관도식(cochleagram)으로 불리게 되었다. Kates는(10) 정상 혹은 저하된 청각 기능을 표현하도록 설계된 디지털 시간 영역 달팽이관 모델을 제시하였다. 이 달팽이관 모델은 직렬로 연결된 디지털 필터 구역들로 모델링 되었다. 각 필터 구역에는 진행파 필터, 압력-속도 변환 필터, 미세 응답 조정 필터, 내유모세포 모델, 그리고 Q값 조절을 위한 되먹임 경로가 포함된다. Meddis는(11) 생리학을 기반으로 내유모세포의 모델을 개발하였다. 이 모델에서 투과성 함수(permeability function)는 신경전달물질(neurotransmitter)이 시냅스 간극(synaptic cleft)으로 방출되는 것을 제어한다. 청신경의 특정 신경세포에 대한 발화 확률은 시냅스 간극에 있는 신경 전달 물질의 양에 관한 함수로 정하였다. 또한, 전위 간격(inter-spike interval)이 1 ms 미만에서 발생할 수 없도록 하였다. Meddis의 내유모세포 모델은 청각 연구자들 사이에서 널리 사용되었는데, Patterson et al.은(12) 청각 이미지 모델(auditory image model, AIM)을 개발할 때 Meddis의 모델을 적용하였다. 또한, Sumner et al.은(13) 내유모세포에 대한 새로운 생리학 결과를 반영하여 Meddis의 모델을 개선하였다.
그러나 이상의 청각모델은 미지의 매개 변수가 많고 계산상 비효율적이며 잡음에 취약하여 음성인식을 위한 음성특징으로 적합하지 않다. 따라서 Kim et al.은(14) ZCPA (zero-crossing peak-amplitudes) 모델을 제안하였다. 이 모델은 필터뱅크를 통과한 각 기저막 응답에 대해 상향 영교차(upward zero-crossing) 지점 간 주기와 진폭을 사용하여 내유모세포의 신경 발화 무늬(neural firing pattern)을 모사한 것으로서, 잡음 환경에서 강건한 음성특징을 추출하는데 유용하다.
3. 인간의 청각모델을 응용한 ITD 추정기법
좌우 두 마이크로폰 입력 채널 간의 ITD는 다음과 같이 정의한다.
| (1) |
여기서 tL 및 tR은 각각 좌측 및 우측 입력 채널에 대한 음원의 도착시간이고, ITD는 이 두 시간의 차이이다. 이것은 음원의 방향에 대한 단서를 제공하기 때문에 음원의 위치를 파악하는 데 중요하다.
이 연구에서는 기존의 청각모델을 응용하여, 잡음 환경에서 두 채널 간 ITD를 추정할 수 있는 기법을 제안한다. 이를 위해 달팽이관 내부의 기저막을 통한 진행파 전달 과정 및 내유모세포의 기전변환(mechano-electrical transduction, MET) 과정 그리고 뇌줄기의 ITD 검출 과정을 디지털 필터 및 신호처리 기법으로 각각 모사하였다.
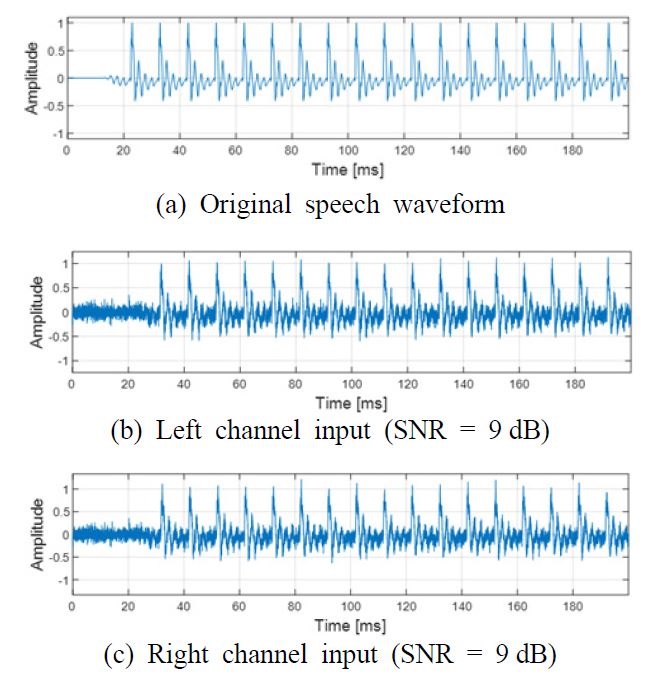
이 기법의 각 단계별 청각 신호처리 과정을 시각화하기 위해 Fig. 3의 음성 파형을 예시로 사용하였다. 이 음성 신호는 남성의 유성음 발화 “er”을 녹음한 것으로서 표본 주파수(sampling frequency)는 48 kHz이다. 화자와의 거리를 3 m로 가정하여 원 신호에 8.8 ms의 시간 지연을 주었으며, ITD 설정을 위해 추가로 –900 μs ~ +900 μs의 시간 지연을 주어 좌우측 각 채널 신호로 정하였다. 또한 좌우 채널 각각 정규분포를 갖는 잡음(SNR = 9 dB)을 부가하였다.
3.1 달팽이관의 필터뱅크 모델
난원창의 진동을 통해 달팽이관의 내부로 전달된 음성 신호는 림프액의 압력 구배로 인해 기저막의 진행파로 변환된다. 이때 기저막의 물리적 변위는 달팽이관의 길이 방향으로 주파수에 대한 선택성을 나타낸다. Greenwood는(15) 인간의 달팽이관에 대한 주파수-위치 함수를 식 (2)와 같이 제시하였다.
| (2) |
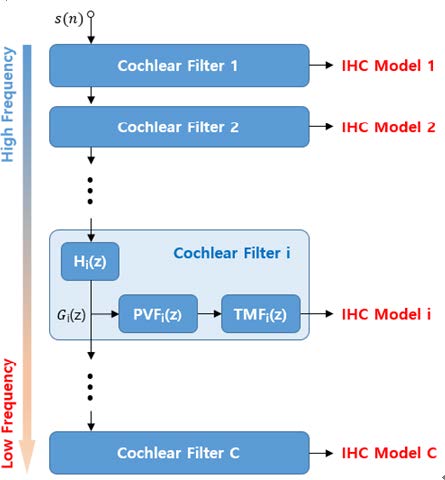
여기서 x는 달팽이관의 길이를 0에서 1사이로 정규화(normalization)한 것으로서, 달팽이관 기저부(고주파 공진부)가 1이고 꼭대기(저주파 공진부)가 0이다. 따라서 식 (2)를 사용하여 등간격의 위치에 대한 주파수를 달팽이관의 중심 주파수 fc로 설정하면 연속적인 기저막을 fc별로 이산화할 수 있다. 따라서 이 연구에서는 이를 기반으로 Kates가 제안한 디지털 필터뱅크 모델을 적용하여 각 fc별로 기저막의 응답을 모사하였다. 단, 계산 효율을 위해 원 모델의 Q값 조절을 위한 되먹임 경로는 제외하였다. 이는 외유모세포의 작용을 모사한 것으로서 ITD 추정을 위한 이 기법에서는 불필요하다. 적용된 달팽이관 필터뱅크의 블록 선도는 Fig. 4와 같다.
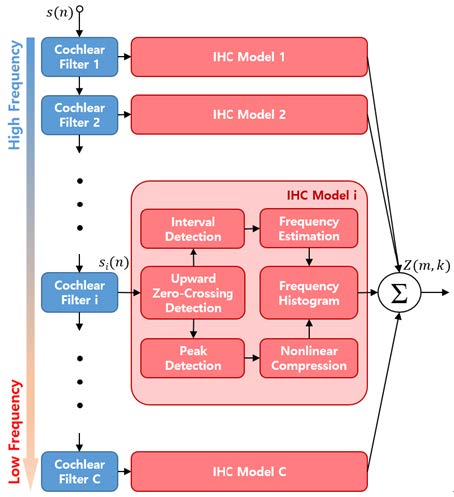
여기서 s(n)는 음성 신호이며, C개의 fc별로 달팽이관 필터(cochlear filter)를 통과하여 내유모세포 모델(IHC model)로 입력된다. 각 달팽이관 필터는 세 개의 디지털 필터로 이루어져 있는데, Hi(z), PVFi(z) 그리고 TMFi(z)이다. Hi(z)는 i번째 fc에 해당하는 기저막 진행파 필터이고, Gi(z)는 i번째 fc지점까지의 기저막 순진행파(net traveling wave) 필터로서 다음과 같다.
| (3) |
Hi(z)는 해당 fc지점의 응답을 모사한 전달함수를 쌍일차 변환(bilinear transformation)을 통해 디지털화한 것으로 식 (4)와 같다.
| (4) |
식 (4)에서 ai는 필터 계수이고, μ와 b는 원하는 주파수 응답 및 군지연(group delay)을 위한 변수로서 일반적으로 각각 0.5로 정한다. 그리고 Qi는 해당 필터의 Q값으로 다음과 같다.
| (5) |
여기서 x는 식 (2)의 정규화된 달팽이관 길이이다. 진행파 필터의 설계 목적은 각 Gi(z)의 오름(peak)이 해당 fc에서 발생하도록 필터 계수 ai를 설정하는 것이다. 이를 위해 식 (3)에 z = e-jw를 대입한 후, 양변에 절대값을 취하여 제곱하고, 로그를 씌우면 식 (6)과 같이 된다.
| (6) |
식 (6)의 최대값은 식 (7)과 같이 그 미분 계수가 0이 되는 조건을 만족할 때 발생한다.
| (7) |
따라서 필터 계수 ai는 식 (7)에 이전의 필터 계수 [a1, a2, ⋯, ai-1] 및 i 번째 fc에 해당하는 ω = ωc를 대입하여 수치적으로 구한다. 결과적으로 Gi(z)의 주파수 응답은 fc 근처에서 증폭하고, 그 이하에서 1로 수렴하며, 그 이상에서 감소한다.
Fig. 4에서 PVFi(z)는 i 번째 fc에 해당하는 진행파의 압력-속도 변환 필터로서, 기저막의 진행파 압력이 속도로 변환될 때의 주파수 특성을 모사한 것이다. 해당 fc보다 2옥타브(octave) 아래에 하나의 극점(pole)을 갖는 1차 고역 통과 필터(high pass filter, HPF)로 모델링하였으며 식 (8)과 같다.
| (8) |
| (9) |
| (10) |
식 (10)에서 fs는 표본 주파수이고, wc는 fc에 대한 디지털 각주파수(digital angular frequency)이다. 그리고 식 (9)에서 ap는 ωc의 휨전 주파수(prewarped frequency)의 1/4에 해당하는 주파수이다. PVFi(z)의 이득(gain)은 나이키스트 주파수(Nyquist frequen-cy)에서 1이 되도록 조정하였다.
진행파 필터는 달팽이관의 측정된 물리적 거동을 완전하게 모사하지 못한다. Kiang과 Moxon이(16) 측정한 동조 곡선(tuning curve)은 중심 주파수보다 약 1옥타브 아래의 주파수 응답에서 홈(notch)을 나타낸다. 또한 Robles et al.이(17) 측정한 위상 응답은 동일한 홈의 주파수에서 π의 위상 변화를 나타낸다. 이러한 현상은 덮개막과 기저막의 상대운동에 의한 공진에 기인하는 것으로 추정된다(18). 따라서 이를 모사하기 위해 Fig. 4와 같이 내유모세포 모델 입력 전에 필터를 추가하였다. TMFi(z)는 i번째 fc에 해당하는 덮개막-기저막 상대운동 필터이며 식 (11)과 같이 2차 필터로 모델링하였다.
| (11) |
| (12) |
| (13) |
식 (11)에서 b0 및 Q0는 각각 영점(zero)에 대한 휨전 주파수 및 Q값이고, bp 및 Qp는 각각 극점에 대한 휨전 주파수 및 Q값이다. 위에서 언급된 동조 곡선에 기반하여 bp는 fc에 설정하였고, b0는 한 옥타브 아래인 bp의 절반에 설정하였다. 또한 홈의 Q값은 fc보다 날카롭고, fc의 Q값은 주파수가 증가할수록 커지기 때문에 Qp와 Q0를 각각 다음과 같이 설정하였다.
| (14) |
| (15) |
그리고 TMFi(z)의 이득(gain)은 ω = 0에서 1이 되도록 조정하였다.
결과적으로, i번째 fc에 해당하는 달팽이관 필터 CFi(z)는 식 (16)과 같이 되며, C개의 CFi(z)를 일렬로 연결하면 달팽이관의 필터뱅크 모델이 된다.
| (16) |
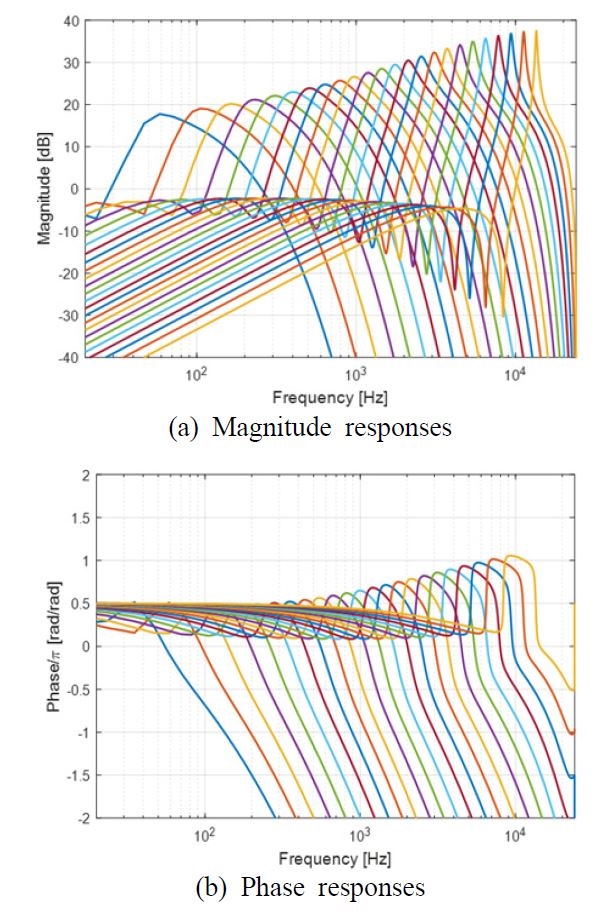
식 (16)의 응답을 시각화하기 위해, 식 (2)를 사용 하여 임계 대역(critical band)의 중심 주파수 하한인 50 Hz 지점과 상한인 13.5 kHz 지점 사이의 24개 등간격 지점에 대한 주파수 열을 fc로 정하고, 각 fc에 대한 주파수 응답을 Fig. 5에 나타내었다. 표본 주파수는 48 kHz이고, FFT 크기는 4096이다.
Fig. 5(a)의 크기 응답을 보면, 공진점과 그 아래의 홈이 fc가 고주파로 갈수록 날카로워 짐을 볼 수 있다. 또한 형상이 공진점을 기준으로 비대칭이라서, 공진점 이하에서는 완만한 꼬리가 나타나지만, 그 이상에서는 가파르게 내려간다. 그리고 (b)의 위상 응답을 보면, 공진점과 홈의 주파수에서 대략 π의 위상 변화가 나타나는데, fc가 고주파로 갈수록 뚜렷해진다. 또한 공진점 이하에서는 위상이 서서히 상승하지만, 그 이하에서는 급격히 하강한다.
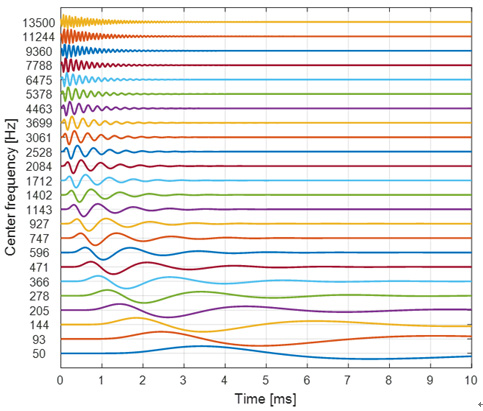
그리고 Fig. 5의 각 주파수 응답을 역 푸리에 변환(inverse Fourier transform, IFT)하면 Fig. 6과 같이 각 fc별 충격응답(impulse response)을 구할 수 있다.
마지막으로, Fig. 6의 충격응답을 Fig. 3의 음성 파형에 합성곱(convolution)하면, Fig. 7과 같이 각 fc별 기저막 응답을 모사할 수 있다. 참고로, Fig. 6과 Fig. 7의 응답은 진폭이 1 이하가 되도록 각 응답의 최대값으로 정규화하여 나타낸 것이다.
3.2 내유모세포의 ZCPA 모델
각 공진 부위 별 기저막 응답은 내유모세포의 기전변환 과정을 통해 전기적 신호로 변환된 후, 청신경으로 발화된다. 이때 발화된 청각 신호는 앞에서 설명한 바와 같이 부동섬모가 한 방향으로 꺾일 때만 반응하기 때문에 위상동기(phase-locking)되어 반파 정류된 신경 가시 형태로 나타난다. 그러므로 이 연구에서는 이와 같은 청각 메커니즘에 근거하여 Kim et al.이 제안한 ZCPA 모델을 적용하여 각 fc별로 내유모세포의 신경 발화 무늬를 모사하였다. 단, 정밀한 ITD 추정 및 계산 효율을 위해 각 fc별 창길이(window length)를 대폭 줄였다. 이에 관한 사항은 아래에서 자세히 설명하였다. 적용된 ZCPA 모델의 블록 선도는 Fig. 8과 같다.
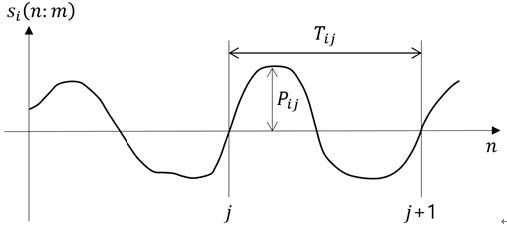
여기서 si(n)은 i번째 달팽이관 필터를 통과한 음성 신호 s(n)이며, Z(m,k)는 ZCPA 모델로 모사된 내유모세포의 신경 발화 무늬이다. 참고로, m과 k는 각각 시간과 주파수의 색인이다. si(n)이 내유모세포 모델로 입력되면 시간틀(time frame) 단위로 처리된다. 시간 m에서 si(n)의 시간틀을 si(n:m)이라 하면, 다음과 같이 나타낼 수 있다.
| (17) |
여기서 wi(n)은 유한한 길이를 갖는 사각 창함수(rectangular window function)이며, C는 달팽이관 필터의 개수이다. 이때 창함수의 길이는 각 대역별로 다르게 사용하는 것이 분해능(resolution) 측면에서 유리하다. 즉, 저주파 대역에서 긴 창함수를 사용하여 높은 주파수 분해능을, 고주파 대역에서 짧은 창함수를 사용하여 높은 시간 분해능을 얻을 수 있다. 게다가 이러한 특성은 심리음향(psychoacoustic) 관찰결과 와도 일치한다. 기존 ZCPA 모델은 음성인식을 위한 특징 추출용으로 ZCPA 무늬를 사용했기 때문에 각 대역별 창길이를 fc 주기의 10배로 하였다. 그러나 창길이가 너무 길어지면 시간 분해능이 떨어지고 계산 효율이 낮아져서, 정밀하고 신속한 ITD 추정에 불리하다. 따라서 이 연구에서는 각 대역별 창길이를 해당 fc 주기의 1배 ~ 3배로 하였다.
내유모세포 모델에서는 Fig. 8에 나타난 바와 같이 si(n:m)의 상향 영교차 지점이 먼저 검출된다. 그리고 이를 기반으로 상향 영교차점들 간의 간격과 진폭이 Fig. 9의 도해와 같이 각각 감지된다.
Fig. 9에서 Tij와 Pij는 각각 i 번째 내유모세포 모델의 j번째 상향 영교차 구간에 대한 간격과 진폭이다. 다음 단계에서는 이를 바탕으로 식 (18), (19)와 같이 해당 구간의 주파수 추정 및 진폭의 비선형 압축이 진행된다.
| (18) |
| (19) |
여기서 fij는 i번째 내유모세포 모델의 j번째 상향 영교차 구간 주파수이고, Lij는 해당 구간에서 청신경의 자극 강도에 대한 감각 정도를 모사한 것이다. 식 (19)의 로그 함수에 1을 더한 이유는 Lij가 음수가 되는 것을 방지하기 위함이다. 따라서 si(n:m)의 상향 영교차점 개수를 Zi라 하면, i번째 내유모세포 모델은 총 Zi-1개의 주파수 정보 벡터 (fij, Lij)를 갖게 된다.
그 후, 이 주파수 정보를 주파수 분포도(frequency histogram)로 나타내면 i번째 내유모세포 모델에 대한 출력을 얻을 수 있다. 마지막으로, 전체 C개의 내유모세포 모델에 대한 주파수 분포도를 구하여 합하면, 식 (20)과 같이 Z(m,k)를 구할 수 있다.
| (20) |
| (21) |
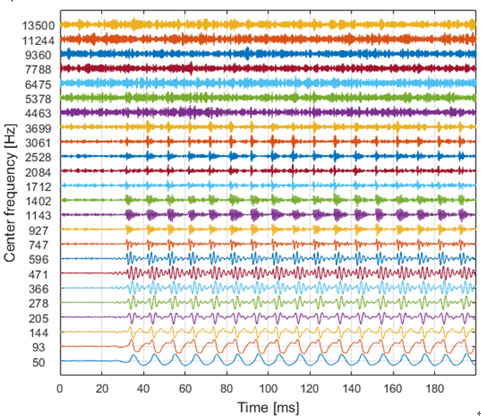
식 (21)에서 Fk는 fc를 중심으로 하는 주파수 구간(frequency bin)이다. Fk의 범위는 각 fc사이의 경계 주파수에 의해 한정되는데, 옥타브 대역 계산식을 통해 이를 구하였다. 그리고 IFk(fij)는 지시 함수(indicator function)로서, fij가 Fk의 구간에 속하면 1을, 속하지 않으면 0을 출력한다. 따라서 식 (20)에 의해 시간 m에서 각 Fk에 해당하는 모든 Lij를 누적하여 Fig. 10과 같이 ZCPA 무늬를 구하였다.
3.3 내측 상올리브의 상호상관도 모델
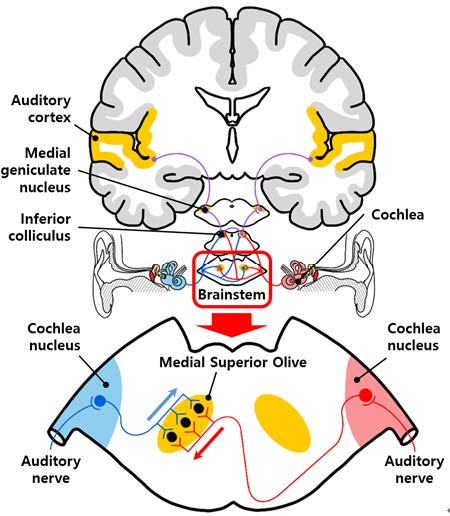
청신경으로 발화된 좌우의 전기적 신호 열은 먼저 뇌줄기의 달팽이핵(cochlear nucleus, CN)에 집결한다. 뇌줄기는 숨뇌(medulla), 다리뇌(pons), 그리고 중뇌(midbrain)로 이루어져 있는데, 숨뇌와 다리뇌 사이에 상올리브 복합체(superior olivary complex, SOC)가 있다. 상올리브 복합체는 좌우 달팽이핵의 신호를 공유한 후에 중뇌의 하구(inferior colliculus)로 정보를 전달한다. 마지막으로 하구의 좌우 청각 정보는 시상(thalamus)의 내측 무릎핵(medial geniculate nucleus)을 거쳐 대뇌(cerebrum)의 청각 피질로 전달된다. 여기서 상올리브 복합체는 뇌줄기 핵의 집합체로서 내측 상올리브(medial superior olive, MSO)를 포함하는데, ITD의 처리는 내측 상올리브가 담당하는 것으로 알려져 있다(19).
이 연구에서는 기존의 신경 생리학 연구에 근거하여 내측 상올리브의 ITD 처리과정을 Jeffress가 제안한 인간의 음원 추적 구조(mechanism)로 모사하였다. 그는 두 귀의 동일 임계 대역에서 발생하는 신경 발화가 한 쌍의 지연선(delay line)을 따라 이동하는 신경 회로를 제시하였다(20). 지연선 간의 순 지연이 ITD에 다다르면, 두 지연선 상의 신경 발화 양상이 일치하게 되고 그 일치점으로부터 ITD가 추정된다. 이 과정은 Fig. 11에 나타난 내측 상올리브의 ITD 처리과정과 유사하며, 좌우 신경 발화 간의 주파수 별 상호상관(cross-correlation)으로 모사할 수 있다. 따라서 상호상관도(cross-correlogram, CC)는 식 (22)와 같다.
| (22) |
여기서 ZL(m,k)와 ZR(m,k)는 각각 좌우의 ZCPA 신경 발화 무늬이다. 그리고 d는 시간 지연의 색인이며, W(l)은 길이가 L인 사각 창함수이다. 또한 식 (22)의 결과를 강조하기 위해 각 주파수 별 상호상관을 모두 합하면 식 (23)과 같이 요약 상호상관도(summary cross-correlogram, SCC)로 간추릴 수 있다.
Fig. 12는 예시로 사용된 Fig. 3의 음성 파형에 대해 상호상관도 및 요약 상호상관도를 구한 결과이다. 상호상관도는 ITD를 중심으로 등고선이 형성되며, 요약 상호상관도는 ITD 부근에서 큰 오름이 형성되어 그 변화를 따라가는 것을 볼 수 있다. 0 μs의 작은 오름은 잡음에 의한 것으로서, SNR이 낮아질수록 커져서 정확한 ITD 추정을 방해한다.
| (23) |
4. 모의실험
이 기법의 ITD 추정 성능을 평가하기 위해 잡음이 부가된 음성 신호에 대해 ITD를 추정한 후, 기존의 상호상관함수(cross-correlation function, CCF)에 의한 ITD 추정 결과와 비교해 보았다.
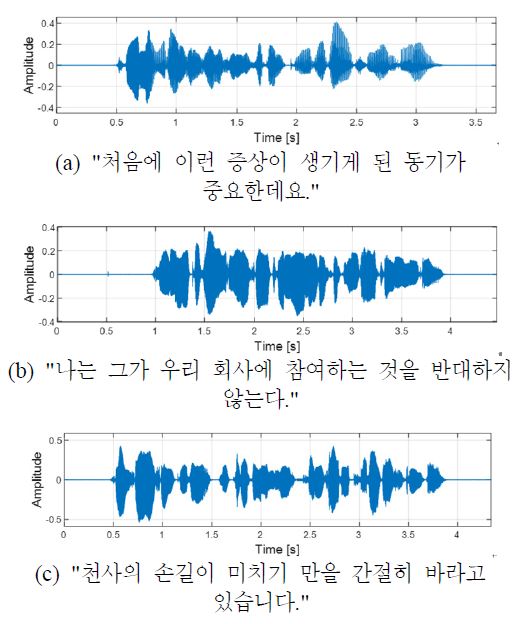
화자는 총 50명의 대한민국 성인으로 각각 25명의 남녀로 구성되었다. 음성 신호는 각 화자가 약 4초 간 말한 것을 표본 주파수 48 kHz의 웨이브 파일(wave file)로 녹음한 것으로 총 50개다. 그 중 일부의 음성 파형 및 발화 내용을 Fig. 13에 나타내었다. 마이크로폰과 화자 간의 거리를 3 m로 가정하여 음성 신호에 8.8 ms의 시간 지연을 주였으며, 추가로 ITD 설정을 위해 100 μs, 200 μs, 300 μs 그리고 400 μs의 시간차를 주어 좌우 채널의 신호로 배정하였다. 그리고 시간차가 반영된 좌우 채널의 신호에 정규분포를 갖는 백색잡음(white noise)을 SNR 0 dB에서 9 dB까지 1 dB씩 증가시켜서 각각 부가하였다.
달팽이관 필터뱅크의 중심 주파수 fc는 녹음된 음성 신호의 주파수 특성을 감안하여 90 Hz에서 3 kHz까지 8개 등간격 지점에 대한 주파수 열로 정하였다. 그리고 ZCPA 모델의 상향 영교차점 검출을 위한 각 대역별 창함수의 길이는 정밀하고 신속한 ITD 추정을 위해 해당 fc주기의 1배로 정하였다.
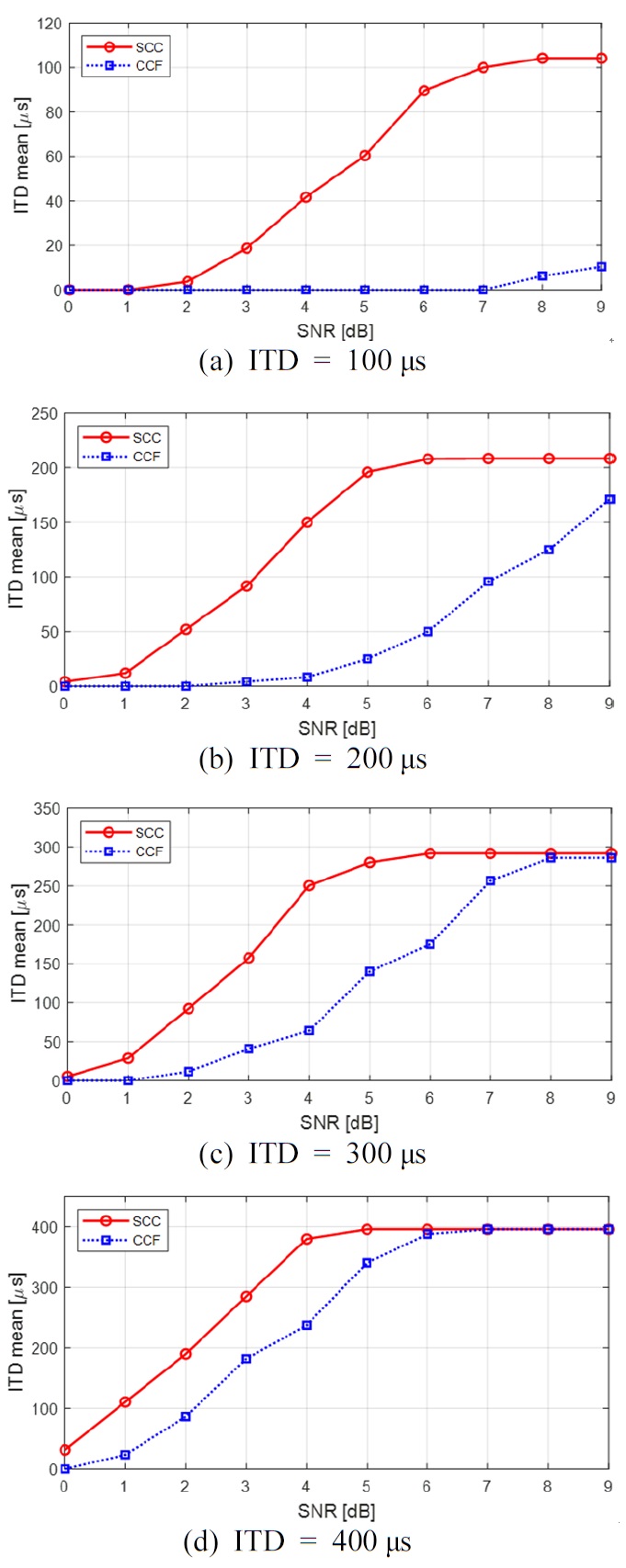
식 (23)의 요약 상호상관도 및 상호상관함수는 최대값이 1이 되도록 정규화한 것으로서, 그 최대값에 해당하는 시간 지연을 검출함으로써 ITD가 추정된다. 50명의 화자로부터 추정된 각각의 ITD는 SNR별로 평균을 내어 Fig. 14에 나타내었다. 각각의 ITD 설정에 대한 SNR별 ITD 추정 오차는 Tables 1 ~ 4와 같다.
Fig. 14(a) 및 Table 1을 보면 실제 ITD값이 100 μs일 때, 이 기법은 SNR이 7 dB 이후부터 오차가 4 %로 수렴하는 반면에 상호상관함수는 모든 SNR에서 90% 이상의 오차가 발생하여 ITD 추정이 불가능함을 알 수 있다. Fig. 14(b) 및 Table 2를 보면 실제 ITD값이 200 μs일 때, 이 기법은 SNR이 5 dB 이후부터 오차가 4 %로 수렴하는 반면에 상호상관함수는 9 dB에서 오차가 15 %로 나타나 9 dB 이상에서 10 % 이내로 수렴할 것으로 예상된다. Fig. 14(c) 및 Table 3을 보면 실제 ITD값이 300 μs일 때, 이 기법은 SNR이 6 dB 이후부터 오차가 3 %로 수렴하는 반면에 상호상관함수는 8 dB 이후부터 오차가 5 %로 수렴하는 것을 볼 수 있다. Fig. 14(d) 및 Table 4를 보면 실제 ITD값이 400 μs일 때, 이 기법은 SNR이 5 dB 이후부터 오차가 1 %로 수렴하는 반면에 상호상관함수는 7 dB 이후부터 오차가 1 %로 수렴하여 이 기법과 동등한 ITD 추정 성능을 나타내는 것을 볼 수 있다.
5. 고 찰
모의실험 결과, 잡음이 부가된 음성 신호의 경우 이 기법의 ITD 추정값이 기존의 상호상관함수의 추정값보다 실제 ITD값에 더 근접하는 것을 확인할 수 있었다. 따라서 잡음 환경에서 최소의 입력 채널로 화자의 위치를 추정하기 위해 인간의 청각계를 모사하는 것이 효과적임을 알 수 있다.
이 기법에서 음성 신호는 달팽이관 필터뱅크를 통해 중심 주파수 대역별로 나눠지고, ZCPA 모델을 거치며 신경 발화 무늬로 변환된다. 이 과정 중에 내유모세포의 위상동기 현상을 모사하기 위해 적용된 ZCPA 모델의 상향 영교차 검출 과정에서 잡음에 덜 민감한 음성특징이 추출되게 된다. 따라서 이 기법이 잡음에 대해 비교적 정확하게 ITD를 추정할 수 있는 이유는 바로 여기에 있다고 생각한다. 또한 모의실험에서 SNR이 작아질수록 ITD 추정 성능이 저하되는 것을 볼 수 있었는데, 그 이유는 잡음의 에너지 상승에 의해 요약 상호상관도에서 0 μs의 오름이 커져서 정확한 ITD 추정을 방해하기 때문이다. 잡음은 시간차 없이 좌우 채널에 부가되기 때문에 0 μs의 오름은 불가피하다. 따라서 잡음에 의한 0 μs의 오름만 선별적으로 제거할 수 있다면, 낮은 SNR에서도 비교적 정확한 ITD 추정이 가능할 것이다.
일반적으로 ITD는 저주파 음에 영향을 받는 반면, 두 귀의 음압차(interaural level difference, ILD)는 고주파 음에 영향을 받는다. 그 이유는 머리 모양에 의한 그림자 효과 때문이다. 향후에는 고주파 대역에서 더욱 정밀한 화자위치추정을 위해 ILD를 처리하는 외측 상올리브(lateral superior olive, LSO)를 모사하여 이 기법에 반영하고자 한다.
6. 결 론
인간의 청각모델을 사용하여 잡음 환경에서 ITD를 추정할 수 있는 방법을 제시하였고, 그 성능을 평가하여 유효성을 확인하였다. 이 기법을 통해 잡음 환경에서 화자의 위치를 더욱 정확하게 파악할 수 있다면, 기존 음성인식기술의 인식성능을 크게 향상시킬 수 있을 것으로 예상한다.
기 호 설 명
| CC(m, d, k) : | 상호상관도 |
| fc : | 달팽이관 중심 주파수 |
| Gi (z) : | i번째 기저막 순진행파 필터 |
| Hi (z) : | i번째 기저막 진행파 필터 |
| PVFi(z) : | i번째 진행파 압력-속도 변환 필터 |
| Pij : | i번째 fc의 j번째 상향 영교차 구간 진폭 |
| SCC(m, d) : | 요약 상호상관도 |
| TMFi(z) : | i번째 덮개막-기저막 상대운동 필터 |
| Tij : | i번째 fc의 j번째 상향 영교차 구간 간격 |
| ZL/R(m,k) : | 좌/우 ZCPA 신경 발화 무늬 |
Acknowledgments
이 연구는 KAIST 기본 연구비에 의해 지원되었습니다.
References
- Lee, G. T. and Park, Y. H., 2019, Method for Estimating Interaural Time Difference by Modeling the Human Auditory System, Proceedings of the KSNVE Annual Spring Conference, pp. 229~229.
- Hwang, S. M., Park, Y. S. and Park, Y. J., 2005, Detection of Speaker Position for Robot Using HRTF, Proceedings of the KSNVE Annual Autumn Conference, pp. 637~640.
-
Go, Y. J., Lee, J. H., Choi, J. S. and Ha, J. H., 2016, Localization of Moving Sound Source Using Various Beamforming Methods, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 26, No. 5, pp. 501~510.
[https://doi.org/10.5050/KSNVE.2016.26.5.501]

-
Sasaki, Y., Kagami, S. and Mizoguchi, H., 2006, Multiple Sound Source Mapping for a Mobile Robot by Self-motion Triangulation, Proceedings of the 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems, pp. 380~385.
[https://doi.org/10.1109/IROS.2006.281797]

- Raangs, R. and Druyvesteyn, W. F., 2002, Sound Source Localization Using Sound Intensity Measured by a Three Dimensional PU-probe, Proceedings of the 112th AES Convention, No. 5589.
-
Zhang, L., Ding, D., Yang, D., Wang, J. and Shi, J., 2017, Sound Source Localization Using Non-conformal Surface Sound Field Transformation Based on Spherical Harmonic Wave Decomposition, Sensors, Vol. 17, No. 5, pp. 1087~1098.
[https://doi.org/10.3390/s17051087]

- Békésy, G. V., 1960, Experiments in Hearing, McGraw-Hill, New York.
-
Flanagan, J. L., 1972, Speech Analysis, Synthesis and Perception, Springer-Verlag, Berlin.
[https://doi.org/10.1007/978-3-662-01562-9]

-
Lyon, R. F. and Mead, C., 1988, An Analog Electronic Cochlea, IEEE Transactions on Acoustics, Speech, and Signal Processing, Vol. 36, No. 7, pp. 1119~1134.
[https://doi.org/10.1109/29.1639]

-
Kates, J. M., 1991, A Time-domain Digital Cochlear Model, IEEE Transactions on Signal Processing, Vol. 39, No. 12, pp. 2573~2592.
[https://doi.org/10.1109/78.107409]

-
Meddis, R., 1986, Simulation of Mechanical to Neural Transduction in the Auditory Receptor, Journal of the Acoustical Society of America, Vol. 79, No. 3, pp. 702~711.
[https://doi.org/10.1121/1.393460]

-
Patterson, R. D., Allerhand, M. H. and Giguere, C., 1995, Time-domain Modelling of Peripheral Auditory Processing: A Modular Architecture and a Software Platform, Journal of the Acoustical Society of America, Vol. 98, No. 4, pp. 1890~1894.
[https://doi.org/10.1121/1.414456]

-
Sumner, C. J., Lopes-Poveda, E. A., O’Mard, L. P. and Meddis, R., 2002, A Revised Model of the Inner-hair Cell and Auditory-nerve Complex, Journal of the Acoustical Society of America, Vol. 111, No. 5, pp. 2178~2188.
[https://doi.org/10.1121/1.1453451]

-
Kim, D. S., Lee, S. Y. and Kil, R. M., 1999, Auditory Processing of Speech Signals for Robust Speech Recognition in Real-world Noisy Environments, IEEE Transactions on Speech and Audio Processing, Vol. 7, No. 1, pp. 55~69.
[https://doi.org/10.1109/89.736331]

-
Greenwood, D. D., 1990, A Cochlear Frequency-position Function for Several Species-29 Years Later, Journal of the Acoustical Society of America, Vol. 87, No. 6, pp. 2592~2605.
[https://doi.org/10.1121/1.399052]

-
Kiang, N. Y. S. and Moxon, E. C., 1974, Tails of Tuning Curves of Auditory-nerve Fibers, Journal of the Acoustical Society of America, Vol. 55, No. 3, pp. 620~630.
[https://doi.org/10.1121/1.1914572]

-
Robles, L., Ruggero, M. A. and Rich, N. C., 1986, Basilar Membrane Mechanics at the Base of the Chinchilla Cochlea. I. Input-output Functions, Tuning Curves, and Response Phases, Journal of the Acoustical Society of America, Vol. 80, No. 5, pp. 1364~1374.
[https://doi.org/10.1121/1.394389]

-
Allen, J. B., 1980, Cochlear Micromechanics - A Physical Model of Transduction, Journal of the Acoustical Society of America, Vol. 68, No. 6, pp. 1660~1670.
[https://doi.org/10.1121/1.385198]

-
Yin, T. C. and Chan, J. C., 1990, Interaural Time Sensitivity in Medial Superior Olive of Cat, Journal of Neurophysiology, Vol. 64, No. 2, pp. 465~488.
[https://doi.org/10.1152/jn.1990.64.2.465]

-
Jeffress, L. A., 1948, A Place Theory of Sound Localization, Journal of Comparative and Physiological Psychology, Vol. 41, No. 1, pp. 35~39.
[https://doi.org/10.1037/h0061495]


Gyeong-Tae Lee received B.S. degree in mechanical engineering from Kyonggi Univ. in 2005 and M.S. degree in mechanical engineering from Hanyang Univ. in 2007. He is currently a Ph.D. candidate in mechanical engineering at KAIST. His research interest includes electro-acoustics, audio signal processing and computational auditory scene analysis.

Yong-Hwa Park received B.S., M.S. and Ph.D. degree from KAIST in 1991, 1993 and 1999. He is currently an associate professor of mechanical engineering department at KAIST. His research interest includes 3D scene recognition, acoustic recognition, wearable health sensors and structure dynamics.