지진하중 하에서 로킹모드에 의한 캐비닛의 응답특성 분석

1. 서 론

최근 전 세계적으로 지진발생 빈도와 지진피해가 증가하고 있으며 우리나라 또한 2016년과 2017년에 경주와 포항에서 발생한 지진으로 시설물의 피해가 상당수 발생하였다⁽¹⁾. 최근 국내외 지진피해사례를 살펴보면 비구조요소에 많은 피해가 발생되는 경향이 있다. 비구조요소 중 전기캐비닛은 시설물의 제어와 통신 등 기능유지를 담당하고 있다. 따라서 이러한 전기캐비닛의 손상은 시설물 고유기능에 장애를 유발할 수 있으며, 이는 재산피해와 함께 인명피해를 동반하는 중대사고로 이어질 수 있다. 그러므로 주요한 기능을 담당하는 전기캐비닛의 내진성능은 확보되어야 한다.

전기캐비닛의 내진성능을 확보하기 위해 많은 연구자들이 수치해석과 함께 시험적인 연구를 수행하였으며^(2~4) 캐비닛 내부 부품의 독립적인 내진성능 평가의 수행을 위하여 캐비닛의 내부 응답을 추정하기 위한 연구 또한 진행된 바 있다⁽⁵⁾. 그뿐만 아니라 로킹현상이 캐비닛의 응답에 미치는 영향을 분석하기 위하여 로킹강성(rocking stiffness)을 계산하고자 하는 연구도 진행되고 있다^(6,7). 일반적으로 수치해석적인 접근에 의한 연구들은 캐비닛이 바닥에 단단히 고정되어 있다고 가정한다. 하지만 이 가정은 캐비닛이 고정되는 방법에 따라 유효하지 않을 수 있다. 특히 캐비닛이 앵커볼트로 정착된 경우 하부 판재의 국부 변형이 발생할 수 있다. 이러한 현상은 캐비닛의 로킹 또는 들림을 유발하게 되며 들어 올려진 캐비닛은 바닥과 충돌하여 충격이 발생한다. 그러나 수치해석으로 캐비닛과 바닥의 충돌과 충격을 묘사하는 것은 난해한 문제이다. 그러므로 실증시험을 통한 평가와 분석이 필요할 수 있다. 하지만 시험적인 접근으로 로킹에 의한 충돌영향을 분석한 사례는 많지 않다.

최근 국내에서 로킹에 의한 충격이 캐비닛을 고정하는 앵커에 미치는 영향을 분석하기 위한 연구가 윤다운 등에 의해 진행되었으나 앵커하중의 증폭경향에 집중하였으며 캐비닛의 응답증폭은 고려되지 않았다⁽⁸⁾. 따라서 이 연구에서는 볼트로 고정된 캐비닛의 진동대 시험을 수행하였다. 그 결과, 캐비닛에서 로킹이 발생하였으며, 캐비닛에서 계측된 응답신호로부터 로킹에 의한 캐비닛의 진동전달 특성을 분석하였다.

2. 입력지진동

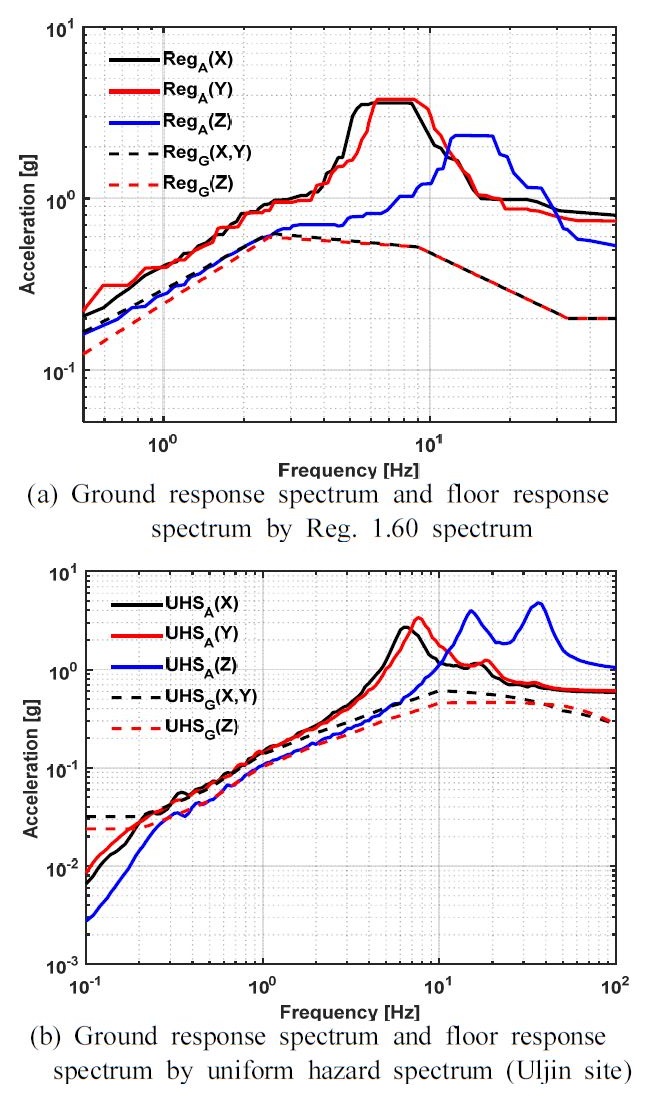
대상 캐비닛은 울진 원자력발전소(OPR1000) 보조건물 165 ft에 위치한다고 가정을 하였다. Table 1과 Fig. 1은 가속도시간이력의 작성을 위한 응답스펙트럼(response spectrum)으로서 모든 응답스펙트럼의 감쇠비는 5 %이다. 국내에 많은 원자력발전소는 regulatory guide 1.60 설계응답스펙트럼을 바탕으로 내진설계가 수행되었으며, 등재해도응답스펙트럼은 원자력발전소의 지진 안전성 평가에 활용되어 이 연구에서는 regulatory guide 1.60 원자력발전소 설계응답스펙트럼과 등재해도응답스펙트럼(UHS)에 대하여 진동대 시험을 수행하였다. Table 1과 Fig. 1에서 Reg_G는 regulatory guide 1.60⁽⁹⁾에서 제시된 응답스펙트럼의 PGA (peak ground acceleration)의 가속도 배율을 0.2 g로 조정한 것이다. 그리고 Reg_A는 Reg_G응답스펙트럼을 입력지진동으로 하였을 경우의 보조건물 165 ft 위치의 층응답스펙트럼이다. UHS_G는 울진부지의 등재해도 응답스펙트럼이고⁽¹⁰⁾, UHS_A는 UHS_G를 입력으로 하였을 경우의 보조건물 165 ft 위치의 층응답스펙트럼이다. Reg_A 수평방향의 영주기가속도(zero period acceleration)값이 가장 높으며 10 Hz 이하의 스펙트럼 가속도 성분이 크다. UHS_A는 수직방향의 영주기 가속도가 가장 높다.

Table 1

Description of response spectrum for input motion

Fig. 1

Response spectrum for shaking table

진동대 시험을 위하여 수평 두 방향과 수직 한 방향에 대한 가속도 시간이력 세트를 MTS의 STEX프로그램을 이용하여 생성하였다. 가속도 시간이력의 진동지속시간은 30초, 강진지속시간은 20초이며 Fig. 2와 같은 사다리꼴 포락함수가 적용되었다^(11,12). 그리고 서로 다른 두 방향의 시간이력은 상관계수 값이 0.3이하가 되도록 하였다.

Fig. 2

Envelope function for artificial time history

3. 진동대 시험

3.1 캐비닛 및 센서의 설치

로킹에 의한 캐비닛의 거동을 살펴보기 위하여 단문형 캐비닛을 진동대에 설치하였다. Fig. 3의 왼쪽 그림은 진동대에 고정된 모형 캐비닛과 설치된 계측기의 위치를 나타낸 것이며, 오른쪽 그림은 캐비닛의 정면도이다. 캐비닛의 크기는 가로와 세로가 각각 800 mm이고 높이는 2350 mm이며 무게는 480 kg이다. 캐비닛은 강재프레임을 이용하여 진동대에 고정하였다. 캐비닛과 강재 프레임은 8개의 M16 볼트로 연결하였으며 Fig. 4와 같이 하중계(load cell)를 설치하여 각 앵커볼트의 인발하중을 계측하였다. 진동대 바닥과 고정프레임 상단에 3축 가속도계를 설치하였다. 캐비닛의 최상부와 문 중앙, 외함 중앙, 내부의 각 층에도 3축 가속도계가 설치되어 지진동과 로킹에 의한 충격으로 인한 진동 전달특성을 검토하고자 하였다. 그리고 캐비닛의 상단과 하단의 단방향 상대변위를 계산하기 위하여 변위계를 설치하였다.

Fig. 3

Sensor location and single door cabinet drawing

Fig. 4

Anchor bolt with ring type load cell

3.2 시험절차

시험절차는 Table 2와 같다. 진동대를 이용하여 지진을 모사한 시간이력 시험(time history test)은 Table 1의 입력지진동에 대하여 Reg_G, Reg_A, UHS_G, UHS_A의 순서로 수행하였다. 그리고 모형 캐비닛의 동특성 변화를 확인하기 위하여 시간이력 시험 전과 후에 공진탐색 시험(resonance search test)을 수행하였다. 시험은 부산대학교 지진방재연구센터의 고성능 6 자유도 진동대를 이용하여 수행하였으며 Table 3은 진동대의 사양이다.

Table 2

Shaking table tests procedure

Table 3

Shaking table specification

3.3 시험 가진의 적절성 확인

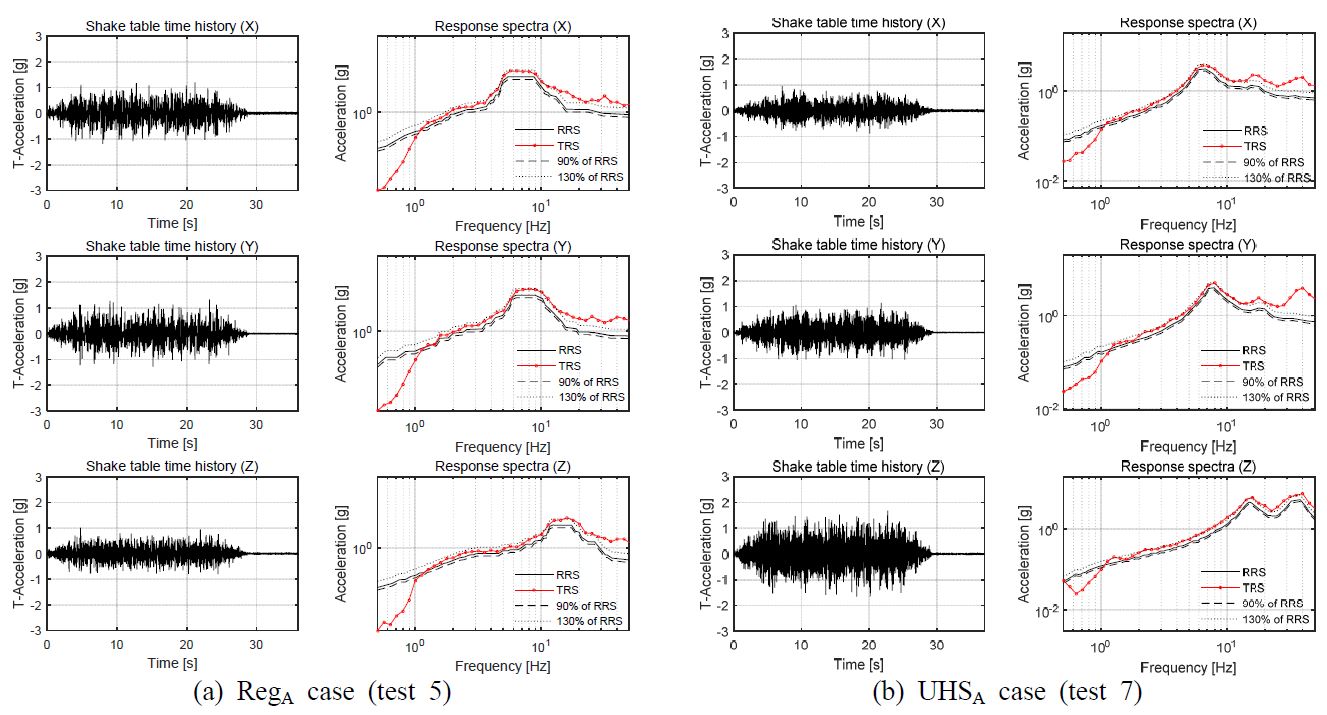
이 연구에서는 진동대 바닥의 응답으로 시험응답스펙트럼(test response spectrum)을 작성하여 목표응답스펙트럼(target response spectrum)과 비교를 하였다. 그 결과 1.3 Hz 이상의 주파수 영역에서 모든 시험의 응답스펙트럼은 목표응답스펙트럼을 포락하는 것으로 확인되었다. Fig. 5는 UHS_A의 가진에 의해 진동대에서 계측된 가속도 시간이력 및 목표응답스펙트럼과 시험응답스펙트럼의 비교 그래프이다.

Fig. 5

Acc. time histories and test response spectrum/target response spectrum

4. 공진탐색 시험 결과

식 (1)과 같이 진동전달함수 H_xy(f)는 진동대 바닥에서 계측된 가속도 신호인 P_xx(f)와 응답가속도신호의 전달함수P_yx(f)를 이용하여 결정하였다. Table 4는 공진탐색시험의 결과이다. 지진모사시험 전과 후의 공진점의 변화가 5 % 이하이다. 그러나 A4의 y축 방향의 공진점이 크게 변하여 국부적인 손상이 의심되었으나, 시험 종료 후 캐비닛에서 육안으로 확인 가능한 파손은 발견되지 않았다.

Table 4

Results of resonance search tests

5. 캐비닛 로킹의 응답영향 분석

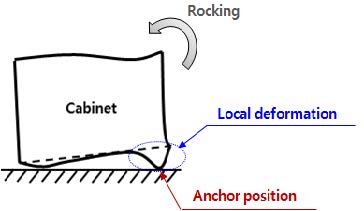
일반적으로 수치해석 시 캐비닛의 하부기초 경계조건은 대부분 바닥에 고정된다고 가정을 한다. 하지만 박판으로 구성된 캐비닛 바닥판은 강한 지진동에 의해 앵커볼트 주변에서 국부적인 변형이 발생될 가능성이 있다. 따라서 Fig. 6과 같이 앵커를 제외한 바닥판은 들림 현상이 발생하고 이는 캐비닛의 로킹을 유발한다. 뿐만 아니라 들어 올려진 캐비닛이 구조물의 바닥과 충돌하여 충격을 발생시키며 캐비닛의 가속도 응답을 증폭시킬 수 있다⁽¹³⁾. 따라서 이 연구에서는 진동대 실험을 통하여 로킹이 캐비닛 의 지진응답에 미치는 영향을 분석하고자 하였다.

Fig. 6

Cabinet uplifting and rocking

진동대 시험 수행 시 카메라를 활용하여 캐비닛의 거동을 촬영한 결과, 캐비닛에서 로킹과 들어올려짐이 발생하는 것을 확인 할 수 있었다. Fig. 7은 로킹현상 발생 시점의 캐비닛이다. 로킹현상이 있을 때, 캐비닛의 바닥부분에서 캐비닛이 바닥에 있을 때와 캐비닛이 들어 올려진 경우 한 픽셀 정도 차이가 발생하는 것을 확인 할 수 있다.

Fig. 7

Uplifting of cabinet

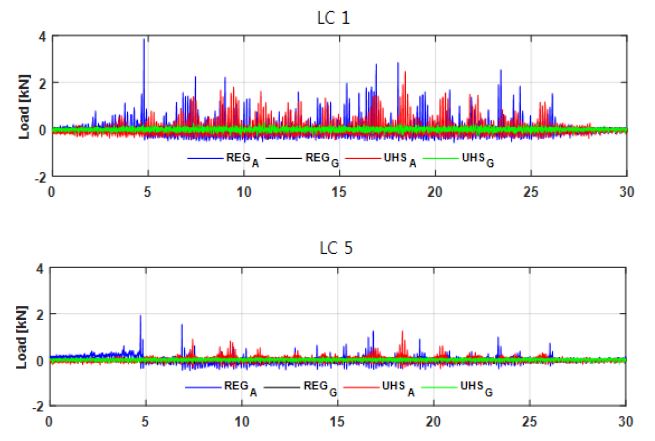
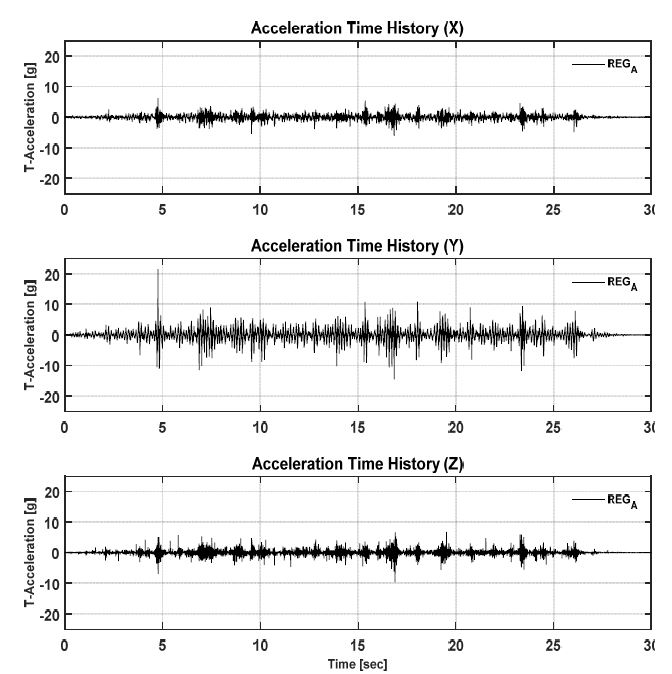
로킹현상에 의한 앵커 인발력과 캐비닛의 진동전달 특성을 분석하기 위하여 응답신호의 분석을 수행 하였다. 먼저, Fig. 8은 지진모사시험 수행 시 앵커볼트에 설치된 로드셀에서 계측된 하중응답이다. Fig. 8의 LC1과 LC5 그래프에서 파란색인 Reg_A의 앵커하중응답이 5초 부분에서 rocking에 의한 충격으로 판단되는 신호가 계측되었다. LC1과 LC5는 모형 캐비닛의 바깥쪽에 위치한 로드셀이다. LC1은 Reg_A의 가진 시 타 시험의 응답과 비교하여 9배 이상, UHS_A의 경우와 비교하여 1.5배 이상 높은 하중이 계측되었다. Fig. 9는 모형 캐비닛 상단(A7)에서 계측된 Reg_A시험의 가속도 시간이력이다. 앵커하중응답과 같이 동일한 시간에서 충격신호가 확인된다. Fig. 10은 캐비닛 상단 Z방향의 지진응답을 STFT(short time fourier transform)를^(14,15) 한 결과이다. 빨간 선은 Fig. 8과 Fig. 9로부터 충격이 감지된 지점이며 STFT에서 저주파수에서 고주파수까지 신호가 측정되었다. Fig. 8, Fig. 9와 Fig. 10의 결과를 바탕으로 로킹에 의한 캐비닛과 강재 프레임의 충돌에 의해 지진응답신호가 증폭되는 것을 확인 할 수 있다.

Fig. 8

Response of anchorage load

Fig. 9

Response acceleration time histories at cabinet top (A7)

Fig. 10

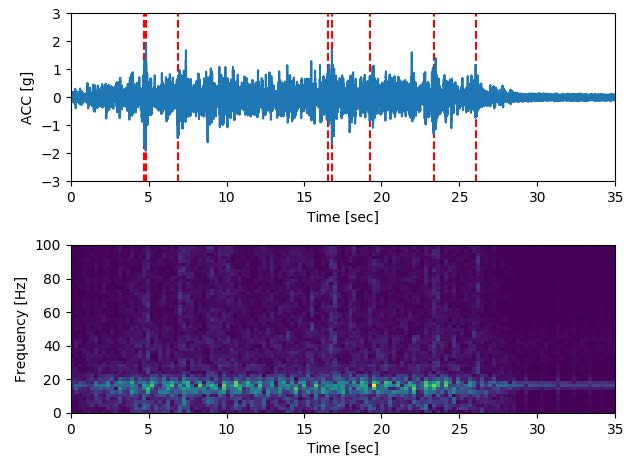
Short time fourier transform of response acceleration time histories (Z-directional) at cabinet top (A7)

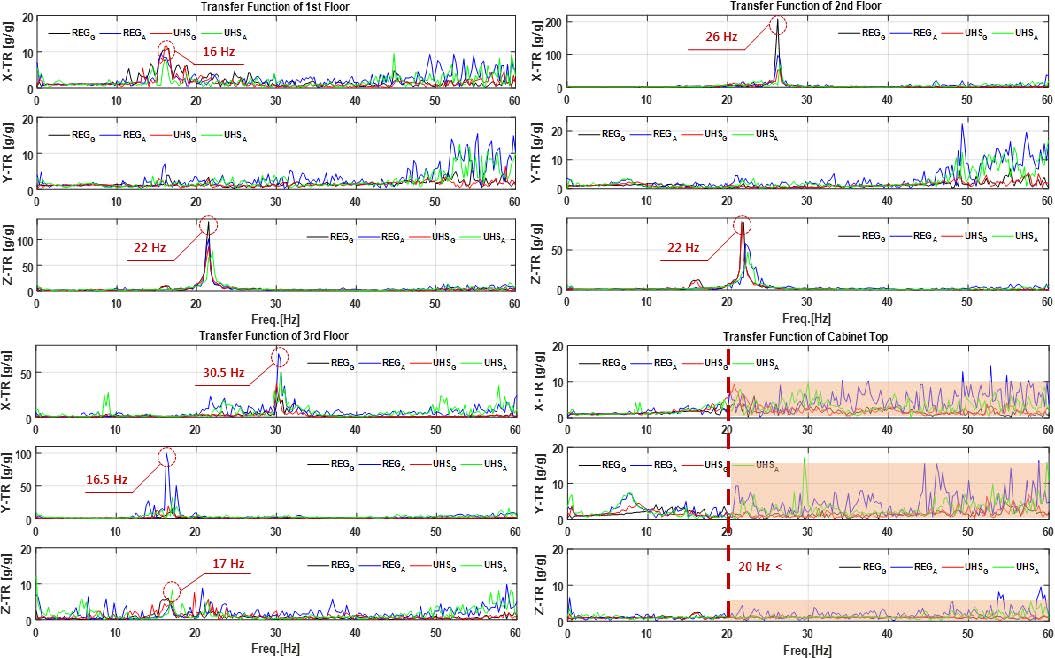
이 연구에서는 입력지진에 의한 캐비닛의 가속도 증폭현상을 분석하기 위하여 전달함수(transfer function)를 사용하였다. Fig. 11은 시간이력 시험의 가속도응답으로부터 구해진 전달함수이다. Fig. 11에서 검은 선과 푸른 선은 각각 Reg_G와 Reg_A이며 붉은 선과 초록색 선은 UHS_G와 UHS_A의 전달함수이다. 여기서 로킹이 발생한 경우는 Reg_A이며 UHS_A는 연직방향 입력가속도 값이 가장 큰 경우이다. 모형 캐비닛 내부 각 층에서의 전달함수에서 가장 큰 값이 나타나는 주파수는 공진탐색 결과와 비슷하다. Fig. 11에서 모형캐비닛 내부의 1층과 2층의 경우, 로킹으로 인한 응답의 증폭은 크지 않은 것으로 나타났다. 3층의 경우, Reg_A가진에 의한 수평방향의 진동전달함수값의 증폭이 다른 시험의 응답과 비교하여 크다. 특히 Y축은 진동전달함수의 값이 2배 이상 높은 것으로 확인되었다. 상단에서 계측된 결과에서 로킹이 발생한 Reg_A의 경우, 로킹이 발생하지 않은 경우와 비교를 하여 20 Hz이상에서 전달함수의 증폭 비율값 크게 나타나는 경향이 확인된다. 이는 로킹으로 인하여 모형캐비닛의 바닥과 강재 지그의 충돌에 의해 발생한 충격이 모형 캐비닛의 프레임을 통하여 캐비닛의 상부로 전달되며 내부 층응답의 증폭에 기여한 것으로 판단된다.

Fig. 11

Transfer function of acceleration responses

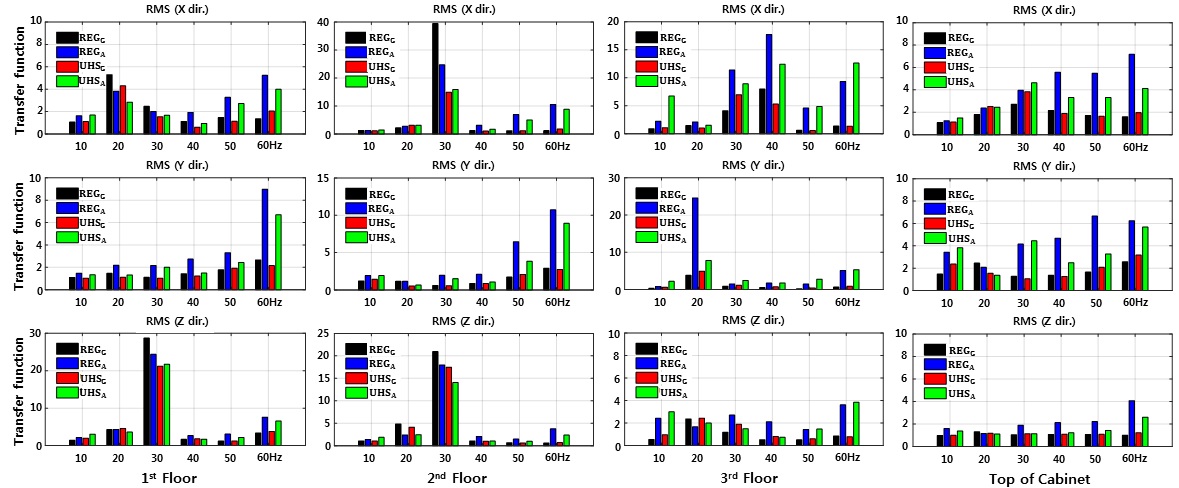
이 연구에서는 캐비닛의 로킹이 가속도응답에 미치는 영향을 분석하기 위하여 각 계측위치의 진동전달함수를 Fig. 12와 같이 정리하였다. 전달함수의 증폭비율을 평균적으로 계산하기 위하여 가속도응답의 진동전달함수를 10 Hz 구간 간격에 대한 RMS값으로 정리하였다. 식 (2)는 RMS값을 계산하기 위한 식이며 여기서 H는 진동전달함수값이다⁽¹⁶⁾.

Fig. 12

RMS values of transfer functions in the 10 Hz ranges (0.5 Hz to 60 Hz)

10 Hz 구간단위로 계산한 진동전달함수의 RMS값은 Fig. 12와 같다. 캐비닛 내부 1층과 2층의 진동전달함수는 모든 시험에 대하여 각 위치의 공진 영역에서 높은 값이 확인된다. 그러나 3층에서는 로킹이 발생한 Reg_A의 진동전달함수값이 크다. 그리고 캐비닛 상단에서는 20 Hz 이상 모든 주파수영역에서 Reg_A가진 시의 진동전달함수값이 크게 나타났다.

캐비넷 상단과 하단의 변위계에서 계측된 변위응답의 차를 이용하여 상대변위를 계산하였다. Table 5는 캐비넷 상단과 하단의 최대상대변위이다. Reg_A의 최대 상대변위가 가장 크며, Reg_G의 최대 상대변위가 가장 작다. 저주기 성분과 수평방형 가속도값이 큰 Reg_A의 경우가 수직방향의 가속도값의 크기는 크지만 저주기 성분이 낮은 UHS_A와 비교하여 높은 최대상대변위가 계산되었다. 따라서 로킹은 저주기 스펙트럼 가속도 성분이 크고 수평방향 가속도값이 높은 입력지진동에 의해 발생할 수 있으며, 캐비닛의 단방향 최대상대변위를 증폭시키는 것으로 판단된다.

Table 5

Relative displacement of cabinet bottom with top

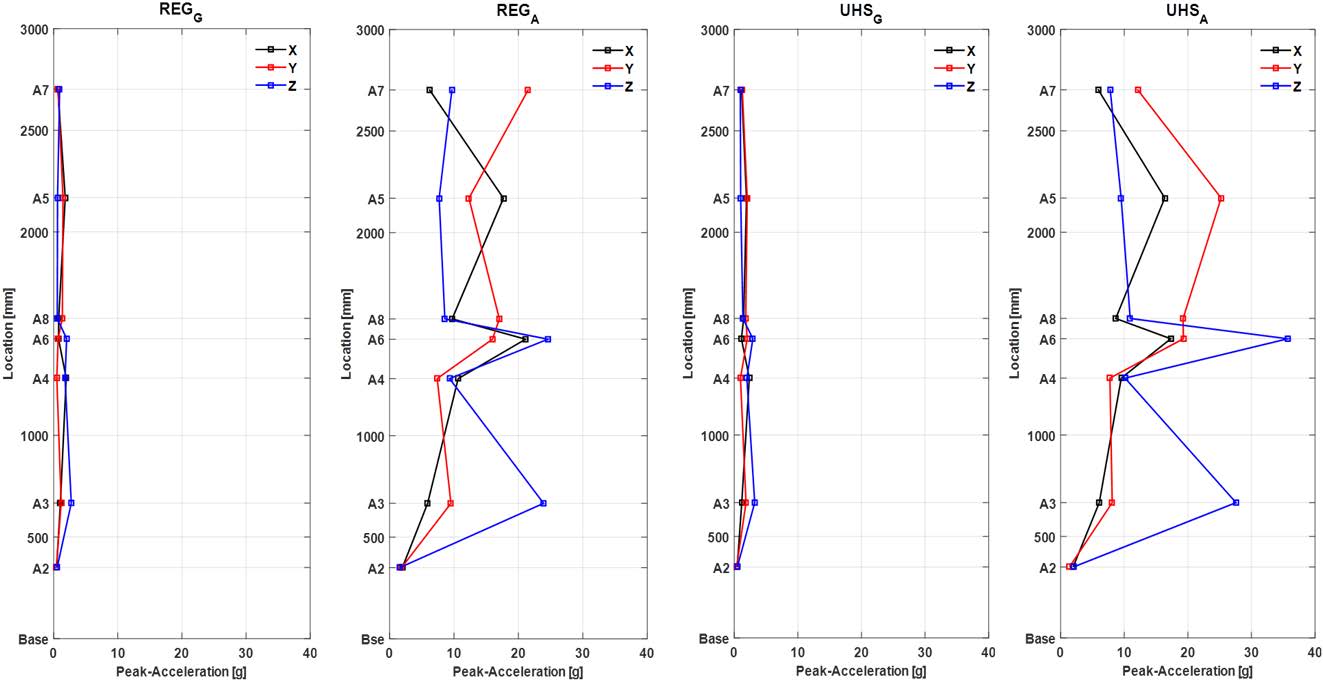
Fig. 13은 각각의 입력지진동에 대하여 캐비닛에 설치된 가속도계에서 계측된 최대가속도응답들을 정리한 것이다. 파란색은 수직방향(Z), 검은색은 좌우방향(X), 파란색은 전후방향(Y)이다. 지반에서의 지진동이 구조물에 의해 증폭된 층응답을 입력지진동으로 하는 Reg_A와 UHS_A의 시간이력시험의 경우, 높은 지진가속도에 의한 영향으로 캐비닛 문의 덜컹거림, 쿵쾅거림과 국부모드(local mode) 증폭 등의 영향으로 인하여 최대가속도응답이 Reg_G 및 UHS_G와 비교하여 상당히 높게 나타났다. Fig. 13에서 입력지진동의 영주기가속도 크기가 가장 높은 UHS_A의 시간이력 시험에서 최대가속도응답이 대부분 크게 계측되었다. 특히 문 중앙에서의 수직방향 최대가속도응답은 UHS_A가 Reg_A와 비교하여 30 % 이상 높게 나타났다. 그러나 캐비닛 상단에서는 Reg_A의 최대가속도응답이 더 높게 계측되었다.

Fig. 13

Peak acceleration responses

Table 6은 Reg_A와 UHS_A의 최대가속도응답을 정리한 것이다. 좌우방향(X)을 제외하고 UHS_A의 최대가속도 응답이 대부분 크게 나왔으나, 최상층에서는 모든 방향에서 Reg_A의 최대가속도응답이 높게 나타난 것이 확인된다. 따라서 앞서 Fig. 12와 Fig. 13의 결과와 같이 캐비닛의 바닥과 강재 지그의 충돌에 의해 발생한 충격이 캐비닛의 프레임을 통하여 상부로 전달되는 것으로 판단된다.

Table 6

Peak acceleration responses of RegA and UHSA case

6. 결 론

이 연구에서는 지진하중으로 야기되는 로킹으로 인한 캐비닛의 응답특성을 분석하기 위하여 진동대 시험을 수행하였다. 입력지진동에 따른 캐비닛의 앵커하중, 가속도응답, 진동전달특성을 분석하였으며 로킹의 발생 여부에 따른 차이를 확인하였다.

캐비닛이 앵커 볼트에 의해 고정되었을 경우 큰 지진 하중으로 인해 로킹과 들림이 발생할 수 있다. 이때 캐비닛 하부는 구조물 바닥과 충돌하여 충격을 발생시킬 수 있다. 입력 지진동의 크기가 작으면 캐비닛의 로킹이 발생하지 않을 수 있으며, 저주파 영역에서 스펙트럼 가속도 값이 높고 수평방향 성분이 강한 입력 지진에서 로킹이 발생할 수 있음을 진동대 시험을 통하여 확인하였다.

로킹과 들림으로 유발되는 충격은 캐비닛의 프레임을 통해 상단으로 전달되는 것으로 추정된다. 로킹이 발생한 Reg_A경우의 캐비닛 최상단에서 계측된 최대가속도응닶이 영주기 가속도 값이 가장 높은 UHS_A의 경우와 비교하여 모든 방향에서 더 크다.

로킹으로 인한 충격은 캐비닛 상부에서 20 Hz 이상의 주파수 영역의 진동전달함수의 값을 크게 증가시키는 것으로 분석 되었다. 캐비닛 내부 3층의 진동전달함수는 로킹과 충격의 영향으로 크게 증가한 것이 확인되었다. 그러나 캐비닛 1층과 2층의 응답은 크게 영향을 받지 않는 것으로 판단되었다. 따라서 라킹 또는 들림과 동반되는 충격의 영향이 캐비닛 상부에 집중되는 것으로 추정할 수 있다.

이 연구의 결과는 지진 하중으로 인한 전기 캐비닛의 로킹 또는 들림에 의한 캐비닛의 거동특성을 분석하는 데 필요한 기본 데이터로 활용될 수 있을 것으로 판단된다.

Acknowledgments

이 연구는 산업통상자원부(MOTIE)와 한국에너지기술평가원(KETEP)의 지원을 받아 수행한 연구 과제입니다. (No. 20171510101910).

References

• Eem, S. H., Yang, B. and Jeon, H., 2018, Earthquake Damage Assessment of Buildings Using Opendata in the Pohang and the Gyeongju Earthquakes, Journal of the Earthquake Engineering Society of Korea, Vol. 22, No, 3, pp. 121~128. [https://doi.org/10.5000/EESK.2018.22.3.121]
• Lin, F. R., Chai, J. F., Lai, Z. Y., Chen, M. Y., Huang, Y. N. and Chang, K. C., 2017, A Simplified Method for the Evaluation of Seismic Demands on In-cabinet Equipment in Motor Control Center Type Cabinets in Nuclear Power Plants, Journal of the Chinese Institute of Engineers, Vol. 40, No. 3, pp. 179~190. [https://doi.org/10.1080/02533839.2017.1303403]
• Cosenza, E., Di Sarno, L., Maddaloni, G., Magliulo, G., Petrone, C. and Prota, A., 2015, Shake Table Tests for the Seismic Fragility Evaluation of Hospital Rooms, Journal of the Earthquake Engineering Structural Dynamics, Vol. 44, No. 1, pp. 23~40. [https://doi.org/10.1002/eqe.2456]
• Kim, D. K., Cho, S. G., Joe, Y. H., Yi, J. H. and Ko, S. H., 2009, Modal Parameter Identification of Cabinets of Nuclear Power Plant, Proceedings of the Earthquake Engineering Society of Korea Conference, Yongin, Korea.
• Gupta, A., Rustogi, S. K. and Gupta, A. K., 1999, Ritz Vector Approach for Evaluating In-cabinet Response Spectra, Nuclear Engineering and Design, Vol. 190, No. 3, pp. 255~272. [https://doi.org/10.1016/S0029-5493(99)00076-X]
• Yang, J., Rustogi, S. K. and Gupta, A., 2003, Rocking Stiffness of Mounting Arrangements in Electrical Cabinets and Control Panels, Nuclear Engineering and Design, Vol. 219, No. 2, pp. 127~141. [https://doi.org/10.1016/S0029-5493(02)00279-0]
• Han, M. S., Cho, S. K., Hong, K. J. and Gupta, A., 2018, Rocking Stiffness of Electric Cabinet Considering the Local Deformation at the Base, Transactions of the Korean Nuclear Society Spring Meeting, Jeju, Korea, https://www.kns.org/files/pre_paper/39/18S-381%ED%95%9C%EB%AF%BC%EC%88%98.pdf, .
• Yun, D. W., Jeon, B. G., Jung, W. Y., Chang, S. J. and Shin, Y. J., 2019, Analysis of Anchorage Behavior Characteristics of the Electrical Cabinet Using Shaking Table Tests, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 29, No. 1, pp. 43~50. [https://doi.org/10.5050/KSNVE.2019.29.1.043]
• Nuclear Regulatory Commission, 1973, Design Response Spectra for Seismic Design of Nuclear Power Plants, Regulatory Guide 1.60, https://www.nrc.gov/docs/ML0037/ML003740207.pdf, .
• Rhee, H. M., Kim, M. K., Sheen, D. H. and Chol, I. K., 2013, Analysis of Uniform Hazard Spectra for Metropolises in the Korean Peninsula, Journal of the Earthquake Engineering Society of Korea, Vol. 17, No. 2, pp. 71~77. [https://doi.org/10.5000/EESK.2013.17.2.071]
• American Society of Civil Engineering, 2000, Seismic Analysis of Safety-related Nuclear Structures and Commentary, ASCE 4-98. [https://doi.org/10.1061/9780784404331]
• ICC Evaluation Service, 2018, Seismic Certification by Shake-table Testing of Nonstructural Components, ICC-ES AC156, https://icc-es.org/acceptance-criteria/ac156, /.
• Di Sarno, L., Magliulo, G., D’Angela, D. and Cosenza, E., 2019, Experimental Assessment of the Seismic Performance of Hospital Cabinets Using Shake Table Testing, Earthquake Engineering Structural Dynamics, Vol. 48, No. 1, pp. 103~123. [https://doi.org/10.1002/eqe.3127]
• Oppenheim, A. V., Ronald W. S. and John, R. B., 1999, Discrete-time Signal Processing, Prentice Hall, Upper Saddle River, NJ, USA.
• Griffin, D., Lim, J., 1984, Signal Estimation from Modified Short-time Fourier Transform, 1984, IEEE Transactions on Acoustics, Speech, and Signal Processing, Vol. 32, No. 2, pp. 236~242. [https://doi.org/10.1109/TASSP.1984.1164317]
• Institute of Electrical and Electronics Engineers, 2003, IEEE Standard on Transitions, Pulses, and Related Waveforms, IEEE Std 181-2003. [https://doi.org/10.1109/IEEESTD.2003.94394]