[ Article ]

Transactions of the Korean Society for Noise and Vibration Engineering - Vol. 30, No. 1, pp.37-44

ISSN: 1598-2785 (Print) 2287-5476 (Online)

Print publication date 20 Feb 2020

Received 02 Dec 2019 Revised 08 Jan 2020 Accepted 08 Jan 2020

DOI: https://doi.org/10.5050/KSNVE.2020.30.1.037

차량 도어 래치의 작동력 계산을 위한 수식 유도 : 파트 1- 캐치, 파울 및 릴리스 래버

이예호^* ; 이태훈^** ; 최승복^† ; 윤근하^*** ; 김완현^*** ; 정병대^*** ; 이진복^*** ; 김다빈^*** ; 신진용^***

Calculation Formula for Operating Force of Vehicle Door Latch : Part 1- Catch, Pawl and Release Lever

Ye-Ho Lee^* ; Tae-Hoon Lee^** ; Seung-Bok Choi^† ; Gun-Ha Yoon^*** ; Wan-Hyun Kim^*** ; Byoung-Dae Jung^*** ; Jin-Bok Lee^*** ; Da-Bin Kim^*** ; Jin-Young Shin^***

*Dept. of Construction Machinery Eng., Inha University, Student
**Dept. of Mechanical Eng., Inha University, Student
***Part Design 1 Team, Pyeonghwa Automotive Co., Researcher

Correspondence to: ^†Fellow Member, Dept. of mechanical Eng., Inha University, Professor E-mail : seungbok@inha.ac.kr ‡ Recommended by Editor Jun hong Park

Abstract

Numerous studies on improving the emotional quality and automatic functionality of automobiles have recently been conducted based on various aspects. The first components touched by passengers are the vehicle doors, and thus the feeling of the opening and closing of the doors is a significant emotional quality and should be treated seriously. In this regard, mathematical equations calculating the operating force of the door latch, which have yet to be reported elsewhere, are formulated in this study. The forces acting on each component are gravity, elasticity, friction, and the normal force. Therefore, the door latch operating force has been formulated as the moment of the force action because all parts rotate about the axis of rotation. Because there are numerous parts used in a door latch, this study is divided into two parts. In part 1, formulas used to calculate the operating force of the catch, pawl, and release lever are determined. And formulas for calculating the OS levers, IS levers and the maximum operating force are analyzed in part 2. In addition, a clear definition of the opening point and the operating force up to the release lever is formulated.

Keywords:

Door Latch, Operating Force, Vehicle Sensibility, Maximum Torque, Various Levers

키워드:

도어 래치, 작동력, 차량감성, 최대토크, 다양한 래버

1. 서 론

최근 차량에 대한 소비자들이 느끼는 ‘고급감’, ‘심미감’과 같은 감성 요인들을 향상시켜 차량의 경쟁력을 향상시키는 방안이 강조되고 있다. 기존의 차량 성능 향상뿐만 아니라 감성 품질 향상으로 소비자에게 만족감을 줄 수 있기 때문에, 기업들은 감성 품질 향상을 위한 연구⁽¹⁾를 진행 중이다. 차량 감성 품질로 소비자가 느낄 수 있는 요소로는 차량의 여러 부분에서 청각⁽²⁾, 시각, 촉각을 들 수 있다. 이중 소비자가 차량에 가장 먼저 접할 수 있는 차량 도어(door)에 감성 품질에 대한 다양한 연구⁽³⁾가 진행 중이다. 예를 들어, 소음 개선을 위한 차량 도어 래치(door latch)의 소음진동 특성 평가⁽⁴⁾와 열림감 향상을 위한 도어 래치 매커니즘 연구 그리고 도어 래치의 충격 소음 개선을 위한 연구가 진행되었다.

도어 래치는 도어 락(door lock)이라고 불리며 자동차의 도어에 장착되며, 차체의 스트라이커(striker)와 맞물려 닫힘 상태를 유지하고 자동차 내부 인명의 안전 및 물품의 보안성을 확보하는 역할을 한다. 도어 손잡이의 촉각에 대한 감성품질을 향상시키기 위해서는 이 도어 래치의 정밀한 설계가 필요하다. 차량 도어의 손잡이를 잡는 순간부터 열림 상태가 되는 순간까지는 도어 래치에 의해 결정된다. 도어 래치의 부품들은 동전크기의 작은 형태들이기 때문에 정확한 부품 간의 작동력을 구할 수 있어야 각각의 요소가 전체 작동력에 어떠한 영향을 주는지 알 수 있다^(5,6). 하지만 이전의 도어 래치의 수학적 모델을 구성한 도어 개폐 필링 개선을 위한 도어 래치 설계인자 및 최적화 논문⁽⁷⁾에서는 작동력에 지배적으로 영향을 주는 토션 스프링과 무게중심 등을 고려하지 않고 진행하였다. 또한 손잡이를 잡은 순간부터 열리는 시점까지의 전체적인 작동력 경향성을 파악하기 위해선 명확한 열리는 시점의 정의가 필요하다.

따라서 이 논문에서는 이와 같은 문제를 해결하기 위해 도어 래치 모듈의 부품간 기구학적 수식을 차량 문이 완전히 닫힌 상태인 ‘세컨드 락(second's lock)’ 상태부터 캐치와 파울의 접촉에 의한 ‘열림 상태’까지 정확하게 수립하도록 한다. 도어 래치에는 여러 부품들이 구성되어있기 때문에 파트1과 파트2로 나누었다. 파트1에서는 손잡이에 연결되어있는 캐치부터 바깥문과 안쪽 문이 나뉘어지는 릴리스 래버까지 수식화 하도록 하며 문이 열리는 열림 시점을 명확히 정의한다. 이를 통해 제품의 정확한 최대 작동력을 도출할 수 있도록 하며, 작동력의 경향성을 파악할 수 있도록 한다. 나아가 이를 바탕으로 각각의 요소가 작동력에 기여하는 경향성을 분석하고 도어 열림의 감성 품질 향상에 도움이 될 수 있는 설계 방향을 제시한다.

2. 도어 래치의 구조 및 캐치작동력 계산

2.1 도어 래치의 구조

손잡이로부터 영향을 주는 부품은 총 6가지로 정의할 수 있으며, 사용자가 느끼는 작동력은 손잡이에 따라 아래와 같이 두 가지 순서로 전달된다.

(1) 캐치(catch) → 파울(pawl) → 락 링크(lock link) → 릴리스 래버(release lever) → IS 래버(IS lever)

(2) 캐치 → 파울 → 락 링크 → 릴리스 래버 → OS 래버(OS lever)

도어 래치 각 파트의 부품 형상과 역할은 Fig. 1에 도식화 하였다.

Fig. 1

Name and function of door latch parts

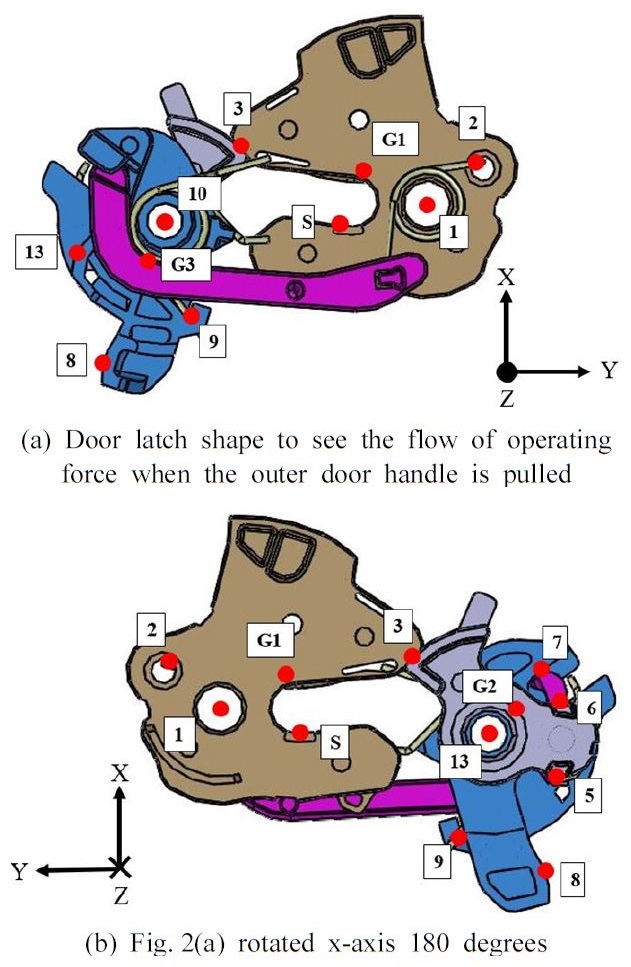
Fig. 2(a)는 바깥문의 손잡이를 당겼을 경우 전체 작동력의 흐름을 볼 수 있는 형상으로 Fig. 2(b)는 Fig. 2(a)의 그림을 x축으로 180˚ 회전한 형상이다. 바깥 손잡이의 경우 점 15에서 바깥문과 케이블이 연결된 부분으로 작동력이 가해지는 시작점이다. 점 1, 4, 10, 12는 각 부품의 회전 중심을 나타낸다. 점1은 캐치의 회전 중심, 점12는 OS래버의 회전 중심이다. 점4는 파울의 회전중심이고 점10은 릴리스 래버의 회전 중심으로 같은 핀에 연결되어있다. 각 부품 별로 비틀림(torsion) 스프링이 1개씩 부착되어 있고 점 2, 5, 9, 14에 각각 적용 되어있다. 점 2는 캐치의 스프링, 점 5는 파울의 스프링, 점 9는 릴리스 래버의 스프링, 점 14는 OS래버의 스프링이 가해지는 지점이다. 점 3은 캐치와 파울이 마찰력에 의해 붙어있는 지점으로 열림(open)시점을 결정하는 부분이다. G1, G2, G3, G4, G5는 각각 캐치, 파울, 릴리스 래버, OS래버, IS래버 부품의 무게중심으로 중력이 작용하는 지점이다. 점 S는 스트라이커(striker)의 반력(seal force)가 적용되는 지점으로 자동차 본체에 부착되어 있는 스트라이커에 의해 작용한다.

Fig. 2

Free body diagram of door latch

이 논문에서는 각 요소에서 발생하는 작동력을 각각 정의하고, 이를 통해 최종적으로 IS 래버와 OS 래버로 전달되는 최종 작동력을 도출하여 사용자가 느끼는 힘의 값이 어느 정도가 될 수 있는지 계산한 후 매개변수를 변화하여 최대 작동력의 영향을 주는 요인에 대하여 분석한다.

2.2 캐치 작동력 계산 수식

차량 문이 잠겨있는 상태를 부품의 측면에서 볼 때 캐치와 파울이 마찰력에 의해 고정되어 있는 상태인 Fig. 2의 형상을 ‘세컨드 락 상태’라고 한다. 세컨드 락 상태에서 캐치는 항상 정지하고 있기 때문에 수식은 정역학에 기인하여 수립될 수 있다. 세컨드 락 상태에서 캐치의 회전 중심점과 힘의 작용점은 Fig. 2(a)와 같이 정의된다. 점 1은 캐치의 회전 중심점을 나타내며 점 2는 비틀림 스프링의 탄성력의 작용점, 점 3은 캐치와 파울 사이의 수직항력과 마찰력의 작용점을 나타낸다. 점 S는 스트라이커에 걸리는 반력으로 x축과 평행한 방향으로 300 N 크기로 고정한다. G1은 캐치의 무게중심점을 나타낸다. 정지 상태이기 때문에 관성력을 배제할 경우, 점1에서 모멘트의 합은 0으로 정의할 수 있다.

여기서 캐치 스프링에 의한 모멘트(M_ck)는 다음과 같다. 스프링 계수(k_catch)는 k_catch = 0.066 kgf·mm/deg이며, 도어가 완전히 닫혀있는 상태의 캐치 스프링의 초기 응축각도(θ_0catch)는 119˚이다.

M c k = k c a t c h θ 0 c a t c h - θ c k g f ⋅ m m = k c a t c h θ 0 c a t c h - θ c ∕ 0.102 N ⋅ m m

(1)

Fig. 2(a)의 점 G1에서 중력(F_G1)과 점1과 G1까지의 거리(r_G1,1)에 의한 캐치의 모멘트(M_G1)는 다음과 같다. g는 중력가속도이다. 중력은 y방향으로 작용하기 때문에 점 1과 G1사이 거리의 x방향길이(r_G1,1)_x를 적용한다.

M G 1 = F G 1 ⋅ r G 1,1 x = m c ⋅ g ⋅ r G 1,1 x

(2)

Fig. 2(a)의 점 S에서 도어 외부 반력(F_seal)과 점 1, S의 사이거리(r_1,s)에 의한 캐치의 모멘트(M_S)는 다음과 같다.

M s = F s e a l ⋅ r 1, s

(3)

Fig. 2(a)의 점 3에서 캐치와 파울이 접촉한 면의 수직항력(F₃)과 마찰력(F_3f)에 의한 모멘트는 점 1과 3사이 거리(r_1,3)에 의해 x축 방향 힘과 y축 방향 힘으로 다음과 같이 나타낼 수 있다. (r_1,3)_x는 점 1과 3사이 거리의 x축 길이, (r_1,3)_y는 y축 길이이다.

M 3 + M 3 f = F 3 x ⋅ r 1,3 y - F 3 y ⋅ r 1,3 x + F 3 f x ⋅ r 1,3 y - F 3 f y ⋅ r 1,3 x

(4)

여기서 수직항력(F₃)과 마찰력(F_3f)의 x축 방향 힘과 y축 방향 힘은 x축과 힘의 방향(α)에 의해 다음과 같다. α_F3x는 수직항력과 x축 사이각, α_F3fx는 마찰력과 x축 사이각이다. μ는 점 3에서의 마찰계수이다.

F 3 x = F 3 ⋅ cos ⁡ α F 3 x F 3 y = F 3 ⋅ sin ⁡ α F 3 x F 3 f x = μ F 3 ⋅ cos ⁡ α F 3 f x F 3 f y = μ F 3 ⋅ sin ⁡ α F 3 f x

(5)

Fig. 2(a)의 점 3의 힘 F₃은 아래와 같이 수립될 수 있다.

M 3 + M 3 f = F 3 x ⋅ r 1,3 y - F 3 y ⋅ r 1,3 x - F 3 f y ⋅ r 1,3 x + F 3 f x ⋅ r 1,3 y = F 3 ⋅ cos ⁡ α F 3 x ⋅ r 1,3 y - F 3 ⋅ sin ⁡ α F 3 x ⋅ r 1,3 x - μ F 3 ⋅ sin ⁡ α F 3 f x ⋅ r 1,3 x + μ F 3 ⋅ cos ⁡ α F 3 f x ⋅ r 1,3 y = F 3 ⋅ cos ⁡ α F 3 x ⋅ r 1,3 y - sin ⁡ α F 3 x ⋅ r 1,3 x - μ ⋅ sin ⁡ α F 3 f x ⋅ r 1,3 x + μ ⋅ cos ⁡ α F 3 f x ⋅ r 1,3 y

(6)

F 3 = - k c a t c h θ 0 c a t c h - θ c ∕ 0.102 - m c ⋅ g ⋅ r G 1,1 x - F s e a l ⋅ r 1, s y ∕ cos ⁡ α F 3 x ⋅ r 1,3 y - sin ⁡ α F 3 x ⋅ r 1,3 x - μ ⋅ sin ⁡ α F 3 f x ⋅ r 1,3 x + μ ⋅ cos ⁡ α F 3 f x ⋅ r 1,3 y ∑ M 1 = M c k + M G 1 + M 3 + M 3 f + M S = 0 = k c a t c h 119 ° - θ c / 0.10197 + m c ⋅ g ⋅ r G 1,1 x + F 3 ⋅ cos ⁡ α F 3 x ⋅ r 1,3 y - sin ⁡ α F 3 x ⋅ r 1,3 x - μ ⋅ sin ⁡ α F 3 f x ⋅ r 1,3 x + μ ⋅ cos ⁡ α F 3 f x ⋅ r 1,3 y + F s e a l ⋅ r 1, s = 0

(7)

캐치의 모멘트 방향은 시계방향을 +로 지정되었으며, 마찰계수 μ는 0.2로 정의한다. 최종적으로 주어진 변수에 따른 캐치와 파울 사이의 전달력 F₃의 크기는 190.1969 N로 도출된다. Table 1은 캐치에 관련된 변수들의 정의를 나타낸다.

Table 1

Variables used in dynamic equation at catch

2.3 파울 작동력 계산 수식

Fig. 2(a)의 점 3에서 운동마찰력과 수직항력, 점 G2에서 질량중심에 의한 중력, Fig. 2(b)에서 점 5에서 토션 스프링(torsion spring)의 탄성력, 점 6에서 릴리스 래버와 연결된 락 링크의 반력이 작용한다. 점 6에 작용하는 모멘트(M₆)는 나머지 모멘트들의 합보다 커야 세컨드 락에서 열림 상태로 갈 수 있다. 따라서 이의 관계를 아래 부등식과 같이 표현 할 수 있다.

M 6 - M p k - M 3 f + M G 2 ≥ 0 M 6 ≥ M p k + M 3 f - M G 2

(8)

여기서 스프링에 의한 모멘트(M_pk)는 파울의 스프링 회전각도(θ_p)에 따라 다음과 같다. 파울의 스프링 계수(k_pawl)는 0.1138 kgf·mm/deg이며, 도어가 완전히 닫혀있는 상태의 파울 스프링 초기 응축각도(θ_0pawl)는 56°이다.

M p k = k p a w l ⋅ θ 0 p a w l + θ p k g f ⋅ m m = k p a w l θ 0 p a w l + θ p ∕ 0.10197 N ⋅ m m

(9)

중력(F_G2)에 의한 모멘트(M_G2)는 점 G2와 4사이거리 x축 길이(r_G2,4)_x에 의해 다음과 같다.

M G 2 = F G 2 ⋅ r G 2,4 x = m p ⋅ g ⋅ r G 2,4 x

(10)

점 3에서 파울에 작용하는 수직항력의 방향은 세컨드 락에서 열림 상태까지 회전중심으로 지나가기 때문에 수직항력에 의한 모멘트는 없다. 마찰력에 의한 모멘트는 다음과 같다. 여기서 파울이 open상태로 회전하면서 캐치의 움직임은 없다고 가정한다.

M 3 f = μ F 3 ⋅ r 3,4

(11)

점 6에 작용하는 모멘트는 아래와 같이 정의될 수 있다. Table 2는 파울에 관련된 변수들의 정의를 나타낸다.

M 6 - M p k - M 3 f + M G 2 ≥ 0 M 6 ≥ M p k + M 3 f - M G 2 = k p a w l θ 0 p a w l + θ p / 0.102 + μ F 3 ⋅ r 3,4 - m p ⋅ g ⋅ r G 2,4 x N ⋅ m m

(12)

Table 2

Variables used in dynamic equation at PAWL

2.4 릴리스 래버 계산 수식

릴리스 래버의 움직임은 아래와 같이 회전 각도(θ_R)에 따라 2가지 스텝(step)으로 구분한다. 첫 번째 단계는 릴리스 래버가 Fig. 2(a)의 점13과 Fig. 2(b)의 점8에서 각각 OS래버와 IS래버의 비 접촉부터 접촉이 되는 순간까지의 구간이다. 두 번째 단계는 접촉 이후부터 Fig. 2(a)의 점 3에서 캐치와 파울이 분리되는 열림 상태까지의 구간을 말한다.

(1) Step 1

0°≤ θ_R ≤ 2.5116°: 릴리스 래버가 IS 래버 또는 OS 래버와 충돌 후 파울과 충돌 전 회전각도

(2) Step 2

2.5116°≤ θ_R ≤12°: 릴리스 래버가 파울과 충돌 후 open 상태까지의 회전 각도

모든 충돌은 완전 비 탄성 충돌로 가정하여 충돌 이후 두 부품이 붙어서 운동한다. 락 링크는 릴리스 래버의 위 아래쪽 면과 붙어있다고 가정한다. 파울이 열림 상태로 갈 수 있는 Fig. 2(b)의 점 6에서 최소 모멘트를 적용한다. 점 7에서의 모멘트(M₇)는 점 6과점 7의 회전중심으로부터 거리 비율로 나타낼 수 있다. 점 9는 릴리스 래버의 토션 스프링이 작용하는 지점이다. 점 8과 점 13은 각각 IS 래버와 OS 래버의 전달되는 힘이 작용하는 지점이다. 이 부분부터 작동력은 2가지로 수식화 된다. 점 10에서의 모멘트의 합은 점 8, 또는 점 13의 모멘트 경우에서 보다 작아야 하며 이는 아래의 식처럼 나타낼 수 있다.

M 7 = r 7,10 r 4,6 M 6 = r 7,10 r 4,6 k p a w l θ 0 p a w l + θ p / 0.102 + μ F 3 ⋅ r 3,4 - m p ⋅ g ⋅ r G 2,4 x

(13)

M 8 - M 7 + M G 3 - M R k ≥ 0 M 8 ≥ M 7 - M G 3 + M R k

(14)

릴리스 래버 회전반경(θ_R)과 스프링에 의한 모멘트(M_Rk)는 다음과 같다. 스프링 계수는 0.095 kgf·mm/deg이며, 도어가 완전히 닫혀있는 상태의 스프링 사이 각(θ_0release)은 37.6°이다.

M R k = k r e l e a s e ⋅ θ 0 r e l e a s e + θ R k g f ⋅ m m = k r e l e a s e ⋅ θ 0 r e l e a s e + θ R ∕ 0.102 N ⋅ m m

(15)

중력(F_3G)에 의한 모멘트(M_G3)는 다음과 같다.

M G 3 = F G 3 ⋅ r G 3,10 x = m R ⋅ g ⋅ r G 3,10 x

(16)

릴리스 래버에서 OS래버의 경우 점 13과 IS 래버의 경우 점 8에서 필요한 최소 모멘트는 아래와 같이 각각 step에 따라 정의될 수 있다.

1 S t e p 1 M 13 + M G 3 - M R k ≥ 0 M 13 ≥ - M G 3 + M R k = - m R ⋅ g ⋅ r G 3,10 x + k r e l e a s e ⋅ θ 0 r e l e a s e + θ R ∕ 0.102

(17)

2 S t e p 2 M 13 - M 7 + M G 3 - M R k ≥ 0 M 13 ≥ M 7 - M G 3 + M R k = r 7,10 r 4,6 k p a w l θ 0 p a w l + θ p / 0.10197 + μ F 3 ⋅ r 3,4 - m p ⋅ g ⋅ r G 2,4 x - m R ⋅ g ⋅ r G 3,10 x + k r e l e a s e ⋅ θ 0 r e l e a s e + θ R ∕ 0.102

(18)

Table 3

Variables used in dynamic equation at release lever

IS 래버의 경우 모멘트는 아래와 같이 정의될 수 있다.

1 S t e p 1 M 8 ≥ - M G 3 + M R k = - m R ⋅ g ⋅ r G 3,10 x + k r e l e a s e ⋅ θ 0 r e l e a s e + θ R ∕ 0.102

(19)

2 S t e p 2 M 8 - M 7 + M G 3 - M R k ≥ 0 M 8 ≥ M 7 - M G 3 + M R k = r 7,10 r 4,6 k p a w l θ 0 p a w l + θ p / 0.10197 + μ F 3 ⋅ r 3,4 - m p ⋅ g ⋅ r G 2,4 x - m R ⋅ g ⋅ r G 3,10 x + k r e l e a s e ⋅ θ 0 r e l e a s e + θ R ∕ 0.102

(20)

2.5 열림 시점 수립

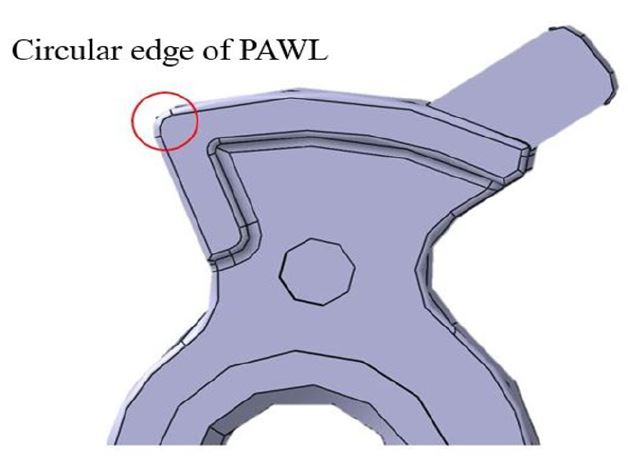
파울과 캐치의 접촉부분 Fig. 2(a)의 점 3에서 수직항력은 파울의 회전중심을 지나기 때문에 모멘트를 고려하지 않아도 무방했다. 그리고 파울의 캐치와 접촉하는 부분은 Fig. 3처럼 파울의 형상이 원이 형태이기 때문에 파울이 회전하면서 수직항력은 항상 파울의 회전중심을 지났다.

Fig. 3

Circular edge of pawl

Fig. 3에서 적색 원 부분은 파울의 모서리로 원의 형태이기 때문에 모서리 시작부터 열림 순간 전까지 수직항력이 파울의 회전중심을 지나지 않고, 모서리 부분의 작은 원의 중심을 지나게 된다. 마찰력뿐만 아니라 수직항력 또한 파울 모멘트에 영향을 주기 때문에 정확한 열림 시점에 대한 정의가 필요하다.

파울 작동력 수식 수립에서 Fig. 2(b)의 점 6은 릴리스 래버에 전달되는 모멘트로 나머지 모멘트의 총합과 같거나 크다고 정의했다. 따라서 수직항력에 의한 모멘트가 포함된다면 점 6에서 정의한 모멘트 식 (8)에서 수직항력에 의한 모멘트를 추가해준다. 그리고 총합이 0이 되는 순간을 열림 시점으로 정의한다.

M 6 - M p k - M 3 f + M G 2 + M n o r m a l f o r c e = 0

(21)

2.6 수식화를 통한 모멘트 분석

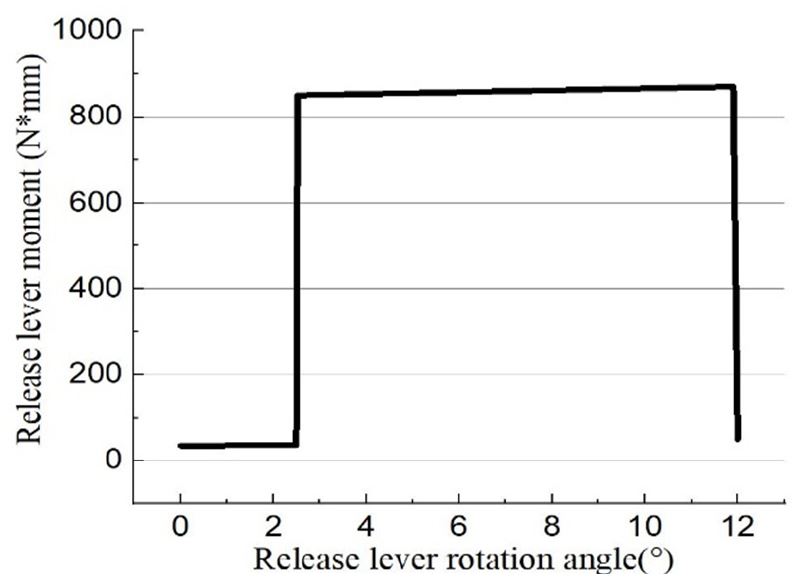
Fig. 4는 릴리스 래버가 파울과 충돌하기 전부터 열림 시점까지 Fig. 2(b) 점 7에서 회전하기 위한 최소 모멘트를 나타낸 그림이다. 파울과 충돌하기 전후 2.5°부근에 37 N·mm에서 850 N·mm만큼 증가하는 것을 확인할 수 있다.

Fig. 4

Release lever moment

도어 래치 감성품질을 결정할 수 있는 최대 작동력은 870.7435 N·mm이며, 릴리스 래버의 회전각도 12°부근에서 열림 시점이 적용되어 점 7에서 회전하기 위한 최소 모멘트가 급격히 떨어지는 형상을 확인할 수 있다. 이를 통해 최대 작동력의 크기를 조절하면서 사용자의 기호에 맞게 최대 작동력을 변화시켜 감성품질 향상에 도움을 줄 수 있다.

3. 결 론

이 논문에서는 차량 도어의 감성품질 향상을 위해 도어 래치의 작동력 수식화 및 열림 시점을 정의하였다. 도어 래치의 부품 중 캐치, 파울, 릴리스 래버를 단계적으로 수식화하고 캐치와 파울 사이의 열림 시점을 정의하였다. 부품의 가해지는 모멘트나 작동력을 구하기 위해 캐치와 파울은 마찰력, 탄성력 그리고 스트라이커에 의한 반력에 의해 서로 접촉되어 있고, 이보다 큰 모멘트가 파울에 작용해야 두 부품이 해체 될 수 있다. 여기서 파울의 힘은 릴리스 래버로부터 전달된다. 작동력을 구하기 위해 자유 물체도를 바탕으로 구조의 수식화를 진행하였으며, 최종적으로 회전각도에 따른 모멘트 그래프를 얻을 수 있다. 릴리스 래버와 파울이 충돌하기 전후에 급격히 변화하였으며 열림 시점에 급격히 감소하는 것을 알 수 있다.

향후 심화된 연구를 통해 도어 래치의 전체 작동력을 수식화하고 수식을 통해 각 부품들의 변수를 변화하여 최대 작동력에 기여하는 부분을 확인할 것이다. 이를 통해 최대 작동력에 가장 큰 기여가 있는 부품의 변수를 변화하여 차량 감성품질 향상에 도움을 줄 수 있다.

Acknowledgments

이 논문은 ㈜평화정공의 지원을 받아 작성된 논문입니다(과제번호: 59646-01).

References

Nam, J. W., Lee, S. H., Seo, S. W. and Jung, C. H., 2014, Research Door Latch Mechanism for Improving Door Open Feeling, Proceedings of the KSAE Annual Autumn Conference, pp. 1095~1096.
Zhang, Z. and Young, S, 2005, Low Frequency Transient CAE Analysis for Vehicle Door Closure Sound Quality, Proceedings of the SAE Noise and Vibration Conference, pp. 1~10. [https://doi.org/10.4271/2005-01-2339]
Kim, B. S., 2011, A Study on the Advancement of Door Opening & Closing Effort, Proceedings of the KSAE Annual Autumn Conference, pp. 2291~2300.
Hur, S. B., Oh, J. C., Ahn, S. J., Byeon, S. G. and Cho, H. D., 2014, Study of Claw Shock Noise Improvement to Automotive Door Latch, Proceedings of the KSNVE Annual Spring Conference, pp. 269~270.
Jung, Y. H., 1996, Assembly-centric Modeling Methodology for Large Assembly Design, Proceedings of the KSAE Annual Autumn Conference, pp. 200~208.
Lee, H. W. and Park, N. G., 2005, A Study on Dynamic Characteristics of Gear-system, Journal of the Korean Society for Precision Engineering, Vol. 22, No. 11, pp. 111~117.
Son, J. H., Hur, S. B., Oh, J. C., Byun S. G. and Cho, H. D., 2013, Optimization & Design Factors of Door Latch for Improved Feeling of Door Open & Close, Proceedings of the KSAE Annual Conference, pp. 15~18.

Seung-Bok Choi received the B.S. degree in Mechanical Engineering from Inha University in 1979, MS degree and Ph.D. degrees from Michigan State University in 1986 and 1990, respectively. He is currently Dean of the Graduate School and fellow professor in Inha University. He is a fellow of NAEK (National Academy Engineering of Korea), KAST (The Korean Academy of Science and Technology). His research interests are robust controller design and control of various systems using smart actuators.

Symbol	Specification
m_c	Catch mass
k_catch	Spring constant of catch spring
θ_c	Rotation angle of Catch
α_G1,1	Angle between point G1 and 1
r_G1,1	Length between point G1 and 1
r_1,3	Length between point 1 and 3
r_1,s	Length between point 1 and point S
α_r1,3x	Angle between point 1 and point 3 distance direction and x axis
α_F3x	Angle between vertical drag and x-axis
α_F3fx	Angle between frictional force and x-axis
F_seal	Seal force
M_ck	Moment of catch spring
M_s	Moment of seal force
M₃	Moment of vertical drag at point 3
M_3f	Moment of friction force at point 3
θ_0catch	Initial angle of Catch spring with door fully closed

Symbol	Specification
m_p	Mass of PAWL
K_pawl	The spring constant of PAWL
θ_p	Rotation angle of PAWL
α_G2,4x	Angle between point G2 and point 4 distance direction and x axis
r_G2,4	Distance between point G2 and point 4
(r_G2,4)_x	The x-direction length of the distance between point G2 and point 4
r_3,4	Distance between points 3 and 4
M_pk	Moment of pawl spring
M_G2	Pawl moment of gravity
M₆	Moment of point 6
θ_0pawl	Initial angle of Pawl spring with door fully closed

Symbol	Specification
m_R	Mass of release lever
k_release	Spring constant of release lever
θ_R	Rotation angle of release lever
α_G3,10	Angle between distance G3,10 and x axis
r_G3,10	Distance between points G3 and 10
(r_G3,10)x	The x-direction length of the distance between points G3 and 10
M₇	Moment of point 7
M_Rk	Moment of release lever spring
M₈	Moment of point 8
M_G3	Release lever moment of gravity
M₁₃	Moment of point 13
θ_0release	Initial angle of Release lever spring with door fully closed