연료 슬로싱 효과를 고려한 위성 기동 간의 SAR 안테나 반사판의 진동 분석
‡ Recommended by Editor Won Ju Jeon
© The Korean Society for Noise and Vibration Engineering
Abstract
Sloshing refers to the movement of a liquid free surface caused by disturbances of a liquid partially filled in a container. Sloshing generates forces and moments owing to the pressure distribution on the liquid free surface, which affect the dynamic stability of the vessel. An equivalent mechanical model that exerts the same amount of force and moment on the vessel wall as sloshing is used to analyze the sloshing effect on the vessel. This phenomenon also occurs in the fuel tank of a satellite structure that controls the attitude using a propulsion system with a liquid propellant. A satellite with a deployable synthetic-aperture radar (SAR) antenna, which is made of a thinner and lighter material, is likely to be more susceptible to various disturbances, including liquid sloshing. In this study, an analysis of a deployable SAR antenna reflector vibrating from the liquid fuel sloshing between the changes in the satellite’s attitude was conducted. The equivalent mechanical model is used to simulate the sloshing effect, and the vibrations of the reflector are compared and analyzed with and without the sloshing effect for the specified torque input.
Keywords:
Sloshing, Equivalent Mechanical Model, SAR Antenna키워드:
슬로싱, 등가 기계 모델, SAR 안테나1. 서 론
슬로싱(sloshing)은 용기에 부분적으로 채워진 액체의 자유유체표면(free liquid surface)의 움직임을 말한다. 이러한 슬로싱은 용기에 있어 외란을 발생시키고, 이는 용기와 용기를 포함하는 구조체의 동적 안정성에 영향을 끼칠 수 있다. 이러한 영향 때문에, 1960년대부터 액체 연료 슬로싱이 우주 발사체의 비행 안정성에 미치는 영향이 연구되었으며(1), 선박이나 자동차의 액체 화물의 슬로싱을 저감하는 연구가 진행되었다(2,3).
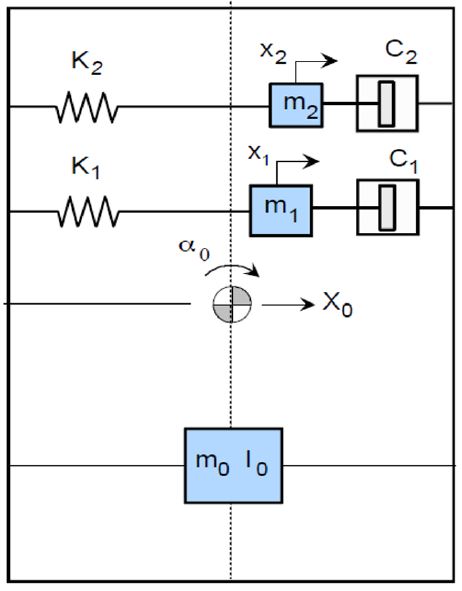
슬로싱은 일반적으로 수치해석을 통해 자유 경계면의 변위와 압력분포를 계산하여 용기에 미치는 영향을 분석한다(4,5). 이러한 방법은 실제 유체의 움직임을 보다 정확히 표현할 수 있는 장점이 있지만, 해석시간이 오래 걸린다는 단점이 있다. 이러한 단점을 해결하기 위해, Fig. 1과 같이 실제 슬로싱에 의한 힘과 모멘트와 동일한 크기의 힘과 모멘트를 발생시키는 등가 기계 모델(equivalent mechanical model, E.M.M.)이 사용되어왔다(6). 이러한 등가 기계 모델은 이전에 실험적으로 검증된 바 있으며, 용기와 구조물에 가해지는 슬로싱에 의한 외란을 예측하기 위해 사용되어왔다. 슬로싱은 유체 연료를 이용하는 위성체의 탱크 내부에서도 발생할 수 있는데, 특히 전개형 SAR(synthetic aperture radar) 안테나를 탑재한 위성체의 경우, 안테나 반사판에 얇고, 가벼운 소재를 사용하기 때문에 다른 외란 뿐 아니라 슬로싱에 의한 진동에도 더욱 민감할 가능성이 있다(7,8).
이 연구는 향후 위성에 탑재되는 전개형 SAR 안테나의 beam pointing error 분석을 수행하기 위한 목적으로, 위성의 자세 변화 기동 간 SAR 안테나 반사판에서 발생하는 진동을 분석하고, 등가 기계 모델을 이용한 슬로싱 모사를 통해, 슬로싱의 유무에 따른 SAR 안테나 반사판의 진동 변화와 그에 따른 안테나 성능 저하에 대한 분석을 수행하였다.
2. 슬로싱 분석 기법
2.1 슬로싱 해석해 및 등가 기계 모델
슬로싱의 해석해는 일반적으로 비점성 유동(inviscid flow)을 가정하며, 용기 형상에 따른 자유 경계면과 용기의 경계조건을 이용해 속도 포텐셜(velocity potential)과 자유 경계면의 모드 주파수(mode frequency)를 구한다. 속도 포텐셜과 모드 주파수를 구하면 특정한 가진에 대한 압력 분포를 계산해 슬로싱에 의한 힘과 모멘트를 구할 수 있다.
슬로싱의 해석해를 구하면 자유 경계면의 변위나 시간에 따른 유체의 전체적 형상을 구할 수 있다. 그러나 단지 슬로싱에 의한 힘과 모멘트를 구하는 것이 목적이라면 슬로싱 해석해를 구하는 것은 계산 시간 측면에서 비효율적일 수 있다. 그 점에서, 슬로싱에 의한 힘과 모멘트와 동일한 크기의 힘과 모멘트를 발생시키는 등가 기계 모델이 제안되었다(6).
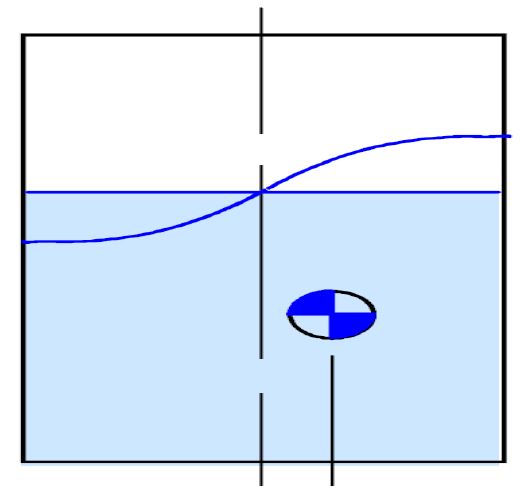
Fig. 1은 대표적 등가 기계 모델 중 하나인 질량-스프링 모델(mass-spring model)이다(9). 질량-스프링 등가 기계 모델은 크게 스프링과 이동 질량(moving mass), 그리고 고정 질량(fixed mass)으로 구성된다. 등가 기계 모델은 슬로싱 모사를 위해 식 (1)과 같은 조건들을 만족해야 한다(9).
| (1.a) |
| (1.b) |
| (1.c) |
등가 기계 모델은 슬로싱의 감쇠를 상대적으로 쉽게 표현할 수 있다. 슬로싱의 감쇠비는 일반적으로 배플(baffle)을 포함하더라도 5 %를 넘지 않는다고 알려져 있다(10). 이렇듯, 감쇠가 크지 않기 때문에 등가 기계 모델에서는 이를 선형 댐퍼로 모사한다. 유체는 연속체이기 때문에 슬로싱의 모드 또한 무수히 많이 존재한다. 그에 비해 등가 기계 모델은 이동 질량의 개수(N)만큼 슬로싱 모드를 표현할 수 있다. 다만 슬로싱의 고차 모드는 1차 모드(fundamental mode)에 비해 힘과 모멘트 측면에서는 그 영향이 미미하므로, 일반적으로 1개의 이동 질량으로도 유의미한 결과를 얻을 수 있다(11).
위성체 연료탱크 내부의 슬로싱을 다룰 때 궤도 상에서 운용되는 위성체 상의 중력은 지상보다 낮다는 점을 고려해야 한다. 이는 고중력(high-gravity) 환경에서와 저중력(low-gravity) 환경에서의 슬로싱 거동이 다소 다르기 때문인데, 이러한 고중력 환경과 저중력 환경을 구분하는 기준으로 본드 수(bond number)를 이용한다. 본드 수는 중력과 표면장력의 비를 나타내는 무차원 수로 식 (2)와 같이 정의한다.
| (2) |
식 (2)의 ρ는 유체 밀도, g는 중력가속도, R0는 용기 반지름, σ는 표면장력을 의미한다. 본드 수 Bo > 100인 경우를 고중력 환경, 그보다 작은 경우를 저중력 환경으로 분류한다. 저중력 환경의 슬로싱에서는 표면장력의 영향을 고려해야 하며, 그에 따라 슬로싱의 모드 주파수도 변한다.
저중력 환경에서 원통형 용기의 횡방향 슬로싱의 1차 모드 주파수는 식 (3)과 같은 관계를 갖는 것으로 알려져 있다(12).
| (3) |
본드 수가 100보다 크거나 100보다 조금 작은 경우에는 표면장력의 영향을 고려하지 않은 고중력 등가 기계 모델을 사용해도 수치상 큰 차이가 없으나, 100보다 확연히 작은 본드 수에서는 표면장력의 영향을 고려한 등가 기계 모델이 필요하다. 이에 대해 Dodge. et al.(11)은 원통형 용기에 대해 본드 수 10<Bo<100의 저중력 환경에서의 표면장력의 영향으로 인한 자유 경계면의 곡률 변화와 유체와 용기 사이의 접촉각(contact angle)을 고려한 등가 기계 모델을 정립하고 실험적으로 검증한 바 있다. 동일한 양의 유체를 기준으로, 저중력 환경에서는 슬로싱에 의해 용기에 가해지는 힘과 모멘트가 고중력 환경에 비해 줄어들게 되는데, 이것은 유체가 저중력 환경에서 중력의 영향 보다 표면장력의 영향을 크게 받는 것에 의한 결과로, 전체 유체 중 더 많은 유체가 용기의 움직임을 따라가기 때문에 나타나는 결과이다. 이는 같은 크기의 용기와 같은 양의 유체일 때 등가 기계 모델의 이동 질량에 더 적은 질량이 배정되는 것으로 이해할 수 있다. Dodge. et al.의 연구에서는, Bo=0의 저중력 환경에서 등가 기계 모델의 이동 질량이 고중력 환경에서보다 약 10 % 정도 줄어든 결과를 보여주었다.
3. SAR 안테나 반사판 진동 분석
3.1 전개형 SAR 안테나 탑재 위성체
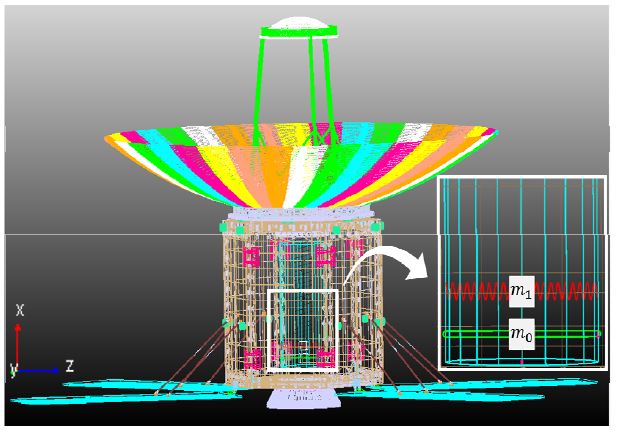
이 연구에서는, MSC사의 상용 동역학 해석 소프트웨어인 Adams를 이용하여 등가 기계 모델을 포함하는 전개형 SAR 안테나를 탑재한 위성체의 기동 및 안테나 반사판의 진동 해석을 수행하였다. 전개형 위성체의 형상은 Fig. 2와 같다.
해석과정에서 SAR 안테나를 탑재한 위성체를 500 kg급으로 가정하였으며, 위성체의 크기를 고려한 원통형 연료탱크를 상정하였다. 위성의 주축 관성모멘트(principal moment of inertia) 값과 연료 탱크의 제원은 다음과 같다.
| (4.a) |
| (4.b) |
| (4.c) |
| (4.d) |
궤도 상 중력을 지상 대비 약 0.5 %인 0.05 m/s2로 가정하고 액체 연료를 단일 추진제로 주로 사용되는(13) 하이드라진(hydrazine)으로 가정하면 이 경우의 본드 수는 약 72.8로 저중력 환경에 해당한다.
위성 기동에 의한 슬로싱 현상을 모사하기 위하여, 원통형 연료탱크에 저중력 환경을 고려한 등가 기계 모델을 수립하였으며, Fig. 2에 나타낸 바와 같이 spring-damper와 translational joint를 이용하여 해석 모델을 구축하였다.
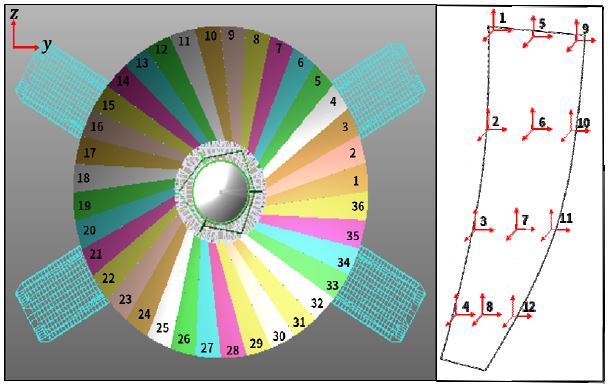
이 해석에 사용된 전개형 SAR 안테나는 총 36개 반사판으로 구성되어 있으며 변위 측정을 위해, 각 반사판 당 12개의 측정점(measuring point)을 Fig. 3와 같이 지정하였다.
3.2 안테나 패널 진동 분석
위성 연료탱크 내부 유체의 높이를 0.5 m, 0.4 m, 0.3 m로 가정하면, 등가 기계 모델의 파라미터들은 Table 1과 같다. 각 경우에 대하여, 모두 1 %의 감쇠비를 적용하였다.
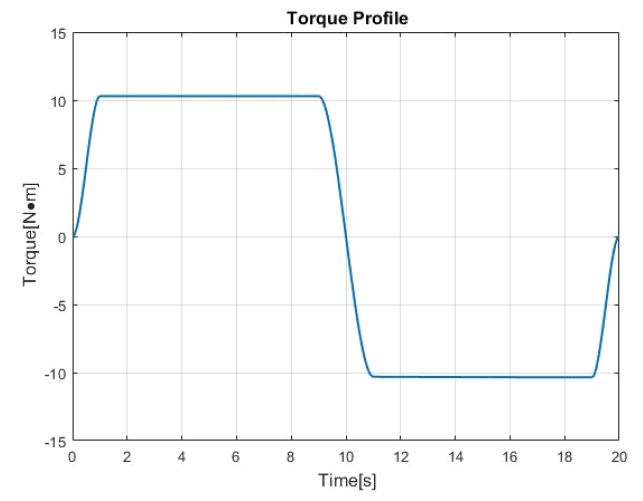
위성의 자세 변화 기동 시 일반적으로 가정되는 토크 입력은 bang-bang 토크 입력이다. 하지만 bang-bang 토크 입력(step input)과 같은 갑작스러운 토크 변화는 현실적으로 구현하기 어렵고 시스템에 무리가 갈 수 있기에 사인 함수나 다항식을 이용한 평탄화된(smoothed) 토크 입력 방식이 제안되었다(14). 다항식을 이용한 평탄화된 토크(T) 입력은 식 (5)와 같다.
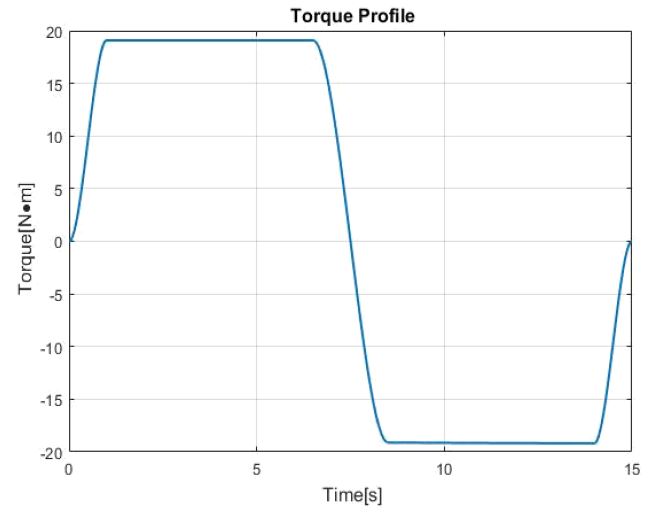
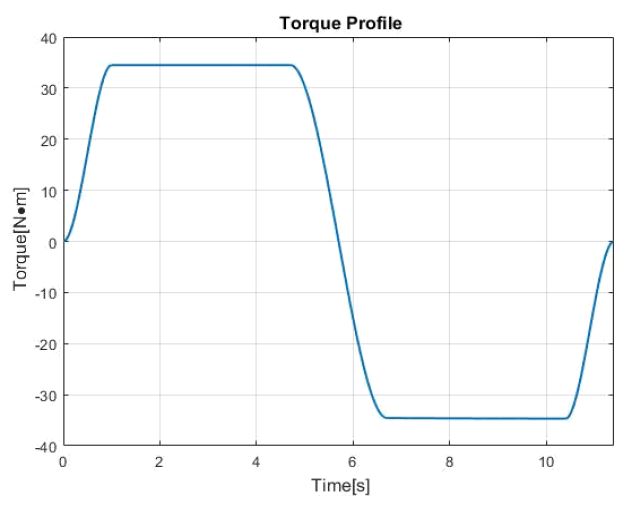
Fig. 4는 ∆t = 1s를 갖는 15초 간의 평탄화된 y방향 토크 입력을 나타낸 것이다.
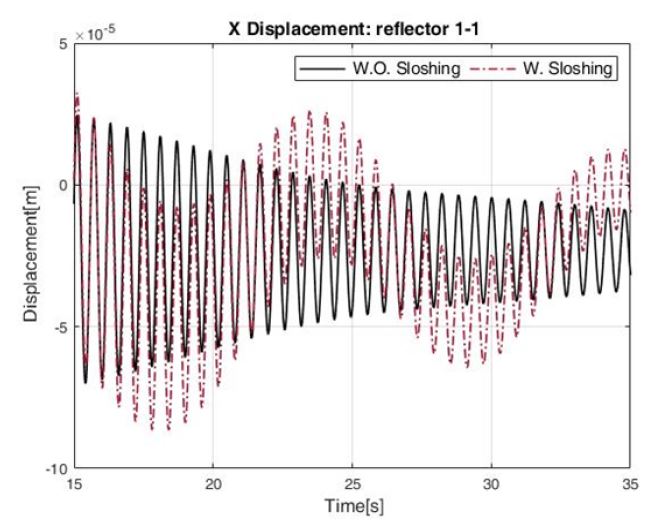
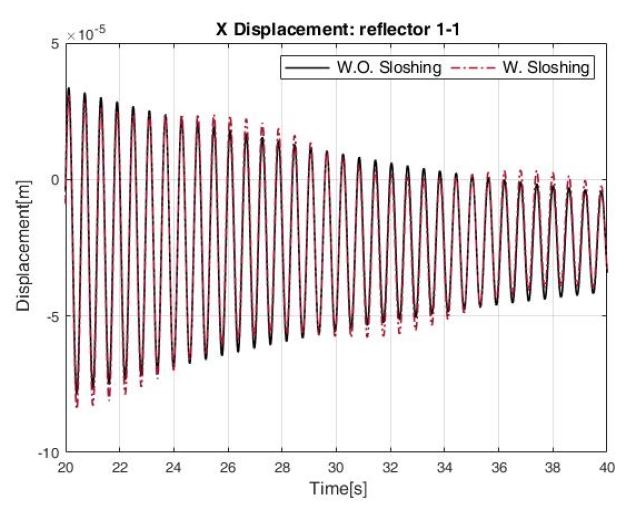
Fig. 4에 해당하는 토크 입력에 대하여, Figs. 5 ~ 7은 위성의 자세 변화 기동 이후 연료탱크 내부의 유체 높이에 따른 1번 반사판의 1번 측정점의 x변위를 나타낸 그래프이며, Table 2는 Figs. 5 ~ 7에서 슬로싱을 고려한 경우의 최대 변위를 나타낸 표다.
Figs. 5 ~ 7과 Table 2에서 h = 0.3 m일 때 슬로싱에 의한 반사판 진동이 가장 큰 것(worst case)을 확인할 수 있다.
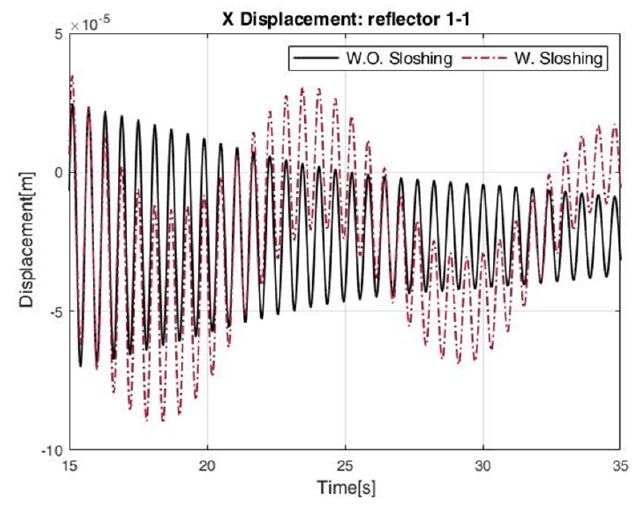
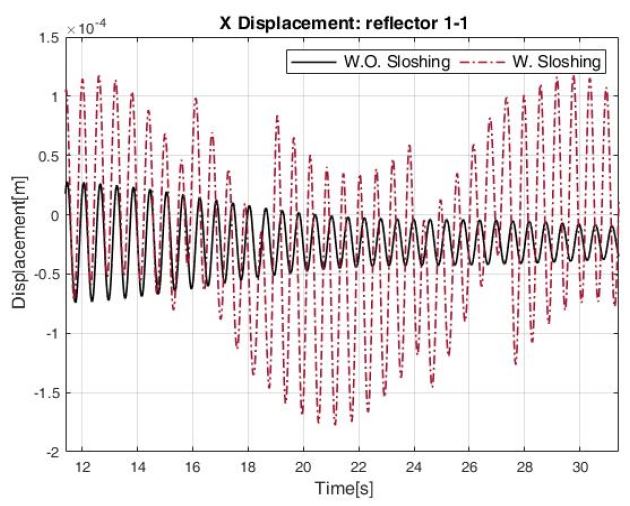
Worst case인 h = 0.3 m인 경우에, Fig. 8과 같이 상대적으로 더 긴 자세 변화 시간을 갖는 ∆t = 1s, 20초 간의 토크 입력을 가했을 때의 결과는 Fig. 9와 같다.
입력 주파수의 성분이 슬로싱의 1차 모드 주파수(ω1)와 유사할 때 SAR 안테나 반사판의 진동 수준이 크게 증가할 수 있다. 일반적인 슬로싱의 1차 모드 형상은 Fig. 10과 같다(9).
이러한 슬로싱 모드 형상은 용기 형상에 따라 전반적인 형상이 결정되고, 중력가속도와 유체 특성에 의해 용기와의 접촉부 형상이 달라진다.
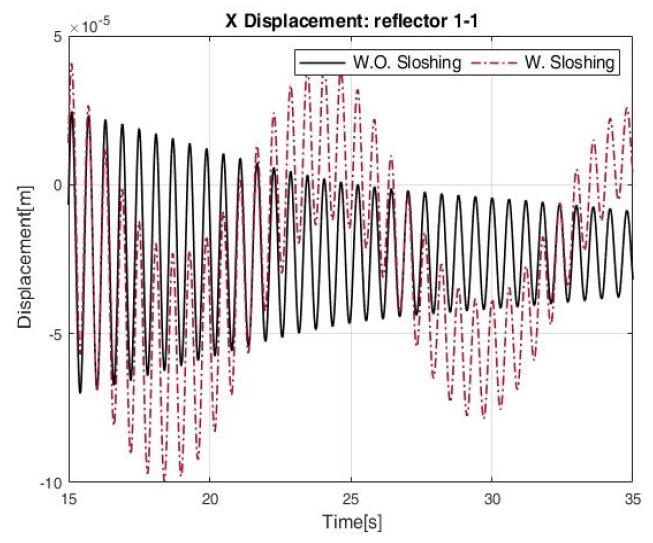
Worst case인 h = 0.3 m에 대해, Fig. 11과 같이 슬로싱의 1차 모드 주파수에 해당하는 주기(11.4s)를 갖는 smoothed 토크 입력을 가했을 때의 결과는 Fig. 12와 같다.
Fig. 12의 결과로 보아 다른 토크 입력보다 입력 토크의 주파수 성분이 슬로싱의 1차 모드 주파수(ω1)와 유사한 경우, SAR 안테나 반사판의 진동에 큰 영향을 주는 것을 확인할 수 있다.
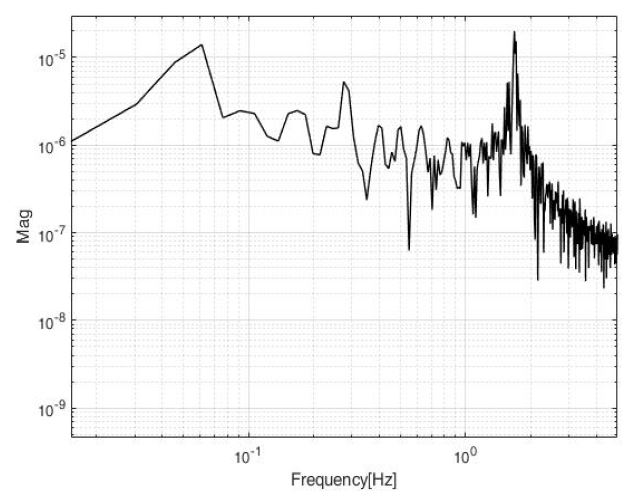
SAR 안테나 반사판 모드와 슬로싱 모드 간의 공진이 발생하면 반사판의 진동이 더 증가할 수 있다. 이를 확인하기 위해, Fig. 12(h = 0.3 m)의 반사판 변위 결과를 주파수 영역에서 분석하였다.
Fig. 13에서 0.06 Hz와 1.67 Hz 부근에서 높은 값을 나타내는데, 상대적으로 저주파인 0.06 Hz 부근의 값이 위성체를 포함한 등가 기계 모델의 슬로싱 1차 모드에 의한 값임을 확인할 수 있고, 1.67 Hz 부근의 값이 SAR 안테나 반사판의 모드 주파수에 의한 값임을 확인할 수 있다. 이 경우, 슬로싱의 1차 모드에 의해 발생하는 SAR 안테나 변위의 주파수 값은 Table 1에 정리된 슬로싱 모드 주파수보다 낮은데, 이는 E.M.M.이 유한한 질량을 갖는 위성과 결합된 계로 안테나에 작용하기 때문이다.
반사판 변위의 주파수 성분 분석을 통하여, h = 0.3 m인 경우에 SAR 안테나 반사판 모드와 슬로싱 모드 간의 공진이 발생하지 않는 것을 확인할 수 있었다. 용기 내부의 연료 충전율이 변하더라도 식 (1)로 유도되는 슬로싱의 1차 모드 주파수의 최대값은 0.09 Hz기 때문에, 이 연구에서 고려한 SAR 안테나 탑재 위성체에서 SAR 안테나 반사판 모드와 슬로싱 모드 간의 공진 발생 가능성이 없음을 확인하였다.
이 연구에서는 위성의 갑작스런 자세 변화 등 슬로싱에 의한 영향이 심각할 수 있는 상황을 가정하였기 때문에 일반적인 위성 운용과정에서 발생하는 유체 슬로싱에 의한 영향은 이 연구에서 제시한 수준보다 훨씬 낮을 수 있다.
4. 결 론
이 연구에서는 슬로싱을 등가 기계 모델을 이용하여 표현하고 전개형 SAR 안테나 탑재 위성체의 기동해석을 수행함으로써 슬로싱이 전개형 SAR 안테나 반사판의 진동에 미치는 영향을 확인하였다. 주어진 조건에서, 연료 충전율이 낮고 기동 시간이 줄어들수록 슬로싱 효과가 다소 증가하였으며, 특히, 토크 입력이 슬로싱의 모드를 가진할 때 슬로싱 효과가 크게 증가하는 것을 확인하였다. 추가로, SAR 안테나 반사판 모드와 슬로싱 모드 간의 공진 가능성을 확인하였다.
기 호 설 명
| h0 : | 고정 질량 높이 |
| hF : | 유체 높이 |
| hn : | n번째 이동 질량 높이 |
| kn : | n번째 등가 기계 모델 스프링 상수 |
| m0 : | 등가 기계 모델 고정 질량 |
| mn : | n번째 등가 기계 모델 이동 질량 |
| mF : | 유체 총 질량 |
| ωn : | n번째 슬로싱 모드 주파수 |
Acknowledgments
이 연구는 ‘위성용 경량화 SAR 안테나 기술 개발’ 사업의 일환으로 방위사업청과 국방과학연구소의 지원(G06180006)으로 수행되었습니다.
References
- Bauer, H. F., 1964, Fluid Oscillations in the Containers of a Space Vehicle and Their Influence on Stability, NASA, TR R-187.
-
Panigrahy, P. K., Saha, U. K. and Maity, D., 2009, Experimental Studies on Sloshing Behavior due to Horizontal Movement of Liquids in Baffled Tanks, Ocean Engineering, Vol. 36, No. 3-4, pp. 213~222.
[https://doi.org/10.1016/j.oceaneng.2008.11.002]

-
Koo, J. H., Cho J. R., Kim D. J. and Jeong, W. B., 2009, Sloshing Reduction Characteristics to Baffle for Cylindrical Liquefied Fuel Tank subject to Dynamic Load, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 19, No. 9, pp. 950~959.
[https://doi.org/10.5050/KSNVN.2009.19.9.950]

-
Godderidge, B., Turnock, S., Tan, M. and Earl, C., 2009, An Investigation of Multiphase CFD Modelling of a Lateral Sloshing Tank, Computers & Fluids, Vol. 38, No. 2, pp. 183~193.
[https://doi.org/10.1016/j.compfluid.2007.11.007]

-
Yang, H. and Peugeot, J., 2010, Propellant Sloshing Parameter Extraction from CFD Analysis, Proceedings of the 46th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, p. 6889.
[https://doi.org/10.2514/6.2010-6889]

-
Abramson, H. N., Chu, W.-H. and Ransleben Jr., G. E., 1961, Representation of Fuel Sloshing in Cylindrical Tanks by an Equivalent Mechanical Model, ARS Journal, Vol. 31, No. 12, pp. 1697~1705.
[https://doi.org/10.2514/8.5896]

-
Shen, Y., Zheng, W. and Wang, X., 2007, Dynamic and Vibration Analysis of a SAR Membrane Antenna, Proceedings of the ASME 2007 International Mechanical Engineering Congress and Exposition, pp. 17~24.
[https://doi.org/10.1115/IMECE2007-41424]

- Kim, D. Y., Suh, J. E., Jung H. Y., Kang K. H. and Han, J. H., 2018, Flexible Structural Analysis of the Antenna Reflector of the Satellite, Proceedings of the KSNVE Annual Spring Conference, p. 248.
- Dodge, F. T., 2000, The New Dynamic Behavior of Liquids in Moving Containers, Southwest Research Institute, San Antonio, TX.
- Stephens, D. G., Leonard, H. W. and Perry, T. W., 1962, Investigation of the Damping of Liquids in Right-circular Cylindrical Tanks, NASA TN D-1367.
-
Dodge, F. T. and Garza, L. R., 1967, Experimental and Theoretical Studies of Liquid Sloshing at Simulated Low Gravity. Journal of Applied Mechanics, Vol. 34, No. 3, pp. 555~562.
[https://doi.org/10.1115/1.3607743]

- Satterlee, H. M. and Reynolds, W. C., 1964, Dynamics of the Free Liquid Surface in Cylindrical Containers under Strong Capillary and Weak Gravity Conditions, Standford University, Dept. Mech. Eng., Tech. Rept. LG2.
- Valentini R., 1997, Hydrazine Thrusters for Space Applications, ESA Attitude and Orbit Control Systems, ESA-SP-128, p. 435.
-
Byers, R. M., Vadali, S. R. and Junkins, J. L., 1990, Near-minimum Time, Closed-loop Slewing of Flexible Spacecraft. Journal of Guidance, Control, and Dynamics, Vol. 13, No. 1, pp. 57~65.
[https://doi.org/10.2514/3.20517]


Ba-Woul Chung received B.S. degree in mechanical and control engineering from Handong Global Univ. in 2019. He is currently a M.S. candidate in aerospace engineering department at KAIST. His research interests include vibration analysis for satellites and space structures.

Tae-Hyun Kim received B.S. degree in mechanical engineering from Korea Aerospace Univ. in 2018. He is currently a M.S. candidate in aerospace engineering department at KAIST. His research interests include structural dynamics and deployable structures.

Jong-Eun Suh received B.S. degree in mechanical engineering from KAIST in 2015. He received M.S. degree in aerospace engineering at KAIST. He is currently a Ph.D. candidate in aerospace engineering at KAIST. His research interests include structural dynamics and deployable structures.

Jae-Hung Han received B.S., M.S. and Ph.D. degree from KAIST in 1991, 1993 and 1998. He is currently a professor and head of aerospace engineering department at KAIST. His research interest includes deployable structure, smart materials, structural dynamics and control.