내부 유체에 의한 고유진동수 분리 효과를 고려한 배관계의 적절한 시간이력해석 방법론

1. 서 론

2011년 동일본 대지진으로 인한 후쿠시마 원전 사후 이후 원자력 발전소에 대한 내진 성능 및 내진 안전성에 대한 재고와 규제의 강화가 지속적으로 이루어져 왔다. 현재는 설계기준초과 지진에 대한 원자력 발전소 및 핵심 기기들의 구조 건전성 평가에 대한 연구들이 화두가 되고 있다. 특히 핵심 기기들 중 배관계에 대한 연구들이 활발하며, 일본과 미국기계학회 등이 설계기준 초과 지진에 대해 선도적인 연구를 진행하고 있다. 설계초과지진 발생으로 인해 배관계는 탄성 영역을 벗어나 소성 거동이 발생한다. 이러한 현상을 기존의 탄성 해석을 통해 구조 건전성을 평가한다면, 배관계의 주요 파괴 모드인 low cycle fatigue 등을 평가 할 수 없을 뿐 아니라, 과도한 마진으로 구조 건전성이 매우 보수적으로 평가된다. 따라서 설계초과지진에 대한 배관계의 구조 건전성 평가 시에는 재료의 탄소성 거동 등을 포함하기 위한 배관계의 시간이력 해석이 필요하다.

배관계의 특성상, 내부 유체로 인해 발생하는 유체-구조 연성 효과(fluid-structure interaction, FSI)를 반영한 연구들이 수행되었다^(1~3). 유체를 포함한 원통형 구조물에서 FSI를 고려한 동역학적 해석을 진행한 결과 연성효과에 의해 고유진동수 분리효과가 존재한다는 것을 확인하였고⁽¹⁾, 원주방향으로 고정된 판형 구조물에 대해 veering(유체의 음향 고유진동수와 구조물의 고유진동수가 강하게 상호작용하는 영역) 구간에서 두 개의 고유진동수가 나타나게 되고, 이를 유체-구조물공진에 의한 고유진동수라는 것을 수치적으로 해석했다^(2,6). 배관에 대해서 Wiggert, D. C. et al.는 모달 해석결과를 바탕으로 전달 행렬을 바탕으로 한 수치해석을 수행하여 유체와 구조물의 연성효과를 나타낼 수 있다는 것을 설명하였다⁽³⁾. 이처럼 여러 선행연구를 통하여 유체-구조물 연성효과를 고려하면 고유진동수 분리가 나타나는 현상이 존재하고, 이를 바탕으로 유체의 영향을 고려했다는 것을 알 수 있다.

하지만 유체-구조물 연성효과에 의한 고유진동수 분리 효과가 시간이력을 기반으로 한 동해석시에는 어떠한 형태로 나타나는지에 대해서는 언급이 없었다. 유체-구조 연성 효과를 포함한 유한요소 해석을 진행하기 위해서 비대칭 행렬 구조방정식이 얻어지고, 재료의 탄소성 거동까지 포함되면 해석 부하가 기하급수적으로 증가한다. 원자력 발전소 내부의 수십, 수백 개 배관계의 구조 건전성을 평가하기 위해서는 해석 비용이 높은 것은 적절하지 않기 때문에 적절한 정확도와 해석 비용을 가지는 해석 방법이 필요하다. 이와 같은 목표를 위해 이 연구에서는 배관 내부 유체에 의한 고유진동수 분리 효과를 고찰하고 내부 유체 효과를 반영하는 적절한 시간이력 해석 방법을 제시하고자 한다. 제시한 해석 방법은 인공지진파의 지진 응답 해석 결과를 통해 검증하였다.

2. 본 론

2.1 고유진동수 분리 효과

유체와 구조물의 유체-구조 연성 효과를 고려한 구조 방정식은 식 (1)이고, 구조 방정식의 강성 행렬과 질량 행렬은 비대칭이고, 연성 행렬은 유체와 구조물의 결합 특성을 포함한다.

$\[ \left[\begin{array}{cc}{\mathbf{M}}_s& 0\\ {\rho }_f{\mathbf{R}}^T& {\mathbf{M}}_f\end{array}\right]\left\{\begin{array}{c}\ddot{u}\\ \ddot{p}\end{array}\right\}+\left[\begin{array}{cc}{\mathbf{K}}_s& -\mathbf{R}\\ 0& {\mathbf{K}}_f\end{array}\right]\left\{\begin{array}{c}u\\ p\end{array}\right\}=f \]$

(1)

식 (1)과 같은 구조 방정식을 가지는 유체-구조 연성 구조물의 동특성은 부가 질량 효과(ρ_fR^T )로 인해 고유진동수가 감소한 FMA(fluid mass added) mode와 내부 유체의 고유진동수가 FMA mode의 고유진동수가 근접할 경우 발생하는 coupled mode로 나뉜다. Zhang, L. et al.은 유체를 포함한 직관 및 원통 용기를 대상으로 실험을 수행하여 유체와 배관의 고유진동수가 가까이에 존재할 때, 고유진동수가 분리되어 FMA mode와 coupled mode로 나뉘는 것을 밝혔다⁽⁴⁾. 이와 유사하지만 Gorman, G. et al.은 원형 평판이 원주방향으로 구속되어 있는 경우에 대해서 유체의 유무에 따른 고유진동수 분리를 밝혔다⁽²⁾. 이러한 고유진동수 분리로 인한 모드 분리를 배관계에 적절히 활용하여, 유체-구조 효과를 반영하되 적절한 해석 비용을 가지는 해석 방법을 고찰하였다.

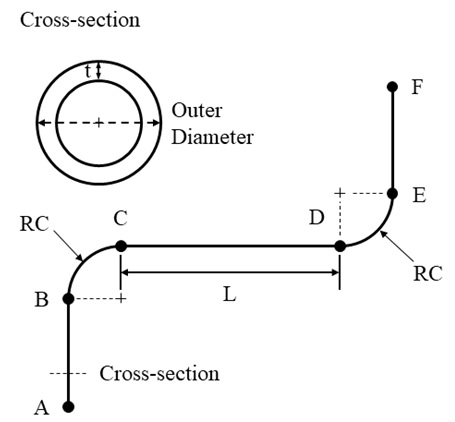
배관계와 같이 복잡한 구조물의 연구에 널리 활용되는 유한요소 해석 방법을 사용했다. 유한요소 해석을 통한 배관계에 고유진동수 분리를 확인하기 앞서 2개의 곡관부를 가지는 비교적 단순한 배관계에 대한 고유진동수 분리 효과의 이론적 고찰과 유한요소 해석 방법의 타당성을 확인하였다. 2개의 곡관부를 가지는 비교적 단순한 배관계에 대해 Moussou, P. et al.은 고유진동수 분리의 이론적 배경을 제시하였다⁽⁵⁾. 해당 선행연구에서 제시된 이론적인 계산 방법을 기준으로 유한요소방법을 적용하여 고유진동수 분리 효과를 확인하기 위해 Moussou, P. et al.이 대상으로한 2개의 곡관부를 가지는 비교적 단순한 배관계를 Fig. 1과 같은 형태로 상용 유한요소 해석 프로그램인 ANSYS 19.2를 이용하여 모사하였다. 수직 직관부 AB, EF의 길이는 1.95 m, 배관의 외경은 0.3 m, 곡관부의 반경(radius of curvature, RC)는 0.45 m, 수평 직관부(L)는 3.88 m, 배관의 두께(t)는 5 mm이다. 배관계의 기하형상에 따라 고유진동수 분리 양상을 확인하기 위해 기하형상의 주요 변수를 선정하였다. 이전에 수행된 곡관부 진동 특성 실험에 사용된 시편들의 치수를 기반으로 기하형상의 주요 변수를 선정하고 Table 1과 같이 case를 나누었다⁽⁶⁾.

Fig. 1

Schematic diagram of finite element model

Table 1

FEM cases geometry & FMA density

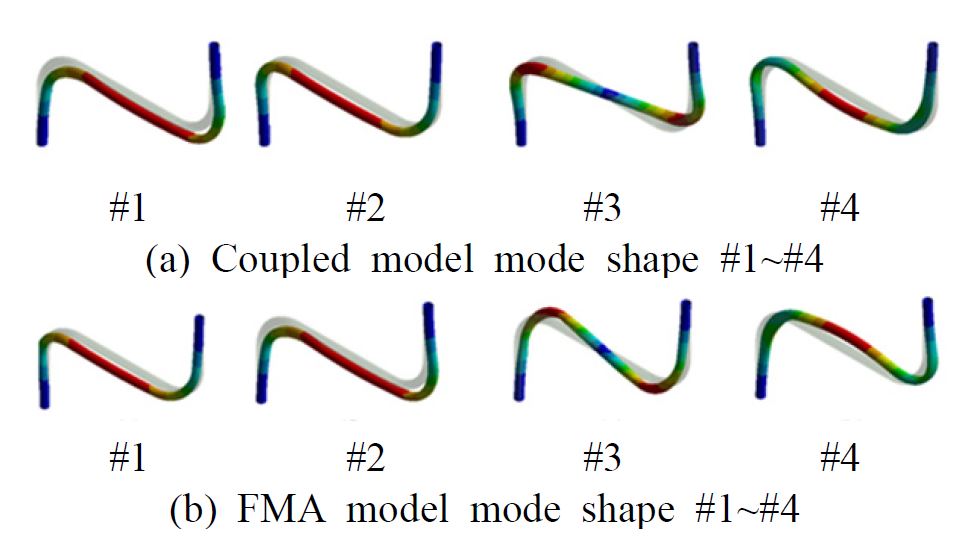
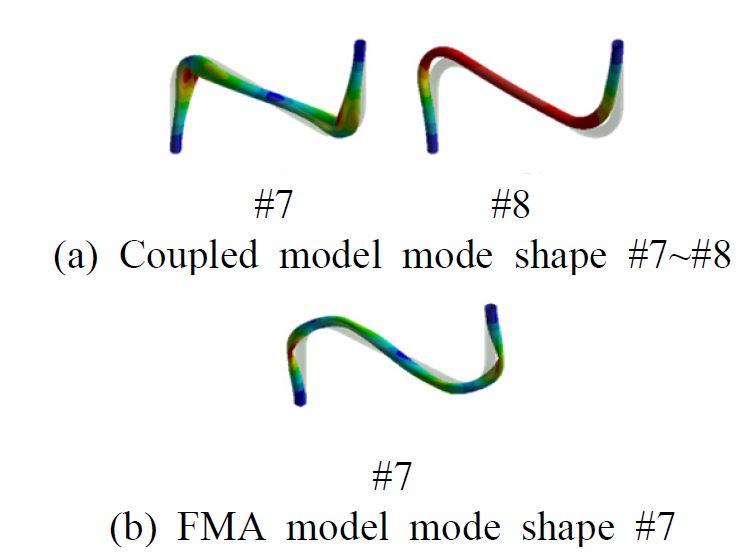
각 case별로 내부 유체를 음향요소로 구현한 coupled model과 유체의 부가 질량 효과만을 고려한 FMA model 두 가지 모델을 각각 구현하였다. 내부유체는 구조물 전체에 영향을 끼친다는 가정 하에, 배관 내부 유체의 부피와 밀도를 통해 총 질량을 계산하여 구조물의 밀도에 추가하는 방식으로 FMA model에서 등가 질량을 모사하였다⁽¹⁾. 각 case 별 계산된 밀도는 Table 1의 ρ_FMA와 같고, 유체의 밀도는 1000 kg/m³, 배관의 밀도는 7800 kg/m³, 유체 내부음속 1000 m/s, 탄성계수 200 GPa, 푸아송비 0.3을 사용하였다. Coupled model에서는 내부 유체를 음향요소로 모사하여 배관계 내부 유체의 효과를 모사하였고, 유한요소 해석을 이용하여 유체 음향 고유진동수와 모드형상을 도출하였다. FMA model과 coupled model의 모드 해석 결과는 Table 2 및 Table 3과 같다. 해당 결과는 지진입력을 가정하고 10 Hz ~ 33 Hz 강진대역을 포함하는 50 Hz 이내의 모드들을 비교하였다. 내부유체의 공진 고유진동수는 구조적으로는 길이, 물성적으로는 유체 내부의 음속에 따라 결정된다. 또한 열린 양 끝단을 가졌다는 가정 하에 압력의 파동형태로 형성되며, f=c/2L로 계산할 수 있다. 유한요소 해석에서 결과와 f=c/2L을 통해 계산한 값과의 오차는 Table 4와 같다. 해당 구간에 존재하는 고유진동수는 Table 2와 Table 3을 통해 큰 차이가 없다는 것을 확인하였고, Fig. 2와 같이 모드형상은 같음을 확인하였다. 하지만 case 3-2의 경우, 유체 고유진동수가 부가 질량 효과를 고려한 FMA mode와 유사한 모드가 존재하기 때문에 이에 따른 coupled mode가 존재하는 것을 Fig. 3을 통해 확인하였다. FMA model과 coupled model을 통해 얻은 해석 결과와 유체 고유진동수를 이용하여 coupled model의 분리된 고유진동수를 계산할 수 있다. 이는 산술적으로 유체의 음향 고유진동수와 부가 질량에 의한 진동수로 나뉘고, 식 (2)와 식 (3)의 조건에 따라 두 가지 해를 갖게 되며, η_c(dimensionless coupling term)과 고유진동수 분리 대역에 따라 식 (4)와 식 (5)로 계산할 수 있다⁽⁵⁾. 여기서 w_f는 내부 유체의 음향 고유진동수, w_s는 부가 질량을 고려한 구조물의 고유진동수다. 계산 결과는 Table 5와 같이 5 %이내의 오차를 가졌다. 따라서 유체의 효과를 고려한 coupled mode는 유체 음향 고유진동수가 FMA mode와 겹치는 경우를 제외하고는 유체의 질량 효과만을 고려하여 나타낼 수 있다. 이를 두 가지 유한요소 모델인 coupled model과 FMA model을 이용하여 고유진동수 분리 현상을 확인할 수 있으며, 이와 같은 유한요소 해석 방법을 통해 복잡한 배관계에도 적용할 수 있는 가능성을 확인하였다.

$\[ \left({{\omega }_s}^2-{\omega }^2\right)\left({{\omega }_f}^2-{\omega }^2\right)-{{\eta }_c}^2{\omega }^4=0 \]$

(2)

$\[ {{\omega }_{\pm }}^2=\frac{{{\omega }_s}^2+{{\omega }_f}^2\pm \sqrt{{\left({{\omega }_s}^2+{{\omega }_f}^2\right)}^2+\left(1-{{\eta }_c}^2\right){\left({{\omega }_s}^2-{{\omega }_f}^2\right)}^2}}{2\left(1-{{\eta }_c}^2\right)} \]$

(3)

$\[ {{\omega }_{+}}^2=\frac{{{\omega }_f}^2}{\left(1-{{\eta }_c}^2\right)} \]$

(4)

$\[ {{\omega }_{-}}^2\approx {{\omega }_s}^2 \]$

(5)

Fig. 2

Case 3-2 coupled/FMA mode shape

Fig. 3

Case 3-2 coupled/FMA different mode shape

Table 2

Coupled model modal frequency [Hz]

Table 3

FMA model modal frequency [Hz]

Table 4

Fluid acoustic frequency [Hz]

Table 5

Separated frequency comparison

2.2 모사 배관계 유한요소 해석

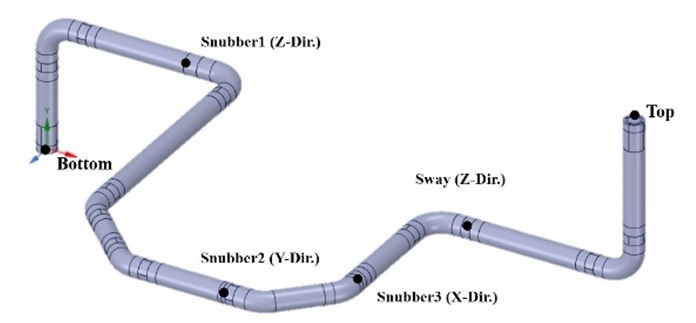
고유진동수 분리로 생성된 모드들이 배관계의 지진 응답에 미치는 영향을 확인하기 위해 실제 배관계와 유사한 모사 배관계를 대상으로 지진 응답 해석을 수행하였다⁽⁷⁾. 상용 원전인 ARP1400의 가압기 밀림관을 모사한 배관계는 Fig. 4와 같다. 반지름 165.1 mm, 두께 33 mm, elbow curvature는 495.3 mm를 가지는 배관계이다. 해당 배관계는 스웨이와 스너버형태의 지지대를 가진다. 이들은 각 지점에서 한 방향 자유도를 구속하여 지지하는 효과가 있기 때문에, Fig. 4와 같이 해석 모델에서는 지지 방향으로 가진 입력이 있다고 가정하였다. 해당 배관계는 복잡한 형상으로 인해 고유진동수 분리를 이론적으로 계산하기 어렵다. 2.1절에서 확인한 FMA mode와 coupled mode를 비교하는 유한요소모델 방법을 통하여 고유진동수 분리 효과를 확인하였다.

Fig. 4

FEM diagram of piping system

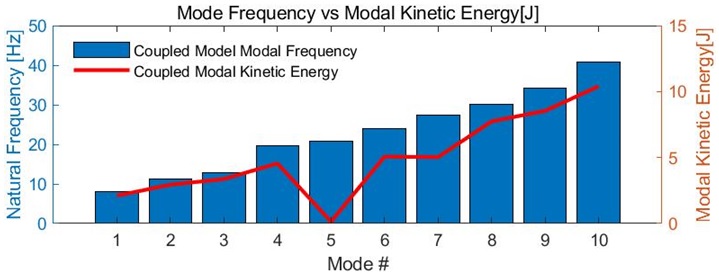
해석에 사용된 모델의 물성치는 Table 6과 같고, 지진 응답 해석 시 주요 관심 진동수 대역인 10 ~ 33 Hz 강진 대역을 포함하도록 1 ~ 40 Hz을 관심 진동수 대역으로 설정하고, 모드형상 및 고유진동수를 분석하였다. 모드 해석 결과는 Table 7과 같다. 해당 배관계의 coupled model의 FMA mode와 coupled mode에 의한 고유진동수 분리 모드를 확인하였다. 해당 배관계의 음향 고유진동수를 통해 고유진동수 분리 모드를 예상할 수 있다. coupled model 기준으로 5, 6번 모드가 분리된 모드이며, FMA model 결과와 비교했을 때, 5번 모드가 음향 공진에 의해 영향을 받은 coupled mode이고 6번 모드가 부가 질량에 의한 FMA mode임을 알 수 있다.

$\[ MK{E}_{pq}={\varphi }_{pq}\sum _{s=1}^n{M}_{ps}{\varphi }_{sq} \]$

(6)

Table 6

Finite element model information

Table 7

Pipe model modal frequency

Modal kinetic energy는 식 (6)과 같이 정의되며, Fig. 5와 같이 coupled mode인 5번 모드의 modal kinetic energy가 낮다. 이를 통해 coupled mode가 외부 가진에 대한 구조물의 응답에 매우 적은 기여도를 가질 것으로 예상된다⁽⁸⁾. 즉, coupled model과 FMA model은 지진 응답 해석에서 유사한 응답을 보일 것이다.

Fig. 5

Modal Analysis Results

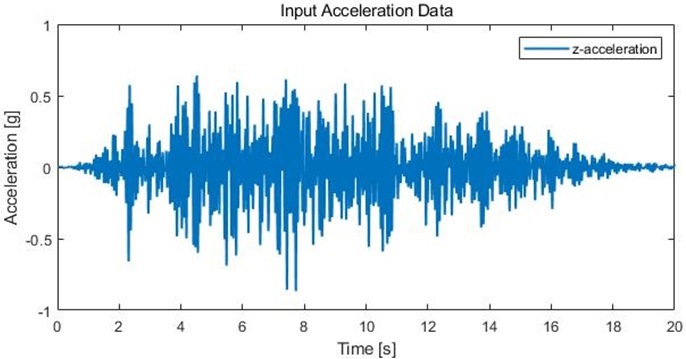
예상한 결과를 검증하기 위해 coupled model과 FMA model의 지진 시간이력 해석을 수행하였다. 지진 시간이력 해석에 사용된 해석 모델의 정보는 Table 7과 같다. 입력 지진 데이터는 Fig. 6과 같고 0.86 g 수준의 인공 지진파의 변위이력이다.

Fig. 6

Input acceleration data

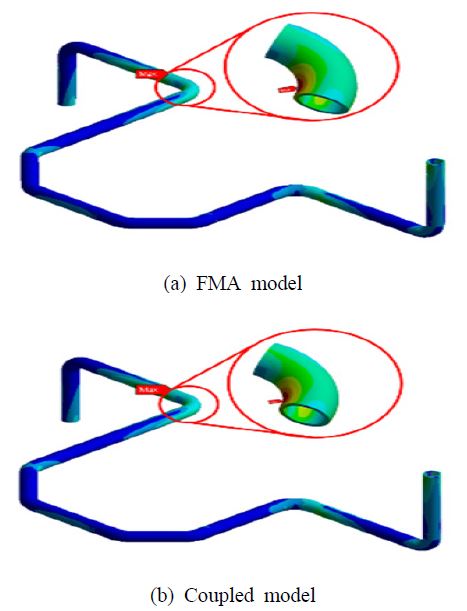
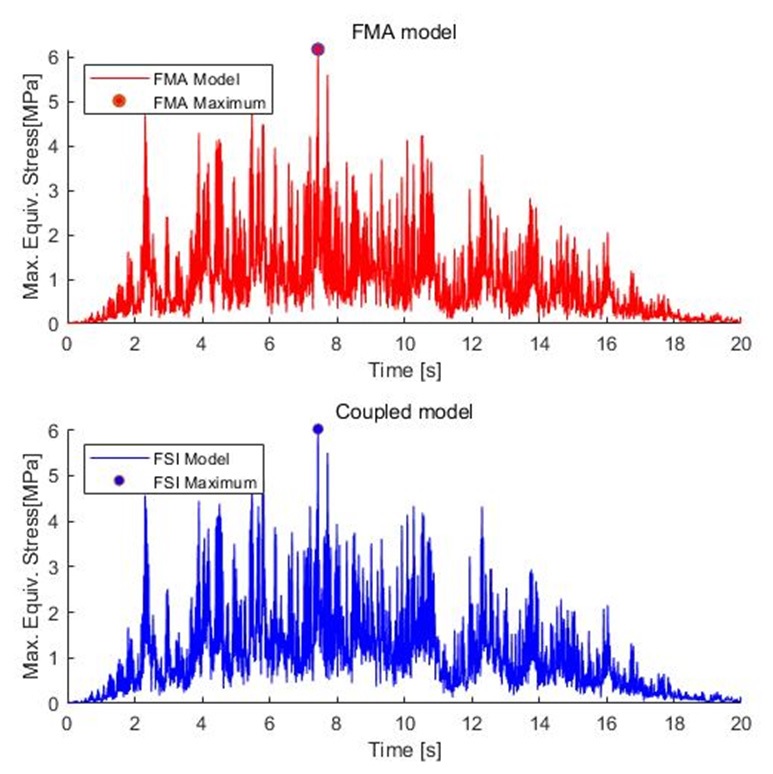
해당 배관계 전체의 최대 응력 발생 시점의 응력 분포는 Fig. 7과 같다. Table 8과 같이, coupled model의 경우 7.44 s에서 최대값 6.02 MPa, FMA model의 경우 7.44 s에 6.17 MPa으로 오차가 약 2.5 %이다. 또한 Fig. 8과 같이 최대 응답 발생 지점에서의 시간 이력이 매우 비슷하며, 두 모델의 응답이 3 % 이내의 오차를 가진다. 시간이력 해석 결과를 통해, 두 모델의 거동 차이는 매우 작다는 것을 확인하였다. 따라서 부가 질량 효과만을 고려한 FMA model을 coupled model과 비교했을 때 적절한 정확도를 가지는 지진 시간이력 해석을 수행할 수 있다.

Fig. 7

Stress distribution at maximum response

Table 8

Maximum stress value(elbows)

Fig. 8

Time history stress at maximum response point

3. 결 론

이 연구를 통해 내부 유체를 포함하는 배관계의 유한요소방법을 이용한 지진 응답 해석 시 적절한 방법에 대해 아래와 같은 결론을 도출하였다.

• ㆍ유한요소 해석을 통해 고유진동수 분리로 부가질량 효과를 나타내는 FMA mode와 유체 공진에 의해 구조가 영향을 받는 coupled mode로 모드 분리가 일어남을 확인하였다.
• ㆍcoupled mode는 modal kinetic energy가 작으므로 지진 응답 해석에 큰 기여를 하지 않는다.
• ㆍ배관계 동해석 시, 음향 유체 요소를 사용하여 유체 구조 연성 효과를 반영한 coupled model을 사용하지 않고 등가 질량법을 통한 FMA model으로도 충분한 정확도를 보장하는 것을 확인하였다.
• ㆍFMA model은 배관 내부 유체를 모사하지 않아 구조 방정식의 크기가 작아지며, 대칭 행렬 구조방정식을 가지므로 해석 비용 측면에서 coupled model에 비해 큰 이점을 가진다.
• ㆍ위 사실을 바탕으로 구조-연성효과를 고려한 해석 모델과 동등한 효과를 나타내면서 해석부하는 적은 FMA model이 배관계의 내진 해석에 적합함을 유한요소 해석을 통해 확인하였다.

Acknowledgments

이 연구는 2019년도 산업통상자원부의 재원으로 한국에너지기술평가원(KETEP)의 지원을 받아 수행한 연구과제입니다. (No. 20193110100020, 해외 내진분석 기술기준을 적용한 표준형 원전 설계초과지진 대응 기술개발).

References

• Sigrist, J. F. and Garreau, S., 2007, Dynamic Analysis of Fluid-structure Interaction Problems with Modal Methods Using Pressure-based Fluid Finite Elements, Finite Elements in Analysis and Design, Vol. 43, No. 4, pp. 287~300. [https://doi.org/10.1016/j.finel.2006.10.002]
• Gorman, D. G. and Horáček, J., 2007, Analysis of the Free Vibration of a Coupled Plate/fluid Interacting System and Interpretation Using Sub-system Modal Energy, Engineering Structures, Vol. 29, No. 5, pp. 754~762. [https://doi.org/10.1016/j.engstruct.2006.06.017]
• Lesmez, M. W., Wiggert, D. C. and Hatfield, F. J., 1987, Modal Analysis of Vibrations in Liquid-Filled Piping Systems, Journal of Fluids Engineering, Vol. 112, No. 3, pp. 311~318. [https://doi.org/10.1115/1.2909406]
• Zhang, L., Tijsseling, A. S. and Vardy, A. E., 1999, FSI Analysis of Liquid-filled Pipes, Journal of Sound and Vibration, Vol. 224, No. 1, pp. 69~99. [https://doi.org/10.1006/jsvi.1999.2158]
• Moussou, P., Vaugrante, P., Guivarch, M., Seligmann, D., Ziada, S. and Staubli, T., 2000, Coupling Effects in a two Elbows Piping System, Proceedings of the 7th International Conference on Flow-induced Vibration, pp. 579~586.
• Salley, L. and Pan, J., 2002, A Study of the Modal Characteristics of Curved Pipes, Applied Acoustics, Vol. 63, No. 2, pp. 189~202. [https://doi.org/10.1016/S0003-682X(01)00027-5]
• Seo, Y. S., Jeong, S. H., Lee, S. H., Hong, C. S. and Jeong, W. B., 2006, Vibration Analysis of Pipes Considering Fluid Pulsation, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 16, No. 10, pp. 1050~1056. [https://doi.org/10.5050/KSNVN.2006.16.10.1050]
• Li, D. S., Li, H. N. and Fritzen, C. P., 2007, The Connection Between Effective Independence and Modal Kinetic Energy Methods for Sensor Placement, Journal of Sound and Vibration, Vol. 305, No. 4~5, pp. 945~955. [https://doi.org/10.1016/j.jsv.2007.05.004]