규칙기반과 딥러닝을 동시에 활용한 앙상블 회전체 이상진단

1. 서 론

상대적으로 중요도가 낮은 발전소의 보조기기는 가격 상의 문제로 실시간 상태 감시 및 진단 시스템이 갖추어지지 않은 경우가 많다. 하지만 보조 기기의 고장 시에도 발전소가 가동을 중단하게 될 위험이 있으며 이에 따른 손실이 계속되는 것이 사실이다. 현재 이러한 문제를 해결하기 위하여 보조기기를 여러 대를 보유하고 있으며 고장 시 대체 가동을 시키는 방식으로 이를 대비하고 있다. 하지만 이는 비용적인 측면에서 비효율적이다. 따라서 가동 중단 상황이 발생하기 전 의심 증상을 발견하면 그 원인을 신속하게 해결하는 것이 중요하다. 이러한 이유로 최근 저비용으로 보조 기기의 상태를 실시간으로 사전 진단 및 분석을 하는 연구에 대한 필요성이 대두되고 있다. 이 논문에서는 이를 진단하기 위한 규칙 기반 알고리듬과 딥러닝 알고리듬을 동시에 사용하는 방법을 소개한다. 규칙 기반 알고리듬을 이용하여 현재 기기에 나타나는 증상들을 측정 후 전문가의 경험에 의존한 규칙 표를 기반으로 그 원인을 추정한다. 또한 진단을 수행하고자 하는 발전소 보조 기기의 주요 파트인 회전체에 대하여 진단 방법으로 궤도 진단을 수행하였다. 진단 방식으로는 합성곱 신경망을 이용하였으며 회전 축에 수직한 두 축의 위치로 생성한 궤도 이미지를 이용하여 합성곱 신경망을 학습시켰다. 합성곱 신경망은 스스로 normal, rubbing, unbalance 세 종류의 원인을 분류하기 위한 필터를 학습하여 이미지를 입력 받을 시 그 이미지에 해당하는 원인을 진단한다. 이 논문에서는 딥러닝의 블랙박스 문제를 보완하면서 스스로 특성 인자를 찾아내는 딥러닝의 장점을 얻기 위하여 이 두 알고리듬의 결과를 동시에 사용하였다. 이처럼 분류기 집합을 구성하여 예측에 가중치를 부여한 뒤 새 데이터 요소를 분류하는 학습 알고리듬은 단일 분류기보다 성능이 우수하며 쉽게 과적합 되지 않는 장점이 있다⁽¹⁾.

2. 보조기기 이상 진단 알고리듬

2.1 알고리듬 소개

(1) 규칙 기반 알고리듬

발전소 보조 기기의 특정 증상이 관측되었을 때 원인을 추정하여 이를 수정하기 위한 알고리듬으로 설비의 육안 점검 결과만을 가지고 설비의 이상 원인을 추정하는 것을 목표로 한다. 하지만 어떤 원인이 존재할 때에 증상이 발생할 확률을 구하는 것은 원인을 설정한 뒤 관측하면 되는 것으로 비교적 쉽게 값을 얻을 수 있는 반면, 특정 증상이 관측되었을 때 그 원인을 역 추적하는 것은 다양한 변수를 함께 고려하여야 하기 때문에 어려운 경우가 많다. 그럼에도 불구하고 실제 현장에서 관측할 수 있는 것은 증상이므로 증상을 관측하여 그 원인을 추적하는 방법을 연구하는 것이 필요하다. 즉, 얻을 수 있는 데이터는 원인 존재 시 증상 발생 확률이며 이를 통해 구해야 할 내용은 증상 발생시 특정 원인의 존재 확률이다. 이를 통하여 설비의 이상 증상의 원인을 확인 및 제거하고 증상을 개선할 수 있다.

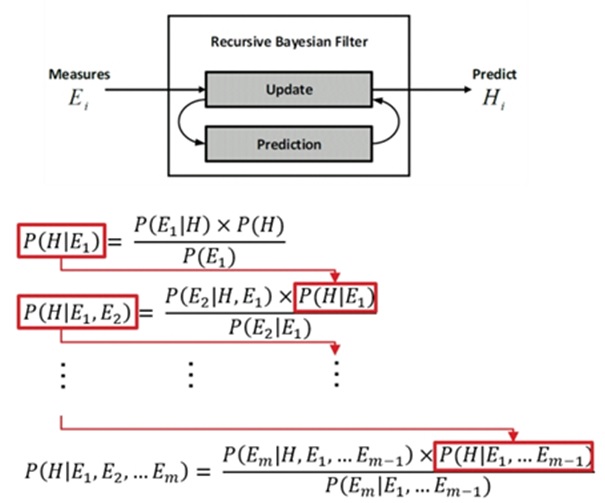
규칙 기반 알고리듬은 베이즈 정리(Bayes’ rule) 에 기반을 두고 있다. 베이즈 정리는 두 확률 변수의 사전 확률과 사후 확률 간의 관계를 나타내는 정리로 아래의 식으로 표현할 수 있다.

$\[ P\left(H|E\right)=\frac{P\left(E|H\right)P\left(H\right)}{P\left(E\right)} \]$

(1)

여기서 P(H)는 H의 사전확률로 E에 대한 어떠한 정보도 없을 때의 H의 확률이다. 또한 P(E|H)는 H를 알고 있을 때의 E의 조건부 확률이며 P(E)는 정규화 파라미터로 정의할 수 있다. 따라서 베이즈 정리를 통하여 원인에 따른 증상의 확률을 이용하여 증상 관측 시 원인의 확률을 계산할 수 있다.

규칙 기반 알고리듬의 기반이 되는 데이터, 즉 사전 확률은 현장에서 기기의 상태를 점검하고 진단하는 전문가의 의견이다. 규칙 표는 현장 전문가가 각각의 원인에 의해 발생할 수 있는 증상들을 체크한 리스트를 기반으로 이의 신뢰도를 0.9로 설정하여 만든 표이다. 아래 Table 1은 이 규칙 기반 알고리듬에 사용한 규칙 표의 일부이다. 행과 열은 각각 설비에서 관측된 증상과 그 원인이다. 표의 내용은 진단 대상 설비에서 특정 원인이 존재 시 증상 발생 확률을 나타낸다.

Table 1

Rule table

즉 이 표에 따르면 ‘과도한 입구 온도’ 원인이 존재할 때 ‘과도한 진동’이 관측될 확률은 10 %, ‘토출압 감소’가 관측될 확률은 90 %이다. 이 표의 표기 값을 P(E|H)로 설정한 후 베이즈 정리의 식을 이용하여 P(H|E)를 계산할 수 있다.

이와 같이 베이즈 정리를 이용하면 단일 증상에서의 사전 확률을 이용하여 사후 확률을 계산할 수 있다. 뿐만 아니라 여러 증상이 복합적으로 발생하는 경우까지 확장가능하다. 한 가지 증상만을 확인하여 어떤 원인의 존재 여부를 따지는 것보다 여러 가지 복합적인 증상의 발생 여부, 관측여부에 따라서 원인의 존재 여부 및 확률을 판단 시 더 높은 신뢰도를 얻을 수 있기 때문이다. 따라서 이처럼 여러 가지 증상의 발생, 미발생, 미측정 등을 한꺼번에 고려하는 방법 또한 필요하다. 이는 단일 증상에서의 원인의 확률을 구할 때 사용한 사전 확률을 똑같이 사용하며 확률변수간의 독립 및 종속 관계를 이용하여 관계식을 정의하여 이를 계산한다. 여러 개의 증상이 관측 되었을 때의 각 원인의 존재 확률은 식 (2)와 같이 정리할 수 있다.

$\[ P\left(H|E_1, E_2,\dots , E_m\right)=\frac{P\left(E_1, E_2,\dots , E_m|H\right)P\left(H\right)}{P\left(E_1, E_2,\dots , E_m\right)} \]$

(2)

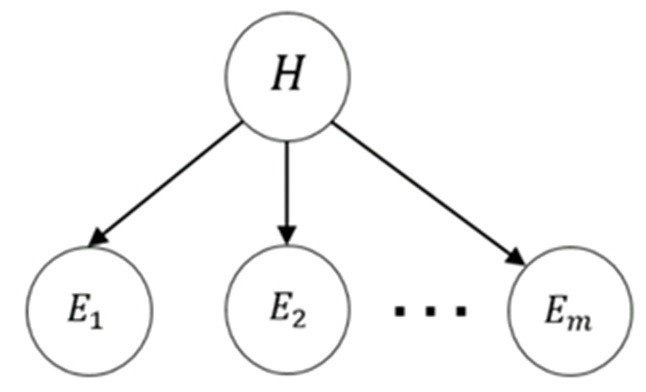
현재 원인과 증상이라는 두 확률 변수 간의 관계는 Fig. 1과 같다. 또한 Fig. 1과 같은 관계를 가질 때 H를 알고 있다면 각 E들은 서로 독립으로 취급할 수 있다.

Fig. 1

Relationship between variables

Fig. 2

Recursive bayesian estimation

따라서 H의 정보가 주어졌을 때의 여러 개의 증상 E가 발생할 확률은 H의 정보가 주어졌을 때 각 E가 발생할 확률의 곱으로 나타낼 수 있다. 따라서 위의 식 (2)를 식 (3)과 같이 정리할 수 있다⁽²⁾.

$\[ P\left(H_1|E_1, E_2,\dots , E_m\right)=\frac{{\prod }_{i=1}^{m}P\left(E_i|H\right)P\left(H\right)}{P\left(E_1, E_2,\dots , E_m\right)} \]$

(3)

이러한 방법으로 확률 변수 간의 관계와 베이즈 정리를 활용하여 여러 증상을 복합적으로 고려한 원인의 확률을 식 (3)을 통해 계산할 수 있다. 또한 현장에서 매번 모든 증상을 측정하는 것이 아니기 때문에 미측정, 측정하였지만 미발생한 것, 그리고 측정을 해서 증상 발생을 확인한 것 3가지로 체크리스트를 만들어서 편의성을 높였다.

앞서 설명한 규칙기반 알고리듬을 이용하여 다양한 증상의 발생, 미발생, 미측정에 따른 원인의 확률을 각각 계산할 수 있다. Fig. 3은 규칙 기반 알고리듬을 통해 가상의 증상을 가정하여 계산한 원인의 확률을 나타내며, 과도한 진동을 측정하고 이의 발생을 확인하였을 때 원인의 확률을 나타낸 것이다. Fig. 3에서 보면 네 가지 원인 모두 과도한 진동을 유발할 수 있는 원인임을 알 수 있다.

Fig. 3

E1 measure & occur

Fig. 4는 이후 토출압 감소를 측정 후 이의 미발생을 확인하였을 때의 원인 확률이다. H2, H3의 확률이 0에 가깝게 줄어들었다.

Fig. 4

E1·E2 measure, E1 occur

Fig. 5는 마지막 증상인 축 정렬 상태의 변화를 측정한 후 발생을 확인하였을 때의 결과이다. 여러 증상을 확인하자 가능한 원인이 배관 변형 한가지로 줄어들었다.

Fig. 5

E1·E2·E3 measure, E1·E3 occur

이와 같이 규칙 기반 알고리듬과 육안 점검 결과를 활용하여 설비의 이상 원인을 알 수 있으며 여러 증상을 확인할수록 그 정확도를 높일 수 있다.

(2) 합성곱 신경망⁽³⁾

현재 진단하고자 하는 설비는 회전기기로서 이를 진단하는 다양한 방법 중 가장 일반적인 방법은 진동 분석 방법이다. 회전체의 이상 발생시 그 결함 유형에 따라 진동 신호의 패턴이 다르기 때문에 이를 이용한 분석과 모드 분석법⁽⁴⁾ 또는 주파수 성분 분석법⁽⁵⁾ 등의 다양한 진동 연구가 선행되어왔다. 이 논문에서는 합성곱 신경망을 이용하여 자동화하는 방법을 사용하였다.

1989년 얀 르쿤 교수에 의해 처음 소개된 합성곱 신경망은 이미지 분석 및 패턴 분석에 특화된 알고리듬으로 성능이 좋을 뿐만 아니라 현재 관련된 선행연구가 많이 진행되어 있어 시기 적절한 활용에 용이하다. 따라서 합성곱 신경망을 진단에 활용하기 위하여 시계열 신호인 진동 신호의 이미지화 하는 전처리 작업이 필요하다. 진동 신호를 이미지화 하는 방법은 대표적으로 단시간 푸리에 변환(STFT, short time Furrier transform), 웨이블렛 변환(wavelet transform)⁽⁶⁾, 그리고 궤도 이미지를 활용한 방법⁽⁷⁾이 있다. 통신상의 문제로 원본 데이터를 전송하지 못하기 때문에 단시간 푸리에 변환 및 웨이블렛 변환은 적용이 어려웠고 따라서 궤도 이미지를 이용한 패턴 분석 및 분류를 진행하였다.

회전체의 회전 축에 수직한 두 축의 변위의 궤도 이미지를 활용한 궤도 분석도 대표적인 진동 분석의 일종이다. 하지만 궤도 형상과 크기의 다양성, 복잡성으로 인해 궤도 분석을 통한 이상 진단은 주로 전문가의 경험에 의지하는 경우가 많다⁽⁸⁾. 따라서 궤도 패턴을 머신러닝 또는 딥러닝으로 분석하여 이를 자동화하는 것은 비용 절감 및 시간 절약의 효과가 있다.

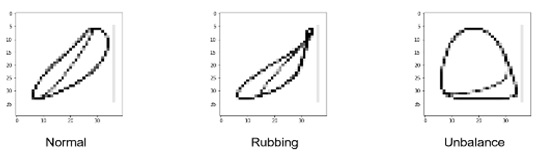
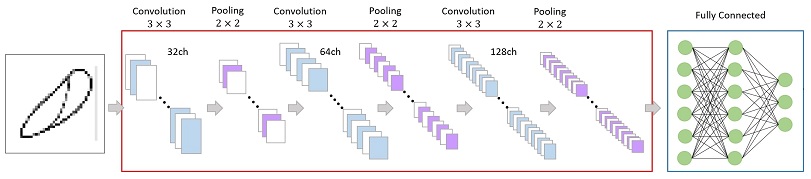
이 논문에서 합성곱 신경망을 적용하여 분류를 진행한 패턴은 정상(normal), 마찰(rubbing), 불균형(unbalance)의 3가지이다. Fig. 6에서 각 양상 별 궤도 이미지의 패턴을 확인할 수 있다. 이 논문에서 사용한 합성곱 신경망 모델은 Fig. 7과 같다.

Fig. 6

Orbit pattern

Fig. 7

CNN model structure

합성곱 신경망의 학습 및 검증을 진행한 데이터는 RK4 데이터를 활용하였으며, 이를 7:3의 비율로 학습 전에 나누어 70 %를 학습에 사용하고 학습에 사용하지 않은 30 %의 데이터를 검증에 사용하였다. 또한, RK4로 측정되지 않은 추가적 검증으로 외부의 마찰 데이터(KEPRI 제공)를 사용하였고 이를 마찰로 진단하였다.

2.2 장단점 및 융합 가능성

규칙 기반 알고리듬은 전문가의 경험을 기반으로 규칙 표를 작성하여 이 규칙 표에 따라 설비의 상태를 진단한다. 따라서 규칙 기반 알고리듬은 결과의 근거가 규칙 표에 있으며 이는 전문가의 진단 및 의견과 비슷한 결과를 낼 수 있다. 이는 자동화 알고리듬을 실제의 시스템에 적용할 때 매우 중요한 부분이다.

또한 규칙 기반 알고리듬은 매우 직관적인 결과를 보여줄 뿐만 아니라 간단한 체크리스트만 확인하면 해당 증상에 따른 원인을 찾을 수 있기 때문에 비전문가도 쉽게 사용할 수 있다는 장점이 있다. 이는 전문 인력 고용에 따른 인건비를 절감할 수 있는 효과가 있다.

하지만 규칙 표를 사람이 직접 작성하여야 하며 미처 고려하지 못한 원인 또는 증상이 존재할 시에는 이에 대한 대처가 불가능하다.

딥러닝 알고리듬은 모든 특성 벡터 추출을 모델 스스로 진행하며 이 연구에서 사용한 합성곱 신경망 알고리듬은 이미지를 분류하기 위한 필터를 스스로 학습하는 모델이다⁽⁹⁾. 딥러닝 알고리듬에서 필터를 학습하는 과정은 규칙 기반 알고리듬에서 규칙 표를 작성하는 부분과 비슷하지만 사람이 직접 이를 작성할 필요가 없어 편리하다. 또한 사람이 미처 고려하지 못한 부분까지 합성곱 신경망의 비선형성을 통해 고려할 수 있다. 이는 결과의 정확도를 향상 시킬 수 있으며 실제로 합성곱 신경망을 통해 궤도 이미지 분류를 수행 시 검증 데이터 분류 정확도 99 % 이상으로 좋은 결과를 얻을 수 있었다.

하지만 딥러닝 알고리듬은 특성 벡터 추출, 즉 필터를 학습하는 과정이 모델에 포함되어 있으며 이 과정에서 수많은 비선형성을 포함하기 때문에 딥러닝 모델의 학습과정에서의 판단 근거를 알기는 쉽지 않다. 즉, 딥러닝 모델을 이용하여 결론을 얻을 수는 있지만 그 근거는 얻기 어렵다. 이러한 블랙박스문제는 딥러닝의 높은 정확도와 낮은 비용, 그리고 높은 효율성에도 산업에서 딥러닝만을 이용하여 설비 진단을 하는 것을 지양하게 하는 원인으로 딥러닝의 블랙박스 문제를 해결하기 위한 시도가 다양한 분야에서 시도되어 왔다⁽¹⁰⁾.

이 논문에서는 블랙박스 문제를 해결하기 위하여 앞서 소개한 규칙 기반 알고리듬과 합성곱 신경망을 동시에 사용하여 두 알고리듬의 단점을 서로 보완하며 정확도와 신뢰도를 모두 높일 수 있는 모델을 제시한다.

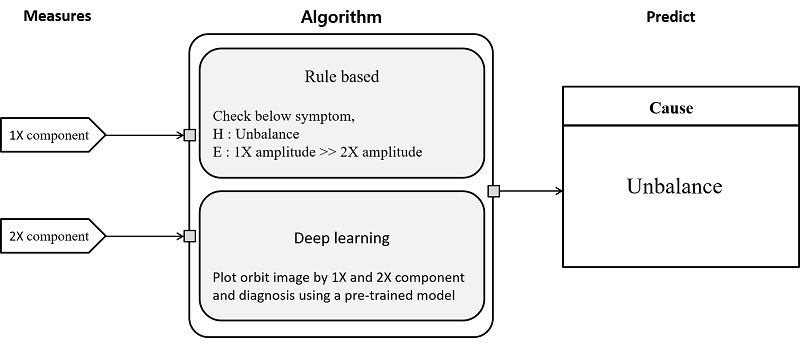
Fig. 8과 같이 앙상블 모델을 활용할 수 있다. 불균형 문제가 발생시 주파수 1X 성분이 2X성분에 비해 매우 크게 측정되는 특성이 있다. 이 경우 규칙 기반 알고리듬에서 1X와 2X 성분에 대한 내용을 입력하여 불균형이라는 결론을 얻고 합성곱 신경망의 진단 결과로 불균형이라는 결론을 얻어 이를 불균형의 문제라고 최종 진단할 수 있다.

Fig. 8

Ensemble example

3. 결 론

규칙기반 알고리듬은 전문가의 의견을 기반으로 하여 신뢰도는 높다는 장점이 있지만 전문가가 직접 규칙 표를 작성하여야 하며 규칙 표에 표기되지 않은 내용에 대해서는 고려할 수 없는 단점이 있다. 그리고 딥러닝 알고리듬은 전문가가 직접 패턴 특성 분석 등의 작업을 하지 않아도 되며 선행 연구에 없는 특성도 모델이 직접 찾아내어 이를 반영하기 때문에 정확도가 높다. 하지만 블랙박스 모델이라는 단점도 존재한다. 따라서 이를 동시에 활용하면 상호보완의 효과가 있어 신뢰도 및 정확도, 편의성을 모두 얻을 수 있다. 이 연구를 통하여 저비용의 딥러닝 기반 강건한 보조기기 진단을 할 수 있다. 다만 두 알고리듬이 추정하는 원인의 종류가 다르기 때문에 이들 알고리듬을 함께 사용하기 위해서 이를 보정하기 위한 연구가 필요하다. 따라서 추후 연구할 내용은 비슷한 증상에서 야기되는 원인들을 범주화하고 물리적 관계 및 데이터간의 상관관계를 분석하여 표현을 통일하는 작업이 필요하다. 또한 원인들 간의 상관관계를 파악하여 표현을 수정하는 연구가 추가적으로 필요하다.

Acknowledgments

이 연구는 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(No. 2020R1A2C1009744), 2019년도 정부(산업통상자원부)의 재원으로 한국산업기술진흥원의 지원을 받아 수행된 연구임(N0008691, 2019년 산업전문인력역량강화사업), 2019년도 정보통신기획평가원의 지원을 받아 수행된 연구임(2019-0-01589, 글로벌 핵심인재 양성 지원 사업), 2019년도 한국전력연구원의 지원을 받아 수행된 연구임(Intelligent Digital Power Plant 구축).

References

• Dietterich, T. G., 2000, Ensemble Methods in Machine Learning, Proceedings of the MCS 2000: International Workshop on Multiple Classifier Systems, Cagliari, Italy, pp. 1~15. [https://doi.org/10.1007/3-540-45014-9_1]
• Jaffer, A. and Gupta, S., 1971, Recursive Bayesian Estimation with Uncertain Observation, IEEE Transactions on Information Theory, Vol. 17, No. 5, pp. 614~616. [https://doi.org/10.1109/TIT.1971.1054684]
• LeCun, Y., Boser, B., Denker, J. S., Henderson, D., Howard, R. E., Hubbard, W. and Jackel, L. D., 1989, Backpropagation Applied to Handwritten Zip Code Recognition. Neural Computation, Vol. 1, No. 4, pp. 541~551. [https://doi.org/10.1162/neco.1989.1.4.541]
• Gao, Q., Duan, C., Fan, H. and Meng, Q., 2008, Rotating Machine Fault Diagnosis Using Empirical Mode Decomposition. Mechanical Systems and Signal Processing, Vol. 22, No. 5, pp. 1072~1081. [https://doi.org/10.1016/j.ymssp.2007.10.003]
• Peng, Z., Chu, F. and He, Y., 2002, Vibration Signal Analysis and Feature Extraction Based on Reassigned Wavelet Scalogram. Journal of Sound and Vibration, Vol. 253, No. 5, pp. 1087~1100. [https://doi.org/10.1006/jsvi.2001.4085]
• Liao, Y., Zeng, X. and Li, W., 2017, Wavelet Transform Based Convolutional Neural Network for Gearbox Fault Classification, Proceedings of the 2017 Prognostics and System Health Management Conference (PHM-Harbin), pp. 1~6. [https://doi.org/10.1109/PHM.2017.8079274]
• Bachschmid, N., Pennacchi, P. and Vania, A., Diagnostic Significance of Orbit Shape Analysis and Its Application to Improve Machine Fault Detection, Journal of the Brazilian Society of Mechanical Sciences and Engineering. Vol. 26, No. 2, pp. 200~208. [https://doi.org/10.1590/S1678-58782004000200012]
• Lee, S. C., Jeong, H. D., Min, H. C., Koo, J. R. and Bae, Y. C., 2015, Rotating Machinery Diagnosis based on Machine Learning of Orbit Image Pattern, Proceedings of the KSNVE Annual Spring Conference, pp. 370~371.
• Lauer, F., Suen, C. Y. and Bloch, G., 2007, Rejection Measurement Based on Linear Discriminant Analysis for Document Recognition, Pattern Recognition, Volume 40, Issue 6, pp. 1816~1824. [https://doi.org/10.1016/j.patcog.2006.10.011]
• Guidotti, R., Monreale, A., Ruggieri, S., Turini, F., Giannotti, F. and Pedreschi, D., 2018, A Survey of Methods for Explaining Black Box Models, ACM Computing Survey, Vol. 51, No. 5, pp. 93:1~93:42. [https://doi.org/10.1145/3236009]